专题(三) 锐角三角函数 (含答案) 2024-2025学年数学苏科版九年级下册
文档属性
| 名称 | 专题(三) 锐角三角函数 (含答案) 2024-2025学年数学苏科版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 293.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 16:24:07 | ||
图片预览


文档简介
专题(三) 锐角三角函数
1.
在△ABC中,∠C=90°,设∠A、∠B、∠C所对的边分别为a、b、c,则下列结论正确的是 ( )
A. c=bsinB B. b=csinB C. a=btanB D. b=ctanB
2. 如图所示为以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过点C作CD⊥AB于点D,且sin∠ACD=,BC=4,则AC的长为 ( )
A. 1 B. 3 C. D.
3. 如图,将宽为1cm的矩形纸条沿BC折叠,使∠CAB=45°,则折叠后重叠部分的面积为 ( )
A. cm2 B. cm2 C. cm2 D. cm2
4. 如图,☉O的直径AB经过弦CD的中点H.若cos∠CDB=,BD=5,则☉O的半径为 ( )
A. B. C. D.
5. 如图,在△ABC中,AB=AC=4,∠C=72°,D是AB的中点,点E在AC上,DE⊥AB,连接BE,则cosA的值为 ( )
A. B. C. D.
6. (2024·武汉)如图,四边形ABCD内接于☉O,∠ABC=60°,∠BAC=∠CAD=45°,AB+AD=2,则☉O的半径是 ( )
A. B. C. D.
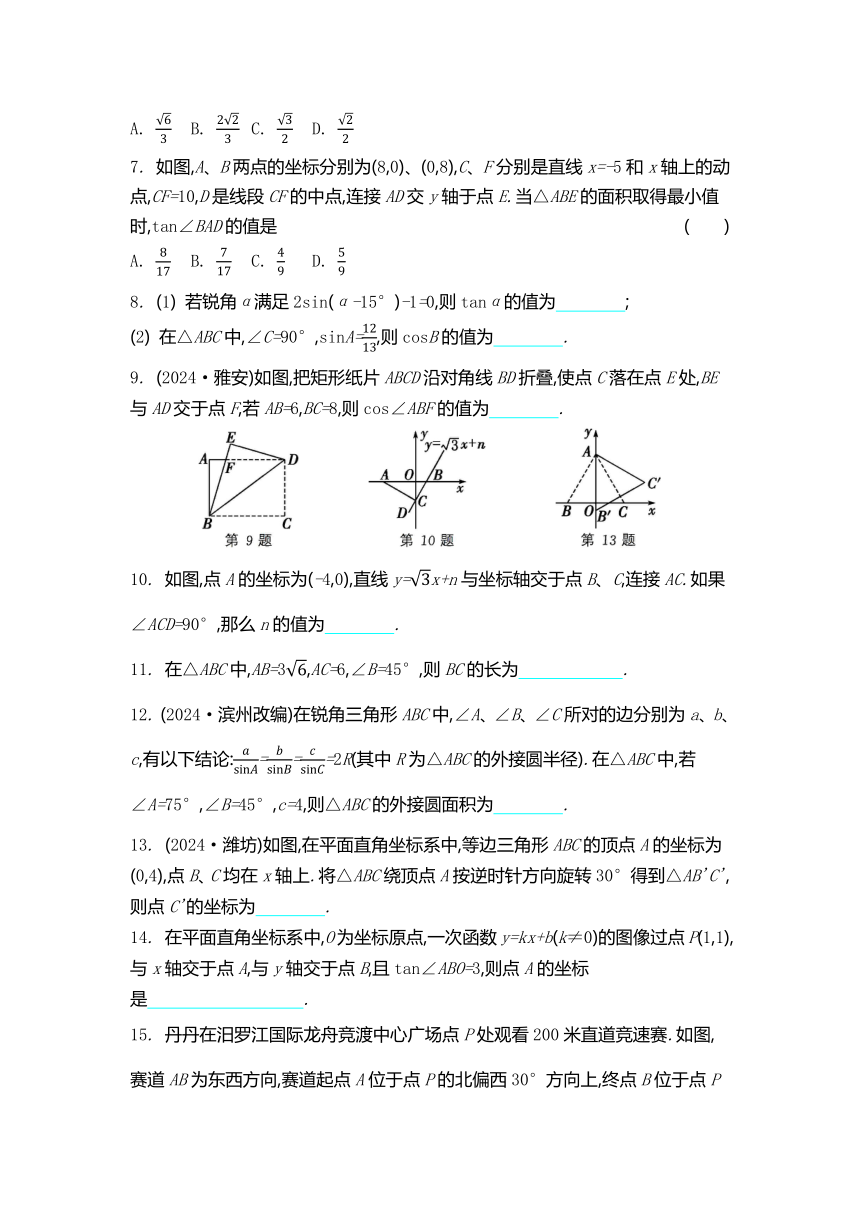
7. 如图,A、B两点的坐标分别为(8,0)、(0,8),C、F分别是直线x=-5和x轴上的动点,CF=10,D是线段CF的中点,连接AD交y轴于点E.当△ABE的面积取得最小值时,tan∠BAD的值是 ( )
A. B. C. D.
8. (1) 若锐角α满足2sin(α-15°)-1=0,则tanα的值为 ;
(2) 在△ABC中,∠C=90°,sinA=,则cosB的值为 .
9. (2024·雅安)如图,把矩形纸片ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F,若AB=6,BC=8,则cos∠ABF的值为 .
10. 如图,点A的坐标为(-4,0),直线y=x+n与坐标轴交于点B、C,连接AC.如果∠ACD=90°,那么n的值为 .
11. 在△ABC中,AB=3,AC=6,∠B=45°,则BC的长为 .
12. (2024·滨州改编)在锐角三角形ABC中,∠A、∠B、∠C所对的边分别为a、b、c,有以下结论:===2R(其中R为△ABC的外接圆半径).在△ABC中,若∠A=75°,∠B=45°,c=4,则△ABC的外接圆面积为 .
13. (2024·潍坊)如图,在平面直角坐标系中,等边三角形ABC的顶点A的坐标为(0,4),点B、C均在x轴上.将△ABC绕顶点A按逆时针方向旋转30°得到△AB'C',则点C'的坐标为 .
14. 在平面直角坐标系中,O为坐标原点,一次函数y=kx+b(k≠0)的图像过点P(1,1),与x轴交于点A,与y轴交于点B,且tan∠ABO=3,则点A的坐标是 .
15. 丹丹在汨罗江国际龙舟竞渡中心广场点P处观看200米直道竞速赛.如图,赛道AB为东西方向,赛道起点A位于点P的北偏西30°方向上,终点B位于点P的北偏东60°方向上,AB=200米,则点P到赛道AB的距离约为 米(结果保留整数,参考数据:≈1.732).
16. 如图,在Rt△ABC中,∠BAC=90°,cosB=,D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使∠ADE=∠B,AE=DE,连接CE,则的值为 .
17. (2024·龙东地区)如图,在Rt△ABC中,∠ACB=90°,tan∠BAC=,BC=2,AD=1,线段AD绕点A旋转,P为CD的中点,则BP长的最大值为 .
18. 计算:
(1) sin 45°+cos 30°·tan 60°-;
(2) 2sin260°+3cos 60°-4tan 45°+tan 30°·cos 45°.
19. 在Rt△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,根据下面的条件解直角三角形.
(1) b=10,∠B=60°; (2) a+b=3+,∠A=30°.
20. 如图,在Rt△ABC中,∠C=90°,D是边BC上的一点,CD=6,cos∠ADC=,tanB=.求:
(1) AC和AB的长;
(2) sin ∠BAD的值.
第20题
21. (2023·泰州)如图,堤坝AB的长为10m,坡度i为1∶0.75,底端A在地面上,堤坝与对面的山之间有一深沟,山顶D处立有高20m的铁塔CD.小明欲测量山高DE,他在A处看到铁塔顶端C刚好在视线AB上,又在坝顶B处测得塔底D的仰角α为26°35'.求堤坝高及山高DE(小明身高忽略不计,精确到1m,参考数据:sin26°35'≈0.45,cos26°35'≈0.89,tan26°35'≈0.50).
第21题
22. (2024·大庆)如图,△ABC为☉O的内接三角形,AB为☉O的直径,将△ABC沿直线AB翻折到△ABD,点D在☉O上.连接CD交AB于点E,延长BD、CA交于点P,过点A作☉O的切线,交BP于点G.
(1) 求证:AG∥CD;
(2) 求证:PA2=PG·PB;
(3) 若sin∠APD=,求tan∠AGB的值.
第22题
专题(三) 锐角三角函数
1. B 2. C 3. D 4. A 5. C
6. A 解析:如图,延长AB到点E,使得BE=AD,连接BD、CE.∵ AB+AD=2,∴ AB+BE=AE=2.∵ 四边形ABCD内接于☉O,∴ ∠ADC+∠ABC=180°.∵ ∠CBE+∠ABC=180°,∴ ∠ADC=∠CBE.∵ ∠BAC=∠CAD,∴ =.∴ ∠DBC=∠CDB.∴ BC=CD.∴ △ADC≌△EBC.∴ ∠ACD=∠ECB,CA=CE.∴ ∠DCB=∠ACE.∵ ∠DAB=∠BAC+∠CAD=45°+45°=90°,∴ BD是☉O的直径.∴ ∠DCB=90°.∴ ∠ACE=90°.∴ 在Rt△ACE中,AC=AE·cos45°=.连接CO并延长,交☉O于点F,连接AF,则∠FAC=90°,∠F=∠ABC=60°.∴ CF==.∴ ☉O的半径为.
7. B 8. (1) 1 (2) 9. 10. - 11. 3+3或3-3 12. 13. 14. (-2,0)或(4,0) 15. 87
16. 2 解析:过点E作EF⊥AD,垂足为F.∵ AE=DE,EF⊥AD,∴ ∠EAD=∠ADE,AF=AD.∵ ∠BAC=90°,D是边BC的中点,∴ AD=BD=CD.∴ ∠B=∠DAB.∵ ∠ADE=∠B,∴ ∠EAD=∠B,∠ADE=∠DAB.∴ AB∥DE.∴ AC⊥DE.∴ 易得ED垂直平分AC.∴ CE=AE.∵ cosB=,∴ cos∠EAD==.∴ =4,即=4.∴ =2.
17. 2+ 解析:如图,取AC的中点Q,连接PQ、BQ.∵ P是CD的中点,Q是AC的中点,∴ PQ是△ACD的中位线.∴ PQ=AD=.∴ 当线段AD绕点A旋转时,点P在以点Q为圆心,PQ长为半径的圆上.延长BQ交☉Q于点P',当点P旋转到点P'的位置时,BP长的值最大.∵ BC=2,tan∠BAC=,∴ AC=4.∴ AQ=CQ=2.∵ ∠ACB=90°,∴ 由勾股定理,得BQ==2.∴ BP长的最大值为2+.
18. (1) (2)
19. (1) ∠A=30°,a=,c= (2) ∠B=60°,a=,b=3,c=2
20. (1) ∵ 在Rt△ACD中,cos ∠ADC==,CD=6,∴ AD=10.∴ 由勾股定理,得AC==8.∵ 在Rt△ABC中,tan B==,∴ BC=12.∴ 由勾股定理,得AB==4 (2) 过点D作DE⊥AB于点E.由(1),得BD=BC-CD=6.∵ 在Rt△BDE中,tan B==,DE2+BE2=BD2,∴ DE2+=36.∴ DE=(负值舍去).∴ 在Rt△ADE中,sin ∠BAD==
21. 如图,过点B作BH⊥AE于点H.∵ 坡度i为1∶0.75,∴ 设BH=4x(x>0)m,则AH=3xm.∴ 在Rt△AHB中,AB==5xm.∴ 5x=10,解得x=2.∴ AH=6m,BH=8m.过点B作BF⊥CE于点F,则四边形BHEF为矩形.∴ EF=BH=8m,BF=EH.设DF=ym.∵ 在Rt△BFD中,tanα=,∴ BF=≈=2y(m).∴ AE=(6+2y)m.∵ 坡度i为1∶0.75,∴ CE∶AE=(20+y+8)∶(6+2y)=1∶0.75,解得y=12.∴ DF=12m.∴ DE=DF+EF=12+8=20(m).∴ 堤坝高为8m,山高DE约为20m
22. (1) ∵ 将△ABC沿直线AB翻折到△ABD,∴ AB⊥CD.∴ ∠DEB=90°.∵ AB为☉O的直径,AG是☉O的切线,∴ AG⊥AB.∴ ∠GAB=90°.∴ ∠DEB=∠GAB.∴ AG∥CD (2) 由(1),得AG⊥AB,∴ ∠GAD+∠BAD=90°.∵ AB为☉O的直径,∴ ∠ADB=90°.∴ ∠BAD+∠ABD=90°.∴ ∠ABD=∠GAD.由翻折,可得∠ABD=∠ABC,∴ ∠DBC=2∠ABD.∵ 四边形ADBC是☉O的内接四边形,∴ ∠DAC+∠DBC=180°.∵ ∠DAC+∠PAD=180°,∴ ∠PAD=∠DBC=2∠ABD.∴ ∠PAG=∠PAD-∠GAD=2∠ABD-∠ABD=∠ABD.又∵ ∠APG=∠BPA,∴ △APG∽△BPA.∴ =,即PA2=PG·PB (3) ∵ AB为☉O的直径,∴ ∠ACB=∠ADB=∠ADP=90°.∴ 在△ADG中,∠AGB+∠GAD=90°.由(2),得∠GAD+∠BAD=90°,∴ ∠AGB=∠BAD.由sin∠APD==,设AD=a,则AP=3a.∴ 由勾股定理,得PD==2a.∴ tan∠APD===.由翻折,可得AC=AD=a,BD=BC,∴ PC=PA+AC=3a+a=4a.∵ 在Rt△PCB中,tan∠CPB==,∴ BD=BC=PC=a.∴ tan∠AGB=tan∠DAB===
1.
在△ABC中,∠C=90°,设∠A、∠B、∠C所对的边分别为a、b、c,则下列结论正确的是 ( )
A. c=bsinB B. b=csinB C. a=btanB D. b=ctanB
2. 如图所示为以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过点C作CD⊥AB于点D,且sin∠ACD=,BC=4,则AC的长为 ( )
A. 1 B. 3 C. D.
3. 如图,将宽为1cm的矩形纸条沿BC折叠,使∠CAB=45°,则折叠后重叠部分的面积为 ( )
A. cm2 B. cm2 C. cm2 D. cm2
4. 如图,☉O的直径AB经过弦CD的中点H.若cos∠CDB=,BD=5,则☉O的半径为 ( )
A. B. C. D.
5. 如图,在△ABC中,AB=AC=4,∠C=72°,D是AB的中点,点E在AC上,DE⊥AB,连接BE,则cosA的值为 ( )
A. B. C. D.
6. (2024·武汉)如图,四边形ABCD内接于☉O,∠ABC=60°,∠BAC=∠CAD=45°,AB+AD=2,则☉O的半径是 ( )
A. B. C. D.
7. 如图,A、B两点的坐标分别为(8,0)、(0,8),C、F分别是直线x=-5和x轴上的动点,CF=10,D是线段CF的中点,连接AD交y轴于点E.当△ABE的面积取得最小值时,tan∠BAD的值是 ( )
A. B. C. D.
8. (1) 若锐角α满足2sin(α-15°)-1=0,则tanα的值为 ;
(2) 在△ABC中,∠C=90°,sinA=,则cosB的值为 .
9. (2024·雅安)如图,把矩形纸片ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F,若AB=6,BC=8,则cos∠ABF的值为 .
10. 如图,点A的坐标为(-4,0),直线y=x+n与坐标轴交于点B、C,连接AC.如果∠ACD=90°,那么n的值为 .
11. 在△ABC中,AB=3,AC=6,∠B=45°,则BC的长为 .
12. (2024·滨州改编)在锐角三角形ABC中,∠A、∠B、∠C所对的边分别为a、b、c,有以下结论:===2R(其中R为△ABC的外接圆半径).在△ABC中,若∠A=75°,∠B=45°,c=4,则△ABC的外接圆面积为 .
13. (2024·潍坊)如图,在平面直角坐标系中,等边三角形ABC的顶点A的坐标为(0,4),点B、C均在x轴上.将△ABC绕顶点A按逆时针方向旋转30°得到△AB'C',则点C'的坐标为 .
14. 在平面直角坐标系中,O为坐标原点,一次函数y=kx+b(k≠0)的图像过点P(1,1),与x轴交于点A,与y轴交于点B,且tan∠ABO=3,则点A的坐标是 .
15. 丹丹在汨罗江国际龙舟竞渡中心广场点P处观看200米直道竞速赛.如图,赛道AB为东西方向,赛道起点A位于点P的北偏西30°方向上,终点B位于点P的北偏东60°方向上,AB=200米,则点P到赛道AB的距离约为 米(结果保留整数,参考数据:≈1.732).
16. 如图,在Rt△ABC中,∠BAC=90°,cosB=,D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使∠ADE=∠B,AE=DE,连接CE,则的值为 .
17. (2024·龙东地区)如图,在Rt△ABC中,∠ACB=90°,tan∠BAC=,BC=2,AD=1,线段AD绕点A旋转,P为CD的中点,则BP长的最大值为 .
18. 计算:
(1) sin 45°+cos 30°·tan 60°-;
(2) 2sin260°+3cos 60°-4tan 45°+tan 30°·cos 45°.
19. 在Rt△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,根据下面的条件解直角三角形.
(1) b=10,∠B=60°; (2) a+b=3+,∠A=30°.
20. 如图,在Rt△ABC中,∠C=90°,D是边BC上的一点,CD=6,cos∠ADC=,tanB=.求:
(1) AC和AB的长;
(2) sin ∠BAD的值.
第20题
21. (2023·泰州)如图,堤坝AB的长为10m,坡度i为1∶0.75,底端A在地面上,堤坝与对面的山之间有一深沟,山顶D处立有高20m的铁塔CD.小明欲测量山高DE,他在A处看到铁塔顶端C刚好在视线AB上,又在坝顶B处测得塔底D的仰角α为26°35'.求堤坝高及山高DE(小明身高忽略不计,精确到1m,参考数据:sin26°35'≈0.45,cos26°35'≈0.89,tan26°35'≈0.50).
第21题
22. (2024·大庆)如图,△ABC为☉O的内接三角形,AB为☉O的直径,将△ABC沿直线AB翻折到△ABD,点D在☉O上.连接CD交AB于点E,延长BD、CA交于点P,过点A作☉O的切线,交BP于点G.
(1) 求证:AG∥CD;
(2) 求证:PA2=PG·PB;
(3) 若sin∠APD=,求tan∠AGB的值.
第22题
专题(三) 锐角三角函数
1. B 2. C 3. D 4. A 5. C
6. A 解析:如图,延长AB到点E,使得BE=AD,连接BD、CE.∵ AB+AD=2,∴ AB+BE=AE=2.∵ 四边形ABCD内接于☉O,∴ ∠ADC+∠ABC=180°.∵ ∠CBE+∠ABC=180°,∴ ∠ADC=∠CBE.∵ ∠BAC=∠CAD,∴ =.∴ ∠DBC=∠CDB.∴ BC=CD.∴ △ADC≌△EBC.∴ ∠ACD=∠ECB,CA=CE.∴ ∠DCB=∠ACE.∵ ∠DAB=∠BAC+∠CAD=45°+45°=90°,∴ BD是☉O的直径.∴ ∠DCB=90°.∴ ∠ACE=90°.∴ 在Rt△ACE中,AC=AE·cos45°=.连接CO并延长,交☉O于点F,连接AF,则∠FAC=90°,∠F=∠ABC=60°.∴ CF==.∴ ☉O的半径为.
7. B 8. (1) 1 (2) 9. 10. - 11. 3+3或3-3 12. 13. 14. (-2,0)或(4,0) 15. 87
16. 2 解析:过点E作EF⊥AD,垂足为F.∵ AE=DE,EF⊥AD,∴ ∠EAD=∠ADE,AF=AD.∵ ∠BAC=90°,D是边BC的中点,∴ AD=BD=CD.∴ ∠B=∠DAB.∵ ∠ADE=∠B,∴ ∠EAD=∠B,∠ADE=∠DAB.∴ AB∥DE.∴ AC⊥DE.∴ 易得ED垂直平分AC.∴ CE=AE.∵ cosB=,∴ cos∠EAD==.∴ =4,即=4.∴ =2.
17. 2+ 解析:如图,取AC的中点Q,连接PQ、BQ.∵ P是CD的中点,Q是AC的中点,∴ PQ是△ACD的中位线.∴ PQ=AD=.∴ 当线段AD绕点A旋转时,点P在以点Q为圆心,PQ长为半径的圆上.延长BQ交☉Q于点P',当点P旋转到点P'的位置时,BP长的值最大.∵ BC=2,tan∠BAC=,∴ AC=4.∴ AQ=CQ=2.∵ ∠ACB=90°,∴ 由勾股定理,得BQ==2.∴ BP长的最大值为2+.
18. (1) (2)
19. (1) ∠A=30°,a=,c= (2) ∠B=60°,a=,b=3,c=2
20. (1) ∵ 在Rt△ACD中,cos ∠ADC==,CD=6,∴ AD=10.∴ 由勾股定理,得AC==8.∵ 在Rt△ABC中,tan B==,∴ BC=12.∴ 由勾股定理,得AB==4 (2) 过点D作DE⊥AB于点E.由(1),得BD=BC-CD=6.∵ 在Rt△BDE中,tan B==,DE2+BE2=BD2,∴ DE2+=36.∴ DE=(负值舍去).∴ 在Rt△ADE中,sin ∠BAD==
21. 如图,过点B作BH⊥AE于点H.∵ 坡度i为1∶0.75,∴ 设BH=4x(x>0)m,则AH=3xm.∴ 在Rt△AHB中,AB==5xm.∴ 5x=10,解得x=2.∴ AH=6m,BH=8m.过点B作BF⊥CE于点F,则四边形BHEF为矩形.∴ EF=BH=8m,BF=EH.设DF=ym.∵ 在Rt△BFD中,tanα=,∴ BF=≈=2y(m).∴ AE=(6+2y)m.∵ 坡度i为1∶0.75,∴ CE∶AE=(20+y+8)∶(6+2y)=1∶0.75,解得y=12.∴ DF=12m.∴ DE=DF+EF=12+8=20(m).∴ 堤坝高为8m,山高DE约为20m
22. (1) ∵ 将△ABC沿直线AB翻折到△ABD,∴ AB⊥CD.∴ ∠DEB=90°.∵ AB为☉O的直径,AG是☉O的切线,∴ AG⊥AB.∴ ∠GAB=90°.∴ ∠DEB=∠GAB.∴ AG∥CD (2) 由(1),得AG⊥AB,∴ ∠GAD+∠BAD=90°.∵ AB为☉O的直径,∴ ∠ADB=90°.∴ ∠BAD+∠ABD=90°.∴ ∠ABD=∠GAD.由翻折,可得∠ABD=∠ABC,∴ ∠DBC=2∠ABD.∵ 四边形ADBC是☉O的内接四边形,∴ ∠DAC+∠DBC=180°.∵ ∠DAC+∠PAD=180°,∴ ∠PAD=∠DBC=2∠ABD.∴ ∠PAG=∠PAD-∠GAD=2∠ABD-∠ABD=∠ABD.又∵ ∠APG=∠BPA,∴ △APG∽△BPA.∴ =,即PA2=PG·PB (3) ∵ AB为☉O的直径,∴ ∠ACB=∠ADB=∠ADP=90°.∴ 在△ADG中,∠AGB+∠GAD=90°.由(2),得∠GAD+∠BAD=90°,∴ ∠AGB=∠BAD.由sin∠APD==,设AD=a,则AP=3a.∴ 由勾股定理,得PD==2a.∴ tan∠APD===.由翻折,可得AC=AD=a,BD=BC,∴ PC=PA+AC=3a+a=4a.∵ 在Rt△PCB中,tan∠CPB==,∴ BD=BC=PC=a.∴ tan∠AGB=tan∠DAB===
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
