反比例函数与几何综合 (2) 同步练习(含答案)2024-2025学年人教版九年级数学下册
文档属性
| 名称 | 反比例函数与几何综合 (2) 同步练习(含答案)2024-2025学年人教版九年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 537.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 17:57:57 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
反比例函数与几何综合
一、知识梳理
【例】如图12-1所示,正比例函数 与反比例函数 的图象相交于点A, C, 点C的坐标为 (2, n) .
(1) 求k和n的值;
(2)利用函数图象,直接写出不等式 的解集;
(3) 点 B 是x 轴上的一个动点, 连接 AB, BC,作点 A 关于直线BC 的对称点Q,在点 B 的移动过程中,是否存在点 B,使得四边形 ABQC 为菱形 若存在,求出点 B 的坐标;若不存在,请说明理由.
解: (1) ∵把点 C的坐标 (2, n) 代入 解得n=3,
∴点C的坐标为 (2, 3) .
∵点C在正比例函数 的图象上,
∴把点C (2, 3) 代入 得3=2k, 解得
(2) 由函数图象可知, 的解集为x<-2或0(3)存在点 B,使得四边形 ABQC为菱形,分两种情况讨论.
◆如图12-2所示,作AH⊥x轴于点H, 当点B在x轴的正半轴且AB=AC时, 四边形ABQC为菱形, 证明如下.
∵点 A 与点Q 关于直线BC 对称,
∴AC=QC, AB=QB.
∵AB=AC,
∴AC=QC=AB=QB.
∴四边形 ABQC 为菱形.
∵由 (1) 可知, 点 C的坐标为 (2, 3),
∵点 A 与点C 关于原点对称,
∴点 A 的坐标为 (-2, - 3) .
∴在 Rt△AHB中,
又∵OH=2,
∴点B的坐标为
◆如图 12--3 所示, 作 AT⊥x轴于点T, 当点 B在x 轴的负半轴且AB=AC时, 四边形 ABQC 为菱形,证明如下.
同理可求得, 又∵OT=2,
∴点 B的坐标为
综上所述, 当点 B的坐标为
或 时, 四边形 ABQC 为菱形.
二、分层练习
1.如图12-4所示, 一次函数 的图象与x轴、y轴分别相交于点A,B,以线段AB 为边在第一象限作等边△ABC.
(1)若点 C在反比例函数 的图象上,求该反比例函数的解析式;
(2) 点 在第一象限,过点P 作x轴的垂线,垂足为点D, 当 与 相似时,点P 是否在 (1)中反比例函数的图象上 如果在,求出点 P 的坐标;如果不在,请说明理由.
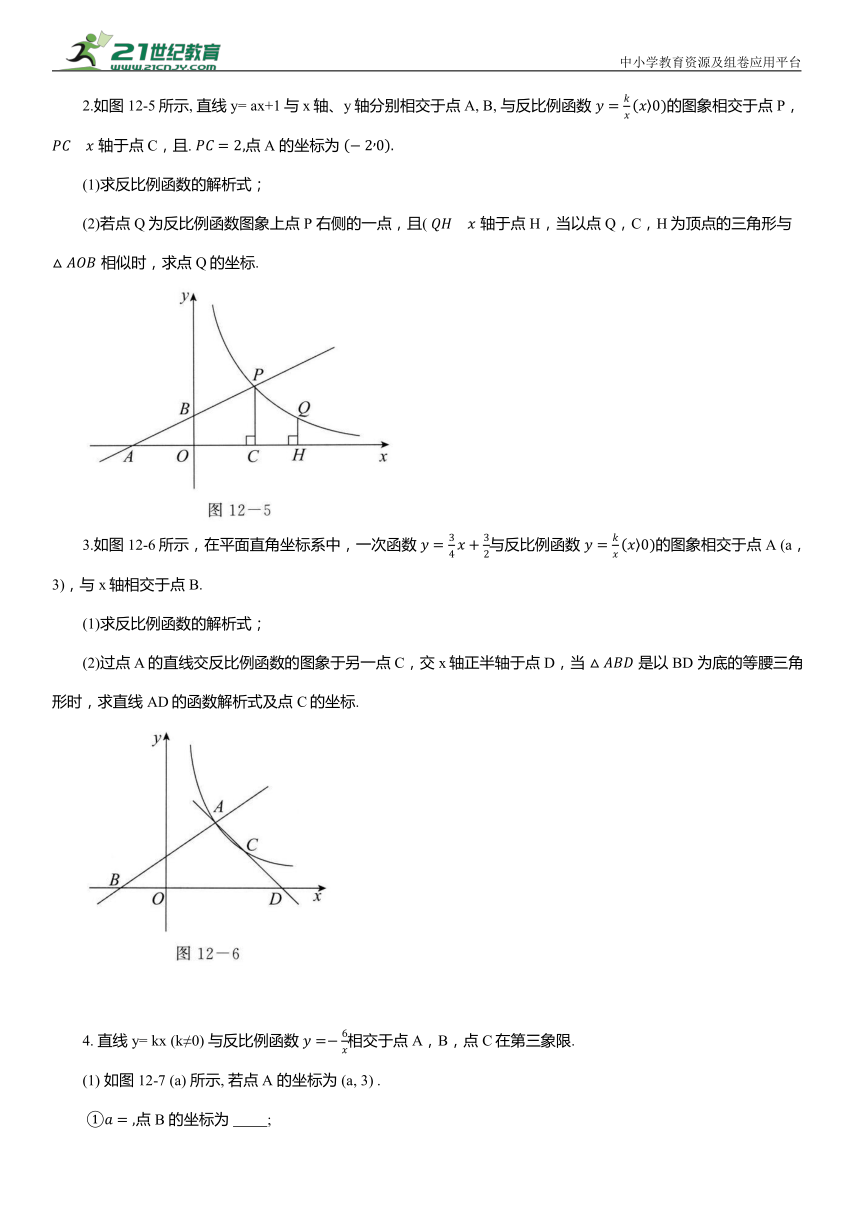
2.如图12-5所示, 直线y= ax+1与x轴、y轴分别相交于点A, B, 与反比例函数 的图象相交于点 P, 轴于点C,且. 点 A 的坐标为
(1)求反比例函数的解析式;
(2)若点 Q为反比例函数图象上点 P 右侧的一点,且( 轴于点 H,当以点 Q,C,H为顶点的三角形与 相似时,求点 Q的坐标.
3.如图12-6所示,在平面直角坐标系中,一次函数 与反比例函数 的图象相交于点 A (a,3),与x轴相交于点B.
(1)求反比例函数的解析式;
(2)过点A的直线交反比例函数的图象于另一点C,交x轴正半轴于点D,当 是以BD 为底的等腰三角形时,求直线 AD的函数解析式及点C的坐标.
4. 直线 y= kx (k≠0) 与反比例函数 相交于点A,B,点C在第三象限.
(1) 如图12-7 (a) 所示, 若点A 的坐标为 (a, 3) .
点 B 的坐标为 ;
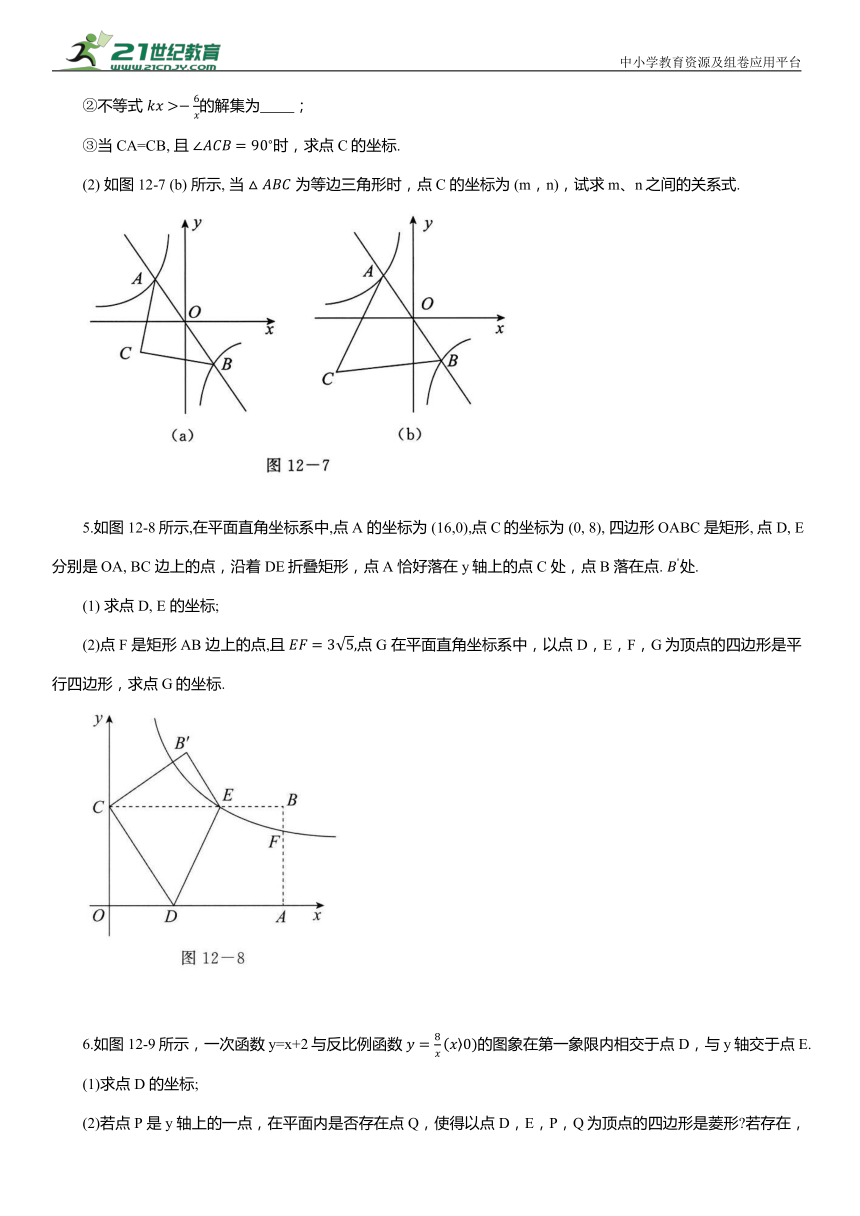
②不等式 的解集为 ;
③当CA=CB, 且 时,求点 C的坐标.
(2) 如图12-7 (b) 所示, 当 为等边三角形时,点C 的坐标为 (m,n),试求m、n之间的关系式.
5.如图12-8所示,在平面直角坐标系中,点 A 的坐标为 (16,0),点 C的坐标为 (0, 8), 四边形OABC 是矩形, 点 D, E 分别是OA, BC 边上的点,沿着DE折叠矩形,点A 恰好落在y轴上的点C 处,点B 落在点. 处.
(1) 求点 D, E 的坐标;
(2)点 F 是矩形AB 边上的点,且 点 G 在平面直角坐标系中,以点 D,E,F,G为顶点的四边形是平行四边形,求点G的坐标.
6.如图12-9所示,一次函数y=x+2与反比例函数 的图象在第一象限内相交于点 D,与y轴交于点E.
(1)求点 D 的坐标;
(2)若点 P 是y 轴上的一点,在平面内是否存在点 Q,使得以点 D,E,P,Q为顶点的四边形是菱形 若存在,请求出点Q的坐标,若不存在,请说明理由.
7. 如图12--10 所示, 直线 y=x--1与反比例函数 的图象相交于点 A(3, m) .
(1)求直线与反比例函数另一个交点B 的坐标和k的值;
(2)点C为x轴上的一点,点D为平面内一点,若以点A,B,C,D为顶点的四边形是矩形,请直接写出满足条件的点C的坐标.
8.【探究归纳】如图12--11 (a) 所示, 已知△ABC与△ABD的面积相等,试判断AB与CD 的位置关系,并说明理由.
【结论应用】 (1) 如图12--11 (b) 所示, 点 M, N 在反比例函数 (k>0,x>0)的图象上, 过点M作ME⊥y轴, 过点N作NF⊥x轴, 垂足分别为点 E, F, 试证明MN∥EF;
(2) 如图12--11 (c) 所示, 点 M, N在反比例函数 的图象上, 且点M的坐标为 (2,m),点N 是反比例函数 在第三象限的图象上的动点. 过点M作ME⊥y轴, 过点 N作EF⊥x轴, 垂足分别为点E, F, 说明MN∥EF,并求出当四边形 MEFN的面积为12时,点 N的坐标.
1. 解: (1) ∵一次函数 的图象分别与x轴、y轴相交于点A, B,
∴将x=0代入 得, y=1;
将y=0代入 得
∴点A的坐标为( 点 B 的坐标为 (0, 1) .
即∠BAO=30°.
∵△ABC是等边三角形,
∴AB=AC=BC, ∠BAC=60°.
∴∠BAO=∠BAO+∠BAC=90°.
∵在 Rt△BOA中,由勾股定理可得,
∴AC=2.
∴点C的坐标为 ( , 2) .
∵点 C在反比例函数 的图象上,
∴反比例函数的解析式为
(2) ∵点 P (2 , m) 在第一象限,
当△ADP∽△AOB时, 则有 即 解得m=1,此时点 P 的坐标为(
当△PDA∽△AOB时, 则有 即 解得m=3,此时点 P 的坐标为(
将点. 代入反比例函数 得
故点 在反比例函数的图象上.
将点 代入反比例函数 得
故点 不在反比例函数的图象上.
综上所述,点P 的坐标为((2 , 1) .
2. 解: (1) ∵点A (-2, 0) 在直线y= ax+1的图象上,∴将点 A (-2, 0) 代入y= ax+1, 得0=-2a+1,解得 即
∴直线的解析式为
∵PC=2, 点 P 在直线 的图象上,
∴将 y=2代入 得 解得x=2, 即点 P 的坐标为(2, 2) .
∵点 P (2,2)在反比例函数 的图象上,
∴k=2×2=4.
∴反比例函数的解析式为
(2) 如图37所示, 连接QC, 设点Q的坐标为 (m, n) .
∵点 Q (m,n)在反比例函数 的图象上,
∵当△QCH∽△BAO时, 可得 即 整理得m-2=2n,
∴代入 得 整理得 解得m=4或m=-2 (舍去) .
∴点 Q的坐标为 (4, 1) .
∵当△QCH∽△ABO时, 可得 即 整理得
解得 或 (舍去),
∴点 Q的坐标为
综上所述,点Q 的坐标为 (4,1)或
3. 解: (1) ∵一次函数 的图象经过点A (a, 3),
∴将 y=3代入 得 解得a=2.
∴点 A 的坐标为 (2, 3) .
∵点 A (2,3)在反比例函数 的图象上,
∴k=2×3=6.
∴反比例函数的解析式为
(2) 如图38所示, 过点 A 作AE⊥x轴于点E.
∵一次函数 交x轴于点B,
∴将y=0代入 得 解得x=-2.
∴点 B 的坐标为 (-2, 0) .
∵AE⊥x轴于点E, 点 A的坐标为 (2, 3),
∴点 E 的坐标为 (2, 0) .
∴BE=2 - (-2) =4.
∵△ABD 是以BD 为底边的等腰三角形,
∴AB=AD, DE=BE=4.
∴点 D 的坐标为 (6, 0) .
设直线 AD的函数解析式为y=mx+n.
∵点 A (2, 3), D (6, 0) 在直线AD上,
解得
∴直线 AD 的函数解析式为
∵联立方程解得 (舍去)
∴点C的坐标为(4,
4. 解: (1) ①∵点 A (a, 3) 在反比例函数 的图象上,
∴将 y=3代入 得 解得a=-2.
∴点 A 的坐标为(-2, 3) .
∵点 A在直线y= kx (k≠0) 的图象上,
∴将A (-2, 3) 代入 y= kx, 得3=-2k, 解得
∴直线的函数解析式为
∵点 A,B 是直线 与反比例函数 的交点,且点 A 的坐标为 (-2, 3),
∴由图象的对称性可得,点B 的坐标为 (2, -3).
②由图象可得,不等式 的解集为x<-2或0③如图39所示, 连接CO, 作AD⊥y轴于点D, 作CE⊥y轴于点E.
∵AD⊥y轴于点D, 点 A 的坐标为 (--2, 3),
∴OD=3, AD=2.
∵∠ACB=90°, CA=CB,
∵∠AOD+∠COE=90°, ∠COE+∠OCE=90°,
∴∠OCE=∠AOD.
在△ADO和△OEC中,
∴△ADO≌△OEC (AAS) .
∴CE=OD=3, EO=DA=2.
∴点 C的坐标为 (--3, - 2) .
(2) 如图40所示, 连接CO, 作AD⊥y轴于点D, 作( 轴于点E.
∵反比例函数和正比例函数都是中心对称图形,且关于原点对称,
∴OA=OB.
又∵△ABC为等边三角形,
∴∠AOC=∠BOC=90°.
,∠DOA=∠BOE,
∴△ADO∽△OEC.
∵∠ACO=30°,
即
∵设点C的坐标为 (m, n),
∴CE=-m, OE=-n.
∴点 A 的坐标为
∵点 A 在反比例函数 的图象上,
∴将点 代入 得 整理得 mn=18.
欲穷千里目,更上一层楼
5. 解: (1) ∵点A的坐标为 (16, 0), 点C的坐标为 (0, 8),
∴OA=16, OC=8.
∴设OD=m, 则CD=DA=16-m.
∵在Rt△COD中, 即 解得m=6,
∴点 D 的坐标为 (6, 0) .
∵四边形OABC是矩形,
∴OA∥CB.
∴∠CED=∠EDA.
∵∠EDA=∠CDE,
∴CE=CD=16-m=10.
∴点 E 的坐标为 (10, 8) .
(2)设过点 E,F的反比例函数的解析式为 如图41所示,过点 B'作 B'M⊥BC于点M.
∴点 B'的坐标为 (6.4, 12.8) .
∵点 E (10, 8) 在反比例函数 的图象上,
∴k=10×8=80, 即
设点 F的坐标为
∵点 F 是矩形AB 边上的点,且在反比例函数 的图象上,
∴将x=16代入 得
∴点 F 的坐标为 (16, 5) .
如图42所示, 以 D,E,F,G为顶点的平行四边形有三种情况.
①把线段 DE 先向右平移10 个单位长度,再向上平移5个单位长度,端点 E 落在点G 处,点G 的坐标为 (20, 13) .
②把线段EF先向左平移4个单位长度,再向下平移8个单位长度,端点 F落在点G 处, 点G 的坐标为 (12, — 3) .
③把线段DF先向左平移6个单位长度,再向上平移3个单位长度,端点 D落在点 G 处, 点 G 的坐标为 (0, 3) .
综上所述, 在平面直角坐标系中, 存在点G (20, 13), G (12, — 3),G (0,3),使得以点 D,E,F,G为顶点的四边形是平行四边形.
6. 解: (1) ∵一次函数y=x+2与反比例函数 的图象在第一象限内相交于点 D,
∴联立方程 整理得 解得 (舍去) .
∴点 D的坐标为 (2, 4) .
(2) ∵点 E 的坐标为 (0, 2), 点 D 的坐标为 (2, 4),
如图43所示, 当ED=EP 或ED=EP 时,
存在菱形 EDQ P 或菱形 EDQ P ,
此时点 P 的坐标为(
点 Q 的坐标为(2,
此时点 P 的坐标为 点 Q 的坐标为 (2
如图44 所示, 当DE=DP 时, 过点 D 作DH⊥y轴于点 H, 存在菱形 DEQ P .
∵DE=DP , DH⊥y轴,
∴点 P 的坐标为 (0, 6), 点 Q 的坐标为(--2, 4) .
如图45 所示,当 时,存在菱形 P EQ D.
∵设点 P 的坐标为 (0, m),
. ,即 解得m=4.
∴点 P 的坐标为 (0, 4), 点 Q 的坐标为(2, 2) .综上所述,当点 P 在 y 轴上时,平面内存在点Q,使得以点 D,E,P,Q为顶点的四边形为菱形,点Q的坐标为(2, 2 +4)或(2, 或(-2, 4) 或 (2, 2) .
7. 解: (1) ∵直线 y=x--1与反比例函数 的图象相交于点A (3,m),
∴将x=3代入直线y=x--1, 得y=3-1=2.
∴点 A 的坐标为 (3, 2) .
∴k=3×2=6.
∴反比例函数的解析式为
∵联立方程 解得 或
∴点 B 的坐标为 (-2, - 3) .
(2) 如图46所示, 当CB⊥AB时, 设CB所在直线的解析式为 则有 解得 5, 则CB所在直线的解析式为y=-x-5.
将y=0代入y=-x-5, 得-x--5=0, 解得x=-5.
∵点C为x轴上的一点,
∴点 C的坐标为 (-5, 0) .
如图47 所示,当CA⊥AB时,设CA 所在直线的解析式为
则有 解得
则 CB 所在直线的解析式为y=-x+5.
∵将y=0代入y=-x+5, 得-x+5=0, 解得x=5,∴点 C的坐标为 (5, 0) .
如图48 和图49所示,当CA⊥BC时,设点 C 的坐标为 (m, 0) .
∵由勾股定理得, 即( ,整理得 解得
∴点 C 的坐标为 (-3, 0) 或 (4, 0) .
综上所述, 点C的坐标为(-5, 0) 或 (5, 0) 或(-3, 0) 或(4, 0) .
8. (1) 证明: AB∥CD, 理由如下.
如图50所示, 分别过点C, D作CG⊥AB于点G, DH⊥AB于点H.
∵CG⊥AB, DH⊥AB,
∴∠CGA=∠DHB=90°.
∴∠CGA+∠DHA=180°.
∴CG∥DH.
∵△ABC 与△ABD的面积相等,
∴CG=DH.
∴四边形CGHD为平行四边形.
∴AB∥CD.
(2) ①证明: 如图51所示, 连接MF, NE.
设点 M 的坐标为 (x ,y ),点 N 的坐标为(
∵点 M,N 在反比例函数 的图象上,
∵ME⊥y轴, NF⊥x轴,
∴OE=y , OF=x , EM=x , NF=y .
∴S△EFM=S△EFN.
∴由 (1) 中的结论可知, MN∥EF.
②解: 如图52所示, 连接FM, EN, MN 和x轴的交点为点G.
∵点 M 的坐标为 (2,m),且在反比例函数 的图象上,
∴EM=2, OE=m, 2m=10.
∵由 (2) ①中的结论可知, MN∥EF,
∴四边形 EFGM为平行四边形.
∴FG=EM=2.
∵S四边形EFNM=S平行四边形EFGM+S△FNG,
=10+FN.
∴FN=2.
∵点 N 是反比例函数 在第三象限内的图象上的动点,
∴将x=-2代入 得
∴点 N 的坐标为 (--2, - 5) .
反比例函数与几何综合
一、知识梳理
【例】如图12-1所示,正比例函数 与反比例函数 的图象相交于点A, C, 点C的坐标为 (2, n) .
(1) 求k和n的值;
(2)利用函数图象,直接写出不等式 的解集;
(3) 点 B 是x 轴上的一个动点, 连接 AB, BC,作点 A 关于直线BC 的对称点Q,在点 B 的移动过程中,是否存在点 B,使得四边形 ABQC 为菱形 若存在,求出点 B 的坐标;若不存在,请说明理由.
解: (1) ∵把点 C的坐标 (2, n) 代入 解得n=3,
∴点C的坐标为 (2, 3) .
∵点C在正比例函数 的图象上,
∴把点C (2, 3) 代入 得3=2k, 解得
(2) 由函数图象可知, 的解集为x<-2或0
◆如图12-2所示,作AH⊥x轴于点H, 当点B在x轴的正半轴且AB=AC时, 四边形ABQC为菱形, 证明如下.
∵点 A 与点Q 关于直线BC 对称,
∴AC=QC, AB=QB.
∵AB=AC,
∴AC=QC=AB=QB.
∴四边形 ABQC 为菱形.
∵由 (1) 可知, 点 C的坐标为 (2, 3),
∵点 A 与点C 关于原点对称,
∴点 A 的坐标为 (-2, - 3) .
∴在 Rt△AHB中,
又∵OH=2,
∴点B的坐标为
◆如图 12--3 所示, 作 AT⊥x轴于点T, 当点 B在x 轴的负半轴且AB=AC时, 四边形 ABQC 为菱形,证明如下.
同理可求得, 又∵OT=2,
∴点 B的坐标为
综上所述, 当点 B的坐标为
或 时, 四边形 ABQC 为菱形.
二、分层练习
1.如图12-4所示, 一次函数 的图象与x轴、y轴分别相交于点A,B,以线段AB 为边在第一象限作等边△ABC.
(1)若点 C在反比例函数 的图象上,求该反比例函数的解析式;
(2) 点 在第一象限,过点P 作x轴的垂线,垂足为点D, 当 与 相似时,点P 是否在 (1)中反比例函数的图象上 如果在,求出点 P 的坐标;如果不在,请说明理由.
2.如图12-5所示, 直线y= ax+1与x轴、y轴分别相交于点A, B, 与反比例函数 的图象相交于点 P, 轴于点C,且. 点 A 的坐标为
(1)求反比例函数的解析式;
(2)若点 Q为反比例函数图象上点 P 右侧的一点,且( 轴于点 H,当以点 Q,C,H为顶点的三角形与 相似时,求点 Q的坐标.
3.如图12-6所示,在平面直角坐标系中,一次函数 与反比例函数 的图象相交于点 A (a,3),与x轴相交于点B.
(1)求反比例函数的解析式;
(2)过点A的直线交反比例函数的图象于另一点C,交x轴正半轴于点D,当 是以BD 为底的等腰三角形时,求直线 AD的函数解析式及点C的坐标.
4. 直线 y= kx (k≠0) 与反比例函数 相交于点A,B,点C在第三象限.
(1) 如图12-7 (a) 所示, 若点A 的坐标为 (a, 3) .
点 B 的坐标为 ;
②不等式 的解集为 ;
③当CA=CB, 且 时,求点 C的坐标.
(2) 如图12-7 (b) 所示, 当 为等边三角形时,点C 的坐标为 (m,n),试求m、n之间的关系式.
5.如图12-8所示,在平面直角坐标系中,点 A 的坐标为 (16,0),点 C的坐标为 (0, 8), 四边形OABC 是矩形, 点 D, E 分别是OA, BC 边上的点,沿着DE折叠矩形,点A 恰好落在y轴上的点C 处,点B 落在点. 处.
(1) 求点 D, E 的坐标;
(2)点 F 是矩形AB 边上的点,且 点 G 在平面直角坐标系中,以点 D,E,F,G为顶点的四边形是平行四边形,求点G的坐标.
6.如图12-9所示,一次函数y=x+2与反比例函数 的图象在第一象限内相交于点 D,与y轴交于点E.
(1)求点 D 的坐标;
(2)若点 P 是y 轴上的一点,在平面内是否存在点 Q,使得以点 D,E,P,Q为顶点的四边形是菱形 若存在,请求出点Q的坐标,若不存在,请说明理由.
7. 如图12--10 所示, 直线 y=x--1与反比例函数 的图象相交于点 A(3, m) .
(1)求直线与反比例函数另一个交点B 的坐标和k的值;
(2)点C为x轴上的一点,点D为平面内一点,若以点A,B,C,D为顶点的四边形是矩形,请直接写出满足条件的点C的坐标.
8.【探究归纳】如图12--11 (a) 所示, 已知△ABC与△ABD的面积相等,试判断AB与CD 的位置关系,并说明理由.
【结论应用】 (1) 如图12--11 (b) 所示, 点 M, N 在反比例函数 (k>0,x>0)的图象上, 过点M作ME⊥y轴, 过点N作NF⊥x轴, 垂足分别为点 E, F, 试证明MN∥EF;
(2) 如图12--11 (c) 所示, 点 M, N在反比例函数 的图象上, 且点M的坐标为 (2,m),点N 是反比例函数 在第三象限的图象上的动点. 过点M作ME⊥y轴, 过点 N作EF⊥x轴, 垂足分别为点E, F, 说明MN∥EF,并求出当四边形 MEFN的面积为12时,点 N的坐标.
1. 解: (1) ∵一次函数 的图象分别与x轴、y轴相交于点A, B,
∴将x=0代入 得, y=1;
将y=0代入 得
∴点A的坐标为( 点 B 的坐标为 (0, 1) .
即∠BAO=30°.
∵△ABC是等边三角形,
∴AB=AC=BC, ∠BAC=60°.
∴∠BAO=∠BAO+∠BAC=90°.
∵在 Rt△BOA中,由勾股定理可得,
∴AC=2.
∴点C的坐标为 ( , 2) .
∵点 C在反比例函数 的图象上,
∴反比例函数的解析式为
(2) ∵点 P (2 , m) 在第一象限,
当△ADP∽△AOB时, 则有 即 解得m=1,此时点 P 的坐标为(
当△PDA∽△AOB时, 则有 即 解得m=3,此时点 P 的坐标为(
将点. 代入反比例函数 得
故点 在反比例函数的图象上.
将点 代入反比例函数 得
故点 不在反比例函数的图象上.
综上所述,点P 的坐标为((2 , 1) .
2. 解: (1) ∵点A (-2, 0) 在直线y= ax+1的图象上,∴将点 A (-2, 0) 代入y= ax+1, 得0=-2a+1,解得 即
∴直线的解析式为
∵PC=2, 点 P 在直线 的图象上,
∴将 y=2代入 得 解得x=2, 即点 P 的坐标为(2, 2) .
∵点 P (2,2)在反比例函数 的图象上,
∴k=2×2=4.
∴反比例函数的解析式为
(2) 如图37所示, 连接QC, 设点Q的坐标为 (m, n) .
∵点 Q (m,n)在反比例函数 的图象上,
∵当△QCH∽△BAO时, 可得 即 整理得m-2=2n,
∴代入 得 整理得 解得m=4或m=-2 (舍去) .
∴点 Q的坐标为 (4, 1) .
∵当△QCH∽△ABO时, 可得 即 整理得
解得 或 (舍去),
∴点 Q的坐标为
综上所述,点Q 的坐标为 (4,1)或
3. 解: (1) ∵一次函数 的图象经过点A (a, 3),
∴将 y=3代入 得 解得a=2.
∴点 A 的坐标为 (2, 3) .
∵点 A (2,3)在反比例函数 的图象上,
∴k=2×3=6.
∴反比例函数的解析式为
(2) 如图38所示, 过点 A 作AE⊥x轴于点E.
∵一次函数 交x轴于点B,
∴将y=0代入 得 解得x=-2.
∴点 B 的坐标为 (-2, 0) .
∵AE⊥x轴于点E, 点 A的坐标为 (2, 3),
∴点 E 的坐标为 (2, 0) .
∴BE=2 - (-2) =4.
∵△ABD 是以BD 为底边的等腰三角形,
∴AB=AD, DE=BE=4.
∴点 D 的坐标为 (6, 0) .
设直线 AD的函数解析式为y=mx+n.
∵点 A (2, 3), D (6, 0) 在直线AD上,
解得
∴直线 AD 的函数解析式为
∵联立方程解得 (舍去)
∴点C的坐标为(4,
4. 解: (1) ①∵点 A (a, 3) 在反比例函数 的图象上,
∴将 y=3代入 得 解得a=-2.
∴点 A 的坐标为(-2, 3) .
∵点 A在直线y= kx (k≠0) 的图象上,
∴将A (-2, 3) 代入 y= kx, 得3=-2k, 解得
∴直线的函数解析式为
∵点 A,B 是直线 与反比例函数 的交点,且点 A 的坐标为 (-2, 3),
∴由图象的对称性可得,点B 的坐标为 (2, -3).
②由图象可得,不等式 的解集为x<-2或0
∵AD⊥y轴于点D, 点 A 的坐标为 (--2, 3),
∴OD=3, AD=2.
∵∠ACB=90°, CA=CB,
∵∠AOD+∠COE=90°, ∠COE+∠OCE=90°,
∴∠OCE=∠AOD.
在△ADO和△OEC中,
∴△ADO≌△OEC (AAS) .
∴CE=OD=3, EO=DA=2.
∴点 C的坐标为 (--3, - 2) .
(2) 如图40所示, 连接CO, 作AD⊥y轴于点D, 作( 轴于点E.
∵反比例函数和正比例函数都是中心对称图形,且关于原点对称,
∴OA=OB.
又∵△ABC为等边三角形,
∴∠AOC=∠BOC=90°.
,∠DOA=∠BOE,
∴△ADO∽△OEC.
∵∠ACO=30°,
即
∵设点C的坐标为 (m, n),
∴CE=-m, OE=-n.
∴点 A 的坐标为
∵点 A 在反比例函数 的图象上,
∴将点 代入 得 整理得 mn=18.
欲穷千里目,更上一层楼
5. 解: (1) ∵点A的坐标为 (16, 0), 点C的坐标为 (0, 8),
∴OA=16, OC=8.
∴设OD=m, 则CD=DA=16-m.
∵在Rt△COD中, 即 解得m=6,
∴点 D 的坐标为 (6, 0) .
∵四边形OABC是矩形,
∴OA∥CB.
∴∠CED=∠EDA.
∵∠EDA=∠CDE,
∴CE=CD=16-m=10.
∴点 E 的坐标为 (10, 8) .
(2)设过点 E,F的反比例函数的解析式为 如图41所示,过点 B'作 B'M⊥BC于点M.
∴点 B'的坐标为 (6.4, 12.8) .
∵点 E (10, 8) 在反比例函数 的图象上,
∴k=10×8=80, 即
设点 F的坐标为
∵点 F 是矩形AB 边上的点,且在反比例函数 的图象上,
∴将x=16代入 得
∴点 F 的坐标为 (16, 5) .
如图42所示, 以 D,E,F,G为顶点的平行四边形有三种情况.
①把线段 DE 先向右平移10 个单位长度,再向上平移5个单位长度,端点 E 落在点G 处,点G 的坐标为 (20, 13) .
②把线段EF先向左平移4个单位长度,再向下平移8个单位长度,端点 F落在点G 处, 点G 的坐标为 (12, — 3) .
③把线段DF先向左平移6个单位长度,再向上平移3个单位长度,端点 D落在点 G 处, 点 G 的坐标为 (0, 3) .
综上所述, 在平面直角坐标系中, 存在点G (20, 13), G (12, — 3),G (0,3),使得以点 D,E,F,G为顶点的四边形是平行四边形.
6. 解: (1) ∵一次函数y=x+2与反比例函数 的图象在第一象限内相交于点 D,
∴联立方程 整理得 解得 (舍去) .
∴点 D的坐标为 (2, 4) .
(2) ∵点 E 的坐标为 (0, 2), 点 D 的坐标为 (2, 4),
如图43所示, 当ED=EP 或ED=EP 时,
存在菱形 EDQ P 或菱形 EDQ P ,
此时点 P 的坐标为(
点 Q 的坐标为(2,
此时点 P 的坐标为 点 Q 的坐标为 (2
如图44 所示, 当DE=DP 时, 过点 D 作DH⊥y轴于点 H, 存在菱形 DEQ P .
∵DE=DP , DH⊥y轴,
∴点 P 的坐标为 (0, 6), 点 Q 的坐标为(--2, 4) .
如图45 所示,当 时,存在菱形 P EQ D.
∵设点 P 的坐标为 (0, m),
. ,即 解得m=4.
∴点 P 的坐标为 (0, 4), 点 Q 的坐标为(2, 2) .综上所述,当点 P 在 y 轴上时,平面内存在点Q,使得以点 D,E,P,Q为顶点的四边形为菱形,点Q的坐标为(2, 2 +4)或(2, 或(-2, 4) 或 (2, 2) .
7. 解: (1) ∵直线 y=x--1与反比例函数 的图象相交于点A (3,m),
∴将x=3代入直线y=x--1, 得y=3-1=2.
∴点 A 的坐标为 (3, 2) .
∴k=3×2=6.
∴反比例函数的解析式为
∵联立方程 解得 或
∴点 B 的坐标为 (-2, - 3) .
(2) 如图46所示, 当CB⊥AB时, 设CB所在直线的解析式为 则有 解得 5, 则CB所在直线的解析式为y=-x-5.
将y=0代入y=-x-5, 得-x--5=0, 解得x=-5.
∵点C为x轴上的一点,
∴点 C的坐标为 (-5, 0) .
如图47 所示,当CA⊥AB时,设CA 所在直线的解析式为
则有 解得
则 CB 所在直线的解析式为y=-x+5.
∵将y=0代入y=-x+5, 得-x+5=0, 解得x=5,∴点 C的坐标为 (5, 0) .
如图48 和图49所示,当CA⊥BC时,设点 C 的坐标为 (m, 0) .
∵由勾股定理得, 即( ,整理得 解得
∴点 C 的坐标为 (-3, 0) 或 (4, 0) .
综上所述, 点C的坐标为(-5, 0) 或 (5, 0) 或(-3, 0) 或(4, 0) .
8. (1) 证明: AB∥CD, 理由如下.
如图50所示, 分别过点C, D作CG⊥AB于点G, DH⊥AB于点H.
∵CG⊥AB, DH⊥AB,
∴∠CGA=∠DHB=90°.
∴∠CGA+∠DHA=180°.
∴CG∥DH.
∵△ABC 与△ABD的面积相等,
∴CG=DH.
∴四边形CGHD为平行四边形.
∴AB∥CD.
(2) ①证明: 如图51所示, 连接MF, NE.
设点 M 的坐标为 (x ,y ),点 N 的坐标为(
∵点 M,N 在反比例函数 的图象上,
∵ME⊥y轴, NF⊥x轴,
∴OE=y , OF=x , EM=x , NF=y .
∴S△EFM=S△EFN.
∴由 (1) 中的结论可知, MN∥EF.
②解: 如图52所示, 连接FM, EN, MN 和x轴的交点为点G.
∵点 M 的坐标为 (2,m),且在反比例函数 的图象上,
∴EM=2, OE=m, 2m=10.
∵由 (2) ①中的结论可知, MN∥EF,
∴四边形 EFGM为平行四边形.
∴FG=EM=2.
∵S四边形EFNM=S平行四边形EFGM+S△FNG,
=10+FN.
∴FN=2.
∵点 N 是反比例函数 在第三象限内的图象上的动点,
∴将x=-2代入 得
∴点 N 的坐标为 (--2, - 5) .
