26.1.1反比例函数 同步练习(含答案)2024-2025学年人教版九年级数学下册
文档属性
| 名称 | 26.1.1反比例函数 同步练习(含答案)2024-2025学年人教版九年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 97.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 17:43:56 | ||
图片预览


文档简介
26.1.1反比例函数
一、知识梳理
(一)反比例函数的定义
函数 (k为常数,k≠0)叫作反比例函数,其中k叫作比例系数,x是自变量,y是函数, 自变量x的取值范围是不等于0的一切实数.
(二)反比例函数解析式的求法
反比例函数的解析式 中,只有一个系数k,确定了k的值,也就确定了反比例函数的解析式.因此,只要给出一组x、y的对应值或图象上一点的坐标,利用待定系数法,即可确定反比例函数的解析式.
【例】如图1--1所示,在平面直角坐标系中,直线y=--3x+6与x轴、y轴分别相交于点A,B,以AB为边在第一象限作正方形ABCD,则过点D的反比例函数的解析式为 .
解: 如图1—2所示, 作 DF⊥x轴于点F.
∵在直线y=-3x+6中, 令x=0, 则y=6,即点 B的坐标为 (0, 6);
令y=0, 则--3x+6=0, 解得:x=2,即点A 的坐标为 (2, 0),
∴OB=6, OA=2.
∵四边形 ABCD 为正方形,
∴∠BAD=90°, AB=AD.
∴∠BAO+∠DAF=90°.
∵∠BOA=90°,
∴∠BAO+∠OBA=90°.
∴∠DAF=∠OBA.
在△OAB 和△FDA中,
∴△OAB≌△FDA (AAS).
∴AF=OB=6, DF=OA=2.
∴OF=OA+AF=6+2=8.
∴点 D的坐标为 (8, 2).
∵点 D 在反比例函数的图象上, 则有k=8×2=16,
∴过点 D 的反比例函数的解析式为
二、分层练习
1.下列函数属于反比例函数的有 (填序号).
⑤y=x-1; (k为常数,k≠0).
2.下列函数中反比例函数的个数有 ( )个.
①xy=2; ②y=3x; (k为常数,
A.1 B.2 C.3 D.4
3.已知函数 是反比例函数,则m 的值为 .
4.若函数 (k为常数)是反比例函数,则k的值为 ,函数解析式为 .
5.已知函数 回答下列问题.
(1)当m、n为何值时,此函数是一次函数
(2)当m、n为何值时,此函数是正比例函数
6.若一个反比例函数的图象与直线 y=2x-6的一个交点为点. 则这个反比例函数的解析式为 .
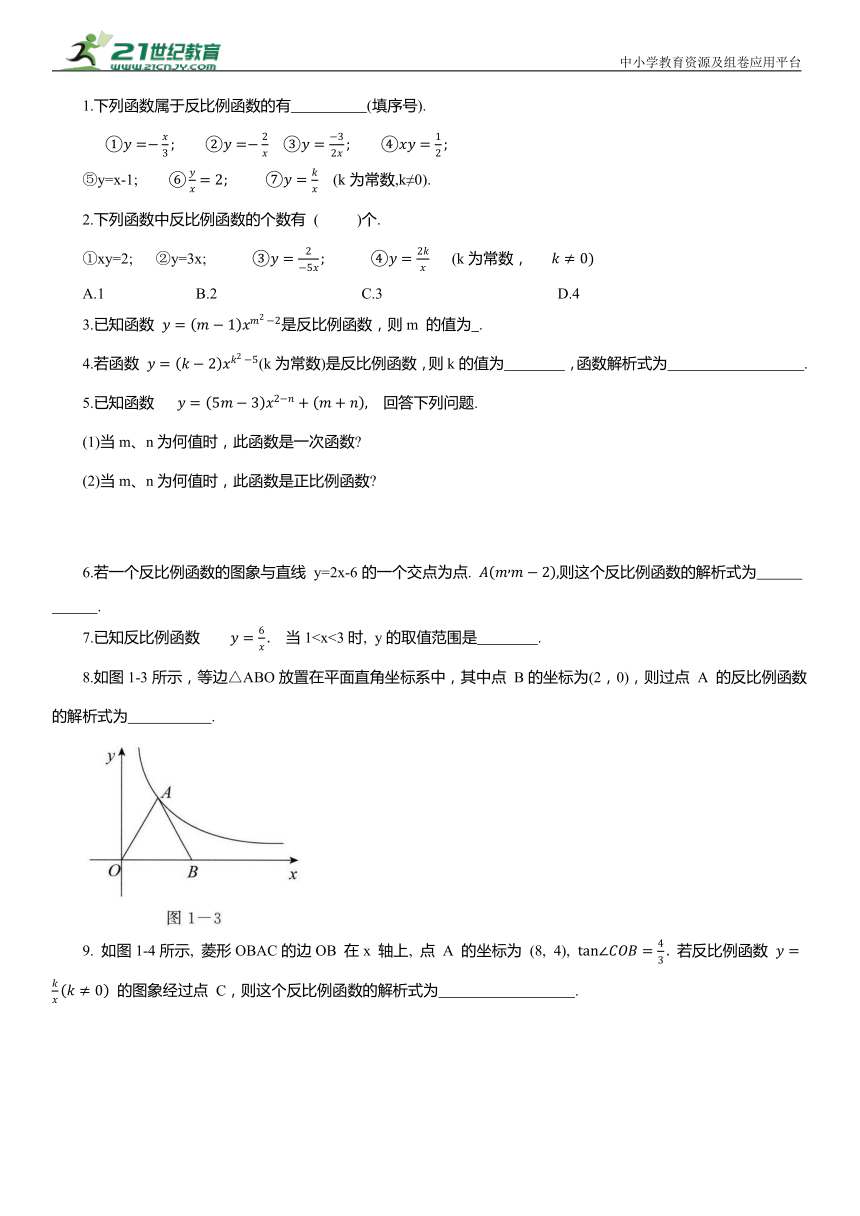
7.已知反比例函数 当18.如图1-3所示,等边△ABO放置在平面直角坐标系中,其中点 B的坐标为(2,0),则过点 A 的反比例函数的解析式为 .
9. 如图1-4所示, 菱形OBAC的边OB 在x 轴上, 点 A 的坐标为 (8, 4), 若反比例函数 的图象经过点 C,则这个反比例函数的解析式为 .
10.在平面直角坐标系中,若函数 (a为常数)的图象经过点 A (-2,3), B (1, 6),C (-4, m) 中的两点, 则:
11.已知函数 其中y 为x的反比例函数,y 为x的正比例函数,且 和x=1时,y的值都是1.求y关于x的函数解析式.
12. 如图1-5 所示, 已知 是边长为 的等边三角形,点E,F分别在CB 和BC 的延长线上,且 设
(1)求y关于x的函数解析式,并求出自变量x的取值范围;
(2)当x为何值时,
1. 解: 是一次函数;
是反比例函数;
是反比例函数;
可变形为 是反比例函数;
⑤y=x--1是一次函数;
可变形为y=2x,是一次函数;
(k为常数, k≠0) 是反比例函数.
2.解: ①xy=2可变形为 是反比例函数;
②y=3x是正比例函数;
是反比例函数;
(k为常数, k≠0) 是反比例函数.
故选C.
3. 解: ∵函数 是反比例函数,
且m-1≠0.
∴m=-1.
4. 解: ∵函数
(k为常数)是反比例函数,
且k-2≠0.
∴k=-2,
该函数的解析式为
5.解: (1) 当函数 y= (5m--3) 是一次函数时,有 解得n=1, m≠
(2)当函数 (m+n)是正比例函数时,
有 解得n=1, m=-1.
6.解:∵反比例函数的图象与直线y=2x--6的一个交点为点 A (m,m--2),
∴m--2=2m--6, 解得m=4.
中小学教育资源及组卷应用平台
∴点 A 的坐标为 (4, 2) .
设反比例函数的解析式为
7. 解: ∵k=6>0,
∴在每个象限内y随x 的增大而减小.
解得k=8.
又∵当x=1时, y=6;
当x=3时, y=2,
∴反比例函数的解析式为
∴当18.解:如图1所示,过点A作AC⊥OB于点C,设过点A 的反比例函数的解析式为
∵△OAB是等边三角形,
∴OA=2, ∠AOC=60°.
∴点 A 的坐标为 (1, ) .
∵点 A 在反比例函数 的图象上,
解得
∴过点 A 的反比例函数的解析式为
9. 解: 如图2所示, 过点 C作CM⊥OB 于点 M.
∵四边形OBAC是菱形, 点 A 的坐标为 (8, 4),
∴CM=4.
又
∴OM=3.
∴点 C的坐标为 (3, 4) .
∵点 C (3,4)在反比例函数 的图象上,
∴k=3×4=12.
∴反比例函数的解析式为
10. 解: ∵在函数 (a为常数)中,
∴函数图象位于第二、第四象限.
∵点A (--2, 3) 在第二象限, 点 B (1, 6) 在第一象限, 函数 y= (a为常数) 的图象经过点 A (-2, 3), B (1, 6), C (-4, m)中的两点,
∴点 C (-4, m) 在第二象限.
∴-2×3=-4m,解得
11. 解: ∵y 与x成反比例, y 与x成正比例,
∵当 和x=1时,
y的值都是1,
解得
12. 解: (1) ∵△ABC是等边三角形,∴∠BAC=60°.
∵∠EAF=120°,
∴∠EAB+∠CAF=60°.
∵∠EAB+∠E=∠ABC=60°,
∴∠E=∠CAF.
∵∠EBA=∠ACF=120°,
∴△ABE∽△FCA.
即
整理得
故 y关于x的函数解析式为
(2) ∵△ABE≌△FCA,
∴BE=CA, 即
故当 时,
△ABE≌△FCA.
一、知识梳理
(一)反比例函数的定义
函数 (k为常数,k≠0)叫作反比例函数,其中k叫作比例系数,x是自变量,y是函数, 自变量x的取值范围是不等于0的一切实数.
(二)反比例函数解析式的求法
反比例函数的解析式 中,只有一个系数k,确定了k的值,也就确定了反比例函数的解析式.因此,只要给出一组x、y的对应值或图象上一点的坐标,利用待定系数法,即可确定反比例函数的解析式.
【例】如图1--1所示,在平面直角坐标系中,直线y=--3x+6与x轴、y轴分别相交于点A,B,以AB为边在第一象限作正方形ABCD,则过点D的反比例函数的解析式为 .
解: 如图1—2所示, 作 DF⊥x轴于点F.
∵在直线y=-3x+6中, 令x=0, 则y=6,即点 B的坐标为 (0, 6);
令y=0, 则--3x+6=0, 解得:x=2,即点A 的坐标为 (2, 0),
∴OB=6, OA=2.
∵四边形 ABCD 为正方形,
∴∠BAD=90°, AB=AD.
∴∠BAO+∠DAF=90°.
∵∠BOA=90°,
∴∠BAO+∠OBA=90°.
∴∠DAF=∠OBA.
在△OAB 和△FDA中,
∴△OAB≌△FDA (AAS).
∴AF=OB=6, DF=OA=2.
∴OF=OA+AF=6+2=8.
∴点 D的坐标为 (8, 2).
∵点 D 在反比例函数的图象上, 则有k=8×2=16,
∴过点 D 的反比例函数的解析式为
二、分层练习
1.下列函数属于反比例函数的有 (填序号).
⑤y=x-1; (k为常数,k≠0).
2.下列函数中反比例函数的个数有 ( )个.
①xy=2; ②y=3x; (k为常数,
A.1 B.2 C.3 D.4
3.已知函数 是反比例函数,则m 的值为 .
4.若函数 (k为常数)是反比例函数,则k的值为 ,函数解析式为 .
5.已知函数 回答下列问题.
(1)当m、n为何值时,此函数是一次函数
(2)当m、n为何值时,此函数是正比例函数
6.若一个反比例函数的图象与直线 y=2x-6的一个交点为点. 则这个反比例函数的解析式为 .
7.已知反比例函数 当1
9. 如图1-4所示, 菱形OBAC的边OB 在x 轴上, 点 A 的坐标为 (8, 4), 若反比例函数 的图象经过点 C,则这个反比例函数的解析式为 .
10.在平面直角坐标系中,若函数 (a为常数)的图象经过点 A (-2,3), B (1, 6),C (-4, m) 中的两点, 则:
11.已知函数 其中y 为x的反比例函数,y 为x的正比例函数,且 和x=1时,y的值都是1.求y关于x的函数解析式.
12. 如图1-5 所示, 已知 是边长为 的等边三角形,点E,F分别在CB 和BC 的延长线上,且 设
(1)求y关于x的函数解析式,并求出自变量x的取值范围;
(2)当x为何值时,
1. 解: 是一次函数;
是反比例函数;
是反比例函数;
可变形为 是反比例函数;
⑤y=x--1是一次函数;
可变形为y=2x,是一次函数;
(k为常数, k≠0) 是反比例函数.
2.解: ①xy=2可变形为 是反比例函数;
②y=3x是正比例函数;
是反比例函数;
(k为常数, k≠0) 是反比例函数.
故选C.
3. 解: ∵函数 是反比例函数,
且m-1≠0.
∴m=-1.
4. 解: ∵函数
(k为常数)是反比例函数,
且k-2≠0.
∴k=-2,
该函数的解析式为
5.解: (1) 当函数 y= (5m--3) 是一次函数时,有 解得n=1, m≠
(2)当函数 (m+n)是正比例函数时,
有 解得n=1, m=-1.
6.解:∵反比例函数的图象与直线y=2x--6的一个交点为点 A (m,m--2),
∴m--2=2m--6, 解得m=4.
中小学教育资源及组卷应用平台
∴点 A 的坐标为 (4, 2) .
设反比例函数的解析式为
7. 解: ∵k=6>0,
∴在每个象限内y随x 的增大而减小.
解得k=8.
又∵当x=1时, y=6;
当x=3时, y=2,
∴反比例函数的解析式为
∴当1
∵△OAB是等边三角形,
∴OA=2, ∠AOC=60°.
∴点 A 的坐标为 (1, ) .
∵点 A 在反比例函数 的图象上,
解得
∴过点 A 的反比例函数的解析式为
9. 解: 如图2所示, 过点 C作CM⊥OB 于点 M.
∵四边形OBAC是菱形, 点 A 的坐标为 (8, 4),
∴CM=4.
又
∴OM=3.
∴点 C的坐标为 (3, 4) .
∵点 C (3,4)在反比例函数 的图象上,
∴k=3×4=12.
∴反比例函数的解析式为
10. 解: ∵在函数 (a为常数)中,
∴函数图象位于第二、第四象限.
∵点A (--2, 3) 在第二象限, 点 B (1, 6) 在第一象限, 函数 y= (a为常数) 的图象经过点 A (-2, 3), B (1, 6), C (-4, m)中的两点,
∴点 C (-4, m) 在第二象限.
∴-2×3=-4m,解得
11. 解: ∵y 与x成反比例, y 与x成正比例,
∵当 和x=1时,
y的值都是1,
解得
12. 解: (1) ∵△ABC是等边三角形,∴∠BAC=60°.
∵∠EAF=120°,
∴∠EAB+∠CAF=60°.
∵∠EAB+∠E=∠ABC=60°,
∴∠E=∠CAF.
∵∠EBA=∠ACF=120°,
∴△ABE∽△FCA.
即
整理得
故 y关于x的函数解析式为
(2) ∵△ABE≌△FCA,
∴BE=CA, 即
故当 时,
△ABE≌△FCA.
