26.1.2反比例函数的图象与性质 同步练习(含答案)2024-2025学年人教版九年级数学下册
文档属性
| 名称 | 26.1.2反比例函数的图象与性质 同步练习(含答案)2024-2025学年人教版九年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 211.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 17:48:11 | ||
图片预览




文档简介
26.1.2反比例函数的图象与性质(1)
一、知识梳理
反比例函数的图象与性质如表2—1所示.
表2—1 反比例函数的图象与性质
定义 反比例函数y= kx(k为常数,k≠0)的图象由两条曲线组成,每条曲线随着x的不断增大(或减小)越来越接近坐标轴,反比例函数的图象属于双曲线
图象 当k>0时,函数图象的两支分别位于第一、第三象限,它们关于原点对称,且在每一个象限内,y随x 的增大而减小
当k<0时,函数图象的两支分别位于第二、第四象限,它们关于原点对称,且在每一个象限内,y随x的增大而增大
性质 对称性:图象关于直线y=x与直线y=-x轴对称 ;图象关于原点中心对称
【例】对于反比例函数 下列说法不正确的是 ().
A.图象位于第二、第四象限
B. 图象经过点 (1, - 120)
C.当x>0时,y随x 的增大而增大
D. 若点 A (x , y ), B (x , y ) 都在反比例函数的图象上, 当 时,则
解:k=--120<0, 则它的图象位于第二、 第四象限, 故A选项正确;当x=1时, 则点 (1,—120)在它的图象上,故B选项正确;
k=-120<0, 当x>0时, y随x的增大而增大, 故C选项正确;
k=--120<0,在第二、 第四象限内, y随x的增大而增大, 当 0故选 D.
二、分层练习
1.对于反比例函数 下列说法正确的是 ().
A. 图象经过点 (1, - 1)
B.图象位于第二、第四象限
C.图象是中心对称图形
D.当x<0时,y随x的增大而增大
2.已知函数 的图象如图2--1所示,以下结论正确的个数是 ( ).
①m<0;②在每一支上,y随x的增大而增大;③若点A (-1, a), B (2, b) 在图象上, 则aA.1个 B.2个
C.3个 D.4个
3.一次函数y=kx+k,且y随x的增大而减小,那么反比例函数 满足( ) .
A. 当x>0时, y>0
B.在每个象限内,y随x的增大而减小
C.图象位于第一、第三象限
D.图象位于第二、第四象限
4.若反比例函数 的图象位于第二、第四象限,则k 的取值可以为 ( ).
A.0 B.1
C.2 D.以上都不是
5.若反比例函数 的图象在其每个象限内均有y随x的增大而减小,则k的值可以为( ).
A. --1 B.3
C.0 D. -3
6.已知反比例函数 若x≥-2, 则y的取值范围为 ( ) .
A. y<-4 B. y>0
C.y≤-4 D.y≤-4或y>0
7.已知反比例函数 的图象位于第二、第四象限,则a 的取值范围为 ( ).
A. a<2 B. a>2 C. a≤2 D. a≥2
8.反比例函数 的图象位于第二、第四象限,则点 (m, --m+1)在第 象限.
9.图2—2所示是三个反比例函数 在x轴上方的图象,由此观察可得, k 、k 、k 的大小关系为 ( ) .
10.已知反比例函数 当--3≤x≤--1时, y的最大值是 4; 则当x≥6时, y有 ( ) .
A.最大值 B. 最大值
C.最小值 D. 最小值--1
11. 如图2-3所示, 点 M, N, P, Q, T均为坐标系中. 的正方形网格的顶点 (网格的横线都与x轴平行,纵线都与y轴平行,每个小正方形的边长为1),点N 的坐标为 (2,2),在反比例函数 的常数k的值从1逐渐增大到9的过程中,关于反比例函数l依次经过的格点顺序,下列说法正确的是 ( ).
A. 点 M→点 P→同时经过点 N, Q→点 T
B. 点 M→点 N→同时经过点 P, Q→点 T
C. 点 M→同时经过点 P, Q→点 N→点 T
D. 点 P→点 M→同时经过点 N, Q→点 T
反比例函数的图象与性质 (2)
一、知识梳理
【例1】若 ab>0, 则一次函数y= ax--b与反比例函数 在同一平面直角坐标系中的大致图象是 ().
解:A选项中,根据一次函数可判断a>0,b<0, 即 ab<0, 故错误;B选项中,根据一次函数可判断a<0,b>0, 即 ab<0, 故错误;C选项中,根据一次函数可判断a<0,b<0, 即 ab>0,根据反比例函数可判断 ab>0,故正确;
D选项中,根据反比例函数可判断 ab<0,故错误.
故选C.
【例2】在反比例函数 的图象上有两点 (x , y ), (x , y ).若解: ∵反比例函数 的图象上有两点 (x , y ), (x , y ), 且
∴该反比例函数位于第二、第四象限.
∴k+3<0,即k<-3.
二、分层练习
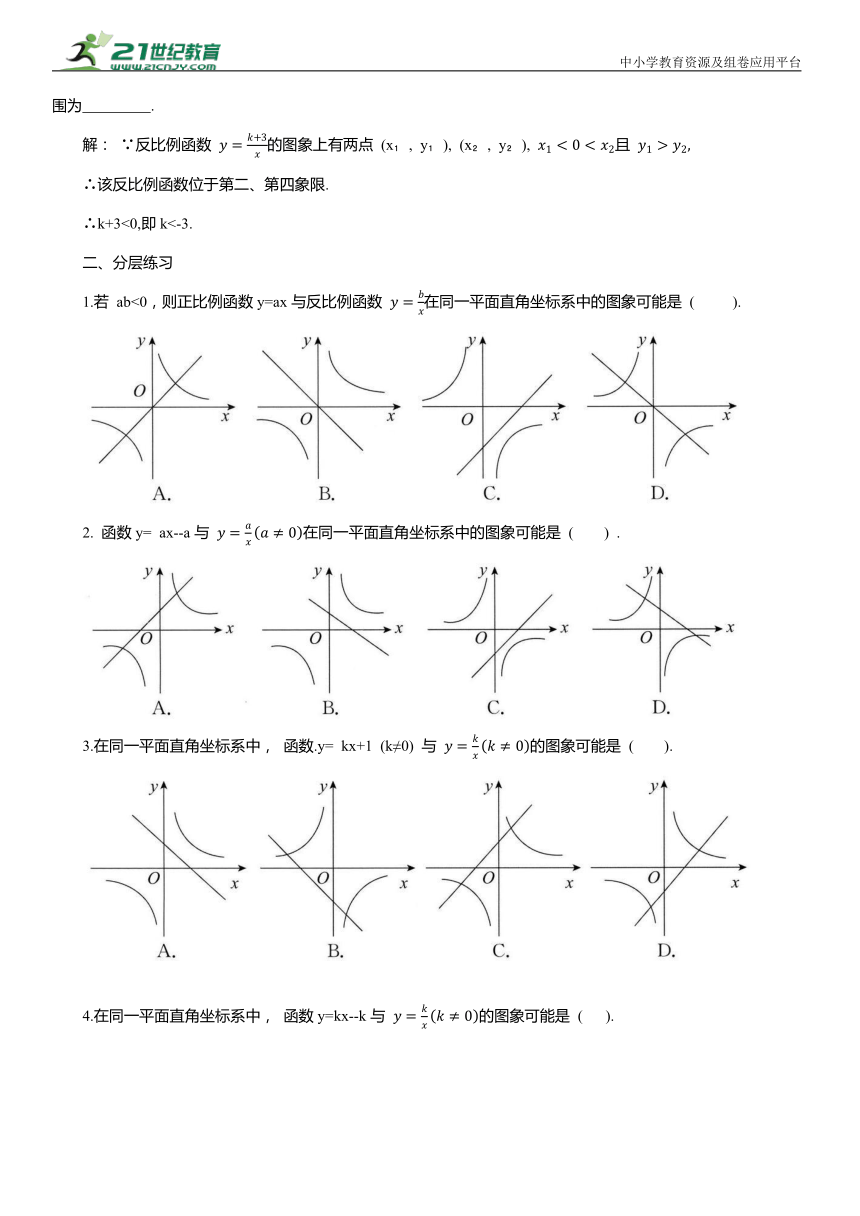
1.若 ab<0,则正比例函数y=ax与反比例函数 在同一平面直角坐标系中的图象可能是 ( ).
2. 函数y= ax--a与 在同一平面直角坐标系中的图象可能是 ( ) .
3.在同一平面直角坐标系中, 函数.y= kx+1 (k≠0) 与 的图象可能是 ( ).
4.在同一平面直角坐标系中, 函数y=kx--k与 的图象可能是 ( ).
5.在同一平面直角坐标系中,函数 与y= kx+k的图象可能是 ( ).
6.如图3--1 所示,正方形 ABOC的边长为2,反比例函数 的一支经过点A. 若点 (-1, y ), (2, y ), (4, y ) 都在该反比例函数的图象上,则 y , y , y 的大小关系为 (用“<”连接) .
7.已知点 和 都在反比例函数 的图象上,则 按从小到大的排列顺序为 .
8.已知反比例函数 的图象上两点. 当 09. 函数 (k为常数)的图象上有三点 则y , y , y 的大小关系为 (用“<”连接) .
10.关于反比例函数 的说法正确的是( ).
①若其图象位于第一、第三象限,则
②若其图象上有两点. 当 时, y , 则p>1;
③其图象与坐标轴没有公共点.
A.① B.①② C.①②③ D.②③
中小学教育资源及组卷应用平台
26.1.2反比例函数的图象与性质 (1)
1. 解: 1× (--1) =--1≠1, 点 (1,—1)不在反比例函数 的图象上,故A 选项错误;
k=1>0, 反比例函数 的图象在第一、 第三象 限, 故B 选项错误;
函数 是反比例函数,此函数的图象是中心对称图形,故C 选项正确;
k=1>0,此函数的图象在每一个象限内,y随x 的增大而减小,故D选项错误.
故选 C.
2.解:①反比例函数图象的两支分别位于第一、 第三象限, 则m>0,故错误;
②由图象可知,在每一支上,y随x 的增大而减小,故错误;
③若点 A (--1, a), B (2, b) 在图象上, 由图象可知a<0, b>0,则a④反比例函数的图象关于原点中心对称,若点 P (x,y)在图象上,则点 P (--x, - y) 也在图象上,正确.
故选 B.
3. 解: ∵一次函数 y= kx+k, 且 y随x的增大而减小,
∴k<0.
∴反比例函数 的图象位于第
二、第四象限.
故选 D.
欲穷千里目,更上一层楼
4.解: ∵反比例函数 的图象位于第二、第四象限,∴k--1<0, 即k<1.
故选 A.
5.解: ∵反比例函数 的图象在其每个象限内均有y 随x 的增大而减小,
∴k--1>0, 即 k>1.
故选 B.
6. 解: 当-2≤x<0时, y≤-4;
当x>0时, y>0.
故选 D.
7.解: ∵反比例函数 的图象位于第二、第四象限,∴a--2<0, 即a<2.
故选 A.
8.解: ∵反比例函数 的图象位于第二、第四象限,
∴m<0.
∴-m+1>1, 故点 (m, - m+1)在第二象限.
9.解:反比例函数 的图象在第二象限, 故k <0;
反比例函数 的图象在第一象限,且 的图象距原点较远,故
综上可得,
故选 C.
10.解: ∵反比例函数 当--3≤x≤--1时, y的最大值是4,
∴k<0,在每一个象限内,y随x增大而增大.
∵当x= 1时, y取最大值4,则k=--1×4=-4.
∴当x=6时,
∴当x≥6时,
故 y有最小值
故选 C.
11.解:∵根据题意可知,各点坐标分别为点 N (2, 2), M (1, 2),Q (1, 3), T (2, 3), P (3, 1),∴KN=2×2=4, KM=1×2=2,
∴常数k的值从1逐渐增大到9的过程中,反比例函数l依次经过的格点顺序为点 M→同时经过点 P,Q→点 N→点 T.
故选 C.
反比例函数的图象与性质 (2)
1. 解: ab<0, 故分两种情况.
当a>0, b<0时, 正比例函数的图象过原点和第一、第三象限,反比例函数的图象在第二、第四象限,无此选项;
◆当a<0, b>0时, 正比例函数的图象过原点和第二、第四象限,反比例函数的图象在第一、第三象限,B选项符合.
故选 B.
2.解:A选项中,从反比例函数的图象得a>0,则对应的一次函数y=ax-a的图象经过第一、 第三、第四象限,故错误;
B选项中,从反比例函数的图象得a>0, 则对应的一次函数y= ax-a的图象经过第一、第三、第四象限,故错误;
C选项中,从反比例函数的图象得a<0, 则对应的一次函数y= ax-a的图象经过第一、第二、第四象限,故错误;
D选项中,从反比例函数的图象得a<0, 则对应的一次函数y= ax-a的图象经过第一、第二、第四象限,故正确.
故选 D.
3.解: 分两种情况.
◆当k>0时, y= kx+1的图象经过第一、第二、第三象限; 的图象经过第一、第三象限;
◆当k<0时, y= kx+1的图象经过第一、第二、第四象象限; y=kx的图象经过第二、第四象限.
故选 C.
4.解:分两种情况.
◆当k>0时, y= kx-k的图象经过第一、第三、第四象限.
的图象经过第一、第三象限.
◆当k<0时, y= kx-k的图象经过第一、第二、第四象限,
的图象经过第二、第四象限.
故选 B.
5.解:分两种情况.
◆当k>0时, y= kx+k的图象经过第一、第二、第三象限, 的图象经过第一、第三象限.
◆当k<0时, y= kx+k的图象经过第二、第三、第四象限,
的图象经过第二、第四象限.
故选 D.
6.解: 由图象可知,点A 的坐标为(--2, 2) .
∵反比例函数 的一支经过点A,
∴k=-2×2=-4.
∴反比例函数的解析式为
∴当x=-1时, 当x=2时, 当x=4时,
7. 解: ∵点 A (-2, y ), B (--1,y ) 和 C (3, y ) 都在反比例函数 的图象上,
解: ∵反比例函数 的图象上有两 点 A (x , y ), B (x ,y ), 当 时,有 ∴1-m>0, 解得 m<1.
9. 解:
∴该函数的图象位于第二、第四象限.
∵点 (--2, y ), (-1, y ) 位于第二象限, 且--2<--1,
又∵点 位于第四象限,
会当凌绝顶,一览众山小
10.解: ∵反比例函数
∴若其图象位于第一、第三象限,则1--p>0, 即p<1, 故①正确.
∵其图象上有两点 M (x , y ),N (x , y ),当 时,
∴图象位于第二、第四象限,1—p<0, 即 p>1, 故②正确.
反比例函数的图象与坐标轴没有公共点,故③正确.
故选C.
一、知识梳理
反比例函数的图象与性质如表2—1所示.
表2—1 反比例函数的图象与性质
定义 反比例函数y= kx(k为常数,k≠0)的图象由两条曲线组成,每条曲线随着x的不断增大(或减小)越来越接近坐标轴,反比例函数的图象属于双曲线
图象 当k>0时,函数图象的两支分别位于第一、第三象限,它们关于原点对称,且在每一个象限内,y随x 的增大而减小
当k<0时,函数图象的两支分别位于第二、第四象限,它们关于原点对称,且在每一个象限内,y随x的增大而增大
性质 对称性:图象关于直线y=x与直线y=-x轴对称 ;图象关于原点中心对称
【例】对于反比例函数 下列说法不正确的是 ().
A.图象位于第二、第四象限
B. 图象经过点 (1, - 120)
C.当x>0时,y随x 的增大而增大
D. 若点 A (x , y ), B (x , y ) 都在反比例函数的图象上, 当 时,则
解:k=--120<0, 则它的图象位于第二、 第四象限, 故A选项正确;当x=1时, 则点 (1,—120)在它的图象上,故B选项正确;
k=-120<0, 当x>0时, y随x的增大而增大, 故C选项正确;
k=--120<0,在第二、 第四象限内, y随x的增大而增大, 当 0
二、分层练习
1.对于反比例函数 下列说法正确的是 ().
A. 图象经过点 (1, - 1)
B.图象位于第二、第四象限
C.图象是中心对称图形
D.当x<0时,y随x的增大而增大
2.已知函数 的图象如图2--1所示,以下结论正确的个数是 ( ).
①m<0;②在每一支上,y随x的增大而增大;③若点A (-1, a), B (2, b) 在图象上, 则a
C.3个 D.4个
3.一次函数y=kx+k,且y随x的增大而减小,那么反比例函数 满足( ) .
A. 当x>0时, y>0
B.在每个象限内,y随x的增大而减小
C.图象位于第一、第三象限
D.图象位于第二、第四象限
4.若反比例函数 的图象位于第二、第四象限,则k 的取值可以为 ( ).
A.0 B.1
C.2 D.以上都不是
5.若反比例函数 的图象在其每个象限内均有y随x的增大而减小,则k的值可以为( ).
A. --1 B.3
C.0 D. -3
6.已知反比例函数 若x≥-2, 则y的取值范围为 ( ) .
A. y<-4 B. y>0
C.y≤-4 D.y≤-4或y>0
7.已知反比例函数 的图象位于第二、第四象限,则a 的取值范围为 ( ).
A. a<2 B. a>2 C. a≤2 D. a≥2
8.反比例函数 的图象位于第二、第四象限,则点 (m, --m+1)在第 象限.
9.图2—2所示是三个反比例函数 在x轴上方的图象,由此观察可得, k 、k 、k 的大小关系为 ( ) .
10.已知反比例函数 当--3≤x≤--1时, y的最大值是 4; 则当x≥6时, y有 ( ) .
A.最大值 B. 最大值
C.最小值 D. 最小值--1
11. 如图2-3所示, 点 M, N, P, Q, T均为坐标系中. 的正方形网格的顶点 (网格的横线都与x轴平行,纵线都与y轴平行,每个小正方形的边长为1),点N 的坐标为 (2,2),在反比例函数 的常数k的值从1逐渐增大到9的过程中,关于反比例函数l依次经过的格点顺序,下列说法正确的是 ( ).
A. 点 M→点 P→同时经过点 N, Q→点 T
B. 点 M→点 N→同时经过点 P, Q→点 T
C. 点 M→同时经过点 P, Q→点 N→点 T
D. 点 P→点 M→同时经过点 N, Q→点 T
反比例函数的图象与性质 (2)
一、知识梳理
【例1】若 ab>0, 则一次函数y= ax--b与反比例函数 在同一平面直角坐标系中的大致图象是 ().
解:A选项中,根据一次函数可判断a>0,b<0, 即 ab<0, 故错误;B选项中,根据一次函数可判断a<0,b>0, 即 ab<0, 故错误;C选项中,根据一次函数可判断a<0,b<0, 即 ab>0,根据反比例函数可判断 ab>0,故正确;
D选项中,根据反比例函数可判断 ab<0,故错误.
故选C.
【例2】在反比例函数 的图象上有两点 (x , y ), (x , y ).若
∴该反比例函数位于第二、第四象限.
∴k+3<0,即k<-3.
二、分层练习
1.若 ab<0,则正比例函数y=ax与反比例函数 在同一平面直角坐标系中的图象可能是 ( ).
2. 函数y= ax--a与 在同一平面直角坐标系中的图象可能是 ( ) .
3.在同一平面直角坐标系中, 函数.y= kx+1 (k≠0) 与 的图象可能是 ( ).
4.在同一平面直角坐标系中, 函数y=kx--k与 的图象可能是 ( ).
5.在同一平面直角坐标系中,函数 与y= kx+k的图象可能是 ( ).
6.如图3--1 所示,正方形 ABOC的边长为2,反比例函数 的一支经过点A. 若点 (-1, y ), (2, y ), (4, y ) 都在该反比例函数的图象上,则 y , y , y 的大小关系为 (用“<”连接) .
7.已知点 和 都在反比例函数 的图象上,则 按从小到大的排列顺序为 .
8.已知反比例函数 的图象上两点. 当 0
10.关于反比例函数 的说法正确的是( ).
①若其图象位于第一、第三象限,则
②若其图象上有两点. 当 时, y , 则p>1;
③其图象与坐标轴没有公共点.
A.① B.①② C.①②③ D.②③
中小学教育资源及组卷应用平台
26.1.2反比例函数的图象与性质 (1)
1. 解: 1× (--1) =--1≠1, 点 (1,—1)不在反比例函数 的图象上,故A 选项错误;
k=1>0, 反比例函数 的图象在第一、 第三象 限, 故B 选项错误;
函数 是反比例函数,此函数的图象是中心对称图形,故C 选项正确;
k=1>0,此函数的图象在每一个象限内,y随x 的增大而减小,故D选项错误.
故选 C.
2.解:①反比例函数图象的两支分别位于第一、 第三象限, 则m>0,故错误;
②由图象可知,在每一支上,y随x 的增大而减小,故错误;
③若点 A (--1, a), B (2, b) 在图象上, 由图象可知a<0, b>0,则a
故选 B.
3. 解: ∵一次函数 y= kx+k, 且 y随x的增大而减小,
∴k<0.
∴反比例函数 的图象位于第
二、第四象限.
故选 D.
欲穷千里目,更上一层楼
4.解: ∵反比例函数 的图象位于第二、第四象限,∴k--1<0, 即k<1.
故选 A.
5.解: ∵反比例函数 的图象在其每个象限内均有y 随x 的增大而减小,
∴k--1>0, 即 k>1.
故选 B.
6. 解: 当-2≤x<0时, y≤-4;
当x>0时, y>0.
故选 D.
7.解: ∵反比例函数 的图象位于第二、第四象限,∴a--2<0, 即a<2.
故选 A.
8.解: ∵反比例函数 的图象位于第二、第四象限,
∴m<0.
∴-m+1>1, 故点 (m, - m+1)在第二象限.
9.解:反比例函数 的图象在第二象限, 故k <0;
反比例函数 的图象在第一象限,且 的图象距原点较远,故
综上可得,
故选 C.
10.解: ∵反比例函数 当--3≤x≤--1时, y的最大值是4,
∴k<0,在每一个象限内,y随x增大而增大.
∵当x= 1时, y取最大值4,则k=--1×4=-4.
∴当x=6时,
∴当x≥6时,
故 y有最小值
故选 C.
11.解:∵根据题意可知,各点坐标分别为点 N (2, 2), M (1, 2),Q (1, 3), T (2, 3), P (3, 1),∴KN=2×2=4, KM=1×2=2,
∴常数k的值从1逐渐增大到9的过程中,反比例函数l依次经过的格点顺序为点 M→同时经过点 P,Q→点 N→点 T.
故选 C.
反比例函数的图象与性质 (2)
1. 解: ab<0, 故分两种情况.
当a>0, b<0时, 正比例函数的图象过原点和第一、第三象限,反比例函数的图象在第二、第四象限,无此选项;
◆当a<0, b>0时, 正比例函数的图象过原点和第二、第四象限,反比例函数的图象在第一、第三象限,B选项符合.
故选 B.
2.解:A选项中,从反比例函数的图象得a>0,则对应的一次函数y=ax-a的图象经过第一、 第三、第四象限,故错误;
B选项中,从反比例函数的图象得a>0, 则对应的一次函数y= ax-a的图象经过第一、第三、第四象限,故错误;
C选项中,从反比例函数的图象得a<0, 则对应的一次函数y= ax-a的图象经过第一、第二、第四象限,故错误;
D选项中,从反比例函数的图象得a<0, 则对应的一次函数y= ax-a的图象经过第一、第二、第四象限,故正确.
故选 D.
3.解: 分两种情况.
◆当k>0时, y= kx+1的图象经过第一、第二、第三象限; 的图象经过第一、第三象限;
◆当k<0时, y= kx+1的图象经过第一、第二、第四象象限; y=kx的图象经过第二、第四象限.
故选 C.
4.解:分两种情况.
◆当k>0时, y= kx-k的图象经过第一、第三、第四象限.
的图象经过第一、第三象限.
◆当k<0时, y= kx-k的图象经过第一、第二、第四象限,
的图象经过第二、第四象限.
故选 B.
5.解:分两种情况.
◆当k>0时, y= kx+k的图象经过第一、第二、第三象限, 的图象经过第一、第三象限.
◆当k<0时, y= kx+k的图象经过第二、第三、第四象限,
的图象经过第二、第四象限.
故选 D.
6.解: 由图象可知,点A 的坐标为(--2, 2) .
∵反比例函数 的一支经过点A,
∴k=-2×2=-4.
∴反比例函数的解析式为
∴当x=-1时, 当x=2时, 当x=4时,
7. 解: ∵点 A (-2, y ), B (--1,y ) 和 C (3, y ) 都在反比例函数 的图象上,
解: ∵反比例函数 的图象上有两 点 A (x , y ), B (x ,y ), 当 时,有 ∴1-m>0, 解得 m<1.
9. 解:
∴该函数的图象位于第二、第四象限.
∵点 (--2, y ), (-1, y ) 位于第二象限, 且--2<--1,
又∵点 位于第四象限,
会当凌绝顶,一览众山小
10.解: ∵反比例函数
∴若其图象位于第一、第三象限,则1--p>0, 即p<1, 故①正确.
∵其图象上有两点 M (x , y ),N (x , y ),当 时,
∴图象位于第二、第四象限,1—p<0, 即 p>1, 故②正确.
反比例函数的图象与坐标轴没有公共点,故③正确.
故选C.
