26.2 实际问题与反比例函数 同步练习(含答案)2024-2025学年人教版九年级数学下册
文档属性
| 名称 | 26.2 实际问题与反比例函数 同步练习(含答案)2024-2025学年人教版九年级数学下册 | 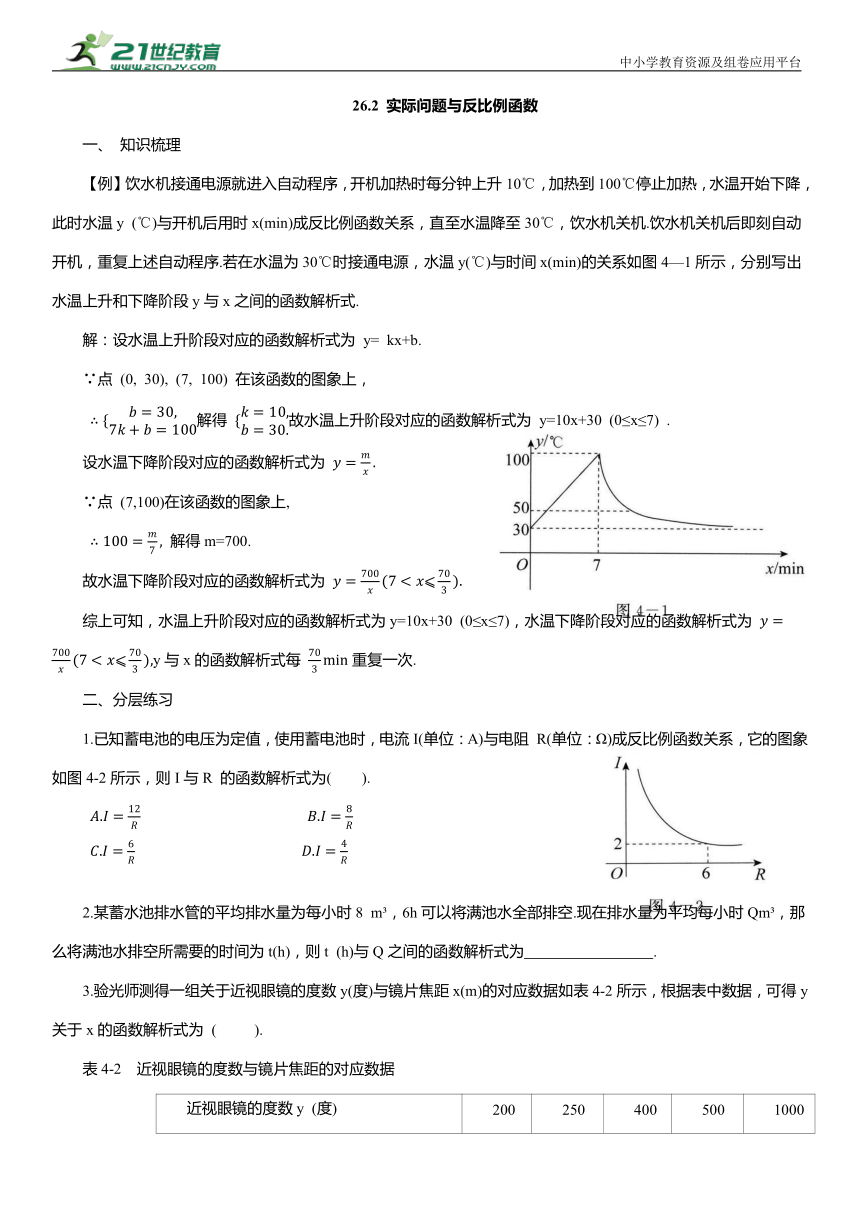 | |
| 格式 | docx | ||
| 文件大小 | 126.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 17:54:20 | ||
图片预览

文档简介
26.2 实际问题与反比例函数
一、 知识梳理
【例】饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃停止加热,水温开始下降,此时水温y (℃)与开机后用时x(min)成反比例函数关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温y(℃)与时间x(min)的关系如图4—1所示,分别写出水温上升和下降阶段y与x之间的函数解析式.
解:设水温上升阶段对应的函数解析式为 y= kx+b.
∵点 (0, 30), (7, 100) 在该函数的图象上,
解得 故水温上升阶段对应的函数解析式为 y=10x+30 (0≤x≤7) .
设水温下降阶段对应的函数解析式为
∵点 (7,100)在该函数的图象上,
解得m=700.
故水温下降阶段对应的函数解析式为
综上可知,水温上升阶段对应的函数解析式为y=10x+30 (0≤x≤7),水温下降阶段对应的函数解析式为 y与x的函数解析式每 重复一次.
二、分层练习
1.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻 R(单位:Ω)成反比例函数关系,它的图象如图4-2所示,则I与R 的函数解析式为( ).
2.某蓄水池排水管的平均排水量为每小时8 m ,6h可以将满池水全部排空.现在排水量为平均每小时Qm ,那么将满池水排空所需要的时间为t(h),则t (h)与Q之间的函数解析式为 .
3.验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(m)的对应数据如表4-2所示,根据表中数据,可得y关于x的函数解析式为 ( ).
表4-2 近视眼镜的度数与镜片焦距的对应数据
近视眼镜的度数y (度) 200 250 400 500 1000
镜片焦距x (m) 0.50 0.40 0.25 0.20 0.10
4.一辆汽车匀速通过某段公路所需时间t(h)与行驶速度v (km/h)满足函数关系 其图象为如图4—3所示的一段曲线,且端点为A (40, 1) 和 B (m, 0.5) . 若行驶速度不得超过60 km/h,则汽车通过该路段最少需要的时间为 ( ).
B.40 min C.60 min
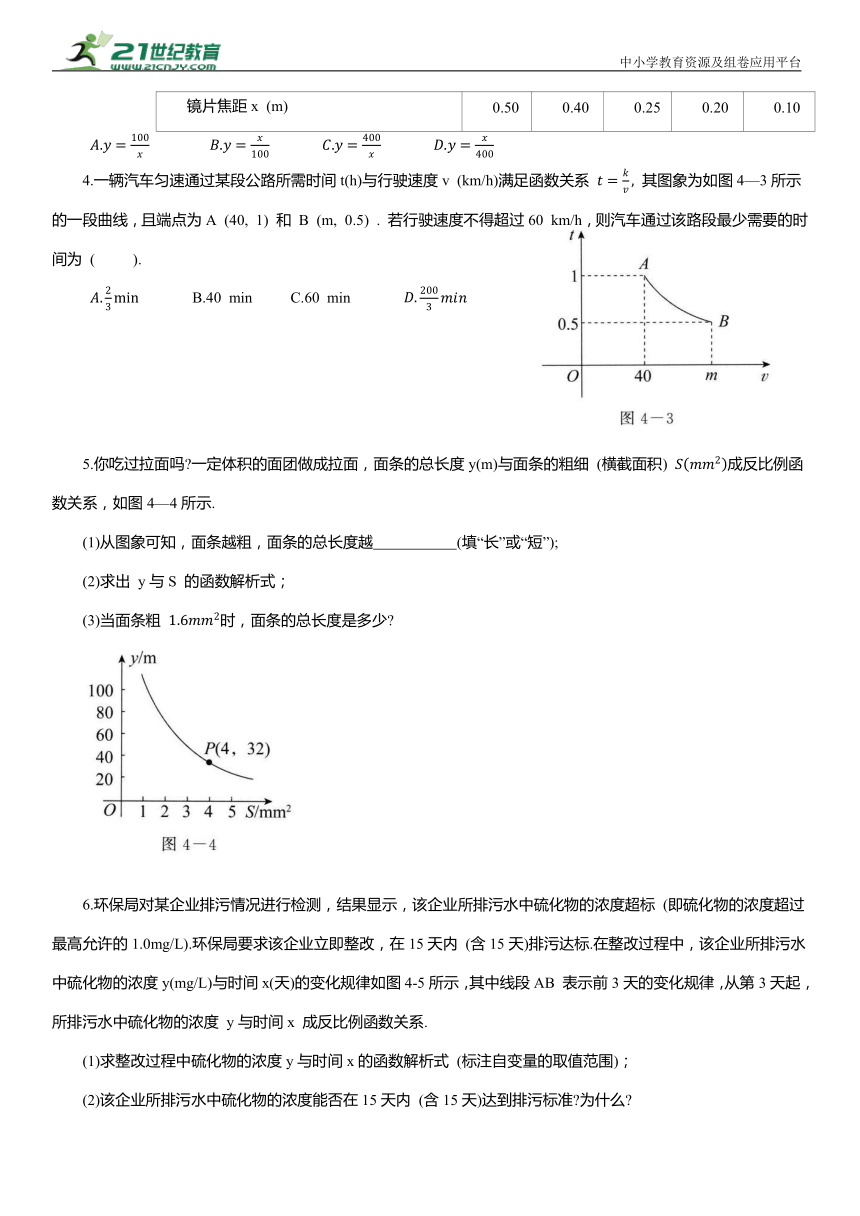
5.你吃过拉面吗 一定体积的面团做成拉面,面条的总长度y(m)与面条的粗细 (横截面积) 成反比例函数关系,如图4—4所示.
(1)从图象可知,面条越粗,面条的总长度越 (填“长”或“短”);
(2)求出 y与S 的函数解析式;
(3)当面条粗 时,面条的总长度是多少
6.环保局对某企业排污情况进行检测,结果显示,该企业所排污水中硫化物的浓度超标 (即硫化物的浓度超过最高允许的1.0mg/L).环保局要求该企业立即整改,在15天内 (含15天)排污达标.在整改过程中,该企业所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图4-5所示,其中线段AB 表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度 y与时间x 成反比例函数关系.
(1)求整改过程中硫化物的浓度y与时间x的函数解析式 (标注自变量的取值范围);
(2)该企业所排污水中硫化物的浓度能否在15天内 (含15天)达到排污标准 为什么
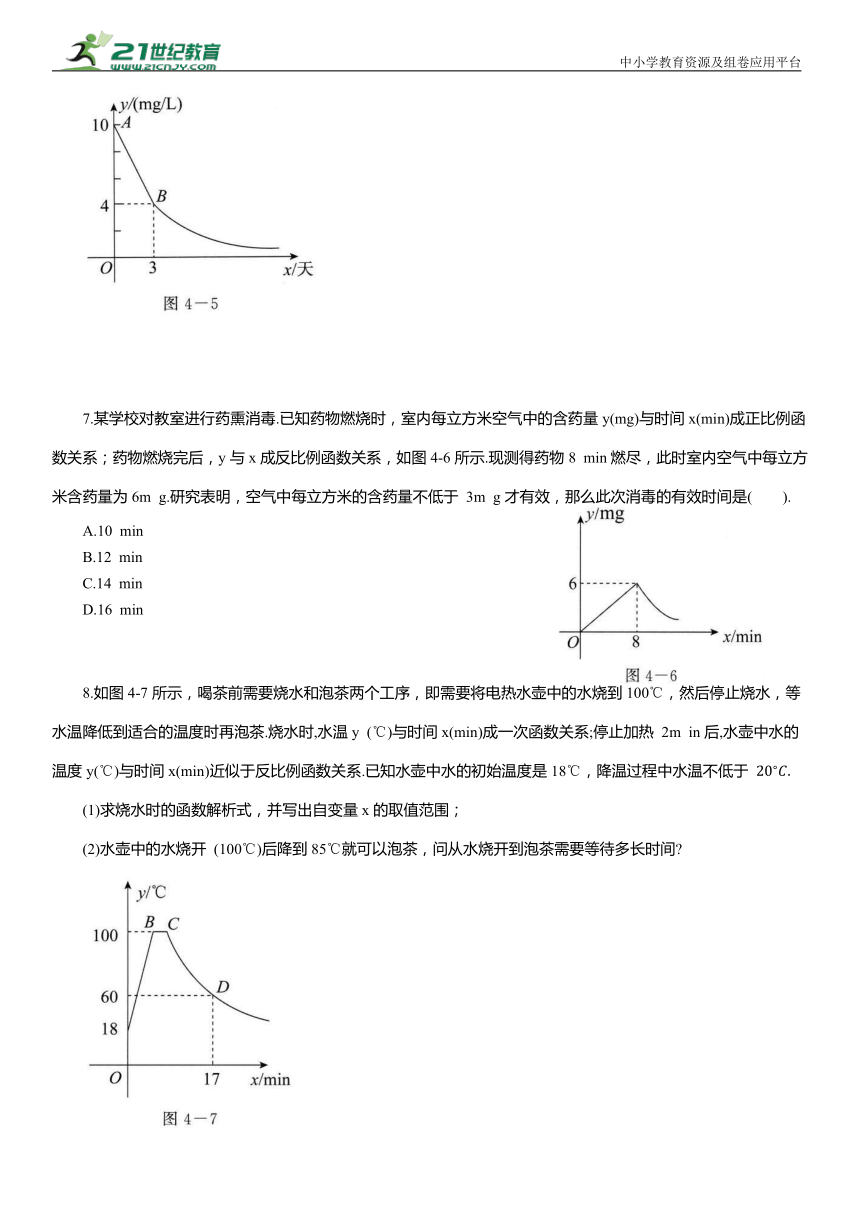
7.某学校对教室进行药熏消毒.已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例函数关系;药物燃烧完后,y与x成反比例函数关系,如图4-6所示.现测得药物8 min燃尽,此时室内空气中每立方米含药量为6m g.研究表明,空气中每立方米的含药量不低于 3m g才有效,那么此次消毒的有效时间是( ).
A.10 min
B.12 min
C.14 min
D.16 min
8.如图4-7所示,喝茶前需要烧水和泡茶两个工序,即需要将电热水壶中的水烧到100℃,然后停止烧水,等水温降低到适合的温度时再泡茶.烧水时,水温y (℃)与时间x(min)成一次函数关系;停止加热 2m in后,水壶中水的温度y(℃)与时间x(min)近似于反比例函数关系.已知水壶中水的初始温度是18℃,降温过程中水温不低于
(1)求烧水时的函数解析式,并写出自变量x的取值范围;
(2)水壶中的水烧开 (100℃)后降到85℃就可以泡茶,问从水烧开到泡茶需要等待多长时间
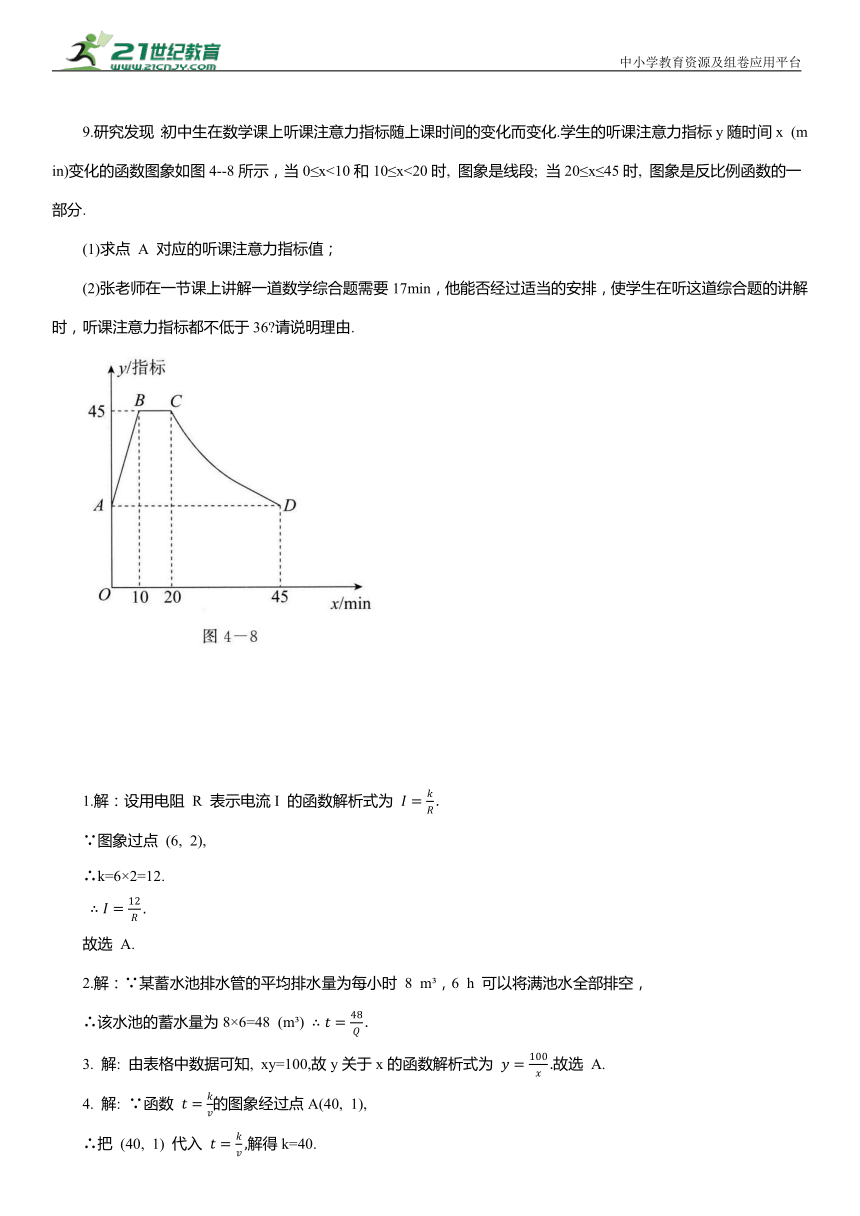
9.研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化.学生的听课注意力指标y随时间x (min)变化的函数图象如图4--8所示,当0≤x<10和10≤x<20时, 图象是线段; 当20≤x≤45时, 图象是反比例函数的一部分.
(1)求点 A 对应的听课注意力指标值;
(2)张老师在一节课上讲解一道数学综合题需要17min,他能否经过适当的安排,使学生在听这道综合题的讲解时,听课注意力指标都不低于36 请说明理由.
1.解:设用电阻 R 表示电流I 的函数解析式为
∵图象过点 (6, 2),
∴k=6×2=12.
故选 A.
2.解:∵某蓄水池排水管的平均排水量为每小时 8 m ,6 h 可以将满池水全部排空,
∴该水池的蓄水量为8×6=48 (m )
3. 解: 由表格中数据可知, xy=100,故y关于x的函数解析式为 故选 A.
4. 解: ∵函数 的图象经过点A(40, 1),
∴把 (40, 1) 代入 解得k=40.
∴函数解析式为
∵函数 的图象经过点 B (m,0.5),
∴把 (m, 0.5) 代入 解得m=80.
∴当v=60时, 代入 解得
则汽车通过该路段最少需要
中小学教育资源及组卷应用平台
故选 B.
5.解:(1)∵由图象可知,面条的总长度和面条的横截面积成反比,∴面条越粗,面条的总长度越短.
(2)根据图象设 y与S 的函数解析式为
∵反比例函数的图象经过点 (4,32),
解得k=128.
∴y与S的函数解析式为
(3) 当、 时,
故当面条粗1.6 mm 时,面条的总长度是 80 m.
6.解: (1)分两种情况讨论.
◆当0≤x≤3时, 设线段AB 对应的函数解析式为y= kx+b.
∵点 A (0, 10), B (3, 4) 在函数y= kx+b的图象上,
解得
∴y=-2x+10.
◆当x>3时,设其函数解析式为
∵点 (3, 4) 在函数 的图象上,
∴m=3×4=12.
综上所述,y与x的函数解析式为
(2)能,理由如下.
∵令 y=1, 则 解得x=12<15,
∴该企业能在15天内达到排污标准.
7.解:(1)设药物燃烧时y关于x的函数解析式为
∵点 (8, 6) 在函数. 的图象上,
∴6=8k ,解得
设药物燃烧后y关于x的函数解析式为
∵点 (8, 6) 在函数 的图象上,
解得
∴y关于x的函数解析式为
∵把y=3代入 解得x=4; 把y=3代入 解得x=16,16-4=12,
∴此次消毒的有效时间是 12 min.
故选 B.
8.解:(1)设停止加热2m in后,y与x的函数解析式为
∵点 D (17, 60) 在函数 的图象上,
解得k=1020.
∴y与x的函数解析式为
∵当y=100时, 有 解得x=10.2,
∴点 C的坐标为 (10.2, 100) .
∴点 B 的坐标为 (8.2, 100) .
设烧水时y与x的函数解析式为y=ax+18.
∵由题意得, 100=8.2a+18, 解得a=10,
∴烧水时y与x的函数解析式为y=10x+18 (0≤x≤8.2) .
(2) ∵当y=85时, 有 解得x=12,
∴从水烧开到泡茶需要等待的时间为12-8.2=3.8 (min) .
会当凌绝顶,一览众山小
9.解:(1)设当20≤x≤45时,反比例函数的解析式为
∵点C (20, 45) 在函数 的图象上,
解得k=900.
∴反比例函数的解析式为
∴当x=45时, 有
∴点 D 的坐标为 (45, 20) .
∴点 A 对应的听课注意力指标值为20.
(2) 设当0≤x<10时, AB段的函数解析式为y= mx+n.
∵点A (0, 20), B (10, 45) 在函数y= mx+n的图象上,
解得
∴AB段的函数解析式为
∵当 y≥36时,代入一次函数,得 解得
当 y≥36时,代入反比例函数,得 解得x≤25,
时,听课注意力指标都不低于 36.
∴张老师能经过适当的安排,使学生在听这道综合题的讲解时,听课注意力指标都不低于 36.
一、 知识梳理
【例】饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃停止加热,水温开始下降,此时水温y (℃)与开机后用时x(min)成反比例函数关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温y(℃)与时间x(min)的关系如图4—1所示,分别写出水温上升和下降阶段y与x之间的函数解析式.
解:设水温上升阶段对应的函数解析式为 y= kx+b.
∵点 (0, 30), (7, 100) 在该函数的图象上,
解得 故水温上升阶段对应的函数解析式为 y=10x+30 (0≤x≤7) .
设水温下降阶段对应的函数解析式为
∵点 (7,100)在该函数的图象上,
解得m=700.
故水温下降阶段对应的函数解析式为
综上可知,水温上升阶段对应的函数解析式为y=10x+30 (0≤x≤7),水温下降阶段对应的函数解析式为 y与x的函数解析式每 重复一次.
二、分层练习
1.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻 R(单位:Ω)成反比例函数关系,它的图象如图4-2所示,则I与R 的函数解析式为( ).
2.某蓄水池排水管的平均排水量为每小时8 m ,6h可以将满池水全部排空.现在排水量为平均每小时Qm ,那么将满池水排空所需要的时间为t(h),则t (h)与Q之间的函数解析式为 .
3.验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(m)的对应数据如表4-2所示,根据表中数据,可得y关于x的函数解析式为 ( ).
表4-2 近视眼镜的度数与镜片焦距的对应数据
近视眼镜的度数y (度) 200 250 400 500 1000
镜片焦距x (m) 0.50 0.40 0.25 0.20 0.10
4.一辆汽车匀速通过某段公路所需时间t(h)与行驶速度v (km/h)满足函数关系 其图象为如图4—3所示的一段曲线,且端点为A (40, 1) 和 B (m, 0.5) . 若行驶速度不得超过60 km/h,则汽车通过该路段最少需要的时间为 ( ).
B.40 min C.60 min
5.你吃过拉面吗 一定体积的面团做成拉面,面条的总长度y(m)与面条的粗细 (横截面积) 成反比例函数关系,如图4—4所示.
(1)从图象可知,面条越粗,面条的总长度越 (填“长”或“短”);
(2)求出 y与S 的函数解析式;
(3)当面条粗 时,面条的总长度是多少
6.环保局对某企业排污情况进行检测,结果显示,该企业所排污水中硫化物的浓度超标 (即硫化物的浓度超过最高允许的1.0mg/L).环保局要求该企业立即整改,在15天内 (含15天)排污达标.在整改过程中,该企业所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图4-5所示,其中线段AB 表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度 y与时间x 成反比例函数关系.
(1)求整改过程中硫化物的浓度y与时间x的函数解析式 (标注自变量的取值范围);
(2)该企业所排污水中硫化物的浓度能否在15天内 (含15天)达到排污标准 为什么
7.某学校对教室进行药熏消毒.已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例函数关系;药物燃烧完后,y与x成反比例函数关系,如图4-6所示.现测得药物8 min燃尽,此时室内空气中每立方米含药量为6m g.研究表明,空气中每立方米的含药量不低于 3m g才有效,那么此次消毒的有效时间是( ).
A.10 min
B.12 min
C.14 min
D.16 min
8.如图4-7所示,喝茶前需要烧水和泡茶两个工序,即需要将电热水壶中的水烧到100℃,然后停止烧水,等水温降低到适合的温度时再泡茶.烧水时,水温y (℃)与时间x(min)成一次函数关系;停止加热 2m in后,水壶中水的温度y(℃)与时间x(min)近似于反比例函数关系.已知水壶中水的初始温度是18℃,降温过程中水温不低于
(1)求烧水时的函数解析式,并写出自变量x的取值范围;
(2)水壶中的水烧开 (100℃)后降到85℃就可以泡茶,问从水烧开到泡茶需要等待多长时间
9.研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化.学生的听课注意力指标y随时间x (min)变化的函数图象如图4--8所示,当0≤x<10和10≤x<20时, 图象是线段; 当20≤x≤45时, 图象是反比例函数的一部分.
(1)求点 A 对应的听课注意力指标值;
(2)张老师在一节课上讲解一道数学综合题需要17min,他能否经过适当的安排,使学生在听这道综合题的讲解时,听课注意力指标都不低于36 请说明理由.
1.解:设用电阻 R 表示电流I 的函数解析式为
∵图象过点 (6, 2),
∴k=6×2=12.
故选 A.
2.解:∵某蓄水池排水管的平均排水量为每小时 8 m ,6 h 可以将满池水全部排空,
∴该水池的蓄水量为8×6=48 (m )
3. 解: 由表格中数据可知, xy=100,故y关于x的函数解析式为 故选 A.
4. 解: ∵函数 的图象经过点A(40, 1),
∴把 (40, 1) 代入 解得k=40.
∴函数解析式为
∵函数 的图象经过点 B (m,0.5),
∴把 (m, 0.5) 代入 解得m=80.
∴当v=60时, 代入 解得
则汽车通过该路段最少需要
中小学教育资源及组卷应用平台
故选 B.
5.解:(1)∵由图象可知,面条的总长度和面条的横截面积成反比,∴面条越粗,面条的总长度越短.
(2)根据图象设 y与S 的函数解析式为
∵反比例函数的图象经过点 (4,32),
解得k=128.
∴y与S的函数解析式为
(3) 当、 时,
故当面条粗1.6 mm 时,面条的总长度是 80 m.
6.解: (1)分两种情况讨论.
◆当0≤x≤3时, 设线段AB 对应的函数解析式为y= kx+b.
∵点 A (0, 10), B (3, 4) 在函数y= kx+b的图象上,
解得
∴y=-2x+10.
◆当x>3时,设其函数解析式为
∵点 (3, 4) 在函数 的图象上,
∴m=3×4=12.
综上所述,y与x的函数解析式为
(2)能,理由如下.
∵令 y=1, 则 解得x=12<15,
∴该企业能在15天内达到排污标准.
7.解:(1)设药物燃烧时y关于x的函数解析式为
∵点 (8, 6) 在函数. 的图象上,
∴6=8k ,解得
设药物燃烧后y关于x的函数解析式为
∵点 (8, 6) 在函数 的图象上,
解得
∴y关于x的函数解析式为
∵把y=3代入 解得x=4; 把y=3代入 解得x=16,16-4=12,
∴此次消毒的有效时间是 12 min.
故选 B.
8.解:(1)设停止加热2m in后,y与x的函数解析式为
∵点 D (17, 60) 在函数 的图象上,
解得k=1020.
∴y与x的函数解析式为
∵当y=100时, 有 解得x=10.2,
∴点 C的坐标为 (10.2, 100) .
∴点 B 的坐标为 (8.2, 100) .
设烧水时y与x的函数解析式为y=ax+18.
∵由题意得, 100=8.2a+18, 解得a=10,
∴烧水时y与x的函数解析式为y=10x+18 (0≤x≤8.2) .
(2) ∵当y=85时, 有 解得x=12,
∴从水烧开到泡茶需要等待的时间为12-8.2=3.8 (min) .
会当凌绝顶,一览众山小
9.解:(1)设当20≤x≤45时,反比例函数的解析式为
∵点C (20, 45) 在函数 的图象上,
解得k=900.
∴反比例函数的解析式为
∴当x=45时, 有
∴点 D 的坐标为 (45, 20) .
∴点 A 对应的听课注意力指标值为20.
(2) 设当0≤x<10时, AB段的函数解析式为y= mx+n.
∵点A (0, 20), B (10, 45) 在函数y= mx+n的图象上,
解得
∴AB段的函数解析式为
∵当 y≥36时,代入一次函数,得 解得
当 y≥36时,代入反比例函数,得 解得x≤25,
时,听课注意力指标都不低于 36.
∴张老师能经过适当的安排,使学生在听这道综合题的讲解时,听课注意力指标都不低于 36.
