反比例函数系数k的几何意义 同步练习(含答案)2024-2025学年人教版九年级数学下册
文档属性
| 名称 | 反比例函数系数k的几何意义 同步练习(含答案)2024-2025学年人教版九年级数学下册 | 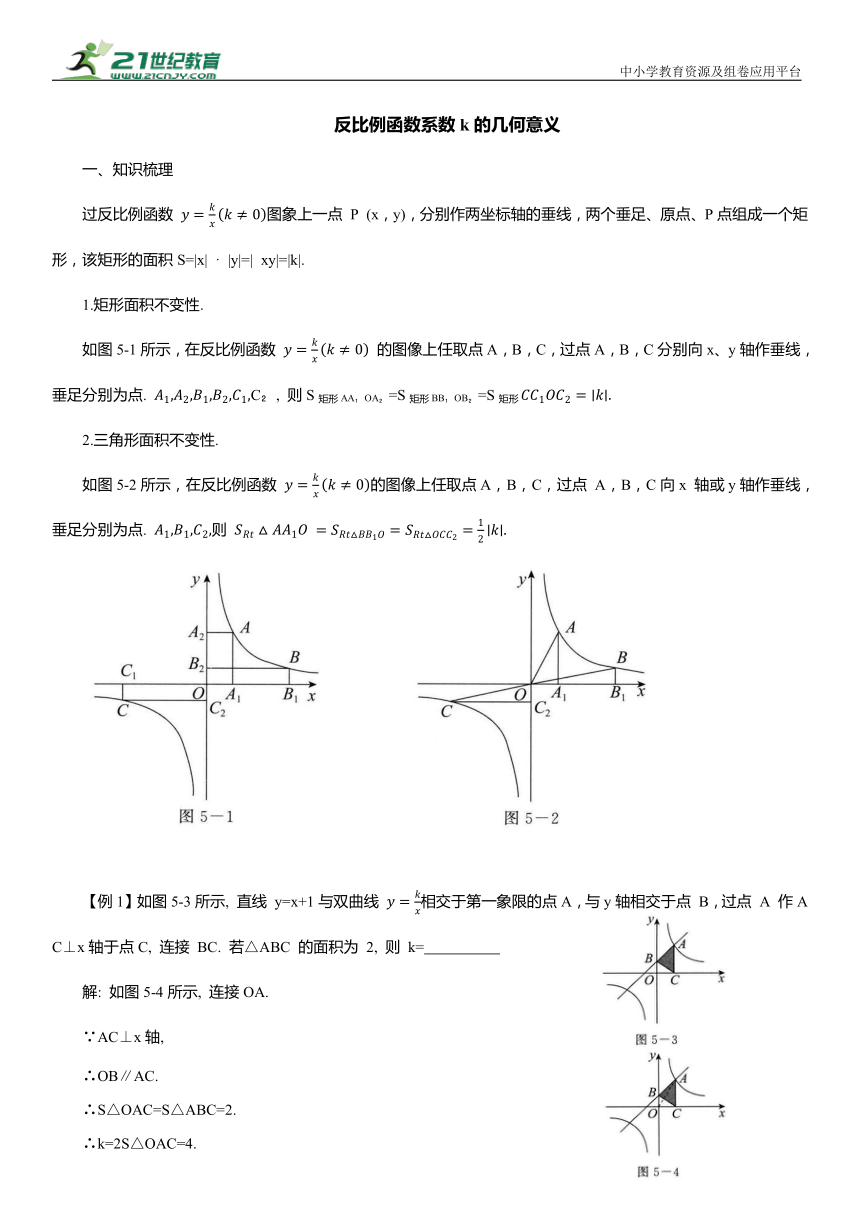 | |
| 格式 | docx | ||
| 文件大小 | 245.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 17:42:17 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
反比例函数系数k的几何意义
一、知识梳理
过反比例函数 图象上一点 P (x,y),分别作两坐标轴的垂线,两个垂足、原点、P点组成一个矩形,该矩形的面积S=|x| · |y|=| xy|=|k|.
1.矩形面积不变性.
如图5-1所示,在反比例函数 的图像上任取点A,B,C,过点A,B,C分别向x、y轴作垂线,垂足分别为点. C , 则S矩形AA OA =S矩形BB OB =S矩形
2.三角形面积不变性.
如图5-2所示,在反比例函数 的图像上任取点A,B,C,过点 A,B,C向x 轴或y轴作垂线,垂足分别为点. 则
【例1】如图5-3所示, 直线 y=x+1与双曲线 相交于第一象限的点A,与y轴相交于点 B,过点 A 作AC⊥x轴于点C, 连接 BC. 若△ABC 的面积为 2, 则 k=
解: 如图5-4所示, 连接OA.
∵AC⊥x轴,
∴OB∥AC.
∴S△OAC=S△ABC=2.
∴k=2S△OAC=4.
【例2】如图5-5 所示,已知点 P 是y轴正半轴上的一点,过点 P作EF∥x轴,分别交反比例函数 和 的图象于点 E,F,以EF 为对角线作EM∥FN. 若点N在x轴上, □EMFN的面积为6, 则k的值为 .
解: 如图5-6所示, 连接OF, OE.
∵EF∥x轴,
又∵EF为□EMFN的对角线,
∵由反比例函数系数k的几何意义可知,
解得k=-4或k=4>0 (舍去) .
二、分层练习
1.如图5-7所示,已知点 A 是反比例函数 图象上的一点,过点A作AB∥y轴,交反比例函数 于点 B, 过点 B作BC⊥AB交y 轴于点C, 连接AC, 则△ABC 的面积为 .
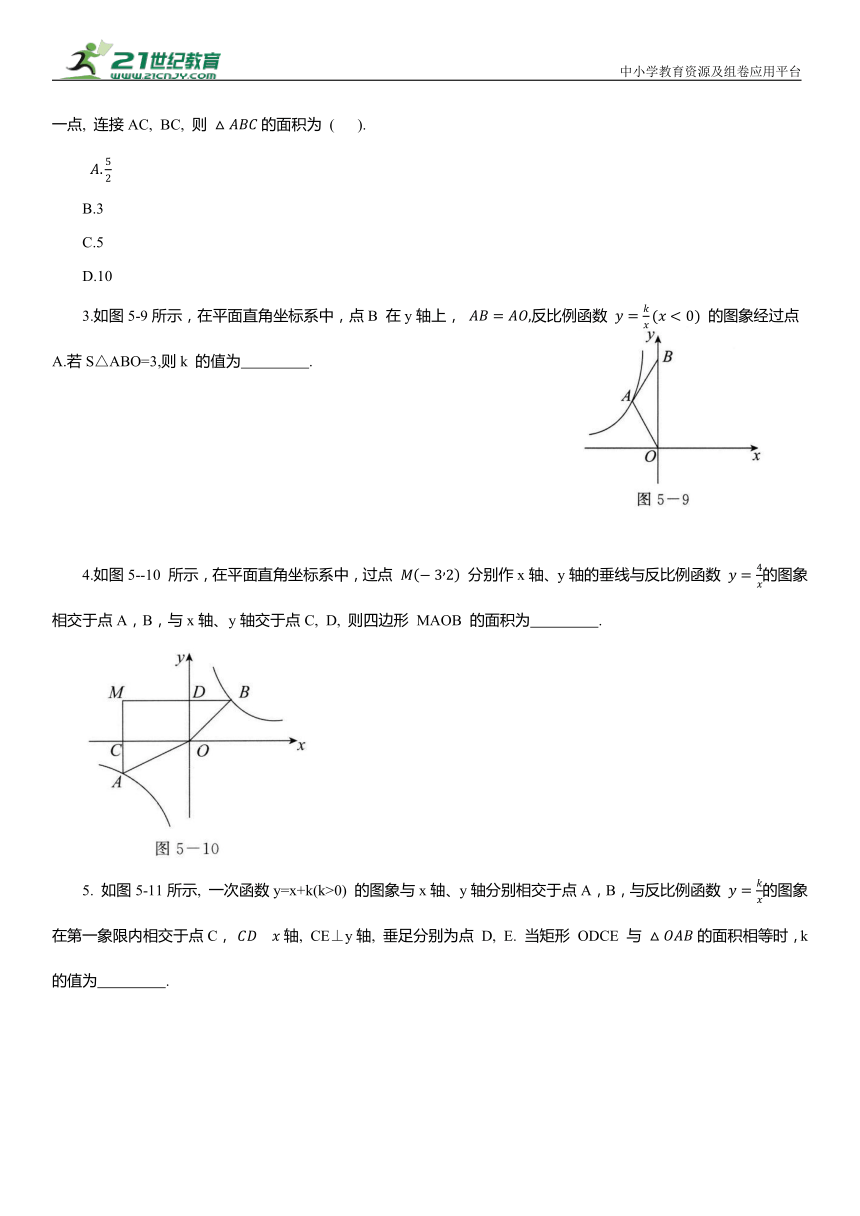
2.如图5-8所示,点A 是反比例函数 图象上的一点,过点 A作AB⊥x轴于点B, 点C为y轴上的一点, 连接AC, BC, 则 的面积为 ( ).
B.3
C.5
D.10
3.如图5-9所示,在平面直角坐标系中,点B 在y轴上, 反比例函数 的图象经过点 A.若S△ABO=3,则k 的值为 .
4.如图5--10 所示,在平面直角坐标系中,过点 分别作x轴、y轴的垂线与反比例函数 的图象相交于点A,B,与x轴、y轴交于点C, D, 则四边形 MAOB 的面积为 .
5. 如图5-11所示, 一次函数y=x+k(k>0) 的图象与x轴、y轴分别相交于点A,B,与反比例函数 的图象在第一象限内相交于点C, 轴, CE⊥y轴, 垂足分别为点 D, E. 当矩形 ODCE 与 的面积相等时,k的值为 .
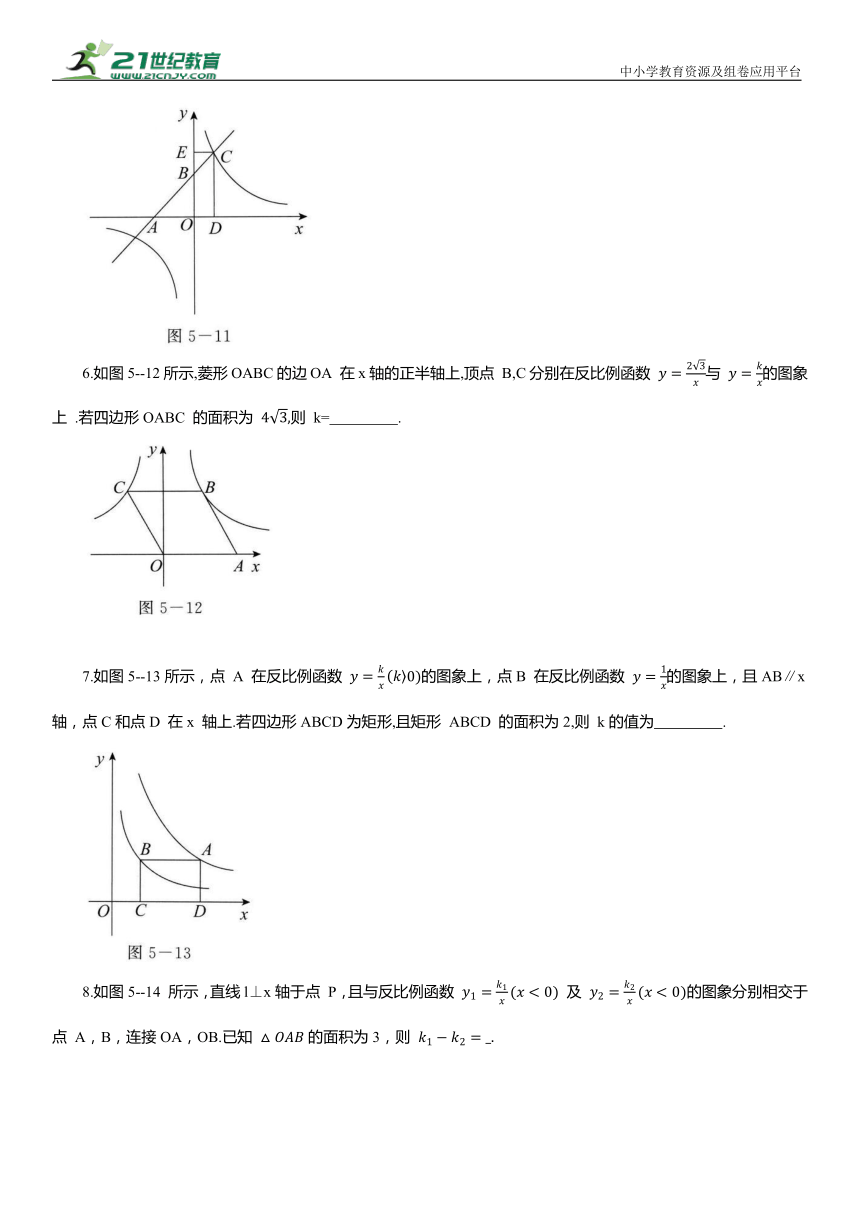
6.如图5--12所示,菱形OABC的边OA 在x轴的正半轴上,顶点 B,C分别在反比例函数 与 的图象上 .若四边形OABC 的面积为 则 k= .
7.如图5--13所示,点 A 在反比例函数 的图象上,点B 在反比例函数 的图象上,且AB∥x轴,点C和点D 在x 轴上.若四边形ABCD为矩形,且矩形 ABCD 的面积为2,则 k的值为 .
8.如图5--14 所示,直线l⊥x轴于点 P,且与反比例函数 及 的图象分别相交于点 A,B,连接OA,OB.已知 的面积为3,则
9. 如图5--15 所示, 的顶点A 在反比例函数 的图象上, 点B在y轴上,点C, D在x轴上,AD与y轴相交于点E.若 的面积为9,则k的值为 .
10.如图5-16 所示,矩形 ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,交坐标轴于点 E,F,G,H,点C在反比例函数 的图象上. 若点A的坐标为 (-2, --2),则k的值为 ( ).
A.3
B.4
C. -4
D. -5
11.如图5-17所示,四边形OABC是平行四边形,对角线OB在y轴上,位于第一象限的点 A 和第二象限的点C 分别在反比例函数 和 的图象上,过点A,C分别作x轴的垂线,垂足分别为点 M,N.下列结论正确的是 ( ).
①ON=OM; ③阴影部分面积是 ④若四边形OABC是菱形,则图中曲线关于 y轴对称.
A.①④
B.②③
C.①②④
D.①③④
1. 解: 如图3所示, 过点A作AE⊥y轴于点E, 设AB交x轴于点D.
∵AB∥y轴,
∴AB⊥x轴.
∵BC⊥AB,
∴四边形ABCE 是矩形.
∵点 A 是反比例函数 图象上的一点,
∴S四边形ADOE =2.
∵点 B 在反比例函数 的图象上,
∴S四边形BDOC=1.
∴△ABC的面积
2. 解: 连接OA, 如图4 所示.
∵AB⊥x轴,
∴OC∥AB.
∵反比例函数的解析式为
故选 A.
3. 解: 如图5所示, 过点 A作AD⊥y轴于点D.
∵AB=AO, S△ABO=3,
又∵反比例函数的图象位于第二象限,k<0,∴k=--3.
4. 解: 设点A 的坐标为 (a, b), 点B 的坐标为 (c, d) .
∵反比例函数 的图象过点A,B,
∵点 M的坐标为 (-3, 2),
∴S矩形MCOD=3×2=6.
5.解: ∵一次函数y=x+k(k>0) 的图象与x轴、y轴分别相交于点A, B,
∴令x=0, 则y=k; 令y=0, 则x=-k.
∴点 A, B的坐标分别为 (-k, 0), (0, k) .
∵S矩形ODCE=k,
解得k=0 (舍去) 或k=2.
6.解:如图6所示,连接OB,设直线 BC与y轴相交于点 P.
∵四边形OABC 是菱形,且面积为
∴△OBC的面积为
∵BC∥x轴,
∴BC⊥y轴.
∵点 B,C分别在反比例函数 与 的图象上,
解得 (正值舍去).
7.解:延长AB交y轴于点E,如图7所示.
矩形A BCD的面积为2,
, 即|k|-1=2.
∵k>0,
∴k=3.
8. 解:
∵△OAB的面积为3,
即
9. 解: 如图8所示, 过点 A作AF⊥x轴于点 F.
∵△BCE的面积为9,
∴S平行四边形ABCD=2S△BCE=18.
∵S矩形ABOF=S平行四边形ABCD,
∴S矩形ABOF=18.
∴|k|=18.
∵反比例函数的图象位于第一象限,
∴k=18.
10.解:∵矩形 ABCD的对角线BD 经过坐标原点,矩形的边分别平行于坐标轴,
∵点 A 的坐标为 (-2, - 2),
∴k+1=4, 即k=3.
故选 A.
11. 解: 作 AE⊥y轴于点E, CF⊥y轴于点F, 如图9所示.
∵四边形OABC是平行四边形,
∴AE=CF.
∴OM=ON, 故①正确.
故②正确.
且
故③错误.
∵若OABC是菱形, 则OA=OC, 而OM=ON,
∴Rt△AOM≌Rt△CON (HL).
∴AM=CN.
即
∴曲线关于 y轴对称,故④正确.
故选 C.
反比例函数系数k的几何意义
一、知识梳理
过反比例函数 图象上一点 P (x,y),分别作两坐标轴的垂线,两个垂足、原点、P点组成一个矩形,该矩形的面积S=|x| · |y|=| xy|=|k|.
1.矩形面积不变性.
如图5-1所示,在反比例函数 的图像上任取点A,B,C,过点A,B,C分别向x、y轴作垂线,垂足分别为点. C , 则S矩形AA OA =S矩形BB OB =S矩形
2.三角形面积不变性.
如图5-2所示,在反比例函数 的图像上任取点A,B,C,过点 A,B,C向x 轴或y轴作垂线,垂足分别为点. 则
【例1】如图5-3所示, 直线 y=x+1与双曲线 相交于第一象限的点A,与y轴相交于点 B,过点 A 作AC⊥x轴于点C, 连接 BC. 若△ABC 的面积为 2, 则 k=
解: 如图5-4所示, 连接OA.
∵AC⊥x轴,
∴OB∥AC.
∴S△OAC=S△ABC=2.
∴k=2S△OAC=4.
【例2】如图5-5 所示,已知点 P 是y轴正半轴上的一点,过点 P作EF∥x轴,分别交反比例函数 和 的图象于点 E,F,以EF 为对角线作EM∥FN. 若点N在x轴上, □EMFN的面积为6, 则k的值为 .
解: 如图5-6所示, 连接OF, OE.
∵EF∥x轴,
又∵EF为□EMFN的对角线,
∵由反比例函数系数k的几何意义可知,
解得k=-4或k=4>0 (舍去) .
二、分层练习
1.如图5-7所示,已知点 A 是反比例函数 图象上的一点,过点A作AB∥y轴,交反比例函数 于点 B, 过点 B作BC⊥AB交y 轴于点C, 连接AC, 则△ABC 的面积为 .
2.如图5-8所示,点A 是反比例函数 图象上的一点,过点 A作AB⊥x轴于点B, 点C为y轴上的一点, 连接AC, BC, 则 的面积为 ( ).
B.3
C.5
D.10
3.如图5-9所示,在平面直角坐标系中,点B 在y轴上, 反比例函数 的图象经过点 A.若S△ABO=3,则k 的值为 .
4.如图5--10 所示,在平面直角坐标系中,过点 分别作x轴、y轴的垂线与反比例函数 的图象相交于点A,B,与x轴、y轴交于点C, D, 则四边形 MAOB 的面积为 .
5. 如图5-11所示, 一次函数y=x+k(k>0) 的图象与x轴、y轴分别相交于点A,B,与反比例函数 的图象在第一象限内相交于点C, 轴, CE⊥y轴, 垂足分别为点 D, E. 当矩形 ODCE 与 的面积相等时,k的值为 .
6.如图5--12所示,菱形OABC的边OA 在x轴的正半轴上,顶点 B,C分别在反比例函数 与 的图象上 .若四边形OABC 的面积为 则 k= .
7.如图5--13所示,点 A 在反比例函数 的图象上,点B 在反比例函数 的图象上,且AB∥x轴,点C和点D 在x 轴上.若四边形ABCD为矩形,且矩形 ABCD 的面积为2,则 k的值为 .
8.如图5--14 所示,直线l⊥x轴于点 P,且与反比例函数 及 的图象分别相交于点 A,B,连接OA,OB.已知 的面积为3,则
9. 如图5--15 所示, 的顶点A 在反比例函数 的图象上, 点B在y轴上,点C, D在x轴上,AD与y轴相交于点E.若 的面积为9,则k的值为 .
10.如图5-16 所示,矩形 ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,交坐标轴于点 E,F,G,H,点C在反比例函数 的图象上. 若点A的坐标为 (-2, --2),则k的值为 ( ).
A.3
B.4
C. -4
D. -5
11.如图5-17所示,四边形OABC是平行四边形,对角线OB在y轴上,位于第一象限的点 A 和第二象限的点C 分别在反比例函数 和 的图象上,过点A,C分别作x轴的垂线,垂足分别为点 M,N.下列结论正确的是 ( ).
①ON=OM; ③阴影部分面积是 ④若四边形OABC是菱形,则图中曲线关于 y轴对称.
A.①④
B.②③
C.①②④
D.①③④
1. 解: 如图3所示, 过点A作AE⊥y轴于点E, 设AB交x轴于点D.
∵AB∥y轴,
∴AB⊥x轴.
∵BC⊥AB,
∴四边形ABCE 是矩形.
∵点 A 是反比例函数 图象上的一点,
∴S四边形ADOE =2.
∵点 B 在反比例函数 的图象上,
∴S四边形BDOC=1.
∴△ABC的面积
2. 解: 连接OA, 如图4 所示.
∵AB⊥x轴,
∴OC∥AB.
∵反比例函数的解析式为
故选 A.
3. 解: 如图5所示, 过点 A作AD⊥y轴于点D.
∵AB=AO, S△ABO=3,
又∵反比例函数的图象位于第二象限,k<0,∴k=--3.
4. 解: 设点A 的坐标为 (a, b), 点B 的坐标为 (c, d) .
∵反比例函数 的图象过点A,B,
∵点 M的坐标为 (-3, 2),
∴S矩形MCOD=3×2=6.
5.解: ∵一次函数y=x+k(k>0) 的图象与x轴、y轴分别相交于点A, B,
∴令x=0, 则y=k; 令y=0, 则x=-k.
∴点 A, B的坐标分别为 (-k, 0), (0, k) .
∵S矩形ODCE=k,
解得k=0 (舍去) 或k=2.
6.解:如图6所示,连接OB,设直线 BC与y轴相交于点 P.
∵四边形OABC 是菱形,且面积为
∴△OBC的面积为
∵BC∥x轴,
∴BC⊥y轴.
∵点 B,C分别在反比例函数 与 的图象上,
解得 (正值舍去).
7.解:延长AB交y轴于点E,如图7所示.
矩形A BCD的面积为2,
, 即|k|-1=2.
∵k>0,
∴k=3.
8. 解:
∵△OAB的面积为3,
即
9. 解: 如图8所示, 过点 A作AF⊥x轴于点 F.
∵△BCE的面积为9,
∴S平行四边形ABCD=2S△BCE=18.
∵S矩形ABOF=S平行四边形ABCD,
∴S矩形ABOF=18.
∴|k|=18.
∵反比例函数的图象位于第一象限,
∴k=18.
10.解:∵矩形 ABCD的对角线BD 经过坐标原点,矩形的边分别平行于坐标轴,
∵点 A 的坐标为 (-2, - 2),
∴k+1=4, 即k=3.
故选 A.
11. 解: 作 AE⊥y轴于点E, CF⊥y轴于点F, 如图9所示.
∵四边形OABC是平行四边形,
∴AE=CF.
∴OM=ON, 故①正确.
故②正确.
且
故③错误.
∵若OABC是菱形, 则OA=OC, 而OM=ON,
∴Rt△AOM≌Rt△CON (HL).
∴AM=CN.
即
∴曲线关于 y轴对称,故④正确.
故选 C.
