反比例函数系数k的代数意义 同步练习(含答案)2024-2025学年人教版九年级数学下册
文档属性
| 名称 | 反比例函数系数k的代数意义 同步练习(含答案)2024-2025学年人教版九年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 291.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
反比例函数系数k的代数意义 (1)
一、知识梳理
点 A (x , y ) 是反比例函数 图象上的一点.
设点 A 的横坐标为a,则点 A 的纵坐标为 即
【例】如图6--1所示,在平面直角坐标系中,点O为坐标原点,正方形ABCO的两边OA,OC分别与x 轴、y轴重合,点 E,F 分别是BC,AB 边上的中点,且在反比例函数 的图象上,连接lEF, S△OEF=3,则k的值为 .
解:设正方形ABCO的边长为a,则点 E的坐标为 点 F 的坐标为
∵点 E, F分别是BC, AB边上的中点,
7
∵S△OEF =3,
解得
∵点E,F 在反比例函数 的图象上,
二、分层练习
1.如图6-2所示,反比例函数 经过 Rt△OAB斜边OA 的中点D, 且与直角边AB相交于点C. 若点A 的坐标为(--6, 4), 则△AOC的面积为 .
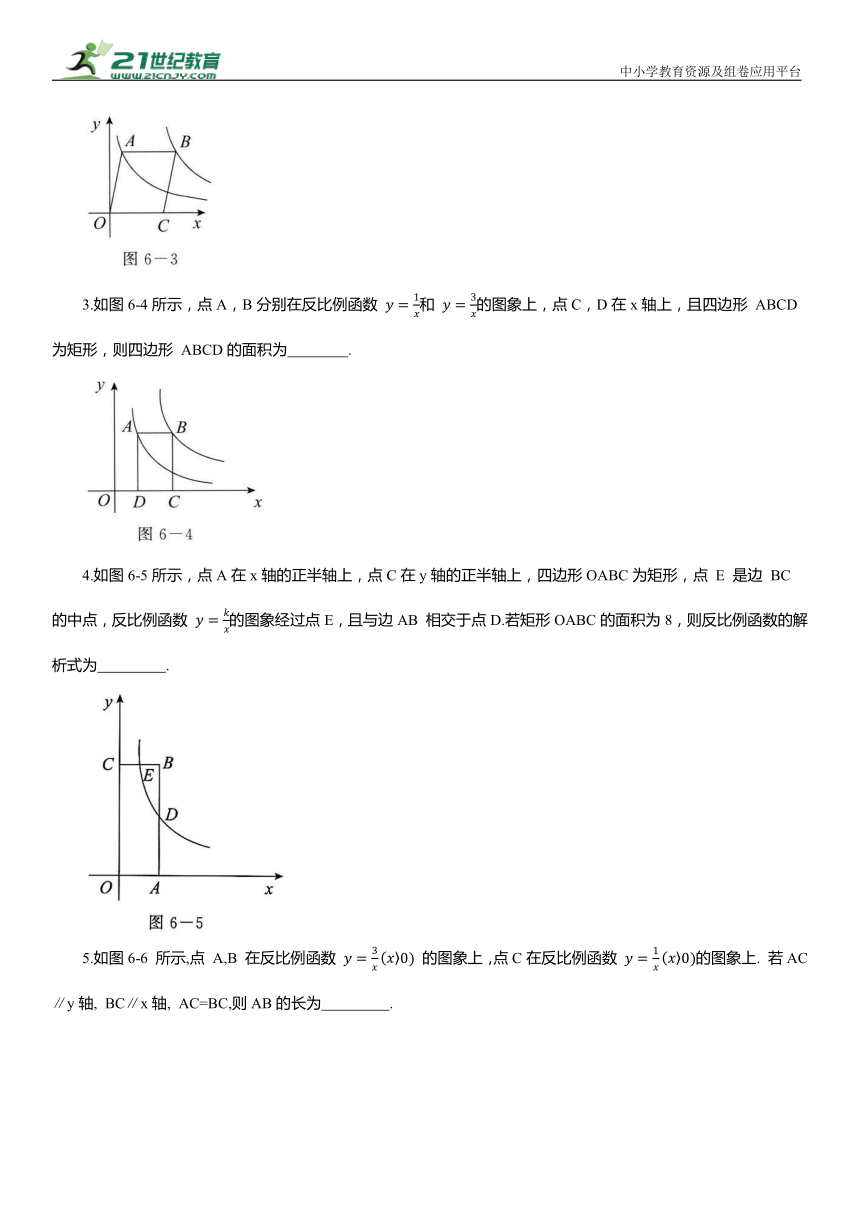
2.如图6-3所示,点O为坐标原点,点A 在反比例函数 的图象上,点B 在反比例函数 的图象上,点C 在x 轴的正半轴上.若四边形 OABC是平行四边形,则四边形 OABC的面积为 .
3.如图6-4所示,点A,B分别在反比例函数 和 的图象上,点C,D在x轴上,且四边形 ABCD为矩形,则四边形 ABCD的面积为 .
4.如图6-5所示,点A在x轴的正半轴上,点C在y轴的正半轴上,四边形OABC为矩形,点 E 是边 BC 的中点,反比例函数 的图象经过点E,且与边AB 相交于点D.若矩形OABC的面积为8,则反比例函数的解析式为 .
5.如图6-6 所示,点 A,B 在反比例函数 的图象上,点C在反比例函数 的图象上. 若AC∥y轴, BC∥x轴, AC=BC,则AB的长为 .
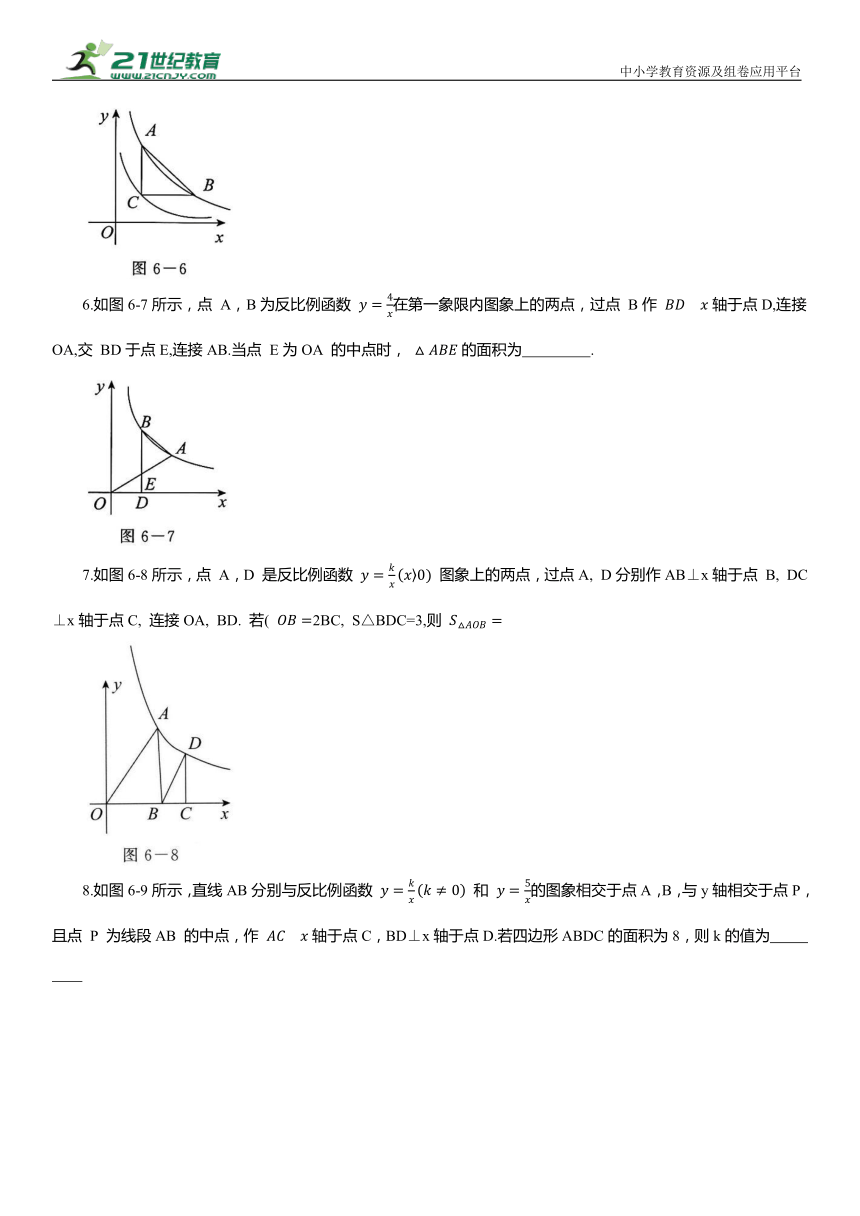
6.如图6-7所示,点 A,B为反比例函数 在第一象限内图象上的两点,过点 B作 轴于点D,连接OA,交 BD于点E,连接AB.当点 E为OA 的中点时, 的面积为 .
7.如图6-8所示,点 A,D 是反比例函数 图象上的两点,过点A, D分别作AB⊥x轴于点 B, DC⊥x轴于点C, 连接OA, BD. 若( 2BC, S△BDC=3,则
8.如图6-9所示,直线AB分别与反比例函数 和 的图象相交于点A,B,与y轴相交于点P,且点 P 为线段AB 的中点,作 轴于点C,BD⊥x轴于点D.若四边形ABDC的面积为8,则k的值为
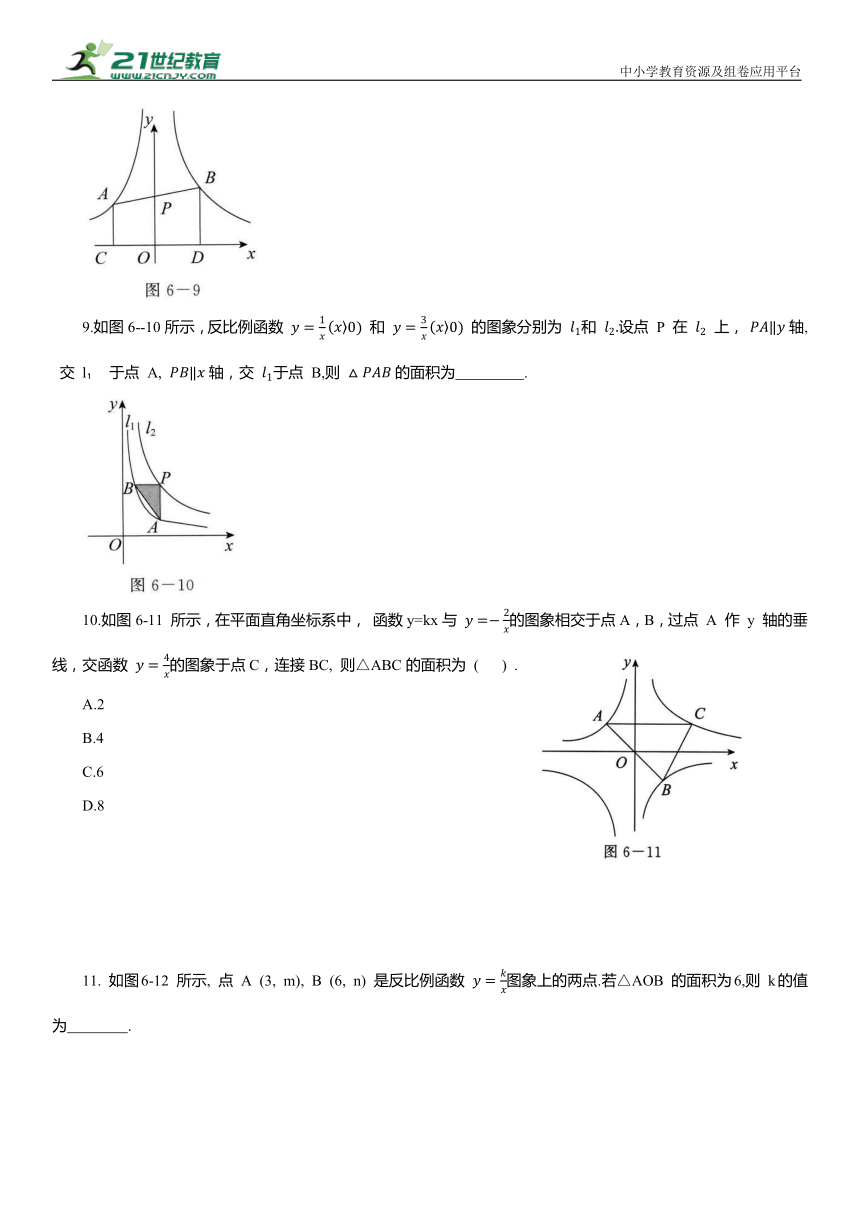
9.如图6--10所示,反比例函数 和 的图象分别为 和 设点 P 在 上, 轴, 交 l 于点 A, 轴,交 于点 B,则 的面积为 .
10.如图6-11 所示,在平面直角坐标系中, 函数y=kx与 的图象相交于点A,B,过点 A 作 y 轴的垂线,交函数 的图象于点C,连接BC, 则△ABC的面积为 ( ) .
A.2
B.4
C.6
D.8
11. 如图6-12 所示, 点 A (3, m), B (6, n) 是反比例函数 图象上的两点.若△AOB 的面积为6,则 k的值为 .
反比例函数系数 k 的代 数 意义 (2)
一、 知识梳理
如图7-1所示, 点 A (x , y ), B (x , y ) 是反比例函数 图象上的两点,则 即
结论:反比例函数 (k为常数,k≠0)图象上任意一点的横纵坐标之积等于比例系数k.
【例】如图7--2所示, 点 A , A 在 的图象上,点 在x轴的正半轴上.若 均为等边三角形,则点 的坐标为
解: 如图7--3所示, 作. 垂足为 y点C,作 垂足为点D .
为等边三角形,
即
设A 的坐标为 (m, m) .
∵点A 在 的图象上,
解得m=3(负值已舍) .
设 则 的坐标为 (
反比例函数系数k的代数意义 (2)
∵点 在反比例函数 的图象上,
化简得 解得
∵a>0,
故点 B 的坐标为(
二、分层练习
1. 如图7--4 所示, 矩形 ABCD 的边AB 与y 轴平行, 点 A 的坐标为 (1,m),点C的坐标为 (3,m+6),则图象同时经过点 B,D的反比例函数的解析式为 .
2.如图7--5所示,在平面直角坐标系中, 已知 的边AD 平行于x轴,点A 的坐标为 点 B 的坐标为 若在第一象限内,反比例函数 的图象恰好经过点C,D,则该反比例函数的解析式为
3.如图7-6所示,正比例函数y=2x的图象与反比例函数 的图象在第一象限内相交于点A,将线段OA沿x轴向右平移3个单位长度得到线段O'A',其中点 A 与点A'对应.若O'A'的中点B 恰好也在该反比例函数的图象上,则k的值为 .
4. 如图7-7 所示, 正方形OABC, ADEF的顶点A, D, C在坐标轴上,点F在AB 上,点 B,E在反比例函数 的图象上,则点 E 的横坐标是 ( ).
5.如图7-8所示,直线AB经过原点分别交反比例函数 的图象于点A,B, 过点A作AC⊥x轴于点C, 连接BC交y轴于点D, 则△BOD的面积为 .
6.如图7-9所示,点 A,B 在反比例函数 的图象上,过点 A 作AC⊥x轴,交OB 于点D,垂足为点C,连接OA.若△ADO的面积为2,点 D为OB 的中点,则k的值为 ( ).
C.6 D.8
反比例函数系数k的代数意义 (2)
7.如图7--10所示,已知在平面直角坐标系中,Rt△OAB的直角顶点B 在x轴的正半轴上,点A 在第一象限,反比例函数 的图象经过OA的中点C, 交AB于点D, 连接CD. 若△ACD的面积为2, 则k的值为 .
8.如图7--11所示,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数 的图象经过顶点 D,分别与对角线AC, 边BC相交于点E, F, 连接EF, AF. 若点 E为AC 的中点,△AEF 的面积为2, 则k的值为 .
9.已知点 在同一个反比例函数的图象上.若 且 则这个反比例函数的解析式为 .
10. 如图7--12所示, 直线y= kx (k<0) 与反比例函数 的图象相交于点 则 的值为 .
反比例系数k的代数意义 (1)
1. 解: 连接OC, 如图 10 所示.
∵点 A 的坐标为 (-6, 4), 点 D 为斜边OA 的中点,
∴点 D 的坐标为 (-3, 2) .
∵点 D 在反比例函数 的图象上,
∴k=-3×2=-6, 即反比例函数的解析式为
2.解:设点 A 的坐标为
∵四边形OABC是平行四边形,
∴AB∥OC.
∴点 B的纵坐标为 /m,
∵点 B 在反比例函数 的图象上,
∴将 代入 得 解得x=5m.
∴点 B 的坐标为
3. 解: 设OD=a, 则点 A 的横坐标为a.
∵点 A 在反比例函数 的图象上,
∴把x=a代入 得 即
∵四边形 ABCD为矩形,点 B 在反比例函数 的图象上,
∴将 代入 得 解得x=3a, 即OC=3a.
∴CD=OC--OD=2a.
4. 解: 设点 B 的坐标是 (a, b) .
∵矩形OABC 的面积为8,
∴ab=8.
∵四边形OABC是矩形,
∴BC∥OA (即BC∥x轴) .
∵点 E 是边 BC 的中点,
即点 E的坐标为
∵点 E 在反比例函数 的图象上,
即反比例函数的解析式为
5.解: ∵点C在反比例函数 的图象上, AC∥y轴, BC∥x轴,点 A,B在反比例函数 的图象上,
∴设点 C 的坐标为 则点 B 的坐标为( 点 A 的坐标为
∵AC=BC,
解得a=1(负值已舍去).
∴点C的坐标为 (1, 1), 点B的坐标为 (3, 1), 点A的坐标为 (1, 3) .
∴AC=BC=2.
∴在 Rt△ABC中,
6.解:设点 B 的坐标为 (x, ),则
∵BD⊥x轴,
∴点 E 的横坐标为x.
∵点 E 为OA 的中点,
∴点 A 的横坐标为2x.
∴点 A 的坐标为
∴点 E 的坐标为 则
7. 解: 设 BC=x, 则OB=2x, OC=3x.
∵点 A,D在反比例函数 的图象上, AB⊥x轴, 轴,
∴点 A,D 的坐标分别为
解得k=18.
8. 解: ∵AC⊥x轴, BD⊥x轴,
∴AC∥PO∥BD.
∵点 P 为线段AB 的中点,
∴OC=OD.
∴设点 A 的坐标为 点 B 的坐标为
解得k=-3.
9. 解: 设点 P 的坐标为 (m, n).
∵点 P 在反比例函数 的图象上,
∴点 P 的坐标为
∵PB∥x轴,
∴点B的纵坐标为
∵将 代入 得 解得
∴点 B 的坐标为 同理可得点 A 的坐标为
10. 解: ∵函数 y= kx与 的图象相交于点A,B,由图象可知点 A,B关于原点对称,
∴设点 A 的坐标为 点B的坐标为 则点C的坐标为
故选 C.
会当凌绝顶,一览众山小
11. 解: 如图11所示, 作 AD⊥x轴于点D, BC⊥x轴于点C.
∵点 A (3, m), B (6, n) 是反比例函数 图象上的两点,
∴3m=6n=k.
∴点 A 的坐标为( 点 B 的坐标为
∴S△AOB=S梯形ABCD=6.
解得k=-8.
反比例系数k的代数意义 (2)
1. 解: ∵矩形ABCD的边AB 与y轴平行, 点A 的坐标为 (1, m), 点C的坐标为
∴点 B 的坐标为 (1, m+6), 点D 的坐标为 (3, m) .
∵点 B,D在反比例函数的图象上,
∴1· (m+6) =3m, 解得m=3.
∴点 B 的坐标为 (1, 9) .
∴反比例函数的解析式为
2.解:设AD=m,根据平行四边形的性质可知,BC=m.
∵ ABCD的边AD 平行于x 轴,点 A 的坐标为 点 B 的坐标为(
∴点 D 的坐标为 点C的坐标为
∵反比例函数 的图象恰好经过点C,D,
解得
∴点 D的坐标为 (3, 2) .
∴k=3×2=6.
∴该反比例函数的解析式为
3.解: ∵点 A 在正比例函数y=2x的图象上,
∴设点 A 的坐标为 (m, 2m) .
∵将线段OA 沿x 轴向右平移3个单位长度得到线段(
∴点 A'的坐标为 (m+3, 2m), 点O'的坐标为 (3, 0) .
∵点 B 为线段O'A'的中点,
∴点 B 的坐标为
∵点 A,B都在反比例函数 的图象上,
解得: (舍去),
∴点 A 的坐标为 (2, 4) .
∴k=2×4=8.
4. 解: 设点 B 的坐标为 (a, a) .
∵点 B 在反比例函数 的图象上,
解得a=1(负值已舍),即点B的坐标为 (1, 1) .
∴设点E 坐标为 (1+b, b) .
∵点 E 在反比例函数 的图象上,
∴ (1+b) ·b=1, 解得
∵b>0,
∴点 E 的横坐标
故选 C.
欲穷千里目,更上一层楼
5. 解: 设点 A 的坐标为 (m, n), 则 mn=6.
∵直线 AB过原点,
∴点O是线段AB 的中点.
∵AC⊥x轴,
∴AC∥OD, 则OD 是△BAC的中位线,
6. 解: 如图12所示, 过点 B 作BE⊥x轴于点E.
∵点 D 为OB 的中点,
∴CD 是△OBE 的中位线, 即
设点 A 的坐标为 则点 B 的坐标为
∵△ADO的面积为2,
解得
故选 B.
7. 解: 如图13所示, 连接OD, 过点C作CE∥AB, 交x轴于点E.
∵∠ABO=90°, 反比例函数 的图象经过OA 的中点C,
∵CE∥AB,
∴△OCE∽△OAB.
即 4S△OCE=S△OAB·
解得
8.解:设点 D 的坐标为(
∵四边形ABCD是矩形,且点 E 为AC 的中点,
∴点E的纵坐标为 将 代入反比例函数 得x=2m.
∴点 E 的坐标为
∴点 B 的横坐标为3m.
∴点F 的横坐标为3m,将x=3m代入反比例函数 得
∴点 F 的坐标为
∵△AEF的面积为2,
∴△ACF的面积为4.
∵AB=3m--m=2m,
解得k=6.
9.解:设反比例函数的解析式为
∵点 在该反比例函数的图象上,
且
即
解得k=-3,经检验,k=-3是原分式方程的解.
∴反比例函数的解析式为
10. 解: ∵点 A (x , y ), B (x , y ) 在反比例函数 的图象上,
∵直线y= kx (k<0) 与反比例函数 的图象相交于点A (x , y ),B (x , y ),
∴ -6.
反比例函数系数k的代数意义 (1)
一、知识梳理
点 A (x , y ) 是反比例函数 图象上的一点.
设点 A 的横坐标为a,则点 A 的纵坐标为 即
【例】如图6--1所示,在平面直角坐标系中,点O为坐标原点,正方形ABCO的两边OA,OC分别与x 轴、y轴重合,点 E,F 分别是BC,AB 边上的中点,且在反比例函数 的图象上,连接lEF, S△OEF=3,则k的值为 .
解:设正方形ABCO的边长为a,则点 E的坐标为 点 F 的坐标为
∵点 E, F分别是BC, AB边上的中点,
7
∵S△OEF =3,
解得
∵点E,F 在反比例函数 的图象上,
二、分层练习
1.如图6-2所示,反比例函数 经过 Rt△OAB斜边OA 的中点D, 且与直角边AB相交于点C. 若点A 的坐标为(--6, 4), 则△AOC的面积为 .
2.如图6-3所示,点O为坐标原点,点A 在反比例函数 的图象上,点B 在反比例函数 的图象上,点C 在x 轴的正半轴上.若四边形 OABC是平行四边形,则四边形 OABC的面积为 .
3.如图6-4所示,点A,B分别在反比例函数 和 的图象上,点C,D在x轴上,且四边形 ABCD为矩形,则四边形 ABCD的面积为 .
4.如图6-5所示,点A在x轴的正半轴上,点C在y轴的正半轴上,四边形OABC为矩形,点 E 是边 BC 的中点,反比例函数 的图象经过点E,且与边AB 相交于点D.若矩形OABC的面积为8,则反比例函数的解析式为 .
5.如图6-6 所示,点 A,B 在反比例函数 的图象上,点C在反比例函数 的图象上. 若AC∥y轴, BC∥x轴, AC=BC,则AB的长为 .
6.如图6-7所示,点 A,B为反比例函数 在第一象限内图象上的两点,过点 B作 轴于点D,连接OA,交 BD于点E,连接AB.当点 E为OA 的中点时, 的面积为 .
7.如图6-8所示,点 A,D 是反比例函数 图象上的两点,过点A, D分别作AB⊥x轴于点 B, DC⊥x轴于点C, 连接OA, BD. 若( 2BC, S△BDC=3,则
8.如图6-9所示,直线AB分别与反比例函数 和 的图象相交于点A,B,与y轴相交于点P,且点 P 为线段AB 的中点,作 轴于点C,BD⊥x轴于点D.若四边形ABDC的面积为8,则k的值为
9.如图6--10所示,反比例函数 和 的图象分别为 和 设点 P 在 上, 轴, 交 l 于点 A, 轴,交 于点 B,则 的面积为 .
10.如图6-11 所示,在平面直角坐标系中, 函数y=kx与 的图象相交于点A,B,过点 A 作 y 轴的垂线,交函数 的图象于点C,连接BC, 则△ABC的面积为 ( ) .
A.2
B.4
C.6
D.8
11. 如图6-12 所示, 点 A (3, m), B (6, n) 是反比例函数 图象上的两点.若△AOB 的面积为6,则 k的值为 .
反比例函数系数 k 的代 数 意义 (2)
一、 知识梳理
如图7-1所示, 点 A (x , y ), B (x , y ) 是反比例函数 图象上的两点,则 即
结论:反比例函数 (k为常数,k≠0)图象上任意一点的横纵坐标之积等于比例系数k.
【例】如图7--2所示, 点 A , A 在 的图象上,点 在x轴的正半轴上.若 均为等边三角形,则点 的坐标为
解: 如图7--3所示, 作. 垂足为 y点C,作 垂足为点D .
为等边三角形,
即
设A 的坐标为 (m, m) .
∵点A 在 的图象上,
解得m=3(负值已舍) .
设 则 的坐标为 (
反比例函数系数k的代数意义 (2)
∵点 在反比例函数 的图象上,
化简得 解得
∵a>0,
故点 B 的坐标为(
二、分层练习
1. 如图7--4 所示, 矩形 ABCD 的边AB 与y 轴平行, 点 A 的坐标为 (1,m),点C的坐标为 (3,m+6),则图象同时经过点 B,D的反比例函数的解析式为 .
2.如图7--5所示,在平面直角坐标系中, 已知 的边AD 平行于x轴,点A 的坐标为 点 B 的坐标为 若在第一象限内,反比例函数 的图象恰好经过点C,D,则该反比例函数的解析式为
3.如图7-6所示,正比例函数y=2x的图象与反比例函数 的图象在第一象限内相交于点A,将线段OA沿x轴向右平移3个单位长度得到线段O'A',其中点 A 与点A'对应.若O'A'的中点B 恰好也在该反比例函数的图象上,则k的值为 .
4. 如图7-7 所示, 正方形OABC, ADEF的顶点A, D, C在坐标轴上,点F在AB 上,点 B,E在反比例函数 的图象上,则点 E 的横坐标是 ( ).
5.如图7-8所示,直线AB经过原点分别交反比例函数 的图象于点A,B, 过点A作AC⊥x轴于点C, 连接BC交y轴于点D, 则△BOD的面积为 .
6.如图7-9所示,点 A,B 在反比例函数 的图象上,过点 A 作AC⊥x轴,交OB 于点D,垂足为点C,连接OA.若△ADO的面积为2,点 D为OB 的中点,则k的值为 ( ).
C.6 D.8
反比例函数系数k的代数意义 (2)
7.如图7--10所示,已知在平面直角坐标系中,Rt△OAB的直角顶点B 在x轴的正半轴上,点A 在第一象限,反比例函数 的图象经过OA的中点C, 交AB于点D, 连接CD. 若△ACD的面积为2, 则k的值为 .
8.如图7--11所示,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数 的图象经过顶点 D,分别与对角线AC, 边BC相交于点E, F, 连接EF, AF. 若点 E为AC 的中点,△AEF 的面积为2, 则k的值为 .
9.已知点 在同一个反比例函数的图象上.若 且 则这个反比例函数的解析式为 .
10. 如图7--12所示, 直线y= kx (k<0) 与反比例函数 的图象相交于点 则 的值为 .
反比例系数k的代数意义 (1)
1. 解: 连接OC, 如图 10 所示.
∵点 A 的坐标为 (-6, 4), 点 D 为斜边OA 的中点,
∴点 D 的坐标为 (-3, 2) .
∵点 D 在反比例函数 的图象上,
∴k=-3×2=-6, 即反比例函数的解析式为
2.解:设点 A 的坐标为
∵四边形OABC是平行四边形,
∴AB∥OC.
∴点 B的纵坐标为 /m,
∵点 B 在反比例函数 的图象上,
∴将 代入 得 解得x=5m.
∴点 B 的坐标为
3. 解: 设OD=a, 则点 A 的横坐标为a.
∵点 A 在反比例函数 的图象上,
∴把x=a代入 得 即
∵四边形 ABCD为矩形,点 B 在反比例函数 的图象上,
∴将 代入 得 解得x=3a, 即OC=3a.
∴CD=OC--OD=2a.
4. 解: 设点 B 的坐标是 (a, b) .
∵矩形OABC 的面积为8,
∴ab=8.
∵四边形OABC是矩形,
∴BC∥OA (即BC∥x轴) .
∵点 E 是边 BC 的中点,
即点 E的坐标为
∵点 E 在反比例函数 的图象上,
即反比例函数的解析式为
5.解: ∵点C在反比例函数 的图象上, AC∥y轴, BC∥x轴,点 A,B在反比例函数 的图象上,
∴设点 C 的坐标为 则点 B 的坐标为( 点 A 的坐标为
∵AC=BC,
解得a=1(负值已舍去).
∴点C的坐标为 (1, 1), 点B的坐标为 (3, 1), 点A的坐标为 (1, 3) .
∴AC=BC=2.
∴在 Rt△ABC中,
6.解:设点 B 的坐标为 (x, ),则
∵BD⊥x轴,
∴点 E 的横坐标为x.
∵点 E 为OA 的中点,
∴点 A 的横坐标为2x.
∴点 A 的坐标为
∴点 E 的坐标为 则
7. 解: 设 BC=x, 则OB=2x, OC=3x.
∵点 A,D在反比例函数 的图象上, AB⊥x轴, 轴,
∴点 A,D 的坐标分别为
解得k=18.
8. 解: ∵AC⊥x轴, BD⊥x轴,
∴AC∥PO∥BD.
∵点 P 为线段AB 的中点,
∴OC=OD.
∴设点 A 的坐标为 点 B 的坐标为
解得k=-3.
9. 解: 设点 P 的坐标为 (m, n).
∵点 P 在反比例函数 的图象上,
∴点 P 的坐标为
∵PB∥x轴,
∴点B的纵坐标为
∵将 代入 得 解得
∴点 B 的坐标为 同理可得点 A 的坐标为
10. 解: ∵函数 y= kx与 的图象相交于点A,B,由图象可知点 A,B关于原点对称,
∴设点 A 的坐标为 点B的坐标为 则点C的坐标为
故选 C.
会当凌绝顶,一览众山小
11. 解: 如图11所示, 作 AD⊥x轴于点D, BC⊥x轴于点C.
∵点 A (3, m), B (6, n) 是反比例函数 图象上的两点,
∴3m=6n=k.
∴点 A 的坐标为( 点 B 的坐标为
∴S△AOB=S梯形ABCD=6.
解得k=-8.
反比例系数k的代数意义 (2)
1. 解: ∵矩形ABCD的边AB 与y轴平行, 点A 的坐标为 (1, m), 点C的坐标为
∴点 B 的坐标为 (1, m+6), 点D 的坐标为 (3, m) .
∵点 B,D在反比例函数的图象上,
∴1· (m+6) =3m, 解得m=3.
∴点 B 的坐标为 (1, 9) .
∴反比例函数的解析式为
2.解:设AD=m,根据平行四边形的性质可知,BC=m.
∵ ABCD的边AD 平行于x 轴,点 A 的坐标为 点 B 的坐标为(
∴点 D 的坐标为 点C的坐标为
∵反比例函数 的图象恰好经过点C,D,
解得
∴点 D的坐标为 (3, 2) .
∴k=3×2=6.
∴该反比例函数的解析式为
3.解: ∵点 A 在正比例函数y=2x的图象上,
∴设点 A 的坐标为 (m, 2m) .
∵将线段OA 沿x 轴向右平移3个单位长度得到线段(
∴点 A'的坐标为 (m+3, 2m), 点O'的坐标为 (3, 0) .
∵点 B 为线段O'A'的中点,
∴点 B 的坐标为
∵点 A,B都在反比例函数 的图象上,
解得: (舍去),
∴点 A 的坐标为 (2, 4) .
∴k=2×4=8.
4. 解: 设点 B 的坐标为 (a, a) .
∵点 B 在反比例函数 的图象上,
解得a=1(负值已舍),即点B的坐标为 (1, 1) .
∴设点E 坐标为 (1+b, b) .
∵点 E 在反比例函数 的图象上,
∴ (1+b) ·b=1, 解得
∵b>0,
∴点 E 的横坐标
故选 C.
欲穷千里目,更上一层楼
5. 解: 设点 A 的坐标为 (m, n), 则 mn=6.
∵直线 AB过原点,
∴点O是线段AB 的中点.
∵AC⊥x轴,
∴AC∥OD, 则OD 是△BAC的中位线,
6. 解: 如图12所示, 过点 B 作BE⊥x轴于点E.
∵点 D 为OB 的中点,
∴CD 是△OBE 的中位线, 即
设点 A 的坐标为 则点 B 的坐标为
∵△ADO的面积为2,
解得
故选 B.
7. 解: 如图13所示, 连接OD, 过点C作CE∥AB, 交x轴于点E.
∵∠ABO=90°, 反比例函数 的图象经过OA 的中点C,
∵CE∥AB,
∴△OCE∽△OAB.
即 4S△OCE=S△OAB·
解得
8.解:设点 D 的坐标为(
∵四边形ABCD是矩形,且点 E 为AC 的中点,
∴点E的纵坐标为 将 代入反比例函数 得x=2m.
∴点 E 的坐标为
∴点 B 的横坐标为3m.
∴点F 的横坐标为3m,将x=3m代入反比例函数 得
∴点 F 的坐标为
∵△AEF的面积为2,
∴△ACF的面积为4.
∵AB=3m--m=2m,
解得k=6.
9.解:设反比例函数的解析式为
∵点 在该反比例函数的图象上,
且
即
解得k=-3,经检验,k=-3是原分式方程的解.
∴反比例函数的解析式为
10. 解: ∵点 A (x , y ), B (x , y ) 在反比例函数 的图象上,
∵直线y= kx (k<0) 与反比例函数 的图象相交于点A (x , y ),B (x , y ),
∴ -6.
