反比例函数与方程、不等式 同步练习(含答案)2024-2025学年人教版九年级数学下册
文档属性
| 名称 | 反比例函数与方程、不等式 同步练习(含答案)2024-2025学年人教版九年级数学下册 | 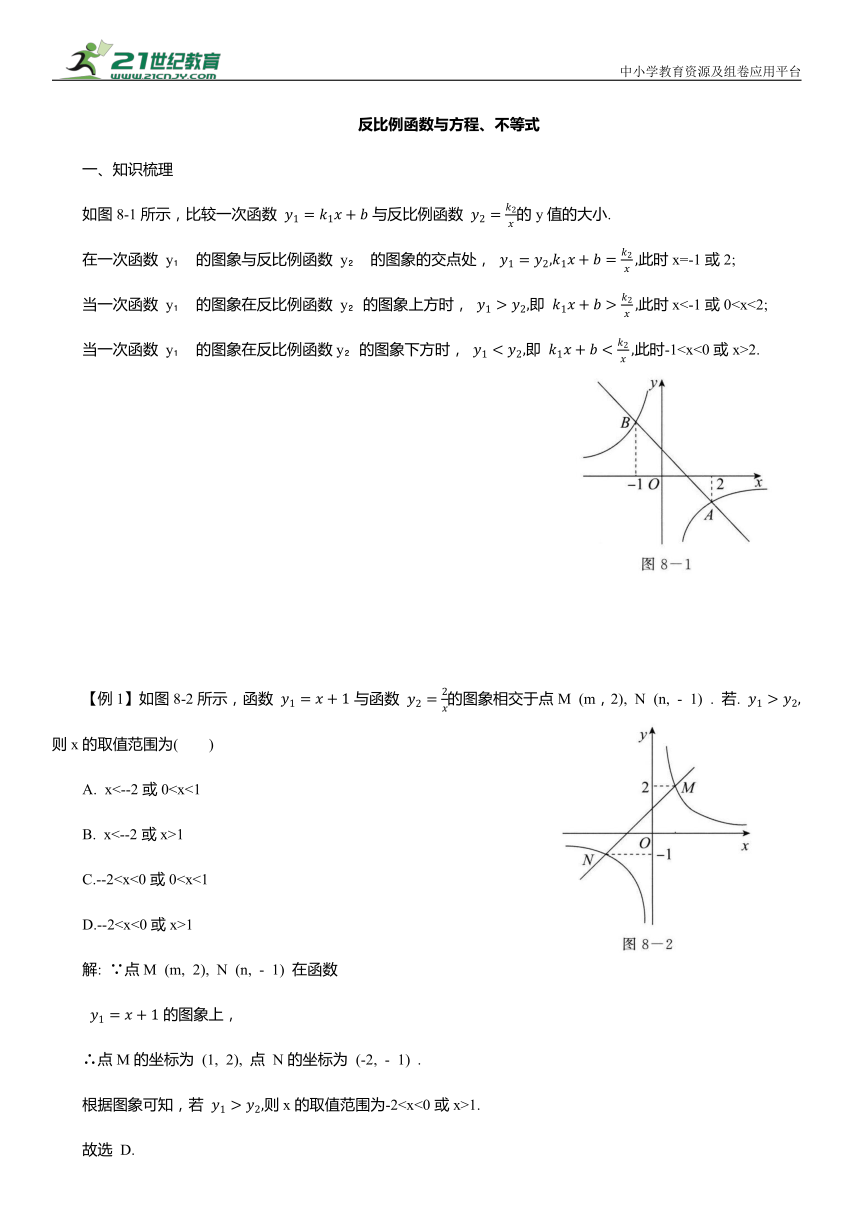 | |
| 格式 | docx | ||
| 文件大小 | 259.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 17:45:09 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
反比例函数与方程、不等式
一、知识梳理
如图8-1所示,比较一次函数 与反比例函数 的y值的大小.
在一次函数 y 的图象与反比例函数 y 的图象的交点处, 此时x=-1或2;
当一次函数 y 的图象在反比例函数 y 的图象上方时, 即 此时x<-1或0当一次函数 y 的图象在反比例函数y 的图象下方时, 即 此时-12.
【例1】如图8-2所示,函数 与函数 的图象相交于点M (m,2), N (n, - 1) . 若. 则x的取值范围为( )
A. x<--2或0B. x<--2或x>1
C.--2D.--21
解: ∵点M (m, 2), N (n, - 1) 在函数
的图象上,
∴点M的坐标为 (1, 2), 点 N的坐标为 (-2, - 1) .
根据图象可知,若 则x的取值范围为-21.
故选 D.
【例2】如图8-3所示, 过点C (2, 1) 作AC∥x轴, BC∥y轴, 点A, B都在直线y=-x+5上.若反比例函数 与△ABC总有公共点,则k的取值范围为 .
解: 如图8-4所示,作直线 y=x交直线AB于点 D.
∵点A, B都在直线y=-x+5上,
∴点 A 的坐标为 (4, 1), 点 B 的坐标为 (2, 3) .
∵联立方程 解得
∴点 D 的坐标为 (2.5, 2.5) .
∴点D 在线段AB 上.
∴当反比例函数的图象过点 C时,则有 k=2×1=2;
当反比例函数的图象过点 D 时,则有
∵反比例函数 与△ABC总有公共点,
∴k的取值范围为
二、分层练习
1.如图8--5所示,反比例函数 与一次函数y=kx+b的图象相交于点M,N,已知点M的坐标为 (1,3),点N 的纵坐标为--1.根据图象信息可得,关于x的方程 的解为 .
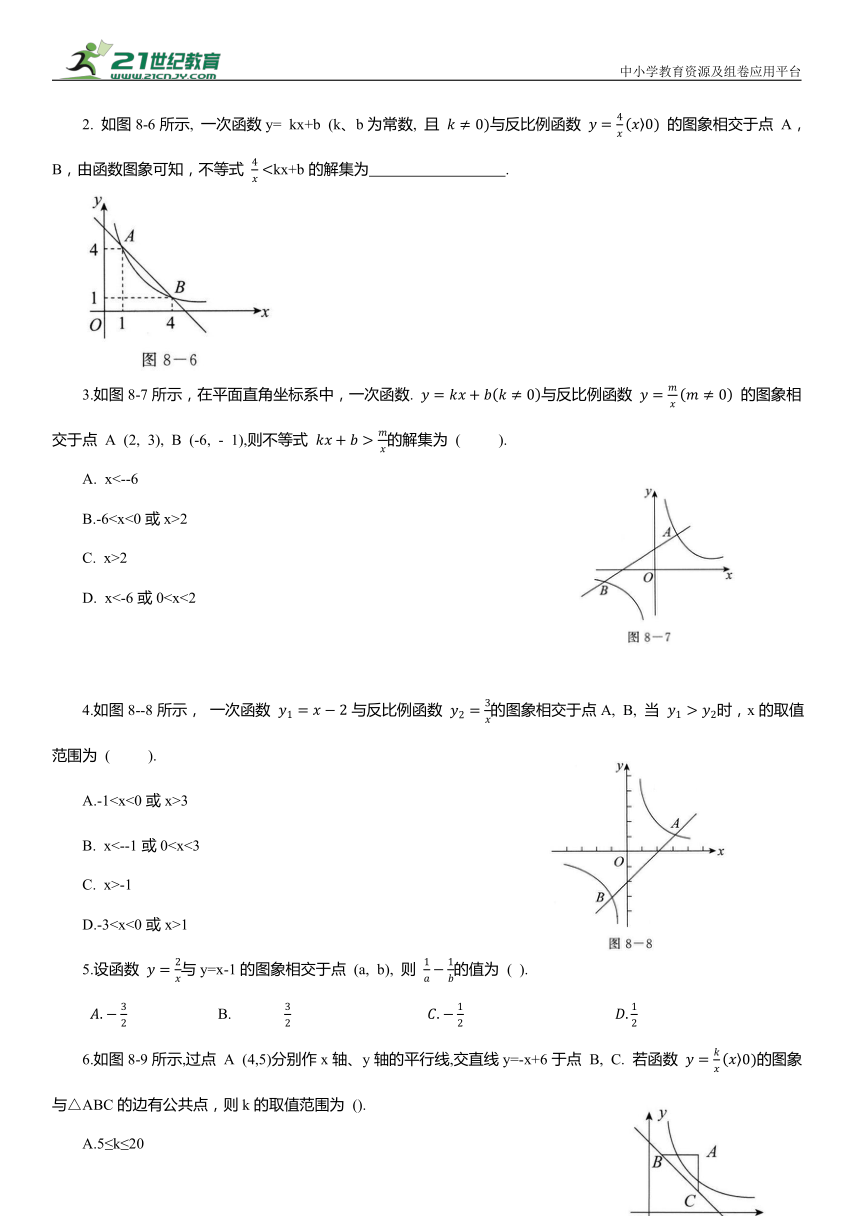
2. 如图8-6所示, 一次函数y= kx+b (k、b为常数, 且 与反比例函数 的图象相交于点 A,B,由函数图象可知,不等式 kx+b的解集为 .
3.如图8-7所示,在平面直角坐标系中,一次函数. 与反比例函数 的图象相交于点 A (2, 3), B (-6, - 1),则不等式 的解集为 ( ).
A. x<--6
B.-62
C. x>2
D. x<-6或04.如图8--8所示, 一次函数 与反比例函数 的图象相交于点A, B, 当 时,x的取值范围为 ( ).
A.-13
B. x<--1或0C. x>-1
D.-31
5.设函数 与y=x-1的图象相交于点 (a, b), 则 的值为 ( ).
B.
6.如图8-9所示,过点 A (4,5)分别作x轴、y轴的平行线,交直线y=-x+6于点 B, C. 若函数 的图象与△ABC的边有公共点,则k的取值范围为 ().
A.5≤k≤20
B.8≤k≤20
C.5≤k≤8
D.9≤k≤20
7.如图8-10所示,等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中点 A 的横坐标为1,且两条直角边AB,AC分别平行于x轴、y轴.若反比例函数 与△ABC有交点,则k的取值范围为 ( ).
A.1B.1≤k≤3
C.1≤k≤4
D.1≤k<4
8. 直线 y=x+b过点A (1, 0), 并与反比例函数 的图象只有一个公共点 B,则k 的值为 .
9.已知反比例函数 和一次函数y=kx+4,讨论k的值.
(1)反比例函数与一次函数没有交点;
(2)反比例函数与一次函数有一个交点;
(3)反比例函数与一次函数有两个交点.
10.如图8-11所示,在平面直角坐标系中,一次函数 的图象上有点 A (0, 5), C (10, 0), 且与反比例函数 的图象交于点 B (8, t) .
(1)求一次函数和反比例函数的函数解析式;
(2)将一次函数的图象向下平移m个单位,恰好与反比例函数的图象只有一个交点,求m的值.
1. 解: 设点 N 的坐标为 (a, - 1) .
∵点 M 的坐标为 (1,3),点 M,N在反比例函数 的图象上,
∴-a=1×3, 解得a=-3.
∴点 N 的坐标为 (-3, - 1) .
∴两个函数图象的交点为 (1, 3), (--3, - 1) .
∴关于x的方程 的解为
2.解: ∵由图象可知, 点A, B的坐标分别为 (1, 4), (4, 1), 且反比例函数有x>0,
∴不等式 的解集为13. 解: ∵由图象可知, 点A, B的坐标分别为 (2, 3), (-6, - 1),
∴不等式 的解集为-62.
故选 B.
4.解: ∵联立方程 解得 或
∴点 A, B的坐标分别为 (3, 1), (--1, - 3) .
∴当 时, x的取值范围为x>3或--1故选 A.
5. 解: ∵函数 与y=x-1的图象相交于点 (a, b),
即 ab=2, b-a=-1.
故选 C.
6.解: ∵过点A (4,5)分别作x轴、y轴的平行线,交直线 于点B, C,
∴点 B 的纵坐标为5,点C 的横坐标为4.
∵点 B, C在直线y=x+6的图象上,
∴将y=5代入y=-x+6得, x=1; 将x=4代入y=-x+6得,
∴点 B 的坐标为 (1, 5), 点 C的坐标为 (4, 2) .
∵函数 的图象与△ABC的边有公共点,
∴当公共点为点 A时,k=20; 当公共点为点 B时,k=5.
∴k的取值范围为5≤k≤20.
故选 A.
7.解: ∵点A在直线y=x的图象上,且点 A的横坐标为1,
∴把x=1代入y=x, 解得y=1, 则点A的坐标为 (1, 1) .
∵AB=AC=2,
∴点 B 的坐标为 (3, 1), 点 C的坐标为 (1, 3) .
∴线段 BC的中点坐标为 (2, 2) .
∴当反比例函数 经过点 (1, 1) 时, k=1;
当反比例函数 经过点 (2, 2) 时, k=4.
∴k的取值范围为1≤k≤4.
故选 C.
8. 解: ∵直线y=x+b过点A (1, 0),
∴1+b=0, 解得b=--1.
∴一次函数的解析式为y=x--1.
∵一次函数与反比例函数 的图象只有一个公共点 B,∴联立方程 整理得 则有 解得
9.解:联立方程 整理得
(1) ∵反比例函数与一次函数没有交点,则△<0,即 解得
∴当 时,反比例函数与一次函数没有交点.
(2) ∵反比例函数与一次函数有一个交点,则△=0,
即4 -4k× (--6) =0,解得
当k=0时,一次函数为y=6,与反比例函数有一个交点,
∴当 或k=0时,反比例函数与一次函数有一个交点.
(3) ∵反比例函数与一次函数有两个交点,则△>0,
即4 -4k× (-6) >0,解得
∴当 且k≠0时,反比例函数与一次函数有两个交点.
☆会当凌绝顶,一览众山小
10. 解: (1) ∵点A (0, 5), C (10, 0) 在一次函数y= kx+b(b≠0) 的图象上,
解得
∴一次函数的解析式为
∵点 B (8,t)在一次函数的图象上,
∴点 B的坐标为(8, 1) .
又∵点 B (8,1)在反比例函数 的图象上,
∴反比例函数的解析式为
(2)直线AB向下平移m个单位长度后得到新的直线解析式为
∵直线 AB 向下平移m个单位长度后恰好与反比例函数的图象只有一个交点,
整理得x -2 (5-m) x+16=0,则 解得m=9或m=1.
反比例函数与方程、不等式
一、知识梳理
如图8-1所示,比较一次函数 与反比例函数 的y值的大小.
在一次函数 y 的图象与反比例函数 y 的图象的交点处, 此时x=-1或2;
当一次函数 y 的图象在反比例函数 y 的图象上方时, 即 此时x<-1或0
【例1】如图8-2所示,函数 与函数 的图象相交于点M (m,2), N (n, - 1) . 若. 则x的取值范围为( )
A. x<--2或0
C.--2
解: ∵点M (m, 2), N (n, - 1) 在函数
的图象上,
∴点M的坐标为 (1, 2), 点 N的坐标为 (-2, - 1) .
根据图象可知,若 则x的取值范围为-2
故选 D.
【例2】如图8-3所示, 过点C (2, 1) 作AC∥x轴, BC∥y轴, 点A, B都在直线y=-x+5上.若反比例函数 与△ABC总有公共点,则k的取值范围为 .
解: 如图8-4所示,作直线 y=x交直线AB于点 D.
∵点A, B都在直线y=-x+5上,
∴点 A 的坐标为 (4, 1), 点 B 的坐标为 (2, 3) .
∵联立方程 解得
∴点 D 的坐标为 (2.5, 2.5) .
∴点D 在线段AB 上.
∴当反比例函数的图象过点 C时,则有 k=2×1=2;
当反比例函数的图象过点 D 时,则有
∵反比例函数 与△ABC总有公共点,
∴k的取值范围为
二、分层练习
1.如图8--5所示,反比例函数 与一次函数y=kx+b的图象相交于点M,N,已知点M的坐标为 (1,3),点N 的纵坐标为--1.根据图象信息可得,关于x的方程 的解为 .
2. 如图8-6所示, 一次函数y= kx+b (k、b为常数, 且 与反比例函数 的图象相交于点 A,B,由函数图象可知,不等式 kx+b的解集为 .
3.如图8-7所示,在平面直角坐标系中,一次函数. 与反比例函数 的图象相交于点 A (2, 3), B (-6, - 1),则不等式 的解集为 ( ).
A. x<--6
B.-6
C. x>2
D. x<-6或0
A.-1
B. x<--1或0
D.-3
5.设函数 与y=x-1的图象相交于点 (a, b), 则 的值为 ( ).
B.
6.如图8-9所示,过点 A (4,5)分别作x轴、y轴的平行线,交直线y=-x+6于点 B, C. 若函数 的图象与△ABC的边有公共点,则k的取值范围为 ().
A.5≤k≤20
B.8≤k≤20
C.5≤k≤8
D.9≤k≤20
7.如图8-10所示,等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中点 A 的横坐标为1,且两条直角边AB,AC分别平行于x轴、y轴.若反比例函数 与△ABC有交点,则k的取值范围为 ( ).
A.1
C.1≤k≤4
D.1≤k<4
8. 直线 y=x+b过点A (1, 0), 并与反比例函数 的图象只有一个公共点 B,则k 的值为 .
9.已知反比例函数 和一次函数y=kx+4,讨论k的值.
(1)反比例函数与一次函数没有交点;
(2)反比例函数与一次函数有一个交点;
(3)反比例函数与一次函数有两个交点.
10.如图8-11所示,在平面直角坐标系中,一次函数 的图象上有点 A (0, 5), C (10, 0), 且与反比例函数 的图象交于点 B (8, t) .
(1)求一次函数和反比例函数的函数解析式;
(2)将一次函数的图象向下平移m个单位,恰好与反比例函数的图象只有一个交点,求m的值.
1. 解: 设点 N 的坐标为 (a, - 1) .
∵点 M 的坐标为 (1,3),点 M,N在反比例函数 的图象上,
∴-a=1×3, 解得a=-3.
∴点 N 的坐标为 (-3, - 1) .
∴两个函数图象的交点为 (1, 3), (--3, - 1) .
∴关于x的方程 的解为
2.解: ∵由图象可知, 点A, B的坐标分别为 (1, 4), (4, 1), 且反比例函数有x>0,
∴不等式 的解集为1
∴不等式 的解集为-6
故选 B.
4.解: ∵联立方程 解得 或
∴点 A, B的坐标分别为 (3, 1), (--1, - 3) .
∴当 时, x的取值范围为x>3或--1
5. 解: ∵函数 与y=x-1的图象相交于点 (a, b),
即 ab=2, b-a=-1.
故选 C.
6.解: ∵过点A (4,5)分别作x轴、y轴的平行线,交直线 于点B, C,
∴点 B 的纵坐标为5,点C 的横坐标为4.
∵点 B, C在直线y=x+6的图象上,
∴将y=5代入y=-x+6得, x=1; 将x=4代入y=-x+6得,
∴点 B 的坐标为 (1, 5), 点 C的坐标为 (4, 2) .
∵函数 的图象与△ABC的边有公共点,
∴当公共点为点 A时,k=20; 当公共点为点 B时,k=5.
∴k的取值范围为5≤k≤20.
故选 A.
7.解: ∵点A在直线y=x的图象上,且点 A的横坐标为1,
∴把x=1代入y=x, 解得y=1, 则点A的坐标为 (1, 1) .
∵AB=AC=2,
∴点 B 的坐标为 (3, 1), 点 C的坐标为 (1, 3) .
∴线段 BC的中点坐标为 (2, 2) .
∴当反比例函数 经过点 (1, 1) 时, k=1;
当反比例函数 经过点 (2, 2) 时, k=4.
∴k的取值范围为1≤k≤4.
故选 C.
8. 解: ∵直线y=x+b过点A (1, 0),
∴1+b=0, 解得b=--1.
∴一次函数的解析式为y=x--1.
∵一次函数与反比例函数 的图象只有一个公共点 B,∴联立方程 整理得 则有 解得
9.解:联立方程 整理得
(1) ∵反比例函数与一次函数没有交点,则△<0,即 解得
∴当 时,反比例函数与一次函数没有交点.
(2) ∵反比例函数与一次函数有一个交点,则△=0,
即4 -4k× (--6) =0,解得
当k=0时,一次函数为y=6,与反比例函数有一个交点,
∴当 或k=0时,反比例函数与一次函数有一个交点.
(3) ∵反比例函数与一次函数有两个交点,则△>0,
即4 -4k× (-6) >0,解得
∴当 且k≠0时,反比例函数与一次函数有两个交点.
☆会当凌绝顶,一览众山小
10. 解: (1) ∵点A (0, 5), C (10, 0) 在一次函数y= kx+b(b≠0) 的图象上,
解得
∴一次函数的解析式为
∵点 B (8,t)在一次函数的图象上,
∴点 B的坐标为(8, 1) .
又∵点 B (8,1)在反比例函数 的图象上,
∴反比例函数的解析式为
(2)直线AB向下平移m个单位长度后得到新的直线解析式为
∵直线 AB 向下平移m个单位长度后恰好与反比例函数的图象只有一个交点,
整理得x -2 (5-m) x+16=0,则 解得m=9或m=1.
