反比例函数与三垂直 同步练习(含答案)2024-2025学年人教版九年级数学下册
文档属性
| 名称 | 反比例函数与三垂直 同步练习(含答案)2024-2025学年人教版九年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 389.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 17:49:51 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
反比例函数与三垂直
一、 知识梳理
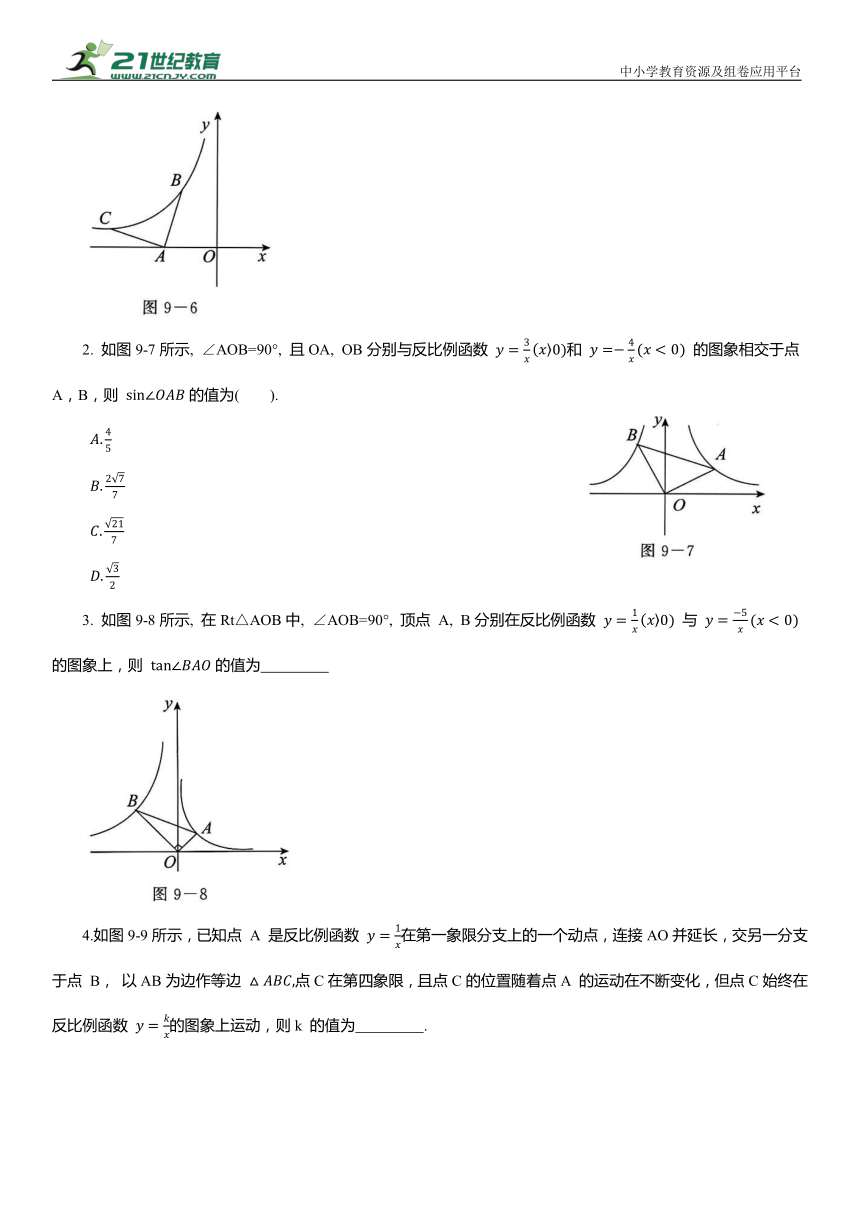
如图9-1和图9-2所示, 点 B, C, E在同一直线上, AC=CD, AC⊥CD, ∠B=∠E=90°, 则有△ABC≌△CED, 像这样的图形被称为“三垂直”全等模型.
模型构造三步走:
①作一个等腰直角即AC=CD, AC⊥CD;
②作一条过直角顶点的直线l,即过点 C作直线BE;
③过直角的两个锐角顶点向直线l作垂线,即过点 A,D作 于点B, DE⊥BE于点E.
【例1】如图9-3所示,正方形ACBE的边长是 点B,C分别在x轴和y轴的正半轴上,BO=2,ED⊥x轴于点 D,ED 的中点 F 在反比例函数 的图象上, 则k= .
解: ∵正方形ACBE 的边长是
∵∠CBE=90°,
∴∠OBC+∠EBD=90°.
∵∠OBC+∠OCB=90°,
∴∠OCB=∠EBD.
在△OBC和△DEB中,
∴△OBC≌△DEB (AAS) .
∴BD=OC=1, DE=OB=2.
∴OD=3.
∴点 E的坐标为 (3, 2) .
∵点F是ED的中点,
∴点 F的坐标为 (3, 1) .
∵点 F 在反比例函数 的图象上,
∴k=3×1=3.
【例2】如图9-4所示,点A,B分别在反比例函数 与
(x>0) 的图象上, 且 则k= .
解: 过点 A 作AC⊥y轴于点C, 过点 B 作BD⊥y轴于点 D, 如图9-5所示.
∵AC⊥y轴, BD⊥y轴, OA⊥OB,
∵∠OAC+∠AOC=90°,
∴∠AOC=∠OBD.
∴△AOC∽△OBD.
∵反比例函数 在第四象限有图象,
∴k<0.
解得k=-8.
二、分层练习
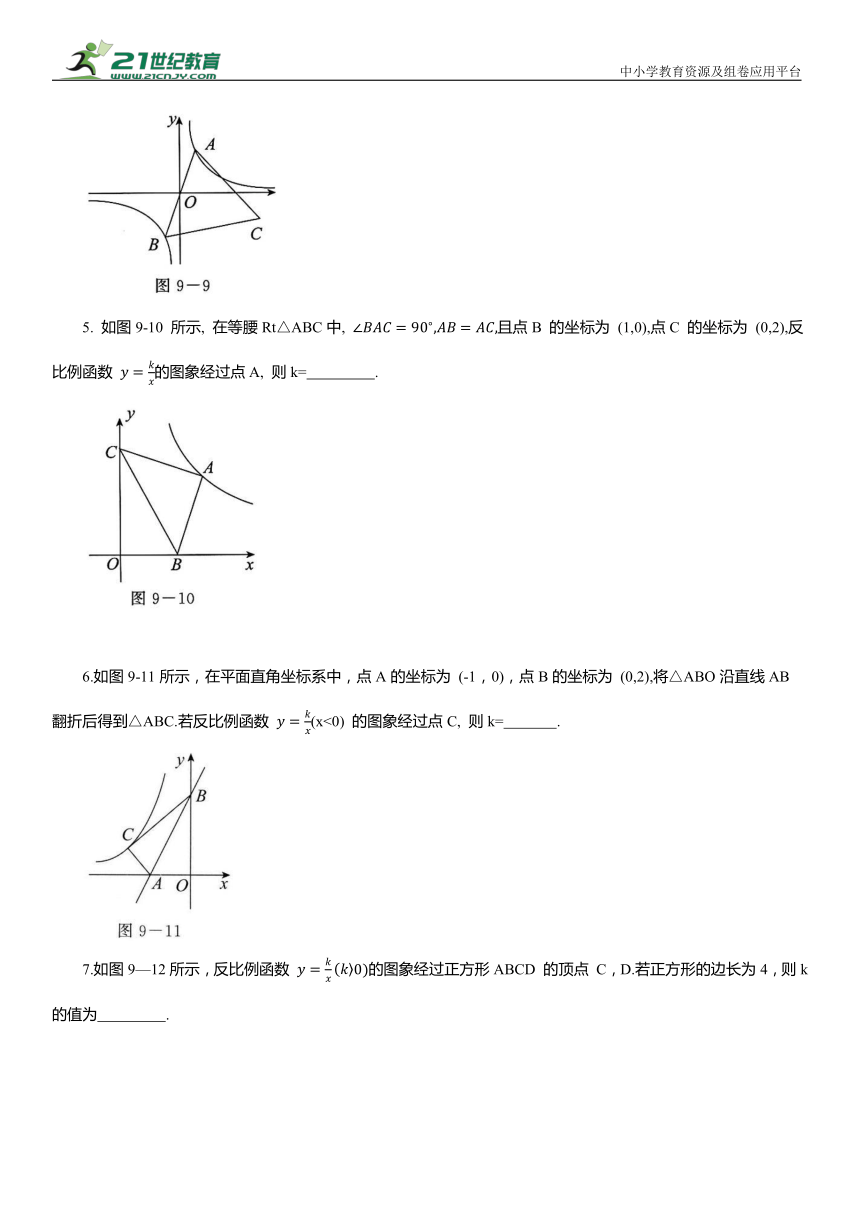
1.如图9-6所示,点B 为反比例函数 图象上的一点,点A 为x轴负半轴上的一点,连接AB,将线段AB绕点A 逆时针旋转 点 B 的对应点为点C.若点 C恰好也在反比例函数 的图象上,点B,C的纵坐标分别为4和1,则k= .
2. 如图9-7所示, ∠AOB=90°, 且OA, OB分别与反比例函数 和 的图象相交于点 A,B,则 的值为( ).
3. 如图9-8所示, 在Rt△AOB中, ∠AOB=90°, 顶点 A, B分别在反比例函数 与 的图象上,则 的值为
4.如图9-9所示,已知点 A 是反比例函数 在第一象限分支上的一个动点,连接AO并延长,交另一分支于点 B, 以AB为边作等边 点C在第四象限,且点C的位置随着点A 的运动在不断变化,但点C始终在反比例函数 的图象上运动,则k 的值为 .
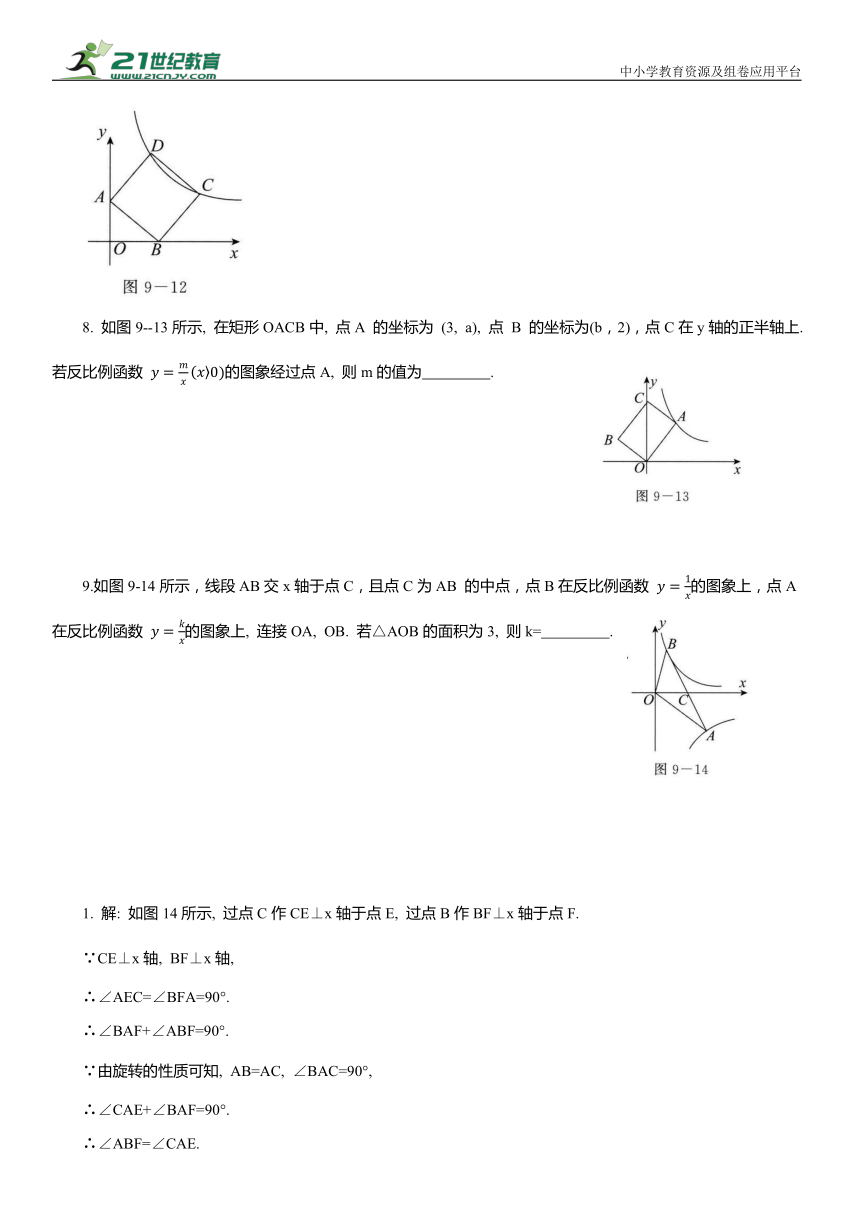
5. 如图9-10 所示, 在等腰Rt△ABC中, 且点B 的坐标为 (1,0),点C 的坐标为 (0,2),反比例函数 的图象经过点A, 则k= .
6.如图9-11所示,在平面直角坐标系中,点A的坐标为 (-1,0),点B的坐标为 (0,2),将△ABO沿直线AB 翻折后得到△ABC.若反比例函数 (x<0) 的图象经过点C, 则k= .
7.如图9—12所示,反比例函数 的图象经过正方形ABCD 的顶点 C,D.若正方形的边长为4,则k的值为 .
8. 如图9--13所示, 在矩形OACB中, 点A 的坐标为 (3, a), 点 B 的坐标为(b,2),点C在y轴的正半轴上.若反比例函数 的图象经过点A, 则m的值为 .
9.如图9-14所示,线段AB交x轴于点C,且点C为AB 的中点,点B在反比例函数 的图象上,点A 在反比例函数 的图象上, 连接OA, OB. 若△AOB的面积为3, 则k= .
1. 解: 如图14所示, 过点C作CE⊥x轴于点E, 过点B作BF⊥x轴于点F.
∵CE⊥x轴, BF⊥x轴,
∴∠AEC=∠BFA=90°.
∴∠BAF+∠ABF=90°.
∵由旋转的性质可知, AB=AC, ∠BAC=90°,
∴∠CAE+∠BAF=90°.
∴∠ABF=∠CAE.
∴△ABF≌△CAE (AAS) .
∴AF=CE, BF=AE.
∵点 B,C的纵坐标分别为4 和1,
∴CE=1, BF=4.
∴AF=1, AE=4.
设点 B的坐标为 (x, 4), 则点C的坐标为 (x-5, 1) .
∵点 B,C在反比例函数 的图象上,
∴4x=x-5,解得
∴点 B 的坐标为
2. 解: 如图15 所示, 过点A, B分别作AM⊥x轴于点 M, BN⊥x轴于点 N.
∵点 A 在反比例函数 的图象上,
∵点 B 在反比例函数 的图象上,
∵∠AOB=90°,
∴△BON∽△OAM.
即
∵在 Rt△AOB中, 设OB=2m, 则
故选 B.
3.解: 如图16所示, 过点 A作AC⊥x轴于点C, 过点B作BD⊥x轴于点D, 则∠BDO=∠ACO=90°.
∵顶点 A,B分别在反比例函数 与 的图象上,
∵∠AOB=90°,
∴△BDO∽△OCA.
即
4. 解: 连接OC, 如图17所示, 过点A作AE⊥y轴于点E, 过点C作( 轴于点 F.
∵反比例函数 关于原点对称,
∴点 A 与点 B 关于原点对称.
∴OA=OB.
又∵△ABC是等边三角形,
∴OC⊥AB, ∠BAC=60°.
即
∵AE⊥y轴, CF⊥y轴, OC⊥AB,
∴∠AEO=∠OFC, ∠AOE=90°-∠FOC=∠OCF.
∴△AEO∽△OFC.
设点 A 的坐标为 (a, b) .
∵点 A位于第一象限,
∴AE=a, OE=b.
∵点 A在反比例函数 的图象上,
∴ab=1.
设点C的坐标为(x, y) .
∵点C位于第四象限,
∴FC=x, OF=-y.
∴FC·OF=x· (-y) =-xy=3.
∴xy=-3.
∵点 C在反比例函数 的图象上,
∴k= xy=-3.
5. 解: 过点 A 作AH⊥x轴于点 H, 过点 C 作( 于点G, 如图18所示,
则有∠AHB=∠CGA=90°.
∵∠AHB=90°,
∴∠ABH+∠BAH=90°.
∵∠BAC=90°,
∴∠BAH+∠CAG=90°.
又∵AB=AC,
∴△ABH≌△CAG (AAS) .
∴AH=CG, BH=AG.
设BH=m.
∵点 B 的坐标为 (1, 0), 点C的坐标为 (0, 2),
∴OB=1, OC=2.
∴CG=OB+BH=1+m.
∵GH=OC, 即1+m+m=2, 解得
∴点A的坐标为
∵点 A 在反比例函数 的图象上,
6.解:如图19 所示,过点C作CD⊥x轴于点D,过点 B 作 轴且与DC 的延长线相交于点 E.
由折叠可知, AO=AC=1, BO=BC=2.
∵∠E=∠CDA=∠ACB=90°,
∴∠ECB+∠EBC=90°, ∠ECB+∠ACD=90°.
∴∠EBC=∠ACD.
∴△ACD∽△CBE.
设CD=m, 则BE=2m, CE=2-m, AD=2m-1.
∵在 Rt△ACD中, 由勾股定理得( 即 1 , 解得 (舍去),
∴点 C 的坐标为
∵点 C 在反比例函数 的图象上,
7. 解: 如图20所示, 作CE⊥x轴于点E, DF⊥y轴于点F, 设点 A 的坐标为 (0, m), 点 B 的坐标为 (n, 0) .
∵四边形ABCD为正方形,
∴BC=BA, ∠ABC=90°.
∴∠ABO+∠CBE=90°.
∵∠ABO+∠OAB=90°,
∴∠CBE=∠OAB.
∵∠AOB=∠BEC,
∴△AOB≌△BEC (AAS) .
∴OA=BE=m, OB=CE=n.
∴点 C的坐标为 (m+n, n) .
∵同理可证, △AOB≌△DFA (AAS) .
∴OA=DF=m, OB=AF=n.
∴点 D 的坐标为 (m, m+n) .
∵反比例函数 经过正方形ABCD的顶点C,D,
∴ (m+n) n=m (m+n), 即m=n.
即 解得
∴点 C的坐标为
8.解:如图21所示,过点A作AE⊥y轴于点E,过点 B作 轴于点F.
∵AE⊥y轴, BF⊥y轴,
∴∠AEC=∠BFO=90°.
∵四边形OACB为矩形,
∴AC=BO, AC∥OB.
∴∠ACE=∠BOF.
∴△ACE≌△BOF (AAS) .
∴CE=OF, AE=BF.
∴点 A 的坐标为 (3, a), 点 B的坐标为 (b, 2) .
∴CE=OF=2, AE=BF=3, OC=a+2.
a ,
,解得
∴点 A 的坐标为
∵反比例函数 的图象经过点 A,
会当凌绝顶,一览众山小
9. 解: 如图22所示, 作 BD⊥x轴于点D, AE⊥x轴于点E.
∵点 B 在反比例函数 的图象上,点A 在反比例函数 的图象上,
∵点 C为AB 的中点,
∴BC=AC.
在△BCD和△ACE中,
∴△BCD≌△ACE (AAS) .
∴S△BDC=S△ACE.
∴S△BOD+S△AOE=S△AOB =3, 即 解得|k|=5.
∵k<0, ∴k=-5
反比例函数与三垂直
一、 知识梳理
如图9-1和图9-2所示, 点 B, C, E在同一直线上, AC=CD, AC⊥CD, ∠B=∠E=90°, 则有△ABC≌△CED, 像这样的图形被称为“三垂直”全等模型.
模型构造三步走:
①作一个等腰直角即AC=CD, AC⊥CD;
②作一条过直角顶点的直线l,即过点 C作直线BE;
③过直角的两个锐角顶点向直线l作垂线,即过点 A,D作 于点B, DE⊥BE于点E.
【例1】如图9-3所示,正方形ACBE的边长是 点B,C分别在x轴和y轴的正半轴上,BO=2,ED⊥x轴于点 D,ED 的中点 F 在反比例函数 的图象上, 则k= .
解: ∵正方形ACBE 的边长是
∵∠CBE=90°,
∴∠OBC+∠EBD=90°.
∵∠OBC+∠OCB=90°,
∴∠OCB=∠EBD.
在△OBC和△DEB中,
∴△OBC≌△DEB (AAS) .
∴BD=OC=1, DE=OB=2.
∴OD=3.
∴点 E的坐标为 (3, 2) .
∵点F是ED的中点,
∴点 F的坐标为 (3, 1) .
∵点 F 在反比例函数 的图象上,
∴k=3×1=3.
【例2】如图9-4所示,点A,B分别在反比例函数 与
(x>0) 的图象上, 且 则k= .
解: 过点 A 作AC⊥y轴于点C, 过点 B 作BD⊥y轴于点 D, 如图9-5所示.
∵AC⊥y轴, BD⊥y轴, OA⊥OB,
∵∠OAC+∠AOC=90°,
∴∠AOC=∠OBD.
∴△AOC∽△OBD.
∵反比例函数 在第四象限有图象,
∴k<0.
解得k=-8.
二、分层练习
1.如图9-6所示,点B 为反比例函数 图象上的一点,点A 为x轴负半轴上的一点,连接AB,将线段AB绕点A 逆时针旋转 点 B 的对应点为点C.若点 C恰好也在反比例函数 的图象上,点B,C的纵坐标分别为4和1,则k= .
2. 如图9-7所示, ∠AOB=90°, 且OA, OB分别与反比例函数 和 的图象相交于点 A,B,则 的值为( ).
3. 如图9-8所示, 在Rt△AOB中, ∠AOB=90°, 顶点 A, B分别在反比例函数 与 的图象上,则 的值为
4.如图9-9所示,已知点 A 是反比例函数 在第一象限分支上的一个动点,连接AO并延长,交另一分支于点 B, 以AB为边作等边 点C在第四象限,且点C的位置随着点A 的运动在不断变化,但点C始终在反比例函数 的图象上运动,则k 的值为 .
5. 如图9-10 所示, 在等腰Rt△ABC中, 且点B 的坐标为 (1,0),点C 的坐标为 (0,2),反比例函数 的图象经过点A, 则k= .
6.如图9-11所示,在平面直角坐标系中,点A的坐标为 (-1,0),点B的坐标为 (0,2),将△ABO沿直线AB 翻折后得到△ABC.若反比例函数 (x<0) 的图象经过点C, 则k= .
7.如图9—12所示,反比例函数 的图象经过正方形ABCD 的顶点 C,D.若正方形的边长为4,则k的值为 .
8. 如图9--13所示, 在矩形OACB中, 点A 的坐标为 (3, a), 点 B 的坐标为(b,2),点C在y轴的正半轴上.若反比例函数 的图象经过点A, 则m的值为 .
9.如图9-14所示,线段AB交x轴于点C,且点C为AB 的中点,点B在反比例函数 的图象上,点A 在反比例函数 的图象上, 连接OA, OB. 若△AOB的面积为3, 则k= .
1. 解: 如图14所示, 过点C作CE⊥x轴于点E, 过点B作BF⊥x轴于点F.
∵CE⊥x轴, BF⊥x轴,
∴∠AEC=∠BFA=90°.
∴∠BAF+∠ABF=90°.
∵由旋转的性质可知, AB=AC, ∠BAC=90°,
∴∠CAE+∠BAF=90°.
∴∠ABF=∠CAE.
∴△ABF≌△CAE (AAS) .
∴AF=CE, BF=AE.
∵点 B,C的纵坐标分别为4 和1,
∴CE=1, BF=4.
∴AF=1, AE=4.
设点 B的坐标为 (x, 4), 则点C的坐标为 (x-5, 1) .
∵点 B,C在反比例函数 的图象上,
∴4x=x-5,解得
∴点 B 的坐标为
2. 解: 如图15 所示, 过点A, B分别作AM⊥x轴于点 M, BN⊥x轴于点 N.
∵点 A 在反比例函数 的图象上,
∵点 B 在反比例函数 的图象上,
∵∠AOB=90°,
∴△BON∽△OAM.
即
∵在 Rt△AOB中, 设OB=2m, 则
故选 B.
3.解: 如图16所示, 过点 A作AC⊥x轴于点C, 过点B作BD⊥x轴于点D, 则∠BDO=∠ACO=90°.
∵顶点 A,B分别在反比例函数 与 的图象上,
∵∠AOB=90°,
∴△BDO∽△OCA.
即
4. 解: 连接OC, 如图17所示, 过点A作AE⊥y轴于点E, 过点C作( 轴于点 F.
∵反比例函数 关于原点对称,
∴点 A 与点 B 关于原点对称.
∴OA=OB.
又∵△ABC是等边三角形,
∴OC⊥AB, ∠BAC=60°.
即
∵AE⊥y轴, CF⊥y轴, OC⊥AB,
∴∠AEO=∠OFC, ∠AOE=90°-∠FOC=∠OCF.
∴△AEO∽△OFC.
设点 A 的坐标为 (a, b) .
∵点 A位于第一象限,
∴AE=a, OE=b.
∵点 A在反比例函数 的图象上,
∴ab=1.
设点C的坐标为(x, y) .
∵点C位于第四象限,
∴FC=x, OF=-y.
∴FC·OF=x· (-y) =-xy=3.
∴xy=-3.
∵点 C在反比例函数 的图象上,
∴k= xy=-3.
5. 解: 过点 A 作AH⊥x轴于点 H, 过点 C 作( 于点G, 如图18所示,
则有∠AHB=∠CGA=90°.
∵∠AHB=90°,
∴∠ABH+∠BAH=90°.
∵∠BAC=90°,
∴∠BAH+∠CAG=90°.
又∵AB=AC,
∴△ABH≌△CAG (AAS) .
∴AH=CG, BH=AG.
设BH=m.
∵点 B 的坐标为 (1, 0), 点C的坐标为 (0, 2),
∴OB=1, OC=2.
∴CG=OB+BH=1+m.
∵GH=OC, 即1+m+m=2, 解得
∴点A的坐标为
∵点 A 在反比例函数 的图象上,
6.解:如图19 所示,过点C作CD⊥x轴于点D,过点 B 作 轴且与DC 的延长线相交于点 E.
由折叠可知, AO=AC=1, BO=BC=2.
∵∠E=∠CDA=∠ACB=90°,
∴∠ECB+∠EBC=90°, ∠ECB+∠ACD=90°.
∴∠EBC=∠ACD.
∴△ACD∽△CBE.
设CD=m, 则BE=2m, CE=2-m, AD=2m-1.
∵在 Rt△ACD中, 由勾股定理得( 即 1 , 解得 (舍去),
∴点 C 的坐标为
∵点 C 在反比例函数 的图象上,
7. 解: 如图20所示, 作CE⊥x轴于点E, DF⊥y轴于点F, 设点 A 的坐标为 (0, m), 点 B 的坐标为 (n, 0) .
∵四边形ABCD为正方形,
∴BC=BA, ∠ABC=90°.
∴∠ABO+∠CBE=90°.
∵∠ABO+∠OAB=90°,
∴∠CBE=∠OAB.
∵∠AOB=∠BEC,
∴△AOB≌△BEC (AAS) .
∴OA=BE=m, OB=CE=n.
∴点 C的坐标为 (m+n, n) .
∵同理可证, △AOB≌△DFA (AAS) .
∴OA=DF=m, OB=AF=n.
∴点 D 的坐标为 (m, m+n) .
∵反比例函数 经过正方形ABCD的顶点C,D,
∴ (m+n) n=m (m+n), 即m=n.
即 解得
∴点 C的坐标为
8.解:如图21所示,过点A作AE⊥y轴于点E,过点 B作 轴于点F.
∵AE⊥y轴, BF⊥y轴,
∴∠AEC=∠BFO=90°.
∵四边形OACB为矩形,
∴AC=BO, AC∥OB.
∴∠ACE=∠BOF.
∴△ACE≌△BOF (AAS) .
∴CE=OF, AE=BF.
∴点 A 的坐标为 (3, a), 点 B的坐标为 (b, 2) .
∴CE=OF=2, AE=BF=3, OC=a+2.
a ,
,解得
∴点 A 的坐标为
∵反比例函数 的图象经过点 A,
会当凌绝顶,一览众山小
9. 解: 如图22所示, 作 BD⊥x轴于点D, AE⊥x轴于点E.
∵点 B 在反比例函数 的图象上,点A 在反比例函数 的图象上,
∵点 C为AB 的中点,
∴BC=AC.
在△BCD和△ACE中,
∴△BCD≌△ACE (AAS) .
∴S△BDC=S△ACE.
∴S△BOD+S△AOE=S△AOB =3, 即 解得|k|=5.
∵k<0, ∴k=-5
同课章节目录
