反比例函数与几何综合 同步练习(含答案)2024-2025学年人教版九年级数学下册
文档属性
| 名称 | 反比例函数与几何综合 同步练习(含答案)2024-2025学年人教版九年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 321.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 17:53:50 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
反比例函数与几何综合
一、知识梳理
【例】如图11--1所示,一次函数y=ax+4与反比例函数 的图象相交于点A, B. 点A的横坐标为1, 过点A作AC⊥x轴于点C, 连接BC.
(1)求一次函数与反比例函数的解析式;
(2) 求 sin∠BAC的值;
(3)求点 B 的坐标,并直接写出不等式 的解集.
解: (1) ∵把x=1代入 得y=8-a,
∴点 A的坐标为 (1, 8--a) .
∵把点A (1, 8-a) 代入y= ax+4,得8--a=a+4, 解得a=2,
∴一次函数的解析式为 y=2x+4,反比例函数的解析式为
(2) ∵a=2,
∴点A的坐标为 (1, 6) .
∴AC=6, OC=1.
设直线y=2x+4与x轴的交点为点D.
∵当 y=0时, 有2x+4=0, 解得x=--2,故点 D的坐标为 (--2, 0),
∴OD=2.
∴CD=3.
(3) ∵联立方程 解得 或
∴点 B 的坐标为 (-3, - 2) .
由图象可知,不等式 的解集为x<-3或0二、分层练习
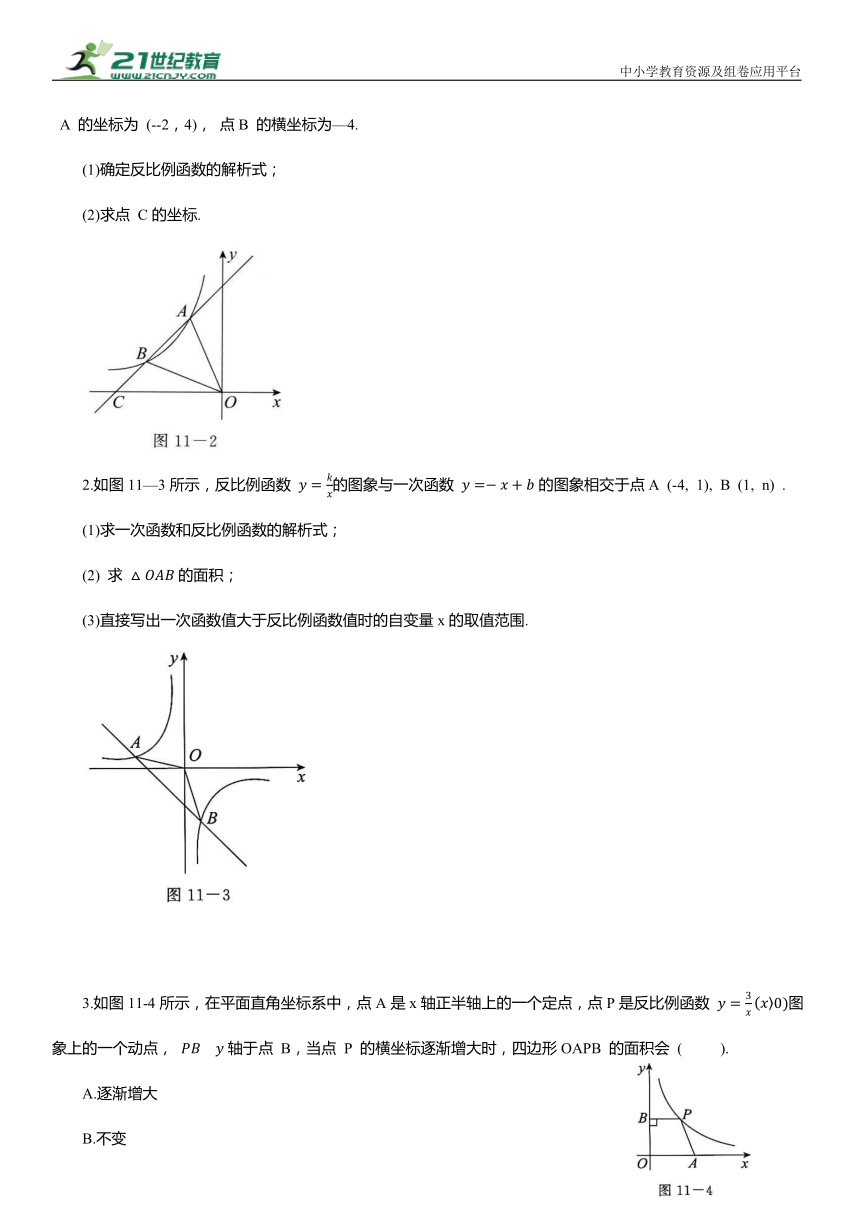
1. 如图11-2所示, 直线. 与反比例函数 的图象相交于点A,B,与x轴相交于点C,其中点 A 的坐标为 (--2,4), 点B 的横坐标为—4.
(1)确定反比例函数的解析式;
(2)求点 C的坐标.
2.如图11—3所示,反比例函数 的图象与一次函数 的图象相交于点A (-4, 1), B (1, n) .
(1)求一次函数和反比例函数的解析式;
(2) 求 的面积;
(3)直接写出一次函数值大于反比例函数值时的自变量x的取值范围.
3.如图11-4所示,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是反比例函数 图象上的一个动点, 轴于点 B,当点 P 的横坐标逐渐增大时,四边形OAPB 的面积会 ( ).
A.逐渐增大
B.不变
C.逐渐减小
D.先增大后减小
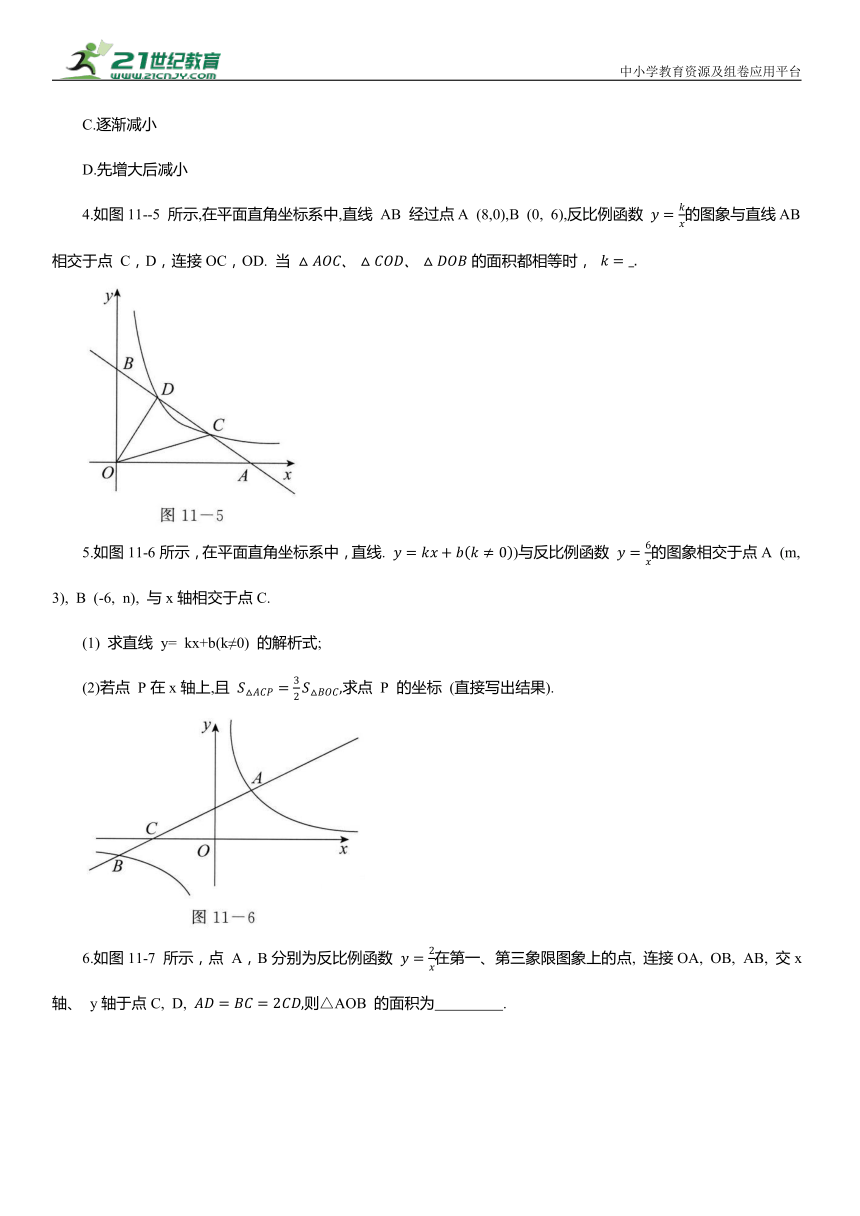
4.如图11--5 所示,在平面直角坐标系中,直线 AB 经过点A (8,0),B (0, 6),反比例函数 的图象与直线AB 相交于点 C,D,连接OC,OD. 当 的面积都相等时,
5.如图11-6所示,在平面直角坐标系中,直线. )与反比例函数 的图象相交于点A (m, 3), B (-6, n), 与x轴相交于点C.
(1) 求直线 y= kx+b(k≠0) 的解析式;
(2)若点 P在x轴上,且 求点 P 的坐标 (直接写出结果).
6.如图11-7 所示,点 A,B分别为反比例函数 在第一、第三象限图象上的点, 连接OA, OB, AB, 交x轴、 y轴于点C, D, 则△AOB 的面积为 .
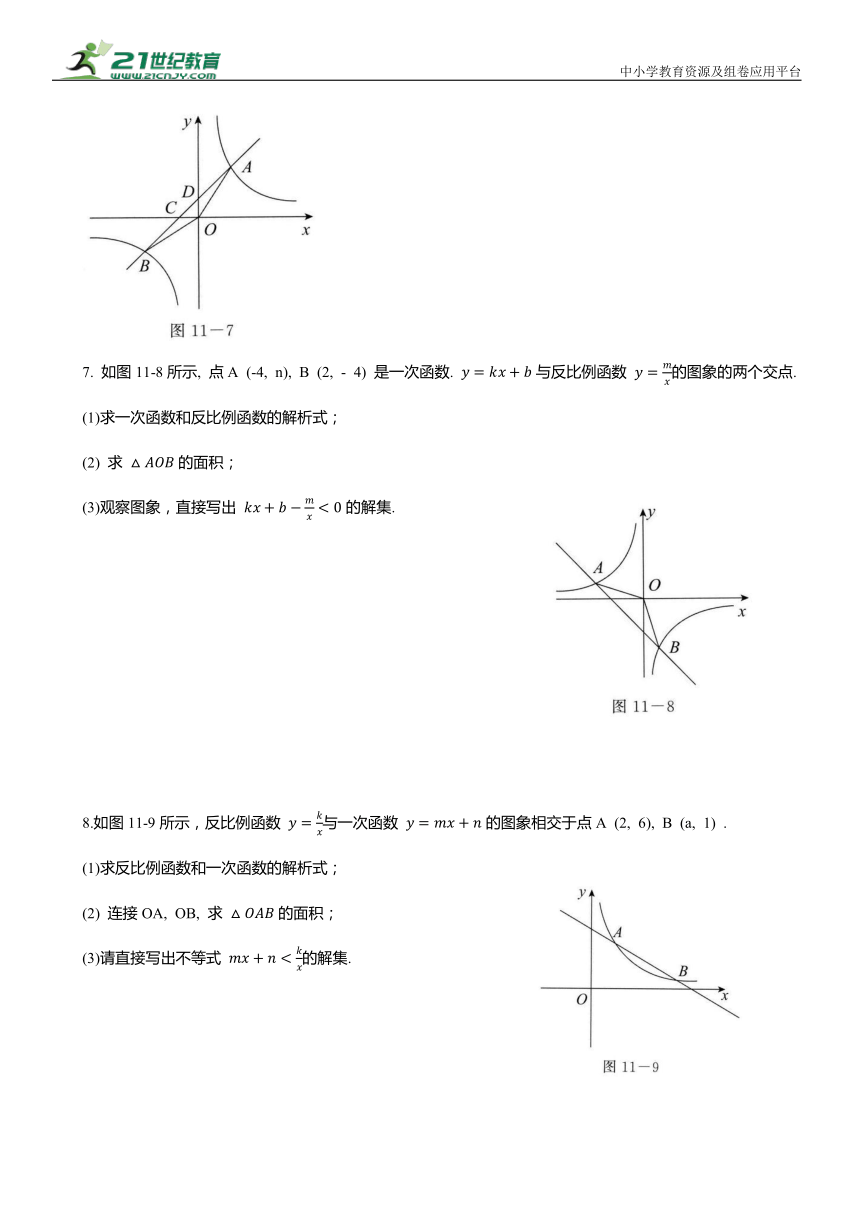
7. 如图11-8所示, 点A (-4, n), B (2, - 4) 是一次函数. 与反比例函数 的图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2) 求 的面积;
(3)观察图象,直接写出 的解集.
8.如图11-9所示,反比例函数 与一次函数 的图象相交于点A (2, 6), B (a, 1) .
(1)求反比例函数和一次函数的解析式;
(2) 连接OA, OB, 求 的面积;
(3)请直接写出不等式 的解集.
9.如图11-10所示,在平面直角坐标系中,直线l与x轴相交于点 M (3,0),与y轴相交于点 反比例函数 的图象经过线段 MN的中点 A.
(1)求直线l和反比例函数的解析式;
(2)在函数 的图象上取不同于点 A 的一点B,作. 轴于点C,连接OB 交直线l 于点 P.若 的面积是 的面积的3倍,求点 P 的坐标.
10. 如图11--11 所示, 一次函数 与反比例函数 的图象相交于点A,B,点 A 的横坐标为1.
(1)求反比例函数的解析式;
(2)求点 B 的坐标,并直接写出 时,x的取值范围;
(3) 当 时,在反比例函数的图象上有一点 C,使得 的面积为21,求点C的坐标.
11. 如图11-12所示, 直线 与反比例函数 的图象相交于点 A,B,点 B 的坐标为( ,点C为反比例函数 的图象在第一象限的点.若 的面积为6,则点 C的坐标为 .
反比例函数与四边形
1. 解: ∵矩形ABCD的两边AD, AB的长分别为3和8, 点E是DC的中点,
∵AF-AE=2,
∴AF=7.
设点 B的坐标为 (t,0),则点F的坐标为 (t, 1),点C的坐标为 点 E的坐标为 (t+3, 4) .
∵点 E (t+3, 4), F (t, 1) 在反比例函数 的图象上,
∴4 (t+3) =t·1, 解得t=--4.
∴点 F 的坐标为 (-4, 1) .
∴m=-4×1=-4.
∴反比例函数的解析式为
2. 解: ∵直线 经过点B,
∴设点 B 的坐标为 则OC=AC=AE=OE=a.
设反比例函数的解析式为
∵点 B 在反比例函数的图象上,
即
∵四边形 ACOE 是正方形,点 D 在AE 上,
∴点 D 的纵坐标为a,
∴把 y=a代入反比例函数. 得 解得
故选 A.
3. 解: 设点 A 的坐标为 (m, n) .
∵过点A作x轴的平行线交y 于点 B,交y轴于点C;过点A作x轴的垂线交 y 于点 D,交x轴于点E,
∴点 B 的坐标为 点C 的坐标为 (0,n),点D 的坐标为
点E的坐标为 (m, 0) .
又∵∠A=∠A,
∴△ABD∽△ACE.
4. 解: 连接AC, 过点C作CE⊥OA 于点E, 如图23所示.
∵四边形OABC是菱形,
∴OC=OA, OC∥AB.
∴△COD 与△COA 同底等高.
∴S△∞a=S△coD=10.
∵在 Rt△OCE中,
∴设CE=4k, 则OE=3k.
∴OA=OC=5k.
即OE·CE=12.
∴k=OE·CE=12.
5.解:设矩形的对称中心为点 E,连接OA,OE,过点 E作 于点F,如图24所示.
∵点 E 是矩形ABCD 的对称中心,
设OB=a, AB=b.
∵矩形ABCD 的面积为6,
∴点 E 的坐标为
即k= ab=3.
6. 解: 设AF=a (a<2) .
∵正方形 ABCD 的边长为2,点 E,F在反比例函数 的图象上,
∴点 F 的坐标为 (a, 2), 点 E的坐标为 (2, a) .
∴FD=DE=2-a.
解得 或 (不合题意,舍去).
∴点F的坐标为(
7. 解: 设点 B 的坐标为 (a, b) .
∵点 E, F 分别为边BC, AB的中点,
∴点E的坐标为( 点 F 的坐标为(
∵四边形OEBF 的面积为1,
∴S矩形OABC—S△OCE—S△OAF=1,
即 解得
8. 解: 如图25所示, 过点M作MG⊥y轴于点G, 作 MN⊥x轴于点N, 则
∵点 D,E,M在反比例函数 的图象上,
又∵M为矩形ABCO 对角线的交点,
∵反比例函数的图象位于第一象限, 解得k=4.
9. 解: (1) ∵点 B的坐标为 (4, 2), 四边形OABC是矩形,∴OA=BC=2, OC=AB=4.
∵点 M在AB 上,且反比例函数 经过点M,
∴将y=2代入 得 解得
∴点 M的坐标为
∴同理可知,将x=4代入 得
∴点 N的坐标为(
(2) ∵点 在直线 的图象上,
解得k=4.
∴反比例函数的解析式为
(3)由题意可得,
∵△OPM 的面积与四边形BMON 的面积相等,
解得OP=4.
∴点 P 的坐标为 (4, 0) 或 (-4, 0) .
10. 解: 如图26所示, 过点 D作 DN⊥x轴于点 N, 过点 A作. 轴于点 M.
∵四边形ABCO是平行四边形,
∴OA∥BC, OA=BC.
∵tan∠AOC=2,
设点 A 的坐标为 (a, 2a), 则OM=a, AM=2a.
∵点 D 是边 BC 的中点,
∴DN=a.
∵顶点 C 的坐标为 (2, 0),
∴点 D 的坐标为
∵过点 A 的反比例函数 的图象过BC 边的中点D,
解得 或a=0 (舍去) .
11. 解: 如图27所示, 过点 D作DF⊥BC于点 F.
∵AD⊥y轴, 四边形ABCD 是菱形,
∴AD∥BC, DC=BC.
∴四边形 BEDF 是矩形.
∴DF=BE, BF=DE=1.
∵BE=3DE,
∴DF=BE=3.
设CD=CB=a, 则CF=a--1.
∵在 Rt△DFC中, 即 解得a=5,
∴设点 C的坐标为 (5,m),则点 D 的坐标为(
∵反比例函数 的图象同时经过点 C,D,
∴5m=1· (m+3),解得
∴点 C 的坐标为
12. 解: 如图28所示, 过点A作AM⊥x轴于点M, 过点 E作. 轴于点N, 设点 A 的坐标为 (a, b), 点E的坐标为 (c, d), 则. AM=b, OM=a, ON=c, EN=d, k= ab= cd.
∵点A,E在反比例函数 的图象上,
∴△AOM 与△EON 的面积相等.
∵四边形AOBC是平行四边形,点E 为对角线的交点,
∴AE=BE.
∵AM∥EN,
∴MN=NB.
即
∵k= ab= cd,
即
∵根据三角形的中位线性质可得,MN=BN,
∴OM=MN=BN.
∴OB=3OM=3a.
∵平行四边形AOBC的面积=OB·AM=18,
∴3a·b=18, 即 ab=6.
∴k=6.
1.解:(1)∵点A 在反比例函数 的图象上,点A 的坐标为 (-2,4).
∴反比例函数的解析式为
(2)∵点 B 在反比例函数 的图象上,且点 B 的横坐标为-4,∴把x=-4代入 得
∴点 B的坐标为(-4, 2) .
∵点 A,B均在直线 的图象上,
∴把点 A (--2, 4), B (-4, 2) 代入函数解析式得, 解得
∴直线的解析式为 y=x+6.
∵点C是直线y=x+6与x轴的交点,
∴把y=0代入y=x+6, 得0=x+6, 解得x=--6.
∴点 C的坐标为 (-6, 0) .
2.解: (1) 把点A (-4, 1) 分别代入反比例函数 和一次函数y=-x+
b, 得 解得k=-4, b=-3.
故反比例函数的解析式为 一次函数的解析式为y=-x--3.
(2) 如图29所示, 设直线y=-x--3与y轴的交点为点C.
∵点 B 在直线y=-x--3的图象上,且点 B 的坐标为 (1, n),
∴把x=1代入y=-x--3, 得y=-4.
∴点 B 的坐标为 (1, - 4) .
∵点C为直线y=-x--3与 y轴的交点,
∴把x=0代入y=-x-3, 得y=-0-3=-3.
∴点C的坐标为 (0, - 3) .
(3) ∵点A 的坐标为 (-4, 1), 点 B 的坐标为 (1, - 4),
∴由图29可知,当x<-4或03.解:设点 P 的坐标为
∵PB⊥y轴于点B,点A是x轴正半轴上的一个定点,
∴四边形OAPB 是直角梯形.
∵AO是定值,
∴点 P 的横坐标逐渐增大时,四边形OAPB的面积逐渐减小.故选 C.
4.解:如图30所示,过点C作x轴的垂线于点 F.设直线 AB的解析式为y= kx+b.
∵直线 AB 过点A (8, 0), B (0, 6), 解得
∴直线 AB的解析式为
∵△AOC、△COD、△DOB的面积都相等,
即 即 解得CF=2.
∴点 C 的纵坐标为2.
∵点C在直线 的图象上,
∴把 y=2代入 得 解得
∴点 C的坐标为
∵反比例函数 的图象经过点C,
欲穷千里目,更上一层楼
5. 解: (1) ∵点A (m, 3), B (-6, n) 在反比例函数 的图象上,∴m=2, n=--1.
∴点 A 的坐标为 (2, 3), 点 B 的坐标为 (-6, - 1) .
∵点 A, B在直线y= kx+b (k≠0) 的图象上,
∴将 A (2, 3), B (--6, - 1) 代入函数解析式,
解得
∴直线的解析式为
(2) 如图31所示, 设点 P 的坐标为 (x, 0) .
∵点C是直线 与x轴的交点,
∴将y=0代入
得 解得x=-4.
∴点 C 的坐标为 (-4, 0) .
点 A 的坐标为 (2, 3),点 B 的坐标为 (-6, - 1),
即 解得
∴点 P 的坐标为 (-6, 0) 或 (
6.解:如图32所示,过点 A 作 轴于点E,过点B作 轴于点F.
∵点 A 在反比例函数 的图象上,
∴AE∥CO.
∵AD=2CD,
∴DE=2DO.
∵同理可得,
7. 解: (1) ∵点 B (2, - 4) 在反比例函数 的图象上,
∴m=2× (-4) =-8.
∴反比例函数的解析式为
∵点 A (-4, n) 在反比例函数 的图象上,
∴n=2.
∴点 A 的坐标为 (-4, 2) .
∵y= kx+b经过点A (-4, 2), B (2, - 4),
解得
∴一次函数的解析式为y=-x-2.
(2)设点 C是直线AB 与y轴的交点.
∵把x=0代入y=-x-2, 得y=--2,
∴点 C的坐标为 (0, - 2) .
∴OC=2.
(3) ∵由图象可知, 当x>2或-4的解集为x>2或-48. 解: (1) 点 A (2, 6) 在反比例函数 的图象上,
∴把点 A (2, 6) 代入 得k=12.
∴反比例函数的解析式为
∵点 B (a,1)在反比例函数 的图象上,
∴把y=1代入 得x=12, 即a=12.
∴点 B 的坐标为 (12, 1) .
∵点A (2, 6), B (12, 1) 在一次函数y= mx+n的图象上,
解得
∴一次函数的解析式为
(2) 如图33所示, 连接OA, OB, 设一次函数 的图象与x轴相交于点C, 则点C的坐标为 (14, 0), OC=14.
∵点A 的坐标为 (2, 6),
∴点 A 到x轴的距离为6,即△AOC的高为6.
∵点 B 的坐标为 (12, 1),
∴B 点到x 轴的距离为1,即△BOC的高为1.
(3)由图33可知,不等式 的解集为012.
9. 解: (1) 设直线l的解析式为y= mx+n (m≠0) .
∵点 M (3, 0), N (0, - 1) 在直线l上,
解得
∴直线 l的解析式为
∵点A 为线段MN 的中点,
∴点 A 的坐标为
∵点 在反比例函数 的图象上,
解得
∴反比例函数的解析式为
∵点 N 的坐标为 (0, - 1),
∴ON=1.
∵点 P 在直线l 上,设点 P 的坐标为
解得
∴点 P的坐标为
10. 解: (1) ∵点 A 在一次函数. 的图象上,且点 A 的横坐标为1,∴把x=1代入. 得
∴点A 的坐标为 (1, 6) .
又∵点A在反比例函数 的图象上,
∴k=1×6=6.
∴反比例函数的解析式为
(2) ∵一次函数 与反比例函数 的图象相交于点A,B,
∴将 代入 得 即
解得
∵当x=-6时,
∴点 B 的坐标为 (--6, - 1) .
∵由图象可知, 当x<-6或0时, x的取值范围为x<-6或0(3) 过点C作CD∥y轴, 交直线 AB于点D, 如图34所示.
设点C的坐标为 则点 D的坐标为 (m, m+5) .
∵点 A 的坐标为 (1, 6), 点 B 的坐标为 (-6, - 1),
∴S△ABC=S△BCD-S△ACD=21,
即 1) =21,
整理得 解得m=3或m=--2 (舍去),
经检验m=3是原方程的解.
∴点C的坐标为 (3, 2) .
11. 解: ∵点 B (-4, - 2) 在反比例函数 的图象上,∴k=-4× (-2) =8.
∵根据中心对称性可知,点A,B关于原点对称,
∴点 A 的坐标为 (4, 2) .
如图35和图36所示,过点A作AE⊥x轴于点E,过点C作CF⊥x轴于点F,设点C的坐标为(a, ).
当S△AOC=S△COF+S梯形ACFE—S△AOE时,如图35 所示,则有
∵△AOC的面积为6,
整理得 解得 (舍去) .
∴点C的坐标为 (2, 4) .
当S△AOC=S△AOE+S梯形ACFE-S△COF|时,如图36 所示,则有
∵△AOC的面积为6,
解得a=8或a=-2 (舍去).
∴点C的坐标为 (8, 1) .
故点 C的坐标为 (2, 4) 或 (8, 1) .
反比例函数与几何综合
一、知识梳理
【例】如图11--1所示,一次函数y=ax+4与反比例函数 的图象相交于点A, B. 点A的横坐标为1, 过点A作AC⊥x轴于点C, 连接BC.
(1)求一次函数与反比例函数的解析式;
(2) 求 sin∠BAC的值;
(3)求点 B 的坐标,并直接写出不等式 的解集.
解: (1) ∵把x=1代入 得y=8-a,
∴点 A的坐标为 (1, 8--a) .
∵把点A (1, 8-a) 代入y= ax+4,得8--a=a+4, 解得a=2,
∴一次函数的解析式为 y=2x+4,反比例函数的解析式为
(2) ∵a=2,
∴点A的坐标为 (1, 6) .
∴AC=6, OC=1.
设直线y=2x+4与x轴的交点为点D.
∵当 y=0时, 有2x+4=0, 解得x=--2,故点 D的坐标为 (--2, 0),
∴OD=2.
∴CD=3.
(3) ∵联立方程 解得 或
∴点 B 的坐标为 (-3, - 2) .
由图象可知,不等式 的解集为x<-3或0
1. 如图11-2所示, 直线. 与反比例函数 的图象相交于点A,B,与x轴相交于点C,其中点 A 的坐标为 (--2,4), 点B 的横坐标为—4.
(1)确定反比例函数的解析式;
(2)求点 C的坐标.
2.如图11—3所示,反比例函数 的图象与一次函数 的图象相交于点A (-4, 1), B (1, n) .
(1)求一次函数和反比例函数的解析式;
(2) 求 的面积;
(3)直接写出一次函数值大于反比例函数值时的自变量x的取值范围.
3.如图11-4所示,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是反比例函数 图象上的一个动点, 轴于点 B,当点 P 的横坐标逐渐增大时,四边形OAPB 的面积会 ( ).
A.逐渐增大
B.不变
C.逐渐减小
D.先增大后减小
4.如图11--5 所示,在平面直角坐标系中,直线 AB 经过点A (8,0),B (0, 6),反比例函数 的图象与直线AB 相交于点 C,D,连接OC,OD. 当 的面积都相等时,
5.如图11-6所示,在平面直角坐标系中,直线. )与反比例函数 的图象相交于点A (m, 3), B (-6, n), 与x轴相交于点C.
(1) 求直线 y= kx+b(k≠0) 的解析式;
(2)若点 P在x轴上,且 求点 P 的坐标 (直接写出结果).
6.如图11-7 所示,点 A,B分别为反比例函数 在第一、第三象限图象上的点, 连接OA, OB, AB, 交x轴、 y轴于点C, D, 则△AOB 的面积为 .
7. 如图11-8所示, 点A (-4, n), B (2, - 4) 是一次函数. 与反比例函数 的图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2) 求 的面积;
(3)观察图象,直接写出 的解集.
8.如图11-9所示,反比例函数 与一次函数 的图象相交于点A (2, 6), B (a, 1) .
(1)求反比例函数和一次函数的解析式;
(2) 连接OA, OB, 求 的面积;
(3)请直接写出不等式 的解集.
9.如图11-10所示,在平面直角坐标系中,直线l与x轴相交于点 M (3,0),与y轴相交于点 反比例函数 的图象经过线段 MN的中点 A.
(1)求直线l和反比例函数的解析式;
(2)在函数 的图象上取不同于点 A 的一点B,作. 轴于点C,连接OB 交直线l 于点 P.若 的面积是 的面积的3倍,求点 P 的坐标.
10. 如图11--11 所示, 一次函数 与反比例函数 的图象相交于点A,B,点 A 的横坐标为1.
(1)求反比例函数的解析式;
(2)求点 B 的坐标,并直接写出 时,x的取值范围;
(3) 当 时,在反比例函数的图象上有一点 C,使得 的面积为21,求点C的坐标.
11. 如图11-12所示, 直线 与反比例函数 的图象相交于点 A,B,点 B 的坐标为( ,点C为反比例函数 的图象在第一象限的点.若 的面积为6,则点 C的坐标为 .
反比例函数与四边形
1. 解: ∵矩形ABCD的两边AD, AB的长分别为3和8, 点E是DC的中点,
∵AF-AE=2,
∴AF=7.
设点 B的坐标为 (t,0),则点F的坐标为 (t, 1),点C的坐标为 点 E的坐标为 (t+3, 4) .
∵点 E (t+3, 4), F (t, 1) 在反比例函数 的图象上,
∴4 (t+3) =t·1, 解得t=--4.
∴点 F 的坐标为 (-4, 1) .
∴m=-4×1=-4.
∴反比例函数的解析式为
2. 解: ∵直线 经过点B,
∴设点 B 的坐标为 则OC=AC=AE=OE=a.
设反比例函数的解析式为
∵点 B 在反比例函数的图象上,
即
∵四边形 ACOE 是正方形,点 D 在AE 上,
∴点 D 的纵坐标为a,
∴把 y=a代入反比例函数. 得 解得
故选 A.
3. 解: 设点 A 的坐标为 (m, n) .
∵过点A作x轴的平行线交y 于点 B,交y轴于点C;过点A作x轴的垂线交 y 于点 D,交x轴于点E,
∴点 B 的坐标为 点C 的坐标为 (0,n),点D 的坐标为
点E的坐标为 (m, 0) .
又∵∠A=∠A,
∴△ABD∽△ACE.
4. 解: 连接AC, 过点C作CE⊥OA 于点E, 如图23所示.
∵四边形OABC是菱形,
∴OC=OA, OC∥AB.
∴△COD 与△COA 同底等高.
∴S△∞a=S△coD=10.
∵在 Rt△OCE中,
∴设CE=4k, 则OE=3k.
∴OA=OC=5k.
即OE·CE=12.
∴k=OE·CE=12.
5.解:设矩形的对称中心为点 E,连接OA,OE,过点 E作 于点F,如图24所示.
∵点 E 是矩形ABCD 的对称中心,
设OB=a, AB=b.
∵矩形ABCD 的面积为6,
∴点 E 的坐标为
即k= ab=3.
6. 解: 设AF=a (a<2) .
∵正方形 ABCD 的边长为2,点 E,F在反比例函数 的图象上,
∴点 F 的坐标为 (a, 2), 点 E的坐标为 (2, a) .
∴FD=DE=2-a.
解得 或 (不合题意,舍去).
∴点F的坐标为(
7. 解: 设点 B 的坐标为 (a, b) .
∵点 E, F 分别为边BC, AB的中点,
∴点E的坐标为( 点 F 的坐标为(
∵四边形OEBF 的面积为1,
∴S矩形OABC—S△OCE—S△OAF=1,
即 解得
8. 解: 如图25所示, 过点M作MG⊥y轴于点G, 作 MN⊥x轴于点N, 则
∵点 D,E,M在反比例函数 的图象上,
又∵M为矩形ABCO 对角线的交点,
∵反比例函数的图象位于第一象限, 解得k=4.
9. 解: (1) ∵点 B的坐标为 (4, 2), 四边形OABC是矩形,∴OA=BC=2, OC=AB=4.
∵点 M在AB 上,且反比例函数 经过点M,
∴将y=2代入 得 解得
∴点 M的坐标为
∴同理可知,将x=4代入 得
∴点 N的坐标为(
(2) ∵点 在直线 的图象上,
解得k=4.
∴反比例函数的解析式为
(3)由题意可得,
∵△OPM 的面积与四边形BMON 的面积相等,
解得OP=4.
∴点 P 的坐标为 (4, 0) 或 (-4, 0) .
10. 解: 如图26所示, 过点 D作 DN⊥x轴于点 N, 过点 A作. 轴于点 M.
∵四边形ABCO是平行四边形,
∴OA∥BC, OA=BC.
∵tan∠AOC=2,
设点 A 的坐标为 (a, 2a), 则OM=a, AM=2a.
∵点 D 是边 BC 的中点,
∴DN=a.
∵顶点 C 的坐标为 (2, 0),
∴点 D 的坐标为
∵过点 A 的反比例函数 的图象过BC 边的中点D,
解得 或a=0 (舍去) .
11. 解: 如图27所示, 过点 D作DF⊥BC于点 F.
∵AD⊥y轴, 四边形ABCD 是菱形,
∴AD∥BC, DC=BC.
∴四边形 BEDF 是矩形.
∴DF=BE, BF=DE=1.
∵BE=3DE,
∴DF=BE=3.
设CD=CB=a, 则CF=a--1.
∵在 Rt△DFC中, 即 解得a=5,
∴设点 C的坐标为 (5,m),则点 D 的坐标为(
∵反比例函数 的图象同时经过点 C,D,
∴5m=1· (m+3),解得
∴点 C 的坐标为
12. 解: 如图28所示, 过点A作AM⊥x轴于点M, 过点 E作. 轴于点N, 设点 A 的坐标为 (a, b), 点E的坐标为 (c, d), 则. AM=b, OM=a, ON=c, EN=d, k= ab= cd.
∵点A,E在反比例函数 的图象上,
∴△AOM 与△EON 的面积相等.
∵四边形AOBC是平行四边形,点E 为对角线的交点,
∴AE=BE.
∵AM∥EN,
∴MN=NB.
即
∵k= ab= cd,
即
∵根据三角形的中位线性质可得,MN=BN,
∴OM=MN=BN.
∴OB=3OM=3a.
∵平行四边形AOBC的面积=OB·AM=18,
∴3a·b=18, 即 ab=6.
∴k=6.
1.解:(1)∵点A 在反比例函数 的图象上,点A 的坐标为 (-2,4).
∴反比例函数的解析式为
(2)∵点 B 在反比例函数 的图象上,且点 B 的横坐标为-4,∴把x=-4代入 得
∴点 B的坐标为(-4, 2) .
∵点 A,B均在直线 的图象上,
∴把点 A (--2, 4), B (-4, 2) 代入函数解析式得, 解得
∴直线的解析式为 y=x+6.
∵点C是直线y=x+6与x轴的交点,
∴把y=0代入y=x+6, 得0=x+6, 解得x=--6.
∴点 C的坐标为 (-6, 0) .
2.解: (1) 把点A (-4, 1) 分别代入反比例函数 和一次函数y=-x+
b, 得 解得k=-4, b=-3.
故反比例函数的解析式为 一次函数的解析式为y=-x--3.
(2) 如图29所示, 设直线y=-x--3与y轴的交点为点C.
∵点 B 在直线y=-x--3的图象上,且点 B 的坐标为 (1, n),
∴把x=1代入y=-x--3, 得y=-4.
∴点 B 的坐标为 (1, - 4) .
∵点C为直线y=-x--3与 y轴的交点,
∴把x=0代入y=-x-3, 得y=-0-3=-3.
∴点C的坐标为 (0, - 3) .
(3) ∵点A 的坐标为 (-4, 1), 点 B 的坐标为 (1, - 4),
∴由图29可知,当x<-4或0
∵PB⊥y轴于点B,点A是x轴正半轴上的一个定点,
∴四边形OAPB 是直角梯形.
∵AO是定值,
∴点 P 的横坐标逐渐增大时,四边形OAPB的面积逐渐减小.故选 C.
4.解:如图30所示,过点C作x轴的垂线于点 F.设直线 AB的解析式为y= kx+b.
∵直线 AB 过点A (8, 0), B (0, 6), 解得
∴直线 AB的解析式为
∵△AOC、△COD、△DOB的面积都相等,
即 即 解得CF=2.
∴点 C 的纵坐标为2.
∵点C在直线 的图象上,
∴把 y=2代入 得 解得
∴点 C的坐标为
∵反比例函数 的图象经过点C,
欲穷千里目,更上一层楼
5. 解: (1) ∵点A (m, 3), B (-6, n) 在反比例函数 的图象上,∴m=2, n=--1.
∴点 A 的坐标为 (2, 3), 点 B 的坐标为 (-6, - 1) .
∵点 A, B在直线y= kx+b (k≠0) 的图象上,
∴将 A (2, 3), B (--6, - 1) 代入函数解析式,
解得
∴直线的解析式为
(2) 如图31所示, 设点 P 的坐标为 (x, 0) .
∵点C是直线 与x轴的交点,
∴将y=0代入
得 解得x=-4.
∴点 C 的坐标为 (-4, 0) .
点 A 的坐标为 (2, 3),点 B 的坐标为 (-6, - 1),
即 解得
∴点 P 的坐标为 (-6, 0) 或 (
6.解:如图32所示,过点 A 作 轴于点E,过点B作 轴于点F.
∵点 A 在反比例函数 的图象上,
∴AE∥CO.
∵AD=2CD,
∴DE=2DO.
∵同理可得,
7. 解: (1) ∵点 B (2, - 4) 在反比例函数 的图象上,
∴m=2× (-4) =-8.
∴反比例函数的解析式为
∵点 A (-4, n) 在反比例函数 的图象上,
∴n=2.
∴点 A 的坐标为 (-4, 2) .
∵y= kx+b经过点A (-4, 2), B (2, - 4),
解得
∴一次函数的解析式为y=-x-2.
(2)设点 C是直线AB 与y轴的交点.
∵把x=0代入y=-x-2, 得y=--2,
∴点 C的坐标为 (0, - 2) .
∴OC=2.
(3) ∵由图象可知, 当x>2或-4
∴把点 A (2, 6) 代入 得k=12.
∴反比例函数的解析式为
∵点 B (a,1)在反比例函数 的图象上,
∴把y=1代入 得x=12, 即a=12.
∴点 B 的坐标为 (12, 1) .
∵点A (2, 6), B (12, 1) 在一次函数y= mx+n的图象上,
解得
∴一次函数的解析式为
(2) 如图33所示, 连接OA, OB, 设一次函数 的图象与x轴相交于点C, 则点C的坐标为 (14, 0), OC=14.
∵点A 的坐标为 (2, 6),
∴点 A 到x轴的距离为6,即△AOC的高为6.
∵点 B 的坐标为 (12, 1),
∴B 点到x 轴的距离为1,即△BOC的高为1.
(3)由图33可知,不等式 的解集为0
9. 解: (1) 设直线l的解析式为y= mx+n (m≠0) .
∵点 M (3, 0), N (0, - 1) 在直线l上,
解得
∴直线 l的解析式为
∵点A 为线段MN 的中点,
∴点 A 的坐标为
∵点 在反比例函数 的图象上,
解得
∴反比例函数的解析式为
∵点 N 的坐标为 (0, - 1),
∴ON=1.
∵点 P 在直线l 上,设点 P 的坐标为
解得
∴点 P的坐标为
10. 解: (1) ∵点 A 在一次函数. 的图象上,且点 A 的横坐标为1,∴把x=1代入. 得
∴点A 的坐标为 (1, 6) .
又∵点A在反比例函数 的图象上,
∴k=1×6=6.
∴反比例函数的解析式为
(2) ∵一次函数 与反比例函数 的图象相交于点A,B,
∴将 代入 得 即
解得
∵当x=-6时,
∴点 B 的坐标为 (--6, - 1) .
∵由图象可知, 当x<-6或0
设点C的坐标为 则点 D的坐标为 (m, m+5) .
∵点 A 的坐标为 (1, 6), 点 B 的坐标为 (-6, - 1),
∴S△ABC=S△BCD-S△ACD=21,
即 1) =21,
整理得 解得m=3或m=--2 (舍去),
经检验m=3是原方程的解.
∴点C的坐标为 (3, 2) .
11. 解: ∵点 B (-4, - 2) 在反比例函数 的图象上,∴k=-4× (-2) =8.
∵根据中心对称性可知,点A,B关于原点对称,
∴点 A 的坐标为 (4, 2) .
如图35和图36所示,过点A作AE⊥x轴于点E,过点C作CF⊥x轴于点F,设点C的坐标为(a, ).
当S△AOC=S△COF+S梯形ACFE—S△AOE时,如图35 所示,则有
∵△AOC的面积为6,
整理得 解得 (舍去) .
∴点C的坐标为 (2, 4) .
当S△AOC=S△AOE+S梯形ACFE-S△COF|时,如图36 所示,则有
∵△AOC的面积为6,
解得a=8或a=-2 (舍去).
∴点C的坐标为 (8, 1) .
故点 C的坐标为 (2, 4) 或 (8, 1) .
