3.4基本不等式
图片预览








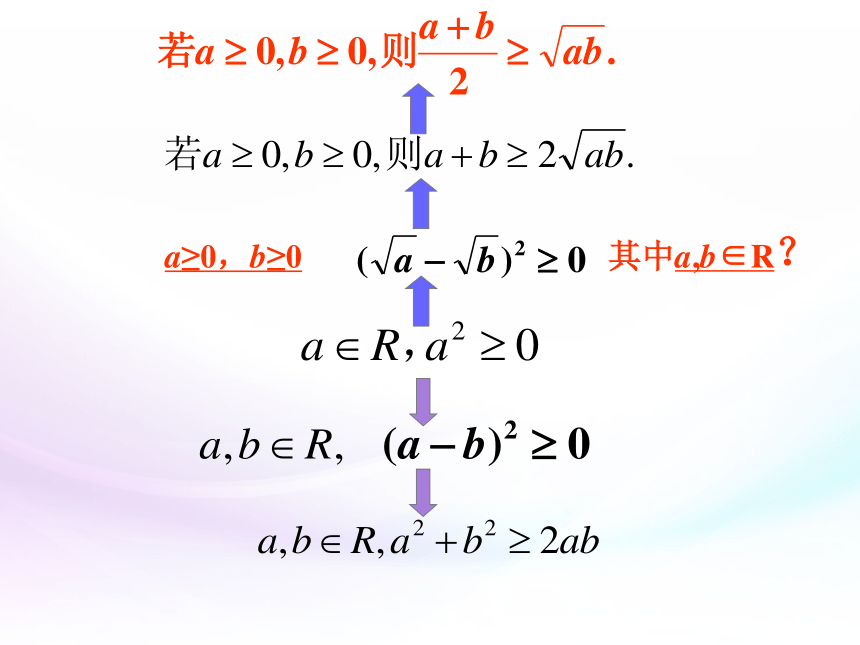

文档简介
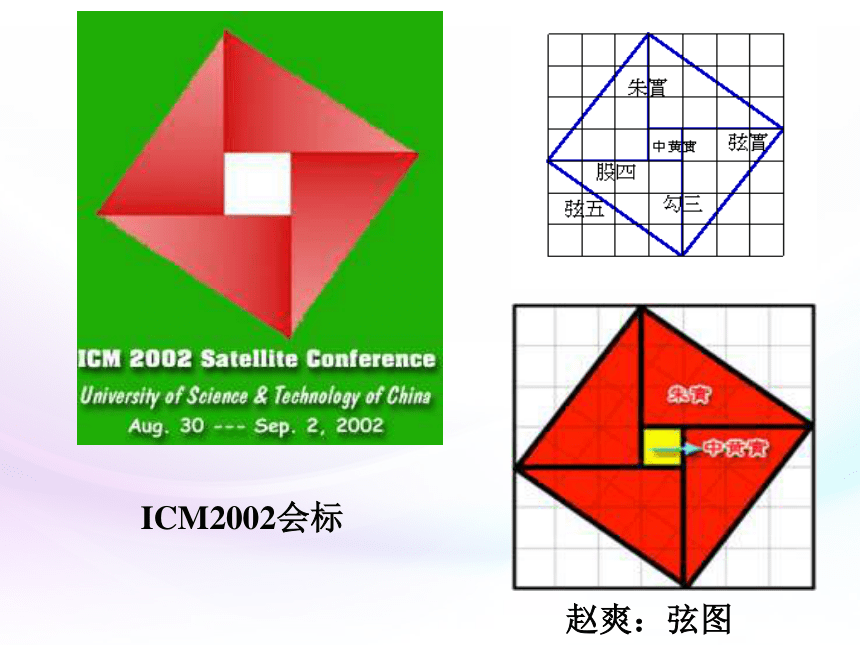
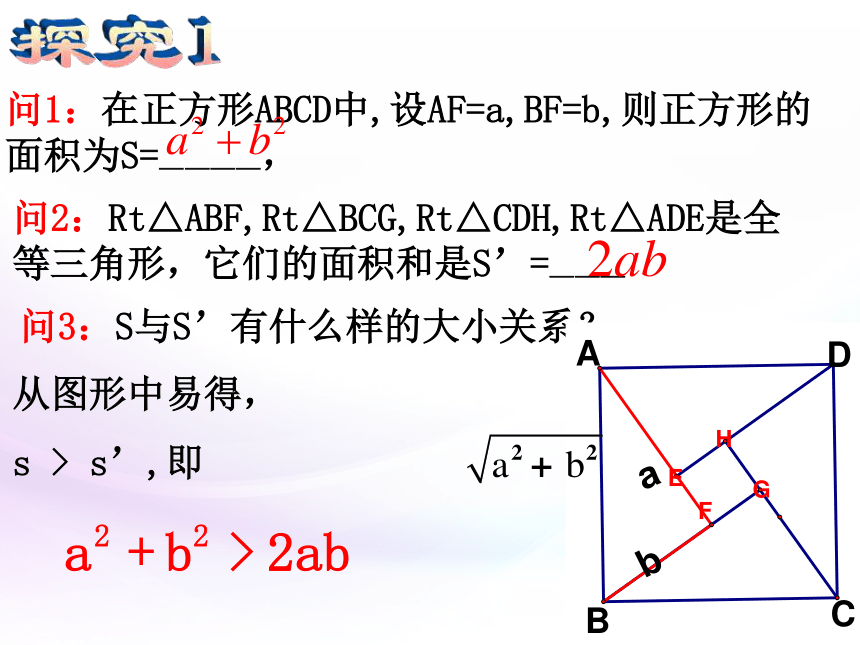
课件45张PPT。3.4 基本不等式:2002年国际数学家大会会标三国时期吴国数学家赵爽ICM2002会标赵爽:弦图思考:这会标中含有怎样的几何图形?思考:你能否在这个图案中找出一些相等关系或不等关系? 问2:Rt△ABF,Rt△BCG,Rt△CDH,Rt△ADE是全等三角形,它们的面积和是S’=———问1:在正方形ABCD中,设AF=a,BF=b,则正方形的面积为S=————,问3:S与S’有什么样的大小关系? 从图形中易得,
s > s’,即探究1ab探究2问题:s, S’有相等的情况吗?何时相等? 图片说明:当直角三角形变为等腰直角三角形,即a=b时,正方形EFGH缩为一个点,这时有 形的角度数的角度a2+b2-2ab =(a-b)2=0
∴ a=b结论:一般地,对于任意实数a、b,我们有
当且仅当a=b时,等号成立此不等式称为重要不等式探究3问题:当 a,b为任意实数时, 成立吗? 以上的不等式是我们从几何图形中的面积关系得出的,能否利用不等式的性质直接推导出来呢?证明: 类 比 联 想 推 理 论 证 (特别的)如果 a>0 ,b>0 ,也可写成如果a>0,b>0 ,用 分别代替a,b.我们将得到什么结果?算术平均数几何平均数其中a,b∈R?a≥0,b≥0证明:要证只要证 ① ② 要证②,只要证③ 要证③,只要证( - ) ④证明:当 时, . 探究3oabABPQ1.如图,AB是圆o的直径,Q是AB上任一点,AQ=a,BQ=b,过点Q作垂直于AB的弦PQ,连AP,BP,
则半弦PQ=__ __,半径AO=_____几何意义:圆的半径不小于圆内半弦长探究你能用这个图得出基本不等式的几何解释吗?2.PQ与AO的大小关系怎样? 如果把 看作是正数a、b的等差中项,把 看作是正数a、b的等比中项,那么该定理可以叙述为:两个正数的等差中项不小于它们的等比中项. 基本不等式 代数意义 为a、b的算术平均数, 为几何平均数,那么两个正数的算术平均数不小于它们的几何平均数. 基本不等式:当且仅当a =b时,等号成立.当且仅当a=b时,等号成立.重要不等式:注意:
(1)不同点:两个不等式的适用范围不同。(2)相同点:当且仅当a=b时,等号成立。例1.(1)用篱笆围一个面积为 的矩形菜园, 问该矩形的长、宽各为多少时, 所用篱笆最短,最短的篱笆是多少?解: (1)设矩形菜园的长为 ,宽为 , 则 , 篱笆的长为 . 由因此,这个矩形的长和宽都是10m时,所用的篱笆最短,最短为40m等号当且仅当 时成立,此时得即结论1.两个正数积为定值,则和有最小值例 一段长为36m的篱笆围成一矩形菜园,问这个矩形的长、宽各为多少时,菜园的面积最大。最大面积是多少?解:设矩形菜园的长为xm,宽为ym,
则2x+2y=36, 即x+y=18,矩形菜园的面积为xy m2 当且仅当x=y,即x=9,y=9时等号成立。
因此,这个矩形的长为9m、宽为9m时,菜园的面积最大,最大面积是81 m2 。结论2:两个正数和为定值,则积有最大值.最值定理:若x、y皆为正数,则
(1)当x+y的值是常数S时,当且仅当x=y时,xy有最大值_______;
(2)当xy的值是常数P时,当且仅当x=y时, x+y有最小值_______.
注意:①各项皆为正数;
②和为定值或积为定值;
③注意等号成立的条件.一“正”
二“定”
三“相等”和定积最大,积定和最小注:应用此不等式关键是配凑和一定或积一定1.已知x>0,y>0,
(1).若xy=36,则x+y的最小值是____,此时x=___,y=___;
(2).若x+y=18,则xy的最大值是____,此时x=___,y=___;
(3).若x+2y=4,则xy的最大值是____,此时x=___,y=___;212. 当 x>0 时, 的最小值为 ,此时x= 。思考:当 x<0时表达式又有何最值呢?22112668199练习:课本100页2,3,4例 、若 ,求 的最小值.例 、若 ,求 的最小值.变1:若 求 的最小值例 、若 ,求 的最小值.变2:若 ,求 的最小值.构造条件例 、若 ,求 的最小值.变3:若 ,求 的最小值.【例2】 (1)若x>0,求的值域;【解析】(1)∵x>0,由基本不等式得即x=2时取等号,f(x)取得最小值为12.∴f(x)的值域为[12,+∞).全优58页典例剖析【例2】(2)若x<0,求 【解析】全优58页典例剖析的值域;(2)∵x<0,∴-x>0.即f(x)≤-12,即x=-2时取等号,f(x)取得最大值-12.∴函数f(x)的值域为(-∞,-12].【例2】(3)若00,1-x>0.∴f(x)=x(1-x)当且仅当x=1-x,又因f(x)=x(1-x)>0,5.函数y=x(1-3x)的最大值是________.【解析】∴1-3x>0,全优62页基础夯实全优74页限时规范训练11.已知a,b,c∈R+且a+b+c=1,求证:证明:≥3+2+2+2=9.当且仅当时取等号.全优58页变式训练全优74页限时规范训练2B全优61页典例剖析【例2】 求函数在[4,+∞)上的值域.这道题告诉我们,“三相等”这一步是必须的【例3】 如图所示,动物园要围成相同面积的长方形虎笼四间,一面可利用原有的墙,其他各面用钢筋网围成.
(1)现有可围36 m长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?【解析】(1)设每间虎笼长x m,宽为y m,则由条件知:4x+6y=36,即2x+3y=18.设每间虎笼面积为S,则S=xy.由于2x+3y当且仅当2x=3y时,等号成立.故每间虎笼长为4.5 m,宽为3 m时,可使面积最大.全优61页典例剖析【例3】 如图所示,动物园要围成相同面积的长方形虎笼四间,一面可利用原有的墙,其他各面用钢筋网围成.
(2)若使每间虎笼面积为24 m2,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋网总长最小?【解析】(2)由条件知S=xy=24.全优61页典例剖析设钢筋网总长为l,则l=4x+6y.由xy=24,∴l=4x+6y即y=4时,等号成立,此时x=6.故每间虎笼长6 m,宽4 m时,可使钢筋网总长最小.全优59页能力提升全优60页典例剖析【例1】 求函数(x>-1)的最小值.【解析】∵x>-1,∴x+1>0.当且仅当即x=1时,等号成立.∴当x=1时,函数取得最小值为9.全优59页基础夯实等号成立,当且仅当2a=2b.全优62页基础夯实全优62页基础夯实全优62页基础夯实全优62页基础夯实全优59页能力提升全优74页限时规范训练2全优62页能力提升全优59页能力提升
s > s’,即探究1ab探究2问题:s, S’有相等的情况吗?何时相等? 图片说明:当直角三角形变为等腰直角三角形,即a=b时,正方形EFGH缩为一个点,这时有 形的角度数的角度a2+b2-2ab =(a-b)2=0
∴ a=b结论:一般地,对于任意实数a、b,我们有
当且仅当a=b时,等号成立此不等式称为重要不等式探究3问题:当 a,b为任意实数时, 成立吗? 以上的不等式是我们从几何图形中的面积关系得出的,能否利用不等式的性质直接推导出来呢?证明: 类 比 联 想 推 理 论 证 (特别的)如果 a>0 ,b>0 ,也可写成如果a>0,b>0 ,用 分别代替a,b.我们将得到什么结果?算术平均数几何平均数其中a,b∈R?a≥0,b≥0证明:要证只要证 ① ② 要证②,只要证③ 要证③,只要证( - ) ④证明:当 时, . 探究3oabABPQ1.如图,AB是圆o的直径,Q是AB上任一点,AQ=a,BQ=b,过点Q作垂直于AB的弦PQ,连AP,BP,
则半弦PQ=__ __,半径AO=_____几何意义:圆的半径不小于圆内半弦长探究你能用这个图得出基本不等式的几何解释吗?2.PQ与AO的大小关系怎样? 如果把 看作是正数a、b的等差中项,把 看作是正数a、b的等比中项,那么该定理可以叙述为:两个正数的等差中项不小于它们的等比中项. 基本不等式 代数意义 为a、b的算术平均数, 为几何平均数,那么两个正数的算术平均数不小于它们的几何平均数. 基本不等式:当且仅当a =b时,等号成立.当且仅当a=b时,等号成立.重要不等式:注意:
(1)不同点:两个不等式的适用范围不同。(2)相同点:当且仅当a=b时,等号成立。例1.(1)用篱笆围一个面积为 的矩形菜园, 问该矩形的长、宽各为多少时, 所用篱笆最短,最短的篱笆是多少?解: (1)设矩形菜园的长为 ,宽为 , 则 , 篱笆的长为 . 由因此,这个矩形的长和宽都是10m时,所用的篱笆最短,最短为40m等号当且仅当 时成立,此时得即结论1.两个正数积为定值,则和有最小值例 一段长为36m的篱笆围成一矩形菜园,问这个矩形的长、宽各为多少时,菜园的面积最大。最大面积是多少?解:设矩形菜园的长为xm,宽为ym,
则2x+2y=36, 即x+y=18,矩形菜园的面积为xy m2 当且仅当x=y,即x=9,y=9时等号成立。
因此,这个矩形的长为9m、宽为9m时,菜园的面积最大,最大面积是81 m2 。结论2:两个正数和为定值,则积有最大值.最值定理:若x、y皆为正数,则
(1)当x+y的值是常数S时,当且仅当x=y时,xy有最大值_______;
(2)当xy的值是常数P时,当且仅当x=y时, x+y有最小值_______.
注意:①各项皆为正数;
②和为定值或积为定值;
③注意等号成立的条件.一“正”
二“定”
三“相等”和定积最大,积定和最小注:应用此不等式关键是配凑和一定或积一定1.已知x>0,y>0,
(1).若xy=36,则x+y的最小值是____,此时x=___,y=___;
(2).若x+y=18,则xy的最大值是____,此时x=___,y=___;
(3).若x+2y=4,则xy的最大值是____,此时x=___,y=___;212. 当 x>0 时, 的最小值为 ,此时x= 。思考:当 x<0时表达式又有何最值呢?22112668199练习:课本100页2,3,4例 、若 ,求 的最小值.例 、若 ,求 的最小值.变1:若 求 的最小值例 、若 ,求 的最小值.变2:若 ,求 的最小值.构造条件例 、若 ,求 的最小值.变3:若 ,求 的最小值.【例2】 (1)若x>0,求的值域;【解析】(1)∵x>0,由基本不等式得即x=2时取等号,f(x)取得最小值为12.∴f(x)的值域为[12,+∞).全优58页典例剖析【例2】(2)若x<0,求 【解析】全优58页典例剖析的值域;(2)∵x<0,∴-x>0.即f(x)≤-12,即x=-2时取等号,f(x)取得最大值-12.∴函数f(x)的值域为(-∞,-12].【例2】(3)若0
(1)现有可围36 m长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?【解析】(1)设每间虎笼长x m,宽为y m,则由条件知:4x+6y=36,即2x+3y=18.设每间虎笼面积为S,则S=xy.由于2x+3y当且仅当2x=3y时,等号成立.故每间虎笼长为4.5 m,宽为3 m时,可使面积最大.全优61页典例剖析【例3】 如图所示,动物园要围成相同面积的长方形虎笼四间,一面可利用原有的墙,其他各面用钢筋网围成.
(2)若使每间虎笼面积为24 m2,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋网总长最小?【解析】(2)由条件知S=xy=24.全优61页典例剖析设钢筋网总长为l,则l=4x+6y.由xy=24,∴l=4x+6y即y=4时,等号成立,此时x=6.故每间虎笼长6 m,宽4 m时,可使钢筋网总长最小.全优59页能力提升全优60页典例剖析【例1】 求函数(x>-1)的最小值.【解析】∵x>-1,∴x+1>0.当且仅当即x=1时,等号成立.∴当x=1时,函数取得最小值为9.全优59页基础夯实等号成立,当且仅当2a=2b.全优62页基础夯实全优62页基础夯实全优62页基础夯实全优62页基础夯实全优59页能力提升全优74页限时规范训练2全优62页能力提升全优59页能力提升
