2025年浙江省中考数学一轮复习专题检测 专题23 圆的基本性质(含解析)
文档属性
| 名称 | 2025年浙江省中考数学一轮复习专题检测 专题23 圆的基本性质(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 21:00:20 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专题23 圆的基本性质
一.选择题
1.(2024 西乡塘区模拟)如图,OB,OC是⊙O的半径,∠D=32°,则∠BOC等于( )
A.32° B.58° C.60° D.64°
2.(2024 天府新区模拟)如图,AB是⊙O的弦,若⊙O的半径OA=10,圆心O到弦AB的距离OC=6,则弦AB的长为( )
A.8 B.12 C.16 D.20
3.(2024 宜宾)如图,AB是⊙O的直径,若∠CDB=60°,则∠ABC的度数等于( )
A.30° B.45° C.60° D.90°
4.(2024 凉山州)数学活动课上,同学们要测一个如图所示的残缺圆形工件的半径,小明的解决方案是:在工件圆弧上任取两点A,B,连接AB,作AB的垂直平分线CD交AB于点D,交于点C,测出AB=40cm,CD=10cm,则圆形工件的半径为( )
A.50cm B.35cm C.25cm D.20cm
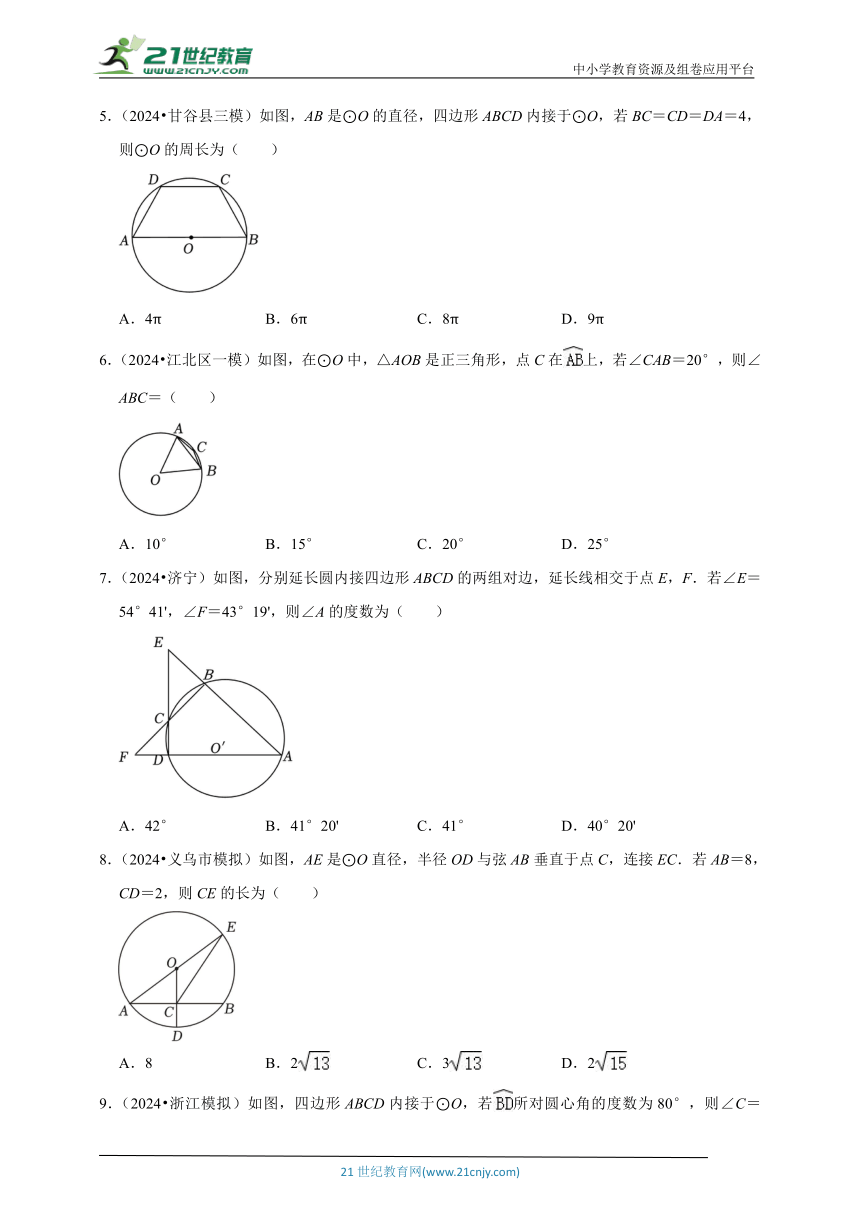
5.(2024 甘谷县三模)如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4,则⊙O的周长为( )
A.4π B.6π C.8π D.9π
6.(2024 江北区一模)如图,在⊙O中,△AOB是正三角形,点C在上,若∠CAB=20°,则∠ABC=( )
A.10° B.15° C.20° D.25°
7.(2024 济宁)如图,分别延长圆内接四边形ABCD的两组对边,延长线相交于点E,F.若∠E=54°41',∠F=43°19',则∠A的度数为( )
A.42° B.41°20' C.41° D.40°20'
8.(2024 义乌市模拟)如图,AE是⊙O直径,半径OD与弦AB垂直于点C,连接EC.若AB=8,CD=2,则CE的长为( )
A.8 B.2 C.3 D.2
9.(2024 浙江模拟)如图,四边形ABCD内接于⊙O,若所对圆心角的度数为80°,则∠C=( )
A.110° B.120° C.135° D.140°
10.(2024 定海区三模)如图所示,⊙O的半径是3,直线l与⊙O相交于A,B两点,点M,N在直线l的异侧,且是⊙O上的两个动点,且∠ANB=135°,则四边形MANB面积的最大值是( )
A.9 B. C.18 D.
二.填空题
11.(2024秋 泗阳县期末)在⊙O中,弦AB=3,圆心角∠A0B=60°,则⊙O的半径为 .
12.(2024 西宁)如图,四边形ABCD内接于⊙O,E为直径CD延长线上一点,=,∠ADE=110°,则∠DAB= .
13.(2024 牡丹江)如图,在⊙O中,直径AB⊥CD于点E,CD=6,BE=1,则弦AC的长为 .
14.(2024 富阳区一模)如图,AB是半圆O的直径,弦CD∥AB,CD=8,弦CD与直径AB之间的距离为3,则AB= .
15.(2024 杭州模拟)江南水乡杭州有很多小河和石拱桥,石拱桥是中国传统桥梁四大基本形式之一,它的主桥拱是圆弧形.如图,已知曲院风荷的一座石拱桥的跨度AB=6米,拱高米,那么桥拱所在圆的半径OA= 米,弧AB的长度为 米.
16.(2024 镇海区校级模拟)如图,AB、CD是⊙O中的两条弦,相交于点E,且AB⊥CD,AE=DE,点H为劣弧AD上一动点,G为HE中点,若CE=1,DE=7,连结AG,则AG最小值为 .
三.解答题
17.(2024 南京)如图,在⊙O的内接四边形ABCD中,AD=BC,对角线AC是⊙O的直径.求证:四边形ABCD是矩形.
18.(2024 凉州区二模)点A,B,C都在⊙O上,且CA=CB,若AB=8,⊙O的半径为5,连接CO,求AC的长.
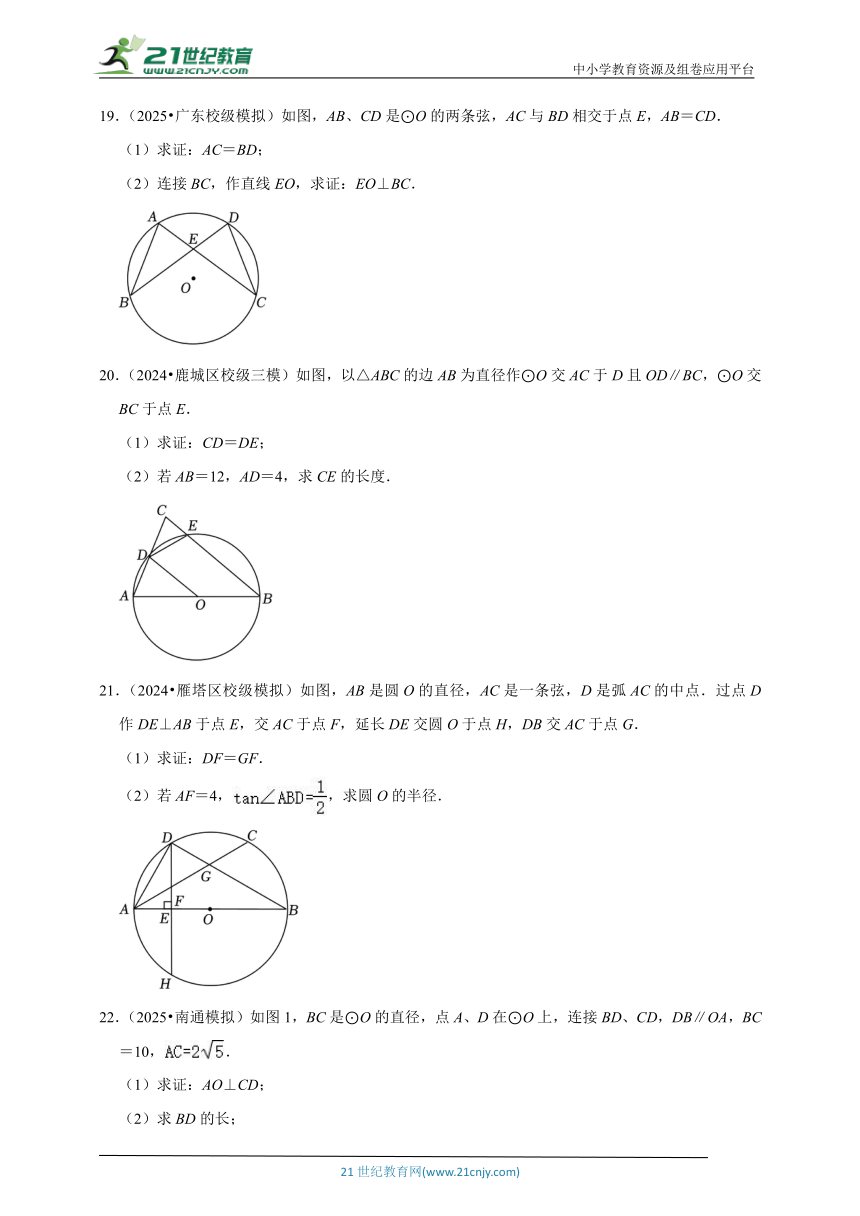
19.(2025 广东校级模拟)如图,AB、CD是⊙O的两条弦,AC与BD相交于点E,AB=CD.
(1)求证:AC=BD;
(2)连接BC,作直线EO,求证:EO⊥BC.
20.(2024 鹿城区校级三模)如图,以△ABC的边AB为直径作⊙O交AC于D且OD∥BC,⊙O交BC于点E.
(1)求证:CD=DE;
(2)若AB=12,AD=4,求CE的长度.
21.(2024 雁塔区校级模拟)如图,AB是圆O的直径,AC是一条弦,D是弧AC的中点.过点D作DE⊥AB于点E,交AC于点F,延长DE交圆O于点H,DB交AC于点G.
(1)求证:DF=GF.
(2)若AF=4,,求圆O的半径.
22.(2025 南通模拟)如图1,BC是⊙O的直径,点A、D在⊙O上,连接BD、CD,DB∥OA,BC=10,.
(1)求证:AO⊥CD;
(2)求BD的长;
(3)如图2,连接AB,作∠CAB的角平分线交⊙O于F,求AF的长度.
23.(2024 十堰一模)如图,在△ABC中,以AB为直径作⊙O,交BC于点D,过O作OE∥BC交⊙O于点E,连接AE,BE,AD.
(1)求证:∠ABE=∠CBE;
(2)若∠C=45°,∠CAE=15°,求∠ABC的度数;
(3)若DF=1,,求AE的长.
24.(2024 金寨县模拟)如图,四边形ABCD内接于⊙O,BD平分∠ABC,交AC于点M.
(1)如图1,求证:AD2=DM DB.
(2)如图2,若AC经过圆心O,且AB=4,BC=3,求BD的长.
答案与解析
一.选择题
1.(2024 西乡塘区模拟)如图,OB,OC是⊙O的半径,∠D=32°,则∠BOC等于( )
A.32° B.58° C.60° D.64°
【点拨】利用同弧所对的圆周角是圆心角的一半即可解得本题.
【解析】解:∵OB、OC是⊙O的半径,∠D=32°,
∴∠BOC=2∠D=64°.
故选:D.
【点睛】本题考查了圆周角定理,同圆或等圆中同弧所对的圆周角是圆心角的一半.
2.(2024 天府新区模拟)如图,AB是⊙O的弦,若⊙O的半径OA=10,圆心O到弦AB的距离OC=6,则弦AB的长为( )
A.8 B.12 C.16 D.20
【点拨】由垂径定理得到AB=2AC,由勾股定理求出AC==8,即可得到AB的长.
【解析】解:∵OC⊥AB,
∴AB=2AC,
∵OA=10,OC=6,
∴AC==8,
∴AB=2×8=16.
故选:C.
【点睛】本题考查垂径定理,勾股定理,关键是由垂径定理得到AB=2AC,由勾股定理求出AC的长.
3.(2024 宜宾)如图,AB是⊙O的直径,若∠CDB=60°,则∠ABC的度数等于( )
A.30° B.45° C.60° D.90°
【点拨】根据直径所对的圆周角是直角可得∠ACB=90°,再根据同弧所对的圆周角相等可得∠A=∠CDB=60°,然后利用直角三角形的两个锐角互余进行计算,即可解答.
【解析】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠CDB=60°,
∴∠A=∠CDB=60°,
∴∠ABC=90°﹣∠A=30°,
故选:A.
【点睛】本题考查了圆周角定理,熟练掌握圆周角定理是解题的关键.
4.(2024 凉山州)数学活动课上,同学们要测一个如图所示的残缺圆形工件的半径,小明的解决方案是:在工件圆弧上任取两点A,B,连接AB,作AB的垂直平分线CD交AB于点D,交于点C,测出AB=40cm,CD=10cm,则圆形工件的半径为( )
A.50cm B.35cm C.25cm D.20cm
【点拨】根据垂径定理可以得到BD的长,再根据勾股定理,即可求得圆形工件的半径.
【解析】解:设圆心为O,连接OB,如图所示,
∵CD垂直平分AB,AB=40cm,
∴BD=20cm,
∵CD=10cm,OC=OB,
∴OD=OB﹣10,
∵∠ODB=90°,
∴OD2+BD2=OB2,
∴(OB﹣10)2+202=OB2,
解得OB=25,
即圆形工件的半径为25cm,
故选:C.
【点睛】本题考查垂径定理的应用、勾股定理,解答本题的关键是明确题意,利用数形结合的思想解答.
5.(2024 甘谷县三模)如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4,则⊙O的周长为( )
A.4π B.6π C.8π D.9π
【点拨】如图,连接OD、OC.根据圆心角、弧、弦的关系证得△AOD是等边三角形,则⊙O的半径长为BC=4cm;然后由圆的周长公式进行计算.
【解析】解:如图,连接OC、OD.
∵AB是⊙O的直径,四边形ABCD内接于⊙O,BC=CD=DA=4,
∴==,
∴∠AOD=∠DOC=∠BOC=60°.
又OA=OD,
∴△AOD是等边三角形,
∴OA=AD=4,
∴⊙O的周长=2×4π=8π.
故选:C.
【点睛】本题考查了圆心角、弧、弦的关系,等边三角形的判定与性质.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距也相等,即四者有一个相等,则其它三个都相等.
6.(2024 江北区一模)如图,在⊙O中,△AOB是正三角形,点C在上,若∠CAB=20°,则∠ABC=( )
A.10° B.15° C.20° D.25°
【点拨】连接OC,根据正三角形的性质求出∠BOC=60°,根据圆周角定理可求解∠COB的度数,根据角的和差求出∠AOC=20°,再利用圆周角定理求解即可.
【解析】解:连接OC,
∵△AOB是正三角形,
∴∠BOC=60°,
∵∠CAB=20°,
∴∠COB=2∠CAB=40°,
∴∠AOC=∠AOB﹣∠BOC=20°,
∴∠ABC=∠AOC=10°,
故选:A.
【点睛】本题主要考查圆周角定理,掌握圆周角定理是解题的关键.
7.(2024 济宁)如图,分别延长圆内接四边形ABCD的两组对边,延长线相交于点E,F.若∠E=54°41',∠F=43°19',则∠A的度数为( )
A.42° B.41°20' C.41° D.40°20'
【点拨】根据圆内接四边形对角互补得出∠A+∠BCD=180°,再根据三角形外角的性质得出∠CDF=∠A+∠E,∠BCD=∠F+∠CDF,由此得到2∠A+∠F+∠E=180°,即可求解.
【解析】解:∵四边形ABCD是圆内接四边形,
∴∠A+∠BCD=180°,
∵∠CDF是△ADE的外角,
∴∠CDF=∠A+∠E,
∵∠BCD是△CDF的外角,
∴∠BCD=∠F+∠CDF,
∴∠BCD=∠F+∠A+∠E,
∵∠A+∠F+∠A+∠E=180°,
∴2∠A+∠F+∠E=180°,
∵∠E=54°41',∠F=43°19',
∴2∠A+54°41'+43°19'=180°,
∴∠A=41°,
故选:C.
【点睛】本题考查了圆内接四边形的性质及三角形外角的性质,度分秒的换算,熟练掌握这些知识点是解题的关键.
8.(2024 义乌市模拟)如图,AE是⊙O直径,半径OD与弦AB垂直于点C,连接EC.若AB=8,CD=2,则CE的长为( )
A.8 B.2 C.3 D.2
【点拨】先根据垂径定理求出AC的长,设⊙O的半径为r,在Rt△OAC中利用勾股定理求出r的值,连接BE,由AE是直径,根据圆周角定理得到∠ABE=90°,利用OC是△ABE的中位线得到BE=2OC=6,然后在Rt△CBE中利用勾股定理可计算出CE.
【解析】解:∵OD⊥AB,AB=8,
∴AC=AB=×8=4,
设⊙O的半径OA=r,
∴OC=OD﹣CD=r﹣2,
在Rt△OAC中,
r2=(r﹣2)2+42,
解得:r=5,
连接BE,如图,
∵OD=5,CD=2,
∴OC=3,
∵AE是直径,
∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE===2.
故选:B.
【点睛】本题考查了垂径定理及圆周角定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧,作出恰当的辅助线是解答此题的关键.
9.(2024 浙江模拟)如图,四边形ABCD内接于⊙O,若所对圆心角的度数为80°,则∠C=( )
A.110° B.120° C.135° D.140°
【点拨】连接OD,根据题意求出∠BOD=80°,根据圆周角定理求出∠A,再根据圆内接四边形的性质求出∠C.
【解析】解:如图,连接OD,
∵所对圆心角的度数为80°,
∴∠BOD=80°,
由圆周角定理得:∠A=∠BOD=40°,
∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°,
∴∠C=180°﹣40°=140°,
故选:D.
【点睛】本题考查的是圆周角定理、圆内接四边形的性质,熟记圆内接四边形的对角互补是解题的关键.
10.(2024 定海区三模)如图所示,⊙O的半径是3,直线l与⊙O相交于A,B两点,点M,N在直线l的异侧,且是⊙O上的两个动点,且∠ANB=135°,则四边形MANB面积的最大值是( )
A.9 B. C.18 D.
【点拨】过点O作OC⊥AB于C,交⊙O于D,E两点,连结OA,OB,DA,DB,EA,EB,先证明∠AOB=90°,得到△OAB为等腰直角三角形,求出AB的长,然后利用S四边形MANB=S△MAB+S△NAB,得出当M点运动到D点,N点运动到E点,四边形MANB面积最大值,由此计算S四边形DAEB,即得答案.
【解析】解:如图,过点O作OC⊥AB于C,交⊙O于D,E两点,连结OA,OB,DA,DB,EA,EB,
∵∠ANB=135°,
∴∠AMB=45°,
∴∠AOB=2∠AMB=90°,
∴△OAB为等腰直角三角形,
∴,
∵S四边形MANB=S△MAB+S△NAB,
∴当点M到AB的距离最大时,△MAB的面积最大,当点N到AB的距离最大时,△NAB的面积最大,
即M点运动到D点,N点运动到E点,
此时四边形MANB面积的最大值
=S四边形DAEB=S△DAB+S△EAB
=
=
=
=
=.
故选:B.
【点睛】本题考查了圆周角定理,勾股定理,找到使四边形MANB面积最大的点M与点N的位置是解题的关键.
二.填空题
11.(2024秋 泗阳县期末)在⊙O中,弦AB=3,圆心角∠A0B=60°,则⊙O的半径为 3 .
【点拨】根据等边三角形的判定定理证明△AOB是等边三角形,根据等边三角形的性质得到答案.
【解析】解:∵OA=OB,∠A0B=60°,
∴△AOB是等边三角形,
∴OA=AB=3.
故答案为:3.
【点睛】本题考查的是圆心角、弧、弦的关系和等边三角形的判定和性质,根据题意证明△AOB是等边三角形是解题的关键.
12.(2024 西宁)如图,四边形ABCD内接于⊙O,E为直径CD延长线上一点,=,∠ADE=110°,则∠DAB= 125° .
【点拨】根据圆的性质和圆内接四边形的性质,可以求得∠DAB的度数.
【解析】解:连接OA、OB,如图所示,
∵∠ADE=110°,∠ADE+∠ADO=180°,
∴∠ADO=70°,
∵OA=OD,
∴∠OAD=∠ODA=70°,
∴∠AOD=40°,
∴∠AOC=140°,
∵=,
∴∠AOB=∠BOC=70°,
∵OB=OC,
∴∠OCB=∠OBC=55°,
∵四边形ABCD为圆内接四边形,
∴∠DAB+∠OCB=180°,
∴∠DAB=125°,
故答案为:125°.
【点睛】本题考查圆内接四边形、圆心角、弧、弦的关系,解答本题的关键是明确题意,利用圆内接四边形的性质解答.
13.(2024 牡丹江)如图,在⊙O中,直径AB⊥CD于点E,CD=6,BE=1,则弦AC的长为 .
【点拨】由垂径定理得,设⊙O的半径为r,则O E=O B﹣E B=r﹣1,在Rt△OED中,由勾股定理得出方程,求出r=5,即可得出AE=9,在Rt△AEC中,由勾股定理即可求解.
【解析】解:∵A B⊥C D,C D=6,
∴,
设⊙O的半径为r,则O E=O B﹣E B=r﹣1,
在Rt△OED中,由勾股定理得:OE2+DE2=OD2,即(r﹣1)2+32=r2,
解得:r=5,
∴OA=5,OE=4,
∴AE=OA+OE=9,
在Rt△AEC中,由勾股定理得:,
故答案为:.
【点睛】本题考查了垂径定理和勾股定理等知识,熟练掌握垂径定理,由勾股定理得出方程是解题的关键.
14.(2024 富阳区一模)如图,AB是半圆O的直径,弦CD∥AB,CD=8,弦CD与直径AB之间的距离为3,则AB= 10 .
【点拨】过O作OH⊥CD于H,由垂径定理得到CH=CD=4,由AB∥CD,得到OH⊥AB,因此OH=3,由勾股定理求出OC==5,即可得到AB=2OC=10.
【解析】解:过O作OH⊥CD于H,
∴CH=CD=×8=4,
∵AB∥CD,
∴OH⊥AB,
∴OH=3,
∴OC==5,
∴AB=2OC=10.
故答案为:10.
【点睛】本题考查垂径定理,勾股定理,关键是由勾股定理求出OC的长.
15.(2024 杭州模拟)江南水乡杭州有很多小河和石拱桥,石拱桥是中国传统桥梁四大基本形式之一,它的主桥拱是圆弧形.如图,已知曲院风荷的一座石拱桥的跨度AB=6米,拱高米,那么桥拱所在圆的半径OA= 2 米,弧AB的长度为 米.
【点拨】根据题意构造直角三角形,进而利用勾股定理求出答案,再根据特殊角的三角函数值求出∠DOB的值,利用弧长公式即可求解.
【解析】解:由题意可知,AD=BD,OD⊥AB,
∵AB=6米,
∴BD=3米,
拱高CD=米,
设OB=x,则DO=x﹣,
BD2+DO2=AO2,
根据题意可得:
32+(x﹣)2=x2
解得:x=2,
即圆弧形桥拱所在圆的半径是2米.
∵sin∠DOB===,
∴∠DOB=60°,
∴∠AOB=120°,
∴弧AB的长度==π.
故答案为:2,π.
【点睛】此题主要考查了垂径定理的应用以及勾股定理,正确应用垂径定理是解题关键.
16.(2024 镇海区校级模拟)如图,AB、CD是⊙O中的两条弦,相交于点E,且AB⊥CD,AE=DE,点H为劣弧AD上一动点,G为HE中点,若CE=1,DE=7,连结AG,则AG最小值为 .
【点拨】连接AO,DO,过点O作OK⊥AE,交AE于点K,OF⊥CD,交DE于点F,构造正方形,计算圆的半径,然后作OE的中点M,连接MG,连接OH,推导出点G的运动轨迹是以M为圆心的圆,连接AM与圆M的交点就是AG的最小值.
【解析】解:如图所示,连接AO,DO,过点O作OK⊥AE,交AE于点K,OF⊥CD,交DE于点F,
∵CE=1,DE=7,∴CD=CE+DE=1+7=8,
∵OF⊥CD,
∴,
∴EF=CF﹣CE=4﹣1=3,
∵AE=DE,OA=OD,OE=OE,
∴△AOE≌△DOE(SSS),
∴,
∵OK⊥AE,OF⊥CD,
∴OK=OF,
∵∠AED=90°,
∴四边形OKEF是正方形,
∴OK=KE=EF=OF=3,
∴,,
如图所示,作OE的中点M,连接MG,连接OH,
∵点M是OE的中点,G为HE中点,
∴,
∴点G在以点M为圆心,以 为半径的圆上运动,
连接AM交⊙M于点G’,过点M作MN⊥AE,
∴当点A,G,M三点共线时,即点G和点G'重合时,AG的值最小,
∵点M是OE的中点,,
∵MN⊥AE,∠NEM=45°,
∴∠NME=45°,
∴△NME是等腰直角三角形,
∴,
∴,
∴,
,
∴ACG的最小值为 ,
故答案为:.
【点睛】本题考查的重点是垂径定理,解直角三角形,中位线等知识,难点是找点G的运动轨迹,当找到点G的运动轨迹以后再利用两点之间直线最短就可以计算出AG的最小值.
三.解答题
17.(2024 南京)如图,在⊙O的内接四边形ABCD中,AD=BC,对角线AC是⊙O的直径.求证:四边形ABCD是矩形.
【点拨】由AC是⊙O的直径,可得∠B=∠D=90°,证明Rt△ABC≌Rt△CDA,得到AB=CD,可证明四边形ABCD是平行四边形,即可解答.
【解析】证明:∵对角线AC是⊙O的直径,
∴∠B=∠D=90°,
∴△ABC和△CDA是直角三角形,
在Rt△ABC和Rt△CDA中,
,
∴Rt△ABC≌Rt△CDA(HL),
∴AB=CD,
又∵AD=BC,
∴四边形ABCD是平行四边形,
∵∠B=90°,
∴平行四边形ABCD是矩形.
【点睛】本题考查了矩形的判定,圆周角定理,全等三角形的判定与性质,解题的关键是掌握相关知识.
18.(2024 凉州区二模)点A,B,C都在⊙O上,且CA=CB,若AB=8,⊙O的半径为5,连接CO,求AC的长.
【点拨】连接OA,OB,根据垂径定理得到,然后利用勾股定理求解即可.
【解析】解:如图,连接OA,OB,
∴OA=OB,
∵CA=CB,
∴OC垂直平分AB,即CO⊥AB,
∵AB=8,
∴,
∵⊙O的半径为5,
∴,
∴CD=OC﹣OD=5﹣3=2,
∴.
【点睛】本题考查了垂径定理,勾股定理,圆的基本性质,解题的关键是利用所判定的垂直,结合垂径定理得到.
19.(2025 广东校级模拟)如图,AB、CD是⊙O的两条弦,AC与BD相交于点E,AB=CD.
(1)求证:AC=BD;
(2)连接BC,作直线EO,求证:EO⊥BC.
【点拨】(1)根据利用弧、弦、圆心角的关系得出,进而可得AC=BD;
(2)因为AB=CD,所以,即∠ACB=∠DBC.结合OB=OC,得出E、O都在BC的垂直平分线上,即可作答.
【解析】证明:(1)∵AB=CD,
∴=,
∴+=+,
即=,
∴AC=BD;
(2)连接OB、OC、BC,
∵AB=CD,
∴=,
∴∠ACB=∠DBC,
∴EB=EC,
∵OB=OC,
∴E、O都在BC的垂直平分线上,
∴EO⊥BC.
【点睛】本题考查了垂直平分线的判定与性质,利用弧、弦、圆心角的关系求证,正确掌握相关性质内容是解题的关键.
20.(2024 鹿城区校级三模)如图,以△ABC的边AB为直径作⊙O交AC于D且OD∥BC,⊙O交BC于点E.
(1)求证:CD=DE;
(2)若AB=12,AD=4,求CE的长度.
【点拨】(1)根据平行线的性质得∠ADO=∠C,根据圆内接四边形的性质得到∠A+∠BED=180°,再根据∠CED+∠BED=180°,OA=OD,∠ODA=∠A,得∠C=∠CED,即可得出结论;
(2)连接AE,根据OD∥BC,得===,所以BC=2OD=12,AC=2AD=8,再根据勾股定理得AE2=AC2﹣CE2=AB2﹣BE2,设CE=x,64﹣x2=144﹣(12﹣x)2,解方程即可得出答案.
【解析】(1)证明:∵OD∥BC,
∴∠ADO=∠C,
∴四边形ABED为⊙O的内接四边形,
∴∠A+∠BED=180°,
∵∠CED+∠BED=180°,
∴∠CED=∠A,
∵OA=OD,
∴∠ODA=∠A,
∴∠C=∠CED,
∴CD=DE;
(2)解:如图,连接AE,
∵AB⊙O的直径,
∴AE⊥BC,
∵OD∥BC,
∴===,
∴BC=2OD=12,AC=2AD=8,
在Rt△ACE和Rt△ABE中,根据勾股定理得,
AE2=AC2﹣CE2=AB2﹣BE2,
设CE=x,
∴64﹣x2=144﹣(12﹣x)2,
解得x=,
∴CE的长度为.
【点睛】本题考查了圆周角定理,平行线的性质以及勾股定理,正确地作出辅助线和利用圆周角定理,平行线的性质以及勾股定理是解题的关键.
21.(2024 雁塔区校级模拟)如图,AB是圆O的直径,AC是一条弦,D是弧AC的中点.过点D作DE⊥AB于点E,交AC于点F,延长DE交圆O于点H,DB交AC于点G.
(1)求证:DF=GF.
(2)若AF=4,,求圆O的半径.
【点拨】(1)D是弧AC的中点,得出=,再由垂径定理得出=,∠ADB=90°,根据等弧所对圆周角相等得出∠ADH=∠CAD,再根据等角的余角相等得∠DGF=∠BDH,最后由等角对等边证明即可;
(2)连接连接OD,根据 ,设AE=x,DE=2x,利用勾股定理求得x,再利用正切函数计算即可.
【解析】(1)证明:∵D是弧AC的中点,
∴=,
∵AB⊥DH,且AB是⊙O的直径,
∴=,∠ADB=90°,
∴=,
∴∠ADH=∠CAD,
∵∠ADB=90°,
∴∠ADH+∠BDH=90°,∠DAC+∠DGF=90°
∴∠DGF=∠BDH,
∴DF=GF;
(2)连接OD,
∵DE⊥AB于点E,AB是⊙O的直径,
∴∠ADE=90°﹣∠DAE=∠ABD,
∵,
∴,
设AE=x,DE=2x,
由(1)得∠ADH=∠CAD,
∴AF=DF=4,
∴EF=DE﹣DF=2x﹣4,
在Rt△AEF中,由勾股定理得:EF2+AE2=AF2,即(2x﹣4)2+x2=42,
解得:或x=0(舍去),
∴,
∵,
∴,
∴,
∴AB=AE+BE=16,
∴⊙O的半径为8.
【点睛】本题考查了垂径定理,勾股定理,圆周角定理,一元二次方程的解法,正切函数,熟练掌握垂径定理,勾股定理,圆周角定理,正切函数是解题的关键.
22.(2025 南通模拟)如图1,BC是⊙O的直径,点A、D在⊙O上,连接BD、CD,DB∥OA,BC=10,.
(1)求证:AO⊥CD;
(2)求BD的长;
(3)如图2,连接AB,作∠CAB的角平分线交⊙O于F,求AF的长度.
【点拨】(1)先根据圆周角定理得出∠BDC=90°,再由DB∥OA即可得出结论;
(2)作AH⊥BC于H,OM⊥BD于M,如图1,则BM=DM,利用勾股定理计算出AB的长,再利用面积法得到AH的长,接着利用勾股定理计算出OH的长,然后证明△AOH≌△OBM得到BM=OH,而得到BD的长;
(3)作CG⊥AF于G,连接CF、BF,如图2,证明△CBF为等腰直角三角形得到CF=BC,利用△ACG为等腰直角三角形得到CG=AG=AC,然后利用勾股定理计算出GF,从而得到AF的长.
【解析】(1)证明:∵BC是⊙O的直径,
∴∠D=90°,
∵OA∥BD,
∴∠CEO=∠D=90°,
∴AO⊥CD;
(2)解:连接AB,作AH⊥BC于H,OM⊥BD于M,如图1,则BM=DM,
∵BC为⊙O的直径,
∴∠CAB=90°,
∴AB==4,
∵AH BC=AC AB,
∴AH==4,
在Rt△OAH中,OH===3,
∵OA∥BD,
∴∠AOH=∠EBO,
在△AOH和△OBM中,
,
∴△AOH≌△OBM(ASA),
∴BM=OH=3,
∴BD=2BM=6;
(3)解:作CG⊥AF于G,连接CF、BF,如图2,
∵AF平分∠CAB,
∴∠CAF=∠BAF=45°,
∴CF=BF,
∴△CBF为等腰直角三角形,
∴CF=BC=5,
在Rt△ACG中,CG=AG=AC=,
在Rt△GFC中,GF==2,
∴AF=AG+GF=+2=3.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了垂径定理.
23.(2024 十堰一模)如图,在△ABC中,以AB为直径作⊙O,交BC于点D,过O作OE∥BC交⊙O于点E,连接AE,BE,AD.
(1)求证:∠ABE=∠CBE;
(2)若∠C=45°,∠CAE=15°,求∠ABC的度数;
(3)若DF=1,,求AE的长.
【点拨】(1)由圆的半径相等可得OB=OE,根据等边对顶角得∠ABE=∠OEB,再由平行线性质可得∠OEB=∠CBE,利用等量代换即可证得结论;
(2)延长AE交BC于G,可证得∠BAE=∠BGE=∠C+∠CAE=45°+15°=60°,运用三角形内角和定理可得答案;
(3)由OA=OB,可得S△AOE=S△ABE,进而可得=,再证得△ABE∽△FBD,可得=,结合DF=1,即可求得答案.
【解析】(1)证明:∵OB=OE,
∴∠ABE=∠OEB,
∵OE∥BC,
∴∠OEB=∠CBE,
∴∠ABE=∠CBE;
(2)解:如图,延长AE交BC于G,
∵AB是⊙O的直径,
∴BE⊥AE,
∵∠ABE=∠CBE,
∴∠BAE=∠BGE=∠C+∠CAE=45°+15°=60°,
∴∠ABC=∠AOE=60°;
(3)∵OA=OB=AB,
∴S△AOE=S△ABE,
∵=,
∴=,
∵∠ABE=∠CBE,即∠ABE=∠FBD,
又∵AB是⊙O的直径,
∴∠AEB=∠BDF=90°,
∴△ABE∽△FBD,
∴=()2,
∴()2=,
∴=,
∵DF=1,
∴AE=.
【点睛】本题考查圆的综合问题,涉及平行线的性质,三角形的外角的性质,三角形中线的性质,圆周角定理,相似三角形的判定与性质等知识,需要学生灵活运用所学知识.
24.(2024 金寨县模拟)如图,四边形ABCD内接于⊙O,BD平分∠ABC,交AC于点M.
(1)如图1,求证:AD2=DM DB.
(2)如图2,若AC经过圆心O,且AB=4,BC=3,求BD的长.
【点拨】(1)由角平分线的定义可得∠ABD=∠CBD,即可得出,结合圆周角定理推出△ADM∽△BDA,由相似三角形的性质可得,即可得证;
(2)由圆周角定理结合角平分线的定义得出,从而得出,推出AD=CD,由勾股定理得出AC=5,结合等腰直角三角形的性质得出,作CE⊥BD于E,求出BE、DE的长,即可得解.
【解析】(1)证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴,
∴∠ABD=∠DAC,
∵∠ADB=∠ADM,
∴△ADM∽△BDA,
∴,
∴AD2=DM DB;
(2)解:∵AC为直径,
∴∠ABC=∠ADC=90°,
∵BD平分∠ABC,
∴,
∴,
∴AD=CD,
∵在Rt△ABC中,AB=4,BC=3,
∴,
在Rt△ADC中,AD=CD,AC=5,
∴,
作CE⊥BD于E,
,
在Rt△BCE中,∠CBE=45°,BC=3,
∴,
在Rt△DCE中,,,
∴,
∴.
【点睛】本题考查了圆周角定理、相似三角形的判定与性质、解直角三角形、等腰直角三角形的判定与性质,熟练掌握以上知识点并灵活运用是解此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专题23 圆的基本性质
一.选择题
1.(2024 西乡塘区模拟)如图,OB,OC是⊙O的半径,∠D=32°,则∠BOC等于( )
A.32° B.58° C.60° D.64°
2.(2024 天府新区模拟)如图,AB是⊙O的弦,若⊙O的半径OA=10,圆心O到弦AB的距离OC=6,则弦AB的长为( )
A.8 B.12 C.16 D.20
3.(2024 宜宾)如图,AB是⊙O的直径,若∠CDB=60°,则∠ABC的度数等于( )
A.30° B.45° C.60° D.90°
4.(2024 凉山州)数学活动课上,同学们要测一个如图所示的残缺圆形工件的半径,小明的解决方案是:在工件圆弧上任取两点A,B,连接AB,作AB的垂直平分线CD交AB于点D,交于点C,测出AB=40cm,CD=10cm,则圆形工件的半径为( )
A.50cm B.35cm C.25cm D.20cm
5.(2024 甘谷县三模)如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4,则⊙O的周长为( )
A.4π B.6π C.8π D.9π
6.(2024 江北区一模)如图,在⊙O中,△AOB是正三角形,点C在上,若∠CAB=20°,则∠ABC=( )
A.10° B.15° C.20° D.25°
7.(2024 济宁)如图,分别延长圆内接四边形ABCD的两组对边,延长线相交于点E,F.若∠E=54°41',∠F=43°19',则∠A的度数为( )
A.42° B.41°20' C.41° D.40°20'
8.(2024 义乌市模拟)如图,AE是⊙O直径,半径OD与弦AB垂直于点C,连接EC.若AB=8,CD=2,则CE的长为( )
A.8 B.2 C.3 D.2
9.(2024 浙江模拟)如图,四边形ABCD内接于⊙O,若所对圆心角的度数为80°,则∠C=( )
A.110° B.120° C.135° D.140°
10.(2024 定海区三模)如图所示,⊙O的半径是3,直线l与⊙O相交于A,B两点,点M,N在直线l的异侧,且是⊙O上的两个动点,且∠ANB=135°,则四边形MANB面积的最大值是( )
A.9 B. C.18 D.
二.填空题
11.(2024秋 泗阳县期末)在⊙O中,弦AB=3,圆心角∠A0B=60°,则⊙O的半径为 .
12.(2024 西宁)如图,四边形ABCD内接于⊙O,E为直径CD延长线上一点,=,∠ADE=110°,则∠DAB= .
13.(2024 牡丹江)如图,在⊙O中,直径AB⊥CD于点E,CD=6,BE=1,则弦AC的长为 .
14.(2024 富阳区一模)如图,AB是半圆O的直径,弦CD∥AB,CD=8,弦CD与直径AB之间的距离为3,则AB= .
15.(2024 杭州模拟)江南水乡杭州有很多小河和石拱桥,石拱桥是中国传统桥梁四大基本形式之一,它的主桥拱是圆弧形.如图,已知曲院风荷的一座石拱桥的跨度AB=6米,拱高米,那么桥拱所在圆的半径OA= 米,弧AB的长度为 米.
16.(2024 镇海区校级模拟)如图,AB、CD是⊙O中的两条弦,相交于点E,且AB⊥CD,AE=DE,点H为劣弧AD上一动点,G为HE中点,若CE=1,DE=7,连结AG,则AG最小值为 .
三.解答题
17.(2024 南京)如图,在⊙O的内接四边形ABCD中,AD=BC,对角线AC是⊙O的直径.求证:四边形ABCD是矩形.
18.(2024 凉州区二模)点A,B,C都在⊙O上,且CA=CB,若AB=8,⊙O的半径为5,连接CO,求AC的长.
19.(2025 广东校级模拟)如图,AB、CD是⊙O的两条弦,AC与BD相交于点E,AB=CD.
(1)求证:AC=BD;
(2)连接BC,作直线EO,求证:EO⊥BC.
20.(2024 鹿城区校级三模)如图,以△ABC的边AB为直径作⊙O交AC于D且OD∥BC,⊙O交BC于点E.
(1)求证:CD=DE;
(2)若AB=12,AD=4,求CE的长度.
21.(2024 雁塔区校级模拟)如图,AB是圆O的直径,AC是一条弦,D是弧AC的中点.过点D作DE⊥AB于点E,交AC于点F,延长DE交圆O于点H,DB交AC于点G.
(1)求证:DF=GF.
(2)若AF=4,,求圆O的半径.
22.(2025 南通模拟)如图1,BC是⊙O的直径,点A、D在⊙O上,连接BD、CD,DB∥OA,BC=10,.
(1)求证:AO⊥CD;
(2)求BD的长;
(3)如图2,连接AB,作∠CAB的角平分线交⊙O于F,求AF的长度.
23.(2024 十堰一模)如图,在△ABC中,以AB为直径作⊙O,交BC于点D,过O作OE∥BC交⊙O于点E,连接AE,BE,AD.
(1)求证:∠ABE=∠CBE;
(2)若∠C=45°,∠CAE=15°,求∠ABC的度数;
(3)若DF=1,,求AE的长.
24.(2024 金寨县模拟)如图,四边形ABCD内接于⊙O,BD平分∠ABC,交AC于点M.
(1)如图1,求证:AD2=DM DB.
(2)如图2,若AC经过圆心O,且AB=4,BC=3,求BD的长.
答案与解析
一.选择题
1.(2024 西乡塘区模拟)如图,OB,OC是⊙O的半径,∠D=32°,则∠BOC等于( )
A.32° B.58° C.60° D.64°
【点拨】利用同弧所对的圆周角是圆心角的一半即可解得本题.
【解析】解:∵OB、OC是⊙O的半径,∠D=32°,
∴∠BOC=2∠D=64°.
故选:D.
【点睛】本题考查了圆周角定理,同圆或等圆中同弧所对的圆周角是圆心角的一半.
2.(2024 天府新区模拟)如图,AB是⊙O的弦,若⊙O的半径OA=10,圆心O到弦AB的距离OC=6,则弦AB的长为( )
A.8 B.12 C.16 D.20
【点拨】由垂径定理得到AB=2AC,由勾股定理求出AC==8,即可得到AB的长.
【解析】解:∵OC⊥AB,
∴AB=2AC,
∵OA=10,OC=6,
∴AC==8,
∴AB=2×8=16.
故选:C.
【点睛】本题考查垂径定理,勾股定理,关键是由垂径定理得到AB=2AC,由勾股定理求出AC的长.
3.(2024 宜宾)如图,AB是⊙O的直径,若∠CDB=60°,则∠ABC的度数等于( )
A.30° B.45° C.60° D.90°
【点拨】根据直径所对的圆周角是直角可得∠ACB=90°,再根据同弧所对的圆周角相等可得∠A=∠CDB=60°,然后利用直角三角形的两个锐角互余进行计算,即可解答.
【解析】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠CDB=60°,
∴∠A=∠CDB=60°,
∴∠ABC=90°﹣∠A=30°,
故选:A.
【点睛】本题考查了圆周角定理,熟练掌握圆周角定理是解题的关键.
4.(2024 凉山州)数学活动课上,同学们要测一个如图所示的残缺圆形工件的半径,小明的解决方案是:在工件圆弧上任取两点A,B,连接AB,作AB的垂直平分线CD交AB于点D,交于点C,测出AB=40cm,CD=10cm,则圆形工件的半径为( )
A.50cm B.35cm C.25cm D.20cm
【点拨】根据垂径定理可以得到BD的长,再根据勾股定理,即可求得圆形工件的半径.
【解析】解:设圆心为O,连接OB,如图所示,
∵CD垂直平分AB,AB=40cm,
∴BD=20cm,
∵CD=10cm,OC=OB,
∴OD=OB﹣10,
∵∠ODB=90°,
∴OD2+BD2=OB2,
∴(OB﹣10)2+202=OB2,
解得OB=25,
即圆形工件的半径为25cm,
故选:C.
【点睛】本题考查垂径定理的应用、勾股定理,解答本题的关键是明确题意,利用数形结合的思想解答.
5.(2024 甘谷县三模)如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4,则⊙O的周长为( )
A.4π B.6π C.8π D.9π
【点拨】如图,连接OD、OC.根据圆心角、弧、弦的关系证得△AOD是等边三角形,则⊙O的半径长为BC=4cm;然后由圆的周长公式进行计算.
【解析】解:如图,连接OC、OD.
∵AB是⊙O的直径,四边形ABCD内接于⊙O,BC=CD=DA=4,
∴==,
∴∠AOD=∠DOC=∠BOC=60°.
又OA=OD,
∴△AOD是等边三角形,
∴OA=AD=4,
∴⊙O的周长=2×4π=8π.
故选:C.
【点睛】本题考查了圆心角、弧、弦的关系,等边三角形的判定与性质.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距也相等,即四者有一个相等,则其它三个都相等.
6.(2024 江北区一模)如图,在⊙O中,△AOB是正三角形,点C在上,若∠CAB=20°,则∠ABC=( )
A.10° B.15° C.20° D.25°
【点拨】连接OC,根据正三角形的性质求出∠BOC=60°,根据圆周角定理可求解∠COB的度数,根据角的和差求出∠AOC=20°,再利用圆周角定理求解即可.
【解析】解:连接OC,
∵△AOB是正三角形,
∴∠BOC=60°,
∵∠CAB=20°,
∴∠COB=2∠CAB=40°,
∴∠AOC=∠AOB﹣∠BOC=20°,
∴∠ABC=∠AOC=10°,
故选:A.
【点睛】本题主要考查圆周角定理,掌握圆周角定理是解题的关键.
7.(2024 济宁)如图,分别延长圆内接四边形ABCD的两组对边,延长线相交于点E,F.若∠E=54°41',∠F=43°19',则∠A的度数为( )
A.42° B.41°20' C.41° D.40°20'
【点拨】根据圆内接四边形对角互补得出∠A+∠BCD=180°,再根据三角形外角的性质得出∠CDF=∠A+∠E,∠BCD=∠F+∠CDF,由此得到2∠A+∠F+∠E=180°,即可求解.
【解析】解:∵四边形ABCD是圆内接四边形,
∴∠A+∠BCD=180°,
∵∠CDF是△ADE的外角,
∴∠CDF=∠A+∠E,
∵∠BCD是△CDF的外角,
∴∠BCD=∠F+∠CDF,
∴∠BCD=∠F+∠A+∠E,
∵∠A+∠F+∠A+∠E=180°,
∴2∠A+∠F+∠E=180°,
∵∠E=54°41',∠F=43°19',
∴2∠A+54°41'+43°19'=180°,
∴∠A=41°,
故选:C.
【点睛】本题考查了圆内接四边形的性质及三角形外角的性质,度分秒的换算,熟练掌握这些知识点是解题的关键.
8.(2024 义乌市模拟)如图,AE是⊙O直径,半径OD与弦AB垂直于点C,连接EC.若AB=8,CD=2,则CE的长为( )
A.8 B.2 C.3 D.2
【点拨】先根据垂径定理求出AC的长,设⊙O的半径为r,在Rt△OAC中利用勾股定理求出r的值,连接BE,由AE是直径,根据圆周角定理得到∠ABE=90°,利用OC是△ABE的中位线得到BE=2OC=6,然后在Rt△CBE中利用勾股定理可计算出CE.
【解析】解:∵OD⊥AB,AB=8,
∴AC=AB=×8=4,
设⊙O的半径OA=r,
∴OC=OD﹣CD=r﹣2,
在Rt△OAC中,
r2=(r﹣2)2+42,
解得:r=5,
连接BE,如图,
∵OD=5,CD=2,
∴OC=3,
∵AE是直径,
∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE===2.
故选:B.
【点睛】本题考查了垂径定理及圆周角定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧,作出恰当的辅助线是解答此题的关键.
9.(2024 浙江模拟)如图,四边形ABCD内接于⊙O,若所对圆心角的度数为80°,则∠C=( )
A.110° B.120° C.135° D.140°
【点拨】连接OD,根据题意求出∠BOD=80°,根据圆周角定理求出∠A,再根据圆内接四边形的性质求出∠C.
【解析】解:如图,连接OD,
∵所对圆心角的度数为80°,
∴∠BOD=80°,
由圆周角定理得:∠A=∠BOD=40°,
∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°,
∴∠C=180°﹣40°=140°,
故选:D.
【点睛】本题考查的是圆周角定理、圆内接四边形的性质,熟记圆内接四边形的对角互补是解题的关键.
10.(2024 定海区三模)如图所示,⊙O的半径是3,直线l与⊙O相交于A,B两点,点M,N在直线l的异侧,且是⊙O上的两个动点,且∠ANB=135°,则四边形MANB面积的最大值是( )
A.9 B. C.18 D.
【点拨】过点O作OC⊥AB于C,交⊙O于D,E两点,连结OA,OB,DA,DB,EA,EB,先证明∠AOB=90°,得到△OAB为等腰直角三角形,求出AB的长,然后利用S四边形MANB=S△MAB+S△NAB,得出当M点运动到D点,N点运动到E点,四边形MANB面积最大值,由此计算S四边形DAEB,即得答案.
【解析】解:如图,过点O作OC⊥AB于C,交⊙O于D,E两点,连结OA,OB,DA,DB,EA,EB,
∵∠ANB=135°,
∴∠AMB=45°,
∴∠AOB=2∠AMB=90°,
∴△OAB为等腰直角三角形,
∴,
∵S四边形MANB=S△MAB+S△NAB,
∴当点M到AB的距离最大时,△MAB的面积最大,当点N到AB的距离最大时,△NAB的面积最大,
即M点运动到D点,N点运动到E点,
此时四边形MANB面积的最大值
=S四边形DAEB=S△DAB+S△EAB
=
=
=
=
=.
故选:B.
【点睛】本题考查了圆周角定理,勾股定理,找到使四边形MANB面积最大的点M与点N的位置是解题的关键.
二.填空题
11.(2024秋 泗阳县期末)在⊙O中,弦AB=3,圆心角∠A0B=60°,则⊙O的半径为 3 .
【点拨】根据等边三角形的判定定理证明△AOB是等边三角形,根据等边三角形的性质得到答案.
【解析】解:∵OA=OB,∠A0B=60°,
∴△AOB是等边三角形,
∴OA=AB=3.
故答案为:3.
【点睛】本题考查的是圆心角、弧、弦的关系和等边三角形的判定和性质,根据题意证明△AOB是等边三角形是解题的关键.
12.(2024 西宁)如图,四边形ABCD内接于⊙O,E为直径CD延长线上一点,=,∠ADE=110°,则∠DAB= 125° .
【点拨】根据圆的性质和圆内接四边形的性质,可以求得∠DAB的度数.
【解析】解:连接OA、OB,如图所示,
∵∠ADE=110°,∠ADE+∠ADO=180°,
∴∠ADO=70°,
∵OA=OD,
∴∠OAD=∠ODA=70°,
∴∠AOD=40°,
∴∠AOC=140°,
∵=,
∴∠AOB=∠BOC=70°,
∵OB=OC,
∴∠OCB=∠OBC=55°,
∵四边形ABCD为圆内接四边形,
∴∠DAB+∠OCB=180°,
∴∠DAB=125°,
故答案为:125°.
【点睛】本题考查圆内接四边形、圆心角、弧、弦的关系,解答本题的关键是明确题意,利用圆内接四边形的性质解答.
13.(2024 牡丹江)如图,在⊙O中,直径AB⊥CD于点E,CD=6,BE=1,则弦AC的长为 .
【点拨】由垂径定理得,设⊙O的半径为r,则O E=O B﹣E B=r﹣1,在Rt△OED中,由勾股定理得出方程,求出r=5,即可得出AE=9,在Rt△AEC中,由勾股定理即可求解.
【解析】解:∵A B⊥C D,C D=6,
∴,
设⊙O的半径为r,则O E=O B﹣E B=r﹣1,
在Rt△OED中,由勾股定理得:OE2+DE2=OD2,即(r﹣1)2+32=r2,
解得:r=5,
∴OA=5,OE=4,
∴AE=OA+OE=9,
在Rt△AEC中,由勾股定理得:,
故答案为:.
【点睛】本题考查了垂径定理和勾股定理等知识,熟练掌握垂径定理,由勾股定理得出方程是解题的关键.
14.(2024 富阳区一模)如图,AB是半圆O的直径,弦CD∥AB,CD=8,弦CD与直径AB之间的距离为3,则AB= 10 .
【点拨】过O作OH⊥CD于H,由垂径定理得到CH=CD=4,由AB∥CD,得到OH⊥AB,因此OH=3,由勾股定理求出OC==5,即可得到AB=2OC=10.
【解析】解:过O作OH⊥CD于H,
∴CH=CD=×8=4,
∵AB∥CD,
∴OH⊥AB,
∴OH=3,
∴OC==5,
∴AB=2OC=10.
故答案为:10.
【点睛】本题考查垂径定理,勾股定理,关键是由勾股定理求出OC的长.
15.(2024 杭州模拟)江南水乡杭州有很多小河和石拱桥,石拱桥是中国传统桥梁四大基本形式之一,它的主桥拱是圆弧形.如图,已知曲院风荷的一座石拱桥的跨度AB=6米,拱高米,那么桥拱所在圆的半径OA= 2 米,弧AB的长度为 米.
【点拨】根据题意构造直角三角形,进而利用勾股定理求出答案,再根据特殊角的三角函数值求出∠DOB的值,利用弧长公式即可求解.
【解析】解:由题意可知,AD=BD,OD⊥AB,
∵AB=6米,
∴BD=3米,
拱高CD=米,
设OB=x,则DO=x﹣,
BD2+DO2=AO2,
根据题意可得:
32+(x﹣)2=x2
解得:x=2,
即圆弧形桥拱所在圆的半径是2米.
∵sin∠DOB===,
∴∠DOB=60°,
∴∠AOB=120°,
∴弧AB的长度==π.
故答案为:2,π.
【点睛】此题主要考查了垂径定理的应用以及勾股定理,正确应用垂径定理是解题关键.
16.(2024 镇海区校级模拟)如图,AB、CD是⊙O中的两条弦,相交于点E,且AB⊥CD,AE=DE,点H为劣弧AD上一动点,G为HE中点,若CE=1,DE=7,连结AG,则AG最小值为 .
【点拨】连接AO,DO,过点O作OK⊥AE,交AE于点K,OF⊥CD,交DE于点F,构造正方形,计算圆的半径,然后作OE的中点M,连接MG,连接OH,推导出点G的运动轨迹是以M为圆心的圆,连接AM与圆M的交点就是AG的最小值.
【解析】解:如图所示,连接AO,DO,过点O作OK⊥AE,交AE于点K,OF⊥CD,交DE于点F,
∵CE=1,DE=7,∴CD=CE+DE=1+7=8,
∵OF⊥CD,
∴,
∴EF=CF﹣CE=4﹣1=3,
∵AE=DE,OA=OD,OE=OE,
∴△AOE≌△DOE(SSS),
∴,
∵OK⊥AE,OF⊥CD,
∴OK=OF,
∵∠AED=90°,
∴四边形OKEF是正方形,
∴OK=KE=EF=OF=3,
∴,,
如图所示,作OE的中点M,连接MG,连接OH,
∵点M是OE的中点,G为HE中点,
∴,
∴点G在以点M为圆心,以 为半径的圆上运动,
连接AM交⊙M于点G’,过点M作MN⊥AE,
∴当点A,G,M三点共线时,即点G和点G'重合时,AG的值最小,
∵点M是OE的中点,,
∵MN⊥AE,∠NEM=45°,
∴∠NME=45°,
∴△NME是等腰直角三角形,
∴,
∴,
∴,
,
∴ACG的最小值为 ,
故答案为:.
【点睛】本题考查的重点是垂径定理,解直角三角形,中位线等知识,难点是找点G的运动轨迹,当找到点G的运动轨迹以后再利用两点之间直线最短就可以计算出AG的最小值.
三.解答题
17.(2024 南京)如图,在⊙O的内接四边形ABCD中,AD=BC,对角线AC是⊙O的直径.求证:四边形ABCD是矩形.
【点拨】由AC是⊙O的直径,可得∠B=∠D=90°,证明Rt△ABC≌Rt△CDA,得到AB=CD,可证明四边形ABCD是平行四边形,即可解答.
【解析】证明:∵对角线AC是⊙O的直径,
∴∠B=∠D=90°,
∴△ABC和△CDA是直角三角形,
在Rt△ABC和Rt△CDA中,
,
∴Rt△ABC≌Rt△CDA(HL),
∴AB=CD,
又∵AD=BC,
∴四边形ABCD是平行四边形,
∵∠B=90°,
∴平行四边形ABCD是矩形.
【点睛】本题考查了矩形的判定,圆周角定理,全等三角形的判定与性质,解题的关键是掌握相关知识.
18.(2024 凉州区二模)点A,B,C都在⊙O上,且CA=CB,若AB=8,⊙O的半径为5,连接CO,求AC的长.
【点拨】连接OA,OB,根据垂径定理得到,然后利用勾股定理求解即可.
【解析】解:如图,连接OA,OB,
∴OA=OB,
∵CA=CB,
∴OC垂直平分AB,即CO⊥AB,
∵AB=8,
∴,
∵⊙O的半径为5,
∴,
∴CD=OC﹣OD=5﹣3=2,
∴.
【点睛】本题考查了垂径定理,勾股定理,圆的基本性质,解题的关键是利用所判定的垂直,结合垂径定理得到.
19.(2025 广东校级模拟)如图,AB、CD是⊙O的两条弦,AC与BD相交于点E,AB=CD.
(1)求证:AC=BD;
(2)连接BC,作直线EO,求证:EO⊥BC.
【点拨】(1)根据利用弧、弦、圆心角的关系得出,进而可得AC=BD;
(2)因为AB=CD,所以,即∠ACB=∠DBC.结合OB=OC,得出E、O都在BC的垂直平分线上,即可作答.
【解析】证明:(1)∵AB=CD,
∴=,
∴+=+,
即=,
∴AC=BD;
(2)连接OB、OC、BC,
∵AB=CD,
∴=,
∴∠ACB=∠DBC,
∴EB=EC,
∵OB=OC,
∴E、O都在BC的垂直平分线上,
∴EO⊥BC.
【点睛】本题考查了垂直平分线的判定与性质,利用弧、弦、圆心角的关系求证,正确掌握相关性质内容是解题的关键.
20.(2024 鹿城区校级三模)如图,以△ABC的边AB为直径作⊙O交AC于D且OD∥BC,⊙O交BC于点E.
(1)求证:CD=DE;
(2)若AB=12,AD=4,求CE的长度.
【点拨】(1)根据平行线的性质得∠ADO=∠C,根据圆内接四边形的性质得到∠A+∠BED=180°,再根据∠CED+∠BED=180°,OA=OD,∠ODA=∠A,得∠C=∠CED,即可得出结论;
(2)连接AE,根据OD∥BC,得===,所以BC=2OD=12,AC=2AD=8,再根据勾股定理得AE2=AC2﹣CE2=AB2﹣BE2,设CE=x,64﹣x2=144﹣(12﹣x)2,解方程即可得出答案.
【解析】(1)证明:∵OD∥BC,
∴∠ADO=∠C,
∴四边形ABED为⊙O的内接四边形,
∴∠A+∠BED=180°,
∵∠CED+∠BED=180°,
∴∠CED=∠A,
∵OA=OD,
∴∠ODA=∠A,
∴∠C=∠CED,
∴CD=DE;
(2)解:如图,连接AE,
∵AB⊙O的直径,
∴AE⊥BC,
∵OD∥BC,
∴===,
∴BC=2OD=12,AC=2AD=8,
在Rt△ACE和Rt△ABE中,根据勾股定理得,
AE2=AC2﹣CE2=AB2﹣BE2,
设CE=x,
∴64﹣x2=144﹣(12﹣x)2,
解得x=,
∴CE的长度为.
【点睛】本题考查了圆周角定理,平行线的性质以及勾股定理,正确地作出辅助线和利用圆周角定理,平行线的性质以及勾股定理是解题的关键.
21.(2024 雁塔区校级模拟)如图,AB是圆O的直径,AC是一条弦,D是弧AC的中点.过点D作DE⊥AB于点E,交AC于点F,延长DE交圆O于点H,DB交AC于点G.
(1)求证:DF=GF.
(2)若AF=4,,求圆O的半径.
【点拨】(1)D是弧AC的中点,得出=,再由垂径定理得出=,∠ADB=90°,根据等弧所对圆周角相等得出∠ADH=∠CAD,再根据等角的余角相等得∠DGF=∠BDH,最后由等角对等边证明即可;
(2)连接连接OD,根据 ,设AE=x,DE=2x,利用勾股定理求得x,再利用正切函数计算即可.
【解析】(1)证明:∵D是弧AC的中点,
∴=,
∵AB⊥DH,且AB是⊙O的直径,
∴=,∠ADB=90°,
∴=,
∴∠ADH=∠CAD,
∵∠ADB=90°,
∴∠ADH+∠BDH=90°,∠DAC+∠DGF=90°
∴∠DGF=∠BDH,
∴DF=GF;
(2)连接OD,
∵DE⊥AB于点E,AB是⊙O的直径,
∴∠ADE=90°﹣∠DAE=∠ABD,
∵,
∴,
设AE=x,DE=2x,
由(1)得∠ADH=∠CAD,
∴AF=DF=4,
∴EF=DE﹣DF=2x﹣4,
在Rt△AEF中,由勾股定理得:EF2+AE2=AF2,即(2x﹣4)2+x2=42,
解得:或x=0(舍去),
∴,
∵,
∴,
∴,
∴AB=AE+BE=16,
∴⊙O的半径为8.
【点睛】本题考查了垂径定理,勾股定理,圆周角定理,一元二次方程的解法,正切函数,熟练掌握垂径定理,勾股定理,圆周角定理,正切函数是解题的关键.
22.(2025 南通模拟)如图1,BC是⊙O的直径,点A、D在⊙O上,连接BD、CD,DB∥OA,BC=10,.
(1)求证:AO⊥CD;
(2)求BD的长;
(3)如图2,连接AB,作∠CAB的角平分线交⊙O于F,求AF的长度.
【点拨】(1)先根据圆周角定理得出∠BDC=90°,再由DB∥OA即可得出结论;
(2)作AH⊥BC于H,OM⊥BD于M,如图1,则BM=DM,利用勾股定理计算出AB的长,再利用面积法得到AH的长,接着利用勾股定理计算出OH的长,然后证明△AOH≌△OBM得到BM=OH,而得到BD的长;
(3)作CG⊥AF于G,连接CF、BF,如图2,证明△CBF为等腰直角三角形得到CF=BC,利用△ACG为等腰直角三角形得到CG=AG=AC,然后利用勾股定理计算出GF,从而得到AF的长.
【解析】(1)证明:∵BC是⊙O的直径,
∴∠D=90°,
∵OA∥BD,
∴∠CEO=∠D=90°,
∴AO⊥CD;
(2)解:连接AB,作AH⊥BC于H,OM⊥BD于M,如图1,则BM=DM,
∵BC为⊙O的直径,
∴∠CAB=90°,
∴AB==4,
∵AH BC=AC AB,
∴AH==4,
在Rt△OAH中,OH===3,
∵OA∥BD,
∴∠AOH=∠EBO,
在△AOH和△OBM中,
,
∴△AOH≌△OBM(ASA),
∴BM=OH=3,
∴BD=2BM=6;
(3)解:作CG⊥AF于G,连接CF、BF,如图2,
∵AF平分∠CAB,
∴∠CAF=∠BAF=45°,
∴CF=BF,
∴△CBF为等腰直角三角形,
∴CF=BC=5,
在Rt△ACG中,CG=AG=AC=,
在Rt△GFC中,GF==2,
∴AF=AG+GF=+2=3.
【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了垂径定理.
23.(2024 十堰一模)如图,在△ABC中,以AB为直径作⊙O,交BC于点D,过O作OE∥BC交⊙O于点E,连接AE,BE,AD.
(1)求证:∠ABE=∠CBE;
(2)若∠C=45°,∠CAE=15°,求∠ABC的度数;
(3)若DF=1,,求AE的长.
【点拨】(1)由圆的半径相等可得OB=OE,根据等边对顶角得∠ABE=∠OEB,再由平行线性质可得∠OEB=∠CBE,利用等量代换即可证得结论;
(2)延长AE交BC于G,可证得∠BAE=∠BGE=∠C+∠CAE=45°+15°=60°,运用三角形内角和定理可得答案;
(3)由OA=OB,可得S△AOE=S△ABE,进而可得=,再证得△ABE∽△FBD,可得=,结合DF=1,即可求得答案.
【解析】(1)证明:∵OB=OE,
∴∠ABE=∠OEB,
∵OE∥BC,
∴∠OEB=∠CBE,
∴∠ABE=∠CBE;
(2)解:如图,延长AE交BC于G,
∵AB是⊙O的直径,
∴BE⊥AE,
∵∠ABE=∠CBE,
∴∠BAE=∠BGE=∠C+∠CAE=45°+15°=60°,
∴∠ABC=∠AOE=60°;
(3)∵OA=OB=AB,
∴S△AOE=S△ABE,
∵=,
∴=,
∵∠ABE=∠CBE,即∠ABE=∠FBD,
又∵AB是⊙O的直径,
∴∠AEB=∠BDF=90°,
∴△ABE∽△FBD,
∴=()2,
∴()2=,
∴=,
∵DF=1,
∴AE=.
【点睛】本题考查圆的综合问题,涉及平行线的性质,三角形的外角的性质,三角形中线的性质,圆周角定理,相似三角形的判定与性质等知识,需要学生灵活运用所学知识.
24.(2024 金寨县模拟)如图,四边形ABCD内接于⊙O,BD平分∠ABC,交AC于点M.
(1)如图1,求证:AD2=DM DB.
(2)如图2,若AC经过圆心O,且AB=4,BC=3,求BD的长.
【点拨】(1)由角平分线的定义可得∠ABD=∠CBD,即可得出,结合圆周角定理推出△ADM∽△BDA,由相似三角形的性质可得,即可得证;
(2)由圆周角定理结合角平分线的定义得出,从而得出,推出AD=CD,由勾股定理得出AC=5,结合等腰直角三角形的性质得出,作CE⊥BD于E,求出BE、DE的长,即可得解.
【解析】(1)证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴,
∴∠ABD=∠DAC,
∵∠ADB=∠ADM,
∴△ADM∽△BDA,
∴,
∴AD2=DM DB;
(2)解:∵AC为直径,
∴∠ABC=∠ADC=90°,
∵BD平分∠ABC,
∴,
∴,
∴AD=CD,
∵在Rt△ABC中,AB=4,BC=3,
∴,
在Rt△ADC中,AD=CD,AC=5,
∴,
作CE⊥BD于E,
,
在Rt△BCE中,∠CBE=45°,BC=3,
∴,
在Rt△DCE中,,,
∴,
∴.
【点睛】本题考查了圆周角定理、相似三角形的判定与性质、解直角三角形、等腰直角三角形的判定与性质,熟练掌握以上知识点并灵活运用是解此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
