2025年浙江省中考数学一轮复习专题检测 专题31 数据分析(含解析)
文档属性
| 名称 | 2025年浙江省中考数学一轮复习专题检测 专题31 数据分析(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 998.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-07 21:01:09 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题31 数据分析
一.选择题
1.(2025 淮安一模)一组数据1,3,5,2,4的平均数是( )
A.1 B.2 C.3 D.6
2.(2024 湖南)某班的5名同学1分钟跳绳的成绩(单位:次)分别为:179,130,192,158,141.这组数据的中位数是( )
A.130 B.158 C.160 D.192
3.(2025 苏州模拟)某初中男子篮球队队员的身高数据是:186,175,187,186,184.这组数据的众数是( )
A.175 B.186 C.184 D.187
4.(2024 宁明县三模)某校举行健美操比赛,甲、乙两个班各选10名学生参加比赛,两个班参赛学生的平均身高都是1.65米,其方差分别是,则参赛学生身高比较整齐的班级是( )
A.甲班 B.乙班 C.同样整齐 D.无法确定
5.(2024 资阳)6名学生一周做家务的天数依次为4,4,5,7,7,7,这组数据的中位数和众数分别为( )
A.5,4 B.6,5 C.6,7 D.7,7
6.(2024 攀枝花)某公司要招聘一名职员,根据实际需要,从学历、能力、经验三个方面对甲、乙、丙、丁四名应聘者进行了测试,测试成绩如表:
项目 应聘者
甲 乙 丙 丁
学历 7 7 9 8
能力 8 9 8 9
经验 8 7 7 7
如果这家公司比较看重员工的能力,将学历、能力、经验三项得分按1:2:1的比例加权平均确定每人的最终得分,录用得分最高者,那么将被录用的是( )
A.甲 B.乙 C.丙 D.丁
7.(2024 宜宾)某校为了解九年级学生在校的锻炼情况,随机抽取10名学生,记录他们某一天在校的锻炼时间(单位:分钟):65,67,75,65,75,80,75,88,78,80.对这组数据判断正确的是( )
A.方差为0 B.众数为75 C.中位数为77.5 D.平均数为75
8.(2024 台州模拟)小明的期中与期末测试成绩如表:
语文 数学 英语
小明期中 88 56 70
年级平均分 75 60 69
小明期末 70 76 68
年级平均分 75 68 65
下列说法不合理的是( )
A.小明期末与期中总分相同 B.小明英语期末名次一定在中等以上
C.小明数学期末成绩比期中有进步 D.小明语文期末成绩比期中有退步
9.(2024 杭州一模)某学校5名教师在一次义务募捐中的捐款额(单位:元)为30,50,50,100,100.若捐款最少的教师又多捐了30元,则分析这5名教师捐款额的数据时,不受影响的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
10.(2025 五华区校级模拟)在一场篮球赛中,某队5名场上队员的身高(单位:cm)分别是:187,188,192,193,194.因身高为194cm的队员受伤,教练让身高为190cm的队员替补上场.与换人前相比,换人后场上队员的身高( )
A.平均数变小,方差变大 B.平均数变小,方差变小
C.平均数变大,方差变小 D.平均数变大,方差变大
二.填空题
11.(2025 永州模拟)数据2、3、5、5、4的众数是 .
12.(2025 盐城一模)一组数据含有三个不同的数:3、8、7,它们的频数分别是3、5、2,则这组数据的平均数是 .
13.(2024 杭州三模)一组数据5,6,7,8,9的标准差为 .
14.(2024 滨江区二模)某校901班共有50名学生,平均身高为m厘米,其中30名男生的平均身高为n厘米,则20名女生的平均身高为 厘米.
15.(2024 海宁市三模)已知某组数据的方差计算公式为,则这组数据的平均数为 .
16.(2024 光山县一模)甲,乙两人在相同条件下各射击10次.两人的成绩(单位:环)如图所示.现有以下三个推断:
①甲的成绩更稳定;②乙的平均成绩更高;③每人再射击一次,乙的成绩一定比甲高.
其中正确的是 .(填序号)
三.解答题
17.(2024 温州模拟)某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:
每人销售件数 1400 880 270 150 130 120
人数 1 1 3 6 3 1
(1)求这15位营销人员该月销售量的平均数、中位数和众数;
(2)为督促并不影响员工的积极性,假设销售负责人把每位营销员的月销售定额定为300件,你认为是否合理,请你制定一个较合理的销售定额,并说明理由.
18.(2024 浙江模拟)由于水资源缺乏,某地区决定利用分段计费的方法引导人们节约用水,即规定每个家庭的月基本用水量为m吨,家庭月用水量不超过m吨的部分按原价收费,超过m吨的部分加倍收费.为了解居民的用水情况,该地区从某社区的1500户家庭中随机抽取了30户家庭的月用水量,结果如表所示:
月用水量(吨) 3 4 5 7 8 9 10
户数(户) 4 2 5 11 4 2 2
(1)求这30户家庭的月平均用水量.
(2)估计该社区的月用水量.
(3)你认为该地区规定每个家庭的月基本用水量m为多少吨比较合理?请你用所学的统计知识说明理由.
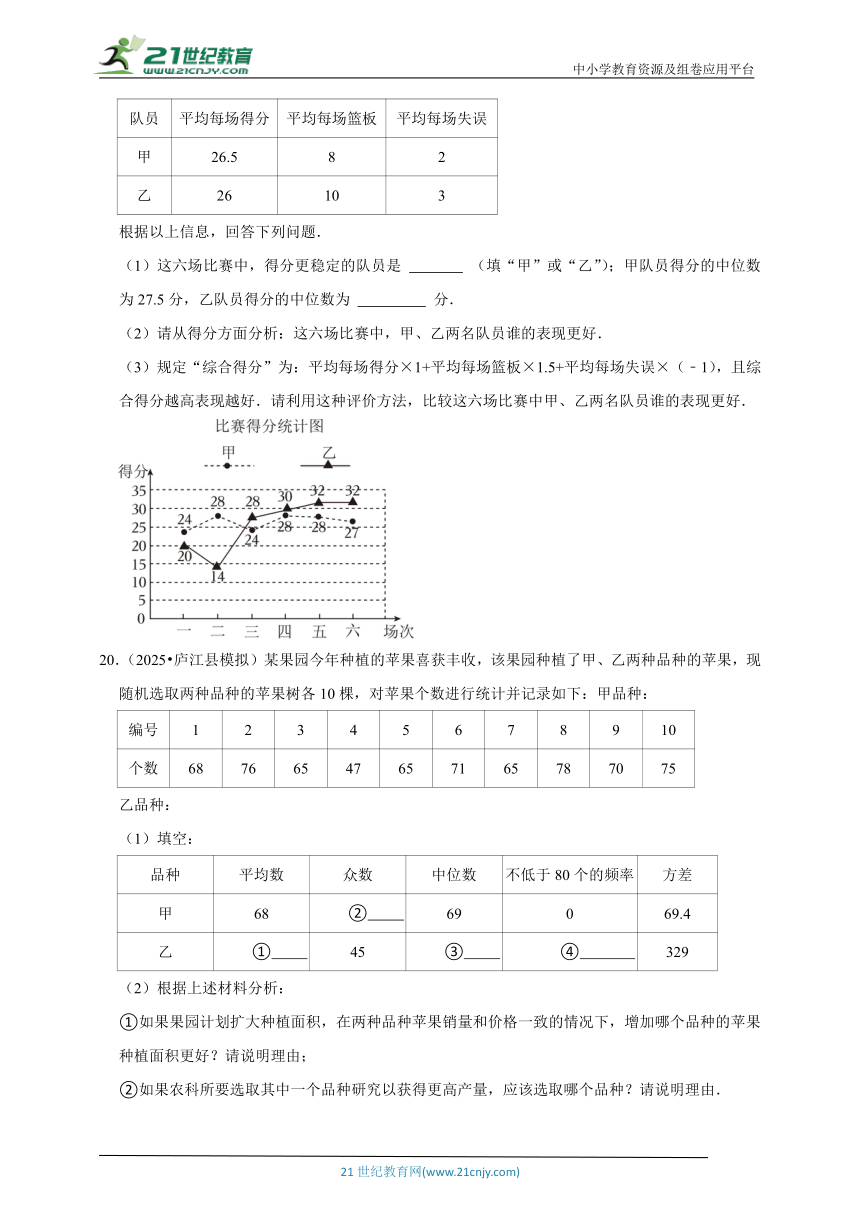
19.(2024 河南)为提升学生体质健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在八年级组织的篮球联赛中,甲、乙两名队员表现优异,他们在近六场比赛中关于得分、篮板和失误三个方面的统计结果如下.
技术统计表
队员 平均每场得分 平均每场篮板 平均每场失误
甲 26.5 8 2
乙 26 10 3
根据以上信息,回答下列问题.
(1)这六场比赛中,得分更稳定的队员是 (填“甲”或“乙”);甲队员得分的中位数为27.5分,乙队员得分的中位数为 分.
(2)请从得分方面分析:这六场比赛中,甲、乙两名队员谁的表现更好.
(3)规定“综合得分”为:平均每场得分×1+平均每场篮板×1.5+平均每场失误×(﹣1),且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好.
20.(2025 庐江县模拟)某果园今年种植的苹果喜获丰收,该果园种植了甲、乙两种品种的苹果,现随机选取两种品种的苹果树各10棵,对苹果个数进行统计并记录如下:甲品种:
编号 1 2 3 4 5 6 7 8 9 10
个数 68 76 65 47 65 71 65 78 70 75
乙品种:
(1)填空:
品种 平均数 众数 中位数 不低于80个的频率 方差
甲 68 ② 69 0 69.4
乙 ① 45 ③ ④ 329
(2)根据上述材料分析:
①如果果园计划扩大种植面积,在两种品种苹果销量和价格一致的情况下,增加哪个品种的苹果种植面积更好?请说明理由;
②如果农科所要选取其中一个品种研究以获得更高产量,应该选取哪个品种?请说明理由.
21.(2024 浙江模拟)法国著名的思想家伏尔泰说过“生命在于运动”,某大学小组为了调查初中同学学生课后运动时间,按照时间分为A、B、C、D四个等级,绘制了如下不完整统计表:
(1)求本次调查的总人数,并且补全人数分布图;
(2)估计本次调查的中位数位于A、B、C、D哪个等级中;
(3)小宁认为我们可以根据本次调查数据精确预测全市初中生为A等的人数,请判断他这句话的正误,并说明理由.
22.(2024 杭州二模)4月24日是中国航天日,为激发青少年崇尚科学、探索未知的热情,某中学开展了“航空航天”知识问答系列活动.为了解活动效果,从七、八年级学生的知识问答成绩中,各随机抽取了20名学生的成绩进行统计分析(6分及6分以上为合格:9分及9分以上为优秀),绘制了如下统计图表:
学生成绩统计表
七年级 八年级
平均数 m 7.55
中位数 8 b
众数 a 7
根据上述信息,解答下列问题:
(1)学生成绩统计表中a= ,b= ;
(2)求七年级学生成绩的平均数m;
(3)根据以上数据,你认为该校七年级和八年级中,哪个年级的学生对航天航空知识掌握更好?并说明理由.
23.(2024 温州模拟)某校举行“知礼 明理”知识问答竞赛,A班、B班各派出5名选手组成代表队参加比赛.两班派出选手的比赛成绩如图所示.
平均数/分 中位数/分 众数/分
A校 85 85 85
B校 85 a b
根据图中信息,整理分析数据得到如下表格:
(1)a= ,b= ;
(2)计算两校比赛成绩的方差,并判断哪个学校派出的代表队选手成绩较为稳定.
(3)请你从平均数、众数、中位数、方差等数据分析,推选一个班级去参加区级比赛.
答案与解析
一.选择题
1.(2025 淮安一模)一组数据1,3,5,2,4的平均数是( )
A.1 B.2 C.3 D.6
【点拨】根据算术平均数的定义列式计算即可.
【解析】解:数据1,3,5,2,4的平均数是=3,
故选:C.
【点睛】本题主要考查算术平均数,解题的关键是掌握算术平均数的定义.
2.(2024 湖南)某班的5名同学1分钟跳绳的成绩(单位:次)分别为:179,130,192,158,141.这组数据的中位数是( )
A.130 B.158 C.160 D.192
【点拨】先将上述数据按照从小到大的顺序排列,根据中位数的定义可知:第3位的数据是中位数.
【解析】解:先将上述数据按照从小到大的顺序排列:130,141,158,179,192,
∴这组数据的中位数是158,
故选:B.
【点睛】本题考查的是中位数,熟练掌握中位数的相关定义和计算方法是解题的关键.
3.(2025 苏州模拟)某初中男子篮球队队员的身高数据是:186,175,187,186,184.这组数据的众数是( )
A.175 B.186 C.184 D.187
【点拨】根据众数的定义求解即可.
【解析】解:∵186出现了2次,出现的次数最多,
∴该组数据的众数是186;
故选:B.
【点睛】本题主要考查众数的定义,众数是一组数据中出现次数最多的数,在一组数据中,众数可能不止一个.
4.(2024 宁明县三模)某校举行健美操比赛,甲、乙两个班各选10名学生参加比赛,两个班参赛学生的平均身高都是1.65米,其方差分别是,则参赛学生身高比较整齐的班级是( )
A.甲班 B.乙班 C.同样整齐 D.无法确定
【点拨】根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
【解析】解:∵=1.9,=2.4,
∴<,
∴参赛学生身高比较整齐的班级是甲班,
故选:A.
【点睛】此题主要考查了方差,方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
5.(2024 资阳)6名学生一周做家务的天数依次为4,4,5,7,7,7,这组数据的中位数和众数分别为( )
A.5,4 B.6,5 C.6,7 D.7,7
【点拨】根据众数和中位数的概念求解.
【解析】解:这组数据的中位数为=6,
所以这组数据的众数为7,
故选:C.
【点睛】本题考查了众数和中位数的概念:一组数据中出现次数最多的数据叫做众数;将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
6.(2024 攀枝花)某公司要招聘一名职员,根据实际需要,从学历、能力、经验三个方面对甲、乙、丙、丁四名应聘者进行了测试,测试成绩如表:
项目 应聘者
甲 乙 丙 丁
学历 7 7 9 8
能力 8 9 8 9
经验 8 7 7 7
如果这家公司比较看重员工的能力,将学历、能力、经验三项得分按1:2:1的比例加权平均确定每人的最终得分,录用得分最高者,那么将被录用的是( )
A.甲 B.乙 C.丙 D.丁
【点拨】根据加权平均数的计算方法可以得到甲、乙、丙、丁的成绩,然后比较大小即可解答本题.
【解析】解:由题意可得,
甲的成绩为:=7.75(分),
乙的成绩为:=8(分),
丙的成绩为:=8(分),
丁的成绩为:=8.25(分),
∴将被录用的是丁.
故选:D.
【点睛】本题考查加权平均数,解答本题的关键是明确加权平均数的计算方法.
7.(2024 宜宾)某校为了解九年级学生在校的锻炼情况,随机抽取10名学生,记录他们某一天在校的锻炼时间(单位:分钟):65,67,75,65,75,80,75,88,78,80.对这组数据判断正确的是( )
A.方差为0 B.众数为75 C.中位数为77.5 D.平均数为75
【点拨】根据平均数和方差、中位数,众数得出答案即可.
【解析】解:65,67,75,65,75,80,75,88,78,80中,
平均数=(65+67+75+65+75+80+75+88+78+80)=74.8,
65,67,75,65,75,80,75,88,78,80按从小到大的顺序排序为65,65,67,75,75,75,78,80,80,88,
∴中位数==75,众数为75,方差=[(65﹣74.8)2×2+(67﹣74.8)2+(75﹣74.8)2×3+(78﹣74.8)2+(80﹣74.8)2×2+(88﹣74.8)2]≈61,
故选:B.
【点睛】本题考查了平均数,方差,中位数,众数等知识点,能熟记中位线、众数的定义和方差的意义是解此题的关键.
8.(2024 台州模拟)小明的期中与期末测试成绩如表:
语文 数学 英语
小明期中 88 56 70
年级平均分 75 60 69
小明期末 70 76 68
年级平均分 75 68 65
下列说法不合理的是( )
A.小明期末与期中总分相同 B.小明英语期末名次一定在中等以上
C.小明数学期末成绩比期中有进步 D.小明语文期末成绩比期中有退步
【点拨】根据表中数据及中位数的定义逐一判断即可.
【解析】解:A.小明期末总分为70+76+68=214(分),期中总分为75+60+69=214(分),期末与期中总分相同,此选项正确,不符合题意;
B.小明英语期末成绩为68分,未给出中位数大小,故不能确定小明英语期末名次一定在中等以上,此选项错误,符合题意;
C.小明数学期末成绩未76分,期中成绩为76分,期末成绩比期中成绩有进步,此选项正确,不符合题意;
D.小明语文期末成绩为70分,期中成绩为88分,期末比期中有退步,此选项正确,不符合题意;
故选:B.
【点睛】本题主要考查算术平均数和中位数,解题的关键是掌握中位数的意义.
9.(2024 杭州一模)某学校5名教师在一次义务募捐中的捐款额(单位:元)为30,50,50,100,100.若捐款最少的教师又多捐了30元,则分析这5名教师捐款额的数据时,不受影响的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
【点拨】根据众数、中位数、平均数及方差的定义求解即可.
【解析】解:依题意,捐款最少的教师又多捐了30元,则数据50、100的个数不变,即众数不变,而平均数,中位数,方差都要用到60,
故不受影响的统计量是众数.
故选:C.
【点睛】本题主要考查算术平均数,解题的关键是掌握众数、中位数、平均数及方差的定义.
10.(2025 五华区校级模拟)在一场篮球赛中,某队5名场上队员的身高(单位:cm)分别是:187,188,192,193,194.因身高为194cm的队员受伤,教练让身高为190cm的队员替补上场.与换人前相比,换人后场上队员的身高( )
A.平均数变小,方差变大 B.平均数变小,方差变小
C.平均数变大,方差变小 D.平均数变大,方差变大
【点拨】根据平均数和方差的定义和意义即可得出答案.
【解析】解:用一名身高190cm的队员换下场上身高194cm的队员,与换人前相比,场上队员身高的和变小,而人数没变,
所以他们的平均数变小,
由于数据的波动性变小,所以数据的方差变小.
故选:B.
【点睛】本题主要考查平均数和方差,熟练掌握方差、平均数的计算公式是解题的关键.
二.填空题
11.(2025 永州模拟)数据2、3、5、5、4的众数是 5 .
【点拨】根据众数的定义即可判断;
【解析】解:数据2、3、5、5、4中,5出现的次数最多,所以这组数据的众数为5,
故答案为5.
【点睛】本题考查众数的定义,解题的关键是记住一组数据中出现次数最多的数据叫做众数.
12.(2025 盐城一模)一组数据含有三个不同的数:3、8、7,它们的频数分别是3、5、2,则这组数据的平均数是 6.3 .
【点拨】本题是求加权平均数,根据加权平均数的公式即可求解.
【解析】解:根据题意可得,这组数据的平均数=(3×3+8×5+7×2)÷(3+5+2)=6.3.
故填6.3.
【点睛】正确理解加权平均数的计算方法是解决本题的关键.
13.(2024 杭州三模)一组数据5,6,7,8,9的标准差为 .
【点拨】要计算方差首先要计算出平均数,再根据方差公式计算.
【解析】解:平均数=(5+6+7+8+9)÷5=7,
方差=[(5﹣7)2+(6﹣7)2+(7﹣7)2+(8﹣7)2+(9﹣7)2]=2.
∴标准差=,
故答案为.
【点睛】本题主要考查平均数、方差、标准差的计算方法,解题的关键是记住有关公式,属于中考常考题型.
14.(2024 滨江区二模)某校901班共有50名学生,平均身高为m厘米,其中30名男生的平均身高为n厘米,则20名女生的平均身高为 厘米.
【点拨】根据题目中的数据和加权平均数的计算方法,可以计算出20名女生的平均身高.
【解析】解:20名女生的平均身高为:=(cm).
故答案为:.
【点睛】本题考查加权平均数,解答本题的关键是明确加权平均数的计算方法.
15.(2024 海宁市三模)已知某组数据的方差计算公式为,则这组数据的平均数为 5 .
【点拨】根据方差的公式可以得到平均数.
【解析】解:由于这组数据的方差是S2=[(x1﹣5)2+(x2﹣5)2+...+(xn﹣5)2],
故平均数是5.
故答案为:5.
【点睛】本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为5,则方差S2=[(x1﹣5)2+(x2﹣5)2+…+(xn﹣5)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
16.(2024 光山县一模)甲,乙两人在相同条件下各射击10次.两人的成绩(单位:环)如图所示.现有以下三个推断:
①甲的成绩更稳定; ②乙的平均成绩更高;③每人再射击一次,乙的成绩一定比甲高.
其中正确的是 ①② .(填序号)
【点拨】①根据方差的意义判断即可;②根据算术平均数的定义判断即可;③根据随机事件的意义判断即可.
【解析】解:由折线统计图可知,
甲的成绩在3和5之间波动,乙的成绩在3和9之间波动,所以甲的成绩更稳定,故①结论正确;
乙的10次成绩中有9次成绩大于甲,其中一次相同,可推知②正确;
每人再射击一次,乙的成绩不一定比甲高,故③的结论错误.
故答案为:①②.
【点睛】本题考查了方差和折线统计图,掌握方差的意义是解答本题的关键.
三.解答题
17.(2024 温州模拟)某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:
每人销售件数 1400 880 270 150 130 120
人数 1 1 3 6 3 1
(1)求这15位营销人员该月销售量的平均数、中位数和众数;
(2)为督促并不影响员工的积极性,假设销售负责人把每位营销员的月销售定额定为300件,你认为是否合理,请你制定一个较合理的销售定额,并说明理由.
【点拨】(1)找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数,众数是一组数据中出现次数最多的数据,注意众数可以不止一个.平均数是指在一组数据中所有数据之和再除以数据的个数.
(2)根据表中数据和平均数、中位数和众数的意义回答.
【解析】解:(1)平均数=(件),
∵最中间的数据为150,
∴这组数据的中位数为150件,
∵150是这组数据中出现次数最多的数据,
∴众数为150件;
答:这15位营销人员该月销售量的平均数为300件,中位数和众数都是150件;
(2)不合理,理由:因为15人中有13人的销售额不到300件,300件虽是所给一组数据的平均数,它却不能很好地反映销售人员的一般水平.
销售额定为150件合适些,因为150件既是中位数,又是众数,是大部分人能达到的定额.
【点睛】此题考查了学生对中位数,众数,平均数的掌握情况.它们都是反映数据集中趋势的指标.
18.(2024 浙江模拟)由于水资源缺乏,某地区决定利用分段计费的方法引导人们节约用水,即规定每个家庭的月基本用水量为m吨,家庭月用水量不超过m吨的部分按原价收费,超过m吨的部分加倍收费.为了解居民的用水情况,该地区从某社区的1500户家庭中随机抽取了30户家庭的月用水量,结果如表所示:
月用水量(吨) 3 4 5 7 8 9 10
户数(户) 4 2 5 11 4 2 2
(1)求这30户家庭的月平均用水量.
(2)估计该社区的月用水量.
(3)你认为该地区规定每个家庭的月基本用水量m为多少吨比较合理?请你用所学的统计知识说明理由.
【点拨】(1)根据平均数的定义求解即可,
(2)用社区的总户数乘以平均数列出算式计算即可;
(3)根据平均数、众数、中位数的意义,结合题意选择合适的量即可.
【解析】解:(1)这30户家庭月用水量的平均数=(3×4+4×2+5×5+7×11+8×4+9×2+40×2)÷30=6.4(吨)
答:这30户家庭的月平均用水量为6.4吨;
(2)∵社区共1500户家庭,
∴该社区的月用水量=6.4×1500=9600(吨);
(3)地区规定每个家庭的月基本用水量m为7吨较合理,理由如下:
7出现了11次,出现的次数最多,
则众数是7,
∵共有30个数,
∴中位数是第15、16个数的平均数,
∴中位数是(7+7)÷2=7(吨),
因为平均数容易受到个别极端数据的影响,中位数、众数不容易 受极端数据的影响,中位数和众数都是7吨,作为月基本用水量 既可以满足大多数家庭的用水量,也可以引导用水量高于7吨 的家庭节约用水.
【点睛】本题考查加权平均数,中位数,众数,样本估计总体等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
19.(2024 河南)为提升学生体质健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在八年级组织的篮球联赛中,甲、乙两名队员表现优异,他们在近六场比赛中关于得分、篮板和失误三个方面的统计结果如下.
技术统计表
队员 平均每场得分 平均每场篮板 平均每场失误
甲 26.5 8 2
乙 26 10 3
根据以上信息,回答下列问题.
(1)这六场比赛中,得分更稳定的队员是 甲 (填“甲”或“乙”);甲队员得分的中位数为27.5分,乙队员得分的中位数为 29 分.
(2)请从得分方面分析:这六场比赛中,甲、乙两名队员谁的表现更好.
(3)规定“综合得分”为:平均每场得分×1+平均每场篮板×1.5+平均每场失误×(﹣1),且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好.
【点拨】(1)根据中位数的计算方法求解即可;
(2)根据平均数的概念求解即可;
(3)根据“综合得分”的计算方法求出甲和乙的得分,然后比较求解即可.
【解析】解:(1)由折线图可得甲得分更稳定,
把乙的六次成绩按从小到大的顺序排序,第三次、第四次的成绩分别为28和30,
故中位数为==29,
故答案为:甲,29;
(2)因为甲的平均每场得分大于乙的平均每场得分,且甲的得分更稳定,所以甲队员表现更好.(注:答案不唯一,合理即可);
(3)甲的综合得分为:26.5×1+8×1.5+2×(﹣1)=36.5.
乙的综合得分为:26×1+10×1.5+3×(﹣1)=38.
因为38>36.5,所以乙队员表现更好.
【点睛】本题考查了中位数,加权平均数、方差的计算,掌握以上计算方法是关键.
20.(2025 庐江县模拟)某果园今年种植的苹果喜获丰收,该果园种植了甲、乙两种品种的苹果,现随机选取两种品种的苹果树各10棵,对苹果个数进行统计并记录如下:甲品种:
编号 1 2 3 4 5 6 7 8 9 10
个数 68 76 65 47 65 71 65 78 70 75
乙品种:
(1)填空:
品种 平均数 众数 中位数 不低于80个的频率 方差
甲 68 ② 65 69 0 69.4
乙 ① 68 45 ③ 68 ④ 0.4 329
(2)根据上述材料分析:
①如果果园计划扩大种植面积,在两种品种苹果销量和价格一致的情况下,增加哪个品种的苹果种植面积更好?请说明理由;
②如果农科所要选取其中一个品种研究以获得更高产量,应该选取哪个品种?请说明理由.
【点拨】(1)分别根据平均数、众数和中位数的定义计算即可;
(2)①根据平均数、众数、中位数和方差的意义判断即可;
②根据不低于80个的高产苹果频率判断即可.
【解析】解:(1)乙品种的平均数为=68(个),
甲品种的众数为65,乙品种的中位数为=68,
乙品种不低于80个的频率为=0.4;
故答案为:①68,②65,③68,④0.4;
(2)①增加甲品种的苹果种植面积更好,
理由:甲品种平均产量和乙品种一致,但甲品种方差更小,稳定性更好,同时它的众数和中位数均高于乙品种,大面积种植风险更小,故选甲;
②应该选取乙品种,
理由:因为乙品种不低于80个的高产苹果频率为40%,甲品种为0,故乙品种更容易出现高产苹果.
【点睛】本题考查频数与频率,中位数、众数、平均数和方差,理解中位数、众数、方差的意义和计算方法是正确解答的前提.
21.(2024 浙江模拟)法国著名的思想家伏尔泰说过“生命在于运动”,某大学小组为了调查初中同学学生课后运动时间,按照时间分为A、B、C、D四个等级,绘制了如下不完整统计表:
(1)求本次调查的总人数,并且补全人数分布图;
(2)估计本次调查的中位数位于A、B、C、D哪个等级中;
(3)小宁认为我们可以根据本次调查数据精确预测全市初中生为A等的人数,请判断他这句话的正误,并说明理由.
【点拨】(1)由A等级人数及其所占百分比可得总人数,总人数减去A、B、D人数即可求出C等级人数;
(2)根据中位数的定义求解即可;
(3)利用样本估计总体求解即可.
【解析】解:(1)本次调查的总人数为12÷24%=50(人),
则C等级人数为50﹣(12+24+4)=10(人),
补全人数分布图如下:
(2)本次调查的中位数是第25、26个数据的平均数,而这两个数据均为B等级,
所以本次调查的中位数位于B等级;
(3)错误,
可以根据本次调查数据估计全市初中生为A等的人数,而不能精确预测.
【点睛】本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
22.(2024 杭州二模)4月24日是中国航天日,为激发青少年崇尚科学、探索未知的热情,某中学开展了“航空航天”知识问答系列活动.为了解活动效果,从七、八年级学生的知识问答成绩中,各随机抽取了20名学生的成绩进行统计分析(6分及6分以上为合格:9分及9分以上为优秀),绘制了如下统计图表:
学生成绩统计表
七年级 八年级
平均数 m 7.55
中位数 8 b
众数 a 7
根据上述信息,解答下列问题:
(1)学生成绩统计表中a= 8 ,b= 7.5 ;
(2)求七年级学生成绩的平均数m;
(3)根据以上数据,你认为该校七年级和八年级中,哪个年级的学生对航天航空知识掌握更好?并说明理由.
【点拨】(1)分别根据众数和中位数的定义解答即可;
(2)根据加权平均数的计算公式计算即可;
(3)比较两个年级的平均数、众数和中位数可得答案.
【解析】解:(1)由统计图可知,七年级中8分出现的次数最多,故众数a=8;
把八年级20名学生的成绩从小到大排列,排在中间的两个数分别为7,8,故中位数b==7.5.
故答案为:8,7.5;
(2)七年级学生成绩的平均数m=5×20%+6×10%+7×10%+8×30%+9×15%+10×15%=7.55;
(3)七年级的学生对航天航空知识掌握更好,理由如下:
因为两个年级的平均数相同,但七年级的中位数和众数均高于八年级,所以七年级的学生对航天航空知识掌握更好.
【点睛】本题考查加权平均数,中位数以及众数,掌握相关统计量的计算方法是正确解答的前提.
23.(2024 温州模拟)某校举行“知礼 明理”知识问答竞赛,A班、B班各派出5名选手组成代表队参加比赛.两班派出选手的比赛成绩如图所示.
平均数/分 中位数/分 众数/分
A校 85 85 85
B校 85 a b
根据图中信息,整理分析数据得到如下表格:
(1)a= 80 ,b= 100 ;
(2)计算两校比赛成绩的方差,并判断哪个学校派出的代表队选手成绩较为稳定.
(3)请你从平均数、众数、中位数、方差等数据分析,推选一个班级去参加区级比赛.
【点拨】(1)根据条形图将B校数据重新排列,再根据中位数和众数的概念求解即可;
(2)计算出A、B两校成绩的方差,根据方差的意义可得答案;
(3)从表中数据,利用平均数和中位数和众数的意义可得出答案.
【解析】解:(1)将B校5名选手的成绩重新排列为:70、75、80、100、100,
所以其中位数a=80、众数b=100,
故答案为:80,100;
(2)=[(75﹣85)2+(80﹣85)2+2×(85﹣85)2+(100﹣85)2]=70,
=[(70﹣85)2+(75﹣85)2+(80﹣85)2+2×(100﹣85)2]=160,
∴,
∴A学校派出的代表队选手成绩较为稳定;
(3)①从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是A校;
②从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是B校.
【点睛】本题主要考查方差,解题的关键是掌握中位数、众数的定义及平均数、众数、中位数和方差的意义.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专题31 数据分析
一.选择题
1.(2025 淮安一模)一组数据1,3,5,2,4的平均数是( )
A.1 B.2 C.3 D.6
2.(2024 湖南)某班的5名同学1分钟跳绳的成绩(单位:次)分别为:179,130,192,158,141.这组数据的中位数是( )
A.130 B.158 C.160 D.192
3.(2025 苏州模拟)某初中男子篮球队队员的身高数据是:186,175,187,186,184.这组数据的众数是( )
A.175 B.186 C.184 D.187
4.(2024 宁明县三模)某校举行健美操比赛,甲、乙两个班各选10名学生参加比赛,两个班参赛学生的平均身高都是1.65米,其方差分别是,则参赛学生身高比较整齐的班级是( )
A.甲班 B.乙班 C.同样整齐 D.无法确定
5.(2024 资阳)6名学生一周做家务的天数依次为4,4,5,7,7,7,这组数据的中位数和众数分别为( )
A.5,4 B.6,5 C.6,7 D.7,7
6.(2024 攀枝花)某公司要招聘一名职员,根据实际需要,从学历、能力、经验三个方面对甲、乙、丙、丁四名应聘者进行了测试,测试成绩如表:
项目 应聘者
甲 乙 丙 丁
学历 7 7 9 8
能力 8 9 8 9
经验 8 7 7 7
如果这家公司比较看重员工的能力,将学历、能力、经验三项得分按1:2:1的比例加权平均确定每人的最终得分,录用得分最高者,那么将被录用的是( )
A.甲 B.乙 C.丙 D.丁
7.(2024 宜宾)某校为了解九年级学生在校的锻炼情况,随机抽取10名学生,记录他们某一天在校的锻炼时间(单位:分钟):65,67,75,65,75,80,75,88,78,80.对这组数据判断正确的是( )
A.方差为0 B.众数为75 C.中位数为77.5 D.平均数为75
8.(2024 台州模拟)小明的期中与期末测试成绩如表:
语文 数学 英语
小明期中 88 56 70
年级平均分 75 60 69
小明期末 70 76 68
年级平均分 75 68 65
下列说法不合理的是( )
A.小明期末与期中总分相同 B.小明英语期末名次一定在中等以上
C.小明数学期末成绩比期中有进步 D.小明语文期末成绩比期中有退步
9.(2024 杭州一模)某学校5名教师在一次义务募捐中的捐款额(单位:元)为30,50,50,100,100.若捐款最少的教师又多捐了30元,则分析这5名教师捐款额的数据时,不受影响的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
10.(2025 五华区校级模拟)在一场篮球赛中,某队5名场上队员的身高(单位:cm)分别是:187,188,192,193,194.因身高为194cm的队员受伤,教练让身高为190cm的队员替补上场.与换人前相比,换人后场上队员的身高( )
A.平均数变小,方差变大 B.平均数变小,方差变小
C.平均数变大,方差变小 D.平均数变大,方差变大
二.填空题
11.(2025 永州模拟)数据2、3、5、5、4的众数是 .
12.(2025 盐城一模)一组数据含有三个不同的数:3、8、7,它们的频数分别是3、5、2,则这组数据的平均数是 .
13.(2024 杭州三模)一组数据5,6,7,8,9的标准差为 .
14.(2024 滨江区二模)某校901班共有50名学生,平均身高为m厘米,其中30名男生的平均身高为n厘米,则20名女生的平均身高为 厘米.
15.(2024 海宁市三模)已知某组数据的方差计算公式为,则这组数据的平均数为 .
16.(2024 光山县一模)甲,乙两人在相同条件下各射击10次.两人的成绩(单位:环)如图所示.现有以下三个推断:
①甲的成绩更稳定;②乙的平均成绩更高;③每人再射击一次,乙的成绩一定比甲高.
其中正确的是 .(填序号)
三.解答题
17.(2024 温州模拟)某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:
每人销售件数 1400 880 270 150 130 120
人数 1 1 3 6 3 1
(1)求这15位营销人员该月销售量的平均数、中位数和众数;
(2)为督促并不影响员工的积极性,假设销售负责人把每位营销员的月销售定额定为300件,你认为是否合理,请你制定一个较合理的销售定额,并说明理由.
18.(2024 浙江模拟)由于水资源缺乏,某地区决定利用分段计费的方法引导人们节约用水,即规定每个家庭的月基本用水量为m吨,家庭月用水量不超过m吨的部分按原价收费,超过m吨的部分加倍收费.为了解居民的用水情况,该地区从某社区的1500户家庭中随机抽取了30户家庭的月用水量,结果如表所示:
月用水量(吨) 3 4 5 7 8 9 10
户数(户) 4 2 5 11 4 2 2
(1)求这30户家庭的月平均用水量.
(2)估计该社区的月用水量.
(3)你认为该地区规定每个家庭的月基本用水量m为多少吨比较合理?请你用所学的统计知识说明理由.
19.(2024 河南)为提升学生体质健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在八年级组织的篮球联赛中,甲、乙两名队员表现优异,他们在近六场比赛中关于得分、篮板和失误三个方面的统计结果如下.
技术统计表
队员 平均每场得分 平均每场篮板 平均每场失误
甲 26.5 8 2
乙 26 10 3
根据以上信息,回答下列问题.
(1)这六场比赛中,得分更稳定的队员是 (填“甲”或“乙”);甲队员得分的中位数为27.5分,乙队员得分的中位数为 分.
(2)请从得分方面分析:这六场比赛中,甲、乙两名队员谁的表现更好.
(3)规定“综合得分”为:平均每场得分×1+平均每场篮板×1.5+平均每场失误×(﹣1),且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好.
20.(2025 庐江县模拟)某果园今年种植的苹果喜获丰收,该果园种植了甲、乙两种品种的苹果,现随机选取两种品种的苹果树各10棵,对苹果个数进行统计并记录如下:甲品种:
编号 1 2 3 4 5 6 7 8 9 10
个数 68 76 65 47 65 71 65 78 70 75
乙品种:
(1)填空:
品种 平均数 众数 中位数 不低于80个的频率 方差
甲 68 ② 69 0 69.4
乙 ① 45 ③ ④ 329
(2)根据上述材料分析:
①如果果园计划扩大种植面积,在两种品种苹果销量和价格一致的情况下,增加哪个品种的苹果种植面积更好?请说明理由;
②如果农科所要选取其中一个品种研究以获得更高产量,应该选取哪个品种?请说明理由.
21.(2024 浙江模拟)法国著名的思想家伏尔泰说过“生命在于运动”,某大学小组为了调查初中同学学生课后运动时间,按照时间分为A、B、C、D四个等级,绘制了如下不完整统计表:
(1)求本次调查的总人数,并且补全人数分布图;
(2)估计本次调查的中位数位于A、B、C、D哪个等级中;
(3)小宁认为我们可以根据本次调查数据精确预测全市初中生为A等的人数,请判断他这句话的正误,并说明理由.
22.(2024 杭州二模)4月24日是中国航天日,为激发青少年崇尚科学、探索未知的热情,某中学开展了“航空航天”知识问答系列活动.为了解活动效果,从七、八年级学生的知识问答成绩中,各随机抽取了20名学生的成绩进行统计分析(6分及6分以上为合格:9分及9分以上为优秀),绘制了如下统计图表:
学生成绩统计表
七年级 八年级
平均数 m 7.55
中位数 8 b
众数 a 7
根据上述信息,解答下列问题:
(1)学生成绩统计表中a= ,b= ;
(2)求七年级学生成绩的平均数m;
(3)根据以上数据,你认为该校七年级和八年级中,哪个年级的学生对航天航空知识掌握更好?并说明理由.
23.(2024 温州模拟)某校举行“知礼 明理”知识问答竞赛,A班、B班各派出5名选手组成代表队参加比赛.两班派出选手的比赛成绩如图所示.
平均数/分 中位数/分 众数/分
A校 85 85 85
B校 85 a b
根据图中信息,整理分析数据得到如下表格:
(1)a= ,b= ;
(2)计算两校比赛成绩的方差,并判断哪个学校派出的代表队选手成绩较为稳定.
(3)请你从平均数、众数、中位数、方差等数据分析,推选一个班级去参加区级比赛.
答案与解析
一.选择题
1.(2025 淮安一模)一组数据1,3,5,2,4的平均数是( )
A.1 B.2 C.3 D.6
【点拨】根据算术平均数的定义列式计算即可.
【解析】解:数据1,3,5,2,4的平均数是=3,
故选:C.
【点睛】本题主要考查算术平均数,解题的关键是掌握算术平均数的定义.
2.(2024 湖南)某班的5名同学1分钟跳绳的成绩(单位:次)分别为:179,130,192,158,141.这组数据的中位数是( )
A.130 B.158 C.160 D.192
【点拨】先将上述数据按照从小到大的顺序排列,根据中位数的定义可知:第3位的数据是中位数.
【解析】解:先将上述数据按照从小到大的顺序排列:130,141,158,179,192,
∴这组数据的中位数是158,
故选:B.
【点睛】本题考查的是中位数,熟练掌握中位数的相关定义和计算方法是解题的关键.
3.(2025 苏州模拟)某初中男子篮球队队员的身高数据是:186,175,187,186,184.这组数据的众数是( )
A.175 B.186 C.184 D.187
【点拨】根据众数的定义求解即可.
【解析】解:∵186出现了2次,出现的次数最多,
∴该组数据的众数是186;
故选:B.
【点睛】本题主要考查众数的定义,众数是一组数据中出现次数最多的数,在一组数据中,众数可能不止一个.
4.(2024 宁明县三模)某校举行健美操比赛,甲、乙两个班各选10名学生参加比赛,两个班参赛学生的平均身高都是1.65米,其方差分别是,则参赛学生身高比较整齐的班级是( )
A.甲班 B.乙班 C.同样整齐 D.无法确定
【点拨】根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
【解析】解:∵=1.9,=2.4,
∴<,
∴参赛学生身高比较整齐的班级是甲班,
故选:A.
【点睛】此题主要考查了方差,方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
5.(2024 资阳)6名学生一周做家务的天数依次为4,4,5,7,7,7,这组数据的中位数和众数分别为( )
A.5,4 B.6,5 C.6,7 D.7,7
【点拨】根据众数和中位数的概念求解.
【解析】解:这组数据的中位数为=6,
所以这组数据的众数为7,
故选:C.
【点睛】本题考查了众数和中位数的概念:一组数据中出现次数最多的数据叫做众数;将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
6.(2024 攀枝花)某公司要招聘一名职员,根据实际需要,从学历、能力、经验三个方面对甲、乙、丙、丁四名应聘者进行了测试,测试成绩如表:
项目 应聘者
甲 乙 丙 丁
学历 7 7 9 8
能力 8 9 8 9
经验 8 7 7 7
如果这家公司比较看重员工的能力,将学历、能力、经验三项得分按1:2:1的比例加权平均确定每人的最终得分,录用得分最高者,那么将被录用的是( )
A.甲 B.乙 C.丙 D.丁
【点拨】根据加权平均数的计算方法可以得到甲、乙、丙、丁的成绩,然后比较大小即可解答本题.
【解析】解:由题意可得,
甲的成绩为:=7.75(分),
乙的成绩为:=8(分),
丙的成绩为:=8(分),
丁的成绩为:=8.25(分),
∴将被录用的是丁.
故选:D.
【点睛】本题考查加权平均数,解答本题的关键是明确加权平均数的计算方法.
7.(2024 宜宾)某校为了解九年级学生在校的锻炼情况,随机抽取10名学生,记录他们某一天在校的锻炼时间(单位:分钟):65,67,75,65,75,80,75,88,78,80.对这组数据判断正确的是( )
A.方差为0 B.众数为75 C.中位数为77.5 D.平均数为75
【点拨】根据平均数和方差、中位数,众数得出答案即可.
【解析】解:65,67,75,65,75,80,75,88,78,80中,
平均数=(65+67+75+65+75+80+75+88+78+80)=74.8,
65,67,75,65,75,80,75,88,78,80按从小到大的顺序排序为65,65,67,75,75,75,78,80,80,88,
∴中位数==75,众数为75,方差=[(65﹣74.8)2×2+(67﹣74.8)2+(75﹣74.8)2×3+(78﹣74.8)2+(80﹣74.8)2×2+(88﹣74.8)2]≈61,
故选:B.
【点睛】本题考查了平均数,方差,中位数,众数等知识点,能熟记中位线、众数的定义和方差的意义是解此题的关键.
8.(2024 台州模拟)小明的期中与期末测试成绩如表:
语文 数学 英语
小明期中 88 56 70
年级平均分 75 60 69
小明期末 70 76 68
年级平均分 75 68 65
下列说法不合理的是( )
A.小明期末与期中总分相同 B.小明英语期末名次一定在中等以上
C.小明数学期末成绩比期中有进步 D.小明语文期末成绩比期中有退步
【点拨】根据表中数据及中位数的定义逐一判断即可.
【解析】解:A.小明期末总分为70+76+68=214(分),期中总分为75+60+69=214(分),期末与期中总分相同,此选项正确,不符合题意;
B.小明英语期末成绩为68分,未给出中位数大小,故不能确定小明英语期末名次一定在中等以上,此选项错误,符合题意;
C.小明数学期末成绩未76分,期中成绩为76分,期末成绩比期中成绩有进步,此选项正确,不符合题意;
D.小明语文期末成绩为70分,期中成绩为88分,期末比期中有退步,此选项正确,不符合题意;
故选:B.
【点睛】本题主要考查算术平均数和中位数,解题的关键是掌握中位数的意义.
9.(2024 杭州一模)某学校5名教师在一次义务募捐中的捐款额(单位:元)为30,50,50,100,100.若捐款最少的教师又多捐了30元,则分析这5名教师捐款额的数据时,不受影响的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
【点拨】根据众数、中位数、平均数及方差的定义求解即可.
【解析】解:依题意,捐款最少的教师又多捐了30元,则数据50、100的个数不变,即众数不变,而平均数,中位数,方差都要用到60,
故不受影响的统计量是众数.
故选:C.
【点睛】本题主要考查算术平均数,解题的关键是掌握众数、中位数、平均数及方差的定义.
10.(2025 五华区校级模拟)在一场篮球赛中,某队5名场上队员的身高(单位:cm)分别是:187,188,192,193,194.因身高为194cm的队员受伤,教练让身高为190cm的队员替补上场.与换人前相比,换人后场上队员的身高( )
A.平均数变小,方差变大 B.平均数变小,方差变小
C.平均数变大,方差变小 D.平均数变大,方差变大
【点拨】根据平均数和方差的定义和意义即可得出答案.
【解析】解:用一名身高190cm的队员换下场上身高194cm的队员,与换人前相比,场上队员身高的和变小,而人数没变,
所以他们的平均数变小,
由于数据的波动性变小,所以数据的方差变小.
故选:B.
【点睛】本题主要考查平均数和方差,熟练掌握方差、平均数的计算公式是解题的关键.
二.填空题
11.(2025 永州模拟)数据2、3、5、5、4的众数是 5 .
【点拨】根据众数的定义即可判断;
【解析】解:数据2、3、5、5、4中,5出现的次数最多,所以这组数据的众数为5,
故答案为5.
【点睛】本题考查众数的定义,解题的关键是记住一组数据中出现次数最多的数据叫做众数.
12.(2025 盐城一模)一组数据含有三个不同的数:3、8、7,它们的频数分别是3、5、2,则这组数据的平均数是 6.3 .
【点拨】本题是求加权平均数,根据加权平均数的公式即可求解.
【解析】解:根据题意可得,这组数据的平均数=(3×3+8×5+7×2)÷(3+5+2)=6.3.
故填6.3.
【点睛】正确理解加权平均数的计算方法是解决本题的关键.
13.(2024 杭州三模)一组数据5,6,7,8,9的标准差为 .
【点拨】要计算方差首先要计算出平均数,再根据方差公式计算.
【解析】解:平均数=(5+6+7+8+9)÷5=7,
方差=[(5﹣7)2+(6﹣7)2+(7﹣7)2+(8﹣7)2+(9﹣7)2]=2.
∴标准差=,
故答案为.
【点睛】本题主要考查平均数、方差、标准差的计算方法,解题的关键是记住有关公式,属于中考常考题型.
14.(2024 滨江区二模)某校901班共有50名学生,平均身高为m厘米,其中30名男生的平均身高为n厘米,则20名女生的平均身高为 厘米.
【点拨】根据题目中的数据和加权平均数的计算方法,可以计算出20名女生的平均身高.
【解析】解:20名女生的平均身高为:=(cm).
故答案为:.
【点睛】本题考查加权平均数,解答本题的关键是明确加权平均数的计算方法.
15.(2024 海宁市三模)已知某组数据的方差计算公式为,则这组数据的平均数为 5 .
【点拨】根据方差的公式可以得到平均数.
【解析】解:由于这组数据的方差是S2=[(x1﹣5)2+(x2﹣5)2+...+(xn﹣5)2],
故平均数是5.
故答案为:5.
【点睛】本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为5,则方差S2=[(x1﹣5)2+(x2﹣5)2+…+(xn﹣5)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
16.(2024 光山县一模)甲,乙两人在相同条件下各射击10次.两人的成绩(单位:环)如图所示.现有以下三个推断:
①甲的成绩更稳定; ②乙的平均成绩更高;③每人再射击一次,乙的成绩一定比甲高.
其中正确的是 ①② .(填序号)
【点拨】①根据方差的意义判断即可;②根据算术平均数的定义判断即可;③根据随机事件的意义判断即可.
【解析】解:由折线统计图可知,
甲的成绩在3和5之间波动,乙的成绩在3和9之间波动,所以甲的成绩更稳定,故①结论正确;
乙的10次成绩中有9次成绩大于甲,其中一次相同,可推知②正确;
每人再射击一次,乙的成绩不一定比甲高,故③的结论错误.
故答案为:①②.
【点睛】本题考查了方差和折线统计图,掌握方差的意义是解答本题的关键.
三.解答题
17.(2024 温州模拟)某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:
每人销售件数 1400 880 270 150 130 120
人数 1 1 3 6 3 1
(1)求这15位营销人员该月销售量的平均数、中位数和众数;
(2)为督促并不影响员工的积极性,假设销售负责人把每位营销员的月销售定额定为300件,你认为是否合理,请你制定一个较合理的销售定额,并说明理由.
【点拨】(1)找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数,众数是一组数据中出现次数最多的数据,注意众数可以不止一个.平均数是指在一组数据中所有数据之和再除以数据的个数.
(2)根据表中数据和平均数、中位数和众数的意义回答.
【解析】解:(1)平均数=(件),
∵最中间的数据为150,
∴这组数据的中位数为150件,
∵150是这组数据中出现次数最多的数据,
∴众数为150件;
答:这15位营销人员该月销售量的平均数为300件,中位数和众数都是150件;
(2)不合理,理由:因为15人中有13人的销售额不到300件,300件虽是所给一组数据的平均数,它却不能很好地反映销售人员的一般水平.
销售额定为150件合适些,因为150件既是中位数,又是众数,是大部分人能达到的定额.
【点睛】此题考查了学生对中位数,众数,平均数的掌握情况.它们都是反映数据集中趋势的指标.
18.(2024 浙江模拟)由于水资源缺乏,某地区决定利用分段计费的方法引导人们节约用水,即规定每个家庭的月基本用水量为m吨,家庭月用水量不超过m吨的部分按原价收费,超过m吨的部分加倍收费.为了解居民的用水情况,该地区从某社区的1500户家庭中随机抽取了30户家庭的月用水量,结果如表所示:
月用水量(吨) 3 4 5 7 8 9 10
户数(户) 4 2 5 11 4 2 2
(1)求这30户家庭的月平均用水量.
(2)估计该社区的月用水量.
(3)你认为该地区规定每个家庭的月基本用水量m为多少吨比较合理?请你用所学的统计知识说明理由.
【点拨】(1)根据平均数的定义求解即可,
(2)用社区的总户数乘以平均数列出算式计算即可;
(3)根据平均数、众数、中位数的意义,结合题意选择合适的量即可.
【解析】解:(1)这30户家庭月用水量的平均数=(3×4+4×2+5×5+7×11+8×4+9×2+40×2)÷30=6.4(吨)
答:这30户家庭的月平均用水量为6.4吨;
(2)∵社区共1500户家庭,
∴该社区的月用水量=6.4×1500=9600(吨);
(3)地区规定每个家庭的月基本用水量m为7吨较合理,理由如下:
7出现了11次,出现的次数最多,
则众数是7,
∵共有30个数,
∴中位数是第15、16个数的平均数,
∴中位数是(7+7)÷2=7(吨),
因为平均数容易受到个别极端数据的影响,中位数、众数不容易 受极端数据的影响,中位数和众数都是7吨,作为月基本用水量 既可以满足大多数家庭的用水量,也可以引导用水量高于7吨 的家庭节约用水.
【点睛】本题考查加权平均数,中位数,众数,样本估计总体等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
19.(2024 河南)为提升学生体质健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在八年级组织的篮球联赛中,甲、乙两名队员表现优异,他们在近六场比赛中关于得分、篮板和失误三个方面的统计结果如下.
技术统计表
队员 平均每场得分 平均每场篮板 平均每场失误
甲 26.5 8 2
乙 26 10 3
根据以上信息,回答下列问题.
(1)这六场比赛中,得分更稳定的队员是 甲 (填“甲”或“乙”);甲队员得分的中位数为27.5分,乙队员得分的中位数为 29 分.
(2)请从得分方面分析:这六场比赛中,甲、乙两名队员谁的表现更好.
(3)规定“综合得分”为:平均每场得分×1+平均每场篮板×1.5+平均每场失误×(﹣1),且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好.
【点拨】(1)根据中位数的计算方法求解即可;
(2)根据平均数的概念求解即可;
(3)根据“综合得分”的计算方法求出甲和乙的得分,然后比较求解即可.
【解析】解:(1)由折线图可得甲得分更稳定,
把乙的六次成绩按从小到大的顺序排序,第三次、第四次的成绩分别为28和30,
故中位数为==29,
故答案为:甲,29;
(2)因为甲的平均每场得分大于乙的平均每场得分,且甲的得分更稳定,所以甲队员表现更好.(注:答案不唯一,合理即可);
(3)甲的综合得分为:26.5×1+8×1.5+2×(﹣1)=36.5.
乙的综合得分为:26×1+10×1.5+3×(﹣1)=38.
因为38>36.5,所以乙队员表现更好.
【点睛】本题考查了中位数,加权平均数、方差的计算,掌握以上计算方法是关键.
20.(2025 庐江县模拟)某果园今年种植的苹果喜获丰收,该果园种植了甲、乙两种品种的苹果,现随机选取两种品种的苹果树各10棵,对苹果个数进行统计并记录如下:甲品种:
编号 1 2 3 4 5 6 7 8 9 10
个数 68 76 65 47 65 71 65 78 70 75
乙品种:
(1)填空:
品种 平均数 众数 中位数 不低于80个的频率 方差
甲 68 ② 65 69 0 69.4
乙 ① 68 45 ③ 68 ④ 0.4 329
(2)根据上述材料分析:
①如果果园计划扩大种植面积,在两种品种苹果销量和价格一致的情况下,增加哪个品种的苹果种植面积更好?请说明理由;
②如果农科所要选取其中一个品种研究以获得更高产量,应该选取哪个品种?请说明理由.
【点拨】(1)分别根据平均数、众数和中位数的定义计算即可;
(2)①根据平均数、众数、中位数和方差的意义判断即可;
②根据不低于80个的高产苹果频率判断即可.
【解析】解:(1)乙品种的平均数为=68(个),
甲品种的众数为65,乙品种的中位数为=68,
乙品种不低于80个的频率为=0.4;
故答案为:①68,②65,③68,④0.4;
(2)①增加甲品种的苹果种植面积更好,
理由:甲品种平均产量和乙品种一致,但甲品种方差更小,稳定性更好,同时它的众数和中位数均高于乙品种,大面积种植风险更小,故选甲;
②应该选取乙品种,
理由:因为乙品种不低于80个的高产苹果频率为40%,甲品种为0,故乙品种更容易出现高产苹果.
【点睛】本题考查频数与频率,中位数、众数、平均数和方差,理解中位数、众数、方差的意义和计算方法是正确解答的前提.
21.(2024 浙江模拟)法国著名的思想家伏尔泰说过“生命在于运动”,某大学小组为了调查初中同学学生课后运动时间,按照时间分为A、B、C、D四个等级,绘制了如下不完整统计表:
(1)求本次调查的总人数,并且补全人数分布图;
(2)估计本次调查的中位数位于A、B、C、D哪个等级中;
(3)小宁认为我们可以根据本次调查数据精确预测全市初中生为A等的人数,请判断他这句话的正误,并说明理由.
【点拨】(1)由A等级人数及其所占百分比可得总人数,总人数减去A、B、D人数即可求出C等级人数;
(2)根据中位数的定义求解即可;
(3)利用样本估计总体求解即可.
【解析】解:(1)本次调查的总人数为12÷24%=50(人),
则C等级人数为50﹣(12+24+4)=10(人),
补全人数分布图如下:
(2)本次调查的中位数是第25、26个数据的平均数,而这两个数据均为B等级,
所以本次调查的中位数位于B等级;
(3)错误,
可以根据本次调查数据估计全市初中生为A等的人数,而不能精确预测.
【点睛】本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
22.(2024 杭州二模)4月24日是中国航天日,为激发青少年崇尚科学、探索未知的热情,某中学开展了“航空航天”知识问答系列活动.为了解活动效果,从七、八年级学生的知识问答成绩中,各随机抽取了20名学生的成绩进行统计分析(6分及6分以上为合格:9分及9分以上为优秀),绘制了如下统计图表:
学生成绩统计表
七年级 八年级
平均数 m 7.55
中位数 8 b
众数 a 7
根据上述信息,解答下列问题:
(1)学生成绩统计表中a= 8 ,b= 7.5 ;
(2)求七年级学生成绩的平均数m;
(3)根据以上数据,你认为该校七年级和八年级中,哪个年级的学生对航天航空知识掌握更好?并说明理由.
【点拨】(1)分别根据众数和中位数的定义解答即可;
(2)根据加权平均数的计算公式计算即可;
(3)比较两个年级的平均数、众数和中位数可得答案.
【解析】解:(1)由统计图可知,七年级中8分出现的次数最多,故众数a=8;
把八年级20名学生的成绩从小到大排列,排在中间的两个数分别为7,8,故中位数b==7.5.
故答案为:8,7.5;
(2)七年级学生成绩的平均数m=5×20%+6×10%+7×10%+8×30%+9×15%+10×15%=7.55;
(3)七年级的学生对航天航空知识掌握更好,理由如下:
因为两个年级的平均数相同,但七年级的中位数和众数均高于八年级,所以七年级的学生对航天航空知识掌握更好.
【点睛】本题考查加权平均数,中位数以及众数,掌握相关统计量的计算方法是正确解答的前提.
23.(2024 温州模拟)某校举行“知礼 明理”知识问答竞赛,A班、B班各派出5名选手组成代表队参加比赛.两班派出选手的比赛成绩如图所示.
平均数/分 中位数/分 众数/分
A校 85 85 85
B校 85 a b
根据图中信息,整理分析数据得到如下表格:
(1)a= 80 ,b= 100 ;
(2)计算两校比赛成绩的方差,并判断哪个学校派出的代表队选手成绩较为稳定.
(3)请你从平均数、众数、中位数、方差等数据分析,推选一个班级去参加区级比赛.
【点拨】(1)根据条形图将B校数据重新排列,再根据中位数和众数的概念求解即可;
(2)计算出A、B两校成绩的方差,根据方差的意义可得答案;
(3)从表中数据,利用平均数和中位数和众数的意义可得出答案.
【解析】解:(1)将B校5名选手的成绩重新排列为:70、75、80、100、100,
所以其中位数a=80、众数b=100,
故答案为:80,100;
(2)=[(75﹣85)2+(80﹣85)2+2×(85﹣85)2+(100﹣85)2]=70,
=[(70﹣85)2+(75﹣85)2+(80﹣85)2+2×(100﹣85)2]=160,
∴,
∴A学校派出的代表队选手成绩较为稳定;
(3)①从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是A校;
②从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是B校.
【点睛】本题主要考查方差,解题的关键是掌握中位数、众数的定义及平均数、众数、中位数和方差的意义.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
