2.5 第1课时 气体的等容变化和等压变化(23张PPT)课件 2024-2025学年高二物理教科版(2019)选择性必修3
文档属性
| 名称 | 2.5 第1课时 气体的等容变化和等压变化(23张PPT)课件 2024-2025学年高二物理教科版(2019)选择性必修3 |  | |
| 格式 | pptx | ||
| 文件大小 | 17.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-04-07 19:36:20 | ||
图片预览








文档简介
第二章 固体、液体和气体
第5节 第1课时 气体的等容变化和等压变化
烧瓶上通过橡胶塞连接一根玻璃管,向玻璃管中注入一段水柱。用手捂住烧瓶,会观察到水柱缓慢向外移动,这说明了什么?
1. 掌握查理定律和盖—吕萨克定律的内容、表达式及适用条件。
2. 理解p-T图像与V-T图像的物理意义。
读数次数
1
2
3
4
5
压强/KPa
101.7
103.5
105.6
109.1
111.3
温度/0C
11.7
18.81
25.64
36.05
43.39
1. 气体的等容变化
一定质量的某种气体,在体积不变时,压强随温度变化的过程叫作气体的等容变化。
演示视频:
一、气体的等容变化
2.查理定律:一定质量的某种气体,在体积不变的情况下,压强p与热力学温度T成正比( ????????=常量) .
?
(1)是实验定律,由法国科学家查理通过实验发现的.
查理(1746-l823)
(2)成立条件:气体质量一定,体积不变.
可写成
或
(3)在p/T=C中的C与气体的种类、质量、体积有关.
注意: ①p与热力学温度T成正比,不与摄氏温度成正比;
②但压强的变化?p与摄氏温度?t 的变化成正比.
(4)一定质量的气体在等容时,升高(或降低)相同的温度,所增加(或减小)的压强是相同的.
(5)解题时前后两状态压强的单位要统一.
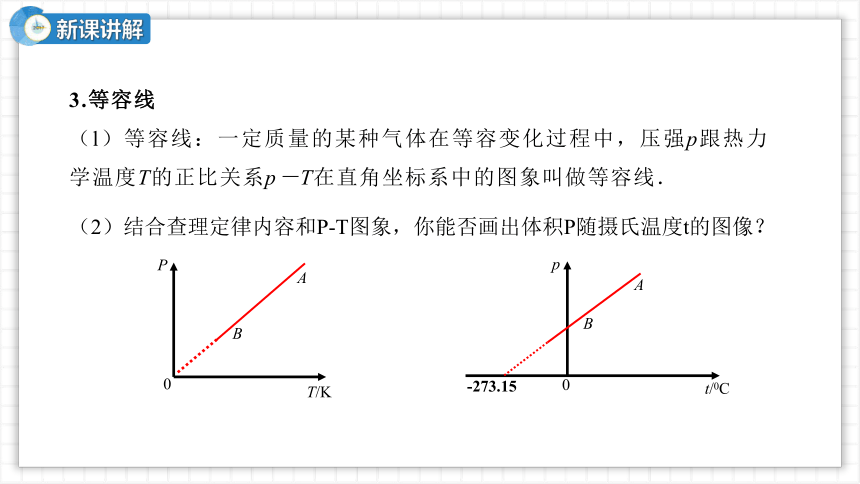
3.等容线
(l)等容线:一定质量的某种气体在等容变化过程中,压强p跟热力学温度T的正比关系p-T在直角坐标系中的图象叫做等容线.
(2)结合查理定律内容和P-T图象,你能否画出体积P随摄氏温度t的图像?
0
T/K
A
B
P
0
p
t/0C
A
B
-273.15
(3)同一气体,不同体积下等容线是不同的,你能判断那条等容线气体的体积比较大吗?你是根据什么理由作出判断的?
结论:等容线斜率越大,体积越小。
(4)一定质量气体的等容线的物理意义.
①图线上每一个点表示气体一个确定的状态,同一根等容线上各状态的体积相同。
②不同体积下的等容线,斜率越大,体积越小(同一温度下,压强大的体积小)如图所示,V2【例题】某种气体的压强为2×105Pa,体积为1m3,温度为200K。它经过等温过程后体积变为2m3。随后,又经过等容过程,温度变为300K,球此时气体的压强。
解:
开始时:p1=2×105Pa,V1=1m3,T1=200K
等温后状态: p=?, V=2m3,T=200K
等容后状态: p2=?,V2=2m3,T2=300K
根据玻意耳定律,有:p1V1=pV
根据查理定律,有:
联立上述各式可得:
P2=1.5×105Pa
应用等容变化规律解题的一般步骤
1.确定研究对象,即被封闭的一定质量的气体。
2.分析被研究气体在状态变化时是否符合定律的适用条件:质量一定,体积不变。
3.确定初、末两个状态的压强、温度。
4.根据等容变化规律列式。
5.求解结果并分析、检验。
二、气体的等压变化
一定质量的某种气体,在压强不变时,体积随温度变化的过程叫作气体的等压变化。
1. 气体的等压变化
实验表明,在保持气体的压强不变的情况下,一定质量气体的体积随温度的升高而增大。
演示视频:
2.盖-吕萨克定律:
一定质量的某种气体,在压强不变的情况下,体积V与热力学温度成正比( ????????=常量).
?
可写成
(1)是实验定律,由法国科学家盖·吕萨克通过实验发现的.
盖·吕萨克(1778—1850年)法国化学家、物理学家.
或
(2)成立条件:气体质量一定,压强不变.
(3)在 V/T=C 中的C与气体的种类、质量、压强有关.
注意: V正比于T而不正比于t,但 ?V??t
(4)一定质量的气体发生等压变化时,升高(或降低)相同的温度,增加(或减小)的体积是相同的.
3.等压线
(1)等压线:一定质量的某种气体在等压变化过程中,体积V与热力学温度T的正比关系在V-T直角坐标系中的图象叫做等压线.
0
V
T
(2)结合盖吕萨克定律内容和V-T图象,你能否画出体积V随摄氏温度t的图象?
(3)同一气体,不同压强下等压线是不同的,你能判断那条等压线气体的压强比较大吗?你是根据什么理由作出判断的?
结论:等压线斜率越大,压强越小。
(4)适用条件:
①压强不太大,温度不太低;②气体的质量和压强都不变。
如图所示,导热良好的固定直立圆筒内用面积S=10 cm2、质量m=1 kg的活塞封闭一定质量的理想气体,活塞能无摩擦滑动。外界环境的热力学温度T1=300 K,平衡时圆筒内活塞处于位置A,活塞到筒底的距离L1=30 cm。竖直向下缓慢推动活塞到达位置B,此时活塞到筒底的距离L2=20 cm。筒壁和活塞的厚度均可忽略不计,
外界大气压强p0=1.0×105 Pa,取重力加速度大小g=10 m/s2。
(1)求此时活塞上的作用力大小F;
(2)缓慢升高环境温度,求活塞回到位置A时筒内气体的热力学温度T2。
解:(1)活塞处于位置A时,根据平衡条件有p1S=p0S+mg
竖直向下缓慢推动活塞到达位置B,根据平衡条件有p2S=p0S+mg+F
活塞从位置A缓慢推动活塞到达位置B,气体做等温变化,有p1SL1=p2SL2
解得此时活塞上的作用力大小为:F=55 N
(2)缓慢升高环境温度,活塞从位置B回到位置A时,
气体做等压变化,有????????2????1=????????1????2
解得活塞回到位置A时筒内气体的热力学温度为:T2=450 K
?
应用等压变化规律解题的一般步骤
1.确定研究对象,即被封闭的一定质量的气体。
2.分析被研究气体在状态变化时是否符合定律的适用条件:质量一定,压强不变。
3.确定初、末两个状态的温度、体积。
4.根据等压变化规律列式。
5.求解结果并分析、检验。
1. 在下列图中,不能反映一定质量的理想气体经历了等温变化→等容变化→等压变化后,又回到初始状态的图是( )
A.
B.
C.
D.
D
2. 一个密闭的钢管内装有空气,在温度为20℃时,压强为1?atm,若温度上升到80℃,管内空气的压强约为( )
A. 4?atm
B. 14atm
C. 1.2?atm
D. 56atm
?
C
3.一定质量的气体在等压变化过程中体积增大了12,若气体原来温度为27 ℃,则温度的变化是( )
A.升高了450 K B.升高了150 ℃
C.降低了150 ℃ D.降低了450 ℃
?
B
3.如图为一定质量的理想气体的V-T图像,该气体经历了从a→b→c的状态变化,图中ab连线平行于V轴,ac是双曲线的一部分,cb连线的延长线通过坐标原点O,则三个状态下的压强满足( )
A.pbC.pc>pa=pb D.pa>pb=pc
B
气体的等容变化
对V-T图像(等压曲线)的理解
气体的等容变化和等压变化
气体的等压变化
适用条件:压强不太大,温度不太低;气体的质量和压强都不变
对p-T图像(等容曲线)的理解
盖—吕萨克定律: V=CT (其中C是常量),或 ????1????1=????2????2
?
查理定律:p=CT (C是常量),或 ????1????1=????2????2
?
适用条件:压强不太大,温度不太低;气体的质量和压强都不变
第5节 第1课时 气体的等容变化和等压变化
烧瓶上通过橡胶塞连接一根玻璃管,向玻璃管中注入一段水柱。用手捂住烧瓶,会观察到水柱缓慢向外移动,这说明了什么?
1. 掌握查理定律和盖—吕萨克定律的内容、表达式及适用条件。
2. 理解p-T图像与V-T图像的物理意义。
读数次数
1
2
3
4
5
压强/KPa
101.7
103.5
105.6
109.1
111.3
温度/0C
11.7
18.81
25.64
36.05
43.39
1. 气体的等容变化
一定质量的某种气体,在体积不变时,压强随温度变化的过程叫作气体的等容变化。
演示视频:
一、气体的等容变化
2.查理定律:一定质量的某种气体,在体积不变的情况下,压强p与热力学温度T成正比( ????????=常量) .
?
(1)是实验定律,由法国科学家查理通过实验发现的.
查理(1746-l823)
(2)成立条件:气体质量一定,体积不变.
可写成
或
(3)在p/T=C中的C与气体的种类、质量、体积有关.
注意: ①p与热力学温度T成正比,不与摄氏温度成正比;
②但压强的变化?p与摄氏温度?t 的变化成正比.
(4)一定质量的气体在等容时,升高(或降低)相同的温度,所增加(或减小)的压强是相同的.
(5)解题时前后两状态压强的单位要统一.
3.等容线
(l)等容线:一定质量的某种气体在等容变化过程中,压强p跟热力学温度T的正比关系p-T在直角坐标系中的图象叫做等容线.
(2)结合查理定律内容和P-T图象,你能否画出体积P随摄氏温度t的图像?
0
T/K
A
B
P
0
p
t/0C
A
B
-273.15
(3)同一气体,不同体积下等容线是不同的,你能判断那条等容线气体的体积比较大吗?你是根据什么理由作出判断的?
结论:等容线斜率越大,体积越小。
(4)一定质量气体的等容线的物理意义.
①图线上每一个点表示气体一个确定的状态,同一根等容线上各状态的体积相同。
②不同体积下的等容线,斜率越大,体积越小(同一温度下,压强大的体积小)如图所示,V2
解:
开始时:p1=2×105Pa,V1=1m3,T1=200K
等温后状态: p=?, V=2m3,T=200K
等容后状态: p2=?,V2=2m3,T2=300K
根据玻意耳定律,有:p1V1=pV
根据查理定律,有:
联立上述各式可得:
P2=1.5×105Pa
应用等容变化规律解题的一般步骤
1.确定研究对象,即被封闭的一定质量的气体。
2.分析被研究气体在状态变化时是否符合定律的适用条件:质量一定,体积不变。
3.确定初、末两个状态的压强、温度。
4.根据等容变化规律列式。
5.求解结果并分析、检验。
二、气体的等压变化
一定质量的某种气体,在压强不变时,体积随温度变化的过程叫作气体的等压变化。
1. 气体的等压变化
实验表明,在保持气体的压强不变的情况下,一定质量气体的体积随温度的升高而增大。
演示视频:
2.盖-吕萨克定律:
一定质量的某种气体,在压强不变的情况下,体积V与热力学温度成正比( ????????=常量).
?
可写成
(1)是实验定律,由法国科学家盖·吕萨克通过实验发现的.
盖·吕萨克(1778—1850年)法国化学家、物理学家.
或
(2)成立条件:气体质量一定,压强不变.
(3)在 V/T=C 中的C与气体的种类、质量、压强有关.
注意: V正比于T而不正比于t,但 ?V??t
(4)一定质量的气体发生等压变化时,升高(或降低)相同的温度,增加(或减小)的体积是相同的.
3.等压线
(1)等压线:一定质量的某种气体在等压变化过程中,体积V与热力学温度T的正比关系在V-T直角坐标系中的图象叫做等压线.
0
V
T
(2)结合盖吕萨克定律内容和V-T图象,你能否画出体积V随摄氏温度t的图象?
(3)同一气体,不同压强下等压线是不同的,你能判断那条等压线气体的压强比较大吗?你是根据什么理由作出判断的?
结论:等压线斜率越大,压强越小。
(4)适用条件:
①压强不太大,温度不太低;②气体的质量和压强都不变。
如图所示,导热良好的固定直立圆筒内用面积S=10 cm2、质量m=1 kg的活塞封闭一定质量的理想气体,活塞能无摩擦滑动。外界环境的热力学温度T1=300 K,平衡时圆筒内活塞处于位置A,活塞到筒底的距离L1=30 cm。竖直向下缓慢推动活塞到达位置B,此时活塞到筒底的距离L2=20 cm。筒壁和活塞的厚度均可忽略不计,
外界大气压强p0=1.0×105 Pa,取重力加速度大小g=10 m/s2。
(1)求此时活塞上的作用力大小F;
(2)缓慢升高环境温度,求活塞回到位置A时筒内气体的热力学温度T2。
解:(1)活塞处于位置A时,根据平衡条件有p1S=p0S+mg
竖直向下缓慢推动活塞到达位置B,根据平衡条件有p2S=p0S+mg+F
活塞从位置A缓慢推动活塞到达位置B,气体做等温变化,有p1SL1=p2SL2
解得此时活塞上的作用力大小为:F=55 N
(2)缓慢升高环境温度,活塞从位置B回到位置A时,
气体做等压变化,有????????2????1=????????1????2
解得活塞回到位置A时筒内气体的热力学温度为:T2=450 K
?
应用等压变化规律解题的一般步骤
1.确定研究对象,即被封闭的一定质量的气体。
2.分析被研究气体在状态变化时是否符合定律的适用条件:质量一定,压强不变。
3.确定初、末两个状态的温度、体积。
4.根据等压变化规律列式。
5.求解结果并分析、检验。
1. 在下列图中,不能反映一定质量的理想气体经历了等温变化→等容变化→等压变化后,又回到初始状态的图是( )
A.
B.
C.
D.
D
2. 一个密闭的钢管内装有空气,在温度为20℃时,压强为1?atm,若温度上升到80℃,管内空气的压强约为( )
A. 4?atm
B. 14atm
C. 1.2?atm
D. 56atm
?
C
3.一定质量的气体在等压变化过程中体积增大了12,若气体原来温度为27 ℃,则温度的变化是( )
A.升高了450 K B.升高了150 ℃
C.降低了150 ℃ D.降低了450 ℃
?
B
3.如图为一定质量的理想气体的V-T图像,该气体经历了从a→b→c的状态变化,图中ab连线平行于V轴,ac是双曲线的一部分,cb连线的延长线通过坐标原点O,则三个状态下的压强满足( )
A.pb
B
气体的等容变化
对V-T图像(等压曲线)的理解
气体的等容变化和等压变化
气体的等压变化
适用条件:压强不太大,温度不太低;气体的质量和压强都不变
对p-T图像(等容曲线)的理解
盖—吕萨克定律: V=CT (其中C是常量),或 ????1????1=????2????2
?
查理定律:p=CT (C是常量),或 ????1????1=????2????2
?
适用条件:压强不太大,温度不太低;气体的质量和压强都不变
同课章节目录
