第八章整式乘法压轴题练习期中复习(含答案)
文档属性
| 名称 | 第八章整式乘法压轴题练习期中复习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 354.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第八章整式乘法压轴题练习期中复习苏科版2024—2025学年七年级下册
一、选择题
1.若x﹣m与3x﹣2的乘积中不含x的一次项,则m的值为( )
A. B. C. D.3
2.如图在边长为a的正方形纸片中剪去一个边长为b的小正方形,把余下的部分沿虚线剪开,拼成一个矩形,分别计算这两个图形阴影部分的面积,可以验证的等式是( )
A.a2﹣b2=(a+b)(a﹣b) B.(a﹣b)2=a2﹣2ab+b2
C.(a+b)2=a2+2ab+b2 D.a2+ab=a(a+b)
3.在展开多项式(x2+x﹣3)(x2﹣2x+2a)中,常数项为﹣30,则a等于( )
A.3 B.4 C.5 D.6
4.图1是长为a,宽为b(a>b)的小长方形纸片将6张如图1的纸片按图2的方式不重叠地放在长方形ABCD内,已知CD的长度固定不变,BC的长度可以变化,图中阴影部分(即两个长方形)的面积分别表示为S1,S2,若a=4,b=2,S1﹣S2的值是( )
A.8 B.16 C.12 D.32
5.已知(x﹣2024)2+(x﹣2026)2=38,则(x﹣2025)2的值是( )
A.4 B.18 C.12 D.16
6.已知实数a,b满足,则3a2+4b2+1012a﹣2024b+1的值是( )
A.65 B.105 C.115 D.2025
二、填空题
7.求值:(2+1)×(22+1)×(24+1)×(28+1)×...×(264+1)= .
8.已知11.已知x=3y+5,且x2﹣7xy+9y2=24,则x2y﹣3xy2的值为 .
9.m2﹣9n2=5,m2+6mn+9n2=5﹣m﹣3n,那么n的值为 .
10.如图,点B是线段CG上一点,以BC,BE为边向两边作正方形,面积分别是S1和S2,设CG=6,两个正方形的面积之和S1+S2=20,则阴影部分△BCE的面积为 .
11.小明将(2022x+2023)2展开后得到;小亮将(2023x﹣2022)2展开后得到,若两人计算过程无误,则c1﹣c2的值为 .
三、解答题
12.在一次测试中,甲、乙两同学计算同一道整式乘法:(2x+a)(3x+b),甲由于抄错了第一个多项式中a的符号,得到的结果为6x2+11x﹣10;乙由于漏抄了第二个多项式中x的系数,得到的结果为2x2﹣9x+10.
(1)试求出式子中a,b的值;
(2)请你计算出这道整式乘法的正确结果.
13.已知关于x的一次二项式ax+b与x2﹣3x+1的积不含二次项,一次项的系数是4.求:
(1)系数a与b的值;
(2)二项式ax+b与x2﹣3x的积.
14.若(x+4)(x2﹣2ax﹣4b)的展开式中不含x的二次项和一次项.
(1)求ba的值;
(2)求(a+1)(a2+1)(a4+1) (a64+1)+1的值.
15.完全平方公式经过适当的变形,可以解决很多数学问题.例如:
若a+b=4,ab=2,求a2+b2的值.
解:∵a+b=4,ab=2,
∴(a+b)2=16,2ab=4.
即a2+b2+2ab=16.
∴a2+b2=12.
根据上面的解题思路与方法解决下列问题:
(1)a+b=3,ab=﹣1,则(a﹣b)2的值为 ;
(2)如图,C是线段AB上的一点,分别以AC,BC为边向两边作正方形,AB=8,两正方形面积的和为24,设AC=a,BC=CF=b,求△AFC的面积;
(3)若(6﹣x)(x﹣2)=3,求(6﹣x)2+(x﹣2)2的值.
16.如图,两个形状大小相同的长方形ABCD和长方形AEFG,点E在AB边上,AB=a,BC=b,且a>b>0.
(1)分别连接BD,DF,BF,试比较△ABD与△DFG的面积大小,并说明理由.
(2)用含a,b的代数式表示图中阴影部分的面积.
(3)当a+b=10,ab=20.求图中阴影部分的面积.
17.在数学中,通常可以运用一些公式来解决问题.比如,运用两数和的完全平方公式(a+b)2=a2+2ab+b2,能够在三个代数式a+b,ab,a2+b2中,当已知其中任意两个代数式的值时,求出第三个代数式的值.例如:已知a+b=3,ab=2,求a2+b2的值.
解:将a+b=3两边同时平方,得(a+b)2=32,
即a2+2ab+b2=9,
因为ab=2,
等量代换,得a2+b2+2×2=9,
所以a2+b2=5.
请根据以上信息,解答下列问题.
(1)已知a﹣b=1,a2+b2=17,求ab的值.
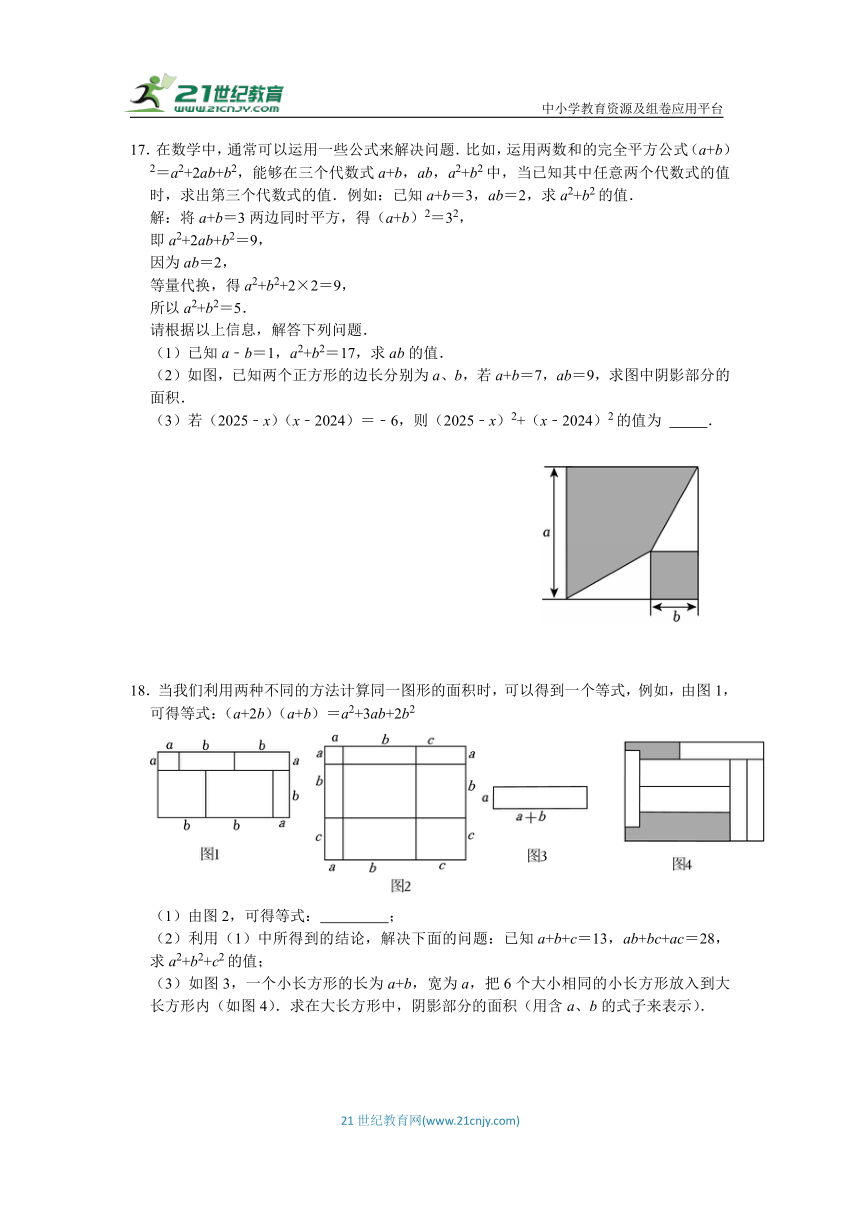
(2)如图,已知两个正方形的边长分别为a、b,若a+b=7,ab=9,求图中阴影部分的面积.
(3)若(2025﹣x)(x﹣2024)=﹣6,则(2025﹣x)2+(x﹣2024)2的值为 .
18.当我们利用两种不同的方法计算同一图形的面积时,可以得到一个等式,例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)由图2,可得等式: ;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=13,ab+bc+ac=28,求a2+b2+c2的值;
(3)如图3,一个小长方形的长为a+b,宽为a,把6个大小相同的小长方形放入到大长方形内(如图4).求在大长方形中,阴影部分的面积(用含a、b的式子来表示).
19.甲、乙两个长方形,它们的边长如图1所示,面积分别S1,S2(m为正整数).
(1)写出S1与S2的大小关系:S1 S2.(填“>”“<”或“=”);
(2)若|S1﹣S2|≤2025,求满足这个不等式的m的最大值;
(3)设有4块长方形甲,3块长方形乙,以及两块面积分别为S3,S4的矩形恰好拼成一个矩形图案,如图2所示.问:是否存在m,使得2S3=S4,若存在,请求出m的值;若不存在,请说明理由.
20.小聪学习多项式研究了多项式值为0的问题,发现当mx+n=0或px+q=0时,多项式A=(mx+n)(px+q)=mpx2+(mq+np)x+nq的值为0,把此时x的值称为多项式A的零点.
(1)已知多项式(3x+2)(x﹣3),则此多项式的零点为 .
(2)已知多项式B=(x﹣2)(x+m)=x2+(a﹣1)x﹣3a有一个零点为2,求多项式B的另一个零点;
(3)订正:小聪继续研究(x﹣4)(x﹣2),x(x﹣6)及等,发现在x轴上表示这些多项式零点的两个点关于直线x=3对称,他把这些多项式称为“3﹣系多项式”.若多项式M=(2x﹣b)(cx﹣7c)=ax2﹣(8a﹣4c)x+5b﹣4是“3﹣系多项式”,则a= ,b= ,c= .
21.有这样一类题:代数式ax﹣y+6+3x﹣5y﹣1的值与x的取值无关,求a的值.
通常的解题方法为把x,y看作字母,a看作系数合并同类项,即原式=(a+3)x﹣6y+5,因为代数式的值与x的取值无关,所以含x项的系数为0,即a+3=0,所以a=﹣3.
[理解应用]
(1)若关于x的多项式(2m﹣3) x+2m2﹣3m的值与x的取值无关,求m的值.
(2)已知3[(2x+1)(x﹣1)﹣x(1﹣3y)]+6(﹣x2+xy﹣1)的值与x无关,求y的值.
(3)如图①,小长方形纸片的长为a、宽为b,有7张如图①所示的纸片按照图②中的方式不重叠地放在大长方形ABCD内,大长方形中有两个部分(图中阴影部分)未被覆盖,设右上角的面积为S1,左下角的面积为S2.当AB的长变化时,S1﹣S2的值始终保持不变,求a与b的等量关系.
22.如图1,将边长(a+b)的正方形剪出两个边长分别为a,b的正方形(阴影部分),观察图形,解答下列问题:
(1)用两种不同的方法表示图一阴影部分的面积,即用两个不同的代数式表示阴影部分的面积.
方法1: ,方法2: ;从中你发现什么结论呢? ;
(2)运用你发现的结论,解决下列问题:
①已知(2023﹣x)2+(x﹣2022)2=9,求(2023﹣x)(x﹣2022)的值;
②如图2,C是线段AB上一点,以AC,BC为边向两边作正方形,AC+BC=8,两个正方形的面积和S1+S2=40,求图中阴影部分的面积.
23.【知识生成】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.
例如图1可以得到(a+b)2=a2+2ab+b2,基于此,请解答下列问题:
【直接应用】(1)若x+y=3,x2+y2=5,求xy的值;
【类比应用】(2)若(x﹣3)(x﹣4)=1,求(x﹣3)2+(x﹣4)2的值;
【知识迁移】(3)两块全等的特制直角三角板(∠AOB=∠COD=90°)如图2所示放置,其中A,O,D在一直线上,连接AC,BD,若AD=16,S△AOC+S△BOD=68,求一块直角三角板的面积.
参考答案
一、选择题
1.【解答】解:(x﹣m)(3x﹣2)
=3x2﹣2x﹣3mx+2m
=3x2﹣(2+3m)x+2m,
由题意得,﹣(2+3m)=0,
解得m,
故选:A.
2.【解答】解:∵图中阴影部分的面积=a2﹣b2,图中阴影部分的面积=(a+b)(a﹣b),
而两个图形中阴影部分的面积相等,
∴阴影部分的面积=a2﹣b2=(a+b)(a﹣b).
故选:A.
3.【解答】解:观察式子(x2+x﹣3)(x2﹣2x+2a)中常数项为﹣3×2a=﹣6a,
∵常数项为﹣30,
∴﹣6a=﹣30,
∴a=5;
故选:C.
4.【解答】解:设EF=x,
S1=(4b+x) 2b=(8+x)×4=32+4x,
S2=(a+x) a=(4+x)×4=16+4x,
∴S1﹣S2=(32+4x)﹣(16+4x)=32+4x﹣16﹣4x=16.
故选:B.
5.【解答】解:设x﹣2025=a,
∵(x﹣2024)2+(x﹣2026)2=38,
∴(x﹣2025+1)2+(x﹣2025﹣1)2=38,
∴(a+1)2+(a﹣1)2=38,
∴a2+2a+1+a2﹣2a+1=38,
∴2a2+2=38,
∴2a2=36,
∴a2=18,
即(x﹣2025)2=18,
故选:B.
6.【解答】解:,
,
,
,
,
,
∴,,
∴a=4,b=2,
∴3a2+4b2+1012a﹣2024b+1
=3×42+4×22+1012×4﹣2024×2+1
=3×16+4×4+4048﹣4048+1
=48+16+1
=65,
故选:A.
二、填空题
7.【解答】解:(2+1)×(22+1)×(24+1)×(28+1)×……×(264+1)
=(2﹣1)(2+1)(22+1)(24+1)(28+1)×……×(264+1)
=(22﹣1)(22+1)(24+1)(28+1)×……×(264+1)
=2128﹣1;
故答案为:2128﹣1.
8.【解答】解:∵x=3y+5,
∴x﹣3y=5,
两边平方,可得x2﹣6xy+9y2=25,
又∵x2﹣7xy+9y2=24,
两式相减,可得xy=1,
∴x2y﹣3xy2=xy(x﹣3y)=1×5=5,
故答案为:5.
9.【解答】解:∵m2﹣9n2=5,
∴(m+3n)(m﹣3n)=5,
又∵m2+6mn+9n2=5﹣m﹣3n,
∴(m+3n)(m+3n+1)=5,
∴m﹣3n=m+3n+1,
解得n,
故答案为:.
10.【解答】解:设BE=a,BC=b,
∴,,a+b=6,
则S1+S2=a2+b2=20,
阴影部分的面积为BE BCab[(a+b)2﹣(a2+b2)][36﹣20]=4,
故答案为:4.
11.【解答】解:∵(2022x+2023)2展开后得到,
∴c1=20232,
∵(2023x﹣2022)2展开后得到,
∴c2=20222,
∴c1﹣c2=20232﹣20222
=(2023+2022)(2023﹣2022)
=4045×1
=4045,
故答案为:4045.
三、解答题
12.【解答】解:(1)由题意得(2x﹣a)(3x+b)
=6x2+(2b﹣3a)x﹣ab
=6x2+11x﹣10,
(2x+a)(x+b)
=2x2+(a+2b)x+ab
=2x2﹣9x+10,
所以2b﹣3a=11,①
a+2b=﹣9.②
由②得2b=﹣9﹣a,代入①得﹣9﹣a﹣3a=11,
所以a=﹣5.
所以2b=﹣4.
所以b=﹣2.
(2)当a=﹣5,b=﹣2时,由(1)得(2x+a)(3x+b)=(2x﹣5)(3x﹣2)=6x2﹣19x+10.
13.【解答】解:(1)根据题意得:
(ax+b)(x2﹣3x+1)
=ax3﹣3ax2+ax+bx2﹣3bx+b
=ax3+(b﹣3a)x2+(a﹣3b)x+b,
∵关于x的一次二项式ax+b与x2﹣3x+1的积不含二次项,一次项的系数是4,
∴,
解得:,
∴系数a的值为,系数b的值为;
(2)由(1)得:系数a的值为,系数b的值为,
∴二项式ax+b与x2﹣3x的积为:
=.
14.【解答】解:(1)(x+4)(x2﹣2ax﹣4b)
=x3﹣2ax2﹣4bx+4x2﹣8ax﹣16b
=x3+(4﹣2a)x2+(﹣4b﹣8a)x﹣16b,
∵(x+4)(x2﹣2ax﹣4b)的展开式中不含x的二次项和一次项,
∴4﹣2a=0,﹣4b﹣8a=0,
∴a=2,b=﹣4,
∴ba=(﹣4)2=16;
(2)由(1)可知a=2,
∴(a+1)(a2+1)(a4+1) (a64+1)+1
=(2+1)(22+1)(24+1)...(264+1)+1,
=(2﹣1)(2+1)(22+1)(24+1)...(264+1)+1
=(22﹣1)(22+1)(24+1)...(264+1)+1
=(24﹣1)(24+1)...(264+1)+1
=(28﹣1)...(264+1)+1
=(264﹣1)(264+1)+1
=2128﹣1+1
=2128.
15.【解答】解:(1)∵a+b=3,ab=﹣1,
∴(a+b)2﹣2ab=a2+b2=32﹣2×(﹣1)=11,
∴(a﹣b)2=a2﹣2ab+b2=11﹣2×(﹣1)=13,
故答案为:13;
(2)设AC=a,BC=CF=b,
由题意得:a2+b2=24,a+b=8,
∴(a+b)2﹣(a2+b2)=2ab,即82﹣24=64﹣24=40,
∴2ab=40,即ab=20,
∴△AFC的面积:;
(3)∵(6﹣x)(x﹣2)=3,
∴设6﹣x=a,x﹣2=b,则a+b=4,
∴(6﹣x)2+(x﹣2)2=a2+b2=(a+b)2﹣2ab=42﹣2×3=16﹣6=10.
16.【解答】解:(1)S△ABD>S△DFG,理由如下:
∵S△ABDAB ADab,
S△DFGDG FG(a﹣b) babb2ab,
∵a>b>0,
∴S△ABD>S△DFG.
(2)如图,延长BC,GF交于I,
S阴影=S ABIG﹣S△ABD﹣S△DFG﹣S△BIF,
∴S阴影=a2ab b (a﹣b) a (a﹣b)a2b2ab;
∴阴影部分的面积用代数式表示为:a2b2ab;
(3)当a+b=10,ab=20时,a2b2ab(a+b)2ab10220=20.
17.【解答】解:(1)∵a﹣b=1,a2+b2=17,(a﹣b)2=a2+b2﹣2ab,
∴12=17﹣2ab,
解得:ab=8;
(2)根据题意可得:
图中阴影部分的面积.
∵a+b=7,
∴(a+b)2=72,
即a2+2ab+b2=49,
∵ab=9,
∴a2+b2+2×9=49,
即a2+b2=31,
∴图中阴影部分的面积=31﹣9=22;
(3)令2025﹣x=m,x﹣2024=n,
则m+n=2025﹣x+x﹣2024=1,
∵(2025﹣x)(x﹣2024)=﹣6,
∴mn=﹣6,
则(2025﹣x)2+(x﹣2024)2=m2+n2=(m+n)2﹣2mn=12﹣2×(﹣6)=13.
故答案为:13.
18.【解答】解:(1)由图示可知:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)由条件可知:
a2+b2+c2
=(a+b+c)2﹣2(ab+ac+bc)
=132﹣2×28
=169﹣56
=113;
(3)大长方形的面积为(a+a+b)(3a+a+b)
=8a2+2ab+4ab+b2
=8a2+6ab+b2,
故阴影部分的面积为:8a2+6ab+b2﹣6a(a+b)
=8a2+6ab+b2﹣6a2﹣6ab
=2a2+b2.
19.【解答】解:(1)S1=(m+7)(m+1)
=m2+m+7m+7
=m2+8m+7;
S2=(m+4)(m+2)
=m2+2m+4m+8
=m2+6m+8;
,
因为m为正整数,
所以2m﹣1>0,
所以S1>S2.
故答案为:>.
(2)因为S1﹣S2=2m﹣1,|S1﹣S2|≤2025,
即|2m﹣1|≤2025,
2m﹣1≤2025,
2m≤2026,
m≤1013.
所以m得最大值是1013.
(3)S3=[(m+4)×3+2m﹣9﹣(m+1)×4]×(m+7)
=(3m+12+2m﹣9﹣4m﹣4)×(m+7)
=(m﹣1)(m+7)
=m2+7m﹣m﹣7
=m2+6m﹣7;
S4=(2m﹣9)(m+2)
=2m2+4m﹣9m﹣18
=2m2﹣5m﹣18;
因为2S3=S4,
所以2×(m2+6m﹣7)=2m2﹣5m﹣18,
即2m2+12m﹣14=2m2﹣5m﹣18,
17m=﹣4,
,
因为m为正整数,
所以m 不存在.
20.【解答】解:(1)根据题意,令(3x+2)(x﹣3)=0,
∴3x+2=0或x﹣3=0,
解得:x=或x=3,
故答案为:或3;
(2)根据题意,把x=2代入B,得B=4+2(a﹣1)﹣3a=0,
解得:a=2,
把a=2代入B,得B=x2+x﹣6=(x﹣2)(x+3),
令x+3=0,
解得:x=﹣3,
∴多项式B的另一个零点是﹣3;
(3)∵M=(2x﹣b)(cx﹣7),
∴M的两个零点分别是或,
根据“3﹣系多项式”的定义,有,
∴bc+14=12c,
∴,
把代入M,
得M=(2x﹣b)(cx﹣7)
=
=,
∵M=ax2﹣(8a﹣4c)x+5b﹣4,
∴,5b﹣4=7b,
解得:b=﹣2,
把b=﹣2代入,
∴.
故答案为:2,﹣2,1.
21.【解答】解:(1)∵关于x的多项式(2m﹣3) x+2m2﹣3m的值与x的取值无关,
∴2m﹣3=0,
解得:m=1.5;
(2)∵3[(2x+1)(x﹣1)﹣x(1﹣3y)]+6(﹣x2+xy﹣1)=(﹣6+15y)x﹣9,
由题意得:﹣6+15y=0,
解得:y=0.4;
(3)设AB=x,由图可知S1=a(x﹣3b),S2=2b(x﹣2a),
∴S1﹣S2=a(x﹣3b)﹣2b(x﹣2a)=(a﹣2b)x+ab,
∵当AB的长变化时,S1﹣S2的值始终保持不变,
∴S1﹣S2取值与x无关,
∴a﹣2b=0,
∴a=2b.
22.【解答】解:(1)根据题意可知,方法1:阴影部分面积是边长为a的正方形面积和边长为b的正方形面积之和,
∴;
方法2:阴影部分面积=边长为(a+b)的正方形面积﹣长为a,宽为b的长方形面积×2,
∴.
又∵两种方式表示的阴影部分面积是相等的:a2+b2=(a+b)2﹣2ab.
故答案为:a2+b2;(a+b)2﹣2ab;a2+b2=(a+b)2﹣2ab;
(2)①设a=2023﹣x,b=x﹣2022,
则a2+b2=9,a+b=2023﹣x+x﹣2022=223﹣2022=1,
根据(1)可知:a2+b2=(a+b)2﹣2ab,即9=12﹣2ab,
∴,
即(2023﹣x)(x﹣2022)=﹣4;
②设AC=x,BC=y,
∵AC+BC=x+y=8,S1+S2=x2+y2=40,
联立方程组可得:,
∴,
∴阴影部分的面积为.
23.【解答】解:(1)∵x+y=3,
∴(x+y)2=32,
∴x2+2xy+y2=9,
即:2xy=9﹣(x2+y2),
又∵x2+y2=5,
∴2xy=9﹣5=4,
∴xy=2;
(2)∵(x﹣3)﹣(x﹣4)=1,
∴[(x﹣3)﹣(x﹣4)]2=1,
∴(x﹣3)2+(x﹣4)2﹣2(x﹣3)(x﹣4)=1,
∴(x﹣3)2+(x﹣4)2=1+2(x﹣3)(x﹣4),
又∵(x﹣3)(x﹣4)=1,
∴(x﹣3)2+(x﹣4)2=1+2×1=3;
(3)设OA=OC=x,OB=OD=y,
∵∠AOB=∠COD=90°,A,O,D在一直线上,
∴S△AOC=OA OC=x2,S△BOD=OB OD=y2,
∵S△AOC+S△BOD=68,
∴x2+y2=68,
∴x2+y2=136,
∵AD=16,
∴x+y=16,
∴(x+y)2=162,
即:x2+y2+2xy=256,
∴2xy=256﹣(x2+y2)=120,
∴xy=60,
∴S△AOB=OA OB=xy=×60=30.
∴一块直角三角板的面积为30.
21世纪教育网(www.21cnjy.com)
第八章整式乘法压轴题练习期中复习苏科版2024—2025学年七年级下册
一、选择题
1.若x﹣m与3x﹣2的乘积中不含x的一次项,则m的值为( )
A. B. C. D.3
2.如图在边长为a的正方形纸片中剪去一个边长为b的小正方形,把余下的部分沿虚线剪开,拼成一个矩形,分别计算这两个图形阴影部分的面积,可以验证的等式是( )
A.a2﹣b2=(a+b)(a﹣b) B.(a﹣b)2=a2﹣2ab+b2
C.(a+b)2=a2+2ab+b2 D.a2+ab=a(a+b)
3.在展开多项式(x2+x﹣3)(x2﹣2x+2a)中,常数项为﹣30,则a等于( )
A.3 B.4 C.5 D.6
4.图1是长为a,宽为b(a>b)的小长方形纸片将6张如图1的纸片按图2的方式不重叠地放在长方形ABCD内,已知CD的长度固定不变,BC的长度可以变化,图中阴影部分(即两个长方形)的面积分别表示为S1,S2,若a=4,b=2,S1﹣S2的值是( )
A.8 B.16 C.12 D.32
5.已知(x﹣2024)2+(x﹣2026)2=38,则(x﹣2025)2的值是( )
A.4 B.18 C.12 D.16
6.已知实数a,b满足,则3a2+4b2+1012a﹣2024b+1的值是( )
A.65 B.105 C.115 D.2025
二、填空题
7.求值:(2+1)×(22+1)×(24+1)×(28+1)×...×(264+1)= .
8.已知11.已知x=3y+5,且x2﹣7xy+9y2=24,则x2y﹣3xy2的值为 .
9.m2﹣9n2=5,m2+6mn+9n2=5﹣m﹣3n,那么n的值为 .
10.如图,点B是线段CG上一点,以BC,BE为边向两边作正方形,面积分别是S1和S2,设CG=6,两个正方形的面积之和S1+S2=20,则阴影部分△BCE的面积为 .
11.小明将(2022x+2023)2展开后得到;小亮将(2023x﹣2022)2展开后得到,若两人计算过程无误,则c1﹣c2的值为 .
三、解答题
12.在一次测试中,甲、乙两同学计算同一道整式乘法:(2x+a)(3x+b),甲由于抄错了第一个多项式中a的符号,得到的结果为6x2+11x﹣10;乙由于漏抄了第二个多项式中x的系数,得到的结果为2x2﹣9x+10.
(1)试求出式子中a,b的值;
(2)请你计算出这道整式乘法的正确结果.
13.已知关于x的一次二项式ax+b与x2﹣3x+1的积不含二次项,一次项的系数是4.求:
(1)系数a与b的值;
(2)二项式ax+b与x2﹣3x的积.
14.若(x+4)(x2﹣2ax﹣4b)的展开式中不含x的二次项和一次项.
(1)求ba的值;
(2)求(a+1)(a2+1)(a4+1) (a64+1)+1的值.
15.完全平方公式经过适当的变形,可以解决很多数学问题.例如:
若a+b=4,ab=2,求a2+b2的值.
解:∵a+b=4,ab=2,
∴(a+b)2=16,2ab=4.
即a2+b2+2ab=16.
∴a2+b2=12.
根据上面的解题思路与方法解决下列问题:
(1)a+b=3,ab=﹣1,则(a﹣b)2的值为 ;
(2)如图,C是线段AB上的一点,分别以AC,BC为边向两边作正方形,AB=8,两正方形面积的和为24,设AC=a,BC=CF=b,求△AFC的面积;
(3)若(6﹣x)(x﹣2)=3,求(6﹣x)2+(x﹣2)2的值.
16.如图,两个形状大小相同的长方形ABCD和长方形AEFG,点E在AB边上,AB=a,BC=b,且a>b>0.
(1)分别连接BD,DF,BF,试比较△ABD与△DFG的面积大小,并说明理由.
(2)用含a,b的代数式表示图中阴影部分的面积.
(3)当a+b=10,ab=20.求图中阴影部分的面积.
17.在数学中,通常可以运用一些公式来解决问题.比如,运用两数和的完全平方公式(a+b)2=a2+2ab+b2,能够在三个代数式a+b,ab,a2+b2中,当已知其中任意两个代数式的值时,求出第三个代数式的值.例如:已知a+b=3,ab=2,求a2+b2的值.
解:将a+b=3两边同时平方,得(a+b)2=32,
即a2+2ab+b2=9,
因为ab=2,
等量代换,得a2+b2+2×2=9,
所以a2+b2=5.
请根据以上信息,解答下列问题.
(1)已知a﹣b=1,a2+b2=17,求ab的值.
(2)如图,已知两个正方形的边长分别为a、b,若a+b=7,ab=9,求图中阴影部分的面积.
(3)若(2025﹣x)(x﹣2024)=﹣6,则(2025﹣x)2+(x﹣2024)2的值为 .
18.当我们利用两种不同的方法计算同一图形的面积时,可以得到一个等式,例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)由图2,可得等式: ;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=13,ab+bc+ac=28,求a2+b2+c2的值;
(3)如图3,一个小长方形的长为a+b,宽为a,把6个大小相同的小长方形放入到大长方形内(如图4).求在大长方形中,阴影部分的面积(用含a、b的式子来表示).
19.甲、乙两个长方形,它们的边长如图1所示,面积分别S1,S2(m为正整数).
(1)写出S1与S2的大小关系:S1 S2.(填“>”“<”或“=”);
(2)若|S1﹣S2|≤2025,求满足这个不等式的m的最大值;
(3)设有4块长方形甲,3块长方形乙,以及两块面积分别为S3,S4的矩形恰好拼成一个矩形图案,如图2所示.问:是否存在m,使得2S3=S4,若存在,请求出m的值;若不存在,请说明理由.
20.小聪学习多项式研究了多项式值为0的问题,发现当mx+n=0或px+q=0时,多项式A=(mx+n)(px+q)=mpx2+(mq+np)x+nq的值为0,把此时x的值称为多项式A的零点.
(1)已知多项式(3x+2)(x﹣3),则此多项式的零点为 .
(2)已知多项式B=(x﹣2)(x+m)=x2+(a﹣1)x﹣3a有一个零点为2,求多项式B的另一个零点;
(3)订正:小聪继续研究(x﹣4)(x﹣2),x(x﹣6)及等,发现在x轴上表示这些多项式零点的两个点关于直线x=3对称,他把这些多项式称为“3﹣系多项式”.若多项式M=(2x﹣b)(cx﹣7c)=ax2﹣(8a﹣4c)x+5b﹣4是“3﹣系多项式”,则a= ,b= ,c= .
21.有这样一类题:代数式ax﹣y+6+3x﹣5y﹣1的值与x的取值无关,求a的值.
通常的解题方法为把x,y看作字母,a看作系数合并同类项,即原式=(a+3)x﹣6y+5,因为代数式的值与x的取值无关,所以含x项的系数为0,即a+3=0,所以a=﹣3.
[理解应用]
(1)若关于x的多项式(2m﹣3) x+2m2﹣3m的值与x的取值无关,求m的值.
(2)已知3[(2x+1)(x﹣1)﹣x(1﹣3y)]+6(﹣x2+xy﹣1)的值与x无关,求y的值.
(3)如图①,小长方形纸片的长为a、宽为b,有7张如图①所示的纸片按照图②中的方式不重叠地放在大长方形ABCD内,大长方形中有两个部分(图中阴影部分)未被覆盖,设右上角的面积为S1,左下角的面积为S2.当AB的长变化时,S1﹣S2的值始终保持不变,求a与b的等量关系.
22.如图1,将边长(a+b)的正方形剪出两个边长分别为a,b的正方形(阴影部分),观察图形,解答下列问题:
(1)用两种不同的方法表示图一阴影部分的面积,即用两个不同的代数式表示阴影部分的面积.
方法1: ,方法2: ;从中你发现什么结论呢? ;
(2)运用你发现的结论,解决下列问题:
①已知(2023﹣x)2+(x﹣2022)2=9,求(2023﹣x)(x﹣2022)的值;
②如图2,C是线段AB上一点,以AC,BC为边向两边作正方形,AC+BC=8,两个正方形的面积和S1+S2=40,求图中阴影部分的面积.
23.【知识生成】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.
例如图1可以得到(a+b)2=a2+2ab+b2,基于此,请解答下列问题:
【直接应用】(1)若x+y=3,x2+y2=5,求xy的值;
【类比应用】(2)若(x﹣3)(x﹣4)=1,求(x﹣3)2+(x﹣4)2的值;
【知识迁移】(3)两块全等的特制直角三角板(∠AOB=∠COD=90°)如图2所示放置,其中A,O,D在一直线上,连接AC,BD,若AD=16,S△AOC+S△BOD=68,求一块直角三角板的面积.
参考答案
一、选择题
1.【解答】解:(x﹣m)(3x﹣2)
=3x2﹣2x﹣3mx+2m
=3x2﹣(2+3m)x+2m,
由题意得,﹣(2+3m)=0,
解得m,
故选:A.
2.【解答】解:∵图中阴影部分的面积=a2﹣b2,图中阴影部分的面积=(a+b)(a﹣b),
而两个图形中阴影部分的面积相等,
∴阴影部分的面积=a2﹣b2=(a+b)(a﹣b).
故选:A.
3.【解答】解:观察式子(x2+x﹣3)(x2﹣2x+2a)中常数项为﹣3×2a=﹣6a,
∵常数项为﹣30,
∴﹣6a=﹣30,
∴a=5;
故选:C.
4.【解答】解:设EF=x,
S1=(4b+x) 2b=(8+x)×4=32+4x,
S2=(a+x) a=(4+x)×4=16+4x,
∴S1﹣S2=(32+4x)﹣(16+4x)=32+4x﹣16﹣4x=16.
故选:B.
5.【解答】解:设x﹣2025=a,
∵(x﹣2024)2+(x﹣2026)2=38,
∴(x﹣2025+1)2+(x﹣2025﹣1)2=38,
∴(a+1)2+(a﹣1)2=38,
∴a2+2a+1+a2﹣2a+1=38,
∴2a2+2=38,
∴2a2=36,
∴a2=18,
即(x﹣2025)2=18,
故选:B.
6.【解答】解:,
,
,
,
,
,
∴,,
∴a=4,b=2,
∴3a2+4b2+1012a﹣2024b+1
=3×42+4×22+1012×4﹣2024×2+1
=3×16+4×4+4048﹣4048+1
=48+16+1
=65,
故选:A.
二、填空题
7.【解答】解:(2+1)×(22+1)×(24+1)×(28+1)×……×(264+1)
=(2﹣1)(2+1)(22+1)(24+1)(28+1)×……×(264+1)
=(22﹣1)(22+1)(24+1)(28+1)×……×(264+1)
=2128﹣1;
故答案为:2128﹣1.
8.【解答】解:∵x=3y+5,
∴x﹣3y=5,
两边平方,可得x2﹣6xy+9y2=25,
又∵x2﹣7xy+9y2=24,
两式相减,可得xy=1,
∴x2y﹣3xy2=xy(x﹣3y)=1×5=5,
故答案为:5.
9.【解答】解:∵m2﹣9n2=5,
∴(m+3n)(m﹣3n)=5,
又∵m2+6mn+9n2=5﹣m﹣3n,
∴(m+3n)(m+3n+1)=5,
∴m﹣3n=m+3n+1,
解得n,
故答案为:.
10.【解答】解:设BE=a,BC=b,
∴,,a+b=6,
则S1+S2=a2+b2=20,
阴影部分的面积为BE BCab[(a+b)2﹣(a2+b2)][36﹣20]=4,
故答案为:4.
11.【解答】解:∵(2022x+2023)2展开后得到,
∴c1=20232,
∵(2023x﹣2022)2展开后得到,
∴c2=20222,
∴c1﹣c2=20232﹣20222
=(2023+2022)(2023﹣2022)
=4045×1
=4045,
故答案为:4045.
三、解答题
12.【解答】解:(1)由题意得(2x﹣a)(3x+b)
=6x2+(2b﹣3a)x﹣ab
=6x2+11x﹣10,
(2x+a)(x+b)
=2x2+(a+2b)x+ab
=2x2﹣9x+10,
所以2b﹣3a=11,①
a+2b=﹣9.②
由②得2b=﹣9﹣a,代入①得﹣9﹣a﹣3a=11,
所以a=﹣5.
所以2b=﹣4.
所以b=﹣2.
(2)当a=﹣5,b=﹣2时,由(1)得(2x+a)(3x+b)=(2x﹣5)(3x﹣2)=6x2﹣19x+10.
13.【解答】解:(1)根据题意得:
(ax+b)(x2﹣3x+1)
=ax3﹣3ax2+ax+bx2﹣3bx+b
=ax3+(b﹣3a)x2+(a﹣3b)x+b,
∵关于x的一次二项式ax+b与x2﹣3x+1的积不含二次项,一次项的系数是4,
∴,
解得:,
∴系数a的值为,系数b的值为;
(2)由(1)得:系数a的值为,系数b的值为,
∴二项式ax+b与x2﹣3x的积为:
=.
14.【解答】解:(1)(x+4)(x2﹣2ax﹣4b)
=x3﹣2ax2﹣4bx+4x2﹣8ax﹣16b
=x3+(4﹣2a)x2+(﹣4b﹣8a)x﹣16b,
∵(x+4)(x2﹣2ax﹣4b)的展开式中不含x的二次项和一次项,
∴4﹣2a=0,﹣4b﹣8a=0,
∴a=2,b=﹣4,
∴ba=(﹣4)2=16;
(2)由(1)可知a=2,
∴(a+1)(a2+1)(a4+1) (a64+1)+1
=(2+1)(22+1)(24+1)...(264+1)+1,
=(2﹣1)(2+1)(22+1)(24+1)...(264+1)+1
=(22﹣1)(22+1)(24+1)...(264+1)+1
=(24﹣1)(24+1)...(264+1)+1
=(28﹣1)...(264+1)+1
=(264﹣1)(264+1)+1
=2128﹣1+1
=2128.
15.【解答】解:(1)∵a+b=3,ab=﹣1,
∴(a+b)2﹣2ab=a2+b2=32﹣2×(﹣1)=11,
∴(a﹣b)2=a2﹣2ab+b2=11﹣2×(﹣1)=13,
故答案为:13;
(2)设AC=a,BC=CF=b,
由题意得:a2+b2=24,a+b=8,
∴(a+b)2﹣(a2+b2)=2ab,即82﹣24=64﹣24=40,
∴2ab=40,即ab=20,
∴△AFC的面积:;
(3)∵(6﹣x)(x﹣2)=3,
∴设6﹣x=a,x﹣2=b,则a+b=4,
∴(6﹣x)2+(x﹣2)2=a2+b2=(a+b)2﹣2ab=42﹣2×3=16﹣6=10.
16.【解答】解:(1)S△ABD>S△DFG,理由如下:
∵S△ABDAB ADab,
S△DFGDG FG(a﹣b) babb2ab,
∵a>b>0,
∴S△ABD>S△DFG.
(2)如图,延长BC,GF交于I,
S阴影=S ABIG﹣S△ABD﹣S△DFG﹣S△BIF,
∴S阴影=a2ab b (a﹣b) a (a﹣b)a2b2ab;
∴阴影部分的面积用代数式表示为:a2b2ab;
(3)当a+b=10,ab=20时,a2b2ab(a+b)2ab10220=20.
17.【解答】解:(1)∵a﹣b=1,a2+b2=17,(a﹣b)2=a2+b2﹣2ab,
∴12=17﹣2ab,
解得:ab=8;
(2)根据题意可得:
图中阴影部分的面积.
∵a+b=7,
∴(a+b)2=72,
即a2+2ab+b2=49,
∵ab=9,
∴a2+b2+2×9=49,
即a2+b2=31,
∴图中阴影部分的面积=31﹣9=22;
(3)令2025﹣x=m,x﹣2024=n,
则m+n=2025﹣x+x﹣2024=1,
∵(2025﹣x)(x﹣2024)=﹣6,
∴mn=﹣6,
则(2025﹣x)2+(x﹣2024)2=m2+n2=(m+n)2﹣2mn=12﹣2×(﹣6)=13.
故答案为:13.
18.【解答】解:(1)由图示可知:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)由条件可知:
a2+b2+c2
=(a+b+c)2﹣2(ab+ac+bc)
=132﹣2×28
=169﹣56
=113;
(3)大长方形的面积为(a+a+b)(3a+a+b)
=8a2+2ab+4ab+b2
=8a2+6ab+b2,
故阴影部分的面积为:8a2+6ab+b2﹣6a(a+b)
=8a2+6ab+b2﹣6a2﹣6ab
=2a2+b2.
19.【解答】解:(1)S1=(m+7)(m+1)
=m2+m+7m+7
=m2+8m+7;
S2=(m+4)(m+2)
=m2+2m+4m+8
=m2+6m+8;
,
因为m为正整数,
所以2m﹣1>0,
所以S1>S2.
故答案为:>.
(2)因为S1﹣S2=2m﹣1,|S1﹣S2|≤2025,
即|2m﹣1|≤2025,
2m﹣1≤2025,
2m≤2026,
m≤1013.
所以m得最大值是1013.
(3)S3=[(m+4)×3+2m﹣9﹣(m+1)×4]×(m+7)
=(3m+12+2m﹣9﹣4m﹣4)×(m+7)
=(m﹣1)(m+7)
=m2+7m﹣m﹣7
=m2+6m﹣7;
S4=(2m﹣9)(m+2)
=2m2+4m﹣9m﹣18
=2m2﹣5m﹣18;
因为2S3=S4,
所以2×(m2+6m﹣7)=2m2﹣5m﹣18,
即2m2+12m﹣14=2m2﹣5m﹣18,
17m=﹣4,
,
因为m为正整数,
所以m 不存在.
20.【解答】解:(1)根据题意,令(3x+2)(x﹣3)=0,
∴3x+2=0或x﹣3=0,
解得:x=或x=3,
故答案为:或3;
(2)根据题意,把x=2代入B,得B=4+2(a﹣1)﹣3a=0,
解得:a=2,
把a=2代入B,得B=x2+x﹣6=(x﹣2)(x+3),
令x+3=0,
解得:x=﹣3,
∴多项式B的另一个零点是﹣3;
(3)∵M=(2x﹣b)(cx﹣7),
∴M的两个零点分别是或,
根据“3﹣系多项式”的定义,有,
∴bc+14=12c,
∴,
把代入M,
得M=(2x﹣b)(cx﹣7)
=
=,
∵M=ax2﹣(8a﹣4c)x+5b﹣4,
∴,5b﹣4=7b,
解得:b=﹣2,
把b=﹣2代入,
∴.
故答案为:2,﹣2,1.
21.【解答】解:(1)∵关于x的多项式(2m﹣3) x+2m2﹣3m的值与x的取值无关,
∴2m﹣3=0,
解得:m=1.5;
(2)∵3[(2x+1)(x﹣1)﹣x(1﹣3y)]+6(﹣x2+xy﹣1)=(﹣6+15y)x﹣9,
由题意得:﹣6+15y=0,
解得:y=0.4;
(3)设AB=x,由图可知S1=a(x﹣3b),S2=2b(x﹣2a),
∴S1﹣S2=a(x﹣3b)﹣2b(x﹣2a)=(a﹣2b)x+ab,
∵当AB的长变化时,S1﹣S2的值始终保持不变,
∴S1﹣S2取值与x无关,
∴a﹣2b=0,
∴a=2b.
22.【解答】解:(1)根据题意可知,方法1:阴影部分面积是边长为a的正方形面积和边长为b的正方形面积之和,
∴;
方法2:阴影部分面积=边长为(a+b)的正方形面积﹣长为a,宽为b的长方形面积×2,
∴.
又∵两种方式表示的阴影部分面积是相等的:a2+b2=(a+b)2﹣2ab.
故答案为:a2+b2;(a+b)2﹣2ab;a2+b2=(a+b)2﹣2ab;
(2)①设a=2023﹣x,b=x﹣2022,
则a2+b2=9,a+b=2023﹣x+x﹣2022=223﹣2022=1,
根据(1)可知:a2+b2=(a+b)2﹣2ab,即9=12﹣2ab,
∴,
即(2023﹣x)(x﹣2022)=﹣4;
②设AC=x,BC=y,
∵AC+BC=x+y=8,S1+S2=x2+y2=40,
联立方程组可得:,
∴,
∴阴影部分的面积为.
23.【解答】解:(1)∵x+y=3,
∴(x+y)2=32,
∴x2+2xy+y2=9,
即:2xy=9﹣(x2+y2),
又∵x2+y2=5,
∴2xy=9﹣5=4,
∴xy=2;
(2)∵(x﹣3)﹣(x﹣4)=1,
∴[(x﹣3)﹣(x﹣4)]2=1,
∴(x﹣3)2+(x﹣4)2﹣2(x﹣3)(x﹣4)=1,
∴(x﹣3)2+(x﹣4)2=1+2(x﹣3)(x﹣4),
又∵(x﹣3)(x﹣4)=1,
∴(x﹣3)2+(x﹣4)2=1+2×1=3;
(3)设OA=OC=x,OB=OD=y,
∵∠AOB=∠COD=90°,A,O,D在一直线上,
∴S△AOC=OA OC=x2,S△BOD=OB OD=y2,
∵S△AOC+S△BOD=68,
∴x2+y2=68,
∴x2+y2=136,
∵AD=16,
∴x+y=16,
∴(x+y)2=162,
即:x2+y2+2xy=256,
∴2xy=256﹣(x2+y2)=120,
∴xy=60,
∴S△AOB=OA OB=xy=×60=30.
∴一块直角三角板的面积为30.
21世纪教育网(www.21cnjy.com)
同课章节目录
