第八章整式的乘法期中复习（含答案）

中小学教育资源及组卷应用平台
第八章整式的乘法期中复习苏科版2024—2025学年七年级下册
一、选择题
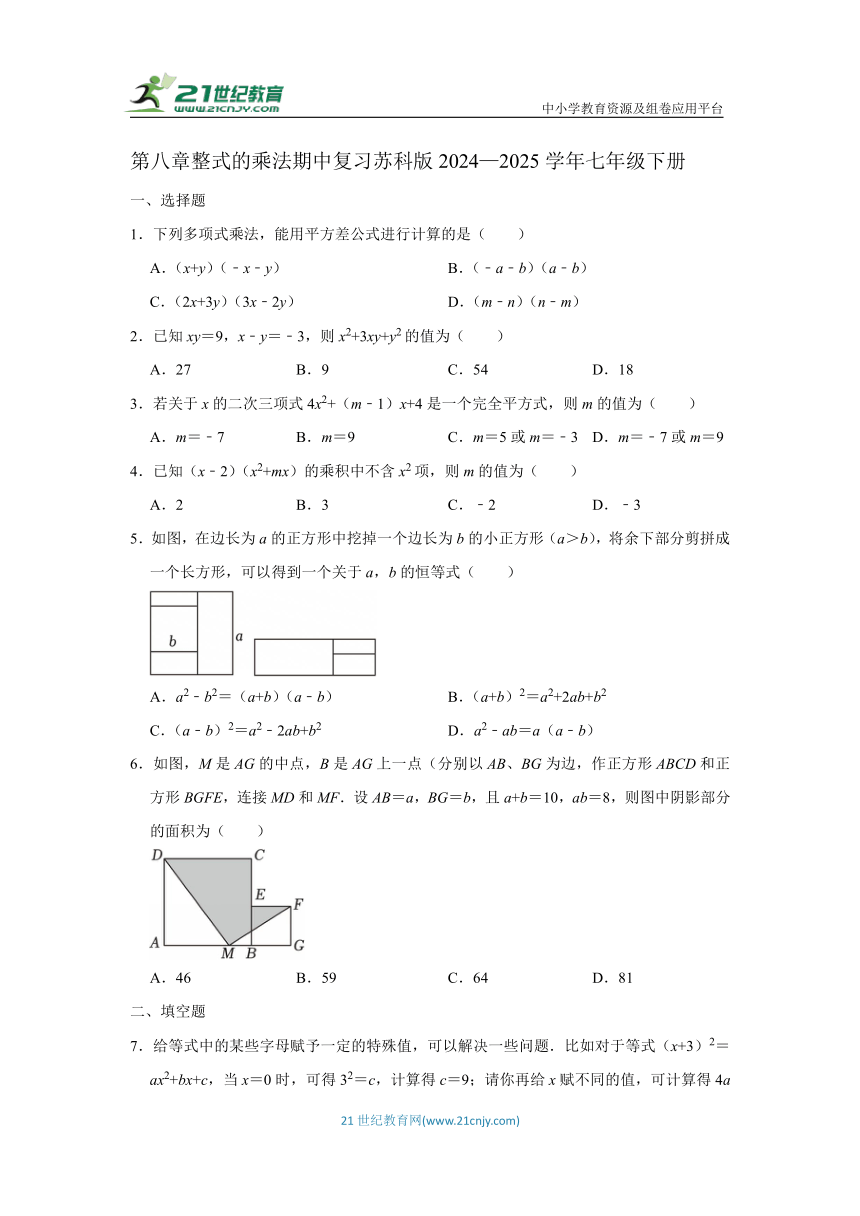
1．下列多项式乘法，能用平方差公式进行计算的是（　　）
A．（x+y）（﹣x﹣y） B．（﹣a﹣b）（a﹣b）
C．（2x+3y）（3x﹣2y） D．（m﹣n）（n﹣m）
2．已知xy＝9，x﹣y＝﹣3，则x2+3xy+y2的值为（　　）
A．27 B．9 C．54 D．18
3．若关于x的二次三项式4x2+（m﹣1）x+4是一个完全平方式，则m的值为（　　）
A．m＝﹣7 B．m＝9 C．m＝5或m＝﹣3 D．m＝﹣7或m＝9
4．已知（x﹣2）（x2+mx）的乘积中不含x2项，则m的值为（　　）
A．2 B．3 C．﹣2 D．﹣3
5．如图，在边长为a的正方形中挖掉一个边长为b的小正方形（a＞b），将余下部分剪拼成一个长方形，可以得到一个关于a，b的恒等式（　　）
A．a2﹣b2＝（a+b）（a﹣b） B．（a+b）2＝a2+2ab+b2
C．（a﹣b）2＝a2﹣2ab+b2 D．a2﹣ab＝a（a﹣b）
6．如图，M是AG的中点，B是AG上一点（分别以AB、BG为边，作正方形ABCD和正方形BGFE，连接MD和MF．设AB＝a，BG＝b，且a+b＝10，ab＝8，则图中阴影部分的面积为（　　）
A．46 B．59 C．64 D．81
二、填空题
7．给等式中的某些字母赋予一定的特殊值，可以解决一些问题．比如对于等式（x+3）2＝ax2+bx+c，当x＝0时，可得32＝c，计算得c＝9；请你再给x赋不同的值，可计算得4a﹣2b＝ 　 　 ．
8．若a＝2025×2024﹣1，b＝20252﹣2025×2024+20242，则a　 　 b．（请用“＞”“＜”或“＝”表示）
9．已知，则ab+bc+ca的值等于 　 ．
10．现有A，B，C三种不同的矩形纸片若干张（边长如图所示）．若要拼成一个长为3a+2b，宽为2a+b的矩形，则需要A种纸片和C种纸片合计　 　 张．
11．已知有甲、乙两个长方形，它们的边长如图所示（m为正整数），甲、乙的面积分别为S1，S2．若满足条件|S1﹣S2|＜n≤2023的整数n有且只有4个，则m的值为 　 　 ．
三、解答题
12．如图，某学校有一块长为（5a+b）m，宽为（2a+b）m的长方形土地，计划在阴影部分的区域进行绿化，中间修建一个边长为（a+b）m的正方形喷水池．
（1）用含a，b的代数式表示绿化面积；
（2）当a＝1，b＝2时，求绿化面积．
13．完全平方公式：（a±b）2＝a2±2ab+b2经过适当变形后可解决很多的数学问题．
例如：若a+b＝3，ab＝1，求a2+b2的值．
解：∵a+b＝3，ab＝1，∴（a+b）2＝a2+2ab+b2＝9，2ab＝2，
∴a2+b2＝（a+b）2﹣2ab＝7．
【探究】（1）若m﹣n＝7，m2+n2＝29，求mn的值；
【延伸】（2）若x（5﹣x）＝1，求x2+（5﹣x）2的值；
【应用】（3）如图，点C在线段AB上，以AC，BC为边向两边作正方形，若AB＝8，两正方形的面积之和，求阴影部分的面积．
14．计算：
（1）（﹣2ab）（3a2﹣2ab﹣4b2）；
（2）（2x﹣1）（x﹣4）﹣（x+3）（x+2）．
15．关于x的代数式（ax﹣3）（2x+1）﹣4x2+m化简后不含有x2项和常数项．
（1）求a和m的值．
（2）若an+mn＝﹣5，求代数式﹣4n2+3m的值．
16．在计算（2x+a）（x+b）时，甲错把b看成了6，得到的结果是2x2+8x﹣24，乙错把a看成了﹣a，得到的结果是2x2+14x+20．
（1）求a、b的值；
（2）求（2x+a）（x+b）的正确结果．
17．通过第1章的学习，我们已经知道，对于一个图形（a+b）2＝a2+2ab+b2；如图2可以得到：（a﹣b）2＝a2﹣2ab+b2；现有长与宽分别为a、b的小长方形若干个，用四个相同的小长方形拼成图3的图形，请认真观察图形．
（1）【探索发现】根据图中条件，猜想并验证（a+b）2与（a﹣b）2之间的关系（用含a、b的代数式表示出来）；图3表示：　 　 ；
（2）【解决问题】①若x+y＝8，x2+y2＝40，则xy＝ 　 　 ；
②当（x﹣300）（200﹣x）＝1996时，求（2x﹣500）2的值；
（3）【拓展提升】如图4，点C是线段AB上的一点，以AC，BC为边向两边作正方形ACDE和BCFG，延长GB和ED交于点H，那么四边形DCBH为长方形，设AB＝10，图中阴影部分面积为42，求两个正方形的面积和S1+S2．
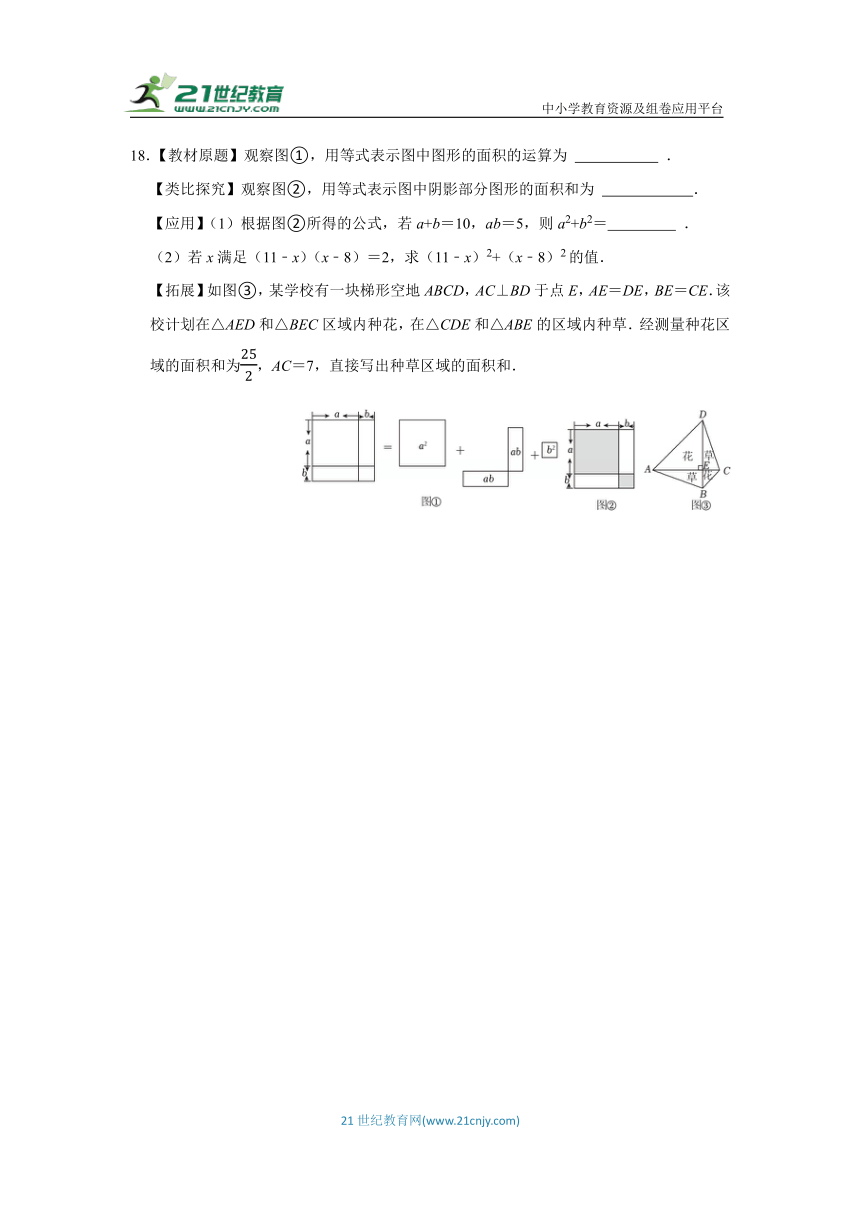
18．【教材原题】观察图①，用等式表示图中图形的面积的运算为 　 ．
【类比探究】观察图②，用等式表示图中阴影部分图形的面积和为 　 ．
【应用】（1）根据图②所得的公式，若a+b＝10，ab＝5，则a2+b2＝　 　 ．
（2）若x满足（11﹣x）（x﹣8）＝2，求（11﹣x）2+（x﹣8）2的值．
【拓展】如图③，某学校有一块梯形空地ABCD，AC⊥BD于点E，AE＝DE，BE＝CE．该校计划在△AED和△BEC区域内种花，在△CDE和△ABE的区域内种草．经测量种花区域的面积和为，AC＝7，直接写出种草区域的面积和．
参考答案
一、选择题
1．【解答】解：根据平方差公式逐项分析判断如下：
A、（x+y）（﹣x﹣y）＝﹣（x+y）（x+y），不符合题意；
B、（﹣a﹣b）（a﹣b）＝﹣（a+b）（a﹣b）＝﹣a2+b2，符合题意；
C、（2x+3y）（3x﹣2y），不符合题意；
D、（m﹣n）（n﹣m）＝﹣（m﹣n）（m﹣n），不符合题意；
故选：B．
2．【解答】解：∵x﹣y＝﹣3，
∴（x﹣y）2＝9，
即x2﹣2xy+y2＝9，
∴x2+3xy+y2＝x2﹣2xy+y2+5xy＝9+45＝54．
故选：C．
3．【解答】解：∵关于x的二次三项式4x2+（m﹣1）x+4是一个完全平方式，
∴m﹣1＝±2×2×2，
解得：m＝9或m＝﹣7．
故选：D．
4．【解答】解：（x﹣2）（x2+mx）
＝x3+mx2﹣2x2﹣2mx
＝x3+（m﹣2）x2﹣2mx，
∵乘积中不含x2项，
∴m﹣2＝0，
∴m＝2．
故选：A．
5．【解答】解：挖掉小正方形后的面积＝a2﹣b2，
新的长方形的面积＝（a+b）（a﹣b），
则a2﹣b2＝（a+b）（a﹣b）．
故选：A．
6．【解答】解：由题知，
∵a+b＝10，且点M是AG的中点，
∴AM＝GM＝5，
∴，
∴．
∵a+b＝10，ab＝8，
∴a2+b2＝（a+b）2﹣2ab＝100﹣16＝84，
∴．
故选：B．
二、填空题
7．【解答】解：当x＝﹣2时，（﹣2+3）2＝4a﹣2b+9，
整理得：1＝4a﹣2b+9，
则4a﹣2b＝﹣8．
故答案为：﹣8．
8．【解答】解：b＝20252﹣2025×2024+20242
＝20252﹣2×2025×2024+20242+2025×2024
＝（2025﹣2024）2+2025×2024
＝1+2025×2024，
∵1+2025×2024＞2025×2024﹣1，
∴a＜b，
故答案为：＜．
9．【解答】解：根据题意，由a﹣b＝b﹣c可得：a﹣c，
由a2+b2+c2＝1可得2（a2+b2+c2）＝2，
再利用完全平方公式可得：2（a2+b2+c2）＝（a﹣b）2+（b﹣c）2+（a﹣c）2+2（ab+bc+ca），
将a2+b2+c2＝1，a﹣b＝b﹣c，a﹣c代入可得：
2×1＝（）2+（）2+（）2+2（ab+bc+ca），
解得ab+bc+ca．
10．【解答】解：（3a+2b）（2a+b）
＝6a2+3ab+4ab+2b2
＝6a2+7ab+2b2，
则6+7＝13（张），
即需要A种纸片和C种纸片合计13张，
故答案为：13．
11．【解答】解：∵，
，
∴S1﹣S2＝2m﹣1，
∵满足条件|S1﹣S2|＜n≤2023的整数n有且只有4个，
∴n可取正整数为2023，2022，2021，2020，
∴2019≤|S1﹣S2|＜2020，
即2019≤|2m﹣1|＜2020，
∵m为正整数，
∴2m﹣1＞0
∴2019≤2m﹣1＜2020，
解得：1010≤m＜1010.5，
∴m＝1010，
故答案为：1010．
三、解答题
12．【解答】解：（1）S草坪＝S长方形一S正方形＝（5a+b）（2a+b）﹣（a+b）2＝10a2+5ab+2ab+b2﹣a2﹣2ab﹣b2＝9a2+5ab，
∴绿化面积为（9a2+5ab）平方米；
（2）当a＝1，b＝2时，
S草坪＝9a2+5ab＝9+10＝19（平方米），
答：绿化面积为19平方米．
13．【解答】解：（1）∵m﹣n＝7，m2+n2＝29，
∴2mn＝（m2+n2）﹣（m﹣n）2＝29﹣72＝29﹣49＝﹣20，
∴mn＝﹣10；
（2）∵x（5﹣x）＝1，
∴x2+（5﹣x）2＝[x+（5﹣x）]2﹣2x（5﹣x）＝23；
（3）AC＝m，BC＝n，
∵AB＝8，
∴m+n＝8，
∵，
∴，
由完全平方公式可得，2mn＝（m+n）2﹣（m2+n2），
∴，
解得：，
∴阴影部分的面积．
14．【解答】解：（1）（﹣2ab）（3a2﹣2ab﹣4b2）
＝﹣6a3b+4a2b2+8ab3；
（2）（2x﹣1）（x﹣4）﹣（x+3）（x+2）
＝2x2﹣8x﹣x+4﹣（x2+5x+6）
＝2x2﹣9x+4﹣x2﹣5x﹣6
＝x2﹣14x﹣2．
15．【解答】解：（1）（ax﹣3）（2x+1）﹣4x2+m
＝2ax2+ax﹣6x﹣3﹣4x2+m
＝（2a﹣4）x2+（a﹣6）x+m﹣3，
∵化简后不含x2项和常数项，
∴2a﹣4＝0，m﹣3＝0，
解得：a＝2，m＝3；
（2）把a＝2，m＝3代入an+mn＝﹣5，
∴2n+3n＝﹣5，
∴n＝﹣1，
∴﹣4n2+3m＝﹣4×（﹣1）2+3×3＝﹣4+9＝5．
16．【解答】解：（1）∵甲错把b看成了6，
∴（2x+a）（x+6）＝2x2+（12+a）x+6a，
又（2x+a）（x+6）＝2x2+8x﹣24，
∴6a＝﹣24，
∴a＝﹣4．
∵乙错把a看成了﹣a，
∴（2x﹣a）（x+b）＝2x2+（2b﹣a）x﹣ab，
又（2x﹣a）（x+b）＝2x2+14x+20，
∴2b﹣a＝14，
∵a＝﹣4，
∴b＝5．
故a＝﹣4，b＝5．
（2）由（1）得：（2x+a）（x+b）＝（2x﹣4）（x+5）＝2x2+6x﹣20．
17．【解答】解：（1）如图3所示：大正方形的边长为（a+b），小正方形的边长为（a﹣b），
∴大正方形的面积为（a+b）2，小正方形的面积为（a﹣b）2，
另一方面：大正方形是由4个长为a，宽为b的长方形和一个边长为（a﹣b）的小正方形构成，
∴（a+b）2＝（a﹣b）2+4ab，
故答案为：（a+b）2＝（a﹣b）2+4ab；
（2）①（x+y）2＝x2+2xy+y2，
∴2xy＝（x+y）2﹣（x2+y2），
∵x+y＝8，x2+y2＝40，
∴2xy＝82﹣40＝24，
∵xy＝12，
故答案为：12；
②设x﹣300＝a，200﹣x＝b，
∴a+b＝x﹣300+200﹣x＝﹣100，a﹣b＝x﹣300﹣（200﹣x）＝2x﹣500，
∴（x﹣300）（200﹣x）＝1996，
∴ab＝1996，
由（1）可知（a+b）2＝（a﹣b）2+4ab，
∴（a﹣b）2＝（a+b）2﹣4ab＝（﹣100）2﹣4×1996＝2016，
∴（2x﹣500）2＝2016；
（3）设AC＝a，BC＝b，
∵AB＝10，
∴a+b＝10，
∵图中阴影部分面积为42，
∴ab＝42，
∵四边形ACDE和BCFG均为正方形，
∴，
∵（a+b）2＝a2+2ab+b2，
∴a2+b2＝（a+b）2﹣2ab＝102﹣2×42＝16，
∴S1+S2＝16．
18．【解答】解：【教材原题】：观察图①可得，（a+b）2＝a2+2ab+b2，
故答案为：（a+b）2＝a2+2ab+b2；
【类比探究】：观察图②可得，图中阴影部分图形的面积和＝a2+b2，
a2+b2＝（a+b）2﹣2ab，
故答案为：a2+b2＝（a+b）2﹣2ab；
【应用】：（1）a2+b2＝（a+b）2﹣2ab＝100﹣10＝90，
故答案为：90；
（2）（11﹣x）2+（x﹣8）2＝[（11﹣x）+（x﹣8）]2﹣2（11﹣x）（x﹣8）＝9﹣4＝5，
∴（11﹣x）2+（x﹣8）2的值是5；
【拓展】：∵AC⊥BD，AE＝DE，BE＝CE，
∴S△ADEAE2，S△BECCE2，
∵种花区域的面积和为，
∴AE2+CE2＝25，
∵AC＝7，
∴AE CE＝12，
∴AE BE＝DE CE＝12，
∴种草区域的面积和（AE BE+DE CE）＝12．
21世纪教育网(www.21cnjy.com)