第二章相交线与平行线章节期中复习(含答案)
文档属性
| 名称 | 第二章相交线与平行线章节期中复习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 353.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 06:44:26 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第二章相交线与平行线章节期中复习北师大版2024—2025学年七年级下册
一、选择题
1.下列说法错误的是( )
A.在同一平面内,若直线a⊥b,b⊥c,则直线a∥c
B.直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
C.相等的两个角一定是对顶角
D.在同一平面内不相交的两条直线是平行线
2.如图,如果∠1=∠2,那么AB∥CD,其依据可以简单说成( )
A.两直线平行,内错角相等
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.同位角相等,两直线平行
3.如图,不能判断l1∥l2的条件是( )
A.∠1=∠3 B.∠4=∠5
C.∠2=∠3 D.∠2+∠4=180°
4.如图,直线a∥b,将直角三角板的直角顶点放在直线b上,已知∠1=55°,则∠2的度数为( )
A.35° B.45° C.55° D.125°
5.如图,直线AB∥CD,点E是平行线外一点,连接AE,CE,若∠A=32°,∠C=60°,则∠E的度数是( )
A.22° B.24° C.26° D.28°
6.如图,AB∥CD,∠PAB=130°,∠PCD=120°,则∠APC的度数为( )
A.140° B.130° C.120° D.110°
7.如图,直线a∥b,CD⊥AB于点D,若∠1=130°,则∠2等于( )
A.60° B.50° C.40° D.30°
二、填空题
8.如图,下列条件中:①∠B+∠BAD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,其中能判定AB∥CD的条件有 (填写序号).
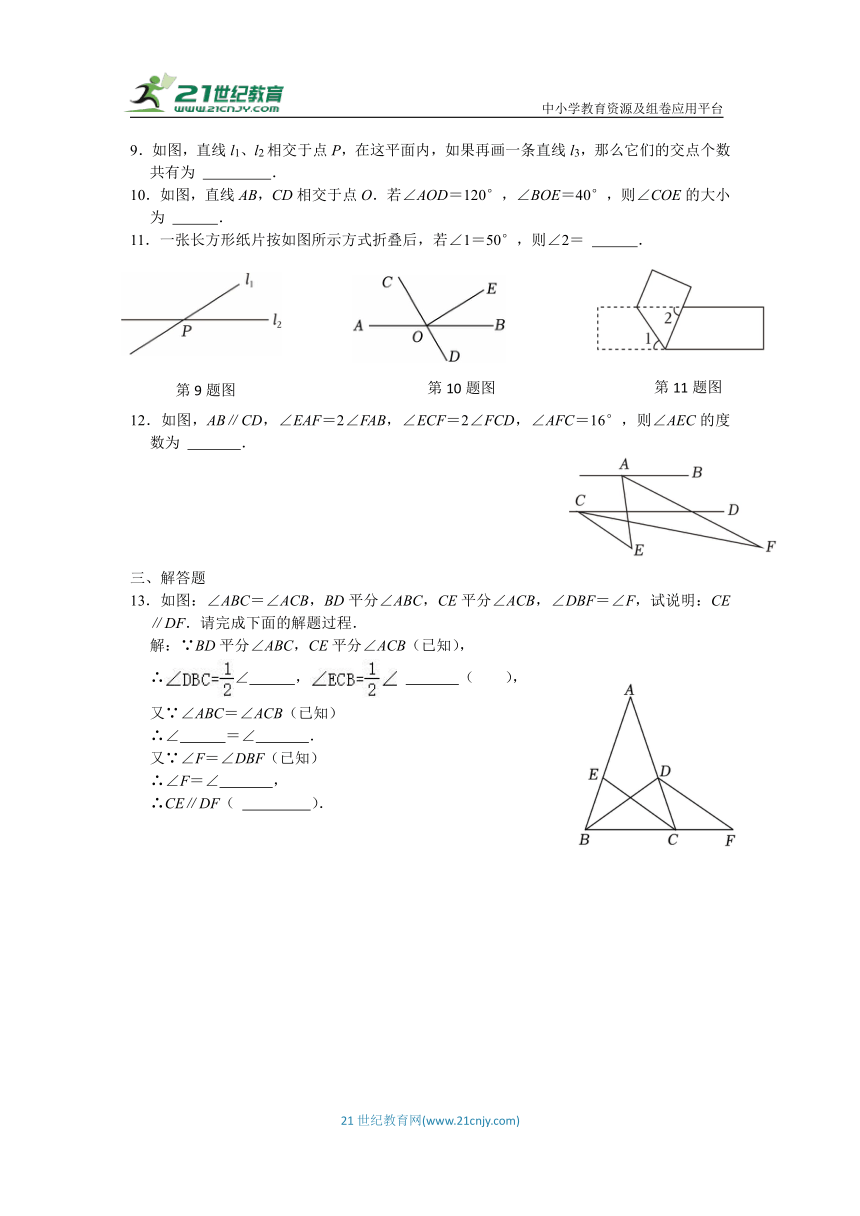
9.如图,直线l1、l2相交于点P,在这平面内,如果再画一条直线l3,那么它们的交点个数共有为 .
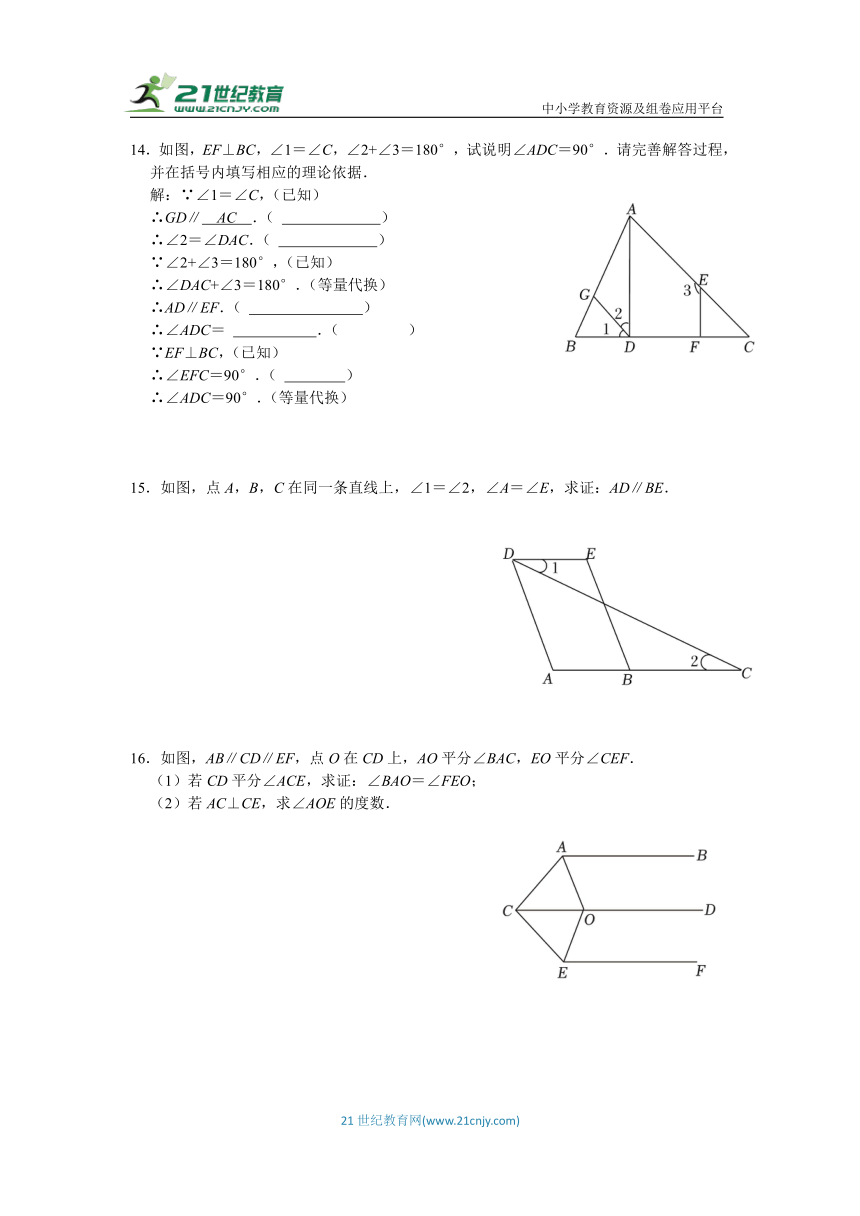
10.如图,直线AB,CD相交于点O.若∠AOD=120°,∠BOE=40°,则∠COE的大小为 .
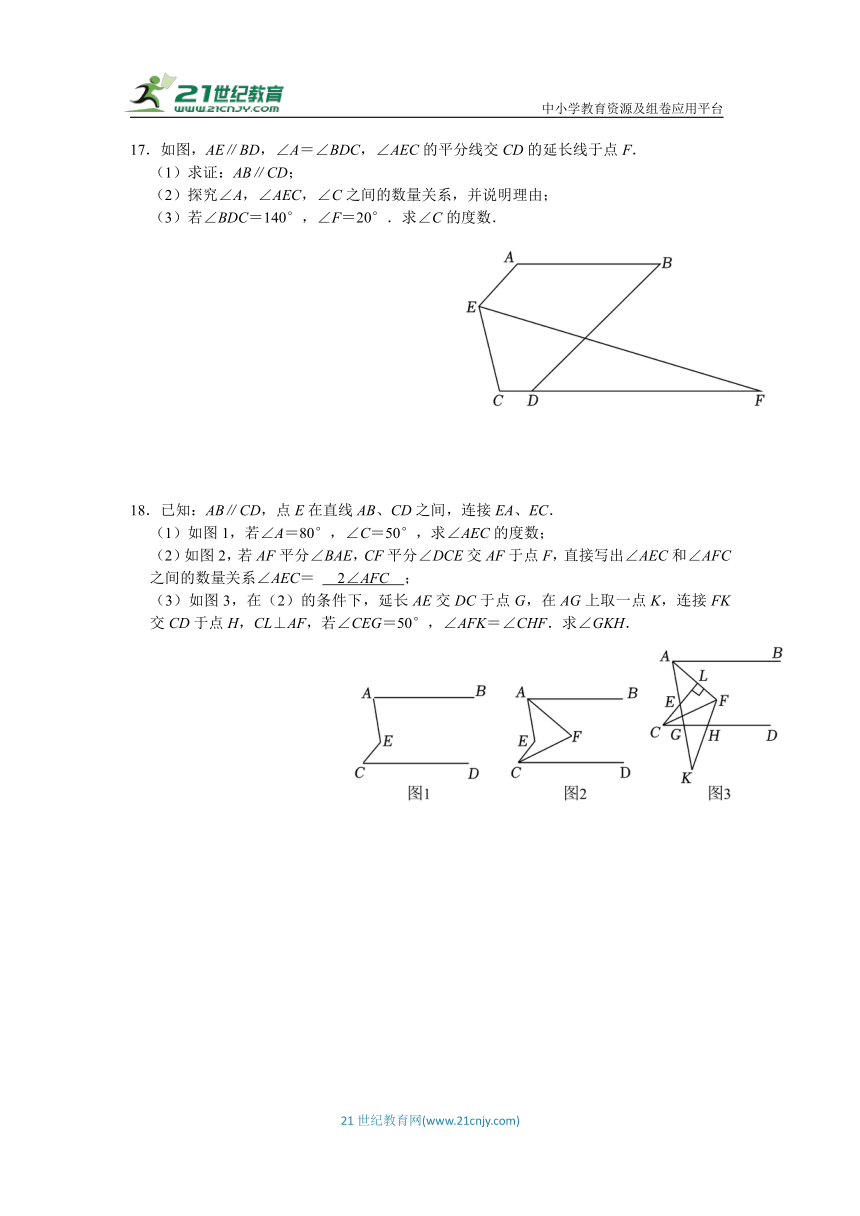
11.一张长方形纸片按如图所示方式折叠后,若∠1=50°,则∠2= .
12.如图,AB∥CD,∠EAF=2∠FAB,∠ECF=2∠FCD,∠AFC=16°,则∠AEC的度数为 .
三、解答题
13.如图:∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,试说明:CE∥DF.请完成下面的解题过程.
解:∵BD平分∠ABC,CE平分∠ACB(已知),
∴∠ , ( ),
又∵∠ABC=∠ACB(已知)
∴∠ =∠ .
又∵∠F=∠DBF(已知)
∴∠F=∠ ,
∴CE∥DF( ).
14.如图,EF⊥BC,∠1=∠C,∠2+∠3=180°,试说明∠ADC=90°.请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠1=∠C,(已知)
∴GD∥ AC .( )
∴∠2=∠DAC.( )
∵∠2+∠3=180°,(已知)
∴∠DAC+∠3=180°.(等量代换)
∴AD∥EF.( )
∴∠ADC= .( )
∵EF⊥BC,(已知)
∴∠EFC=90°.( )
∴∠ADC=90°.(等量代换)
15.如图,点A,B,C在同一条直线上,∠1=∠2,∠A=∠E,求证:AD∥BE.
16.如图,AB∥CD∥EF,点O在CD上,AO平分∠BAC,EO平分∠CEF.
(1)若CD平分∠ACE,求证:∠BAO=∠FEO;
(2)若AC⊥CE,求∠AOE的度数.
17.如图,AE∥BD,∠A=∠BDC,∠AEC的平分线交CD的延长线于点F.
(1)求证:AB∥CD;
(2)探究∠A,∠AEC,∠C之间的数量关系,并说明理由;
(3)若∠BDC=140°,∠F=20°.求∠C的度数.
18.已知:AB∥CD,点E在直线AB、CD之间,连接EA、EC.
(1)如图1,若∠A=80°,∠C=50°,求∠AEC的度数;
(2)如图2,若AF平分∠BAE,CF平分∠DCE交AF于点F,直接写出∠AEC和∠AFC之间的数量关系∠AEC= 2∠AFC ;
(3)如图3,在(2)的条件下,延长AE交DC于点G,在AG上取一点K,连接FK交CD于点H,CL⊥AF,若∠CEG=50°,∠AFK=∠CHF.求∠GKH.
参考答案
一、选择题
1.【解答】解:A、在同一平面内,若直线a⊥b,b⊥c,则直线a∥c,故A不符合题意;
B、直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,故B不符合题意;
C、相等的两个角不一定是对顶角,故C符合题意;
D、在同一平面内不相交的两条直线是平行线,故D不符合题意;
故选:C.
2.【解答】解:∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行),
故选:D.
3.【解答】解:A、∵∠1=∠3,
∴l1∥l2,故此选项不合题意;
B、∵∠4=∠5,
∴l1∥l2,故此选项不合题意;
C、∠2=∠3,无法得出l1∥l2,故此选项符合题意;
D、∵∠2+∠4=180°,
∴l1∥l2,故此选项不合题意;
故选:C.
4.【解答】解:如图:
∵a∥b,
∴∠1=∠3=55°,
∵∠BAC=90°,
∴∠2=180°﹣∠3﹣∠BAC=35°,
故选:A.
5.【解答】解:如图,∵直线AB∥CD,
∴∠1=∠C=60°,
∵∠A=32°,
∴∠E=∠1﹣∠A=28°.
故选:D.
6.【解答】解:过P点作PE∥AB,
∴∠PAB+∠APE=180°,
∵∠PAB=130°,
∴∠APE=180°﹣130°=50°,
∵AB∥CD,
∴PE∥CD,
∴∠PCD+∠CPE=180°,
∵∠PCD=120°,
∴∠CPE=180°﹣120°=60°,
∴∠APC=∠APE+∠CPE=50°+60°=110°,
故选:D.
7.【解答】解:∵a∥b,
∴∠ABC+∠1=180°,
∵∠1=130°,
∴∠ABC=50°,
∵CD⊥AB,
∴∠BDC=90°,
∴∠ABC+∠2=90°,
∴∠2=40°,
故选:C.
二、填空题
8.【解答】解:∵∠B+∠BAD=180°,
∴AD∥BC,故①不符合题意;
∵∠1=∠2,
∴AD∥BC,故②不符合题意;
∵∠3=∠4,
∴AB∥CD,故③符合题意;
∵∠B=∠5,
∴AB∥CD,故④符合题意;
故答案为:③④.
9.【解答】解:当l3平行于l1或l2时,交点的个数为2个;
当l3与l1和l2都不平行,交于P点时,交点的个数为1个;不交于同一点时,交点的个数为3个.
故答案为:1个或2个或3个.
10.【解答】解:∵直线AB,CD相交于点O,∠AOD=120°,
∴∠BOC=∠AOD=120°,
∵∠BOE=40°,
∴∠COE=∠BOC﹣∠BOE=80°,
故答案为:80°.
11..【解答】解:如图:
由折叠的性质可得∠3=∠1=50°,
∴∠4=180°﹣2×50°=80°,
∵长方形的对边平行,
∴∠2=∠4=80°.
故答案为:80°.
12.【解答】解:如图:∵AB∥CD,
∴∠FAB=∠AMC,
∵∠AMC是△MCF的外角,
∴∠AMC=∠F+∠FCD,
∴∠FAB=∠F+∠FCD,
∵∠FAE+∠F+∠ANF=180°,∠E+∠FCE+∠CNE=180°,
∠ANF=∠CNE,
∴∠FAE+∠F=∠E+∠FCE,
∵∠EAF=2∠FAB,∠ECF=2∠FCD,
∴2∠FAB+∠F=∠E+2∠FCD,
∴2(∠F+∠FCD)+∠F=∠E+2∠FCD,
∴2∠F+2∠FCD+∠F=∠E+2∠FCD,
∴∠E=3∠F,
∵∠F=16°,
∴∠E=48°,
故答案为:48°.
三、解答题
13.【解答】解:∵BD平分∠ABC,CE平分∠ACB ( 已知 ),
∴∠DBC=∠ABC,∠ECB=∠ACB( 角平分线的定义).
又∵∠ABC=∠ACB (已知),
∴∠DBC=∠ECB,
又∵∠DBF=∠F(已知),
∴∠F=∠ECB(等量代换),
∴CE∥DF(同位角相等,两直线平行).
故答案为:ABC;ACB;DBC;ECB;ECB;同位角相等,两直线平行.
14.【解答】解:∵∠1=∠C,(已知)
∴GD∥AC.(同位角相等,两直线平行)
∴∠2=∠DAC.(两直线平行,内错角相等)
∵∠2+∠3=180°,(已知)
∴∠DAC+∠3=180°.(等量代换)
∴AD∥EF.(同旁内角互补,两直线平行)
∴∠ADC=∠EFC.(两直线平行,同位角相等)
∵EF⊥BC,(已知)
∴∠EFC=90°.(垂直的定义)
∴∠ADC=90°.(等量代换)
故答案为:AC;同位角相等,两直线平行;两直线平行,内错角相等;同旁内角互补,两直线平行;∠EFC;垂直的定义.
15.【解答】证明:∵∠1=∠2,
∴DE∥AC,
∴∠E+∠ABE=180°,
∵∠A=∠E,
∴∠A+∠ABE=180°,
∴AD∥BE.
16.【解答】(1)证明:∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵CD∥EF,
∴∠DCE+∠CEF=180°,
∵CD平分∠ACE,
∴∠ACD=∠DCE,
∴∠BAC=∠CEF,
∵AO平分∠BAC,EO平分∠CEF,
∴∠BAO=∠BAC,∠FEO=∠CEF,
∴∠BAO=∠FEO;
(2)解:∵AC⊥CE,
∴∠ACE=90°,
∴∠ACD+∠DCE=90°,
由(1)可得:∠BAC+∠ACD=180°,∠DCE+∠CEF=180°,
∴∠BAC+∠CEF=360°﹣(∠ACD+∠DCE)=270°,
∵∠BAO=∠BAC,∠FEO=∠CEF,
∴∠BAO+∠FEO=∠BAC+∠CEF=135°,
∵AB∥CD,
∴∠BAO=∠AOC,
∵CD∥EF,
∴∠COE=∠FEO,
∴∠AOE=∠AOC+∠COE
=∠BAO+∠FEO
=135°,
∴∠AOE的度数为135°.
17.【解答】(1)证明:∵AE∥BD,
∴∠A+∠ABD=180°,
∵∠A=∠BDC,
∴∠BDC+∠ABD=180°,
∴AB∥CD;
(2)解:∠A+∠AEC+∠C=360°,理由:
如图,过点E作EH∥AB,
由(1)知AB∥CD,
∴EH∥CD,
∴∠A+∠AEH=180°,∠C+∠CEH=180°,
∴∠A+∠AEH+∠C+∠CEH=360°,
即∠A+∠AEC+∠C=360°;
(3)解:∵∠AEC 的平分线交CD的延长线于点F,
∴,
在△CEF中,∠F+∠CEF+∠C=180°,
∵∠F=20°,
∴①,
∵∠A=∠BDC,∠BDC=140°,
∴∠A=140°,
∵∠A+∠AEC+∠C=360°,
∴∠AEC+∠C=220°②,
②﹣①得,∠AEC=120°,
∴∠C=100°.
18.【解答】解:(1)如图,过点E作EG∥AB,
∴∠GEA=∠A,∠GEC=∠C,
∵∠A=80°,∠C=50°,
∴∠GEA=80°,∠GEC=50°,
∴∠AEC=∠GEA+∠GEC=130°;
(2)过点E作EG∥AB,
∴∠GEA=∠BAE,∠GEC=∠ECD,
∴∠AEC=∠GEA+∠GEC=∠BAE+∠DCE,
同理∠F=∠FAB+∠FCD,
由题意可得:
,,
∴,
∴∠AEC=2∠AFC,
故答案为:∠AFC;
(3)∵∠CEG=50°,
∴∠AEC=130°,
∵,
又CL⊥AF,
∴∠CLF=90°,
∴∠LCF=25°,
∴设∠CFK=α,∠K=β,∠BAF=∠EAF=x,∠ECF=∠FCD=y,则∠AFK=∠CHF=65°+α,
根据三角形的内角和为180度可得:
∠FCH+∠CFH+∠CHF=180°,
∴x+α+α+65°=180°,
∴x+2α=115°,
由(2)知:∠AFC=∠BAF+∠FCD,
∴x+y=65°,
∵∠AOF=∠OFK+∠K,
∴α+β=25°+50°=75°,
∴α+β+x+y=140°,
∵∠AFK=∠CHF,
∴∠FAK+∠K=∠FCH+∠CFH,即α+x=β+y,
∴α+x=70°,
把α+x=70°代入x+2α=115°,得70°+α=115°,
∴α=45°,
∴∠K=β=30°.
21世纪教育网(www.21cnjy.com)
第二章相交线与平行线章节期中复习北师大版2024—2025学年七年级下册
一、选择题
1.下列说法错误的是( )
A.在同一平面内,若直线a⊥b,b⊥c,则直线a∥c
B.直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
C.相等的两个角一定是对顶角
D.在同一平面内不相交的两条直线是平行线
2.如图,如果∠1=∠2,那么AB∥CD,其依据可以简单说成( )
A.两直线平行,内错角相等
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.同位角相等,两直线平行
3.如图,不能判断l1∥l2的条件是( )
A.∠1=∠3 B.∠4=∠5
C.∠2=∠3 D.∠2+∠4=180°
4.如图,直线a∥b,将直角三角板的直角顶点放在直线b上,已知∠1=55°,则∠2的度数为( )
A.35° B.45° C.55° D.125°
5.如图,直线AB∥CD,点E是平行线外一点,连接AE,CE,若∠A=32°,∠C=60°,则∠E的度数是( )
A.22° B.24° C.26° D.28°
6.如图,AB∥CD,∠PAB=130°,∠PCD=120°,则∠APC的度数为( )
A.140° B.130° C.120° D.110°
7.如图,直线a∥b,CD⊥AB于点D,若∠1=130°,则∠2等于( )
A.60° B.50° C.40° D.30°
二、填空题
8.如图,下列条件中:①∠B+∠BAD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,其中能判定AB∥CD的条件有 (填写序号).
9.如图,直线l1、l2相交于点P,在这平面内,如果再画一条直线l3,那么它们的交点个数共有为 .
10.如图,直线AB,CD相交于点O.若∠AOD=120°,∠BOE=40°,则∠COE的大小为 .
11.一张长方形纸片按如图所示方式折叠后,若∠1=50°,则∠2= .
12.如图,AB∥CD,∠EAF=2∠FAB,∠ECF=2∠FCD,∠AFC=16°,则∠AEC的度数为 .
三、解答题
13.如图:∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,试说明:CE∥DF.请完成下面的解题过程.
解:∵BD平分∠ABC,CE平分∠ACB(已知),
∴∠ , ( ),
又∵∠ABC=∠ACB(已知)
∴∠ =∠ .
又∵∠F=∠DBF(已知)
∴∠F=∠ ,
∴CE∥DF( ).
14.如图,EF⊥BC,∠1=∠C,∠2+∠3=180°,试说明∠ADC=90°.请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠1=∠C,(已知)
∴GD∥ AC .( )
∴∠2=∠DAC.( )
∵∠2+∠3=180°,(已知)
∴∠DAC+∠3=180°.(等量代换)
∴AD∥EF.( )
∴∠ADC= .( )
∵EF⊥BC,(已知)
∴∠EFC=90°.( )
∴∠ADC=90°.(等量代换)
15.如图,点A,B,C在同一条直线上,∠1=∠2,∠A=∠E,求证:AD∥BE.
16.如图,AB∥CD∥EF,点O在CD上,AO平分∠BAC,EO平分∠CEF.
(1)若CD平分∠ACE,求证:∠BAO=∠FEO;
(2)若AC⊥CE,求∠AOE的度数.
17.如图,AE∥BD,∠A=∠BDC,∠AEC的平分线交CD的延长线于点F.
(1)求证:AB∥CD;
(2)探究∠A,∠AEC,∠C之间的数量关系,并说明理由;
(3)若∠BDC=140°,∠F=20°.求∠C的度数.
18.已知:AB∥CD,点E在直线AB、CD之间,连接EA、EC.
(1)如图1,若∠A=80°,∠C=50°,求∠AEC的度数;
(2)如图2,若AF平分∠BAE,CF平分∠DCE交AF于点F,直接写出∠AEC和∠AFC之间的数量关系∠AEC= 2∠AFC ;
(3)如图3,在(2)的条件下,延长AE交DC于点G,在AG上取一点K,连接FK交CD于点H,CL⊥AF,若∠CEG=50°,∠AFK=∠CHF.求∠GKH.
参考答案
一、选择题
1.【解答】解:A、在同一平面内,若直线a⊥b,b⊥c,则直线a∥c,故A不符合题意;
B、直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,故B不符合题意;
C、相等的两个角不一定是对顶角,故C符合题意;
D、在同一平面内不相交的两条直线是平行线,故D不符合题意;
故选:C.
2.【解答】解:∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行),
故选:D.
3.【解答】解:A、∵∠1=∠3,
∴l1∥l2,故此选项不合题意;
B、∵∠4=∠5,
∴l1∥l2,故此选项不合题意;
C、∠2=∠3,无法得出l1∥l2,故此选项符合题意;
D、∵∠2+∠4=180°,
∴l1∥l2,故此选项不合题意;
故选:C.
4.【解答】解:如图:
∵a∥b,
∴∠1=∠3=55°,
∵∠BAC=90°,
∴∠2=180°﹣∠3﹣∠BAC=35°,
故选:A.
5.【解答】解:如图,∵直线AB∥CD,
∴∠1=∠C=60°,
∵∠A=32°,
∴∠E=∠1﹣∠A=28°.
故选:D.
6.【解答】解:过P点作PE∥AB,
∴∠PAB+∠APE=180°,
∵∠PAB=130°,
∴∠APE=180°﹣130°=50°,
∵AB∥CD,
∴PE∥CD,
∴∠PCD+∠CPE=180°,
∵∠PCD=120°,
∴∠CPE=180°﹣120°=60°,
∴∠APC=∠APE+∠CPE=50°+60°=110°,
故选:D.
7.【解答】解:∵a∥b,
∴∠ABC+∠1=180°,
∵∠1=130°,
∴∠ABC=50°,
∵CD⊥AB,
∴∠BDC=90°,
∴∠ABC+∠2=90°,
∴∠2=40°,
故选:C.
二、填空题
8.【解答】解:∵∠B+∠BAD=180°,
∴AD∥BC,故①不符合题意;
∵∠1=∠2,
∴AD∥BC,故②不符合题意;
∵∠3=∠4,
∴AB∥CD,故③符合题意;
∵∠B=∠5,
∴AB∥CD,故④符合题意;
故答案为:③④.
9.【解答】解:当l3平行于l1或l2时,交点的个数为2个;
当l3与l1和l2都不平行,交于P点时,交点的个数为1个;不交于同一点时,交点的个数为3个.
故答案为:1个或2个或3个.
10.【解答】解:∵直线AB,CD相交于点O,∠AOD=120°,
∴∠BOC=∠AOD=120°,
∵∠BOE=40°,
∴∠COE=∠BOC﹣∠BOE=80°,
故答案为:80°.
11..【解答】解:如图:
由折叠的性质可得∠3=∠1=50°,
∴∠4=180°﹣2×50°=80°,
∵长方形的对边平行,
∴∠2=∠4=80°.
故答案为:80°.
12.【解答】解:如图:∵AB∥CD,
∴∠FAB=∠AMC,
∵∠AMC是△MCF的外角,
∴∠AMC=∠F+∠FCD,
∴∠FAB=∠F+∠FCD,
∵∠FAE+∠F+∠ANF=180°,∠E+∠FCE+∠CNE=180°,
∠ANF=∠CNE,
∴∠FAE+∠F=∠E+∠FCE,
∵∠EAF=2∠FAB,∠ECF=2∠FCD,
∴2∠FAB+∠F=∠E+2∠FCD,
∴2(∠F+∠FCD)+∠F=∠E+2∠FCD,
∴2∠F+2∠FCD+∠F=∠E+2∠FCD,
∴∠E=3∠F,
∵∠F=16°,
∴∠E=48°,
故答案为:48°.
三、解答题
13.【解答】解:∵BD平分∠ABC,CE平分∠ACB ( 已知 ),
∴∠DBC=∠ABC,∠ECB=∠ACB( 角平分线的定义).
又∵∠ABC=∠ACB (已知),
∴∠DBC=∠ECB,
又∵∠DBF=∠F(已知),
∴∠F=∠ECB(等量代换),
∴CE∥DF(同位角相等,两直线平行).
故答案为:ABC;ACB;DBC;ECB;ECB;同位角相等,两直线平行.
14.【解答】解:∵∠1=∠C,(已知)
∴GD∥AC.(同位角相等,两直线平行)
∴∠2=∠DAC.(两直线平行,内错角相等)
∵∠2+∠3=180°,(已知)
∴∠DAC+∠3=180°.(等量代换)
∴AD∥EF.(同旁内角互补,两直线平行)
∴∠ADC=∠EFC.(两直线平行,同位角相等)
∵EF⊥BC,(已知)
∴∠EFC=90°.(垂直的定义)
∴∠ADC=90°.(等量代换)
故答案为:AC;同位角相等,两直线平行;两直线平行,内错角相等;同旁内角互补,两直线平行;∠EFC;垂直的定义.
15.【解答】证明:∵∠1=∠2,
∴DE∥AC,
∴∠E+∠ABE=180°,
∵∠A=∠E,
∴∠A+∠ABE=180°,
∴AD∥BE.
16.【解答】(1)证明:∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵CD∥EF,
∴∠DCE+∠CEF=180°,
∵CD平分∠ACE,
∴∠ACD=∠DCE,
∴∠BAC=∠CEF,
∵AO平分∠BAC,EO平分∠CEF,
∴∠BAO=∠BAC,∠FEO=∠CEF,
∴∠BAO=∠FEO;
(2)解:∵AC⊥CE,
∴∠ACE=90°,
∴∠ACD+∠DCE=90°,
由(1)可得:∠BAC+∠ACD=180°,∠DCE+∠CEF=180°,
∴∠BAC+∠CEF=360°﹣(∠ACD+∠DCE)=270°,
∵∠BAO=∠BAC,∠FEO=∠CEF,
∴∠BAO+∠FEO=∠BAC+∠CEF=135°,
∵AB∥CD,
∴∠BAO=∠AOC,
∵CD∥EF,
∴∠COE=∠FEO,
∴∠AOE=∠AOC+∠COE
=∠BAO+∠FEO
=135°,
∴∠AOE的度数为135°.
17.【解答】(1)证明:∵AE∥BD,
∴∠A+∠ABD=180°,
∵∠A=∠BDC,
∴∠BDC+∠ABD=180°,
∴AB∥CD;
(2)解:∠A+∠AEC+∠C=360°,理由:
如图,过点E作EH∥AB,
由(1)知AB∥CD,
∴EH∥CD,
∴∠A+∠AEH=180°,∠C+∠CEH=180°,
∴∠A+∠AEH+∠C+∠CEH=360°,
即∠A+∠AEC+∠C=360°;
(3)解:∵∠AEC 的平分线交CD的延长线于点F,
∴,
在△CEF中,∠F+∠CEF+∠C=180°,
∵∠F=20°,
∴①,
∵∠A=∠BDC,∠BDC=140°,
∴∠A=140°,
∵∠A+∠AEC+∠C=360°,
∴∠AEC+∠C=220°②,
②﹣①得,∠AEC=120°,
∴∠C=100°.
18.【解答】解:(1)如图,过点E作EG∥AB,
∴∠GEA=∠A,∠GEC=∠C,
∵∠A=80°,∠C=50°,
∴∠GEA=80°,∠GEC=50°,
∴∠AEC=∠GEA+∠GEC=130°;
(2)过点E作EG∥AB,
∴∠GEA=∠BAE,∠GEC=∠ECD,
∴∠AEC=∠GEA+∠GEC=∠BAE+∠DCE,
同理∠F=∠FAB+∠FCD,
由题意可得:
,,
∴,
∴∠AEC=2∠AFC,
故答案为:∠AFC;
(3)∵∠CEG=50°,
∴∠AEC=130°,
∵,
又CL⊥AF,
∴∠CLF=90°,
∴∠LCF=25°,
∴设∠CFK=α,∠K=β,∠BAF=∠EAF=x,∠ECF=∠FCD=y,则∠AFK=∠CHF=65°+α,
根据三角形的内角和为180度可得:
∠FCH+∠CFH+∠CHF=180°,
∴x+α+α+65°=180°,
∴x+2α=115°,
由(2)知:∠AFC=∠BAF+∠FCD,
∴x+y=65°,
∵∠AOF=∠OFK+∠K,
∴α+β=25°+50°=75°,
∴α+β+x+y=140°,
∵∠AFK=∠CHF,
∴∠FAK+∠K=∠FCH+∠CFH,即α+x=β+y,
∴α+x=70°,
把α+x=70°代入x+2α=115°,得70°+α=115°,
∴α=45°,
∴∠K=β=30°.
21世纪教育网(www.21cnjy.com)
同课章节目录
