5.1.2复数的几何意义 教学课件(共20张PPT)高中数学北师大版(2019)必修第二册
文档属性
| 名称 | 5.1.2复数的几何意义 教学课件(共20张PPT)高中数学北师大版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 37.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 09:55:05 | ||
图片预览






文档简介
5.1.2复数的几何意义
北师大版(2019)必修第二册
第五章 复数
学习目标
掌握复数的复平面,实轴,虚轴,模,共轭复数的概念
02
理解用复平面内的点或以原点为起点的向量来表示复数及它们之间的一一对应关系
01
掌握用向量的模来表示复数的模的方法
03
问题提出
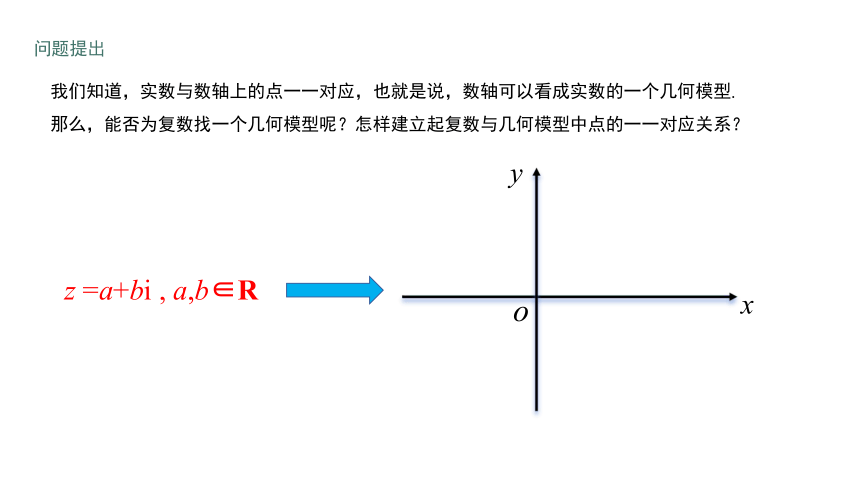
我们知道,实数与数轴上的点一一对应,也就是说,数轴可以看成实数的一个几何模型.
那么,能否为复数找一个几何模型呢?怎样建立起复数与几何模型中点的一一对应关系?
y
x
o
z =a+bi , a,b∈R
分析理解
我们知道,实数与数轴上的点一一对应,也就是说,数轴可以看成实数的一个几何模型。那么,能否为复数找一个几何模型呢?怎样建立起复数与几何模型中点的一一对应关系?
任何一个复数 z= a+bi(a,b∈R),都可以由一个有序数对 (a,b) 唯一确定.
因为有序数对于平面直角坐标系中的点一一对应,所以复数集与平面直角坐标系中的点集是一一对应的.
(3,2)
一一对应
点A
一一对应
复数Z=a+bi
(a,b)
一一对应
点Z(a,b)
一一对应
复平面
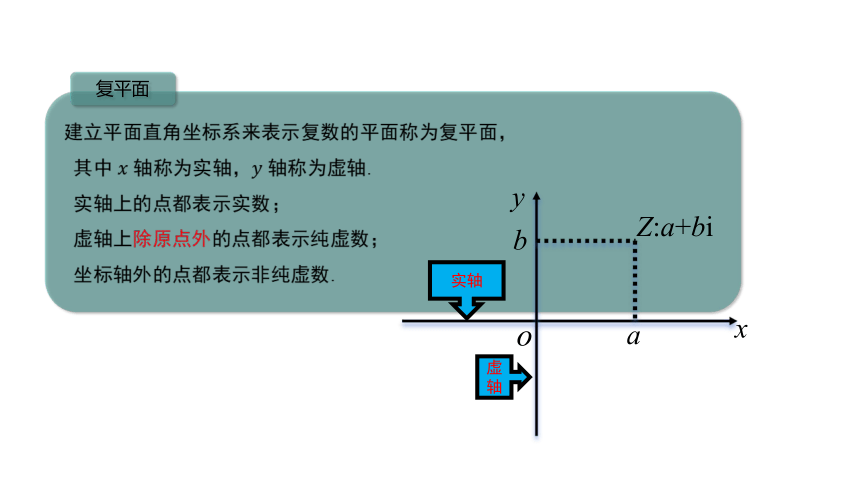
建立平面直角坐标系来表示复数的平面称为复平面,
其中 ???? 轴称为实轴,???? 轴称为虚轴.
实轴上的点都表示实数;
虚轴上除原点外的点都表示纯虚数;
坐标轴外的点都表示非纯虚数.
?
y
x
o
a
b
Z:a+bi
虚轴
实轴
复数的几何意义
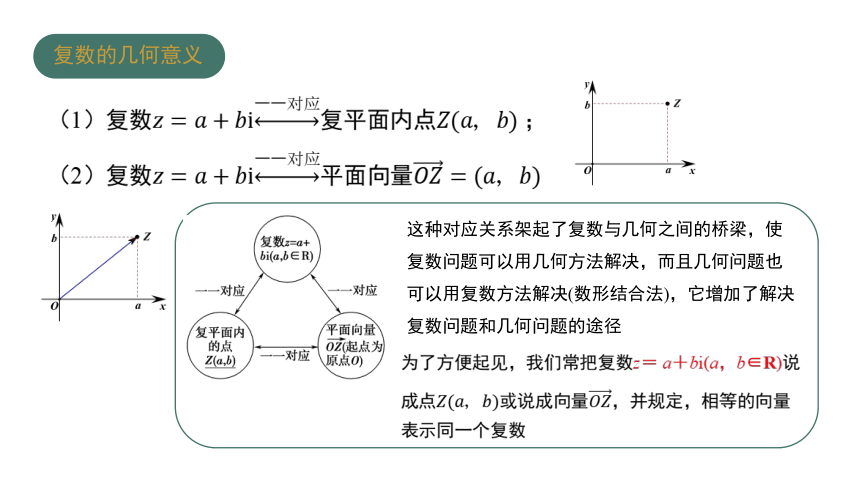
(1)复数????=????+????i一一对应复平面内点????(????,????)?;
?
(2)复数????=????+????i一一对应平面向量????????=(????,????)
?
这种对应关系架起了复数与几何之间的桥梁,使复数问题可以用几何方法解决,而且几何问题也可以用复数方法解决(数形结合法),它增加了解决复数问题和几何问题的途径
为了方便起见,我们常把复数z= a+bi(a,b∈R)说成点????(????,????)或说成向量????????,并规定,相等的向量表示同一个复数
?
复数的模
向量????????的模称为复数 z=a+bi(a,b∈R) 的模,记作|z|或|a+bi|. 由向量模的定义可知,|z|=|a+bi|=????2+????2.
如果b=0,那么 z=a+bi是一个实数a,它的模等于|z|=|a|(a的绝对值).
?
(1)虽然两个复数一般不能比较大小,但它们的模是非负实数,可以比较大小.
知识剖析
(2)复数 z=a+bi(a,b∈R) 的模 |z| 表示的是复平面内对应的点 ????(????,????) 到原点的距离,它是实数的绝对值概念的扩充,因此有 |z|≥0,并且绝对值具有的某些性质可以推广到复数的模
?
例3 在复平面内,表示下列复数的点 Z 的集合是什么图形:
(1)|z|=2 ;(2)2≤|z|≤3
解:(1)复数 z 的模等于2表明,向量????????的模等于2,即点 Z 到原点 O 的距离等于2,因此满足条件 |z|=2 的点 Z 的集合是以原点 O 为圆心,以 2 为半径的圆,如图.
?
(2)不等式2≤|z|≤3可以转化为不等式组|????|≤3|????|≥2.
满足|z|≤3 的点 Z 的集合是以原点 O 为圆心,以3为半径的圆及其内部所有的点构成的集合;满足|z|≥2的点 Z 的集合是以原点 O 为圆心,以2为半径的圆及其外部所有的点构成的集合.因此,满足2≤|z|≤3的点的集合是这两个集合的交集,即以原点 O 为圆心,以 2 和 3 为半径的两圆所夹的圆环,并包括圆环的边界
?
共轭复数
(1)定义:若两个复数的实部相等,而虚部互为相反数,则称这两个复数互为共轭复数,复数 z 的共轭复数用表示 ????.当z=a+bi(a,b∈R)时,????=a-bi.
?
(2)几何意义:在复平面内,表示两个共轭复数的点关于实轴对称,并且它们的模相等.另外,当复数z=a+bi的虚部 b=0 时,有 z=????.也就是说,任意一个实数的共轭复数仍是它本身,反之亦然.
?
例4 在复平面内作出表示下列复数的点,并分别求出它们的模和共轭复数:
(1)????1=3??2i;(2)????2=?1+3i.
?
解:在复平面内作图如图.
(1)????1=3?2i=32+(?2)2=13
????1=3+2i
?
(2)????2=?1+3i=(?2)2+(3)2=2
????2=?1?3i
?
当堂检测
A
ABC
????????
?
????????????????,????∪????,+∞
?
感谢您的聆听与指导
General template of fresh teaching
北师大版(2019)必修第二册
第五章 复数
学习目标
掌握复数的复平面,实轴,虚轴,模,共轭复数的概念
02
理解用复平面内的点或以原点为起点的向量来表示复数及它们之间的一一对应关系
01
掌握用向量的模来表示复数的模的方法
03
问题提出
我们知道,实数与数轴上的点一一对应,也就是说,数轴可以看成实数的一个几何模型.
那么,能否为复数找一个几何模型呢?怎样建立起复数与几何模型中点的一一对应关系?
y
x
o
z =a+bi , a,b∈R
分析理解
我们知道,实数与数轴上的点一一对应,也就是说,数轴可以看成实数的一个几何模型。那么,能否为复数找一个几何模型呢?怎样建立起复数与几何模型中点的一一对应关系?
任何一个复数 z= a+bi(a,b∈R),都可以由一个有序数对 (a,b) 唯一确定.
因为有序数对于平面直角坐标系中的点一一对应,所以复数集与平面直角坐标系中的点集是一一对应的.
(3,2)
一一对应
点A
一一对应
复数Z=a+bi
(a,b)
一一对应
点Z(a,b)
一一对应
复平面
建立平面直角坐标系来表示复数的平面称为复平面,
其中 ???? 轴称为实轴,???? 轴称为虚轴.
实轴上的点都表示实数;
虚轴上除原点外的点都表示纯虚数;
坐标轴外的点都表示非纯虚数.
?
y
x
o
a
b
Z:a+bi
虚轴
实轴
复数的几何意义
(1)复数????=????+????i一一对应复平面内点????(????,????)?;
?
(2)复数????=????+????i一一对应平面向量????????=(????,????)
?
这种对应关系架起了复数与几何之间的桥梁,使复数问题可以用几何方法解决,而且几何问题也可以用复数方法解决(数形结合法),它增加了解决复数问题和几何问题的途径
为了方便起见,我们常把复数z= a+bi(a,b∈R)说成点????(????,????)或说成向量????????,并规定,相等的向量表示同一个复数
?
复数的模
向量????????的模称为复数 z=a+bi(a,b∈R) 的模,记作|z|或|a+bi|. 由向量模的定义可知,|z|=|a+bi|=????2+????2.
如果b=0,那么 z=a+bi是一个实数a,它的模等于|z|=|a|(a的绝对值).
?
(1)虽然两个复数一般不能比较大小,但它们的模是非负实数,可以比较大小.
知识剖析
(2)复数 z=a+bi(a,b∈R) 的模 |z| 表示的是复平面内对应的点 ????(????,????) 到原点的距离,它是实数的绝对值概念的扩充,因此有 |z|≥0,并且绝对值具有的某些性质可以推广到复数的模
?
例3 在复平面内,表示下列复数的点 Z 的集合是什么图形:
(1)|z|=2 ;(2)2≤|z|≤3
解:(1)复数 z 的模等于2表明,向量????????的模等于2,即点 Z 到原点 O 的距离等于2,因此满足条件 |z|=2 的点 Z 的集合是以原点 O 为圆心,以 2 为半径的圆,如图.
?
(2)不等式2≤|z|≤3可以转化为不等式组|????|≤3|????|≥2.
满足|z|≤3 的点 Z 的集合是以原点 O 为圆心,以3为半径的圆及其内部所有的点构成的集合;满足|z|≥2的点 Z 的集合是以原点 O 为圆心,以2为半径的圆及其外部所有的点构成的集合.因此,满足2≤|z|≤3的点的集合是这两个集合的交集,即以原点 O 为圆心,以 2 和 3 为半径的两圆所夹的圆环,并包括圆环的边界
?
共轭复数
(1)定义:若两个复数的实部相等,而虚部互为相反数,则称这两个复数互为共轭复数,复数 z 的共轭复数用表示 ????.当z=a+bi(a,b∈R)时,????=a-bi.
?
(2)几何意义:在复平面内,表示两个共轭复数的点关于实轴对称,并且它们的模相等.另外,当复数z=a+bi的虚部 b=0 时,有 z=????.也就是说,任意一个实数的共轭复数仍是它本身,反之亦然.
?
例4 在复平面内作出表示下列复数的点,并分别求出它们的模和共轭复数:
(1)????1=3??2i;(2)????2=?1+3i.
?
解:在复平面内作图如图.
(1)????1=3?2i=32+(?2)2=13
????1=3+2i
?
(2)????2=?1+3i=(?2)2+(3)2=2
????2=?1?3i
?
当堂检测
A
ABC
????????
?
????????????????,????∪????,+∞
?
感谢您的聆听与指导
General template of fresh teaching
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
