6.6简单几何体的再认识 教学课件(共30张PPT)高中数学北师大版(2019)必修第二册
文档属性
| 名称 | 6.6简单几何体的再认识 教学课件(共30张PPT)高中数学北师大版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 43.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 09:57:44 | ||
图片预览






文档简介
6.6简单几何体的再认识
北师大版(2019)必修第二册
第六章 立体几何初步
学习目标
掌握柱体、锥体、台体的体积公式.
02
掌握柱体、锥体、台体的侧面积公式.
01
理解球的有关概念.
03
掌握球的表面积和体积公式并能解决与球有关的组合体的相关计算问题.
04
知识引入
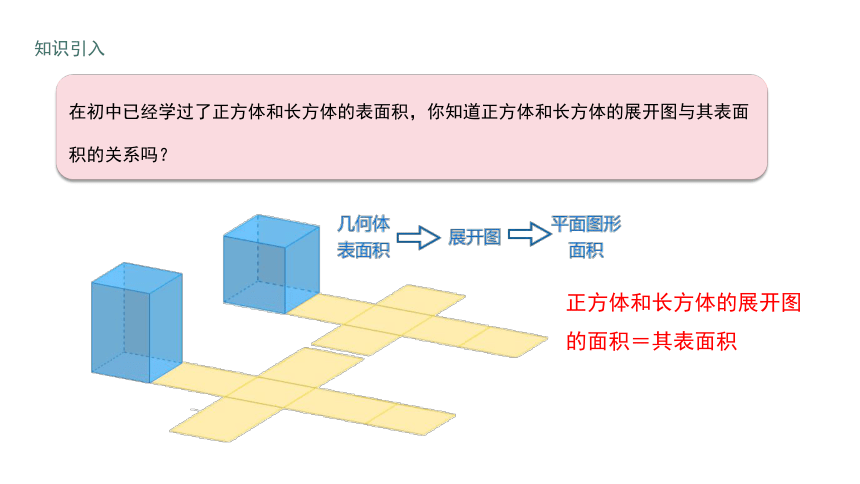
在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
正方体和长方体的展开图的面积=其表面积
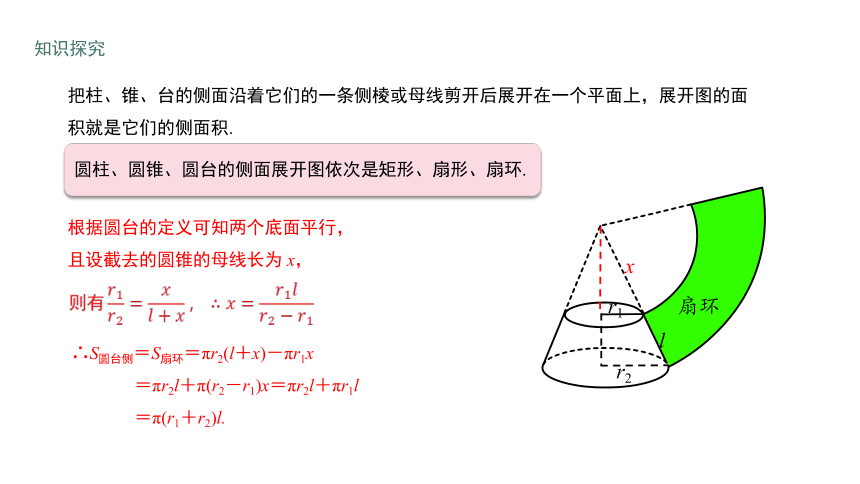
圆柱、圆锥、圆台的侧面展开图依次是矩形、扇形、扇环.
知识探究
把柱、锥、台的侧面沿着它们的一条侧棱或母线剪开后展开在一个平面上,展开图的面积就是它们的侧面积.
S圆柱侧=S长方形=2πrl
长方形
长=2πr
r
宽=l
l
r
l
S圆锥侧=S扇形= =πrl
扇形
圆柱、圆锥、圆台的侧面展开图依次是矩形、扇形、扇环.
知识探究
把柱、锥、台的侧面沿着它们的一条侧棱或母线剪开后展开在一个平面上,展开图的面积就是它们的侧面积.
r2
l
r1
扇环
∴S圆台侧=S扇环=πr2(l+x)-πr1x
=πr2l+π(r2-r1)x=πr2l+πr1l
=π(r1+r2)l.
x
根据圆台的定义可知两个底面平行,
且设截去的圆锥的母线长为 x,
则有????1????2=????????+????,∴????=????1????????2?????1
?
例1 一个圆柱形的锅炉,底面直径d=1m,高h=2.3m.求锅炉的表面积(精确到0.1m2).
因此锅炉的表面积约为 8.8m2.
解:S=S侧面积+2S底面积=πdh+2π(????2)2
=π×1×2.3+2π×14=2.8π≈8.8(m2),
?
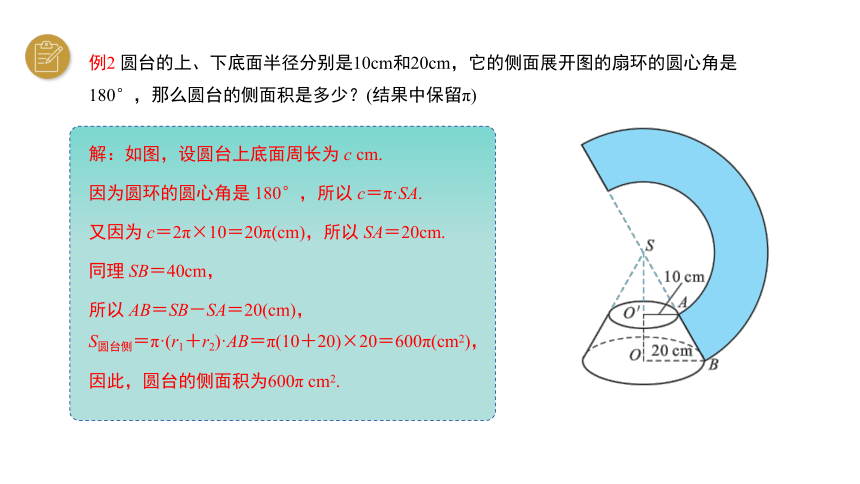
例2 圆台的上、下底面半径分别是10cm和20cm,它的侧面展开图的扇环的圆心角是180°,那么圆台的侧面积是多少?(结果中保留π)
解:如图,设圆台上底面周长为 c cm.
因为圆环的圆心角是 180°,所以 c=π·SA.
又因为 c=2π×10=20π(cm),所以 SA=20cm.
同理 SB=40cm,
所以 AB=SB-SA=20(cm),
S圆台侧=π·(r1+r2)·AB=π(10+20)×20=600π(cm2),
因此,圆台的侧面积为600π cm2.
知识探究
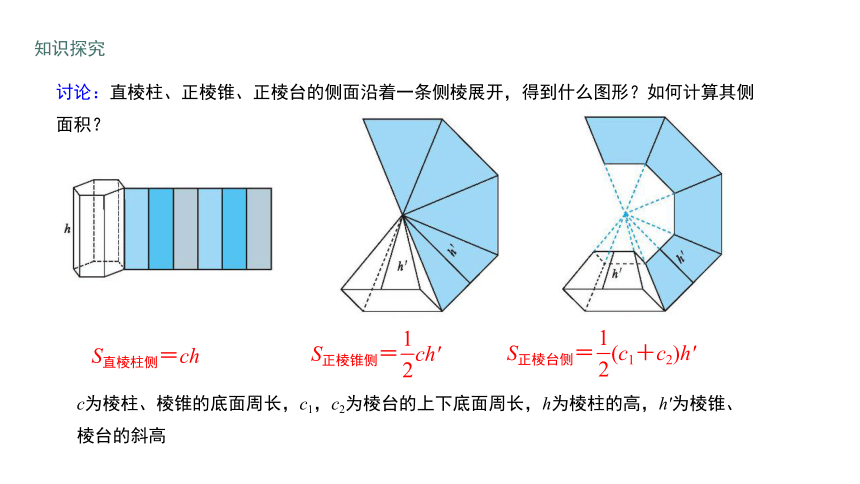
讨论:直棱柱、正棱锥、正棱台的侧面沿着一条侧棱展开,得到什么图形?如何计算其侧面积?
S直棱柱侧=ch
S正棱锥侧= ch'
S正棱台侧= (c1+c2)h'
c为棱柱、棱锥的底面周长,c1,c2为棱台的上下底面周长,h为棱柱的高,h′为棱锥、棱台的斜高
思考交流:将圆柱、圆锥、圆台的侧面积公式进行类比,能发现它们的联系和区别吗?
对于圆台的侧面积S圆台侧=π(r1+r2)l. (r1为上底面半径,r2为下底面半径,l为母线长):
当r1=r2时,得S圆柱侧=2πrl;
当r1=0时,得S圆锥侧=πrl .
所以圆柱可以看作一个上、下底面半径相等的特殊圆台,圆锥可以看作上底面半径为0的特殊圆台.
思考交流:将直棱柱、正棱锥、正棱台的侧面积公式进行类比,能发现它们的联系和区别吗?
对于正棱台的侧面积S正棱台侧=
当c1=c2时,得S直棱柱侧=ch;
当c1=0时,得S正棱锥侧= .
其中c1,c2分别为正棱台上、下底面的周长,c为棱柱、棱锥的底面周长,
?'为正棱台和正棱锥的斜高,h为直棱柱的高
?
12(????1+????2)?'
?
12?????'
?
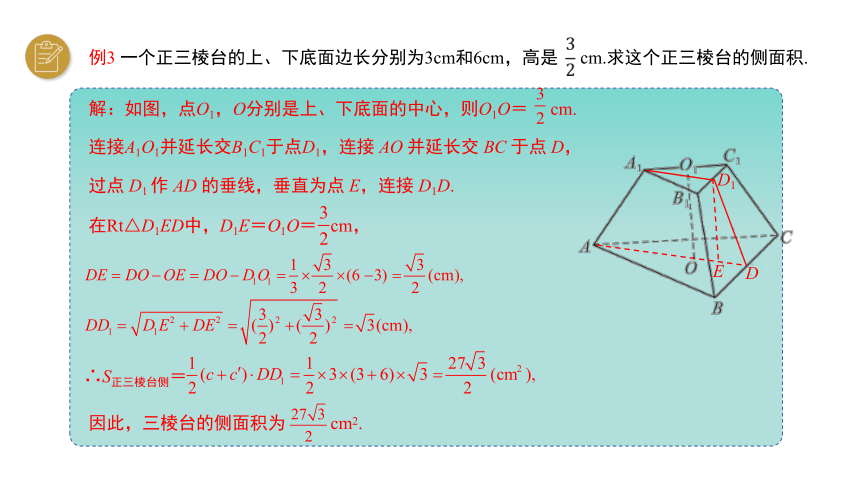
例3 一个正三棱台的上、下底面边长分别为3cm和6cm,高是 cm.求这个正三棱台的侧面积.
32
?
连接A1O1并延长交B1C1于点D1,连接 AO 并延长交 BC 于点 D,
过点 D1 作 AD 的垂线,垂直为点 E,连接 D1D.
解:如图,点O1,O分别是上、下底面的中心,则O1O= cm.
D1
D
E
在Rt△D1ED中,D1E=O1O= cm,
∴S正三棱台侧=
因此,三棱台的侧面积为 cm2.
知识探究
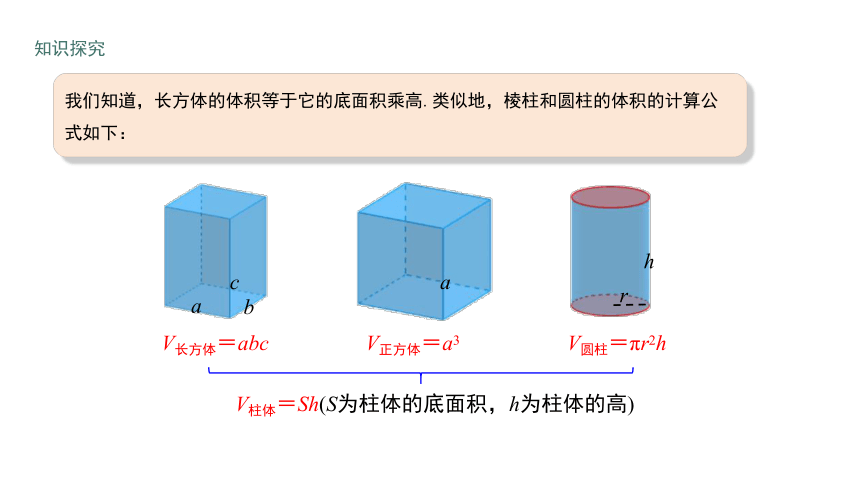
我们知道,长方体的体积等于它的底面积乘高.类似地,棱柱和圆柱的体积的计算公式如下:
V正方体=a3
a
V长方体=abc
a
b
c
V圆柱=πr2h
h
r
V柱体=Sh(S为柱体的底面积,h为柱体的高)
知识探究
问题:如图所示的直三棱柱可以分成3个三棱锥,所得到的3个三棱锥的体积之间有什么关系?由此能得到三棱锥的体积计算公式吗?
V三棱锥= Sh
所得到的3个三棱锥的体积相等.
棱锥和圆锥的体积可用这个公式来计算.
例4 埃及胡夫金字塔大约建于公元前 2580 年,其形状为正四棱锥.塔高约146.6m,底面边长约 230.4m.求这座金字塔的侧面积(精确到0.1m2)和体积(精确到0.1m3).
解:如图,AC 为高,BC 为底面的边心距,
则 AC=146.6m,BC=115.2m,底面周长c=(4×230.4)m.
S侧面积=
=
V= S底·AC=
因此,金字塔的侧面积约为85 914.9m2,体积约为2 594 046.0m3.
知识探究
棱台和圆台的体积都可用两个锥体的体积之差来计算.
如图,四棱台ABCD-A'B'C'D'的高为h,
四边形ABCD面积为S下,四边形A'B'C'D'面积为S上,
设四棱锥P-A'B'C'D'的高为h',
V台=
13(????上+????下+????上?????下 )?
?
例5 已知一正四棱台的上底边长为4cm,下底边长为8cm,高为3cm.求其体积.
因此正四棱台的体积为112cm3.
解:V= (S上+S下+ S上 · S下 )h
=
=112(cm3),
思考交流:柱体、锥体、台体的体积之间有什么关系?
上底扩大
S上=S
S下=S
上底缩小
S上=0
S下=S
知识探究
用一个平面 ???? 去截半径为 R 的球 O,若平面 ???? 经过球心 O,则平面与球面的公共点显然都是共面的且到球心 O 的距离都为 R,这说明过球心的平面截球面所得截线是以球心 O为圆心的圆.
?
当平面 ???? 不经过球心O时(如图)不妨设OO'⊥????于点O',记OO'=d,对于平面与球面的任意一个公共点 P,都满足OO'⊥O'P,所以O'P=????2?????2.此时截线是以点O'为圆心,以为r=????2?????2半径的圆.
?
球面被经过球心的平面截得的圆叫做球的大圆;
球面被不过球心的截面截得的圆叫做球的小圆.
与圆和直线相切类似,当直线与球有唯一交点时,称直线与球相切,这一交点称为直线与球的切点.
思考交流:过球外一点作球的切线,这点和切点之间的线段长称为这点到球的切线长,过球外一点P,可以作球的无数条切线.那么所有切线的切线长相等吗?所有切点组成什么图形?
解:设过点P的直线与球O相切于点A,则平面POA与球面的交线是球的大圆(如图),
由直线与圆相切的性质可得OA⊥AP,所以
设点 A 在OP上的垂足为O',则AO'长度恒定不变.
这说明,过球外一点的所有切线的切线长都相等,这些切点的集合是以点O'为圆心、O'A为半径的圆,圆面O'及所有切线围成了一个圆锥.
球的表面积和体积可用右边公式来计算
S球面=4πR2,V球= (其中R为球的半径)
例6 如图,一个圆锥形的空杯子上面放着一个半球形的冰激凌,如果冰激凌融化了,会溢出杯子吗?(假设冰激凌融化前后体积不变)
V圆锥=
∴V半球<V圆锥,
解:∵V半球=
∴冰激凌融化了,不会溢出杯子.
例7 一个圆柱形的玻璃瓶的内半径为3cm,瓶里所装的水深为8cm,将一个钢球完全浸入水中,瓶中水的高度上升到8.5cm.求钢球的半径.
解得R=1.5,
解:如图,设钢球半径为R cm,
根据题意,得
所以钢球的半径为1.5cm.
当堂检测
B
D
B
D
6
感谢您的聆听与指导
General template of fresh teaching
北师大版(2019)必修第二册
第六章 立体几何初步
学习目标
掌握柱体、锥体、台体的体积公式.
02
掌握柱体、锥体、台体的侧面积公式.
01
理解球的有关概念.
03
掌握球的表面积和体积公式并能解决与球有关的组合体的相关计算问题.
04
知识引入
在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?
正方体和长方体的展开图的面积=其表面积
圆柱、圆锥、圆台的侧面展开图依次是矩形、扇形、扇环.
知识探究
把柱、锥、台的侧面沿着它们的一条侧棱或母线剪开后展开在一个平面上,展开图的面积就是它们的侧面积.
S圆柱侧=S长方形=2πrl
长方形
长=2πr
r
宽=l
l
r
l
S圆锥侧=S扇形= =πrl
扇形
圆柱、圆锥、圆台的侧面展开图依次是矩形、扇形、扇环.
知识探究
把柱、锥、台的侧面沿着它们的一条侧棱或母线剪开后展开在一个平面上,展开图的面积就是它们的侧面积.
r2
l
r1
扇环
∴S圆台侧=S扇环=πr2(l+x)-πr1x
=πr2l+π(r2-r1)x=πr2l+πr1l
=π(r1+r2)l.
x
根据圆台的定义可知两个底面平行,
且设截去的圆锥的母线长为 x,
则有????1????2=????????+????,∴????=????1????????2?????1
?
例1 一个圆柱形的锅炉,底面直径d=1m,高h=2.3m.求锅炉的表面积(精确到0.1m2).
因此锅炉的表面积约为 8.8m2.
解:S=S侧面积+2S底面积=πdh+2π(????2)2
=π×1×2.3+2π×14=2.8π≈8.8(m2),
?
例2 圆台的上、下底面半径分别是10cm和20cm,它的侧面展开图的扇环的圆心角是180°,那么圆台的侧面积是多少?(结果中保留π)
解:如图,设圆台上底面周长为 c cm.
因为圆环的圆心角是 180°,所以 c=π·SA.
又因为 c=2π×10=20π(cm),所以 SA=20cm.
同理 SB=40cm,
所以 AB=SB-SA=20(cm),
S圆台侧=π·(r1+r2)·AB=π(10+20)×20=600π(cm2),
因此,圆台的侧面积为600π cm2.
知识探究
讨论:直棱柱、正棱锥、正棱台的侧面沿着一条侧棱展开,得到什么图形?如何计算其侧面积?
S直棱柱侧=ch
S正棱锥侧= ch'
S正棱台侧= (c1+c2)h'
c为棱柱、棱锥的底面周长,c1,c2为棱台的上下底面周长,h为棱柱的高,h′为棱锥、棱台的斜高
思考交流:将圆柱、圆锥、圆台的侧面积公式进行类比,能发现它们的联系和区别吗?
对于圆台的侧面积S圆台侧=π(r1+r2)l. (r1为上底面半径,r2为下底面半径,l为母线长):
当r1=r2时,得S圆柱侧=2πrl;
当r1=0时,得S圆锥侧=πrl .
所以圆柱可以看作一个上、下底面半径相等的特殊圆台,圆锥可以看作上底面半径为0的特殊圆台.
思考交流:将直棱柱、正棱锥、正棱台的侧面积公式进行类比,能发现它们的联系和区别吗?
对于正棱台的侧面积S正棱台侧=
当c1=c2时,得S直棱柱侧=ch;
当c1=0时,得S正棱锥侧= .
其中c1,c2分别为正棱台上、下底面的周长,c为棱柱、棱锥的底面周长,
?'为正棱台和正棱锥的斜高,h为直棱柱的高
?
12(????1+????2)?'
?
12?????'
?
例3 一个正三棱台的上、下底面边长分别为3cm和6cm,高是 cm.求这个正三棱台的侧面积.
32
?
连接A1O1并延长交B1C1于点D1,连接 AO 并延长交 BC 于点 D,
过点 D1 作 AD 的垂线,垂直为点 E,连接 D1D.
解:如图,点O1,O分别是上、下底面的中心,则O1O= cm.
D1
D
E
在Rt△D1ED中,D1E=O1O= cm,
∴S正三棱台侧=
因此,三棱台的侧面积为 cm2.
知识探究
我们知道,长方体的体积等于它的底面积乘高.类似地,棱柱和圆柱的体积的计算公式如下:
V正方体=a3
a
V长方体=abc
a
b
c
V圆柱=πr2h
h
r
V柱体=Sh(S为柱体的底面积,h为柱体的高)
知识探究
问题:如图所示的直三棱柱可以分成3个三棱锥,所得到的3个三棱锥的体积之间有什么关系?由此能得到三棱锥的体积计算公式吗?
V三棱锥= Sh
所得到的3个三棱锥的体积相等.
棱锥和圆锥的体积可用这个公式来计算.
例4 埃及胡夫金字塔大约建于公元前 2580 年,其形状为正四棱锥.塔高约146.6m,底面边长约 230.4m.求这座金字塔的侧面积(精确到0.1m2)和体积(精确到0.1m3).
解:如图,AC 为高,BC 为底面的边心距,
则 AC=146.6m,BC=115.2m,底面周长c=(4×230.4)m.
S侧面积=
=
V= S底·AC=
因此,金字塔的侧面积约为85 914.9m2,体积约为2 594 046.0m3.
知识探究
棱台和圆台的体积都可用两个锥体的体积之差来计算.
如图,四棱台ABCD-A'B'C'D'的高为h,
四边形ABCD面积为S下,四边形A'B'C'D'面积为S上,
设四棱锥P-A'B'C'D'的高为h',
V台=
13(????上+????下+????上?????下 )?
?
例5 已知一正四棱台的上底边长为4cm,下底边长为8cm,高为3cm.求其体积.
因此正四棱台的体积为112cm3.
解:V= (S上+S下+ S上 · S下 )h
=
=112(cm3),
思考交流:柱体、锥体、台体的体积之间有什么关系?
上底扩大
S上=S
S下=S
上底缩小
S上=0
S下=S
知识探究
用一个平面 ???? 去截半径为 R 的球 O,若平面 ???? 经过球心 O,则平面与球面的公共点显然都是共面的且到球心 O 的距离都为 R,这说明过球心的平面截球面所得截线是以球心 O为圆心的圆.
?
当平面 ???? 不经过球心O时(如图)不妨设OO'⊥????于点O',记OO'=d,对于平面与球面的任意一个公共点 P,都满足OO'⊥O'P,所以O'P=????2?????2.此时截线是以点O'为圆心,以为r=????2?????2半径的圆.
?
球面被经过球心的平面截得的圆叫做球的大圆;
球面被不过球心的截面截得的圆叫做球的小圆.
与圆和直线相切类似,当直线与球有唯一交点时,称直线与球相切,这一交点称为直线与球的切点.
思考交流:过球外一点作球的切线,这点和切点之间的线段长称为这点到球的切线长,过球外一点P,可以作球的无数条切线.那么所有切线的切线长相等吗?所有切点组成什么图形?
解:设过点P的直线与球O相切于点A,则平面POA与球面的交线是球的大圆(如图),
由直线与圆相切的性质可得OA⊥AP,所以
设点 A 在OP上的垂足为O',则AO'长度恒定不变.
这说明,过球外一点的所有切线的切线长都相等,这些切点的集合是以点O'为圆心、O'A为半径的圆,圆面O'及所有切线围成了一个圆锥.
球的表面积和体积可用右边公式来计算
S球面=4πR2,V球= (其中R为球的半径)
例6 如图,一个圆锥形的空杯子上面放着一个半球形的冰激凌,如果冰激凌融化了,会溢出杯子吗?(假设冰激凌融化前后体积不变)
V圆锥=
∴V半球<V圆锥,
解:∵V半球=
∴冰激凌融化了,不会溢出杯子.
例7 一个圆柱形的玻璃瓶的内半径为3cm,瓶里所装的水深为8cm,将一个钢球完全浸入水中,瓶中水的高度上升到8.5cm.求钢球的半径.
解得R=1.5,
解:如图,设钢球半径为R cm,
根据题意,得
所以钢球的半径为1.5cm.
当堂检测
B
D
B
D
6
感谢您的聆听与指导
General template of fresh teaching
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
