6.3.2刻画空间点、线、面位置关系的公理 教学课件(共31张PPT)高中数学北师大版(2019)必修第二册
文档属性
| 名称 | 6.3.2刻画空间点、线、面位置关系的公理 教学课件(共31张PPT)高中数学北师大版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 44.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 10:05:49 | ||
图片预览






文档简介
(共31张PPT)
6.3.2刻画空间点、线、面位置关系的公理
北师大版(2019)必修第二册
第六章 立体几何初步
学习目标
理解异面直线夹角的定义,会求两异面直线夹角.
02
掌握基本事实1,2,3,4,推论及定理,会运用它们解决问题.
01
知识引入
在初中平面几何学习中,曾经学习过以下一些基本事实:
(1)两点确定一条直线.
(2)两点之间线段最短.
(3)过直线外一点有且只有一条直线与这条直线平行.
类似地,人们把经过长期观察与实践总结出的平面的一些最基本性质当作基本事实,作为进一步学习空间中位置关系的基础.
思考:两点确定一条直线,那么怎样确定一个平面呢?
知识探究
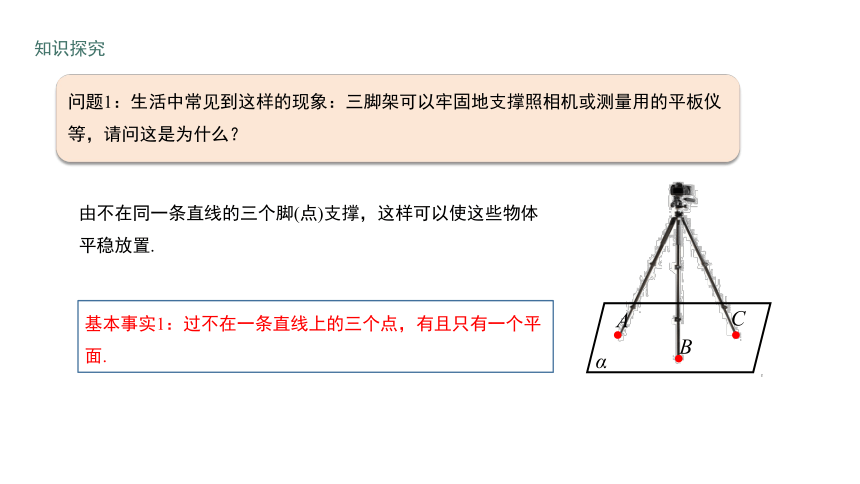
问题1:生活中常见到这样的现象:三脚架可以牢固地支撑照相机或测量用的平板仪等,请问这是为什么?
基本事实1:过不在一条直线上的三个点,有且只有一个平面.
由不在同一条直线的三个脚(点)支撑,这样可以使这些物体平稳放置.
α
C
A
B
知识探究
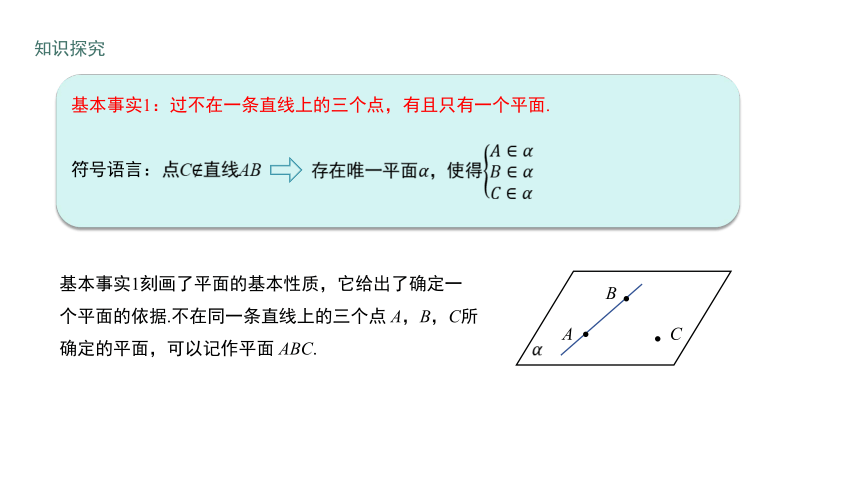
基本事实1:过不在一条直线上的三个点,有且只有一个平面.
符号语言:
点C直线AB
存在唯一平面,使得
A
B
C
基本事实1刻画了平面的基本性质,它给出了确定一个平面的依据.不在同一条直线上的三个点 A,B,C所确定的平面,可以记作平面 ABC.
知识探究
问题2:如何判断直线在平面内呢?
如图,在长方体中,A,B两点在平面ABCD内,那么整条直线AB都在平面ABCD内;A,D1两点在平面A1ADD1内,那么直线AD1上所有点都在平面A1ADD1内.
由此可以概括出下面的基本事实
基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
符号表示:若A∈l,B∈l,且A∈α,B∈α,则l α.
知识探究
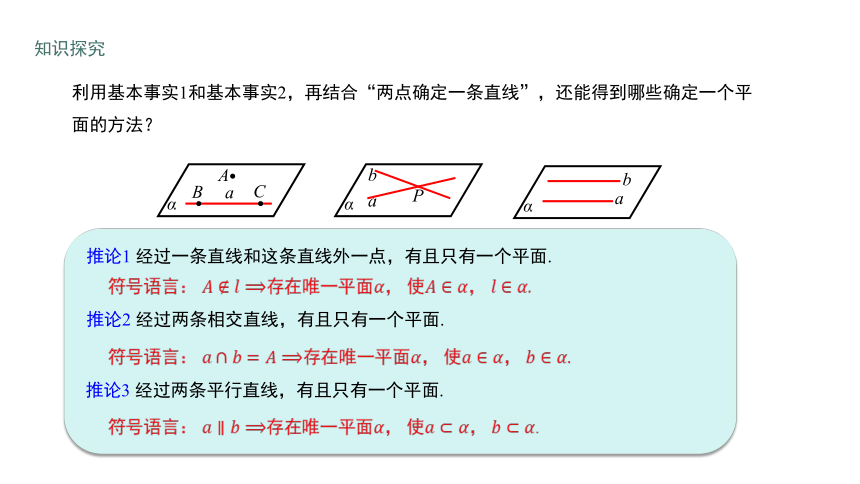
利用基本事实1和基本事实2,再结合“两点确定一条直线”,还能得到哪些确定一个平面的方法?
推论1 经过一条直线和这条直线外一点,有且只有一个平面.
α
a
A
B
C
α
α
b
a
b
a
P
推论3 经过两条平行直线,有且只有一个平面.
推论2 经过两条相交直线,有且只有一个平面.
符号语言: 存在唯一平面, 使, .
符号语言: 存在唯一平面, 使, .
符号语言: 存在唯一平面, 使, .
知识探究
例如,长方体中,不共线的三点A,C,D1确定平面ACD1;
直线BC1和直线外一点 A 确定平面ABC1D1
基本事实1及以上推论给出了确定平面的依据.
知识探究
长方体的任意两个面,要么平行,要么交于一条直线.由此可以抽象出下面的基本事实.
基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线
P,P
P
l
符号语言:
基本事实3表明,如果两个平面有一个公共点,那么它们必定还有另外一个公共点,只要找出这两个平面的两个公共点,就找出了它们的交线.
基本事实3表达了不重合的平面与平面有两种位置关系:两个平面相交于一条直线,两个平面平行.
知识探究
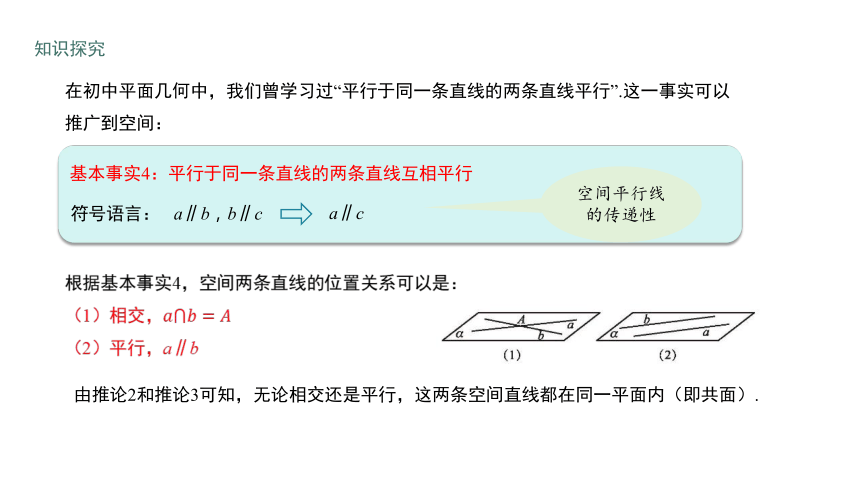
在初中平面几何中,我们曾学习过“平行于同一条直线的两条直线平行”.这一事实可以推广到空间:
基本事实4:平行于同一条直线的两条直线互相平行
符号语言:
根据基本事实4,空间两条直线的位置关系可以是:
(1)相交,
(2)平行,a∥b
a∥b,b∥c
a∥c
空间平行线的传递性
由推论2和推论3可知,无论相交还是平行,这两条空间直线都在同一平面内(即共面).
知识探究
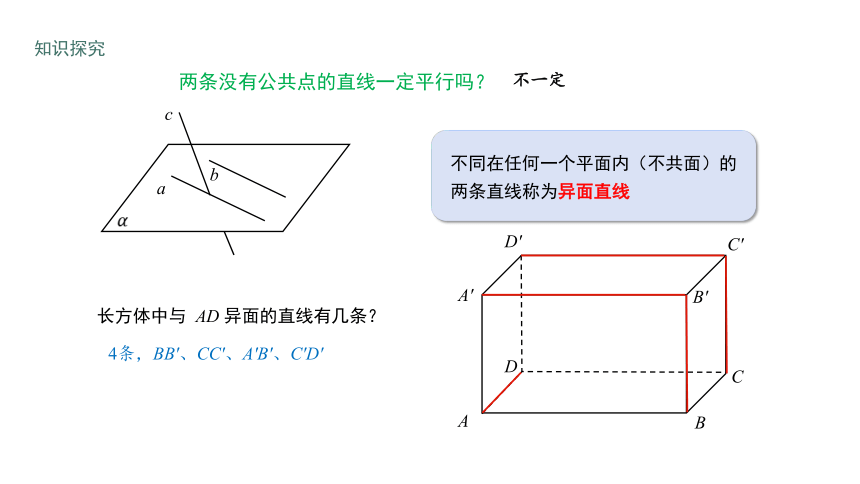
两条没有公共点的直线一定平行吗?
不一定
不同在任何一个平面内(不共面)的
两条直线称为异面直线
a
b
c
A′
D′
B′
C′
A
B
C
D
长方体中与 AD 异面的直线有几条?
4条,BB′、CC′、A′B′、C′D′
知识探究
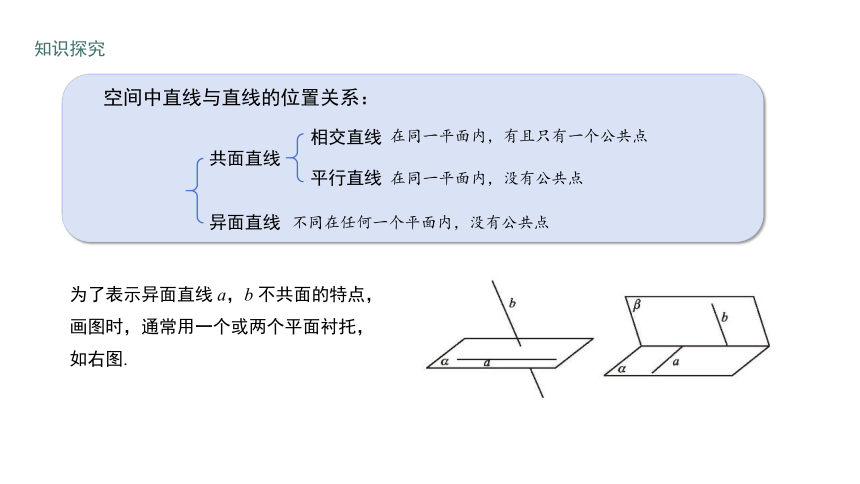
相交直线
平行直线
共面直线
异面直线
不同在任何一个平面内,没有公共点
在同一平面内,没有公共点
在同一平面内,有且只有一个公共点
空间中直线与直线的位置关系:
为了表示异面直线 a,b 不共面的特点,画图时,通常用一个或两个平面衬托,如右图.
思考:如果空间中两个角的两条边分别对应平行,那么这两个角的大小有什么关系?
在平面上,角的边是射线,射线是有方向的.
①两组边方向相同
②两组边方向相反
③一组方向相同,另一组相反
相等
相等
互补
定理:如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补.
知识探究
平面内两条直线相交成了4个角,其中不大于90°的角称为它们的夹角.夹角刻画了一条直线相对于另一条直线的位置关系.两条异面直线之间也存在位置关系的问题,为此引入“异面直线的夹角”的概念.
a
b
如图,已知两条异面直线a,b,过空间任一点O作直线a′∥a,b′∥b,这时a′,b′共面,我们把a′与b′所成的不大于90°的角称为异面直线a,b所成的角(或夹角).
a′
b′
O
若两条异面直线 a,b 所成的角为直角,则称这两条直线互相垂直,记作:a⊥b.
平移使得空间问题转化为平面几何问题
相交垂直
异面垂直
(0°,90°]
异面直线夹角的范围?
垂直
例1 四个顶点不在同一平面内的四边形称为空间四边形.如图,在空间四边形 ABCD 中,点E,F,G,H分别是边AB,BC,CD,DA的中点,求证:四边形EFGH是平行四边形.
A
B
D
C
H
E
F
G
连接BD,构造中位线,凑“一组对边平行且相等”的条件
解:如图,连接BD,
∵FG是△CBD的中位线,∴FG∥BD,FG BD
又∵EH是△ABD的中位线,∴EH∥BD,EH BD
∴FG∥EH,FGEH
∴四边形EFGH是平行四边形
例2 如图,已知正方体 ABCD-A1B1C1D1 的棱长为 a.
(1)正方体的哪些棱所在的直线与直线 BC1 是异面直线?
(2)求异面直线 AA1 与 BC 所成的角;
(3)求异面直线 BC1 与 AC 所成的角.
A
A1
B
D
C
B1
D1
C1
解:(1)正方体共有12条棱,与BC1相交的棱有6条,与BC1平行的棱不存在.
因此余下的6条棱所在的直线分别与直线BC1是异面直线,它们是A1A,A1B1,A1D1,DA,DC,DD1.
例2 如图,已知正方体 ABCD-A1B1C1D1 的棱长为 a.
(1)正方体的哪些棱所在的直线与直线 BC1 是异面直线?
(2)求异面直线 AA1 与 BC 所成的角;
(3)求异面直线 BC1 与 AC 所成的角.
A
A1
B
D
C
B1
D1
C1
解:(2)因为 AD∥BC,∴∠A1AD 即为异面直线 AA1 与 BC 所成的角.
显然∠A1AD=90°,故异面直线 AA1 与 BC 所成的角为90°.
例2 如图,已知正方体 ABCD-A1B1C1D1 的棱长为 a.
(1)正方体的哪些棱所在的直线与直线 BC1 是异面直线?
(2)求异面直线 AA1 与 BC 所成的角;
(3)求异面直线 BC1 与 AC 所成的角.
A
A1
B
D
C
B1
D1
C1
因为A1B,BC1与A1C1都是该正方体的面对角线,
所以A1B=BC1=A1C1,△A1BC1是等边三角形,
从而∠BC1A1=60°,即异面直线BC1与AC所成的角为60°.
(3)如图,连接A1C1,A1B.
因为 ,
所以四边形AA1C1C是平行四边形,AC∥A1C1,
故∠BC1A1就是异面直线BC1与AC所成的角.
当堂检测
B
ABC
BD
1或3
5
基本事实
基本事实1:过不在一条直线的三个点,有且只有一个平面.
基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
推论1:一条直线和该直线外一点确定一个平面.
推论2:两条相交直线确定一个平面.
推论3:两条平行直线确定一个平面.
课堂总结
1、基本事实4:
相交直线
平行直线
共面直线
异面直线
不同在任何一个平面内,没有公共点
在同一平面内,没有公共点
在同一平面内,有且只有一个公共点
3、定理:
平行于同一直线的两条直线平行.
2、空间中直线与直线的位置关系:
如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补.
4、异面直线所成的角
通过平移把空间问题转化为平面几何问题.
课堂总结
感谢您的聆听与指导
General template of fresh teaching
6.3.2刻画空间点、线、面位置关系的公理
北师大版(2019)必修第二册
第六章 立体几何初步
学习目标
理解异面直线夹角的定义,会求两异面直线夹角.
02
掌握基本事实1,2,3,4,推论及定理,会运用它们解决问题.
01
知识引入
在初中平面几何学习中,曾经学习过以下一些基本事实:
(1)两点确定一条直线.
(2)两点之间线段最短.
(3)过直线外一点有且只有一条直线与这条直线平行.
类似地,人们把经过长期观察与实践总结出的平面的一些最基本性质当作基本事实,作为进一步学习空间中位置关系的基础.
思考:两点确定一条直线,那么怎样确定一个平面呢?
知识探究
问题1:生活中常见到这样的现象:三脚架可以牢固地支撑照相机或测量用的平板仪等,请问这是为什么?
基本事实1:过不在一条直线上的三个点,有且只有一个平面.
由不在同一条直线的三个脚(点)支撑,这样可以使这些物体平稳放置.
α
C
A
B
知识探究
基本事实1:过不在一条直线上的三个点,有且只有一个平面.
符号语言:
点C直线AB
存在唯一平面,使得
A
B
C
基本事实1刻画了平面的基本性质,它给出了确定一个平面的依据.不在同一条直线上的三个点 A,B,C所确定的平面,可以记作平面 ABC.
知识探究
问题2:如何判断直线在平面内呢?
如图,在长方体中,A,B两点在平面ABCD内,那么整条直线AB都在平面ABCD内;A,D1两点在平面A1ADD1内,那么直线AD1上所有点都在平面A1ADD1内.
由此可以概括出下面的基本事实
基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
符号表示:若A∈l,B∈l,且A∈α,B∈α,则l α.
知识探究
利用基本事实1和基本事实2,再结合“两点确定一条直线”,还能得到哪些确定一个平面的方法?
推论1 经过一条直线和这条直线外一点,有且只有一个平面.
α
a
A
B
C
α
α
b
a
b
a
P
推论3 经过两条平行直线,有且只有一个平面.
推论2 经过两条相交直线,有且只有一个平面.
符号语言: 存在唯一平面, 使, .
符号语言: 存在唯一平面, 使, .
符号语言: 存在唯一平面, 使, .
知识探究
例如,长方体中,不共线的三点A,C,D1确定平面ACD1;
直线BC1和直线外一点 A 确定平面ABC1D1
基本事实1及以上推论给出了确定平面的依据.
知识探究
长方体的任意两个面,要么平行,要么交于一条直线.由此可以抽象出下面的基本事实.
基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线
P,P
P
l
符号语言:
基本事实3表明,如果两个平面有一个公共点,那么它们必定还有另外一个公共点,只要找出这两个平面的两个公共点,就找出了它们的交线.
基本事实3表达了不重合的平面与平面有两种位置关系:两个平面相交于一条直线,两个平面平行.
知识探究
在初中平面几何中,我们曾学习过“平行于同一条直线的两条直线平行”.这一事实可以推广到空间:
基本事实4:平行于同一条直线的两条直线互相平行
符号语言:
根据基本事实4,空间两条直线的位置关系可以是:
(1)相交,
(2)平行,a∥b
a∥b,b∥c
a∥c
空间平行线的传递性
由推论2和推论3可知,无论相交还是平行,这两条空间直线都在同一平面内(即共面).
知识探究
两条没有公共点的直线一定平行吗?
不一定
不同在任何一个平面内(不共面)的
两条直线称为异面直线
a
b
c
A′
D′
B′
C′
A
B
C
D
长方体中与 AD 异面的直线有几条?
4条,BB′、CC′、A′B′、C′D′
知识探究
相交直线
平行直线
共面直线
异面直线
不同在任何一个平面内,没有公共点
在同一平面内,没有公共点
在同一平面内,有且只有一个公共点
空间中直线与直线的位置关系:
为了表示异面直线 a,b 不共面的特点,画图时,通常用一个或两个平面衬托,如右图.
思考:如果空间中两个角的两条边分别对应平行,那么这两个角的大小有什么关系?
在平面上,角的边是射线,射线是有方向的.
①两组边方向相同
②两组边方向相反
③一组方向相同,另一组相反
相等
相等
互补
定理:如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补.
知识探究
平面内两条直线相交成了4个角,其中不大于90°的角称为它们的夹角.夹角刻画了一条直线相对于另一条直线的位置关系.两条异面直线之间也存在位置关系的问题,为此引入“异面直线的夹角”的概念.
a
b
如图,已知两条异面直线a,b,过空间任一点O作直线a′∥a,b′∥b,这时a′,b′共面,我们把a′与b′所成的不大于90°的角称为异面直线a,b所成的角(或夹角).
a′
b′
O
若两条异面直线 a,b 所成的角为直角,则称这两条直线互相垂直,记作:a⊥b.
平移使得空间问题转化为平面几何问题
相交垂直
异面垂直
(0°,90°]
异面直线夹角的范围?
垂直
例1 四个顶点不在同一平面内的四边形称为空间四边形.如图,在空间四边形 ABCD 中,点E,F,G,H分别是边AB,BC,CD,DA的中点,求证:四边形EFGH是平行四边形.
A
B
D
C
H
E
F
G
连接BD,构造中位线,凑“一组对边平行且相等”的条件
解:如图,连接BD,
∵FG是△CBD的中位线,∴FG∥BD,FG BD
又∵EH是△ABD的中位线,∴EH∥BD,EH BD
∴FG∥EH,FGEH
∴四边形EFGH是平行四边形
例2 如图,已知正方体 ABCD-A1B1C1D1 的棱长为 a.
(1)正方体的哪些棱所在的直线与直线 BC1 是异面直线?
(2)求异面直线 AA1 与 BC 所成的角;
(3)求异面直线 BC1 与 AC 所成的角.
A
A1
B
D
C
B1
D1
C1
解:(1)正方体共有12条棱,与BC1相交的棱有6条,与BC1平行的棱不存在.
因此余下的6条棱所在的直线分别与直线BC1是异面直线,它们是A1A,A1B1,A1D1,DA,DC,DD1.
例2 如图,已知正方体 ABCD-A1B1C1D1 的棱长为 a.
(1)正方体的哪些棱所在的直线与直线 BC1 是异面直线?
(2)求异面直线 AA1 与 BC 所成的角;
(3)求异面直线 BC1 与 AC 所成的角.
A
A1
B
D
C
B1
D1
C1
解:(2)因为 AD∥BC,∴∠A1AD 即为异面直线 AA1 与 BC 所成的角.
显然∠A1AD=90°,故异面直线 AA1 与 BC 所成的角为90°.
例2 如图,已知正方体 ABCD-A1B1C1D1 的棱长为 a.
(1)正方体的哪些棱所在的直线与直线 BC1 是异面直线?
(2)求异面直线 AA1 与 BC 所成的角;
(3)求异面直线 BC1 与 AC 所成的角.
A
A1
B
D
C
B1
D1
C1
因为A1B,BC1与A1C1都是该正方体的面对角线,
所以A1B=BC1=A1C1,△A1BC1是等边三角形,
从而∠BC1A1=60°,即异面直线BC1与AC所成的角为60°.
(3)如图,连接A1C1,A1B.
因为 ,
所以四边形AA1C1C是平行四边形,AC∥A1C1,
故∠BC1A1就是异面直线BC1与AC所成的角.
当堂检测
B
ABC
BD
1或3
5
基本事实
基本事实1:过不在一条直线的三个点,有且只有一个平面.
基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
推论1:一条直线和该直线外一点确定一个平面.
推论2:两条相交直线确定一个平面.
推论3:两条平行直线确定一个平面.
课堂总结
1、基本事实4:
相交直线
平行直线
共面直线
异面直线
不同在任何一个平面内,没有公共点
在同一平面内,没有公共点
在同一平面内,有且只有一个公共点
3、定理:
平行于同一直线的两条直线平行.
2、空间中直线与直线的位置关系:
如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补.
4、异面直线所成的角
通过平移把空间问题转化为平面几何问题.
课堂总结
感谢您的聆听与指导
General template of fresh teaching
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
