2024-2025年北师大版六年级下册数学期中专题训练:应用题(含解析)
文档属性
| 名称 | 2024-2025年北师大版六年级下册数学期中专题训练:应用题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 406.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-08 05:49:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025年北师大版六年级下册数学期中专题训练:应用题
1.两个同样的小圆柱拼成一个高为40厘米的长圆柱,表面积减少了60平方厘米,原来每个小圆柱的体积是多少立方厘米?
2.一个底面半径是6厘米的圆柱形容器,装一部分水,水中浸没着一个高9厘米的圆锥体铅锤。当铅锤从水中取出后,水面下降了2厘米。这个圆锥体的铅锤的底面积是多少平方厘米?
3.如图,先将甲容器注满水,再将水倒入乙容器,这时乙容器中的水有多高?
4.一个圆锥形沙堆,量得底面周长是12.56米,高是1.5米,把这堆沙全部铺在一个圆柱形沙坑内,这个沙坑的底面半径是2米。这堆沙平均能铺多厚?
5.一个底面半径为10厘米的圆柱形容器,里面装有水。将等底等高的一个圆柱形铁块和一个圆锥形铁块同时放入这个容器中,水面上升到9厘米(如图)。这个圆锥形铁块的体积是多少?
6.为了发展农村绿色能源,幸福村要挖一个圆柱形的沼气池,底面半径是4米、深2.5米。(π取值为3.14)
(1)这个沼气池的容积是多少立方米?
(2)如果要在沼气池的底部和四周铺上一种防漏水膜,大约需要铺多大面积的防漏水膜?
7.一个圆柱形水桶,从里面量底面半径是2分米,高是5分米,如果每立方分米水重1千克,这个水桶能盛水多少千克?
8.一个圆柱形储水池,底面直径10米,深5米,在池的四周及底面抹上水泥,抹水泥面积是多少平方米?
9.建筑工地上有一个圆锥形的沙土堆,底面面积是24平方米,高3米。把这些沙土平填在一个长6米,宽4米的长方体土坑中,沙土厚多少米?
10.一个粮仓如图,如果每立方米粮食的质量为700千克,这个粮仓最多能装多少千克粮食?
11.一个长方体的木块,它的长、宽、高的比是。这个长方体木块的长是24厘米,现在将这个长方体木块削成一个体积最大的圆锥,这个圆锥的体积是多少立方厘米?
12.做一个无盖的圆柱形水桶,水桶的底面周长是50.24厘米,高40厘米。
(1)做这样一个水桶至少需要多少平方分米的材料?
(2)这个水桶可以装水多少升?
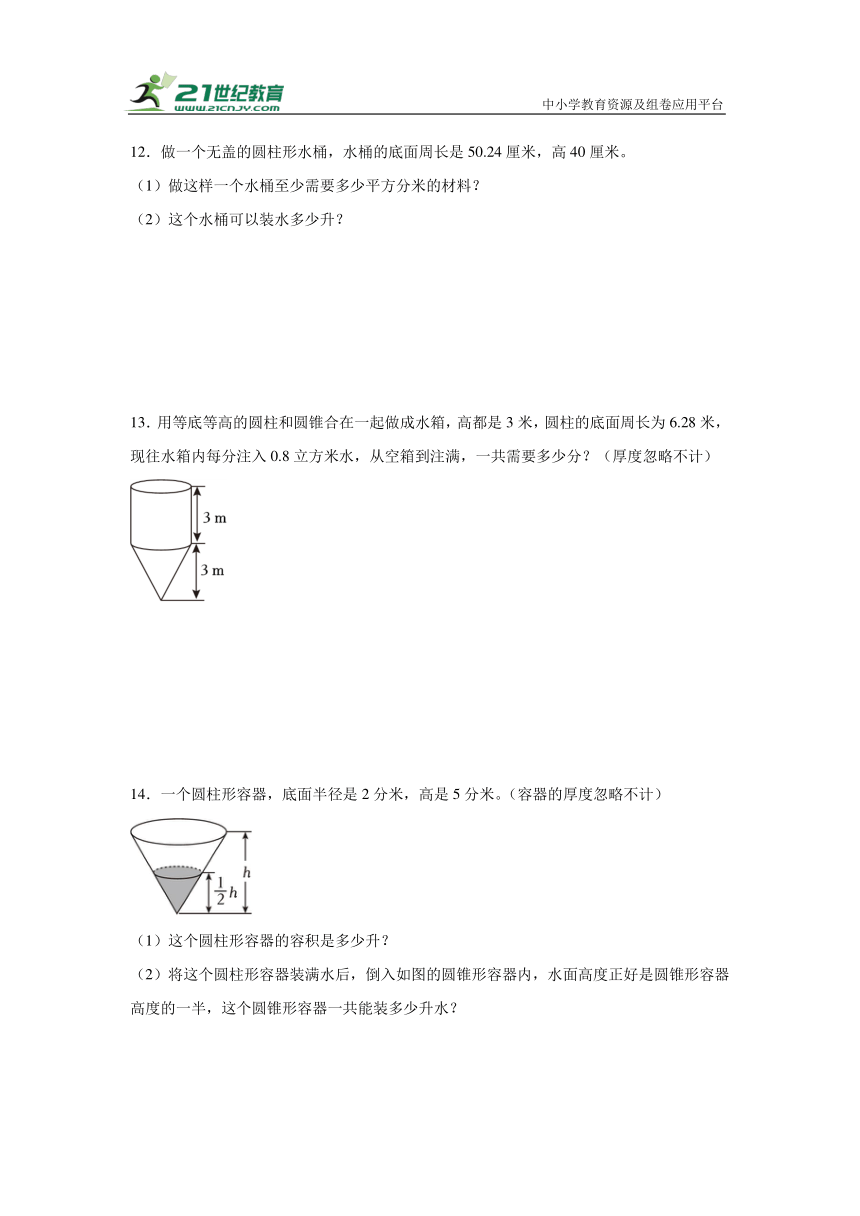
13.用等底等高的圆柱和圆锥合在一起做成水箱,高都是3米,圆柱的底面周长为6.28米,现往水箱内每分注入0.8立方米水,从空箱到注满,一共需要多少分?(厚度忽略不计)
14.一个圆柱形容器,底面半径是2分米,高是5分米。(容器的厚度忽略不计)
(1)这个圆柱形容器的容积是多少升?
(2)将这个圆柱形容器装满水后,倒入如图的圆锥形容器内,水面高度正好是圆锥形容器高度的一半,这个圆锥形容器一共能装多少升水?
15.李师傅要做一个零件(如图),有一个棱长6厘米的正方体铁块,在它的两个底面之间挖一个圆柱形圆孔,圆孔的底面直径是4厘米,剩下的部分就是这个零件了,此时零件的体积是多少立方厘米?
16.在一幅比例尺是1∶600的图纸上量得一个圆柱形水池底面内直径是2厘米,高是1厘米,这个水池最多能装多少吨水?(π取3,1立方米水质量是1吨)
17.一个晒盐场用500千克海水可以晒出15千克盐,照这样计算用200吨海水可以晒出多少吨盐?
18.在一幅比例尺为1∶1000000的地图上,量得甲乙两个港口的距离大约13.5厘米,这两个港口的实际距离为多少千米?一艘每小时行45千米的轮船从甲港出发,需要多少小时才能到达乙港?
19.在一幅比例尺为1∶300的平面图上,量得一间长方形教室的周长是10厘米,长与宽的比是3∶2。这间教室的实际面积是多少平方米?
20.在一幅比例尺是1∶2000000的地图上量得甲、乙两地相距32厘米。
(1)甲、乙两地实际相距多少千米?
(2)A、B两辆汽车同时从甲、乙两地相对开出,A车速度90千米/时,B车速度70千米/时。两车多少小时可以相遇?
21.在一幅比例尺是1∶20000000的地图上,量得A、B两地的距离是6厘米。甲、乙两辆汽车同时从两地相对开出,经过6小时后两车相遇。已知甲、乙两车的速度比是2∶3,相遇时甲、乙两车各行驶了多少千米?
22.两张不同的图纸,A图纸的比例尺是1∶2000,B图纸的比例尺是1∶500。那么,这两张图纸上3厘米长的线段表示的实际长度各是多少米?
23.把一块长与宽的比为5∶3的长方形土地,用1∶500的比例尺在画图纸上,得到的长方形的周长是32厘米,这块长方形土地的实际面积是多少平方米?
24.青白江区城市森林和谐广场位于青白江区华金大道二段,是青白江百姓休闲、娱乐的重要场所。把它绘制在比例尺为1∶5000的地图上,该广场平面图是一个长约是5厘米,宽约是3厘米的长方形。请问该广场实际面积约是多少平方米?
25.在一幅比例尺为1∶6000000的地图上,量得甲乙两地高速公路长为4.1厘米。杨叔叔开车从甲地出发,以每小时90千米的速度行驶了1.5小时。为了尽快到达乙地,他在不超速的情况下将速度提高了30%。剩下的路程他1小时能走完吗?
26.在比例尺是1∶8000000的地图上,量得A、B两地间的距离是6厘米。甲、乙两辆汽车分别从两地同时出发,相向而行,3小时后相遇。已知甲车平均每小时行驶85千米,乙车平均每小时行驶多少千米?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2024-2025年北师大版六年级下册数学期中专题训练:应用题》参考答案
1.600立方厘米
【分析】分析题目,减少的部分是小圆柱的2个底面的面积,据此用60除以2求出小圆柱的底面积,再用40除以2求出小圆柱的高,最后根据圆柱的体积=底面积×高代入数据计算即可。
【详解】60÷2=30(平方厘米)
40÷2=20(厘米)
30×20=600(立方厘米)
答:原来每个小圆柱的体积是600立方厘米。
2.75.36平方厘米
【分析】由题意可知,下降的水的体积就是圆锥的体积,根据圆柱的体积公式,代入数据计算下降的水的体积,即圆锥的体积,再根据的逆运算,用圆锥的体积除以再除以高,即可得解。
【详解】
(平方厘米)
答:这个圆锥体的铅锤的底面积是75.36平方厘米。
3.6厘米
【分析】由图可知,甲乙两个容器等底等高,则甲容器的容积等于乙容器容积的;用18乘,即可求出乙容器中水的高度。
【详解】18×=6(厘米)
答:这时乙容器中的水有6厘米。
4.0.5米
【分析】由题意可知,圆锥的体积与圆柱的体积相等,根据圆的周长公式的逆运算,用周长除以圆周率再除以2可得半径,再根据圆锥的体积公式,代入数据可得圆锥体积,即圆柱体积,最后根据圆柱体积公式的逆运算,用体积除以圆周率再除以半径的平方,即可得解。
【详解】
(米)
答:这堆沙平均能铺0.5米厚。
5.314立方厘米
【分析】水面上升的体积,就是圆柱和圆锥铁块的体积。由题意可知,圆柱形容器水面升高了厘米,根据圆柱的体积计算公式,即可求出水面上升的体积,即圆柱和圆锥的体积和,等底等高的圆柱的体积是圆锥体积的3倍,利用体积除以(3+1)即可求出圆锥的体积。
【详解】3.14×102×(9-5)÷(3+1)
=3.14×100×4÷4
=314(立方厘米)
答:这个圆锥形铁块的体积是314立方厘米。
6.(1)125.6立方米
(2)113.04平方米
【分析】(1)根据圆柱的体积(容积):V=sh=πr2h,代入数据计算即可求出这个沼气池的容积。
(2)防漏水膜的面积=底面面积+侧面积,根据圆的面积:S=πr2,侧面积:S=ch=2πrh,代入数据计算即可。
【详解】(1)3.14×42×2.5
=3.14×16×2.5
=125.6(立方米)
答:这个沼气池的容积是125.6立方米。
(2)3.14×42+3.14×4×2×2.5
=3.14×16+3.14×4×2×2.5
=50.24+62.8
=113.04(平方米)
答:大约需要铺113.04平方米的防漏水膜。
7.62.8千克
【分析】分析题目,先根据圆柱的体积=πr2h求出圆柱的体积,再乘每立方米水的重量即可解答。
【详解】3.14×22×5×1
=3.14×4×5×1
=12.56×5×1
=62.8×1
=62.8(千克)
答:这个水桶能盛水62.8千克。
8.235.5平方米
【分析】根据题意,在圆柱形储水池的四周及底面抹上水泥,那么抹水泥部分的面积=圆柱的侧面积+底面积;根据圆柱的侧面积公式S侧=πdh,圆柱的底面积公式S底=πr2,代入数据计算求解。
【详解】抹水泥部分的面积:
3.14×10×5+3.14×(10÷2)2
=3.14×10×5+3.14×52
=3.14×10×5+3.14×25
=157+78.5
=235.5(平方米)
答:抹水泥面积是235.5平方米。
9.1米
【分析】已知圆锥形沙土堆的底面面积是24平方米,高3米,根据圆锥的体积公式V=Sh,代入数据计算,求出沙土的体积;
把这些沙土平填在一个长6米,宽4米的长方体土坑中,沙土的体积不变;根据长方体的体积=长×宽×高,可知长方体的高=体积÷长÷宽,代入数据计算,求出沙土的厚度。
【详解】×24×3=24(立方米)
24÷6÷4
=4÷4
=1(米)
答:沙土厚1米。
10.3736.6千克
【分析】从图中可知,粮仓的上面是圆锥、下面是圆柱;根据圆柱的体积(容积)公式V=πr2h,圆锥的体积(容积)公式V=πr2h,代入数据计算,求出圆柱、圆锥的容积,再相加,即是这个粮仓的容积;然后用每立方米粮食的质量乘粮仓的容积,即可求出这个粮仓最多能装粮食的质量。
【详解】2÷2=1(米)
3.14×12×1.5+×3.14×12×0.6
=3.14×1×1.5+×3.14×1×0.6
=4.71+0.628
=5.338(立方米)
700×5.338=3736.6(千克)
答:这个粮仓最多能装3736.6千克粮食。
11.1017.36立方厘米
【分析】长方体的12条棱分为三组,互相平行的一组是4条,根据题意,可知长占长+宽+高的和的,已知一个数的几分之几是多少,求这个数,用除法,先求出长+宽+高的和,再用乘法分别求出它的宽、高,再确定“将这个长方体削成一个体积最大的圆锥”,这个圆锥体的底面直径应该是长方体的宽,圆锥体的高等于长方体的高,根据圆锥的体积计算公式解答。
【详解】
(厘米)
(厘米)
(厘米)
体积:
(立方厘米)
答:这个圆锥的体积是1017.36立方厘米。
12.(1)22.1056平方分米
(2)8.0384升
【分析】(1)求做这个水桶需要材料的面积,就是求这个无盖圆柱形水桶的表面积,先根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出水桶底面的半径;根据圆柱的表面积公式:表面积=底面积+侧面积,代入数据,即可解答,注意单位名数的换算;
(2)根据圆柱的容积公式:容积=底面积×高,代入数据,求出圆柱形水桶的容积,据此解答,注意单位名数的换算。
【详解】(1)50.24÷3.14÷2
=16÷2
=8(厘米)
3.14×82+50.24×40
=3.14×64+2009.6
=200.96+2009.6
=2210.56(平方厘米)
2210.56平方厘米=22.1056平方分米
答:做这样一个水桶至少需要22.1056平方分米的材料。
(2)3.14×82×40
=3.14×64×40
=200.96×40
=8038.4(立方厘米)
8038.4立方厘米=8.0384升
答:这个水桶可以装水8.0384升。
13.
15.7分
【分析】根据圆的周长公式C=2πr可知,r=C÷π÷2,求出圆柱、圆锥的底面半径;然后根据体积公式V柱=πr2h,V锥=πr2h,求出圆柱、圆锥的体积,再相加,就是水箱的体积;最后用水箱的容积除以每分钟注入水的容积,即可求出水箱注满需要的时间。
【详解】
(米)
(分)
答:一共需要15.7分。
14.(1)62.8升
(2)502.4升
【分析】(1)根据圆柱的体积计算公式“”即可求出这个圆柱形容器的容积是多少立方分米,再根据“立方分米与升是等量关系二者互化数值不变”转化成升。
(2)如果把这个圆锥沿高剖开,整个圆锥的剖面是一个大三角形,有水部分是一个小三角形,大三角形的高是小三角形高的2倍,则大三角形的底是小三角形底的2倍,即大圆锥的底面半径是小圆锥底面半径的2倍,则大圆锥体积是小圆锥体积的倍,即8倍,即水的体积是整个圆锥容积的。把圆锥的容积看作单位“1”,根据分数除法的意义即可解答。
【详解】(1)
(立方分米)
62.8立方分米升
答:这个圆柱形容器的容积是62.8升。
(2)由题意可知,在圆锥底面半径是小圆锥底面半径的2倍,设小圆锥的底面半径为,则大圆锥的底面半径为
水的体积是:
圆锥的容积是:
62.8÷
=62.8×8
=502.4(升)
答:这个圆锥形容器一共能装502.4升水。
【点睛】(1)根据公式计算即可,不难;(2)关键是求出水的体积占整个圆锥容器的几分之几,这也是解答本题的难点。
15.140.64立方厘米
【分析】根据题意可知,这个最大圆柱的高等于正方体的棱长,根据正方体的体积公式:,圆柱的体积公式:,把数据代入公式求出它们的体积差即可。
【详解】
=
=6×6×6-3.14×4×6
(立方厘米)
答:这个零件的体积是140.64立方厘米。
16.648吨
【分析】先根据“实际距离=图上距离÷比例尺”以及进率“1米=100厘米”,求出圆柱形水池底面内直径和高的实际尺寸;
再根据圆柱的体积(容积)公式V=πr2h,求出圆柱形水池的容积,然后乘1立方米水的质量,即可求出这个水池最多能装水的质量。
【详解】2÷
=2×600
=1200(厘米)
1200厘米=12米
1÷
=1×600
=600(厘米)
600厘米=6米
3×(12÷2)2×6
=3×62×6
=3×36×6
=648(立方米)
648×1=648(吨)
答:这个水池最多能装648吨水。
17.6吨
【分析】分析题目,设用200吨海水可以晒出x吨盐,根据晒出的盐的质量∶海水的质量的比值不变列出比例方程x∶200=15∶500,最后解出比例即可。
【详解】解:设用200吨海水可以晒出x吨盐。
x∶200=15∶500
500x=200×15
500x=3000
500x÷500=3000÷500
x=6
答:用200吨海水可以晒出6吨盐。
18.135千米;3小时
【分析】已知图上距离是13.5厘米,根据图上距离÷比例尺=实际距离,据此即可求出实际距离,再根据1千米=100000厘米,将结果换算成千米即可。已知每小时行45千米(速度),根据时间=路程÷速度,用实际距离÷45即可求出到达乙港所需的时间。
【详解】13.5÷=13.5×1000000=13500000(厘米)
13500000厘米=135千米
135÷45=3(小时)
答:这两个港口的实际距离为135千米,需要3小时才能到达乙港。
19.54平方米
【分析】根据的逆运算,用周长除以2,可得长与宽的和,根据比的意义,把长看作3份,则宽是2份,即长与宽的和是份,长占长与宽的和的,宽占长与宽的和的,根据求一个数的几分之几是多少,用乘法计算,可分别得长与宽的图上距离,再根据实际距离=图上距离÷比例尺,代入数据计算可分别得长与宽的实际距离,把单位转化为米,最后根据长方形的面积=长×宽。据此解答。
【详解】
(厘米)
(厘米)
(厘米)=9(米)
(厘米)=6(米)
(平方米)
答:这间教室的实际面积是54平方米。
20.(1)640千米
(2)4小时
【分析】(1)根据实际距离=图上距离÷比例尺,代入数据,求出甲、乙两地的实际距离,注意单位名数的换算。
(2)根据相遇时间=路程÷速度和,用甲、乙两点的路程÷A车与B车速度和,即可解答。
【详解】(1)32÷
=32×2000000
=64000000(厘米)
64000000厘米=640千米
答:甲、乙两地实际相距640千米。
(2)640÷(90+70)
=640÷160
=4(小时)
答:两车4小时可以相遇。
21.甲车480千米,乙车720千米
【分析】根据“图上距离÷比例尺=实际距离”计算出两地的路程,1千米=1000米=100000厘米,根据进率转换单位;根据“相遇问题速度和=相遇路程÷相遇时间”计算出两车的速度和;根据按比分配的一般方法,把两车的速度和平均分成(2+3)份,分别计算出2份、3份是多少千米,再用甲、乙两车速度分别乘相遇时间即可得到相遇时两车分别行驶的路程;据此解答。
【详解】6÷
=6×20000000
=120000000(厘米)
120000000厘米=1200千米
1200÷6=200(千米/时)
200÷(2+3)×2
=200÷5×2
=40×2
=80(千米/时)
200÷(2+3)×3
=200÷5×3
=40×3
=120(千米/时)
80×6=480(千米)
120×6=720(千米)
答:相遇时甲车行驶了480千米,乙车行驶了720千米。
22.A图60米;B图15米
【分析】根据实际距离=图上距离÷比例尺,代入相关数据分别求出图上距离3厘米分别表示的实际距离是多少厘米,再把厘米化成米即可。
【详解】3÷
=3×2000
=6000(厘米)
6000厘米=60米
3÷
=3×500
=1500(厘米)
1500厘米=15米
答:A图纸上3厘米表示实际长度60米,B图纸上3厘米表示实际长度15米。
23.1500平方米
【分析】已知图上长方形的周长是32厘米,根据长方形的周长=(长+宽)×2可知,长方形的长、宽之和=周长÷2;已知长与宽的比为5∶3,那么长、宽分别占长、宽之和的、,根据求一个数的几分之几是多少,用乘法求出长、宽的图上尺寸;
已知图纸的比例尺是1∶500,根据“实际距离=图上距离÷比例尺”,以及进率“1米=100厘米”,求出长、宽的实际尺寸;
最后根据长方形的面积=长×宽,求出这个长方形土地的实际面积。
【详解】长、宽之和:32÷2=16(厘米)
图上的长:
16×
=16×
=10(厘米)
图上的宽:
16×
=16×
=6(厘米)
实际的长:
10÷
=10×500
=5000(厘米)
5000厘米=50米
实际的宽:
6÷
=6×500
=3000(厘米)
3000厘米=30米
实际面积:50×30=1500(平方米)
答:这块地的实际面积是1500平方米。
24.37500平方米
【分析】由题可知该广场的长和宽的图上距离分别是5厘米和3厘米,根据公式:实际距离=图上距离÷比例尺,代入数据进行计算,可以求出该广场的长和宽的实际距离,再根据1米=100厘米进行单位换算,最后根据长方形的面积=长×宽,代入数据计算,即可求出该广场实际面积,据此解答。
【详解】(厘米)
(厘米)
25000厘米=250米
15000厘米=150米
250×150=37500(平方米)
答:该广场实际面积约是37500平方米。
25.能走完
【分析】根据实际距离=图上距离÷比例尺,代入数据,求出甲乙两地的实际距离。再根据路程=速度×时间,用90×1.5,求出杨叔叔开车1.5小时行驶的路程;再用甲乙两地的实际距离-杨叔叔开车1.5小时行驶的路程,求出剩下的路程;再把原来杨叔叔开车的速度看作单位“1”,速度提高后的速度是原来速度的(1+30%),用原来速度×(1+30%),求出提高后的速度,再根据路程=速度×时间,求出1小时行驶的路程,再和剩下的路程比较,大于剩下的路程,就能走完;小于剩下的路程,就不能走完,据此解答,注意单位名数的统一。
【详解】4.1÷
=4.1×6000000
=24600000(厘米)
24600000厘米=246千米
246-90×1.5
=246-135
=111(千米)
90×(1+30%)×1
=90×1.3×1
=117×1
=117(千米)
111<117,剩下的路程他1小时能走完。
答:剩下的路程他1小时能走完。
26.75千米
【分析】图上距离和比例尺已知,依据“图上距离÷比例尺=实际距离”即可求出两地的实际距离。再根据“速度和=路程÷相遇时间”即可求出两车的速度和,再减甲车的速度,即可求出乙车的速度,据此解答。
【详解】6÷=48000000(厘米)
48000000厘米=480千米
480÷3=160(千米/时)
160-85=75(千米/时)
答:乙车平均每小时行驶75千米。
中小学教育资源及组卷应用平台
2024-2025年北师大版六年级下册数学期中专题训练:应用题
1.两个同样的小圆柱拼成一个高为40厘米的长圆柱,表面积减少了60平方厘米,原来每个小圆柱的体积是多少立方厘米?
2.一个底面半径是6厘米的圆柱形容器,装一部分水,水中浸没着一个高9厘米的圆锥体铅锤。当铅锤从水中取出后,水面下降了2厘米。这个圆锥体的铅锤的底面积是多少平方厘米?
3.如图,先将甲容器注满水,再将水倒入乙容器,这时乙容器中的水有多高?
4.一个圆锥形沙堆,量得底面周长是12.56米,高是1.5米,把这堆沙全部铺在一个圆柱形沙坑内,这个沙坑的底面半径是2米。这堆沙平均能铺多厚?
5.一个底面半径为10厘米的圆柱形容器,里面装有水。将等底等高的一个圆柱形铁块和一个圆锥形铁块同时放入这个容器中,水面上升到9厘米(如图)。这个圆锥形铁块的体积是多少?
6.为了发展农村绿色能源,幸福村要挖一个圆柱形的沼气池,底面半径是4米、深2.5米。(π取值为3.14)
(1)这个沼气池的容积是多少立方米?
(2)如果要在沼气池的底部和四周铺上一种防漏水膜,大约需要铺多大面积的防漏水膜?
7.一个圆柱形水桶,从里面量底面半径是2分米,高是5分米,如果每立方分米水重1千克,这个水桶能盛水多少千克?
8.一个圆柱形储水池,底面直径10米,深5米,在池的四周及底面抹上水泥,抹水泥面积是多少平方米?
9.建筑工地上有一个圆锥形的沙土堆,底面面积是24平方米,高3米。把这些沙土平填在一个长6米,宽4米的长方体土坑中,沙土厚多少米?
10.一个粮仓如图,如果每立方米粮食的质量为700千克,这个粮仓最多能装多少千克粮食?
11.一个长方体的木块,它的长、宽、高的比是。这个长方体木块的长是24厘米,现在将这个长方体木块削成一个体积最大的圆锥,这个圆锥的体积是多少立方厘米?
12.做一个无盖的圆柱形水桶,水桶的底面周长是50.24厘米,高40厘米。
(1)做这样一个水桶至少需要多少平方分米的材料?
(2)这个水桶可以装水多少升?
13.用等底等高的圆柱和圆锥合在一起做成水箱,高都是3米,圆柱的底面周长为6.28米,现往水箱内每分注入0.8立方米水,从空箱到注满,一共需要多少分?(厚度忽略不计)
14.一个圆柱形容器,底面半径是2分米,高是5分米。(容器的厚度忽略不计)
(1)这个圆柱形容器的容积是多少升?
(2)将这个圆柱形容器装满水后,倒入如图的圆锥形容器内,水面高度正好是圆锥形容器高度的一半,这个圆锥形容器一共能装多少升水?
15.李师傅要做一个零件(如图),有一个棱长6厘米的正方体铁块,在它的两个底面之间挖一个圆柱形圆孔,圆孔的底面直径是4厘米,剩下的部分就是这个零件了,此时零件的体积是多少立方厘米?
16.在一幅比例尺是1∶600的图纸上量得一个圆柱形水池底面内直径是2厘米,高是1厘米,这个水池最多能装多少吨水?(π取3,1立方米水质量是1吨)
17.一个晒盐场用500千克海水可以晒出15千克盐,照这样计算用200吨海水可以晒出多少吨盐?
18.在一幅比例尺为1∶1000000的地图上,量得甲乙两个港口的距离大约13.5厘米,这两个港口的实际距离为多少千米?一艘每小时行45千米的轮船从甲港出发,需要多少小时才能到达乙港?
19.在一幅比例尺为1∶300的平面图上,量得一间长方形教室的周长是10厘米,长与宽的比是3∶2。这间教室的实际面积是多少平方米?
20.在一幅比例尺是1∶2000000的地图上量得甲、乙两地相距32厘米。
(1)甲、乙两地实际相距多少千米?
(2)A、B两辆汽车同时从甲、乙两地相对开出,A车速度90千米/时,B车速度70千米/时。两车多少小时可以相遇?
21.在一幅比例尺是1∶20000000的地图上,量得A、B两地的距离是6厘米。甲、乙两辆汽车同时从两地相对开出,经过6小时后两车相遇。已知甲、乙两车的速度比是2∶3,相遇时甲、乙两车各行驶了多少千米?
22.两张不同的图纸,A图纸的比例尺是1∶2000,B图纸的比例尺是1∶500。那么,这两张图纸上3厘米长的线段表示的实际长度各是多少米?
23.把一块长与宽的比为5∶3的长方形土地,用1∶500的比例尺在画图纸上,得到的长方形的周长是32厘米,这块长方形土地的实际面积是多少平方米?
24.青白江区城市森林和谐广场位于青白江区华金大道二段,是青白江百姓休闲、娱乐的重要场所。把它绘制在比例尺为1∶5000的地图上,该广场平面图是一个长约是5厘米,宽约是3厘米的长方形。请问该广场实际面积约是多少平方米?
25.在一幅比例尺为1∶6000000的地图上,量得甲乙两地高速公路长为4.1厘米。杨叔叔开车从甲地出发,以每小时90千米的速度行驶了1.5小时。为了尽快到达乙地,他在不超速的情况下将速度提高了30%。剩下的路程他1小时能走完吗?
26.在比例尺是1∶8000000的地图上,量得A、B两地间的距离是6厘米。甲、乙两辆汽车分别从两地同时出发,相向而行,3小时后相遇。已知甲车平均每小时行驶85千米,乙车平均每小时行驶多少千米?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2024-2025年北师大版六年级下册数学期中专题训练:应用题》参考答案
1.600立方厘米
【分析】分析题目,减少的部分是小圆柱的2个底面的面积,据此用60除以2求出小圆柱的底面积,再用40除以2求出小圆柱的高,最后根据圆柱的体积=底面积×高代入数据计算即可。
【详解】60÷2=30(平方厘米)
40÷2=20(厘米)
30×20=600(立方厘米)
答:原来每个小圆柱的体积是600立方厘米。
2.75.36平方厘米
【分析】由题意可知,下降的水的体积就是圆锥的体积,根据圆柱的体积公式,代入数据计算下降的水的体积,即圆锥的体积,再根据的逆运算,用圆锥的体积除以再除以高,即可得解。
【详解】
(平方厘米)
答:这个圆锥体的铅锤的底面积是75.36平方厘米。
3.6厘米
【分析】由图可知,甲乙两个容器等底等高,则甲容器的容积等于乙容器容积的;用18乘,即可求出乙容器中水的高度。
【详解】18×=6(厘米)
答:这时乙容器中的水有6厘米。
4.0.5米
【分析】由题意可知,圆锥的体积与圆柱的体积相等,根据圆的周长公式的逆运算,用周长除以圆周率再除以2可得半径,再根据圆锥的体积公式,代入数据可得圆锥体积,即圆柱体积,最后根据圆柱体积公式的逆运算,用体积除以圆周率再除以半径的平方,即可得解。
【详解】
(米)
答:这堆沙平均能铺0.5米厚。
5.314立方厘米
【分析】水面上升的体积,就是圆柱和圆锥铁块的体积。由题意可知,圆柱形容器水面升高了厘米,根据圆柱的体积计算公式,即可求出水面上升的体积,即圆柱和圆锥的体积和,等底等高的圆柱的体积是圆锥体积的3倍,利用体积除以(3+1)即可求出圆锥的体积。
【详解】3.14×102×(9-5)÷(3+1)
=3.14×100×4÷4
=314(立方厘米)
答:这个圆锥形铁块的体积是314立方厘米。
6.(1)125.6立方米
(2)113.04平方米
【分析】(1)根据圆柱的体积(容积):V=sh=πr2h,代入数据计算即可求出这个沼气池的容积。
(2)防漏水膜的面积=底面面积+侧面积,根据圆的面积:S=πr2,侧面积:S=ch=2πrh,代入数据计算即可。
【详解】(1)3.14×42×2.5
=3.14×16×2.5
=125.6(立方米)
答:这个沼气池的容积是125.6立方米。
(2)3.14×42+3.14×4×2×2.5
=3.14×16+3.14×4×2×2.5
=50.24+62.8
=113.04(平方米)
答:大约需要铺113.04平方米的防漏水膜。
7.62.8千克
【分析】分析题目,先根据圆柱的体积=πr2h求出圆柱的体积,再乘每立方米水的重量即可解答。
【详解】3.14×22×5×1
=3.14×4×5×1
=12.56×5×1
=62.8×1
=62.8(千克)
答:这个水桶能盛水62.8千克。
8.235.5平方米
【分析】根据题意,在圆柱形储水池的四周及底面抹上水泥,那么抹水泥部分的面积=圆柱的侧面积+底面积;根据圆柱的侧面积公式S侧=πdh,圆柱的底面积公式S底=πr2,代入数据计算求解。
【详解】抹水泥部分的面积:
3.14×10×5+3.14×(10÷2)2
=3.14×10×5+3.14×52
=3.14×10×5+3.14×25
=157+78.5
=235.5(平方米)
答:抹水泥面积是235.5平方米。
9.1米
【分析】已知圆锥形沙土堆的底面面积是24平方米,高3米,根据圆锥的体积公式V=Sh,代入数据计算,求出沙土的体积;
把这些沙土平填在一个长6米,宽4米的长方体土坑中,沙土的体积不变;根据长方体的体积=长×宽×高,可知长方体的高=体积÷长÷宽,代入数据计算,求出沙土的厚度。
【详解】×24×3=24(立方米)
24÷6÷4
=4÷4
=1(米)
答:沙土厚1米。
10.3736.6千克
【分析】从图中可知,粮仓的上面是圆锥、下面是圆柱;根据圆柱的体积(容积)公式V=πr2h,圆锥的体积(容积)公式V=πr2h,代入数据计算,求出圆柱、圆锥的容积,再相加,即是这个粮仓的容积;然后用每立方米粮食的质量乘粮仓的容积,即可求出这个粮仓最多能装粮食的质量。
【详解】2÷2=1(米)
3.14×12×1.5+×3.14×12×0.6
=3.14×1×1.5+×3.14×1×0.6
=4.71+0.628
=5.338(立方米)
700×5.338=3736.6(千克)
答:这个粮仓最多能装3736.6千克粮食。
11.1017.36立方厘米
【分析】长方体的12条棱分为三组,互相平行的一组是4条,根据题意,可知长占长+宽+高的和的,已知一个数的几分之几是多少,求这个数,用除法,先求出长+宽+高的和,再用乘法分别求出它的宽、高,再确定“将这个长方体削成一个体积最大的圆锥”,这个圆锥体的底面直径应该是长方体的宽,圆锥体的高等于长方体的高,根据圆锥的体积计算公式解答。
【详解】
(厘米)
(厘米)
(厘米)
体积:
(立方厘米)
答:这个圆锥的体积是1017.36立方厘米。
12.(1)22.1056平方分米
(2)8.0384升
【分析】(1)求做这个水桶需要材料的面积,就是求这个无盖圆柱形水桶的表面积,先根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出水桶底面的半径;根据圆柱的表面积公式:表面积=底面积+侧面积,代入数据,即可解答,注意单位名数的换算;
(2)根据圆柱的容积公式:容积=底面积×高,代入数据,求出圆柱形水桶的容积,据此解答,注意单位名数的换算。
【详解】(1)50.24÷3.14÷2
=16÷2
=8(厘米)
3.14×82+50.24×40
=3.14×64+2009.6
=200.96+2009.6
=2210.56(平方厘米)
2210.56平方厘米=22.1056平方分米
答:做这样一个水桶至少需要22.1056平方分米的材料。
(2)3.14×82×40
=3.14×64×40
=200.96×40
=8038.4(立方厘米)
8038.4立方厘米=8.0384升
答:这个水桶可以装水8.0384升。
13.
15.7分
【分析】根据圆的周长公式C=2πr可知,r=C÷π÷2,求出圆柱、圆锥的底面半径;然后根据体积公式V柱=πr2h,V锥=πr2h,求出圆柱、圆锥的体积,再相加,就是水箱的体积;最后用水箱的容积除以每分钟注入水的容积,即可求出水箱注满需要的时间。
【详解】
(米)
(分)
答:一共需要15.7分。
14.(1)62.8升
(2)502.4升
【分析】(1)根据圆柱的体积计算公式“”即可求出这个圆柱形容器的容积是多少立方分米,再根据“立方分米与升是等量关系二者互化数值不变”转化成升。
(2)如果把这个圆锥沿高剖开,整个圆锥的剖面是一个大三角形,有水部分是一个小三角形,大三角形的高是小三角形高的2倍,则大三角形的底是小三角形底的2倍,即大圆锥的底面半径是小圆锥底面半径的2倍,则大圆锥体积是小圆锥体积的倍,即8倍,即水的体积是整个圆锥容积的。把圆锥的容积看作单位“1”,根据分数除法的意义即可解答。
【详解】(1)
(立方分米)
62.8立方分米升
答:这个圆柱形容器的容积是62.8升。
(2)由题意可知,在圆锥底面半径是小圆锥底面半径的2倍,设小圆锥的底面半径为,则大圆锥的底面半径为
水的体积是:
圆锥的容积是:
62.8÷
=62.8×8
=502.4(升)
答:这个圆锥形容器一共能装502.4升水。
【点睛】(1)根据公式计算即可,不难;(2)关键是求出水的体积占整个圆锥容器的几分之几,这也是解答本题的难点。
15.140.64立方厘米
【分析】根据题意可知,这个最大圆柱的高等于正方体的棱长,根据正方体的体积公式:,圆柱的体积公式:,把数据代入公式求出它们的体积差即可。
【详解】
=
=6×6×6-3.14×4×6
(立方厘米)
答:这个零件的体积是140.64立方厘米。
16.648吨
【分析】先根据“实际距离=图上距离÷比例尺”以及进率“1米=100厘米”,求出圆柱形水池底面内直径和高的实际尺寸;
再根据圆柱的体积(容积)公式V=πr2h,求出圆柱形水池的容积,然后乘1立方米水的质量,即可求出这个水池最多能装水的质量。
【详解】2÷
=2×600
=1200(厘米)
1200厘米=12米
1÷
=1×600
=600(厘米)
600厘米=6米
3×(12÷2)2×6
=3×62×6
=3×36×6
=648(立方米)
648×1=648(吨)
答:这个水池最多能装648吨水。
17.6吨
【分析】分析题目,设用200吨海水可以晒出x吨盐,根据晒出的盐的质量∶海水的质量的比值不变列出比例方程x∶200=15∶500,最后解出比例即可。
【详解】解:设用200吨海水可以晒出x吨盐。
x∶200=15∶500
500x=200×15
500x=3000
500x÷500=3000÷500
x=6
答:用200吨海水可以晒出6吨盐。
18.135千米;3小时
【分析】已知图上距离是13.5厘米,根据图上距离÷比例尺=实际距离,据此即可求出实际距离,再根据1千米=100000厘米,将结果换算成千米即可。已知每小时行45千米(速度),根据时间=路程÷速度,用实际距离÷45即可求出到达乙港所需的时间。
【详解】13.5÷=13.5×1000000=13500000(厘米)
13500000厘米=135千米
135÷45=3(小时)
答:这两个港口的实际距离为135千米,需要3小时才能到达乙港。
19.54平方米
【分析】根据的逆运算,用周长除以2,可得长与宽的和,根据比的意义,把长看作3份,则宽是2份,即长与宽的和是份,长占长与宽的和的,宽占长与宽的和的,根据求一个数的几分之几是多少,用乘法计算,可分别得长与宽的图上距离,再根据实际距离=图上距离÷比例尺,代入数据计算可分别得长与宽的实际距离,把单位转化为米,最后根据长方形的面积=长×宽。据此解答。
【详解】
(厘米)
(厘米)
(厘米)=9(米)
(厘米)=6(米)
(平方米)
答:这间教室的实际面积是54平方米。
20.(1)640千米
(2)4小时
【分析】(1)根据实际距离=图上距离÷比例尺,代入数据,求出甲、乙两地的实际距离,注意单位名数的换算。
(2)根据相遇时间=路程÷速度和,用甲、乙两点的路程÷A车与B车速度和,即可解答。
【详解】(1)32÷
=32×2000000
=64000000(厘米)
64000000厘米=640千米
答:甲、乙两地实际相距640千米。
(2)640÷(90+70)
=640÷160
=4(小时)
答:两车4小时可以相遇。
21.甲车480千米,乙车720千米
【分析】根据“图上距离÷比例尺=实际距离”计算出两地的路程,1千米=1000米=100000厘米,根据进率转换单位;根据“相遇问题速度和=相遇路程÷相遇时间”计算出两车的速度和;根据按比分配的一般方法,把两车的速度和平均分成(2+3)份,分别计算出2份、3份是多少千米,再用甲、乙两车速度分别乘相遇时间即可得到相遇时两车分别行驶的路程;据此解答。
【详解】6÷
=6×20000000
=120000000(厘米)
120000000厘米=1200千米
1200÷6=200(千米/时)
200÷(2+3)×2
=200÷5×2
=40×2
=80(千米/时)
200÷(2+3)×3
=200÷5×3
=40×3
=120(千米/时)
80×6=480(千米)
120×6=720(千米)
答:相遇时甲车行驶了480千米,乙车行驶了720千米。
22.A图60米;B图15米
【分析】根据实际距离=图上距离÷比例尺,代入相关数据分别求出图上距离3厘米分别表示的实际距离是多少厘米,再把厘米化成米即可。
【详解】3÷
=3×2000
=6000(厘米)
6000厘米=60米
3÷
=3×500
=1500(厘米)
1500厘米=15米
答:A图纸上3厘米表示实际长度60米,B图纸上3厘米表示实际长度15米。
23.1500平方米
【分析】已知图上长方形的周长是32厘米,根据长方形的周长=(长+宽)×2可知,长方形的长、宽之和=周长÷2;已知长与宽的比为5∶3,那么长、宽分别占长、宽之和的、,根据求一个数的几分之几是多少,用乘法求出长、宽的图上尺寸;
已知图纸的比例尺是1∶500,根据“实际距离=图上距离÷比例尺”,以及进率“1米=100厘米”,求出长、宽的实际尺寸;
最后根据长方形的面积=长×宽,求出这个长方形土地的实际面积。
【详解】长、宽之和:32÷2=16(厘米)
图上的长:
16×
=16×
=10(厘米)
图上的宽:
16×
=16×
=6(厘米)
实际的长:
10÷
=10×500
=5000(厘米)
5000厘米=50米
实际的宽:
6÷
=6×500
=3000(厘米)
3000厘米=30米
实际面积:50×30=1500(平方米)
答:这块地的实际面积是1500平方米。
24.37500平方米
【分析】由题可知该广场的长和宽的图上距离分别是5厘米和3厘米,根据公式:实际距离=图上距离÷比例尺,代入数据进行计算,可以求出该广场的长和宽的实际距离,再根据1米=100厘米进行单位换算,最后根据长方形的面积=长×宽,代入数据计算,即可求出该广场实际面积,据此解答。
【详解】(厘米)
(厘米)
25000厘米=250米
15000厘米=150米
250×150=37500(平方米)
答:该广场实际面积约是37500平方米。
25.能走完
【分析】根据实际距离=图上距离÷比例尺,代入数据,求出甲乙两地的实际距离。再根据路程=速度×时间,用90×1.5,求出杨叔叔开车1.5小时行驶的路程;再用甲乙两地的实际距离-杨叔叔开车1.5小时行驶的路程,求出剩下的路程;再把原来杨叔叔开车的速度看作单位“1”,速度提高后的速度是原来速度的(1+30%),用原来速度×(1+30%),求出提高后的速度,再根据路程=速度×时间,求出1小时行驶的路程,再和剩下的路程比较,大于剩下的路程,就能走完;小于剩下的路程,就不能走完,据此解答,注意单位名数的统一。
【详解】4.1÷
=4.1×6000000
=24600000(厘米)
24600000厘米=246千米
246-90×1.5
=246-135
=111(千米)
90×(1+30%)×1
=90×1.3×1
=117×1
=117(千米)
111<117,剩下的路程他1小时能走完。
答:剩下的路程他1小时能走完。
26.75千米
【分析】图上距离和比例尺已知,依据“图上距离÷比例尺=实际距离”即可求出两地的实际距离。再根据“速度和=路程÷相遇时间”即可求出两车的速度和,再减甲车的速度,即可求出乙车的速度,据此解答。
【详解】6÷=48000000(厘米)
48000000厘米=480千米
480÷3=160(千米/时)
160-85=75(千米/时)
答:乙车平均每小时行驶75千米。
同课章节目录
