空间向量与立体几何高频考点 归纳练 2025年高考数学复习备考模拟预测
文档属性
| 名称 | 空间向量与立体几何高频考点 归纳练 2025年高考数学复习备考模拟预测 |  | |
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-08 10:23:42 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
空间向量与立体几何高频考点 归纳练
2025年高考数学复习备考模拟预测
一、单选题
1.已知为圆锥的底面直径,为底面圆心,正三角形内接于,若,圆锥的侧面积为,则与所成角的余弦值为( )
A. B. C. D.
2.已知棱长为的正四面体与一个球相交,球与正四面体的每个面所在平面的交线都为一个面积为的圆,则该球的表面积为( )
A. B. C. D.
3.底面半径为3的圆锥被平行底面的平面所截,截去一个底面半径为1、高为1的圆锥,所得圆台的体积为( )
A. B. C. D.
4.象牙镂雕套球又称“同心球”,制作相当繁复,工艺要求极高.据《格古要论》记载,早在宋代就已出现3层套球,时称“鬼工球”.某象牙镂雕套球的直径为,其表面的圆形孔的直径均为,记其中两个圆形孔的圆心为,如图所示,若,则圆与圆所在平面的夹角的正弦值为( )
A. B. C. D.
5.一个圆锥被平行于底面的平面所截,上下两个几何体的侧面积之比为,则上下两个几何体的体积之比为( )
A. B. C. D.
6.一个密闭的长方体盒子高为4,底面是边长为2的正方形,盒内有一个半径为1的小球,若将盒子任意翻动,则小球不能到达区域的体积是( )
A. B. C. D.
7.折扇是我国古老文化的延续,在我国已有四千年左右的历史.如图所示的某折扇扇面可视为一个圆台的侧面展开图,该扇面的面积为元,若该圆台上、下底面半径分别为5,10,则该圆台的体积为( )
A. B. C. D.
8.已知正方体的棱长为1,点P在正方体的内切球表面上运动,且满足平面,则的最小值为( )
A. B. C. D.
9.在三棱锥中,是以为斜边的等腰直角三角形,且,,点在底面内的射影在的外部,且,则该三棱锥外接球的表面积为( )
A. B. C. D.
二、多选题
10.如图,在四面体中,,,,,,分别为棱上的动点,则( )
A.的最小值为 B.四面体的体积为
C.的最小值为2 D.二面角的余弦值为
11.如图,四棱锥的外接球球心为点O,且底面为正方形,平面.若点M为上靠近点D的三等分点,点P,Q分别为线段与平面上的点,则最小时,下列说法正确的是( )
A.
B.点P为线段的中点
C.平面截四棱锥所得的截面是直角梯形
D.三棱锥的体积为
12.六氟化硫()分子结构为正八面体(可看作是将两个棱长均相等的正四棱锥将底面粘接在一起的几何体).如图,正八面体的棱长为,下列说法中正确的有( )
A.异面直线AE与BF所成的角为45°
B.此八面体的外接球与内切球的体积之比为
C.若点P为棱上的动点,则的最小值为
D.若点为四边形的中心,点为此八面体表面上动点,且,则动点的轨迹长度为
三、填空题
13.已知圆锥的母线长为2,其侧面展开图是一个半圆,则该圆锥的体积为 .
14.台球是球类运动项目之一,是运动员在台球桌上,用一根长的球杆,按照一定的规则,通过击打白色主球,使目标球入袋的一项体育休闲项目.如图,三角架内有15个大小相同的球,且球与球,球与三角架均相切.若三角架为边长是的等边三角形,则球的半径为 .(取)
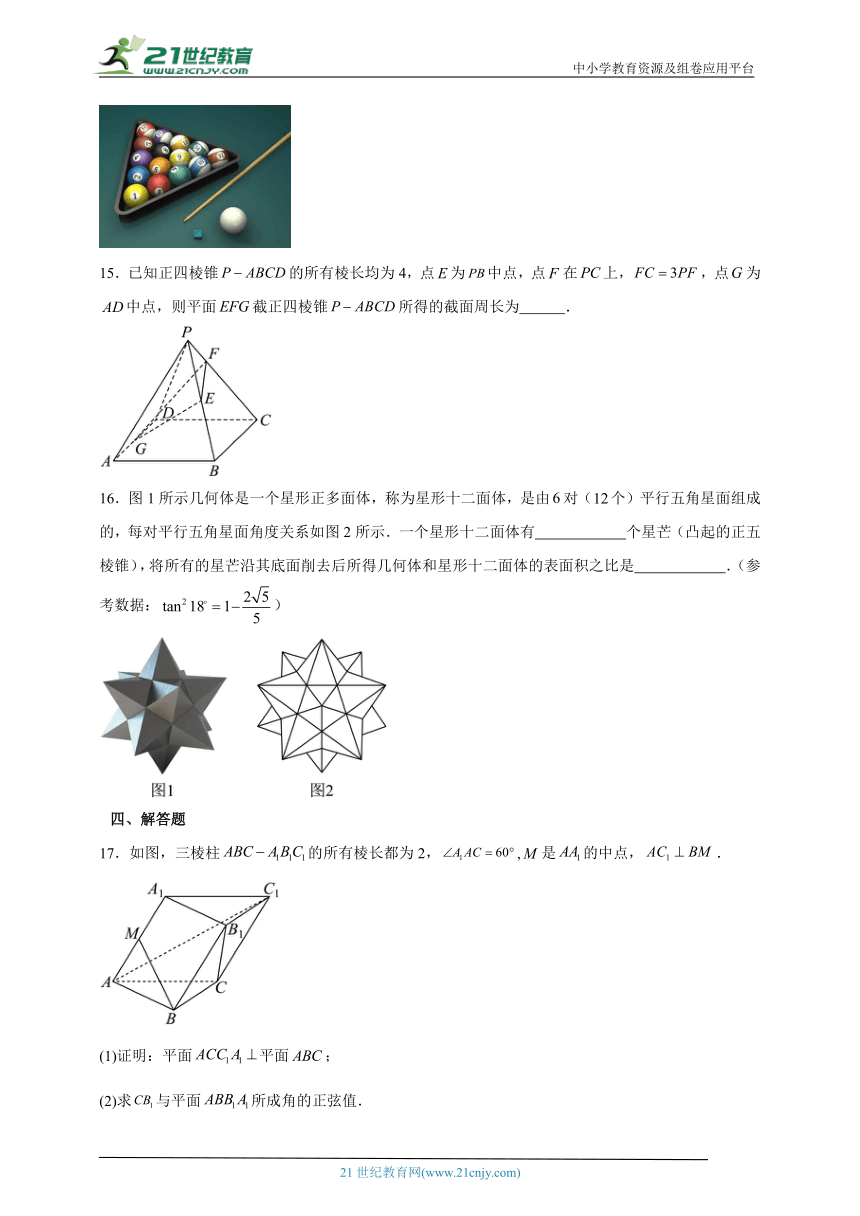
15.已知正四棱锥的所有棱长均为4,点为中点,点在上,,点为中点,则平面截正四棱锥所得的截面周长为 .
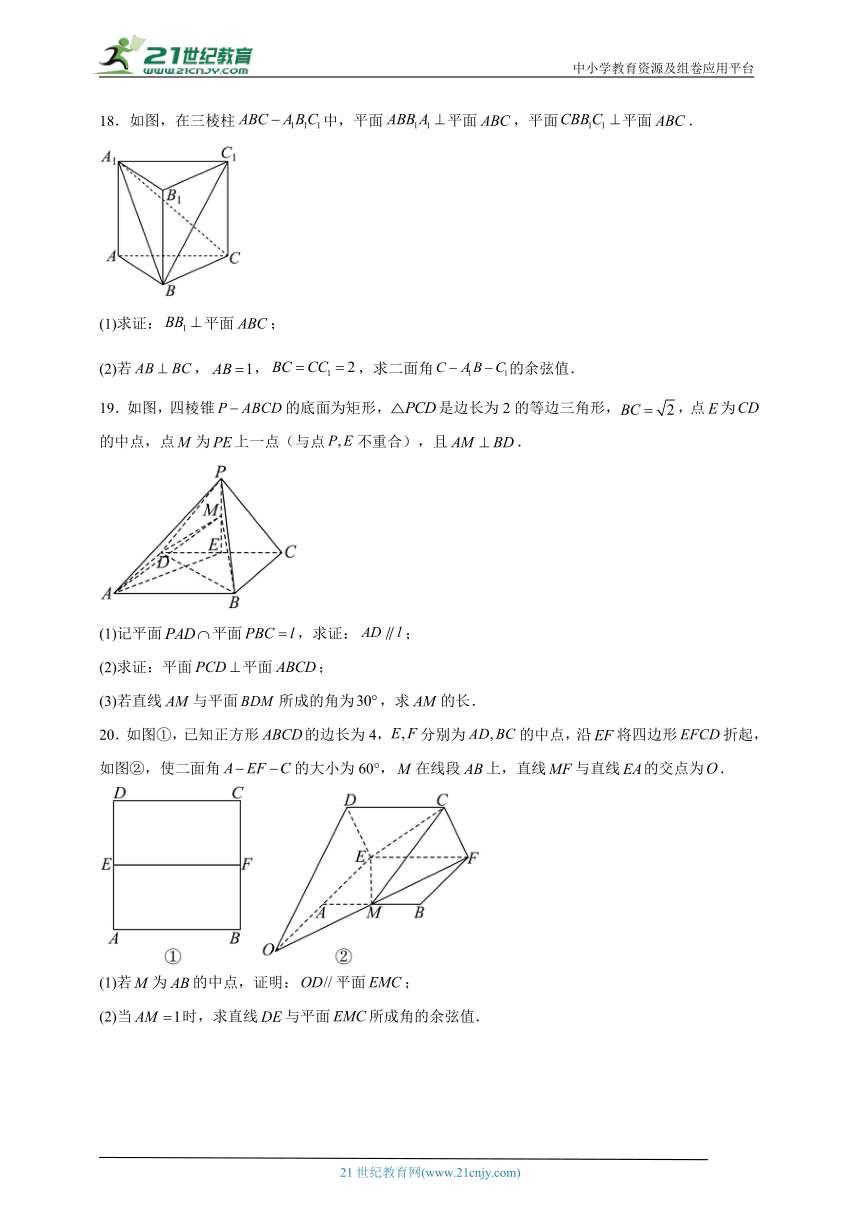
16.图1所示几何体是一个星形正多面体,称为星形十二面体,是由对(个)平行五角星面组成的,每对平行五角星面角度关系如图2所示.一个星形十二面体有 个星芒(凸起的正五棱锥),将所有的星芒沿其底面削去后所得几何体和星形十二面体的表面积之比是 .(参考数据:)
四、解答题
17.如图,三棱柱的所有棱长都为2,,是的中点,.
(1)证明:平面平面;
(2)求与平面所成角的正弦值.
18.如图,在三棱柱中,平面平面,平面平面.
(1)求证:平面;
(2)若,,,求二面角的余弦值.
19.如图,四棱锥的底面为矩形,是边长为2的等边三角形,,点为的中点,点为上一点(与点不重合),且.
(1)记平面平面,求证:;
(2)求证:平面平面;
(3)若直线与平面所成的角为,求的长.
20.如图①,已知正方形的边长为4,分别为的中点,沿将四边形折起,如图②,使二面角的大小为60°,在线段上,直线与直线的交点为.
(1)若为的中点,证明:平面;
(2)当时,求直线与平面所成角的余弦值.
参考答案
1.A
先求出圆锥的底面半径和,过点作交的延长线于点,为与所成角,由余弦定理求解即可.
设圆锥的底面半径为,母线长为,
因为,所以,
所以,所以,
所以,又正三角形内接于,
所以,解得:,所以,
所以,
过点作交的延长线于点,,
所以与所成角即为与所成角或其补角,
所以为与所成角,
由余弦定理可得:,
故选:A.
2.B
根据正弦定理可得外接圆半径,进而根据勾股定理可得四面体的高,即可根据球的性质,结合勾股定理求解半径得解.
由对称性,可知球心与正四面体重心重合,
由于球与正四面体的每个面所在平面的交线都为一个面积为的圆,故每个面的交线为半径为3的圆.
设球心为,为的中心,则,故,故
设球心到任意面的距离为,则由等体积法可得,
故连接球心与任意面中心,则连线长为3,且连线垂直该面,再连交线圆上一点与球心(即为球的半径),由勾股定理得球的半径为,则表面积为.
故选:B.
3.A
根据相似可得原圆锥的高,进而利用圆锥的体积公式即可求解.
由已知,设原圆锥的高为,则,所以,
因为, ,
所以.
故选:A.
4.C
由球的结构特征,结合余弦定理即可求解;
记该象牙镂雕套球的球心为,圆与圆所在平面的夹角即为(或其补角),.
所以,
所以,
故选:C
5.D
由圆锥侧面积公式及体积公式即可求解.
根据定义知上、下两个几何体分别为小圆锥和圆台,设小圆锥的高为,底面半径为,所以母线长为,
原圆锥的高为,底面半径为,所以母线长为
由小圆锥的侧面积为:,大圆锥的侧面积为:,
上下两个几何体的侧面积之比为,
所以,又由相似易得:,
所以得,即,
所以小圆锥和原圆锥的体积比,
所以小圆锥和圆台的体积之比为.
故选:D.
6.B
根据空间想象得出小球不能达到的空间,利用空间几何体的体积公式计算即可.
小球在长方体盒子自由滚动当与长方体三面相切时,
即在正方体的8个顶点处的单位立方体空间内,
不能达到的空间为,
此后当小球移动时与长方体的侧面两面相切,
其不能达到的空间为以长方体的侧棱中间长为2的棱为棱柱减去底面半径为1的圆柱的四分之一体积
(这样的空间有四个),体积为,
故小球达不到的空间体积为:.
故选:B
7.C
根据已知分别求出上下底面面积,最后由圆台的体积计算公式.
,圆台的侧面积为,母线长
圆台的高
则圆台上下底面面积为
由圆台的体积计算公式可得:
故选:C.
8.A
根据平面平面可得点的轨迹是平面与正方体内切球的交线,根据点与圆的位置关系可求得AP的最小值.
由题意得,正方体内切球的球心为正方体的中心,记为点,内切球半径.
∵,平面,平面,
∴平面,同理可得平面,
∵平面,,∴平面平面,
∵平面,∴平面,故点的轨迹是平面与正方体内切球的交线,此交线为圆,记圆心为.
如图,以为原点建立空间直角坐标系,则,,,,
∴,,.
设平面的法向量为,则,
令,则,故,
∴点到平面的距离为,
∴圆的半径为,
由得,,
∴,
∴的最小值为.
9.B
由题设,知且,底面,
若是的中点,而,则,且,
而底面,则,都在平面内,则平面,
由平面,则,又底面,则,
由,则,即,
由点在底面内的射影在的外部,则在边的外侧,如下图,
若在的另一侧,则必与的中点重合,不合题设,
由题意,该三棱锥外接球的球心在过的中点垂直于平面的直线上,
根据几何关系有,则,
所以,可得,
(注意时,不成立),
所以,外接球半径,则,故其表面积.
故选:B
10.BC
先由线面垂直的判定定理证明平面,再由棱锥的体积公式可得B正确;由线面垂直的判定定理得到平面,从而得到二面角的平面角,再由几何关系计算可得D错误;将侧面翻折至点与平面共面,分别得到的最小值为和的最小值为,由解三角形即得A错误,C正确.
对于B,因为,,所以,
又,,平面,所以平面.
因为,,所以,,,
所以四面体的体积为,故B正确;
对于D,由平面,平面,得,
又,,平面,所以平面,
又平面,则,所以为二面角的平面角,
因为,,所以,
所以,故D错误;
对于A、C,将侧面翻折至点与平面共面,如图所示,
过点作于点,过点作于点,
则的最小值为,的最小值为,故A错误,C正确.
故选:BC.
11.AC
对于A,连接,如下图:
因为平面,且平面,
所以,,,
因为在正方形中,,且,平面,
所以平面,因为平面,所以,
同理可得,
因为为的斜边,
所以的中点到的距离都等于的一半,
则球心就是的中点,如下图:
在正方形中,,
在中,,
在中,,
则,,
由,则易知,则,
故A正确;
对于B,由平面,则当平面时,最短,
因为平面,所以,
因为,且平面,所以平面,
将绕旋转到的位置,使得平面,
在平面中,过作,垂足为,如下图:
易知,,由图可知,
在正方形中,由,则,
在中,,则,
易知,所以,,
在中,,
易知为的三等分点,如下图:
故B错误;
对于C,由B可知,易知,
在中,过作,交于,连接,如下图:
易知,,即,,即,
因为平面,所以平面,
因为平面,所以,故C正确;
对于D,由题意可作图如下:
由C易知平面,由,则,
在中,,
因为平面,平面,所以,
在中,,,
所以三棱锥的体积,故D错误.
故选:AC.
12.BD
利用等角定理即可判断A,再利用内切圆和外接圆的性质求的,可判断B,利用展开图可得最小值为菱形的对角线可判断C,由可得轨迹为正八面体与半径为的球的交线,可求出其一个面的长度,再由对称性可求出轨迹的总长.
对于A,由正八面体的结构特征可得,,所以异面直线AE与BF所成的角为,A错误;
对于B,根据对称性易得其外接球与内切球的球心为其中心,所以,内切球切点在面的中线上,
且在四边形中,由等面积法可得,则,B正确;
对于C,因为的展开图为一个角为的菱形,对角线即为的最小值,此时,C错误;
对于D,因为到各棱的距离都等于,则点在各面的轨迹恰好为各个面的内切圆,记其半径为,
因为为等边三角形,
所以,所以在一个面的轨迹长度为,
所以在八个面内的轨迹长度之和为,D正确.
故选:BD
13.
由条件求解底面半径和圆锥的高,即可求得圆锥的体积.
设底面半径为,由题意可知,解得:,
圆锥的高,
所以圆锥的体积.
故答案为:
14.3
根据球与球、球与三角架均相切这些特征构建平面图形,利用平面几何中直线与圆相切并结合等边三角形得到球的半径与三角架边长之间的关系,即可求得半径.
可构建如图所示的平面图形,
设球的半径为,则,
所以,解得.
故答案为:3.
15.
延长与的延长线交于点,连接与交于点,延长与的延长线交于点,连接与交于点,则平面截正四棱锥所得的截面为五边形,即可求解.
延长与的延长线交于点,连接与交于点,延长与的延长线交于点,连接与交于点,
则平面截正四棱锥所得的截面为五边形,
如图所示:
易知,,
,
所以五边形的周长为.
故答案为:
16.
结合图形可判断出星芒的个数;将每个正五棱锥沿着侧面展开与底面在同一个平面上,形成一个正五角星,计算出正五棱锥侧面积和底面积之比即可.
由图可知,每个星形十二面体有个星芒,
将每个正五棱锥沿着侧面展开与底面在同一个平面上,形成一个正五角星,
则这个正五角星的五个顶点在圆上,连接,则垂直平分,设,
正五棱锥的侧面积等于,底面积等于,
正五边形的每个内角为,则,故,
则,所以,,,
设,则,则,
,则,
所以,将所有的星芒沿其底面削去后所得几何体和星形十二面体的表面积之比为
,
故答案为:;.
17.(1)证明见解析
(2)
(1)取的中点,得到,证得,再由,利用线面垂直的判定定理,证得平面,得到,结合,证得平面,进而证得平面平面.
(2)连接,证得平面,以为坐标原点,建立空间直角坐标系,求得平面的一个法向量为和向量,结合向量的夹角公式,即可求解.
(1)证明:取的中点,连接,
因为是的中点,所以,
又因为三棱柱的所有棱长都是2,
所以四边形为菱形,所以,所以,
因为,且,平面,所以平面,
又因为平面,所以,
在等边中,因为为的中点,所以,
又因为,且平面,所以平面,
因为平面,所以平面平面.
(2)解:连接,因为三棱柱的所有棱长都为2,且,
可得为等边三角形,且为的中点,所以,
由(1)知:平面平面,平面平面,
且平面,所以平面,
所以两两垂直,以为坐标原点,以所在的直线分别为轴,轴和轴,建立空间直角坐标系,如图所示,
则,
所以,
设平面的法向量为,则,
取,可得,所以,
因为,
设与平面所成的角为,则,
所以与平面所成的角的正弦值为.
18.(1)证明见解析
(2).
(1)根据面面垂直的性质可得平面,进而可得,同理得,即可利用线面垂直的判定求解,
(2)建立空间直角坐标系,求解平面法向量,即可利用法向量的夹角求解.
(1)如图,取为内一点,作,交于点,作,交于点.
因为平面平面且平面平面,平面,
所以平面.
因为平面,
所以,同理得.
因为,且平面,
所以平面.
(2)因为,,两两垂直,以为原点,建立空间直角坐标系,如图所示.
由题意,得,,,,
则,,,.
设平面的法向量为,则
令,则,,所以.
设平面的法向量为,则
令,则,,所以.
设二面角的平面角为,则由图可得.
故二面角的余弦值为.
19.(1)证明见解析
(2)证明见解析
(3)
(1)因为底面为矩形,
所以.
又因为面,面,
所以面.
又因为面,面面,
所以.
(2)因为三角形是等边三角形,且是的中点,
所以.
如图1,连接,在矩形中,,,
所以.所以.
因为,
所以,即.
因为,,
平面,
所以平面.由平面,得.
又因为,,
平面
所以平面.
因为平面,
所以平面平面.
(3)设是的中点,以为原点,所在直线为轴,所在直线为轴,所在直线为轴建立如图2所示的空间直角坐标系.
由已知得,,,,.
设,
则,,.
设面的法向量为,
则,即,
令,有,
所以,
解得,
所以当直线与平面所成的角为时,.
20.(1)证明见解析;
(2).
(1)连接交于点Q,连接,因为正方形,分别为的中点,所以四边形为矩形,所以为中点,
又为的中点,,所以为的中点,
所以,
又平面,平面,
所以平面.
(2)
由题知:,二面角的大小为60°,
故:是二面角的平面角,,
又,所以为正三角形,
取中点,中点,连接,
则,易证:面,所以,
以为坐标原点,分别为轴建立平面直角坐标系,
则,
所以,
设平面的法向量为,
则,令,则
则,
设直线与平面的夹角为,则,
又,所以,所以,
直线与平面所成角的余弦值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
空间向量与立体几何高频考点 归纳练
2025年高考数学复习备考模拟预测
一、单选题
1.已知为圆锥的底面直径,为底面圆心,正三角形内接于,若,圆锥的侧面积为,则与所成角的余弦值为( )
A. B. C. D.
2.已知棱长为的正四面体与一个球相交,球与正四面体的每个面所在平面的交线都为一个面积为的圆,则该球的表面积为( )
A. B. C. D.
3.底面半径为3的圆锥被平行底面的平面所截,截去一个底面半径为1、高为1的圆锥,所得圆台的体积为( )
A. B. C. D.
4.象牙镂雕套球又称“同心球”,制作相当繁复,工艺要求极高.据《格古要论》记载,早在宋代就已出现3层套球,时称“鬼工球”.某象牙镂雕套球的直径为,其表面的圆形孔的直径均为,记其中两个圆形孔的圆心为,如图所示,若,则圆与圆所在平面的夹角的正弦值为( )
A. B. C. D.
5.一个圆锥被平行于底面的平面所截,上下两个几何体的侧面积之比为,则上下两个几何体的体积之比为( )
A. B. C. D.
6.一个密闭的长方体盒子高为4,底面是边长为2的正方形,盒内有一个半径为1的小球,若将盒子任意翻动,则小球不能到达区域的体积是( )
A. B. C. D.
7.折扇是我国古老文化的延续,在我国已有四千年左右的历史.如图所示的某折扇扇面可视为一个圆台的侧面展开图,该扇面的面积为元,若该圆台上、下底面半径分别为5,10,则该圆台的体积为( )
A. B. C. D.
8.已知正方体的棱长为1,点P在正方体的内切球表面上运动,且满足平面,则的最小值为( )
A. B. C. D.
9.在三棱锥中,是以为斜边的等腰直角三角形,且,,点在底面内的射影在的外部,且,则该三棱锥外接球的表面积为( )
A. B. C. D.
二、多选题
10.如图,在四面体中,,,,,,分别为棱上的动点,则( )
A.的最小值为 B.四面体的体积为
C.的最小值为2 D.二面角的余弦值为
11.如图,四棱锥的外接球球心为点O,且底面为正方形,平面.若点M为上靠近点D的三等分点,点P,Q分别为线段与平面上的点,则最小时,下列说法正确的是( )
A.
B.点P为线段的中点
C.平面截四棱锥所得的截面是直角梯形
D.三棱锥的体积为
12.六氟化硫()分子结构为正八面体(可看作是将两个棱长均相等的正四棱锥将底面粘接在一起的几何体).如图,正八面体的棱长为,下列说法中正确的有( )
A.异面直线AE与BF所成的角为45°
B.此八面体的外接球与内切球的体积之比为
C.若点P为棱上的动点,则的最小值为
D.若点为四边形的中心,点为此八面体表面上动点,且,则动点的轨迹长度为
三、填空题
13.已知圆锥的母线长为2,其侧面展开图是一个半圆,则该圆锥的体积为 .
14.台球是球类运动项目之一,是运动员在台球桌上,用一根长的球杆,按照一定的规则,通过击打白色主球,使目标球入袋的一项体育休闲项目.如图,三角架内有15个大小相同的球,且球与球,球与三角架均相切.若三角架为边长是的等边三角形,则球的半径为 .(取)
15.已知正四棱锥的所有棱长均为4,点为中点,点在上,,点为中点,则平面截正四棱锥所得的截面周长为 .
16.图1所示几何体是一个星形正多面体,称为星形十二面体,是由对(个)平行五角星面组成的,每对平行五角星面角度关系如图2所示.一个星形十二面体有 个星芒(凸起的正五棱锥),将所有的星芒沿其底面削去后所得几何体和星形十二面体的表面积之比是 .(参考数据:)
四、解答题
17.如图,三棱柱的所有棱长都为2,,是的中点,.
(1)证明:平面平面;
(2)求与平面所成角的正弦值.
18.如图,在三棱柱中,平面平面,平面平面.
(1)求证:平面;
(2)若,,,求二面角的余弦值.
19.如图,四棱锥的底面为矩形,是边长为2的等边三角形,,点为的中点,点为上一点(与点不重合),且.
(1)记平面平面,求证:;
(2)求证:平面平面;
(3)若直线与平面所成的角为,求的长.
20.如图①,已知正方形的边长为4,分别为的中点,沿将四边形折起,如图②,使二面角的大小为60°,在线段上,直线与直线的交点为.
(1)若为的中点,证明:平面;
(2)当时,求直线与平面所成角的余弦值.
参考答案
1.A
先求出圆锥的底面半径和,过点作交的延长线于点,为与所成角,由余弦定理求解即可.
设圆锥的底面半径为,母线长为,
因为,所以,
所以,所以,
所以,又正三角形内接于,
所以,解得:,所以,
所以,
过点作交的延长线于点,,
所以与所成角即为与所成角或其补角,
所以为与所成角,
由余弦定理可得:,
故选:A.
2.B
根据正弦定理可得外接圆半径,进而根据勾股定理可得四面体的高,即可根据球的性质,结合勾股定理求解半径得解.
由对称性,可知球心与正四面体重心重合,
由于球与正四面体的每个面所在平面的交线都为一个面积为的圆,故每个面的交线为半径为3的圆.
设球心为,为的中心,则,故,故
设球心到任意面的距离为,则由等体积法可得,
故连接球心与任意面中心,则连线长为3,且连线垂直该面,再连交线圆上一点与球心(即为球的半径),由勾股定理得球的半径为,则表面积为.
故选:B.
3.A
根据相似可得原圆锥的高,进而利用圆锥的体积公式即可求解.
由已知,设原圆锥的高为,则,所以,
因为, ,
所以.
故选:A.
4.C
由球的结构特征,结合余弦定理即可求解;
记该象牙镂雕套球的球心为,圆与圆所在平面的夹角即为(或其补角),.
所以,
所以,
故选:C
5.D
由圆锥侧面积公式及体积公式即可求解.
根据定义知上、下两个几何体分别为小圆锥和圆台,设小圆锥的高为,底面半径为,所以母线长为,
原圆锥的高为,底面半径为,所以母线长为
由小圆锥的侧面积为:,大圆锥的侧面积为:,
上下两个几何体的侧面积之比为,
所以,又由相似易得:,
所以得,即,
所以小圆锥和原圆锥的体积比,
所以小圆锥和圆台的体积之比为.
故选:D.
6.B
根据空间想象得出小球不能达到的空间,利用空间几何体的体积公式计算即可.
小球在长方体盒子自由滚动当与长方体三面相切时,
即在正方体的8个顶点处的单位立方体空间内,
不能达到的空间为,
此后当小球移动时与长方体的侧面两面相切,
其不能达到的空间为以长方体的侧棱中间长为2的棱为棱柱减去底面半径为1的圆柱的四分之一体积
(这样的空间有四个),体积为,
故小球达不到的空间体积为:.
故选:B
7.C
根据已知分别求出上下底面面积,最后由圆台的体积计算公式.
,圆台的侧面积为,母线长
圆台的高
则圆台上下底面面积为
由圆台的体积计算公式可得:
故选:C.
8.A
根据平面平面可得点的轨迹是平面与正方体内切球的交线,根据点与圆的位置关系可求得AP的最小值.
由题意得,正方体内切球的球心为正方体的中心,记为点,内切球半径.
∵,平面,平面,
∴平面,同理可得平面,
∵平面,,∴平面平面,
∵平面,∴平面,故点的轨迹是平面与正方体内切球的交线,此交线为圆,记圆心为.
如图,以为原点建立空间直角坐标系,则,,,,
∴,,.
设平面的法向量为,则,
令,则,故,
∴点到平面的距离为,
∴圆的半径为,
由得,,
∴,
∴的最小值为.
9.B
由题设,知且,底面,
若是的中点,而,则,且,
而底面,则,都在平面内,则平面,
由平面,则,又底面,则,
由,则,即,
由点在底面内的射影在的外部,则在边的外侧,如下图,
若在的另一侧,则必与的中点重合,不合题设,
由题意,该三棱锥外接球的球心在过的中点垂直于平面的直线上,
根据几何关系有,则,
所以,可得,
(注意时,不成立),
所以,外接球半径,则,故其表面积.
故选:B
10.BC
先由线面垂直的判定定理证明平面,再由棱锥的体积公式可得B正确;由线面垂直的判定定理得到平面,从而得到二面角的平面角,再由几何关系计算可得D错误;将侧面翻折至点与平面共面,分别得到的最小值为和的最小值为,由解三角形即得A错误,C正确.
对于B,因为,,所以,
又,,平面,所以平面.
因为,,所以,,,
所以四面体的体积为,故B正确;
对于D,由平面,平面,得,
又,,平面,所以平面,
又平面,则,所以为二面角的平面角,
因为,,所以,
所以,故D错误;
对于A、C,将侧面翻折至点与平面共面,如图所示,
过点作于点,过点作于点,
则的最小值为,的最小值为,故A错误,C正确.
故选:BC.
11.AC
对于A,连接,如下图:
因为平面,且平面,
所以,,,
因为在正方形中,,且,平面,
所以平面,因为平面,所以,
同理可得,
因为为的斜边,
所以的中点到的距离都等于的一半,
则球心就是的中点,如下图:
在正方形中,,
在中,,
在中,,
则,,
由,则易知,则,
故A正确;
对于B,由平面,则当平面时,最短,
因为平面,所以,
因为,且平面,所以平面,
将绕旋转到的位置,使得平面,
在平面中,过作,垂足为,如下图:
易知,,由图可知,
在正方形中,由,则,
在中,,则,
易知,所以,,
在中,,
易知为的三等分点,如下图:
故B错误;
对于C,由B可知,易知,
在中,过作,交于,连接,如下图:
易知,,即,,即,
因为平面,所以平面,
因为平面,所以,故C正确;
对于D,由题意可作图如下:
由C易知平面,由,则,
在中,,
因为平面,平面,所以,
在中,,,
所以三棱锥的体积,故D错误.
故选:AC.
12.BD
利用等角定理即可判断A,再利用内切圆和外接圆的性质求的,可判断B,利用展开图可得最小值为菱形的对角线可判断C,由可得轨迹为正八面体与半径为的球的交线,可求出其一个面的长度,再由对称性可求出轨迹的总长.
对于A,由正八面体的结构特征可得,,所以异面直线AE与BF所成的角为,A错误;
对于B,根据对称性易得其外接球与内切球的球心为其中心,所以,内切球切点在面的中线上,
且在四边形中,由等面积法可得,则,B正确;
对于C,因为的展开图为一个角为的菱形,对角线即为的最小值,此时,C错误;
对于D,因为到各棱的距离都等于,则点在各面的轨迹恰好为各个面的内切圆,记其半径为,
因为为等边三角形,
所以,所以在一个面的轨迹长度为,
所以在八个面内的轨迹长度之和为,D正确.
故选:BD
13.
由条件求解底面半径和圆锥的高,即可求得圆锥的体积.
设底面半径为,由题意可知,解得:,
圆锥的高,
所以圆锥的体积.
故答案为:
14.3
根据球与球、球与三角架均相切这些特征构建平面图形,利用平面几何中直线与圆相切并结合等边三角形得到球的半径与三角架边长之间的关系,即可求得半径.
可构建如图所示的平面图形,
设球的半径为,则,
所以,解得.
故答案为:3.
15.
延长与的延长线交于点,连接与交于点,延长与的延长线交于点,连接与交于点,则平面截正四棱锥所得的截面为五边形,即可求解.
延长与的延长线交于点,连接与交于点,延长与的延长线交于点,连接与交于点,
则平面截正四棱锥所得的截面为五边形,
如图所示:
易知,,
,
所以五边形的周长为.
故答案为:
16.
结合图形可判断出星芒的个数;将每个正五棱锥沿着侧面展开与底面在同一个平面上,形成一个正五角星,计算出正五棱锥侧面积和底面积之比即可.
由图可知,每个星形十二面体有个星芒,
将每个正五棱锥沿着侧面展开与底面在同一个平面上,形成一个正五角星,
则这个正五角星的五个顶点在圆上,连接,则垂直平分,设,
正五棱锥的侧面积等于,底面积等于,
正五边形的每个内角为,则,故,
则,所以,,,
设,则,则,
,则,
所以,将所有的星芒沿其底面削去后所得几何体和星形十二面体的表面积之比为
,
故答案为:;.
17.(1)证明见解析
(2)
(1)取的中点,得到,证得,再由,利用线面垂直的判定定理,证得平面,得到,结合,证得平面,进而证得平面平面.
(2)连接,证得平面,以为坐标原点,建立空间直角坐标系,求得平面的一个法向量为和向量,结合向量的夹角公式,即可求解.
(1)证明:取的中点,连接,
因为是的中点,所以,
又因为三棱柱的所有棱长都是2,
所以四边形为菱形,所以,所以,
因为,且,平面,所以平面,
又因为平面,所以,
在等边中,因为为的中点,所以,
又因为,且平面,所以平面,
因为平面,所以平面平面.
(2)解:连接,因为三棱柱的所有棱长都为2,且,
可得为等边三角形,且为的中点,所以,
由(1)知:平面平面,平面平面,
且平面,所以平面,
所以两两垂直,以为坐标原点,以所在的直线分别为轴,轴和轴,建立空间直角坐标系,如图所示,
则,
所以,
设平面的法向量为,则,
取,可得,所以,
因为,
设与平面所成的角为,则,
所以与平面所成的角的正弦值为.
18.(1)证明见解析
(2).
(1)根据面面垂直的性质可得平面,进而可得,同理得,即可利用线面垂直的判定求解,
(2)建立空间直角坐标系,求解平面法向量,即可利用法向量的夹角求解.
(1)如图,取为内一点,作,交于点,作,交于点.
因为平面平面且平面平面,平面,
所以平面.
因为平面,
所以,同理得.
因为,且平面,
所以平面.
(2)因为,,两两垂直,以为原点,建立空间直角坐标系,如图所示.
由题意,得,,,,
则,,,.
设平面的法向量为,则
令,则,,所以.
设平面的法向量为,则
令,则,,所以.
设二面角的平面角为,则由图可得.
故二面角的余弦值为.
19.(1)证明见解析
(2)证明见解析
(3)
(1)因为底面为矩形,
所以.
又因为面,面,
所以面.
又因为面,面面,
所以.
(2)因为三角形是等边三角形,且是的中点,
所以.
如图1,连接,在矩形中,,,
所以.所以.
因为,
所以,即.
因为,,
平面,
所以平面.由平面,得.
又因为,,
平面
所以平面.
因为平面,
所以平面平面.
(3)设是的中点,以为原点,所在直线为轴,所在直线为轴,所在直线为轴建立如图2所示的空间直角坐标系.
由已知得,,,,.
设,
则,,.
设面的法向量为,
则,即,
令,有,
所以,
解得,
所以当直线与平面所成的角为时,.
20.(1)证明见解析;
(2).
(1)连接交于点Q,连接,因为正方形,分别为的中点,所以四边形为矩形,所以为中点,
又为的中点,,所以为的中点,
所以,
又平面,平面,
所以平面.
(2)
由题知:,二面角的大小为60°,
故:是二面角的平面角,,
又,所以为正三角形,
取中点,中点,连接,
则,易证:面,所以,
以为坐标原点,分别为轴建立平面直角坐标系,
则,
所以,
设平面的法向量为,
则,令,则
则,
设直线与平面的夹角为,则,
又,所以,所以,
直线与平面所成角的余弦值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
