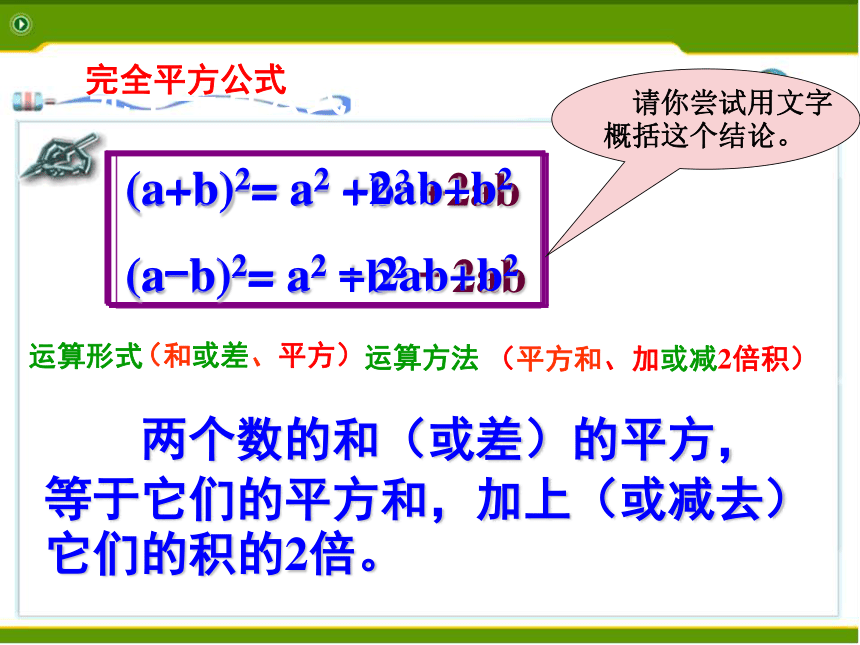
完全平方公式
图片预览







文档简介
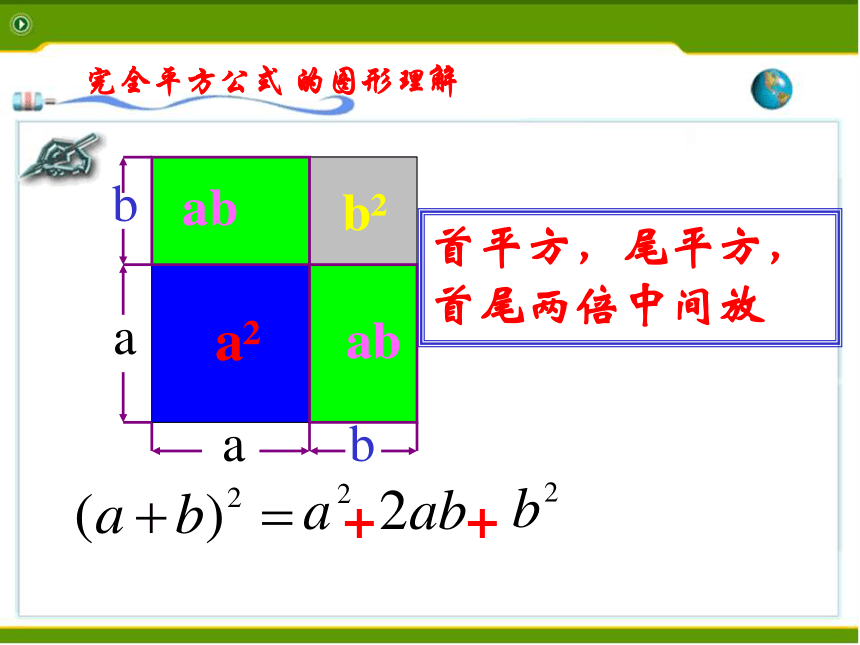
课件26张PPT。 用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.(a+b)(m+n)=am+an+bm+bn多项式的乘法(a+b)2(a-b)2= a2 +2ab+b2= a2 - 2ab+b2= a2 +ab +ab +b2= a2 - ab - ab +b2=(a+b) (a+b)=(a-b) (a-b)计算下列各题:观察以上多项式的乘法,有什么特点?完全平方公式的数学表达式: 两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。完全平方公式 请你尝试用文字概括这个结论。运算形式运算方法(和或差、平方) (平方和、加或减2倍积)(a+b)2a2b2完全平方公式 的图形理解首平方,尾平方,首尾两倍中间放 (a-b)2b2完全平方公式 的图形理解首平方,尾平方,首尾两倍中间放 公式特点:4、公式中的字母a,b可以表示数,单项式和多项式。(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b21、积为二次三项式;2、积中两项为两数的平方和;3、另一项是两数积的2倍,且与乘式中间的符号相同。首平方,尾平方,首尾两倍中间放 完全平方公式做一做:用两数和的完全平方公式计算(填空):
(a+1)2=( )2+2( )( )+( )2
= _____________
(2)(2a+3b)2=( )2+2( )( )+( )2
=__________________八年级 数学第十五章 整式的乘法感受新知----试一试a1a1a2+2a+12a2a3b3b4a2+12ab+9b2下面各式的计算是否正确?如果不正确,应当怎样改正?(x+y)2=x2 +y2(2)(x -y)2 =x2 -y2(3) (x -y)2 =x2+2xy +y2(4) (x+y)2 =x2 +xy +y2错错错错(x +y)2 =x2+2xy +y2(x -y)2 =x2 -2xy +y2(x -y)2 =x2 -2xy +y2(x +y)2 =x2+2xy +y2感受新知----试一试例1 运用完全平方公式计算:解: (x+2y)2==x2(1)(x+2y)2(a +b)2= a2 + 2 ab + b2x2+2?x ?2y+(2y)2+4xy+4y2八年级 数学第十五章 整式的乘法感受新知----看一看(2)(x-2y)2解: (x-2y)2=x2-2?x ?2y+(2y)2=x2(a - b)2= a2 - 2 ab + b2-4xy+4y2例2、运用完全平方公式计算: (1) ( 4a2 - b2 )2解:( 4a2 - b2)2=( )2-2( )·( )+( )2 =16a4-8a2b2+b4记清公式、代准数式、准确计算。解题过程分3步:4a24a2b2b2感受新知----看一看= x2 – 2xy2+4y4+(2y2)2(a - b)2 = a2 - 2ab + b2 (2) ( x – 2y2)2– 2 ?( x) ?(2y2)( x)2解:( x – 2y2)2 =感受新知----看一看运用完全平方公式计算:(1) 1042解: 1042= (100+4)2=10000+800+16=10816(2) 99.992解: 99.992= (100 –0.01)2=10000 -2+0.0001=9998.0001感受新知---试一试继续探索----试一试如何运用完全平方公式使计算更简便(1) (-a+b)2(2) (-2m-1)2(3) (2x+5)(-2x-5)(4) (x+y-1)2= (b-a)2= (2m+1)2= -(2x+5)(2x+5)= -(2x+5)2 添括号时,如果括号前面是正号,括到括号里的各项都不变号;如果括号前面是负号,括到括号里的各项都改变符号.a+(b+c) = a+b+c; a- (b+c) = a - b – c.a + b + c = a + ( b + c) ;
a – b – c = a – ( b + c ) . 运用乘法公式计算:
(1) ( x +2y-3) (x- 2y +3) ; (2) (a + b +c ) 2.解: (1) ( x +2y-3) (x- 2y +3)
= [ x+ (2y – 3 )] [ x- (2y-3) ]
= x2- (2y- 3)2
= x2- ( 4y2-12y+9)
= x2-4y2+12y-9.(a + b +c ) 2
= [ (a+b) +c ]2
= (a+b)2 +2 (a+b)c +c2
= a2+2ab +b2 +2ac +2bc +c2
= a2+b2+c2 +2ab+2bc +2ac.2.运用乘法公式计算:
(a + 2b – 1 ) 2 ;
(2x +y +z ) (2x – y – z )3.如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,求剩下的钢板的面积.1、代数式2xy-x2-y2= ( )
A.(x-y)2 B.(-x-y)2 C.(y-x)2 D.-(x-y)2D2、如果x2-6xy+N是一个完全平方式,那么N为________深入探索----算一算3、如果4x2+mxy+9y2是一个完全平方式,那么m的值是____________9y2±12深入探索----算一算(a+b)2 _a2_b2 =______(a-b)2+2ab= ______公式变形(a-b)2+4ab= ______(a+b)2-4ab=_______(a+b)2_2ab= _____2ab a2 +b2(a+b)2-(a-b)2=______a2 +b24ab(a-b)2(a+b)2深入探索----算一算1、已知(a+b)2=11,ab=1,求(a-b)2的值.2、若(x+y)2=9,(x-y)2=5,则xy=______ 3、多项式 加上一个单项式后,使它成为一个整式的完全平方式,那么加上的单项式可以是__________4、已知 (a+b)2=25 ab=3 则 a2+b2=___5、已知:a+b=5,ab=-6,求下列各式的值(1)(a+b)2 (2)a2+b21. 计算:4x(x-1)2+x(2x+5)·(5-2x)
2. 当x=2,y=-1时。求代数式
(x+y)(x-y)+(x-y)2-(x2-3xy)的值。 3.用简便的方法计算:
1.23452+0.76552+2.469×0.7655深入探索----算一算感受新知----看一看运用乘法公式计算(1)(x+2y-3)(x+2y+3)(2)(x+2y-3)(x-2y+3)(3)(a+b+c)21.(1)(x+3)2-x2
(2) (a+b+3)(a-b-3)
(3)(x+5)2-(x-2)(x-3)2.运用乘法公式计算:
(1) (x+2y- )(x-2y+ )3.已知求下列式子的值:深入探索----算一算(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b21、完全平方公式:2、注意:项数、符号、字母及其指数;3、公式的逆向使用;4、解题时常用结论:(-a-b)2 =(a+b)2 (a-b)2 =(b-a)2a2 +2ab+b2 = (a+b)2
a2 - 2ab+b2= (a-b)2(1) (2a+3)2 (2) (b-3)2
(3) (-2x-3y)2 (4)
(5) (6) (1-3x)(3x-1)
(7) (a?b?3)(a?b+3)。熟练运用----算一算 (1) ( x ? 2y)2 ;
(2) (2xy+ x )2 ;1、利用完全平方公式计算:(n +1)2 ? n2;
(-x-y)2.熟练运用----算一算1.已知:a-b=5,ab=-6,求a2+b2的值 2.计算(a-b-3)(a-b+3)3.二次三项式是一个完全平方式,求m的值?4.已知n为正整数,且是一个完全平方数,你知道n的值吗?熟练运用----算一算
(a-b)2= a2 - 2ab+b21、积为二次三项式;2、积中两项为两数的平方和;3、另一项是两数积的2倍,且与乘式中间的符号相同。首平方,尾平方,首尾两倍中间放 完全平方公式做一做:用两数和的完全平方公式计算(填空):
(a+1)2=( )2+2( )( )+( )2
= _____________
(2)(2a+3b)2=( )2+2( )( )+( )2
=__________________八年级 数学第十五章 整式的乘法感受新知----试一试a1a1a2+2a+12a2a3b3b4a2+12ab+9b2下面各式的计算是否正确?如果不正确,应当怎样改正?(x+y)2=x2 +y2(2)(x -y)2 =x2 -y2(3) (x -y)2 =x2+2xy +y2(4) (x+y)2 =x2 +xy +y2错错错错(x +y)2 =x2+2xy +y2(x -y)2 =x2 -2xy +y2(x -y)2 =x2 -2xy +y2(x +y)2 =x2+2xy +y2感受新知----试一试例1 运用完全平方公式计算:解: (x+2y)2==x2(1)(x+2y)2(a +b)2= a2 + 2 ab + b2x2+2?x ?2y+(2y)2+4xy+4y2八年级 数学第十五章 整式的乘法感受新知----看一看(2)(x-2y)2解: (x-2y)2=x2-2?x ?2y+(2y)2=x2(a - b)2= a2 - 2 ab + b2-4xy+4y2例2、运用完全平方公式计算: (1) ( 4a2 - b2 )2解:( 4a2 - b2)2=( )2-2( )·( )+( )2 =16a4-8a2b2+b4记清公式、代准数式、准确计算。解题过程分3步:4a24a2b2b2感受新知----看一看= x2 – 2xy2+4y4+(2y2)2(a - b)2 = a2 - 2ab + b2 (2) ( x – 2y2)2– 2 ?( x) ?(2y2)( x)2解:( x – 2y2)2 =感受新知----看一看运用完全平方公式计算:(1) 1042解: 1042= (100+4)2=10000+800+16=10816(2) 99.992解: 99.992= (100 –0.01)2=10000 -2+0.0001=9998.0001感受新知---试一试继续探索----试一试如何运用完全平方公式使计算更简便(1) (-a+b)2(2) (-2m-1)2(3) (2x+5)(-2x-5)(4) (x+y-1)2= (b-a)2= (2m+1)2= -(2x+5)(2x+5)= -(2x+5)2 添括号时,如果括号前面是正号,括到括号里的各项都不变号;如果括号前面是负号,括到括号里的各项都改变符号.a+(b+c) = a+b+c; a- (b+c) = a - b – c.a + b + c = a + ( b + c) ;
a – b – c = a – ( b + c ) . 运用乘法公式计算:
(1) ( x +2y-3) (x- 2y +3) ; (2) (a + b +c ) 2.解: (1) ( x +2y-3) (x- 2y +3)
= [ x+ (2y – 3 )] [ x- (2y-3) ]
= x2- (2y- 3)2
= x2- ( 4y2-12y+9)
= x2-4y2+12y-9.(a + b +c ) 2
= [ (a+b) +c ]2
= (a+b)2 +2 (a+b)c +c2
= a2+2ab +b2 +2ac +2bc +c2
= a2+b2+c2 +2ab+2bc +2ac.2.运用乘法公式计算:
(a + 2b – 1 ) 2 ;
(2x +y +z ) (2x – y – z )3.如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,求剩下的钢板的面积.1、代数式2xy-x2-y2= ( )
A.(x-y)2 B.(-x-y)2 C.(y-x)2 D.-(x-y)2D2、如果x2-6xy+N是一个完全平方式,那么N为________深入探索----算一算3、如果4x2+mxy+9y2是一个完全平方式,那么m的值是____________9y2±12深入探索----算一算(a+b)2 _a2_b2 =______(a-b)2+2ab= ______公式变形(a-b)2+4ab= ______(a+b)2-4ab=_______(a+b)2_2ab= _____2ab a2 +b2(a+b)2-(a-b)2=______a2 +b24ab(a-b)2(a+b)2深入探索----算一算1、已知(a+b)2=11,ab=1,求(a-b)2的值.2、若(x+y)2=9,(x-y)2=5,则xy=______ 3、多项式 加上一个单项式后,使它成为一个整式的完全平方式,那么加上的单项式可以是__________4、已知 (a+b)2=25 ab=3 则 a2+b2=___5、已知:a+b=5,ab=-6,求下列各式的值(1)(a+b)2 (2)a2+b21. 计算:4x(x-1)2+x(2x+5)·(5-2x)
2. 当x=2,y=-1时。求代数式
(x+y)(x-y)+(x-y)2-(x2-3xy)的值。 3.用简便的方法计算:
1.23452+0.76552+2.469×0.7655深入探索----算一算感受新知----看一看运用乘法公式计算(1)(x+2y-3)(x+2y+3)(2)(x+2y-3)(x-2y+3)(3)(a+b+c)21.(1)(x+3)2-x2
(2) (a+b+3)(a-b-3)
(3)(x+5)2-(x-2)(x-3)2.运用乘法公式计算:
(1) (x+2y- )(x-2y+ )3.已知求下列式子的值:深入探索----算一算(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b21、完全平方公式:2、注意:项数、符号、字母及其指数;3、公式的逆向使用;4、解题时常用结论:(-a-b)2 =(a+b)2 (a-b)2 =(b-a)2a2 +2ab+b2 = (a+b)2
a2 - 2ab+b2= (a-b)2(1) (2a+3)2 (2) (b-3)2
(3) (-2x-3y)2 (4)
(5) (6) (1-3x)(3x-1)
(7) (a?b?3)(a?b+3)。熟练运用----算一算 (1) ( x ? 2y)2 ;
(2) (2xy+ x )2 ;1、利用完全平方公式计算:(n +1)2 ? n2;
(-x-y)2.熟练运用----算一算1.已知:a-b=5,ab=-6,求a2+b2的值 2.计算(a-b-3)(a-b+3)3.二次三项式是一个完全平方式,求m的值?4.已知n为正整数,且是一个完全平方数,你知道n的值吗?熟练运用----算一算
