期中综合素质评价卷(含答案)鲁教版五四制九年级数学
文档属性
| 名称 | 期中综合素质评价卷(含答案)鲁教版五四制九年级数学 |

|
|
| 格式 | doc | ||
| 文件大小 | 549.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-08 00:00:00 | ||
图片预览




文档简介
期中综合素质评价
一、选择题(每题3分,共30分)
1.[2025·烟台模拟]把△ABC三边的长度都缩小为原来的,则锐角A的正弦值( )
A.不变 B.缩小为原来的 C.扩大为原来的3倍 D.不能确定
2.若A(2,4)与B(-2,a)都是反比例函数y=(k≠0)图象上的点,则a的值是( )
A.4 B.-4 C.2 D.-2
3.在△ABC中,∠A,∠B均为锐角,且|tan B-|+(2sin A-)2=0,则△ABC的形状是( )
A.钝角三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
4. INCLUDEPICTURE "../新趋势·跨学科H.EPS" \* MERGEFORMAT INCLUDEPICTURE "../新趋势·跨学科H.EPS" \* MERGEFORMAT \d 阿基米德说:“给我一个支点,我就能撬动整个地球.”这句话阐明了一个重要的物理学知识——杠杆原理,即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为1 200 N和0.5 m,则这一杠杆的动力F和动力臂l之间的函数图象大致是( )
5.如图,在平面直角坐标系中,一次函数y1=x-2与反比例函数y2=的图象交于A,B两点,下列结论正确的是( )
A.当x>3时,y1B.当x<-1时,y1C.当0y2
D.当-16.如图,在平面直角坐标系中,函数y=(x>0)与y=x-1的图象交于点P(a,b),则代数式-的值为( )
A.-
B.
C.-
D.
7.若ab<0,则正比例函数y=ax与反比例函数y=在同一坐标系中的图象可能是( )
8. INCLUDEPICTURE "../新视角·操作实践题H.EPS" \* MERGEFORMAT INCLUDEPICTURE "../新视角·操作实践题H.EPS" \* MERGEFORMAT \d 按下列方法可求出tan 75°的值,如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB,在CB的延长线上截取线段BD,使BD=AB,连接AD,依据此图可求得tan 75°的值为( )
A.2- B.2+ C.1+ D.-1
9.随着科技的进步,我国的生物医药行业发展迅速,最近某药品研究所开发出一种抗菌新药,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x(小时)之间的函数关系如图所示(当3≤x≤10时,y与x成反比例).根据图中信息可知,血液中药物浓度不低于6微克/毫升的持续时间为( )
A.4小时 B.小时 C.小时 D.小时
10.如图,斜坡AP的坡比为1?2.4,在坡顶A处的同一水平面上有一座古塔BC,在坡底P处测得该塔顶B的仰角∠BPQ为45°,在坡顶A处测得该塔顶B的仰角∠BAC为76°,坡顶A到塔底C处的距离为7米,则斜坡AP的长度约为( )(点P,A,B,C,Q在同一平面内,参考数据:sin 76°≈0.97,cos 76°≈0.24,tan 76°≈4.01)
A.24米 B.26米
C.28米 D.39米
二、填空题(每题3分,共18分)
11.若y=(m-2)xm2-5是反比例函数,则m的值是________.
12.[2025·泰安乳山市月考]在反比例函数y=的图象上有两点A(x1,y1),B(x2,y2),当x1<013.某商场从安全和便利的角度出发,为提升顾客的购物体验,准备将自动扶梯由原来的阶梯式改造成斜坡式,如图,已知商场的层高AD为6 m,原坡角∠ABD=30°,改造后的斜坡式自动扶梯的坡角∠ACB=16°,请你计算改造后的自动扶梯增加的占地长度BC=________(结果精确到0.1 m,参考数据:≈1.73,sin 16°≈0.28,cos 16°≈0.96,tan 16°≈0.29).
14.如图,在△ABC中,∠ABC=30°,tan C=,BC=6,则AB的长为________.
15.如图,一艘渔船正以60海里/时的速度向正东方向航行,在A处测得岛礁P在东北方向,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得位于岛礁P正东方向的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/时的速度继续航行________小时即可到达.(结果保留根号)
16. INCLUDEPICTURE "../新考法分类讨论法2024上海H.EPS" \* MERGEFORMAT INCLUDEPICTURE "../新考法分类讨论法2024上海H.EPS" \* MERGEFORMAT \d 在平行四边形ABCD中,∠ABC是锐角,将CD沿直线l翻折至AB所在直线,对应点分别为C′,D′,若AC′∶AB∶BC=1∶3∶7,则cos∠ABC=________.
三、解答题(17,18题每题6分,19~21题每题12分,22题10分,23题14分,共72分)
17.计算:
(1)2cos 30°-tan 60°+tan 45°-sin 60°; (2)-sin 60°·cos 30°.
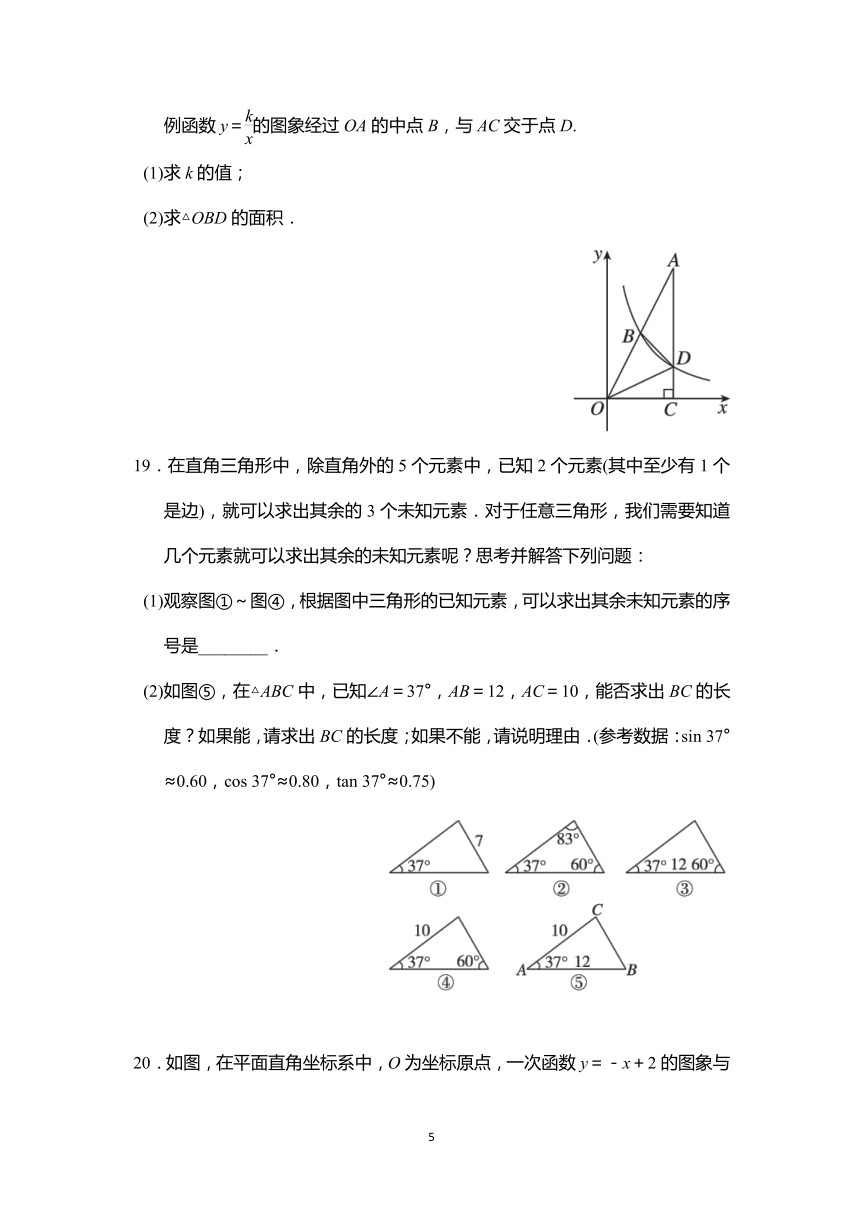
18.如图,点A在第一象限,AC⊥x轴,垂足为C,OA=2,tan A=,反比例函数y=的图象经过OA的中点B,与AC交于点D.
(1)求k的值;
(2)求△OBD的面积.
19.在直角三角形中,除直角外的5个元素中,已知2个元素(其中至少有1个是边),就可以求出其余的3个未知元素.对于任意三角形,我们需要知道几个元素就可以求出其余的未知元素呢?思考并解答下列问题:
(1)观察图①~图④,根据图中三角形的已知元素,可以求出其余未知元素的序号是________.
(2)如图⑤,在△ABC中,已知∠A=37°,AB=12,AC=10,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
20.如图,在平面直角坐标系中,O为坐标原点,一次函数y=-x+2的图象与反比例函数y=在第二象限的图象交于点A(n,3),与x轴交于点B,连接AO并延长交这个反比例函数在第四象限的图象于点C.
(1)求这个反比例函数的表达式;
(2)求△ABC的面积;
(3)当直线AC对应的函数值大于反比例函数y=的函数值时,直接写出x的取值范围.
21. INCLUDEPICTURE "../情境题·生活应用H.EPS" \* MERGEFORMAT INCLUDEPICTURE "../情境题·生活应用H.EPS" \* MERGEFORMAT \d 某水果生产基地在气温较低时用装有恒温系统的大棚栽培一种新品种水果,如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y(℃)与时间x(h)之间的函数关系图象,其中线段AB,BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.请根据图中信息解答下列问题:
(1)求这个恒温系统设定的恒定温度为多少摄氏度;
(2)求全天的温度y与时间x之间的函数表达式;
(3)若大棚内的温度低于12℃不利于新品种水果的生长,则这天内,相对有利于新品种水果生长的时间共有多少小时?
22. INCLUDEPICTURE "../新视角·操作实践题H.EPS" \* MERGEFORMAT INCLUDEPICTURE "../新视角·操作实践题H.EPS" \* MERGEFORMAT \d 【综合与实践】
不借助科学计算器,如何求tan 22.5°的值?小明进行了如下的实践操作:
如图,已知正方形纸片ABCD.
第一步:将正方形纸片ABCD沿AC折叠,展开后得到折痕AC.
第二步:将AB折叠到AF,使点B的对应点F恰好落在AC上,展开后得到折痕AE,点E在线段BC上,连接EF.
【问题解决】
(1)求证:∠BAE=22.5°;
(2)请利用小明的实践操作过程,求tan 22.5°的值.
23. INCLUDEPICTURE "../2025聊城月考新考向传统文化.EPS" \* MERGEFORMAT INCLUDEPICTURE "../2025聊城月考新考向传统文化.EPS" \* MERGEFORMAT \d 【项目式活动探究】光岳楼位于聊城古城中央,始建于明洪武七年(公元1374年),被誉为中国十大名楼,光岳楼为中国既古老又雄伟的木构楼阁,是宋元建筑向明清建筑过渡的代表作,在中国古代建筑史上有着重要地位,1988年光岳楼被列为全国重点文物保护单位,享有“虽黄鹤、岳阳亦当望拜”之誉.某校数学实践小组利用所学数学知识测量光岳楼的高度,他们制订了两个测量方案,并利用课余时间完成了实地测量.在测量仰角的度数以及有关长度时,都分别测量了两次并取它们的平均值作为测量结果.下面是两个方案及测量数据(不完整):
项目 测量光岳楼的高度
方案 方案一:标杆垂直立于地面,借助平行的太阳光线构成相似三角形.测量:标杆长CD,影长ED及同一时刻楼影长DB 方案二:利用锐角三角函数.测量:距离CD,仰角α,仰角β
说明 E,D,B三点在同一条直线上 B,C,D三点在同一条直线上
测量示意图
测量数据 测量项目 第一次 第二次 平均值 测量项目 第一次 第二次 平均值
CD 1.61 m 1.59 m 1.6 m β 29.9° 30.1° 30°
ED 1.18 m 1.22 m 1.2 m α 37.1° 36.9° 37°
DB 25 m 26 m CD 13.2 m 12.8 m 平均值
【问题解决】
(1)“方案一”两次测量楼影长DB的平均值是________;
(2)根据“方案一”的测量数据,可求得光岳楼AB的高度为________;
(3)根据“方案二”的测量数据,求出光岳楼AB的高度;(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,≈1.73;结果保留一位小数)
(4)请对本次实践活动进行评价.(写出一条即可)
答案
一、1.A 2.B 3.B 4.B 5.B 6.C 7.B
8.B 【点拨】在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,∴AB=2k,BC=k.∵BD=AB,∴∠BAD=∠BDA=∠ABC=15°.∴∠CAD=75°.在Rt△ACD中,CD=CB+BD=CB+AB=k+2k,则tan 75°=tan∠CAD===2+.
9.C 【点拨】设正比例函数表达式为y=kx,反比例函数表达式为y=,把(3,8)分别代入表达式,得8=3k,=8,解得k=,m=24,故两个函数的表达式分别为y=x,y=,把y=6分别代入两个表达式中,得6=x,6=,分别解得x=和x=4,故持续时间为4-=(小时),故选C.
10.D 【点拨】延长BC交PQ于点D,过点A作AH⊥PQ于点H.由题易知BC⊥AC,BD⊥PQ,CD=AH,DH=AC.在Rt△BDP中,∵∠BPD=45°,∴PD=BD.在Rt△ABC中,∵tan 76°=,AC=7米,∴BC=7tan 76°≈28.07(米).∵斜坡AP的坡比为1∶2.4,∴==.设AH=5k米,则PH=12k米,由勾股定理,得AP=13k米.易知PH+HD=BC+CD,∴12k+7≈28.07+5k,解得k≈3.01,∴AP=13k≈39米.
二、11.-2 12.k<4
13.10.3 m 【点拨】在Rt△ABD中,∠ABD=30°,AD=6 m,∴AB=2AD=12 m,∴BD==6≈10.38(m),在Rt△ACD中,∠ACD=16°,AD=6 m,∴CD=≈≈20.69(m),∴BC=CD-BD≈20.69-10.38≈10.3(m).
14.6-2 【点拨】作AD⊥BC于D,设AD=x,∵tan C==,∴CD=3x.∵∠ABC=30°,∴AB=2AD=2x,BD==AD=x.∵BC=BD+CD=x+3x=6,∴x=3-,∴AB=2x=6-2.
15. 【点拨】
如图,过点P作PQ⊥AB交AB延长线于点Q,过点M作MN⊥AB交AB延长线于点N,由题易知在Rt△AQP中,∠PAQ=45°,∴AQ=PQ=60×1.5+BQ=90+BQ,∴ BQ=PQ-90.易知在Rt△BPQ中,∠BPQ=30°,∴BQ=PQ·tan 30°=PQ,∴PQ-90=PQ,∴PQ=45(3+)海里,∴易知MN=PQ=45(3+)海里.在Rt△BMN中,易知∠MBN=30°,∴ BM=2MN=90(3+)海里,∴继续航行=(小时)即可到达.
16.或 【点拨】设直线l交BC于点F.当C′在线段AB上时,如图①,根据AC′∶AB∶BC=1∶3∶7,设AC′=1,AB=3,BC=7,由翻折的性质知∠FCD=∠FC′D′,C′F=CF.∵CD沿直线l翻折至AB所在直线,∴∠BC′F+∠FC′D′=180°=∠FCD+∠FBA,∴∠BC′F=∠FBA,∴BF=C′F=CF=.过点F作AB的垂线,垂足为E,∴BE=BC′=(AB-AC′)=1,∴cos∠ABC===;当C′在BA的延长线上时,如图②,根据AC′∶AB∶BC=1∶3∶7,设AC′=1,AB=3,BC=7,同理知CF=C′F=BF=,过点F作AB的垂线,垂足为E,∴BE=BC′=(AB+AC′)=2,∴cos∠ABC===.综上,cos ∠ABC的值为或.
三、17.【解】(1)原式=2×-+1-×=-+1-=1-.
(2)原式=-×=-.
18.【解】(1)在Rt△ACO中,∠ACO=90°,tan A==,
∴AC=2OC.∵OC2+AC2=OA2,∴OC2+(2OC)2=(2)2,∴OC=2,∴AC=4,∴A(2,4).
∵OA的中点是B,∴B(1,2).
∵B在反比例函数y=的图象上,∴2=,解得k=2.
(2)由(1)知y=,当x=2时,y=1,∴D(2,1),
∴AD=4-1=3,∴S△OBD=S△OAD-S△BAD=×3×2-×3×(2-1)=.
19.【解】(1)③④
(2)能.如图,作CD⊥AB于D,则∠ADC=90°.
∵AC=10,∠A=37°,
∴CD=AC·sin 37°≈10×0.6=6,AD=AC·cos 37°≈10×0.8=8.
∵AB=12,∴BD≈12-8=4,
∴BC=≈=2.
∴能求出BC的长度,BC≈2.
20.【解】(1)∵点A(n,3)在一次函数y=-x+2的图象上,
∴3=-n+2,解得n=-1,
∴A(-1,3).又∵点A(-1,3)在反比例函数y=的图象上,∴k=1×(-3)=-3,
∴反比例函数的表达式为y=-.
(2)在y=-x+2中,当y=0时,0=-x+2,解得x=2,
∴B(2,0).
∵点C在反比例函数y=-的图象上,A(-1,3),
∴根据对称性,得点C的坐标为(1,-3),
∴S△ABC=S△AOB+S△BOC=×2×3+×2×3=6.
(3)由图象可得,当直线AC对应的函数值大于反比例函数y=的函数值时,x的取值范围是x<-1或021.【解】(1)设直线AB的表达式为y=kx+b(k≠0).
根据题意,得解得
∴直线AB的表达式为y=2x+10.
当x=5时,y=2×5+10=20,
∴这个恒温系统设定的恒定温度为20 ℃.
(2)由(1)可知,当0≤x≤5时,y=2x+10,
当5<x≤10时,y=20.
设反比例函数表达式为y=,
根据题意,得20=,∴k′=200,
∴反比例函数的表达式为y=.
∴全天的温度y与时间x之间的函数表达式为
y=
(3)当0≤x≤5时,令y=12,则12=2x+10,解得x=1;
当10<x≤24时,令y=12,则12=,解得x=.
∴相对有利于新品种水果生长的时间共有-1=(h).
22.(1)【证明】∵四边形ABCD是正方形,∴∠BAD=90°,
由折叠的性质,得∠BAC=∠DAC=∠BAD=×90°=45°,同理可得,∠BAE=∠EAF=∠BAC=×45°=22.5°.
(2)【解】∵四边形ABCD是正方形,
∴∠B=∠BCD=90°,AB=BC.
由折叠的性质,得BE=EF,∠B=∠AFE=90°,
∠ECF=∠BCD=45°,
∴∠CFE=180°-∠AFE=90°,
∴∠FEC=90°-∠ECF=45°,
∴∠ECF=∠FEC,∴EF=FC.
设BE=a,则EF=FC=a,
∴在Rt△CEF中,EC=a,
∴BC=BE+EC=(1+)a,
∴AB=BC=(1+)a.
在Rt△ABE中,
tan∠BAE=tan 22.5°===-1.
∴tan 22.5°=-1.
23.【解】(1)25.5 m
(2)34 m
(3)设BC=x m,∵CD==13(m),
∴BD=BC+CD=(x+13)m.
在Rt△ABC中,∠ACB=37°,
∴AB=BC·tan 37°≈0.75x m.
在Rt△ABD中,∠ADB=30°,
∴AB=BD·tan 30°=(x+13)m.
∴0.75x≈(x+13),解得x≈44,
∴AB≈0.75x=33 m.
答:光岳楼AB的高度约为33 m.
(4)两种方案均可测量出光岳楼的近似高度,测量时取平均值是减少误差的方式.(答案不唯一)
一、选择题(每题3分,共30分)
1.[2025·烟台模拟]把△ABC三边的长度都缩小为原来的,则锐角A的正弦值( )
A.不变 B.缩小为原来的 C.扩大为原来的3倍 D.不能确定
2.若A(2,4)与B(-2,a)都是反比例函数y=(k≠0)图象上的点,则a的值是( )
A.4 B.-4 C.2 D.-2
3.在△ABC中,∠A,∠B均为锐角,且|tan B-|+(2sin A-)2=0,则△ABC的形状是( )
A.钝角三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
4. INCLUDEPICTURE "../新趋势·跨学科H.EPS" \* MERGEFORMAT INCLUDEPICTURE "../新趋势·跨学科H.EPS" \* MERGEFORMAT \d 阿基米德说:“给我一个支点,我就能撬动整个地球.”这句话阐明了一个重要的物理学知识——杠杆原理,即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为1 200 N和0.5 m,则这一杠杆的动力F和动力臂l之间的函数图象大致是( )
5.如图,在平面直角坐标系中,一次函数y1=x-2与反比例函数y2=的图象交于A,B两点,下列结论正确的是( )
A.当x>3时,y1
D.当-1
A.-
B.
C.-
D.
7.若ab<0,则正比例函数y=ax与反比例函数y=在同一坐标系中的图象可能是( )
8. INCLUDEPICTURE "../新视角·操作实践题H.EPS" \* MERGEFORMAT INCLUDEPICTURE "../新视角·操作实践题H.EPS" \* MERGEFORMAT \d 按下列方法可求出tan 75°的值,如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB,在CB的延长线上截取线段BD,使BD=AB,连接AD,依据此图可求得tan 75°的值为( )
A.2- B.2+ C.1+ D.-1
9.随着科技的进步,我国的生物医药行业发展迅速,最近某药品研究所开发出一种抗菌新药,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x(小时)之间的函数关系如图所示(当3≤x≤10时,y与x成反比例).根据图中信息可知,血液中药物浓度不低于6微克/毫升的持续时间为( )
A.4小时 B.小时 C.小时 D.小时
10.如图,斜坡AP的坡比为1?2.4,在坡顶A处的同一水平面上有一座古塔BC,在坡底P处测得该塔顶B的仰角∠BPQ为45°,在坡顶A处测得该塔顶B的仰角∠BAC为76°,坡顶A到塔底C处的距离为7米,则斜坡AP的长度约为( )(点P,A,B,C,Q在同一平面内,参考数据:sin 76°≈0.97,cos 76°≈0.24,tan 76°≈4.01)
A.24米 B.26米
C.28米 D.39米
二、填空题(每题3分,共18分)
11.若y=(m-2)xm2-5是反比例函数,则m的值是________.
12.[2025·泰安乳山市月考]在反比例函数y=的图象上有两点A(x1,y1),B(x2,y2),当x1<0
14.如图,在△ABC中,∠ABC=30°,tan C=,BC=6,则AB的长为________.
15.如图,一艘渔船正以60海里/时的速度向正东方向航行,在A处测得岛礁P在东北方向,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得位于岛礁P正东方向的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/时的速度继续航行________小时即可到达.(结果保留根号)
16. INCLUDEPICTURE "../新考法分类讨论法2024上海H.EPS" \* MERGEFORMAT INCLUDEPICTURE "../新考法分类讨论法2024上海H.EPS" \* MERGEFORMAT \d 在平行四边形ABCD中,∠ABC是锐角,将CD沿直线l翻折至AB所在直线,对应点分别为C′,D′,若AC′∶AB∶BC=1∶3∶7,则cos∠ABC=________.
三、解答题(17,18题每题6分,19~21题每题12分,22题10分,23题14分,共72分)
17.计算:
(1)2cos 30°-tan 60°+tan 45°-sin 60°; (2)-sin 60°·cos 30°.
18.如图,点A在第一象限,AC⊥x轴,垂足为C,OA=2,tan A=,反比例函数y=的图象经过OA的中点B,与AC交于点D.
(1)求k的值;
(2)求△OBD的面积.
19.在直角三角形中,除直角外的5个元素中,已知2个元素(其中至少有1个是边),就可以求出其余的3个未知元素.对于任意三角形,我们需要知道几个元素就可以求出其余的未知元素呢?思考并解答下列问题:
(1)观察图①~图④,根据图中三角形的已知元素,可以求出其余未知元素的序号是________.
(2)如图⑤,在△ABC中,已知∠A=37°,AB=12,AC=10,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
20.如图,在平面直角坐标系中,O为坐标原点,一次函数y=-x+2的图象与反比例函数y=在第二象限的图象交于点A(n,3),与x轴交于点B,连接AO并延长交这个反比例函数在第四象限的图象于点C.
(1)求这个反比例函数的表达式;
(2)求△ABC的面积;
(3)当直线AC对应的函数值大于反比例函数y=的函数值时,直接写出x的取值范围.
21. INCLUDEPICTURE "../情境题·生活应用H.EPS" \* MERGEFORMAT INCLUDEPICTURE "../情境题·生活应用H.EPS" \* MERGEFORMAT \d 某水果生产基地在气温较低时用装有恒温系统的大棚栽培一种新品种水果,如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y(℃)与时间x(h)之间的函数关系图象,其中线段AB,BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.请根据图中信息解答下列问题:
(1)求这个恒温系统设定的恒定温度为多少摄氏度;
(2)求全天的温度y与时间x之间的函数表达式;
(3)若大棚内的温度低于12℃不利于新品种水果的生长,则这天内,相对有利于新品种水果生长的时间共有多少小时?
22. INCLUDEPICTURE "../新视角·操作实践题H.EPS" \* MERGEFORMAT INCLUDEPICTURE "../新视角·操作实践题H.EPS" \* MERGEFORMAT \d 【综合与实践】
不借助科学计算器,如何求tan 22.5°的值?小明进行了如下的实践操作:
如图,已知正方形纸片ABCD.
第一步:将正方形纸片ABCD沿AC折叠,展开后得到折痕AC.
第二步:将AB折叠到AF,使点B的对应点F恰好落在AC上,展开后得到折痕AE,点E在线段BC上,连接EF.
【问题解决】
(1)求证:∠BAE=22.5°;
(2)请利用小明的实践操作过程,求tan 22.5°的值.
23. INCLUDEPICTURE "../2025聊城月考新考向传统文化.EPS" \* MERGEFORMAT INCLUDEPICTURE "../2025聊城月考新考向传统文化.EPS" \* MERGEFORMAT \d 【项目式活动探究】光岳楼位于聊城古城中央,始建于明洪武七年(公元1374年),被誉为中国十大名楼,光岳楼为中国既古老又雄伟的木构楼阁,是宋元建筑向明清建筑过渡的代表作,在中国古代建筑史上有着重要地位,1988年光岳楼被列为全国重点文物保护单位,享有“虽黄鹤、岳阳亦当望拜”之誉.某校数学实践小组利用所学数学知识测量光岳楼的高度,他们制订了两个测量方案,并利用课余时间完成了实地测量.在测量仰角的度数以及有关长度时,都分别测量了两次并取它们的平均值作为测量结果.下面是两个方案及测量数据(不完整):
项目 测量光岳楼的高度
方案 方案一:标杆垂直立于地面,借助平行的太阳光线构成相似三角形.测量:标杆长CD,影长ED及同一时刻楼影长DB 方案二:利用锐角三角函数.测量:距离CD,仰角α,仰角β
说明 E,D,B三点在同一条直线上 B,C,D三点在同一条直线上
测量示意图
测量数据 测量项目 第一次 第二次 平均值 测量项目 第一次 第二次 平均值
CD 1.61 m 1.59 m 1.6 m β 29.9° 30.1° 30°
ED 1.18 m 1.22 m 1.2 m α 37.1° 36.9° 37°
DB 25 m 26 m CD 13.2 m 12.8 m 平均值
【问题解决】
(1)“方案一”两次测量楼影长DB的平均值是________;
(2)根据“方案一”的测量数据,可求得光岳楼AB的高度为________;
(3)根据“方案二”的测量数据,求出光岳楼AB的高度;(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,≈1.73;结果保留一位小数)
(4)请对本次实践活动进行评价.(写出一条即可)
答案
一、1.A 2.B 3.B 4.B 5.B 6.C 7.B
8.B 【点拨】在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,∴AB=2k,BC=k.∵BD=AB,∴∠BAD=∠BDA=∠ABC=15°.∴∠CAD=75°.在Rt△ACD中,CD=CB+BD=CB+AB=k+2k,则tan 75°=tan∠CAD===2+.
9.C 【点拨】设正比例函数表达式为y=kx,反比例函数表达式为y=,把(3,8)分别代入表达式,得8=3k,=8,解得k=,m=24,故两个函数的表达式分别为y=x,y=,把y=6分别代入两个表达式中,得6=x,6=,分别解得x=和x=4,故持续时间为4-=(小时),故选C.
10.D 【点拨】延长BC交PQ于点D,过点A作AH⊥PQ于点H.由题易知BC⊥AC,BD⊥PQ,CD=AH,DH=AC.在Rt△BDP中,∵∠BPD=45°,∴PD=BD.在Rt△ABC中,∵tan 76°=,AC=7米,∴BC=7tan 76°≈28.07(米).∵斜坡AP的坡比为1∶2.4,∴==.设AH=5k米,则PH=12k米,由勾股定理,得AP=13k米.易知PH+HD=BC+CD,∴12k+7≈28.07+5k,解得k≈3.01,∴AP=13k≈39米.
二、11.-2 12.k<4
13.10.3 m 【点拨】在Rt△ABD中,∠ABD=30°,AD=6 m,∴AB=2AD=12 m,∴BD==6≈10.38(m),在Rt△ACD中,∠ACD=16°,AD=6 m,∴CD=≈≈20.69(m),∴BC=CD-BD≈20.69-10.38≈10.3(m).
14.6-2 【点拨】作AD⊥BC于D,设AD=x,∵tan C==,∴CD=3x.∵∠ABC=30°,∴AB=2AD=2x,BD==AD=x.∵BC=BD+CD=x+3x=6,∴x=3-,∴AB=2x=6-2.
15. 【点拨】
如图,过点P作PQ⊥AB交AB延长线于点Q,过点M作MN⊥AB交AB延长线于点N,由题易知在Rt△AQP中,∠PAQ=45°,∴AQ=PQ=60×1.5+BQ=90+BQ,∴ BQ=PQ-90.易知在Rt△BPQ中,∠BPQ=30°,∴BQ=PQ·tan 30°=PQ,∴PQ-90=PQ,∴PQ=45(3+)海里,∴易知MN=PQ=45(3+)海里.在Rt△BMN中,易知∠MBN=30°,∴ BM=2MN=90(3+)海里,∴继续航行=(小时)即可到达.
16.或 【点拨】设直线l交BC于点F.当C′在线段AB上时,如图①,根据AC′∶AB∶BC=1∶3∶7,设AC′=1,AB=3,BC=7,由翻折的性质知∠FCD=∠FC′D′,C′F=CF.∵CD沿直线l翻折至AB所在直线,∴∠BC′F+∠FC′D′=180°=∠FCD+∠FBA,∴∠BC′F=∠FBA,∴BF=C′F=CF=.过点F作AB的垂线,垂足为E,∴BE=BC′=(AB-AC′)=1,∴cos∠ABC===;当C′在BA的延长线上时,如图②,根据AC′∶AB∶BC=1∶3∶7,设AC′=1,AB=3,BC=7,同理知CF=C′F=BF=,过点F作AB的垂线,垂足为E,∴BE=BC′=(AB+AC′)=2,∴cos∠ABC===.综上,cos ∠ABC的值为或.
三、17.【解】(1)原式=2×-+1-×=-+1-=1-.
(2)原式=-×=-.
18.【解】(1)在Rt△ACO中,∠ACO=90°,tan A==,
∴AC=2OC.∵OC2+AC2=OA2,∴OC2+(2OC)2=(2)2,∴OC=2,∴AC=4,∴A(2,4).
∵OA的中点是B,∴B(1,2).
∵B在反比例函数y=的图象上,∴2=,解得k=2.
(2)由(1)知y=,当x=2时,y=1,∴D(2,1),
∴AD=4-1=3,∴S△OBD=S△OAD-S△BAD=×3×2-×3×(2-1)=.
19.【解】(1)③④
(2)能.如图,作CD⊥AB于D,则∠ADC=90°.
∵AC=10,∠A=37°,
∴CD=AC·sin 37°≈10×0.6=6,AD=AC·cos 37°≈10×0.8=8.
∵AB=12,∴BD≈12-8=4,
∴BC=≈=2.
∴能求出BC的长度,BC≈2.
20.【解】(1)∵点A(n,3)在一次函数y=-x+2的图象上,
∴3=-n+2,解得n=-1,
∴A(-1,3).又∵点A(-1,3)在反比例函数y=的图象上,∴k=1×(-3)=-3,
∴反比例函数的表达式为y=-.
(2)在y=-x+2中,当y=0时,0=-x+2,解得x=2,
∴B(2,0).
∵点C在反比例函数y=-的图象上,A(-1,3),
∴根据对称性,得点C的坐标为(1,-3),
∴S△ABC=S△AOB+S△BOC=×2×3+×2×3=6.
(3)由图象可得,当直线AC对应的函数值大于反比例函数y=的函数值时,x的取值范围是x<-1或0
根据题意,得解得
∴直线AB的表达式为y=2x+10.
当x=5时,y=2×5+10=20,
∴这个恒温系统设定的恒定温度为20 ℃.
(2)由(1)可知,当0≤x≤5时,y=2x+10,
当5<x≤10时,y=20.
设反比例函数表达式为y=,
根据题意,得20=,∴k′=200,
∴反比例函数的表达式为y=.
∴全天的温度y与时间x之间的函数表达式为
y=
(3)当0≤x≤5时,令y=12,则12=2x+10,解得x=1;
当10<x≤24时,令y=12,则12=,解得x=.
∴相对有利于新品种水果生长的时间共有-1=(h).
22.(1)【证明】∵四边形ABCD是正方形,∴∠BAD=90°,
由折叠的性质,得∠BAC=∠DAC=∠BAD=×90°=45°,同理可得,∠BAE=∠EAF=∠BAC=×45°=22.5°.
(2)【解】∵四边形ABCD是正方形,
∴∠B=∠BCD=90°,AB=BC.
由折叠的性质,得BE=EF,∠B=∠AFE=90°,
∠ECF=∠BCD=45°,
∴∠CFE=180°-∠AFE=90°,
∴∠FEC=90°-∠ECF=45°,
∴∠ECF=∠FEC,∴EF=FC.
设BE=a,则EF=FC=a,
∴在Rt△CEF中,EC=a,
∴BC=BE+EC=(1+)a,
∴AB=BC=(1+)a.
在Rt△ABE中,
tan∠BAE=tan 22.5°===-1.
∴tan 22.5°=-1.
23.【解】(1)25.5 m
(2)34 m
(3)设BC=x m,∵CD==13(m),
∴BD=BC+CD=(x+13)m.
在Rt△ABC中,∠ACB=37°,
∴AB=BC·tan 37°≈0.75x m.
在Rt△ABD中,∠ADB=30°,
∴AB=BD·tan 30°=(x+13)m.
∴0.75x≈(x+13),解得x≈44,
∴AB≈0.75x=33 m.
答:光岳楼AB的高度约为33 m.
(4)两种方案均可测量出光岳楼的近似高度,测量时取平均值是减少误差的方式.(答案不唯一)
同课章节目录
