期末综合素质评价卷(含答案)鲁教版五四制九年级数学
文档属性
| 名称 | 期末综合素质评价卷(含答案)鲁教版五四制九年级数学 | 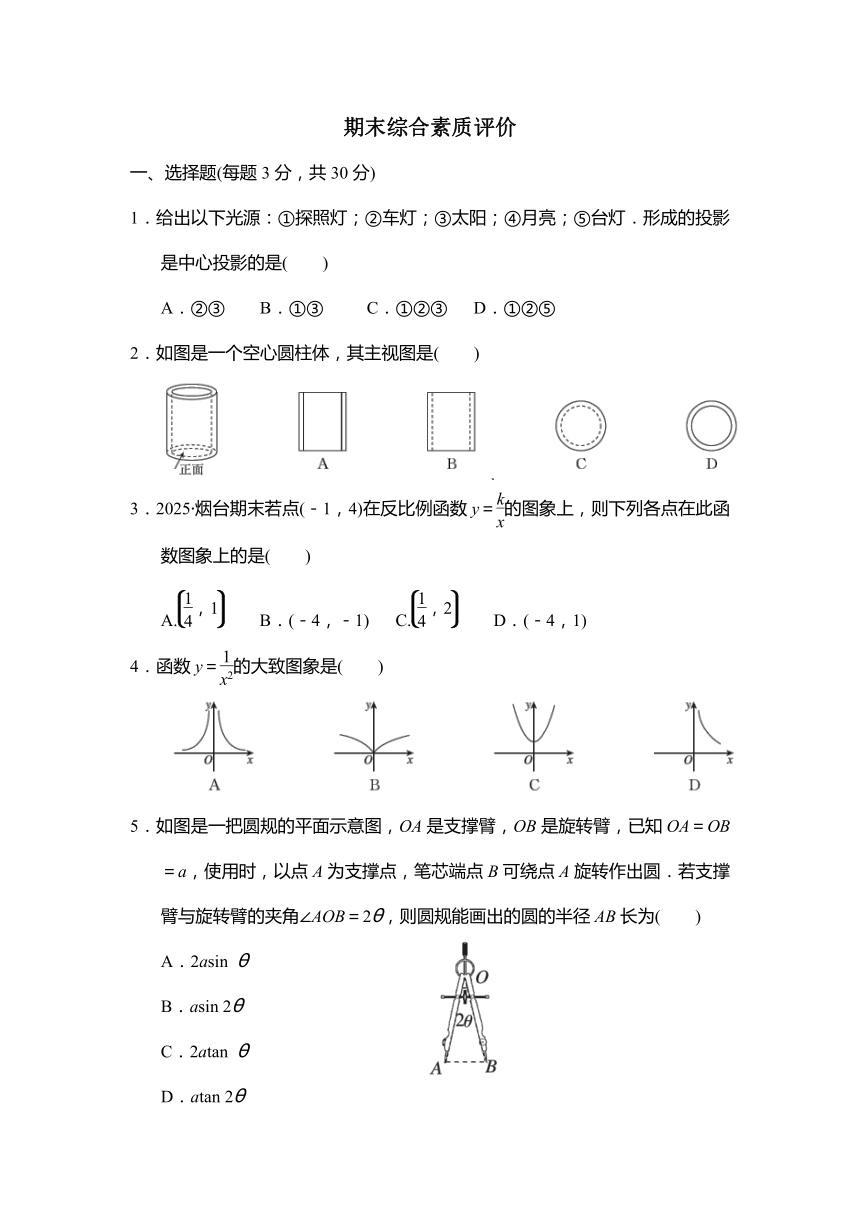 | |
| 格式 | doc | ||
| 文件大小 | 492.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-08 20:26:44 | ||
图片预览



文档简介
期末综合素质评价
一、选择题(每题3分,共30分)
1.给出以下光源:①探照灯;②车灯;③太阳;④月亮;⑤台灯.形成的投影是中心投影的是( )
A.②③ B.①③ C.①②③ D.①②⑤
2.如图是一个空心圆柱体,其主视图是( )
3.2025·烟台期末若点(-1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A. B.(-4,-1) C. D.(-4,1)
4.函数y=的大致图象是( )
5.如图是一把圆规的平面示意图,OA是支撑臂,OB是旋转臂,已知OA=OB=a,使用时,以点A为支撑点,笔芯端点B可绕点A旋转作出圆.若支撑臂与旋转臂的夹角∠AOB=2θ,则圆规能画出的圆的半径AB长为( )
A.2asin θ
B.asin 2θ
C.2atan θ
D.atan 2θ
6. INCLUDEPICTURE "../新考法·构造直角三角形法H.EPS" \* MERGEFORMAT INCLUDEPICTURE "../新考法·构造直角三角形法H.EPS" \* MERGEFORMAT \d 如图,△ABC的顶点都在正方形网格的格点上,则tan A的值为( )
A. B. C. D.
7.如图,△ABC是等边三角形,点A和点B在x轴上,点C在y轴上,AD⊥CB,垂足为点D,反比例函数y=(k>0)的图象经过点D,若△ABC的面积为8,则k的值为( )
A.2 B. C.3 D.4
8.如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线ED交AC于点D,连接BD,若 BC=2,则cos∠BDC的值是 ( )
A.
B.
C.
D.
9.已知二次函数y=mx2-2mx+3(m为常数,且m≠0),当-1≤x≤2时,函数有最小值2,则m的值是( )
A.1 B.
C.1或 D.1或-
10.[2025·日照月考]如图,二次函数y=ax2+bx+c(a≠0)图象的一部分与x轴的一个交点坐标为(-1,0),对称轴为直线x=1,结合图象给出下列结论:
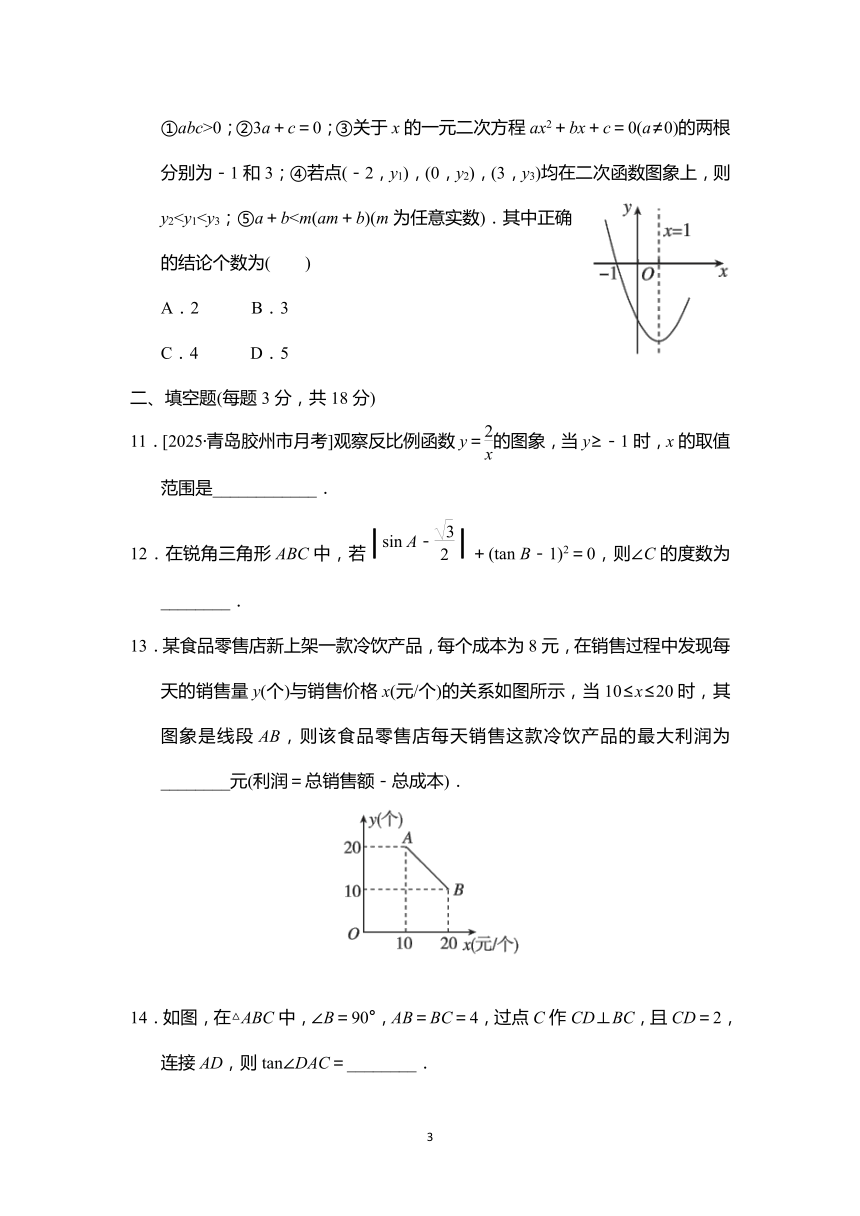
①abc>0;②3a+c=0;③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为-1和3;④若点(-2,y1),(0,y2),(3,y3)均在二次函数图象上,则y2的结论个数为( )
A.2 B.3
C.4 D.5
二、填空题(每题3分,共18分)
11.[2025·青岛胶州市月考]观察反比例函数y=的图象,当y≥-1时,x的取值范围是____________.
12.在锐角三角形ABC中,若+(tan B-1)2=0,则∠C的度数为________.
13.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中发现每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当10≤x≤20时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为________元(利润=总销售额-总成本).
14.如图,在△ABC中,∠B=90°,AB=BC=4,过点C作CD⊥BC,且CD=2,连接AD,则tan∠DAC=________.
15. INCLUDEPICTURE "../母题左灰.eps" \* MERGEFORMAT INCLUDEPICTURE "../母题左灰.eps" \* MERGEFORMAT \d [教材P144复习题T11]一个几何体由若干个大小相同的小正方体搭成,如图分别是它的左视图与俯视图,该几何体所用小正方体的个数是m,则m的最小值是________.
16. INCLUDEPICTURE "../新视角·新定义题H.EPS" \* MERGEFORMAT INCLUDEPICTURE "../新视角·新定义题H.EPS" \* MERGEFORMAT \d 定义:在平面直角坐标系xOy中,如果将点P绕点T(0,t)(t>0)旋转180°得到点Q,那么称线段PQ为“拓展带”,点Q为点P的“拓展点”.
(1)当t=3时,点(-1,1)的“拓展点”坐标为________.
(2)如果t>1,当点M(2,1)的“拓展点”N在函数y=-的图象上时,t的值为________.
三、解答题(17题6分,18,19题每题8分,20~22题每题12分,23题14分,共72分)
17.2025·菏泽月考计算:
(1)cos 30°+2-1-sin 45°-(tan 60°+1)0;
(2)cos 60°-sin 245°+tan 230°-sin 30°.
18.如图①是一种包装盒的平面展开图,将它围起来可得到一个几何体的模型.
(1)这个几何体模型最确切的名称是____________;
(2)如图②是根据a,h的取值画出的几何体的主视图和俯视图,请在网格中画出该几何体的左视图;
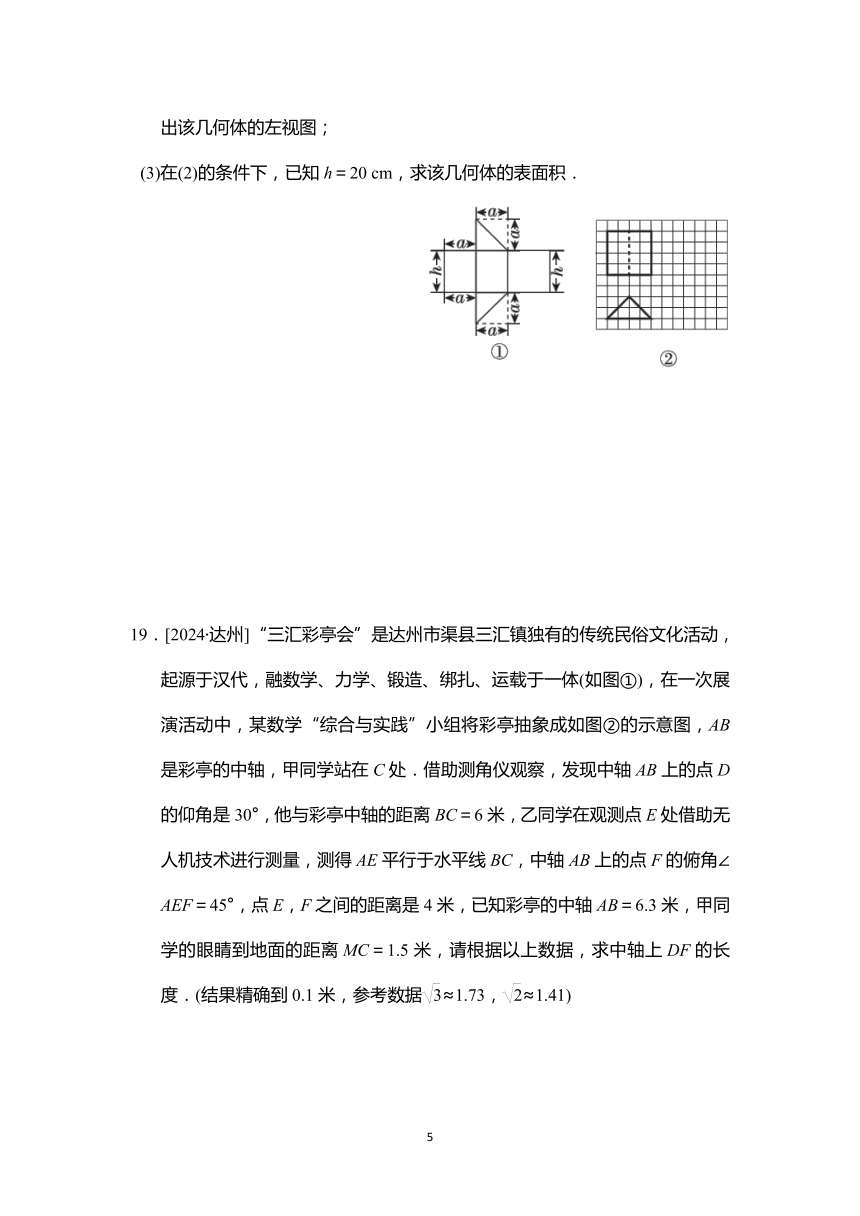
(3)在(2)的条件下,已知h=20 cm,求该几何体的表面积.
19.[2024·达州]“三汇彩亭会”是达州市渠县三汇镇独有的传统民俗文化活动,起源于汉代,融数学、力学、锻造、绑扎、运载于一体(如图①),在一次展演活动中,某数学“综合与实践”小组将彩亭抽象成如图②的示意图,AB是彩亭的中轴,甲同学站在C处.借助测角仪观察,发现中轴AB上的点D的仰角是30°,他与彩亭中轴的距离BC=6米,乙同学在观测点E处借助无人机技术进行测量,测得AE平行于水平线BC,中轴AB上的点F的俯角∠AEF=45°,点E,F之间的距离是4米,已知彩亭的中轴AB=6.3米,甲同学的眼睛到地面的距离MC=1.5米,请根据以上数据,求中轴上DF的长度.(结果精确到0.1米,参考数据≈1.73,≈1.41)
20.如图,一次函数y=ax+b的图象与反比例函数y=的图象相交于A(m,1),B(2,-3)两点,与y轴交于点C.
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出不等式ax+b>的解集;
(3)设D为线段AC上的一个动点(不包括A,C两点),过点D作DE∥y轴交反比例函数图象于点E,连接CE,当△CDE的面积最大时,求点E的坐标,并求出面积的最大值.
21.如图,某光源下有三根竖立的杆子,甲杆GH的影子为GM,乙杆EF的影子一部分落在地面EA上,另一部分落在斜坡AB上的AD处.
(1)请在图中画出形成影子的光线,确定光源所在的位置R,并画出丙杆PQ在地面上的影子;
(2)在(1)的结论下,若过点F的光线FD⊥AB,斜坡与地面的夹角为60°,AD=1 m,AE=2 m,求乙杆EF的高度(结果保留根号).
22.某商场经销一种儿童玩具,该种玩具的进价是每个15元,经过一段时间的销售发现,该种玩具每天的销售量y(个)与每个的售价x(元)之间的函数关系如图所示.
(1)求y关于x的函数关系式,并求出当某天的销售量为78个时,该玩具的销售利润.
(2)每天的销售量不低于18个的情况下,若要每天获得的销售利润最大,求该玩具每个的售价是多少?最大利润是多少?
(3)根据物价部门规定,这种玩具的售价每个不能高于45元.该商场决定每销售一个这种玩具就捐款n元(1≤n≤7),捐款后发现,该商场每天销售这种玩具所获利润随售价的增大而增大,求n的取值范围.
23.如图,抛物线y=ax2+bx-4(a≠0)与x轴交于点A,B(-1,0),与y轴交于点C,且OA=OC,点D(m,0)是线段OA上一动点(不与点O,A重合),过点D作DP⊥x轴交直线AC于点E,交抛物线于点P,连接CP.
(1)求抛物线的表达式;
(2)过点P作PQ⊥AC,垂足为Q,求PQ的最大值;
(3)试探究在点D的运动过程中,是否存在点P,使得△CPE为直角三角形.若存在,求出点P的坐标;若不存在,请说明理由.
答案
一、1.D 2.B 3.D 4.A 5.A 6.A
7.A 【点拨】过点D作DE∥CO,DF∥AB,分别交AB,CO于点E,F,则四边形OEDF是矩形.∵△ABC是等边三角形,CO⊥AB,AD⊥BC,∴AO=OB,CD=DB,∴点D是BC边的中点.又∵DE∥CO,DF∥AB,∴DF=OB,DE=CO,∴S矩形OEDF=DF·DE=OB·OC=S△COB=S△ABC=×8=2.∵点D在反比例函数y=的图象上,∴|k|=2,又∵k>0,∴k=2.
8.B
9.D 【点拨】∵二次函数y=mx2-2mx+3(m为常数,且m≠0),∴抛物线的对称轴为直线x=-=1.当m>0时,抛物线开口向上,对称轴x=1在-1≤x≤2范围内,∴当x=1时,y=mx2-2mx+3取得最小值2,即 2=m-2m+3,解得m=1.当m<0时,抛物线开口向下,对称轴x=1在-1≤x≤2范围内,则离对称轴越远的点的纵坐标越小,∴当x=-1时,y=mx2-2mx+3取得最小值2,即2=m+2m+3,解得m=-.∴ m的值是1或-.
10.B 【点拨】①∵抛物线的开口向上,∴a>0,∵对称轴在y轴右侧,∴->0,∴b<0,∵抛物线与y轴的交点在y轴的负半轴上,∴c<0,∴abc>0,故①正确;②∵对称轴为直线x=-=1,∴b=-2a,由图象可知,当x=-1时,a-b+c=0,∴3a+c=0,故②正确;③∵对称轴为直线x=1,抛物线与x轴的一个交点坐标为(-1,0),∴抛物线与x轴的另一个交点坐标为(3,0),∴关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为-1和3,故③正确;④由图象易得y2二、11.x≤-2或x>0 12.75°
13.121 【点拨】当10≤x≤20时,设y=kx+b,,把(10,20),(20,10)的坐标代入,得 解得 ∴每天的销售量y(个)与销售价格x(元/个)的函数表达式为y=-x+30.设该食品零售店每天销售这款冷饮产品的利润为w元,则w=(x-8)y=(x-8)(-x+30)=-x2+38x-240=-(x-19)2+121,∵-1<0,∴当x=19时,w有最大值为121,故答案为121.
14. 【点拨】过点A作AE⊥CD,交CD的延长线于点E.∵∠B=∠DCB=∠E=90°,AB=BC,∴四边形ABCE是正方形.∴AE=EC=AB=4,∠DCA=45°.又∵CD=2,∴DE=CE-CD=4-2=2.在Rt△AED中,AD===2.过点D作DF⊥AC于点F.∵∠DCA=45°,∠DFC=90°,∴∠CDF=45°=∠DCA.∴FD=FC,∴DC=FD=2,∴FD=.在Rt△AFD中,AF===3,∴tan∠DAC===.
15.9 【点拨】由左视图与俯视图可确定所用小正方体个数最少时的俯视图如图.
所以组成这个几何体所用的小正方体最少有9个,即m的最小值是9.
16.(1)(1,5) (2)2
【点拨】(1)由“拓展点”的定义可得互为“拓展点”的两点的横坐标互为相反数,纵坐标的和的一半等于t,∴当t=3时,点(-1,1)的“拓展点”坐标为(1,5).(2)设N点坐标为(x,y),则=0,=t,解得x=-2,y=2t-1,∵N在函数y=-的图象上,∴-2(2t-1)=-6,解得t=2.
三、17.【解】(1)原式=×+-×-1=+-1-1=0.
(2)原式=-+×-=-+×-=0.
18.【解】(1)直三棱柱
(2)如图所示.
(3)由题可得a==10(cm),
所以该几何体的表面积为×(10)2×2+2×10×20+202=600+400(cm2).
19.【解】过点M作MN⊥AB,垂足为N.由题易知,四边形CMNB是矩形.
∴CM=BN=1.5米,MN=CB=6米,AN=AB-BN=6.3-1.5=4.8(米).
在Rt△DMN中,tan∠DMN=tan 30°=,
∴DN=MN·tan 30°=2米.
在Rt△AEF中,EF=4米,sin∠AEF=sin 45°=,
∴AF=EF·sin 45°=2米.
∵AF+DN=AN+DF,
∴DF=2+2-4.8≈2×1.73+2×1.41-4.8=3.46+2.82-4.8=1.48≈1.5(米).
∴中轴上DF的长度约为1.5米.
20.【解】(1)∵点B(2,-3)在反比例函数图象上,∴k=-6,
∴反比例函数的表达式为y=-.
∵点A(m,1)在反比例函数y=-的图象上,
∴1=-,解得m=-6,∴A(-6,1).
∵A(-6,1),B(2,-3)在一次函数y=ax+b的图象上,
∴解得
∴一次函数的表达式为y=-x-2.
(2)根据图象可得不等式ax+b>的解集为x<-6或0(3)易知C(0,-2),设点D的坐标为(-6∴ED=--=-+t+2,
∴S△CDE=×(-t)×=-t2-t+3=-(t+2)2+4.∵-<0,
∴当t=-2时,S△CDE有最大值为4,此时E(-2,3).
21.【解】(1)如图所示,QN即为丙杆PQ在地面上的影子.
(2)如图,分别延长FD,EA交于点S,易知∠ADS=90°.
∵∠DAS=60°,∴∠S=30°.
∵AD=1 m,∴AS=2 m,
∴ES=AS+AE=2+2=4(m).
在Rt△EFS中,∠FES=90°,∠S=30°,
∴tan S=tan 30°===,∴EF= m.
∴乙杆EF的高度为 m.
22.【解】(1)设y关于x的函数关系式为y=kx+b,
由题意知,图象过(30,120),(45,75)两点,
∴解得
∴y=-3x+210,
当y=78时,-3x+210=78,解得x=44,
此时利润为78×(44-15)=2 262(元),
∴当某天的销售量为78个时,该玩具的销售利润为2 262元.
(2)由题意得,-3x+210≥18,解得x≤64.
设每天的销售利润为W元,
依题意,得W=(x-15)(-3x+210)=-3x2+255x-3 150 =-3(x-42.5)2+2 268.75.
∵-3<0,且销售个数为整数,∴当x=42或43时,W取得最大值,最大值为2 268,∴要每天获得的销售利润最大,该玩具每个的售价是42或43元,最大利润为2 268元.
(3)设捐款后每天所获得的利润为Q元,
依题意得,Q=(x-15-n)(-3x+210)=-3x2+(255+3n)x-3 150-210n,
∵抛物线的对称轴为直线x=42.5+0.5n,-3<0,
∴当x≤42.5+0.5n时,Q随x的增大而增大.
∵物价部门规定这种玩具的售价每个不能高于45元,
∴42.5+0.5n≥45,解得n≥5,
又∵1≤n≤7,∴5≤n≤7.
23.【解】(1)对于y=ax2+bx-4(a≠0),令x=0,则y=-4,∴C(0,-4),∴OC=4,
∵OA=OC,∴OA=4,∴A(4,0).
∵抛物线y=ax2+bx-4(a≠0)与x轴交于点A(4,0),B(-1,0),
∴解得
∴抛物线的表达式为y=x2-3x-4.
(2)设直线AC的表达式为y=kx+n,
把A(4,0),C(0,-4)的坐标代入,得解得
∴直线AC的表达式为y=x-4.
∵DP⊥x轴,D(m,0),
∴E(m,m-4),P(m,m2-3m-4),
∴PE=m-4-(m2-3m-4)=-m2+4m.
∵OA=OC,∠AOC=90°,∴∠OAC=∠OCA=45°.
易知PE∥y轴,∴∠CEP=∠OCA=45°.
∵PQ⊥AC,∴△PQE为等腰直角三角形,
∴PQ=PE=(-m2+4m)=-(m-2)2+2.
∵-<0,0(3)存在点P,使得△CPE为直角三角形.
由(2)知∠CEP=45°≠90°,P(m,m2-3m-4),PE=-m2+4m,∠CAO=45°.∵D(m,0),∴OD=m.
分两种情况讨论:
①当∠PCE=90°时,过点E作EF⊥y轴于点F,则EF=OD=m,
易知OA∥EF,
∴∠CEF=∠CAO=45°,
∴易得CE=EF=m.
∵易知EP=CE,∴EP=2m,
∴-m2+4m=2m,解得m=0(舍去)或m=2.
∴P(2,-6);
②当∠EPC=90°时,易知CP∥x轴,
∴点P与点C的纵坐标相同,为-4,
∴m2-3m-4=-4,解得m=0(舍去)或m=3,
∴P(3,-4).
综上,存在点P,点P的坐标为(3,-4)或(2,-6).
一、选择题(每题3分,共30分)
1.给出以下光源:①探照灯;②车灯;③太阳;④月亮;⑤台灯.形成的投影是中心投影的是( )
A.②③ B.①③ C.①②③ D.①②⑤
2.如图是一个空心圆柱体,其主视图是( )
3.2025·烟台期末若点(-1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A. B.(-4,-1) C. D.(-4,1)
4.函数y=的大致图象是( )
5.如图是一把圆规的平面示意图,OA是支撑臂,OB是旋转臂,已知OA=OB=a,使用时,以点A为支撑点,笔芯端点B可绕点A旋转作出圆.若支撑臂与旋转臂的夹角∠AOB=2θ,则圆规能画出的圆的半径AB长为( )
A.2asin θ
B.asin 2θ
C.2atan θ
D.atan 2θ
6. INCLUDEPICTURE "../新考法·构造直角三角形法H.EPS" \* MERGEFORMAT INCLUDEPICTURE "../新考法·构造直角三角形法H.EPS" \* MERGEFORMAT \d 如图,△ABC的顶点都在正方形网格的格点上,则tan A的值为( )
A. B. C. D.
7.如图,△ABC是等边三角形,点A和点B在x轴上,点C在y轴上,AD⊥CB,垂足为点D,反比例函数y=(k>0)的图象经过点D,若△ABC的面积为8,则k的值为( )
A.2 B. C.3 D.4
8.如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线ED交AC于点D,连接BD,若 BC=2,则cos∠BDC的值是 ( )
A.
B.
C.
D.
9.已知二次函数y=mx2-2mx+3(m为常数,且m≠0),当-1≤x≤2时,函数有最小值2,则m的值是( )
A.1 B.
C.1或 D.1或-
10.[2025·日照月考]如图,二次函数y=ax2+bx+c(a≠0)图象的一部分与x轴的一个交点坐标为(-1,0),对称轴为直线x=1,结合图象给出下列结论:
①abc>0;②3a+c=0;③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为-1和3;④若点(-2,y1),(0,y2),(3,y3)均在二次函数图象上,则y2
A.2 B.3
C.4 D.5
二、填空题(每题3分,共18分)
11.[2025·青岛胶州市月考]观察反比例函数y=的图象,当y≥-1时,x的取值范围是____________.
12.在锐角三角形ABC中,若+(tan B-1)2=0,则∠C的度数为________.
13.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中发现每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当10≤x≤20时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为________元(利润=总销售额-总成本).
14.如图,在△ABC中,∠B=90°,AB=BC=4,过点C作CD⊥BC,且CD=2,连接AD,则tan∠DAC=________.
15. INCLUDEPICTURE "../母题左灰.eps" \* MERGEFORMAT INCLUDEPICTURE "../母题左灰.eps" \* MERGEFORMAT \d [教材P144复习题T11]一个几何体由若干个大小相同的小正方体搭成,如图分别是它的左视图与俯视图,该几何体所用小正方体的个数是m,则m的最小值是________.
16. INCLUDEPICTURE "../新视角·新定义题H.EPS" \* MERGEFORMAT INCLUDEPICTURE "../新视角·新定义题H.EPS" \* MERGEFORMAT \d 定义:在平面直角坐标系xOy中,如果将点P绕点T(0,t)(t>0)旋转180°得到点Q,那么称线段PQ为“拓展带”,点Q为点P的“拓展点”.
(1)当t=3时,点(-1,1)的“拓展点”坐标为________.
(2)如果t>1,当点M(2,1)的“拓展点”N在函数y=-的图象上时,t的值为________.
三、解答题(17题6分,18,19题每题8分,20~22题每题12分,23题14分,共72分)
17.2025·菏泽月考计算:
(1)cos 30°+2-1-sin 45°-(tan 60°+1)0;
(2)cos 60°-sin 245°+tan 230°-sin 30°.
18.如图①是一种包装盒的平面展开图,将它围起来可得到一个几何体的模型.
(1)这个几何体模型最确切的名称是____________;
(2)如图②是根据a,h的取值画出的几何体的主视图和俯视图,请在网格中画出该几何体的左视图;
(3)在(2)的条件下,已知h=20 cm,求该几何体的表面积.
19.[2024·达州]“三汇彩亭会”是达州市渠县三汇镇独有的传统民俗文化活动,起源于汉代,融数学、力学、锻造、绑扎、运载于一体(如图①),在一次展演活动中,某数学“综合与实践”小组将彩亭抽象成如图②的示意图,AB是彩亭的中轴,甲同学站在C处.借助测角仪观察,发现中轴AB上的点D的仰角是30°,他与彩亭中轴的距离BC=6米,乙同学在观测点E处借助无人机技术进行测量,测得AE平行于水平线BC,中轴AB上的点F的俯角∠AEF=45°,点E,F之间的距离是4米,已知彩亭的中轴AB=6.3米,甲同学的眼睛到地面的距离MC=1.5米,请根据以上数据,求中轴上DF的长度.(结果精确到0.1米,参考数据≈1.73,≈1.41)
20.如图,一次函数y=ax+b的图象与反比例函数y=的图象相交于A(m,1),B(2,-3)两点,与y轴交于点C.
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出不等式ax+b>的解集;
(3)设D为线段AC上的一个动点(不包括A,C两点),过点D作DE∥y轴交反比例函数图象于点E,连接CE,当△CDE的面积最大时,求点E的坐标,并求出面积的最大值.
21.如图,某光源下有三根竖立的杆子,甲杆GH的影子为GM,乙杆EF的影子一部分落在地面EA上,另一部分落在斜坡AB上的AD处.
(1)请在图中画出形成影子的光线,确定光源所在的位置R,并画出丙杆PQ在地面上的影子;
(2)在(1)的结论下,若过点F的光线FD⊥AB,斜坡与地面的夹角为60°,AD=1 m,AE=2 m,求乙杆EF的高度(结果保留根号).
22.某商场经销一种儿童玩具,该种玩具的进价是每个15元,经过一段时间的销售发现,该种玩具每天的销售量y(个)与每个的售价x(元)之间的函数关系如图所示.
(1)求y关于x的函数关系式,并求出当某天的销售量为78个时,该玩具的销售利润.
(2)每天的销售量不低于18个的情况下,若要每天获得的销售利润最大,求该玩具每个的售价是多少?最大利润是多少?
(3)根据物价部门规定,这种玩具的售价每个不能高于45元.该商场决定每销售一个这种玩具就捐款n元(1≤n≤7),捐款后发现,该商场每天销售这种玩具所获利润随售价的增大而增大,求n的取值范围.
23.如图,抛物线y=ax2+bx-4(a≠0)与x轴交于点A,B(-1,0),与y轴交于点C,且OA=OC,点D(m,0)是线段OA上一动点(不与点O,A重合),过点D作DP⊥x轴交直线AC于点E,交抛物线于点P,连接CP.
(1)求抛物线的表达式;
(2)过点P作PQ⊥AC,垂足为Q,求PQ的最大值;
(3)试探究在点D的运动过程中,是否存在点P,使得△CPE为直角三角形.若存在,求出点P的坐标;若不存在,请说明理由.
答案
一、1.D 2.B 3.D 4.A 5.A 6.A
7.A 【点拨】过点D作DE∥CO,DF∥AB,分别交AB,CO于点E,F,则四边形OEDF是矩形.∵△ABC是等边三角形,CO⊥AB,AD⊥BC,∴AO=OB,CD=DB,∴点D是BC边的中点.又∵DE∥CO,DF∥AB,∴DF=OB,DE=CO,∴S矩形OEDF=DF·DE=OB·OC=S△COB=S△ABC=×8=2.∵点D在反比例函数y=的图象上,∴|k|=2,又∵k>0,∴k=2.
8.B
9.D 【点拨】∵二次函数y=mx2-2mx+3(m为常数,且m≠0),∴抛物线的对称轴为直线x=-=1.当m>0时,抛物线开口向上,对称轴x=1在-1≤x≤2范围内,∴当x=1时,y=mx2-2mx+3取得最小值2,即 2=m-2m+3,解得m=1.当m<0时,抛物线开口向下,对称轴x=1在-1≤x≤2范围内,则离对称轴越远的点的纵坐标越小,∴当x=-1时,y=mx2-2mx+3取得最小值2,即2=m+2m+3,解得m=-.∴ m的值是1或-.
10.B 【点拨】①∵抛物线的开口向上,∴a>0,∵对称轴在y轴右侧,∴->0,∴b<0,∵抛物线与y轴的交点在y轴的负半轴上,∴c<0,∴abc>0,故①正确;②∵对称轴为直线x=-=1,∴b=-2a,由图象可知,当x=-1时,a-b+c=0,∴3a+c=0,故②正确;③∵对称轴为直线x=1,抛物线与x轴的一个交点坐标为(-1,0),∴抛物线与x轴的另一个交点坐标为(3,0),∴关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为-1和3,故③正确;④由图象易得y2
13.121 【点拨】当10≤x≤20时,设y=kx+b,,把(10,20),(20,10)的坐标代入,得 解得 ∴每天的销售量y(个)与销售价格x(元/个)的函数表达式为y=-x+30.设该食品零售店每天销售这款冷饮产品的利润为w元,则w=(x-8)y=(x-8)(-x+30)=-x2+38x-240=-(x-19)2+121,∵-1<0,∴当x=19时,w有最大值为121,故答案为121.
14. 【点拨】过点A作AE⊥CD,交CD的延长线于点E.∵∠B=∠DCB=∠E=90°,AB=BC,∴四边形ABCE是正方形.∴AE=EC=AB=4,∠DCA=45°.又∵CD=2,∴DE=CE-CD=4-2=2.在Rt△AED中,AD===2.过点D作DF⊥AC于点F.∵∠DCA=45°,∠DFC=90°,∴∠CDF=45°=∠DCA.∴FD=FC,∴DC=FD=2,∴FD=.在Rt△AFD中,AF===3,∴tan∠DAC===.
15.9 【点拨】由左视图与俯视图可确定所用小正方体个数最少时的俯视图如图.
所以组成这个几何体所用的小正方体最少有9个,即m的最小值是9.
16.(1)(1,5) (2)2
【点拨】(1)由“拓展点”的定义可得互为“拓展点”的两点的横坐标互为相反数,纵坐标的和的一半等于t,∴当t=3时,点(-1,1)的“拓展点”坐标为(1,5).(2)设N点坐标为(x,y),则=0,=t,解得x=-2,y=2t-1,∵N在函数y=-的图象上,∴-2(2t-1)=-6,解得t=2.
三、17.【解】(1)原式=×+-×-1=+-1-1=0.
(2)原式=-+×-=-+×-=0.
18.【解】(1)直三棱柱
(2)如图所示.
(3)由题可得a==10(cm),
所以该几何体的表面积为×(10)2×2+2×10×20+202=600+400(cm2).
19.【解】过点M作MN⊥AB,垂足为N.由题易知,四边形CMNB是矩形.
∴CM=BN=1.5米,MN=CB=6米,AN=AB-BN=6.3-1.5=4.8(米).
在Rt△DMN中,tan∠DMN=tan 30°=,
∴DN=MN·tan 30°=2米.
在Rt△AEF中,EF=4米,sin∠AEF=sin 45°=,
∴AF=EF·sin 45°=2米.
∵AF+DN=AN+DF,
∴DF=2+2-4.8≈2×1.73+2×1.41-4.8=3.46+2.82-4.8=1.48≈1.5(米).
∴中轴上DF的长度约为1.5米.
20.【解】(1)∵点B(2,-3)在反比例函数图象上,∴k=-6,
∴反比例函数的表达式为y=-.
∵点A(m,1)在反比例函数y=-的图象上,
∴1=-,解得m=-6,∴A(-6,1).
∵A(-6,1),B(2,-3)在一次函数y=ax+b的图象上,
∴解得
∴一次函数的表达式为y=-x-2.
(2)根据图象可得不等式ax+b>的解集为x<-6或0
∴S△CDE=×(-t)×=-t2-t+3=-(t+2)2+4.∵-<0,
∴当t=-2时,S△CDE有最大值为4,此时E(-2,3).
21.【解】(1)如图所示,QN即为丙杆PQ在地面上的影子.
(2)如图,分别延长FD,EA交于点S,易知∠ADS=90°.
∵∠DAS=60°,∴∠S=30°.
∵AD=1 m,∴AS=2 m,
∴ES=AS+AE=2+2=4(m).
在Rt△EFS中,∠FES=90°,∠S=30°,
∴tan S=tan 30°===,∴EF= m.
∴乙杆EF的高度为 m.
22.【解】(1)设y关于x的函数关系式为y=kx+b,
由题意知,图象过(30,120),(45,75)两点,
∴解得
∴y=-3x+210,
当y=78时,-3x+210=78,解得x=44,
此时利润为78×(44-15)=2 262(元),
∴当某天的销售量为78个时,该玩具的销售利润为2 262元.
(2)由题意得,-3x+210≥18,解得x≤64.
设每天的销售利润为W元,
依题意,得W=(x-15)(-3x+210)=-3x2+255x-3 150 =-3(x-42.5)2+2 268.75.
∵-3<0,且销售个数为整数,∴当x=42或43时,W取得最大值,最大值为2 268,∴要每天获得的销售利润最大,该玩具每个的售价是42或43元,最大利润为2 268元.
(3)设捐款后每天所获得的利润为Q元,
依题意得,Q=(x-15-n)(-3x+210)=-3x2+(255+3n)x-3 150-210n,
∵抛物线的对称轴为直线x=42.5+0.5n,-3<0,
∴当x≤42.5+0.5n时,Q随x的增大而增大.
∵物价部门规定这种玩具的售价每个不能高于45元,
∴42.5+0.5n≥45,解得n≥5,
又∵1≤n≤7,∴5≤n≤7.
23.【解】(1)对于y=ax2+bx-4(a≠0),令x=0,则y=-4,∴C(0,-4),∴OC=4,
∵OA=OC,∴OA=4,∴A(4,0).
∵抛物线y=ax2+bx-4(a≠0)与x轴交于点A(4,0),B(-1,0),
∴解得
∴抛物线的表达式为y=x2-3x-4.
(2)设直线AC的表达式为y=kx+n,
把A(4,0),C(0,-4)的坐标代入,得解得
∴直线AC的表达式为y=x-4.
∵DP⊥x轴,D(m,0),
∴E(m,m-4),P(m,m2-3m-4),
∴PE=m-4-(m2-3m-4)=-m2+4m.
∵OA=OC,∠AOC=90°,∴∠OAC=∠OCA=45°.
易知PE∥y轴,∴∠CEP=∠OCA=45°.
∵PQ⊥AC,∴△PQE为等腰直角三角形,
∴PQ=PE=(-m2+4m)=-(m-2)2+2.
∵-<0,0
由(2)知∠CEP=45°≠90°,P(m,m2-3m-4),PE=-m2+4m,∠CAO=45°.∵D(m,0),∴OD=m.
分两种情况讨论:
①当∠PCE=90°时,过点E作EF⊥y轴于点F,则EF=OD=m,
易知OA∥EF,
∴∠CEF=∠CAO=45°,
∴易得CE=EF=m.
∵易知EP=CE,∴EP=2m,
∴-m2+4m=2m,解得m=0(舍去)或m=2.
∴P(2,-6);
②当∠EPC=90°时,易知CP∥x轴,
∴点P与点C的纵坐标相同,为-4,
∴m2-3m-4=-4,解得m=0(舍去)或m=3,
∴P(3,-4).
综上,存在点P,点P的坐标为(3,-4)或(2,-6).
同课章节目录
