第四章 投影与视图 综合素质评价卷(含答案)鲁教版五四制九年级上册数学
文档属性
| 名称 | 第四章 投影与视图 综合素质评价卷(含答案)鲁教版五四制九年级上册数学 |

|
|
| 格式 | doc | ||
| 文件大小 | 647.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-08 00:00:00 | ||
图片预览




文档简介
第四章 投影与视图综合素质评价
一、选择题(每题3分,共30分)
1.下列关于投影的说法中不正确的是( )
A.正午,某大厦在地面上的投影是平行投影
B.匡衡借光学习时,他在地面上的投影是中心投影
C.三角形木板的正投影是一个点
D.晚上,小强向路灯走去,他的影子越来越短
2.把一个正六棱柱如图放置,一束水平方向的平行光线照射此正六棱柱时的正投影是( )
3.如图是某学校操场上的单杠(图中实线部分)及其在地面上的影子(图中虚线部分),根据图中所示,可判断形成该影子的光线为( )
A.太阳光线 B.灯光光线
C.太阳光线或灯光光线 D.该影子实际不可能存在
4.如图,济南泉城广场上矗立着一座泉标,其取古汉字“泉”字的意象造型.在晴天的日子里,从早到晚的这段时间,泉标在太阳下的影子长度的变化规律是( )
A.保持不变 B.逐渐变长 C.先逐渐变短,后又逐渐变长 D.逐渐变短
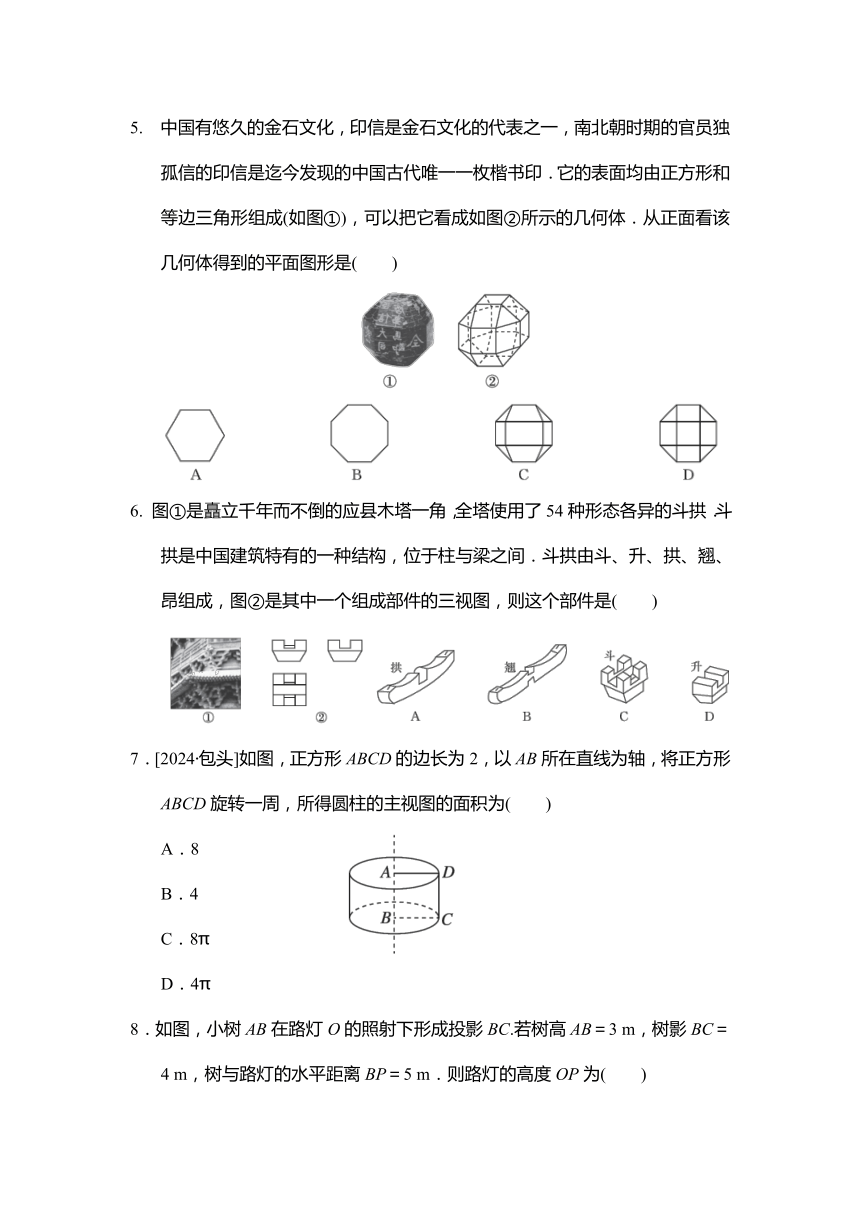
5.INCLUDEPICTURE"新考向传统文化H.EPS" 中国有悠久的金石文化,印信是金石文化的代表之一,南北朝时期的官员独孤信的印信是迄今发现的中国古代唯一一枚楷书印.它的表面均由正方形和等边三角形组成(如图①),可以把它看成如图②所示的几何体.从正面看该几何体得到的平面图形是( )
6.INCLUDEPICTURE"H新考向传统文化.EPS" 图①是矗立千年而不倒的应县木塔一角,全塔使用了54种形态各异的斗拱.斗拱是中国建筑特有的一种结构,位于柱与梁之间.斗拱由斗、升、拱、翘、昂组成,图②是其中一个组成部件的三视图,则这个部件是( )
INCLUDEPICTURE"JL29-5.EPS"
7.[2024·包头]如图,正方形ABCD的边长为2,以AB所在直线为轴,将正方形ABCD旋转一周,所得圆柱的主视图的面积为( )
A.8
B.4
C.8π
D.4π
8.如图,小树AB在路灯O的照射下形成投影BC.若树高AB=3 m,树影BC=4 m,树与路灯的水平距离BP=5 m.则路灯的高度OP为( )
A.4 m B. m C. m D. m
9.由5个形状、大小完全相同的小正方体组合而成的几何体,其主视图和左视图如图所示,则搭建该几何体的方式有( )
A.1种 B.2种 C.3种 D.4种
10.一个正三棱柱的三视图如图所示,若这个正三棱柱的表面积为24+8,则a的值为( )
A.2+ B.2+ C. D.2
二、填空题(每题3分,共18分)
11.对于下列说法:①太阳光线可以看成平行光线,这样的光线形成的投影是平行投影;②物体投影的长短在任何情况下,仅与物体的长短有关;③物体的俯视图是光线垂直照射时,物体的投影;④看书时人们之所以使用台灯,是因为台灯发出的光线是平行光线.其中正确的是________(填序号).
12.某学校操场上立着高度不同的甲、乙两种篮球架,那么在同一时刻的太阳光的照射下,甲种篮球架的高度与其影长的比________(填“大于”“小于”或“等于”)乙种篮球架的高度与其影长的比.
13.如图所示的是一个几何体的三视图,其俯视图是圆心角为270°的扇形,则该几何体的表面积为________.
14.[2025·淄博校级月考]如图,这个几何体是由10个完全相同的小正方体搭成的.如果在这个几何体上添加一些相同的小正方体,并保持其主视图和左视图与添加前的主视图和左视图相同,那么最多可以添加________个小正方体.
15.如图,在平面直角坐标系内,一点光源位于A(0,5)处,线段CD垂直于x轴,D为垂足,C(3,1),则CD在x轴上的影子长DE为________,点C的影子E的坐标为________.
16.如图,在某点光源下有两根直杆MH,NI垂直于平整的地面,甲杆MH的影子为MJ,乙杆NI的影子一部分落在地面上的NG处,一部分落在斜坡GL上的GK处.
(1)点光源所在的位置是________;(填“A”“B”“C”或“D”)
(2)若点光源发出的过点I的光线IK⊥GL,斜坡GL与地面的夹角为30°,NG=1米,GK=米,则乙杆NI的高度为________米.
三、解答题(17题6分,18,19题每题8分,20~22题每题12分,23题14分,共72分)
17.画出如图所示几何体的三视图.
18.如图是一个几何体的三视图,它的俯视图为菱形.
(1)请写出这个几何体的名称;
(2)根据所示数据计算这个几何体的体积.
19.用10个大小相同的小立方块搭成几何体.从上面看到的该几何体的形状图如图①所示.其中小正方形中的数字表示在该位置的小立方块的个数.
(1)请在图②中画出从正面和左面看到的这个几何体的形状图;
(2)如果现在你还有一些大小相同的小立方块,要求保持从正面和左面看到的形状图都不变,最多可以再添加________个小立方块.
20.在一个阳光明媚的上午,数学陈老师组织学生测量小山坡上的一棵大树CD的高度,如图所示,山坡OM与地面ON的夹角为30°(∠MON=30°),站立在水平地面上身高1.7米的小明AB在地面的影长BP为1.2米,此刻大树CD在斜坡上的影长DQ为5米,求大树CD的高度.(结果保留根号)
21.已知线段AB=2 cm,投影面为P.
(1)当AB垂直于投影面P时(如图①),请画出线段AB的正投影;
(2)当AB平行于投影面P时(如图②),请画出线段AB的正投影,并求出正投影的长;
(3)在(2)的基础上,点A不动,线段AB绕点A在垂直于投影面P的平面内逆时针旋转30°(如图③),请在图③中画出线段AB的正投影,并求出其正投影的长.
22.(16分)如图,王琳同学在晚上由路灯A走向路灯B,当他行到P处时发现,他在路灯B下的影长为2 m,且影子顶端恰好位于路灯A的正下方C处,接着他又走了6.5 m到Q处,此时他在路灯A下的影子顶端恰好位于路灯B的正下方D处(已知王琳身高1.8 m,路灯B高9 m).
(1)王琳站在P处时,在路灯B下的影子对应的线段为________;
(2)求王琳站在Q处时,在路灯A下的影长;
(3)求路灯A的高度.
23.[2025·济南期末]通常,路灯、台灯、手电筒……的光可以看成是从一个点发出的,在点光源的照射下,物体所产生的影子称为中心投影.
(1)【画图操作】如图①,三根底部在同一直线上的旗杆直立在地面上,第一根、第二根旗杆在同一灯光下的影长如图所示.请在图中画出光源的位置及第三根旗杆在该灯光下的影子(不写画法);
(2)【数学思考】如图②,夜晚,小明从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图象大致为________;
(3)【解决问题】如图③,河对岸有一灯杆AB,在灯光下,小明在点D处测得自己的影长DF=3 m,沿BD方向前进到达点F处测得自己的影长FG=4 m.已知小明的身高为1.6 m,求灯杆AB的高度.
答案
一、1.C 2.B 3.B 4.C 5.D 6.C 7.A 8.D 9.C
10.D 【点拨】由左视图知底面正三角形的高为2,∴易得正三角形的边长为4,∴两正三角形的面积和为×4×2×2=8.∵正三棱柱的表面积为24+8,∴三个侧面的面积和为24+8-8=24=(4+4+4)a,解得a=2,故选D.
二、11.① 12.等于 13.12+15π 14.4
15.; 【点拨】∵CD⊥x轴,∴CD∥OA,∴△ECD∽△EAO,∴DE∶OE=CD∶AO,∵A(0,5),C(3,1),∴CD=1,AO=5,OD=3,∴DE∶(DE+3)=1∶5,∴DE=,∴OE=3+=,∴点C的影子E的坐标为.
16.(1)C (2)
【点拨】(1)如图所示,点C即为点光源所在的位置.
(2)如图,延长IK交EG于点O.
∵点光源发出的过点I的光线IK⊥GL,
∴∠OKG=90°.∵∠KGE=30°,GK=米,
∴在Rt△OKG中,∠CON=60°,
OK=GK·tan 30°=×=(米),
OG=2OK=2×=(米).
∵NG=1米,∴ON=米.
在Rt△ONI中,∵∠CON=60°,
∴IN=ON·tan 60°=ON=米.
∴乙杆NI的高度为米.
三、17.【解】画图如图所示.
18.【解】(1)这个几何体是直四棱柱.
(2)由三视图知,棱柱底面菱形的对角线长分别为4 cm,3 cm,棱柱的高为6 cm,
∴直四棱柱的体积=×3×4×6=36(cm3),
∴这个几何体的体积为36 cm3.
19.【解】(1)如图所示.
(2)3
20.【解】如图,过点Q作QE⊥DC于点E,由题易得△ABP∽△CEQ,∴=,即=,∴=.
∵EQ∥NO,∴∠1=∠2=30°.
∵QD=5米,∴DE=米,EQ=米,
∴==,解得CE=米,
∴CD=CE+DE=+=(米).
答:大树CD的高度为米.
21.【解】(1)如图①所示,点A′(或B′)即为所求.
(2)如图②所示,线段A′B′即为所求.
∵AB平行于投影面P,∴A′B′=AB=2 cm.
(3)如图③所示,线段A′B′即为所求.
过点A作AD⊥BB′,垂足为点D.则∠ADB=90°,
由题意得A′B′=AD,∠BAD=30°,AB=2 cm,
∴A′B′=AD=AB·cos∠BAD=2×cos 30°=(cm).
22.【解】(1)CP
(2)由题意知CP=2 m,PQ=6.5 m,PE=1.8 m,BD=9 m,PE∥BD,∴△CEP∽△CBD,
∴=,即=,解得QD=1.5 m.
∴王琳站在Q处时,在路灯A下的影长为1.5 m.
(3)由题意知FQ=1.8 m,FQ∥AC,∴△DFQ∽△DAC,
∴=,即=,解得AC=12 m.
∴路灯A的高度为12 m.
23.【解】(1)如图,光源的位置为O,第三根旗杆在该灯光下的影子为线段EF.
(2)D
(3)∵CD∥EF∥AB,
∴△CDF∽△ABF,△ABG∽△EFG.
∴=,=.
又∵CD=EF,∴=.
又∵DF=3 m,FG=4 m,∴=.
∴BD=9 m.∴BF=9+3=12(m).
又∵CD=1.6 m,DF=3 m,
∴=,解得AB=6.4 m.
∴灯杆AB的高度为6.4 m.
一、选择题(每题3分,共30分)
1.下列关于投影的说法中不正确的是( )
A.正午,某大厦在地面上的投影是平行投影
B.匡衡借光学习时,他在地面上的投影是中心投影
C.三角形木板的正投影是一个点
D.晚上,小强向路灯走去,他的影子越来越短
2.把一个正六棱柱如图放置,一束水平方向的平行光线照射此正六棱柱时的正投影是( )
3.如图是某学校操场上的单杠(图中实线部分)及其在地面上的影子(图中虚线部分),根据图中所示,可判断形成该影子的光线为( )
A.太阳光线 B.灯光光线
C.太阳光线或灯光光线 D.该影子实际不可能存在
4.如图,济南泉城广场上矗立着一座泉标,其取古汉字“泉”字的意象造型.在晴天的日子里,从早到晚的这段时间,泉标在太阳下的影子长度的变化规律是( )
A.保持不变 B.逐渐变长 C.先逐渐变短,后又逐渐变长 D.逐渐变短
5.INCLUDEPICTURE"新考向传统文化H.EPS" 中国有悠久的金石文化,印信是金石文化的代表之一,南北朝时期的官员独孤信的印信是迄今发现的中国古代唯一一枚楷书印.它的表面均由正方形和等边三角形组成(如图①),可以把它看成如图②所示的几何体.从正面看该几何体得到的平面图形是( )
6.INCLUDEPICTURE"H新考向传统文化.EPS" 图①是矗立千年而不倒的应县木塔一角,全塔使用了54种形态各异的斗拱.斗拱是中国建筑特有的一种结构,位于柱与梁之间.斗拱由斗、升、拱、翘、昂组成,图②是其中一个组成部件的三视图,则这个部件是( )
INCLUDEPICTURE"JL29-5.EPS"
7.[2024·包头]如图,正方形ABCD的边长为2,以AB所在直线为轴,将正方形ABCD旋转一周,所得圆柱的主视图的面积为( )
A.8
B.4
C.8π
D.4π
8.如图,小树AB在路灯O的照射下形成投影BC.若树高AB=3 m,树影BC=4 m,树与路灯的水平距离BP=5 m.则路灯的高度OP为( )
A.4 m B. m C. m D. m
9.由5个形状、大小完全相同的小正方体组合而成的几何体,其主视图和左视图如图所示,则搭建该几何体的方式有( )
A.1种 B.2种 C.3种 D.4种
10.一个正三棱柱的三视图如图所示,若这个正三棱柱的表面积为24+8,则a的值为( )
A.2+ B.2+ C. D.2
二、填空题(每题3分,共18分)
11.对于下列说法:①太阳光线可以看成平行光线,这样的光线形成的投影是平行投影;②物体投影的长短在任何情况下,仅与物体的长短有关;③物体的俯视图是光线垂直照射时,物体的投影;④看书时人们之所以使用台灯,是因为台灯发出的光线是平行光线.其中正确的是________(填序号).
12.某学校操场上立着高度不同的甲、乙两种篮球架,那么在同一时刻的太阳光的照射下,甲种篮球架的高度与其影长的比________(填“大于”“小于”或“等于”)乙种篮球架的高度与其影长的比.
13.如图所示的是一个几何体的三视图,其俯视图是圆心角为270°的扇形,则该几何体的表面积为________.
14.[2025·淄博校级月考]如图,这个几何体是由10个完全相同的小正方体搭成的.如果在这个几何体上添加一些相同的小正方体,并保持其主视图和左视图与添加前的主视图和左视图相同,那么最多可以添加________个小正方体.
15.如图,在平面直角坐标系内,一点光源位于A(0,5)处,线段CD垂直于x轴,D为垂足,C(3,1),则CD在x轴上的影子长DE为________,点C的影子E的坐标为________.
16.如图,在某点光源下有两根直杆MH,NI垂直于平整的地面,甲杆MH的影子为MJ,乙杆NI的影子一部分落在地面上的NG处,一部分落在斜坡GL上的GK处.
(1)点光源所在的位置是________;(填“A”“B”“C”或“D”)
(2)若点光源发出的过点I的光线IK⊥GL,斜坡GL与地面的夹角为30°,NG=1米,GK=米,则乙杆NI的高度为________米.
三、解答题(17题6分,18,19题每题8分,20~22题每题12分,23题14分,共72分)
17.画出如图所示几何体的三视图.
18.如图是一个几何体的三视图,它的俯视图为菱形.
(1)请写出这个几何体的名称;
(2)根据所示数据计算这个几何体的体积.
19.用10个大小相同的小立方块搭成几何体.从上面看到的该几何体的形状图如图①所示.其中小正方形中的数字表示在该位置的小立方块的个数.
(1)请在图②中画出从正面和左面看到的这个几何体的形状图;
(2)如果现在你还有一些大小相同的小立方块,要求保持从正面和左面看到的形状图都不变,最多可以再添加________个小立方块.
20.在一个阳光明媚的上午,数学陈老师组织学生测量小山坡上的一棵大树CD的高度,如图所示,山坡OM与地面ON的夹角为30°(∠MON=30°),站立在水平地面上身高1.7米的小明AB在地面的影长BP为1.2米,此刻大树CD在斜坡上的影长DQ为5米,求大树CD的高度.(结果保留根号)
21.已知线段AB=2 cm,投影面为P.
(1)当AB垂直于投影面P时(如图①),请画出线段AB的正投影;
(2)当AB平行于投影面P时(如图②),请画出线段AB的正投影,并求出正投影的长;
(3)在(2)的基础上,点A不动,线段AB绕点A在垂直于投影面P的平面内逆时针旋转30°(如图③),请在图③中画出线段AB的正投影,并求出其正投影的长.
22.(16分)如图,王琳同学在晚上由路灯A走向路灯B,当他行到P处时发现,他在路灯B下的影长为2 m,且影子顶端恰好位于路灯A的正下方C处,接着他又走了6.5 m到Q处,此时他在路灯A下的影子顶端恰好位于路灯B的正下方D处(已知王琳身高1.8 m,路灯B高9 m).
(1)王琳站在P处时,在路灯B下的影子对应的线段为________;
(2)求王琳站在Q处时,在路灯A下的影长;
(3)求路灯A的高度.
23.[2025·济南期末]通常,路灯、台灯、手电筒……的光可以看成是从一个点发出的,在点光源的照射下,物体所产生的影子称为中心投影.
(1)【画图操作】如图①,三根底部在同一直线上的旗杆直立在地面上,第一根、第二根旗杆在同一灯光下的影长如图所示.请在图中画出光源的位置及第三根旗杆在该灯光下的影子(不写画法);
(2)【数学思考】如图②,夜晚,小明从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图象大致为________;
(3)【解决问题】如图③,河对岸有一灯杆AB,在灯光下,小明在点D处测得自己的影长DF=3 m,沿BD方向前进到达点F处测得自己的影长FG=4 m.已知小明的身高为1.6 m,求灯杆AB的高度.
答案
一、1.C 2.B 3.B 4.C 5.D 6.C 7.A 8.D 9.C
10.D 【点拨】由左视图知底面正三角形的高为2,∴易得正三角形的边长为4,∴两正三角形的面积和为×4×2×2=8.∵正三棱柱的表面积为24+8,∴三个侧面的面积和为24+8-8=24=(4+4+4)a,解得a=2,故选D.
二、11.① 12.等于 13.12+15π 14.4
15.; 【点拨】∵CD⊥x轴,∴CD∥OA,∴△ECD∽△EAO,∴DE∶OE=CD∶AO,∵A(0,5),C(3,1),∴CD=1,AO=5,OD=3,∴DE∶(DE+3)=1∶5,∴DE=,∴OE=3+=,∴点C的影子E的坐标为.
16.(1)C (2)
【点拨】(1)如图所示,点C即为点光源所在的位置.
(2)如图,延长IK交EG于点O.
∵点光源发出的过点I的光线IK⊥GL,
∴∠OKG=90°.∵∠KGE=30°,GK=米,
∴在Rt△OKG中,∠CON=60°,
OK=GK·tan 30°=×=(米),
OG=2OK=2×=(米).
∵NG=1米,∴ON=米.
在Rt△ONI中,∵∠CON=60°,
∴IN=ON·tan 60°=ON=米.
∴乙杆NI的高度为米.
三、17.【解】画图如图所示.
18.【解】(1)这个几何体是直四棱柱.
(2)由三视图知,棱柱底面菱形的对角线长分别为4 cm,3 cm,棱柱的高为6 cm,
∴直四棱柱的体积=×3×4×6=36(cm3),
∴这个几何体的体积为36 cm3.
19.【解】(1)如图所示.
(2)3
20.【解】如图,过点Q作QE⊥DC于点E,由题易得△ABP∽△CEQ,∴=,即=,∴=.
∵EQ∥NO,∴∠1=∠2=30°.
∵QD=5米,∴DE=米,EQ=米,
∴==,解得CE=米,
∴CD=CE+DE=+=(米).
答:大树CD的高度为米.
21.【解】(1)如图①所示,点A′(或B′)即为所求.
(2)如图②所示,线段A′B′即为所求.
∵AB平行于投影面P,∴A′B′=AB=2 cm.
(3)如图③所示,线段A′B′即为所求.
过点A作AD⊥BB′,垂足为点D.则∠ADB=90°,
由题意得A′B′=AD,∠BAD=30°,AB=2 cm,
∴A′B′=AD=AB·cos∠BAD=2×cos 30°=(cm).
22.【解】(1)CP
(2)由题意知CP=2 m,PQ=6.5 m,PE=1.8 m,BD=9 m,PE∥BD,∴△CEP∽△CBD,
∴=,即=,解得QD=1.5 m.
∴王琳站在Q处时,在路灯A下的影长为1.5 m.
(3)由题意知FQ=1.8 m,FQ∥AC,∴△DFQ∽△DAC,
∴=,即=,解得AC=12 m.
∴路灯A的高度为12 m.
23.【解】(1)如图,光源的位置为O,第三根旗杆在该灯光下的影子为线段EF.
(2)D
(3)∵CD∥EF∥AB,
∴△CDF∽△ABF,△ABG∽△EFG.
∴=,=.
又∵CD=EF,∴=.
又∵DF=3 m,FG=4 m,∴=.
∴BD=9 m.∴BF=9+3=12(m).
又∵CD=1.6 m,DF=3 m,
∴=,解得AB=6.4 m.
∴灯杆AB的高度为6.4 m.
