8.1.2三角形的内角和与外角和(第1课时) 课件(共23张PPT)
文档属性
| 名称 | 8.1.2三角形的内角和与外角和(第1课时) 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 998.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 12:58:50 | ||
图片预览


文档简介
(共23张PPT)
(华师大版)七年级
下
8.1.2三角形的内角和与外角和(第1课时)
三角形
第8章
“八”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.探索三角形内角和的性质,能证明三角形内角和的性质;
2.应用三角形的内角和的性质解决角度问题.
新知导入
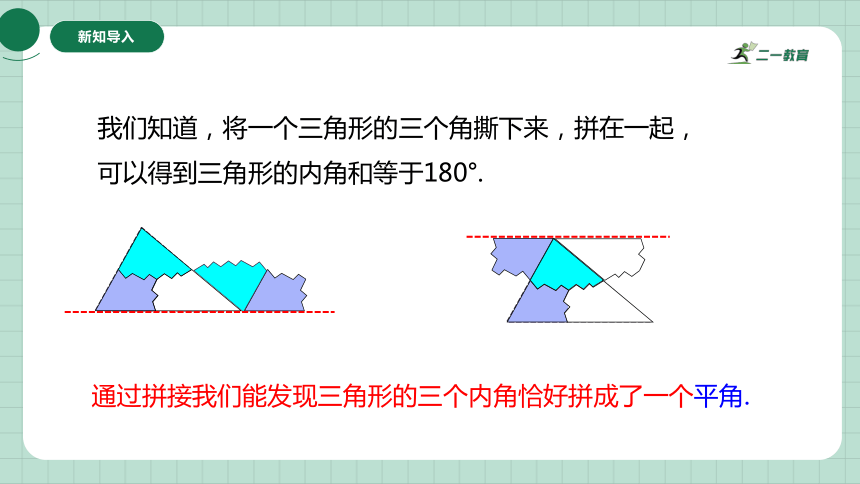
我们知道,将一个三角形的三个角撕下来,拼在一起,可以得到三角形的内角和等于180°.
通过拼接我们能发现三角形的三个内角恰好拼成了一个平角.
新知讲解
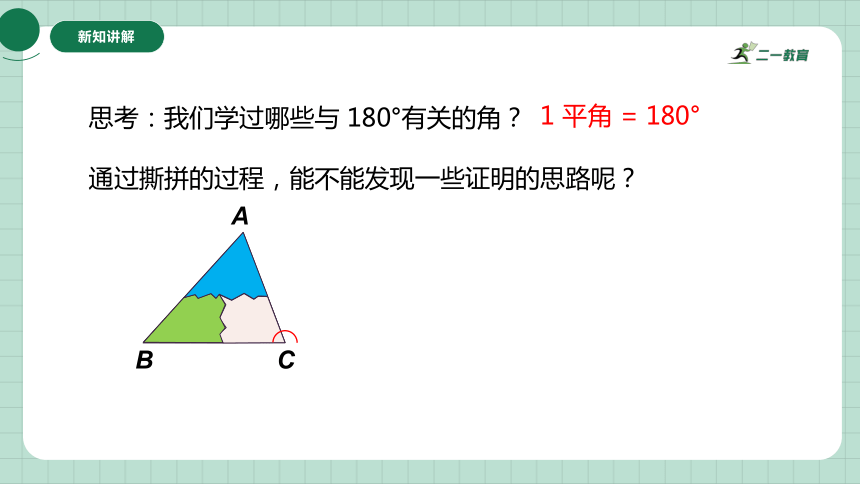
思考:我们学过哪些与 180°有关的角?
A
B
C
1 平角 = 180°
通过撕拼的过程,能不能发现一些证明的思路呢?
新知讲解
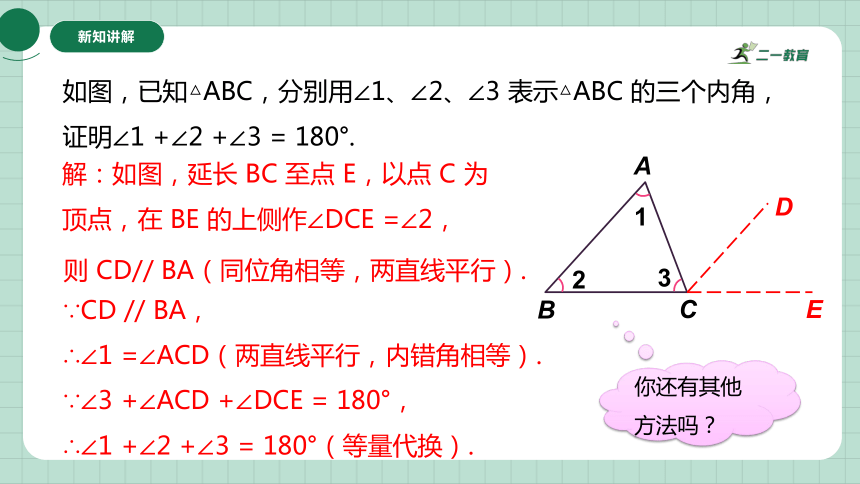
如图,已知△ABC,分别用∠1、∠2、∠3 表示△ABC 的三个内角,证明∠1 +∠2 +∠3 = 180°.
你还有其他方法吗?
A
B
C
1
2
3
解:如图,延长 BC 至点 E,以点 C 为顶点,在 BE 的上侧作∠DCE =∠2,
E
D
∵CD // BA,
∴∠1 =∠ACD(两直线平行,内错角相等).
∵∠3 +∠ACD +∠DCE = 180°,
∴∠1 +∠2 +∠3 = 180°(等量代换).
则 CD// BA(同位角相等,两直线平行).
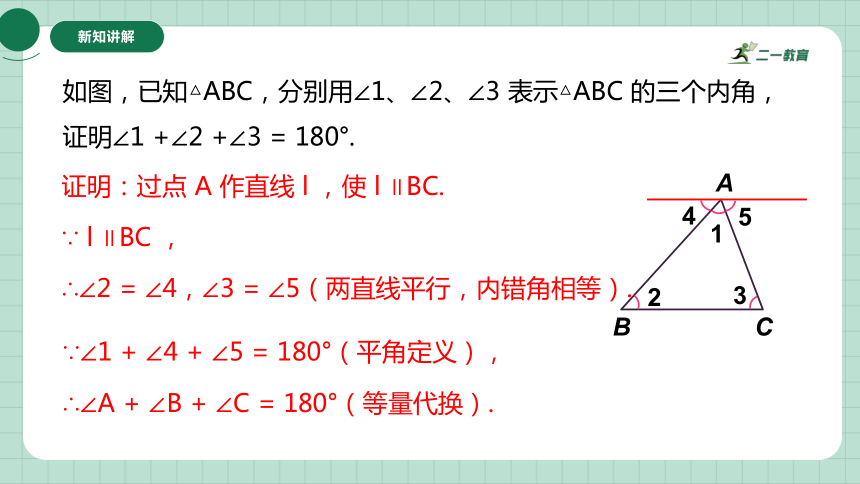
新知讲解
A
B
C
1
2
3
∵∠1 + ∠4 + ∠5 = 180°(平角定义),
∴∠A + ∠B + ∠C = 180°(等量代换).
证明:过点 A 作直线 l ,使 l ∥BC.
∵ l ∥BC ,
∴∠2 = ∠4,∠3 = ∠5(两直线平行,内错角相等).
4
5
如图,已知△ABC,分别用∠1、∠2、∠3 表示△ABC 的三个内角,证明∠1 +∠2 +∠3 = 180°.
新知讲解
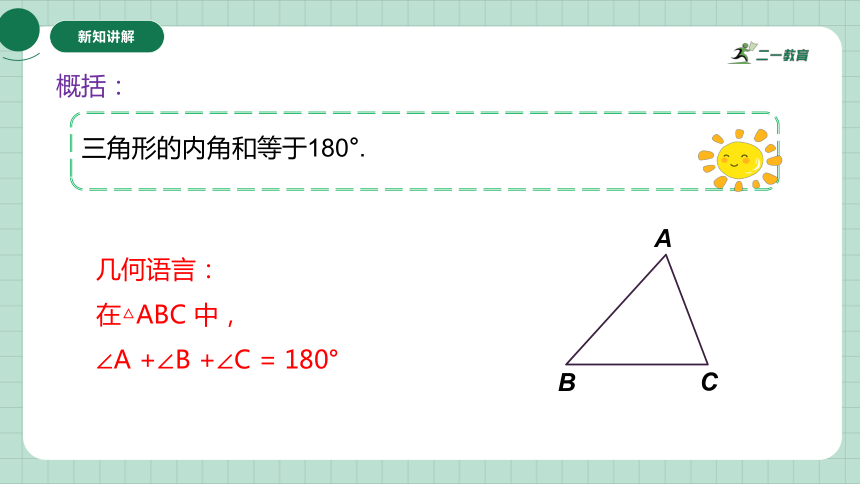
概括:
三角形的内角和等于180°.
几何语言:
在△ABC 中,
∠A +∠B +∠C = 180°
A
B
C
新知讲解
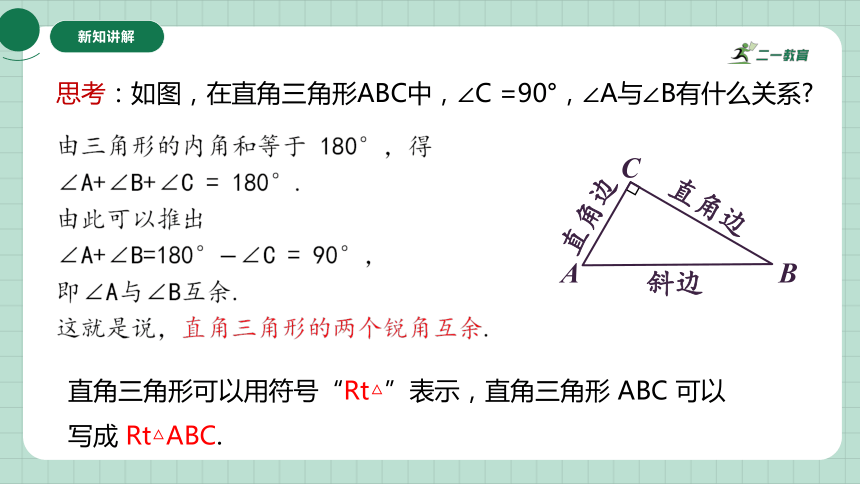
思考:如图,在直角三角形ABC中,∠C =90°,∠A与∠B有什么关系
由三角形的内角和等于 180°,得
∠A+∠B+∠C = 180°.
由此可以推出
∠A+∠B=180°∠C = 90°,
即∠A与∠B互余.
这就是说,直角三角形的两个锐角互余.
A
B
C
直角边
直角边
斜边
直角三角形可以用符号“Rt△”表示,直角三角形 ABC 可以写成 Rt△ABC.
新知讲解
注意
1.“Rt △”后必须紧跟表示直角三角形的三个顶点的大写字母,不能单独使用.如“直角三角形的边”不能写成“Rt △的边”.
2. 三角形的三个内角中最多只有一个钝角或直角,或者说至少有两个锐角.
新知讲解
例1 如图,AD 是△ABC 的边 BC 上的高,∠1 = 45,∠C = 65. 求∠BAC 的度数.
解:在Rt△ABC中,
∵∠1+∠B=90(直角三角形的两个内角互余),
∴∠B=90∠1(等式性质).
又∵∠1=45(已知),
∴∠B=9045=45(等量代换).
A
C
B
1
65
新知讲解
例1 如图,AD 是△ABC 的边 BC 上的高,∠1 = 45,∠C = 65. 求∠BAC 的度数.
在△ABC中,
∵∠B+∠C+∠BAC=180
(三角形的内角和等于180),
∴∠BAC=180∠B∠C(等式性质).
又∵∠B=45,∠C=65(已知),
∴∠BAC=1804565=70(等量代换).
A
C
B
1
65
新知讲解
思考:我们已经知道,直角三角形的两个锐角互余。
反过来,有两个角互余的三角形是直角三角形吗
A
C
B
∠A +∠B +∠C = 180°.
又∵ ∠A +∠B = 90°,
∴∠C = 180°– 90°= 90°.
由三角形的内角和等于180°,得
【知识技能类作业】必做题:
课堂练习
1.如图, 的度数为( )
A. B. C. D.
B
【知识技能类作业】必做题:
课堂练习
2.下列条件不能判定 是直角三角形的是( )
A. B.
C. D. ,
C
【知识技能类作业】必做题:
课堂练习
3. 如图,在△ABC中,∠BAC=89°,AD⊥BC于点D,AE平分∠DAC,∠B=
51°,求∠1的度数.
解:∵ ∠B=51°,∠BAC=89°,
∴ ∠C=180°-51°-89°=40°.
∵ AD⊥BC,∴ ∠ADC=90°.∴ ∠CAD=90°-40°=50°.
∵ AE平分∠DAC,
∴ ∠1=∠DAC=×50°=25°
【知识技能类作业】选做题:
课堂练习
4.已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=3∠A,则此三角形 ( )
A. 一定有一个内角为60°
B. 一定有一个内角为45°
C. 一定是直角三角形
D. 一定是钝角三角形
B
5. 如图,△EFG的三个顶点E、G、F分别在平行线AB、CD上,FH平分∠EFG,交线段EG于点H.若∠AEF=36°,∠BEG=57°,则∠EHF的度数为 .
【知识技能类作业】选做题:
课堂练习
75°
【综合拓展类作业】
课堂练习
6. 如图,在Rt△ABC中,∠ACB=90°,AF平分∠CAB,交CD于点E,交CB于点F,且∠CEF=∠CFE.试说明:CD⊥AB.
解:∵ AF平分∠CAB,∴ ∠CAF=∠BAF.∵ ∠CEF=∠CFE,
∠AED=∠CEF,∴ ∠CFE=∠AED.∵ 在Rt△ACF中,
∠ACF=90°,∴ ∠CAF+∠CFE=90°.∵ ∠CAF=∠BAF,
∠CFE=∠AED,∴ ∠BAF+∠AED=90°.∴ ∠ADE=90°.
∴ CD⊥AB
课堂总结
1.三角形三个内角的和等于180 .
2.直角三角形的两个锐角互余.
3.有两个角互余的三角形是直角三角形.
板书设计
课题:8.1.2三角形的内角和与外角和(第1课时)
1.三角形三个内角的和等于180 .
2.直角三角形的两个锐角互余.
3.有两个角互余的三角形是直角三角形.
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
(华师大版)七年级
下
8.1.2三角形的内角和与外角和(第1课时)
三角形
第8章
“八”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.探索三角形内角和的性质,能证明三角形内角和的性质;
2.应用三角形的内角和的性质解决角度问题.
新知导入
我们知道,将一个三角形的三个角撕下来,拼在一起,可以得到三角形的内角和等于180°.
通过拼接我们能发现三角形的三个内角恰好拼成了一个平角.
新知讲解
思考:我们学过哪些与 180°有关的角?
A
B
C
1 平角 = 180°
通过撕拼的过程,能不能发现一些证明的思路呢?
新知讲解
如图,已知△ABC,分别用∠1、∠2、∠3 表示△ABC 的三个内角,证明∠1 +∠2 +∠3 = 180°.
你还有其他方法吗?
A
B
C
1
2
3
解:如图,延长 BC 至点 E,以点 C 为顶点,在 BE 的上侧作∠DCE =∠2,
E
D
∵CD // BA,
∴∠1 =∠ACD(两直线平行,内错角相等).
∵∠3 +∠ACD +∠DCE = 180°,
∴∠1 +∠2 +∠3 = 180°(等量代换).
则 CD// BA(同位角相等,两直线平行).
新知讲解
A
B
C
1
2
3
∵∠1 + ∠4 + ∠5 = 180°(平角定义),
∴∠A + ∠B + ∠C = 180°(等量代换).
证明:过点 A 作直线 l ,使 l ∥BC.
∵ l ∥BC ,
∴∠2 = ∠4,∠3 = ∠5(两直线平行,内错角相等).
4
5
如图,已知△ABC,分别用∠1、∠2、∠3 表示△ABC 的三个内角,证明∠1 +∠2 +∠3 = 180°.
新知讲解
概括:
三角形的内角和等于180°.
几何语言:
在△ABC 中,
∠A +∠B +∠C = 180°
A
B
C
新知讲解
思考:如图,在直角三角形ABC中,∠C =90°,∠A与∠B有什么关系
由三角形的内角和等于 180°,得
∠A+∠B+∠C = 180°.
由此可以推出
∠A+∠B=180°∠C = 90°,
即∠A与∠B互余.
这就是说,直角三角形的两个锐角互余.
A
B
C
直角边
直角边
斜边
直角三角形可以用符号“Rt△”表示,直角三角形 ABC 可以写成 Rt△ABC.
新知讲解
注意
1.“Rt △”后必须紧跟表示直角三角形的三个顶点的大写字母,不能单独使用.如“直角三角形的边”不能写成“Rt △的边”.
2. 三角形的三个内角中最多只有一个钝角或直角,或者说至少有两个锐角.
新知讲解
例1 如图,AD 是△ABC 的边 BC 上的高,∠1 = 45,∠C = 65. 求∠BAC 的度数.
解:在Rt△ABC中,
∵∠1+∠B=90(直角三角形的两个内角互余),
∴∠B=90∠1(等式性质).
又∵∠1=45(已知),
∴∠B=9045=45(等量代换).
A
C
B
1
65
新知讲解
例1 如图,AD 是△ABC 的边 BC 上的高,∠1 = 45,∠C = 65. 求∠BAC 的度数.
在△ABC中,
∵∠B+∠C+∠BAC=180
(三角形的内角和等于180),
∴∠BAC=180∠B∠C(等式性质).
又∵∠B=45,∠C=65(已知),
∴∠BAC=1804565=70(等量代换).
A
C
B
1
65
新知讲解
思考:我们已经知道,直角三角形的两个锐角互余。
反过来,有两个角互余的三角形是直角三角形吗
A
C
B
∠A +∠B +∠C = 180°.
又∵ ∠A +∠B = 90°,
∴∠C = 180°– 90°= 90°.
由三角形的内角和等于180°,得
【知识技能类作业】必做题:
课堂练习
1.如图, 的度数为( )
A. B. C. D.
B
【知识技能类作业】必做题:
课堂练习
2.下列条件不能判定 是直角三角形的是( )
A. B.
C. D. ,
C
【知识技能类作业】必做题:
课堂练习
3. 如图,在△ABC中,∠BAC=89°,AD⊥BC于点D,AE平分∠DAC,∠B=
51°,求∠1的度数.
解:∵ ∠B=51°,∠BAC=89°,
∴ ∠C=180°-51°-89°=40°.
∵ AD⊥BC,∴ ∠ADC=90°.∴ ∠CAD=90°-40°=50°.
∵ AE平分∠DAC,
∴ ∠1=∠DAC=×50°=25°
【知识技能类作业】选做题:
课堂练习
4.已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=3∠A,则此三角形 ( )
A. 一定有一个内角为60°
B. 一定有一个内角为45°
C. 一定是直角三角形
D. 一定是钝角三角形
B
5. 如图,△EFG的三个顶点E、G、F分别在平行线AB、CD上,FH平分∠EFG,交线段EG于点H.若∠AEF=36°,∠BEG=57°,则∠EHF的度数为 .
【知识技能类作业】选做题:
课堂练习
75°
【综合拓展类作业】
课堂练习
6. 如图,在Rt△ABC中,∠ACB=90°,AF平分∠CAB,交CD于点E,交CB于点F,且∠CEF=∠CFE.试说明:CD⊥AB.
解:∵ AF平分∠CAB,∴ ∠CAF=∠BAF.∵ ∠CEF=∠CFE,
∠AED=∠CEF,∴ ∠CFE=∠AED.∵ 在Rt△ACF中,
∠ACF=90°,∴ ∠CAF+∠CFE=90°.∵ ∠CAF=∠BAF,
∠CFE=∠AED,∴ ∠BAF+∠AED=90°.∴ ∠ADE=90°.
∴ CD⊥AB
课堂总结
1.三角形三个内角的和等于180 .
2.直角三角形的两个锐角互余.
3.有两个角互余的三角形是直角三角形.
板书设计
课题:8.1.2三角形的内角和与外角和(第1课时)
1.三角形三个内角的和等于180 .
2.直角三角形的两个锐角互余.
3.有两个角互余的三角形是直角三角形.
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
