2025学年小升初数学专题训练:探索规律(含解析)
文档属性
| 名称 | 2025学年小升初数学专题训练:探索规律(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 08:00:25 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2025学年小升初数学专题训练:探索规律
一、选择题
1.按规律填空:1、4、9、16、25、( )、49。
A.32 B.33 C.35 D.36
2.班级联欢会上,同学们按“3个红气球、2个黄气球、2个绿气球、1个白气球”的顺序把气球串起来装饰教室。第132个气球是( )的。
A.红色 B.黄色 C.绿色 D.白色
3.认真观察下面这组图,第一幅图的点数为1,第2幅图的点数为5,……
按照上面的规律,第n幅图的点数为( )。
A.4n-3 B.4n+3 C.6n-2 D.6n+4
4.正方形图1作如下操作:第1次:分别连接各边中点如图2,得到5个正方形;第2次:将图2左上角正方形按上述方法再分割如图3,得到9个正方形,……,以此类推,根据以上操作,若要得到53个正方形,需要操作的次数是( )。
A.12 B.13 C.14 D.15
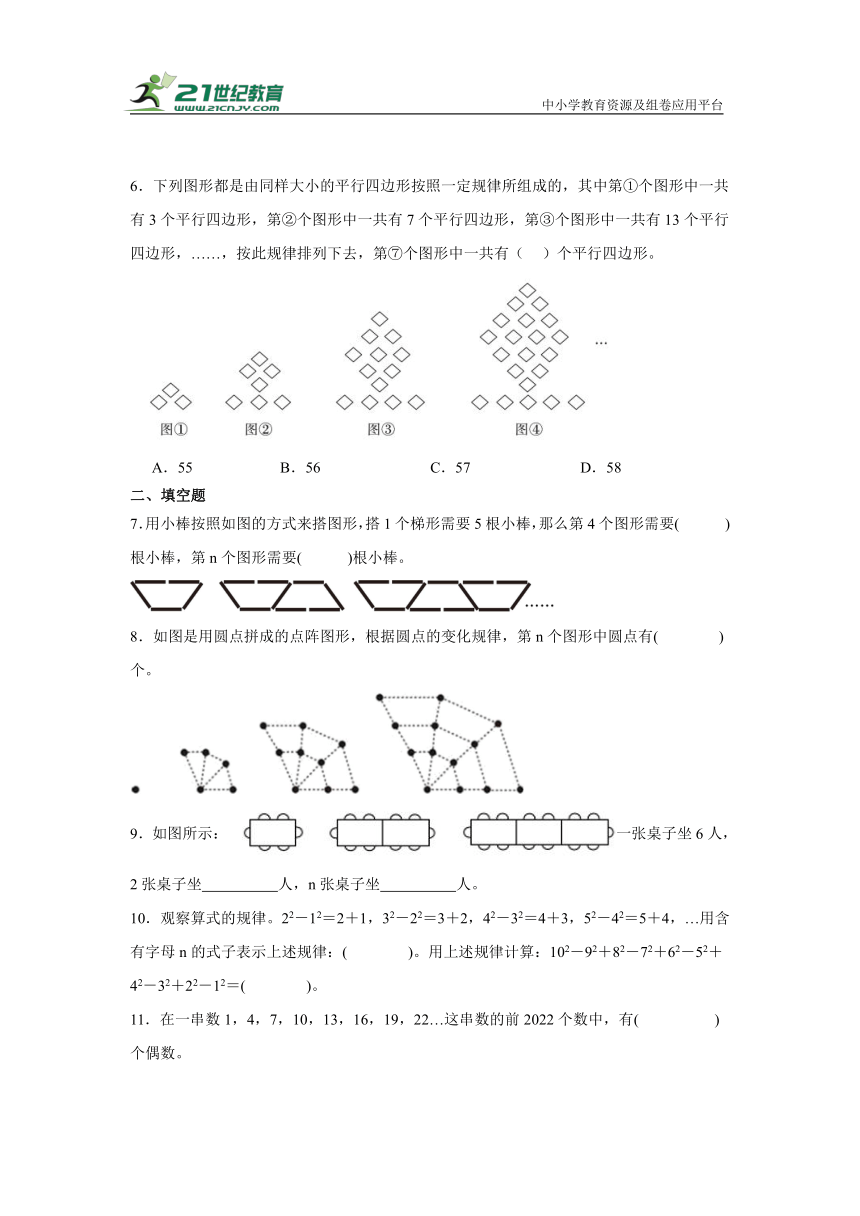
5.观察下边图形,按此规律,第⑩个图中○的个数有( )个。
A.55 B.40 C.36 D.10
6.下列图形都是由同样大小的平行四边形按照一定规律所组成的,其中第①个图形中一共有3个平行四边形,第②个图形中一共有7个平行四边形,第③个图形中一共有13个平行四边形,……,按此规律排列下去,第⑦个图形中一共有( )个平行四边形。
A.55 B.56 C.57 D.58
二、填空题
7.用小棒按照如图的方式来搭图形,搭1个梯形需要5根小棒,那么第4个图形需要( )根小棒,第n个图形需要( )根小棒。
8.如图是用圆点拼成的点阵图形,根据圆点的变化规律,第n个图形中圆点有( )个。
9.如图所示:一张桌子坐6人,2张桌子坐 人,n张桌子坐 人。
10.观察算式的规律。22-12=2+1,32-22=3+2,42-32=4+3,52-42=5+4,…用含有字母n的式子表示上述规律:( )。用上述规律计算:102-92+82-72+62-52+42-32+22-12=( )。
11.在一串数1,4,7,10,13,16,19,22…这串数的前2022个数中,有( )个偶数。
12.1-=,-=,-=,根据你发现的规律,那么+++++=( )。
13.观察如图,找规律。第7幅图中有( )个○,有( )个△。
14.一些小球按如图的方式摆放,那么第16幅有( )个小球。
15.古希腊数学家把1,3,6,10,15,21,……,叫做三角形数,根据它的规律,则第10个三角形数是( )。
16.如下图所示,第1个图案中有2个正方形,第2个图案中有5个正方形,第3个图案中有8个正方形…,则第5个图案中有( )个正方形,第n个图案中有( )个正方形。
17.亮亮准备了一些边长3厘米的正方形纸片,按下图所示的方式摆放,每个重叠部分都是边长1厘米的小正方形,像这样不断摆下去,当亮亮用了n张纸片时,摆成图形的面积是( )平方厘米,周长是( )厘米。
18.用小棒摆正六边形(如图),摆5个正六边形需要( )根小棒,摆n个正六边形需要( )根小棒。
三、判断题
19.……,第103个图形是。( )
20.〇☆☆☆△△〇☆☆☆△△〇☆☆☆△△……第111个图形是☆。( )
21.■◇◇●●●■◇◇●●●■◇◇●●●……照这样的规律,第70个图形是◇。( )
22.像这样用小棒摆下去,第100个图案需要301根小棒。( )
23.1+3+5…+13+15+13+11…+3+1=113。( )
四、解答题
24.(1)用一个长方形像图中那样任意圈出四个数字,你发现了什么规律?
(2)如果长方形中最上面一个数字用表示,最下面一个数字可以怎样表示?
(3)按这样的圈法,小丽圈出的四个数的和是200,你知道她圈的是哪四个数吗?算一算写出来。
25.仔细观察下面的点子图,根据每个图中点子的排列规律,想一想,可以怎样计算每个图中点子的总个数?请你把下表填写完整。
序号 1 2 3 4 5 …
表示点子数的算式 1 1+4 …
点子的总个数 1 …
观察表中数据,如果用A表示第n个图形中点子的总个数,A和n之间的关系可以表示成A= 。
26.下图中,每一个正方形的边长均为1,根据分数的乘法的意义以及相应的图形,回答以下问题.
(1)① 1×=1-←→
② 2×=2-←→
③ 3×=3-←→
④ 4×=4-←→
写出第5个等式,并画出相应的图形.
⑤____________________←→
(2)猜想并写出与第100个图形相对应的等式.
观察下列三行数:
①0,3,8,15,24,…
②2,5,10,17,26,…
③0,6,16,30,48,…
27.第①行数按什么规律排行?
28.第②行,第③行数与第①行数分别有什么关系?
29.分别从①②③行数中取出第a个数,并计算这三个数的和.(结果用含a的式子表示)
30.现有365张大小相同的纸卡,上面分别印着整数1~365,如果按照数字从小到大逆时针方向螺旋由内而外排列,从1开始排列至365为止(如图1)。图2是完成上述排列后,抽出365周围的部分。
(1)在图2的8个空白方格中,其中有些位置不会有数字卡,在这些空格上打“×”。
(2)在其他位置填上与365相邻的数字。
31.观察下面的算式:
32-1=4×2=8
42-1=5×3=15
72-1=8×6=48
92-1=10×8=80
(1)根据你发现的规律,再写一道这样的算式。
(2)运用这个规律计算101×99。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2025学年小升初数学专题训练:探索规律》参考答案
题号 1 2 3 4 5 6
答案 D B A B A C
1.D
【分析】观察可知规律,第一个数是12,第二个数是22,第三个数是32,第四个数是42,第五个数是52,则第六个数是62计算62即可得解。
【详解】
按规律填空:1、4、9、16、25、36、49。
故答案为:D
2.B
【分析】根据题意,这组气球是以3+2+2+1=8个气球为一个循环周期,分别按3红、2黄、2绿、1白的顺序循环排列;
求第132个气球的颜色,就是求132里有几个8,用除法计算,如有余数,余数是几,就是一个循环周期里的第几个气球;如果没有余数,就是一个循环周期里的最后一个气球,据此找到对应的颜色即可。
【详解】132÷8=16……4
余数是4,是一个循环周期里的第4个气球,即黄气球;
第132个气球是黄色的。
故答案为:B
3.A
【分析】观察图形,第1幅图的点数为:1+4×0=1;
第2幅图的点数为:1+4×1=5;
第3幅图的点数为:1+4×2=9;
第4幅图的点数为:1+4×3=13;
……
照这个规律,第n幅图点数应为:1+4(n-1)=4n-3。
【详解】按照上面的规律,第n幅图的点数为(4n-3)。
故答案为:A
4.B
【分析】由题意可知,第1次:分别连接各边中点如图2,得到4+1=5个正方形;
第2次:将图2左上角正方形按上述方法再分割如图3,得到4×2+1=9个正方形……
以此类推,根据以上操作,则第n次得到4n+1个正方形,由此规律代入求得答案即可。
【详解】第1次:得到4×1+1=5(个)正方形;
第2次:将图2左上角正方形按上述方法再分割如图3,得到4×2+1=9(个)正方形……
设第n次得到53个正方形。
4n+1=53,
解:4n+1-1=53-1
4n=52
4n÷4=52÷4
n=13
故答案为:B
【点评】此题主要考查了图形的变化类,根据已知得出正方形个数的变化规律是解题关键。
5.A
【分析】第几个图中就有几层,且每层圆的个数与层数相同,据此把各层圆的个数进行求和解答。
【详解】图①中圆的个数:1=1
图②中圆的个数:3=1+2
图③中圆的个数:6=1+2+3
图④中圆的个数:10=1+2+3+4
……
图⑩中圆的个数:55=1+2+3+4+……+10
故答案为:A
【点睛】本题考查运用数形结合的方法探究数学规律,注意要把图形和数一一对应。
6.C
【分析】第1个图中有3个平行四边形,3=2+1×1,
第2个图中有7个平行四边形,7=3+2×2,
第3个图中有13个平行四边形,13=4+3×3,
……
第n个图中平行四边形的个数:n+1+n×n。
【详解】第n个图中平行四边形的个数:n+1+n×n。
当n=7时,
7+1+7×7=57(个)
第7个图形中一共有57个平行四边形。
故答案为:C
【点睛】解决本题的关键是根据图形的变化找到规律。
7. 17 (4n+1)/(1+4n)
【分析】通过观察图形可知,第一个图形由5根小棒搭成,以后增加4根小棒就可增加一个图形,由此搭n个这样的图形需(4n+1)根小棒;据此解答即可。
【详解】第4个图形需要:
4×4+1
=16+1
=17(根)
搭第n个图形需要(4n+1)或(1+4n)根小棒。
用小棒按照如图的方式来搭图形,搭1个梯形需要5根小棒,那么第4个图形需要17根小棒,搭第n个图形需要(4n+1)或(1+4n)根小棒。
8.4n-3
【分析】第1个图形中圆点有1个,1=1×4-3;
第2个图形中圆点有5个,5=2×4-3;
第3个图形中圆点有9个,9=3×4-3;
第4个图形中圆点有13个,13=4×4-3
规律:第n个图形中圆点有(4n-3)个;按此规律解答。
【详解】由分析可得:如图是用圆点拼成的点阵图形,根据圆点的变化规律,第n个图形中圆点有(4n-3)个。
9. 10 4n+2
【分析】观察可得,一张桌子坐(2+4)人,2张桌子坐(2+4×2)人,……就是有几张桌子就坐几个4加2人。n张桌子坐的人即可求。
【详解】一张桌子坐:
2+4=6(人)
2张桌子坐:
2+4×2
=2+8
=10(人)
n张桌子坐:(4n+2)人。
一张桌子坐6人,2张桌子坐10人,n张桌子坐(4n+2)人。
【点睛】仔细观察,比较总结出规律是解决本题的关键。
10. n2-(n-1)2=2n-1 55
【分析】观察算式,发现规律,相邻两个自然数(0除外)的平方差等于这两个数的和,据此规律写出用字母n表示的式子,并用规律计算出算式的结果。
【详解】n2-(n-1)2
=n+(n-1)
=2n-1
即n2-(n-1)2=2n-1。
102-92+82-72+62-52+42-32+22-12
=10+9+8+7+6+5+4+3+2+1
=(10+1)+(9+2)+(8+3)+(7+4)+(6+5)
=11×5
=55
【点睛】本题考查找规律,观察算式,找到算式的规律,应用发现的规律解决问题是解题的关键。
11.1011
【分析】观察这串数的奇偶性质为:奇数、偶数、奇数、偶数、奇数、偶数、奇数、偶数……发现以2个数为一个组,每组的第1个数是奇数,第2个数是偶数,要求前2022个数中有几个偶数,则用2022除以2,商是几,就有几个偶数。
【详解】以2个数为一个组,每组有1个偶数,
2022÷2=1011
在一串数1,4,7,10,13,16,19,22…这串数的前2022个数中,有1011个偶数。
【点睛】本题主要考查了奇数和偶数的认识以及周期问题,明确奇数和偶数的排列顺序和周期是解题的关键。
12.
【详解】观察加数,发现分母是相邻的自然数的乘积,分子是1的分数,可以将每个加数改写成由分母是相邻的自然数且分子都是1的两个分数相减的形式,据此进行简算。
【解答】
=
=1-
=
【点睛】本题考查找规律,从已知的数列中发现规律,利用规律解答。
13. 13 36
【分析】观察图形可知,○的个数位:序号数减1的差乘2,然后再加上1即可;
△的个数位:序号数减1的差的平方。据此填空即可。
【详解】第7幅图中○的个数有:
(7-1)×2+1
=6×2+1
=12+1
=13(个)
第7幅图中△的个数有:
(7-1)2=62=36(个)
【点睛】本题考查图形的变化规律,发现规律,利用规律是解题的关键。
14.136
【分析】通过观察可得,第一幅图是1个小球,第二幅图是在第一幅图的下面添了两个球,第三幅图是在第二幅图的下面添了三个小球,……照此规律,第16幅图的最下面有16个小球。于是第16幅图的小球可求得。
【详解】第一幅图:1(个)
第二幅图:1+2=3(个)
第三幅图:1+2+3=6(个)
……
第16幅图的小球有:
1+2+3+4+……+16
=(1+16)×16÷2
=17×8
=136(个)
【点睛】本题考查了学生观察比较,善于总结的意识和能力。
15.55
【分析】观察数列可知,第1个三角形数是1,第2个三角形数是1+2=3,第3个三角形数是1+2+3=6,第4个三角形数是1+2+3+4=10,第5个三角形数是1+2+3+4+5=15,根据所给的数据发现:第n个三角形数是1+2+3+…+n,据此解答即可。
【详解】第10个三角形数是:
1+2+3+4+5+6+7+8+9+10
=10×5+5
=50+5
=55
【点睛】此题考查了规律型:数字的变化.要能够发现:第n个数对应的数的规律为:第n个三角形数是1+2+3+…+n。
16. 14 3n-1
【分析】第1个图案有2个正方形;第2个图案比第1个图案增加了2个小正方形和1个由4个小正形组成的正方形,有5个正方形;第3个图案比第2个图案增加了2个小正方形和1个由4个小正形组成的正方形,有8个正方形……后一个图案比前一个图案多3个正方形,图案序数与正方形个数的关系是:正方形个数=图案序数×3-1。
【详解】5×3-1
=15-1
=14(个)
第5个图案中有14个正方形;
第n个图案中有(3n-1)个正方形。
【点睛】本题主要考查数与形结合的规律,发现后一个图案比前一个图案增加2个小正方形和1个由4个小正方形组成的正方形是解本题的关键。
17. 8n+1 8n+4
【分析】用2张纸片时,摆成图形的面积是2个正方形的面积和-1个小正方形的面积;周长是2个正方形的周长和-1个小正方形的周长。
用3张纸片时,摆成图形的面积是3个正方形的面积和-2个小正方形的面积;周长是3个正方形的周长和-2个小正方形的周长。
……
用n张纸片时,摆成图形的面积是n个正方形的面积和-(n-1)个小正方形的面积;周长是n个正方形的周长和-(n - 1)个小正方形的周长。
【详解】3×3=9(平方厘米)
1×1=1(平方厘米)
3×4=12(厘米)
1×4=4(厘米)
9n-1×(n-1)
=9n-n+1
=8n+1
12n-4(n-1)
=12n-4n+4
=8n+4
所以,摆成图形的面积是(8n+1)平方厘米,周长是(8n+4)厘米。
【点睛】本题主要考查数与形集合的规律,发现每多1 个正方形,面积与周长之间的变化规律是解本题的关键。
18. 26 5n+1
【分析】观察图可知,摆1个六边形需要6根小棒,可以写作:5×1+1;摆2个需要11根小棒,可以写作:5×2+1;摆3个需要16根小棒,可以写成:5×3+1;…由此可以推理得出一般规律:摆n个六边形需要:(5n+1)根小棒,据此解答。
【详解】根据分析可知:
摆5个正六边形需要小棒:
5×5+1
=25+1
=26(根)
摆n个正六边形需要小棒:(5n+1)根
【点睛】根据题干中已知的图形的排列特点及其数量关系,推理得出一般的结论进行解答,是此类问题的关键。
19.×
【分析】每4个图形一循环,计算第103个图形是第几组循环零几个图形,即可得出其形状,进而判断即可。
【详解】103÷4=25(组)……3(个)
第103个图形是。所以原题说法错误。
故答案为:×。
【点睛】解答此题的关键是先找到规律,再根据规律求解。
20.√
【分析】根据图示可知,每6个图形一循环,计算第111个图形是第几组循环零几个图形,即可知道其形状,判断即可。
【详解】111÷6=18(组)……3(个)
所有第111个图形是☆。原题说法正确。
故答案为:√。
【点睛】本题主要考查的是找图形规律,解题的关键是观察图形找到规律,再根据规律求解。
21.×
【分析】该图形是以“■◇◇●●●”为一组重复出现,这一组里一共有6个图形,用70÷6所得的商表示有几组这样的“■◇◇●●●”,产生的余数是就是这样的一组的第几个图形,如果没有余数,就是这样的一组的最后一个图形。
【详解】70÷6=11(组)……4(个),第4个图形是●,则第70个图形是●。所以原题说法错误。
故答案为:×。
【点睛】根据题干得出这组图形的排列周期特点是解决此类问题的关键。
22.√
【分析】规律:每多1个正方形就多3根小棒;
第1个图形里共有4根小棒,即3×1+1;
第2个图形里共有7根小棒,即3×2+1;
第3个图形里共有10根小棒,即3×3+1;
第4个图形里共有13根小棒,即3×4+1;
……
第n个图形里需要的小棒数为:3n+1。
【详解】根据分析可知,第n个图形里需要的小棒数为:3n+1,当n=100时,
3n+1
=3×100+1
=300+1
=301(根)
即第100个图形需要301根小棒。
故答案为:√
23.√
【分析】1=12,1+3=22,1+3+5=32,…据此可知,从1开始的连续奇数的和等于奇数个数的平方,所以1+3+5…+13+15=82,1+3+5…+13=72,据此解答。
【详解】1+3+5…+13+15+13+11…+3+1
=(1+3+5…+13+15)+(13+11…+3+1)
=82+72
=64+49
=113
所以原题干说法正确。
故答案为:√
24.(1)每相邻两个之间相差10;
(2);
(3)35、45、55、65。
【分析】(1)观察上下相邻的数之间的大小关系,得出规律;
(2)长方形中一共有4个数,最上面和最下面之间相差30,据此列式;
(3)设小丽圈出的第一个数字为,下面的数依次是a+10、a+20、a+30,根据四个数相加等于200,列出方程,求出第一个数,再分别求出下面的数即可。
【详解】(1)我发现圈出的4个数,每相邻两个之间相差10。
(2)最下面一个数字可以用表示。
(3)解:设小丽圈出的第一个数字为。
4+60=200
4=140
,,。
答:她圈的是35、45、55、65。
【点睛】本题考查了数字的排列规律和列方程解决问题,关键是发现数表中的规律。
25. 1+2×4 1+3×4 1+4×4 5 9 13 17 4n-3
【分析】通过观察发现,第一个图的点子数是1,第二个图的点子数是1+4=5,第三个图的点子数是1+2×4=9,第4个图的点子数是1+3×4=13,第五个图的点子数是1+4×4=17,由此可知用A表示第n个图形中点子的总个数,A和n之间的关系可以表示成A=4n-3,据此解答即可。
【详解】如图:
序号 1 2 3 4 5 …
表示点子数的算式 1 1+4 1+2×4 1+3×4 1+4×4 …
点子的总个数 1 5 9 13 17 …
由分析可得:A=1+4(n-1)=4n-3
【点睛】此题主要考查学生根据图形规律,归纳出规律关系式,然后进行代数解答。
26.(1) 5×=5-
(2)100×=100-
【详解】(1)根据算式的规律,可知⑤的算式为5×=5-
再画出对应的图,每个小正方形可看做“单位1”,表示,将“单位1”平均分成6份,阴影部分占5份,5×可画为
(2)第100个图形对应的算式为100×=100-,即100×=100-
27.第a个数为a2﹣1 28.第②行相对应的数比第①行数多2,第③行相对应的数是第①行数的2倍 29.a2﹣1+a2+1+2(a2﹣1)=4a2﹣2
【分析】探索数与式的规律(1)第①行的每个数均为序数的平方减1;(2)第②行相对应的数比第①行数多2,第③行相对应的数是第①行数的2倍;(3)由(2)得出第②行第a个数为a2+1,第③行第a个数为2(a2﹣1),相加化简即可.
27.解:∵第1个数0=12﹣1,第2个数3=22﹣1,第3个数8=32﹣1,第4个数15=42﹣1,…
∴第a个数为a2﹣1
28.第②行相对应的数比第①行数多2,第③行相对应的数是第①行数的2倍
29.由(2)知,第②行第a个数为a2+1,第③行第a个数为2(a2﹣1),
∴这三个数的和为a2﹣1+a2+1+2(a2﹣1)=4a2﹣2
30.见解答
【分析】(1)(2)如下图所示,数从小到大逆时针方向螺旋由内而外排列出的图形是一个正方形,以1为中心数,每个1×1,3×3,5×5的正方形的右下角的数(即标蓝色方格内的数)均是从1开始的连续奇数的平方(即(2n-1) ),因为19 =361,即最接近365的奇数的平方,据此画出以数361为右下角的数的排列,再画出以数289为右下角的数的排列(如下图),据此解答。
【详解】由分析可知:
(1)如下图所示:
(2)如下图所示:
【点睛】本题考查了数表中的规律的应用。
31.(1)52-1=6×4=24
(2)9999
【分析】(1)观察32-1=4×2=8可得:4=3+1,2=3-1,4和2相差2。
可将算式改写成:32-1=(3+1)×(3-1)=4×2=8
那么42-1=5×3=15可改写成:42-1=(4+1)×(4-1)=5×3=15
72-1=8×6=48可改写成:72-1=(7+1)×(7-1)=8×6=48
92-1=10×8=80可改写成:92-1=(9+1)×(9-1)=10×8=80
可得规律:n2-1=(n+1)×(n-1),据此写出这样的算式即可。
(2)101和99相差2,101=100+1,99=100-1,根据算式的规律n2-1=(n+1)×(n-1),可得101×99=(100+1)×(100-1)=1002-1,据此求解即可。
【详解】(1)根据分析可得规律:n2-1=(n+1)×(n-1)
52-1=6×4=24(答案不唯一)
(2)101×99
=(100+1)×(100-1)
=1002-1
=10000-1
=9999
中小学教育资源及组卷应用平台
2025学年小升初数学专题训练:探索规律
一、选择题
1.按规律填空:1、4、9、16、25、( )、49。
A.32 B.33 C.35 D.36
2.班级联欢会上,同学们按“3个红气球、2个黄气球、2个绿气球、1个白气球”的顺序把气球串起来装饰教室。第132个气球是( )的。
A.红色 B.黄色 C.绿色 D.白色
3.认真观察下面这组图,第一幅图的点数为1,第2幅图的点数为5,……
按照上面的规律,第n幅图的点数为( )。
A.4n-3 B.4n+3 C.6n-2 D.6n+4
4.正方形图1作如下操作:第1次:分别连接各边中点如图2,得到5个正方形;第2次:将图2左上角正方形按上述方法再分割如图3,得到9个正方形,……,以此类推,根据以上操作,若要得到53个正方形,需要操作的次数是( )。
A.12 B.13 C.14 D.15
5.观察下边图形,按此规律,第⑩个图中○的个数有( )个。
A.55 B.40 C.36 D.10
6.下列图形都是由同样大小的平行四边形按照一定规律所组成的,其中第①个图形中一共有3个平行四边形,第②个图形中一共有7个平行四边形,第③个图形中一共有13个平行四边形,……,按此规律排列下去,第⑦个图形中一共有( )个平行四边形。
A.55 B.56 C.57 D.58
二、填空题
7.用小棒按照如图的方式来搭图形,搭1个梯形需要5根小棒,那么第4个图形需要( )根小棒,第n个图形需要( )根小棒。
8.如图是用圆点拼成的点阵图形,根据圆点的变化规律,第n个图形中圆点有( )个。
9.如图所示:一张桌子坐6人,2张桌子坐 人,n张桌子坐 人。
10.观察算式的规律。22-12=2+1,32-22=3+2,42-32=4+3,52-42=5+4,…用含有字母n的式子表示上述规律:( )。用上述规律计算:102-92+82-72+62-52+42-32+22-12=( )。
11.在一串数1,4,7,10,13,16,19,22…这串数的前2022个数中,有( )个偶数。
12.1-=,-=,-=,根据你发现的规律,那么+++++=( )。
13.观察如图,找规律。第7幅图中有( )个○,有( )个△。
14.一些小球按如图的方式摆放,那么第16幅有( )个小球。
15.古希腊数学家把1,3,6,10,15,21,……,叫做三角形数,根据它的规律,则第10个三角形数是( )。
16.如下图所示,第1个图案中有2个正方形,第2个图案中有5个正方形,第3个图案中有8个正方形…,则第5个图案中有( )个正方形,第n个图案中有( )个正方形。
17.亮亮准备了一些边长3厘米的正方形纸片,按下图所示的方式摆放,每个重叠部分都是边长1厘米的小正方形,像这样不断摆下去,当亮亮用了n张纸片时,摆成图形的面积是( )平方厘米,周长是( )厘米。
18.用小棒摆正六边形(如图),摆5个正六边形需要( )根小棒,摆n个正六边形需要( )根小棒。
三、判断题
19.……,第103个图形是。( )
20.〇☆☆☆△△〇☆☆☆△△〇☆☆☆△△……第111个图形是☆。( )
21.■◇◇●●●■◇◇●●●■◇◇●●●……照这样的规律,第70个图形是◇。( )
22.像这样用小棒摆下去,第100个图案需要301根小棒。( )
23.1+3+5…+13+15+13+11…+3+1=113。( )
四、解答题
24.(1)用一个长方形像图中那样任意圈出四个数字,你发现了什么规律?
(2)如果长方形中最上面一个数字用表示,最下面一个数字可以怎样表示?
(3)按这样的圈法,小丽圈出的四个数的和是200,你知道她圈的是哪四个数吗?算一算写出来。
25.仔细观察下面的点子图,根据每个图中点子的排列规律,想一想,可以怎样计算每个图中点子的总个数?请你把下表填写完整。
序号 1 2 3 4 5 …
表示点子数的算式 1 1+4 …
点子的总个数 1 …
观察表中数据,如果用A表示第n个图形中点子的总个数,A和n之间的关系可以表示成A= 。
26.下图中,每一个正方形的边长均为1,根据分数的乘法的意义以及相应的图形,回答以下问题.
(1)① 1×=1-←→
② 2×=2-←→
③ 3×=3-←→
④ 4×=4-←→
写出第5个等式,并画出相应的图形.
⑤____________________←→
(2)猜想并写出与第100个图形相对应的等式.
观察下列三行数:
①0,3,8,15,24,…
②2,5,10,17,26,…
③0,6,16,30,48,…
27.第①行数按什么规律排行?
28.第②行,第③行数与第①行数分别有什么关系?
29.分别从①②③行数中取出第a个数,并计算这三个数的和.(结果用含a的式子表示)
30.现有365张大小相同的纸卡,上面分别印着整数1~365,如果按照数字从小到大逆时针方向螺旋由内而外排列,从1开始排列至365为止(如图1)。图2是完成上述排列后,抽出365周围的部分。
(1)在图2的8个空白方格中,其中有些位置不会有数字卡,在这些空格上打“×”。
(2)在其他位置填上与365相邻的数字。
31.观察下面的算式:
32-1=4×2=8
42-1=5×3=15
72-1=8×6=48
92-1=10×8=80
(1)根据你发现的规律,再写一道这样的算式。
(2)运用这个规律计算101×99。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2025学年小升初数学专题训练:探索规律》参考答案
题号 1 2 3 4 5 6
答案 D B A B A C
1.D
【分析】观察可知规律,第一个数是12,第二个数是22,第三个数是32,第四个数是42,第五个数是52,则第六个数是62计算62即可得解。
【详解】
按规律填空:1、4、9、16、25、36、49。
故答案为:D
2.B
【分析】根据题意,这组气球是以3+2+2+1=8个气球为一个循环周期,分别按3红、2黄、2绿、1白的顺序循环排列;
求第132个气球的颜色,就是求132里有几个8,用除法计算,如有余数,余数是几,就是一个循环周期里的第几个气球;如果没有余数,就是一个循环周期里的最后一个气球,据此找到对应的颜色即可。
【详解】132÷8=16……4
余数是4,是一个循环周期里的第4个气球,即黄气球;
第132个气球是黄色的。
故答案为:B
3.A
【分析】观察图形,第1幅图的点数为:1+4×0=1;
第2幅图的点数为:1+4×1=5;
第3幅图的点数为:1+4×2=9;
第4幅图的点数为:1+4×3=13;
……
照这个规律,第n幅图点数应为:1+4(n-1)=4n-3。
【详解】按照上面的规律,第n幅图的点数为(4n-3)。
故答案为:A
4.B
【分析】由题意可知,第1次:分别连接各边中点如图2,得到4+1=5个正方形;
第2次:将图2左上角正方形按上述方法再分割如图3,得到4×2+1=9个正方形……
以此类推,根据以上操作,则第n次得到4n+1个正方形,由此规律代入求得答案即可。
【详解】第1次:得到4×1+1=5(个)正方形;
第2次:将图2左上角正方形按上述方法再分割如图3,得到4×2+1=9(个)正方形……
设第n次得到53个正方形。
4n+1=53,
解:4n+1-1=53-1
4n=52
4n÷4=52÷4
n=13
故答案为:B
【点评】此题主要考查了图形的变化类,根据已知得出正方形个数的变化规律是解题关键。
5.A
【分析】第几个图中就有几层,且每层圆的个数与层数相同,据此把各层圆的个数进行求和解答。
【详解】图①中圆的个数:1=1
图②中圆的个数:3=1+2
图③中圆的个数:6=1+2+3
图④中圆的个数:10=1+2+3+4
……
图⑩中圆的个数:55=1+2+3+4+……+10
故答案为:A
【点睛】本题考查运用数形结合的方法探究数学规律,注意要把图形和数一一对应。
6.C
【分析】第1个图中有3个平行四边形,3=2+1×1,
第2个图中有7个平行四边形,7=3+2×2,
第3个图中有13个平行四边形,13=4+3×3,
……
第n个图中平行四边形的个数:n+1+n×n。
【详解】第n个图中平行四边形的个数:n+1+n×n。
当n=7时,
7+1+7×7=57(个)
第7个图形中一共有57个平行四边形。
故答案为:C
【点睛】解决本题的关键是根据图形的变化找到规律。
7. 17 (4n+1)/(1+4n)
【分析】通过观察图形可知,第一个图形由5根小棒搭成,以后增加4根小棒就可增加一个图形,由此搭n个这样的图形需(4n+1)根小棒;据此解答即可。
【详解】第4个图形需要:
4×4+1
=16+1
=17(根)
搭第n个图形需要(4n+1)或(1+4n)根小棒。
用小棒按照如图的方式来搭图形,搭1个梯形需要5根小棒,那么第4个图形需要17根小棒,搭第n个图形需要(4n+1)或(1+4n)根小棒。
8.4n-3
【分析】第1个图形中圆点有1个,1=1×4-3;
第2个图形中圆点有5个,5=2×4-3;
第3个图形中圆点有9个,9=3×4-3;
第4个图形中圆点有13个,13=4×4-3
规律:第n个图形中圆点有(4n-3)个;按此规律解答。
【详解】由分析可得:如图是用圆点拼成的点阵图形,根据圆点的变化规律,第n个图形中圆点有(4n-3)个。
9. 10 4n+2
【分析】观察可得,一张桌子坐(2+4)人,2张桌子坐(2+4×2)人,……就是有几张桌子就坐几个4加2人。n张桌子坐的人即可求。
【详解】一张桌子坐:
2+4=6(人)
2张桌子坐:
2+4×2
=2+8
=10(人)
n张桌子坐:(4n+2)人。
一张桌子坐6人,2张桌子坐10人,n张桌子坐(4n+2)人。
【点睛】仔细观察,比较总结出规律是解决本题的关键。
10. n2-(n-1)2=2n-1 55
【分析】观察算式,发现规律,相邻两个自然数(0除外)的平方差等于这两个数的和,据此规律写出用字母n表示的式子,并用规律计算出算式的结果。
【详解】n2-(n-1)2
=n+(n-1)
=2n-1
即n2-(n-1)2=2n-1。
102-92+82-72+62-52+42-32+22-12
=10+9+8+7+6+5+4+3+2+1
=(10+1)+(9+2)+(8+3)+(7+4)+(6+5)
=11×5
=55
【点睛】本题考查找规律,观察算式,找到算式的规律,应用发现的规律解决问题是解题的关键。
11.1011
【分析】观察这串数的奇偶性质为:奇数、偶数、奇数、偶数、奇数、偶数、奇数、偶数……发现以2个数为一个组,每组的第1个数是奇数,第2个数是偶数,要求前2022个数中有几个偶数,则用2022除以2,商是几,就有几个偶数。
【详解】以2个数为一个组,每组有1个偶数,
2022÷2=1011
在一串数1,4,7,10,13,16,19,22…这串数的前2022个数中,有1011个偶数。
【点睛】本题主要考查了奇数和偶数的认识以及周期问题,明确奇数和偶数的排列顺序和周期是解题的关键。
12.
【详解】观察加数,发现分母是相邻的自然数的乘积,分子是1的分数,可以将每个加数改写成由分母是相邻的自然数且分子都是1的两个分数相减的形式,据此进行简算。
【解答】
=
=1-
=
【点睛】本题考查找规律,从已知的数列中发现规律,利用规律解答。
13. 13 36
【分析】观察图形可知,○的个数位:序号数减1的差乘2,然后再加上1即可;
△的个数位:序号数减1的差的平方。据此填空即可。
【详解】第7幅图中○的个数有:
(7-1)×2+1
=6×2+1
=12+1
=13(个)
第7幅图中△的个数有:
(7-1)2=62=36(个)
【点睛】本题考查图形的变化规律,发现规律,利用规律是解题的关键。
14.136
【分析】通过观察可得,第一幅图是1个小球,第二幅图是在第一幅图的下面添了两个球,第三幅图是在第二幅图的下面添了三个小球,……照此规律,第16幅图的最下面有16个小球。于是第16幅图的小球可求得。
【详解】第一幅图:1(个)
第二幅图:1+2=3(个)
第三幅图:1+2+3=6(个)
……
第16幅图的小球有:
1+2+3+4+……+16
=(1+16)×16÷2
=17×8
=136(个)
【点睛】本题考查了学生观察比较,善于总结的意识和能力。
15.55
【分析】观察数列可知,第1个三角形数是1,第2个三角形数是1+2=3,第3个三角形数是1+2+3=6,第4个三角形数是1+2+3+4=10,第5个三角形数是1+2+3+4+5=15,根据所给的数据发现:第n个三角形数是1+2+3+…+n,据此解答即可。
【详解】第10个三角形数是:
1+2+3+4+5+6+7+8+9+10
=10×5+5
=50+5
=55
【点睛】此题考查了规律型:数字的变化.要能够发现:第n个数对应的数的规律为:第n个三角形数是1+2+3+…+n。
16. 14 3n-1
【分析】第1个图案有2个正方形;第2个图案比第1个图案增加了2个小正方形和1个由4个小正形组成的正方形,有5个正方形;第3个图案比第2个图案增加了2个小正方形和1个由4个小正形组成的正方形,有8个正方形……后一个图案比前一个图案多3个正方形,图案序数与正方形个数的关系是:正方形个数=图案序数×3-1。
【详解】5×3-1
=15-1
=14(个)
第5个图案中有14个正方形;
第n个图案中有(3n-1)个正方形。
【点睛】本题主要考查数与形结合的规律,发现后一个图案比前一个图案增加2个小正方形和1个由4个小正方形组成的正方形是解本题的关键。
17. 8n+1 8n+4
【分析】用2张纸片时,摆成图形的面积是2个正方形的面积和-1个小正方形的面积;周长是2个正方形的周长和-1个小正方形的周长。
用3张纸片时,摆成图形的面积是3个正方形的面积和-2个小正方形的面积;周长是3个正方形的周长和-2个小正方形的周长。
……
用n张纸片时,摆成图形的面积是n个正方形的面积和-(n-1)个小正方形的面积;周长是n个正方形的周长和-(n - 1)个小正方形的周长。
【详解】3×3=9(平方厘米)
1×1=1(平方厘米)
3×4=12(厘米)
1×4=4(厘米)
9n-1×(n-1)
=9n-n+1
=8n+1
12n-4(n-1)
=12n-4n+4
=8n+4
所以,摆成图形的面积是(8n+1)平方厘米,周长是(8n+4)厘米。
【点睛】本题主要考查数与形集合的规律,发现每多1 个正方形,面积与周长之间的变化规律是解本题的关键。
18. 26 5n+1
【分析】观察图可知,摆1个六边形需要6根小棒,可以写作:5×1+1;摆2个需要11根小棒,可以写作:5×2+1;摆3个需要16根小棒,可以写成:5×3+1;…由此可以推理得出一般规律:摆n个六边形需要:(5n+1)根小棒,据此解答。
【详解】根据分析可知:
摆5个正六边形需要小棒:
5×5+1
=25+1
=26(根)
摆n个正六边形需要小棒:(5n+1)根
【点睛】根据题干中已知的图形的排列特点及其数量关系,推理得出一般的结论进行解答,是此类问题的关键。
19.×
【分析】每4个图形一循环,计算第103个图形是第几组循环零几个图形,即可得出其形状,进而判断即可。
【详解】103÷4=25(组)……3(个)
第103个图形是。所以原题说法错误。
故答案为:×。
【点睛】解答此题的关键是先找到规律,再根据规律求解。
20.√
【分析】根据图示可知,每6个图形一循环,计算第111个图形是第几组循环零几个图形,即可知道其形状,判断即可。
【详解】111÷6=18(组)……3(个)
所有第111个图形是☆。原题说法正确。
故答案为:√。
【点睛】本题主要考查的是找图形规律,解题的关键是观察图形找到规律,再根据规律求解。
21.×
【分析】该图形是以“■◇◇●●●”为一组重复出现,这一组里一共有6个图形,用70÷6所得的商表示有几组这样的“■◇◇●●●”,产生的余数是就是这样的一组的第几个图形,如果没有余数,就是这样的一组的最后一个图形。
【详解】70÷6=11(组)……4(个),第4个图形是●,则第70个图形是●。所以原题说法错误。
故答案为:×。
【点睛】根据题干得出这组图形的排列周期特点是解决此类问题的关键。
22.√
【分析】规律:每多1个正方形就多3根小棒;
第1个图形里共有4根小棒,即3×1+1;
第2个图形里共有7根小棒,即3×2+1;
第3个图形里共有10根小棒,即3×3+1;
第4个图形里共有13根小棒,即3×4+1;
……
第n个图形里需要的小棒数为:3n+1。
【详解】根据分析可知,第n个图形里需要的小棒数为:3n+1,当n=100时,
3n+1
=3×100+1
=300+1
=301(根)
即第100个图形需要301根小棒。
故答案为:√
23.√
【分析】1=12,1+3=22,1+3+5=32,…据此可知,从1开始的连续奇数的和等于奇数个数的平方,所以1+3+5…+13+15=82,1+3+5…+13=72,据此解答。
【详解】1+3+5…+13+15+13+11…+3+1
=(1+3+5…+13+15)+(13+11…+3+1)
=82+72
=64+49
=113
所以原题干说法正确。
故答案为:√
24.(1)每相邻两个之间相差10;
(2);
(3)35、45、55、65。
【分析】(1)观察上下相邻的数之间的大小关系,得出规律;
(2)长方形中一共有4个数,最上面和最下面之间相差30,据此列式;
(3)设小丽圈出的第一个数字为,下面的数依次是a+10、a+20、a+30,根据四个数相加等于200,列出方程,求出第一个数,再分别求出下面的数即可。
【详解】(1)我发现圈出的4个数,每相邻两个之间相差10。
(2)最下面一个数字可以用表示。
(3)解:设小丽圈出的第一个数字为。
4+60=200
4=140
,,。
答:她圈的是35、45、55、65。
【点睛】本题考查了数字的排列规律和列方程解决问题,关键是发现数表中的规律。
25. 1+2×4 1+3×4 1+4×4 5 9 13 17 4n-3
【分析】通过观察发现,第一个图的点子数是1,第二个图的点子数是1+4=5,第三个图的点子数是1+2×4=9,第4个图的点子数是1+3×4=13,第五个图的点子数是1+4×4=17,由此可知用A表示第n个图形中点子的总个数,A和n之间的关系可以表示成A=4n-3,据此解答即可。
【详解】如图:
序号 1 2 3 4 5 …
表示点子数的算式 1 1+4 1+2×4 1+3×4 1+4×4 …
点子的总个数 1 5 9 13 17 …
由分析可得:A=1+4(n-1)=4n-3
【点睛】此题主要考查学生根据图形规律,归纳出规律关系式,然后进行代数解答。
26.(1) 5×=5-
(2)100×=100-
【详解】(1)根据算式的规律,可知⑤的算式为5×=5-
再画出对应的图,每个小正方形可看做“单位1”,表示,将“单位1”平均分成6份,阴影部分占5份,5×可画为
(2)第100个图形对应的算式为100×=100-,即100×=100-
27.第a个数为a2﹣1 28.第②行相对应的数比第①行数多2,第③行相对应的数是第①行数的2倍 29.a2﹣1+a2+1+2(a2﹣1)=4a2﹣2
【分析】探索数与式的规律(1)第①行的每个数均为序数的平方减1;(2)第②行相对应的数比第①行数多2,第③行相对应的数是第①行数的2倍;(3)由(2)得出第②行第a个数为a2+1,第③行第a个数为2(a2﹣1),相加化简即可.
27.解:∵第1个数0=12﹣1,第2个数3=22﹣1,第3个数8=32﹣1,第4个数15=42﹣1,…
∴第a个数为a2﹣1
28.第②行相对应的数比第①行数多2,第③行相对应的数是第①行数的2倍
29.由(2)知,第②行第a个数为a2+1,第③行第a个数为2(a2﹣1),
∴这三个数的和为a2﹣1+a2+1+2(a2﹣1)=4a2﹣2
30.见解答
【分析】(1)(2)如下图所示,数从小到大逆时针方向螺旋由内而外排列出的图形是一个正方形,以1为中心数,每个1×1,3×3,5×5的正方形的右下角的数(即标蓝色方格内的数)均是从1开始的连续奇数的平方(即(2n-1) ),因为19 =361,即最接近365的奇数的平方,据此画出以数361为右下角的数的排列,再画出以数289为右下角的数的排列(如下图),据此解答。
【详解】由分析可知:
(1)如下图所示:
(2)如下图所示:
【点睛】本题考查了数表中的规律的应用。
31.(1)52-1=6×4=24
(2)9999
【分析】(1)观察32-1=4×2=8可得:4=3+1,2=3-1,4和2相差2。
可将算式改写成:32-1=(3+1)×(3-1)=4×2=8
那么42-1=5×3=15可改写成:42-1=(4+1)×(4-1)=5×3=15
72-1=8×6=48可改写成:72-1=(7+1)×(7-1)=8×6=48
92-1=10×8=80可改写成:92-1=(9+1)×(9-1)=10×8=80
可得规律:n2-1=(n+1)×(n-1),据此写出这样的算式即可。
(2)101和99相差2,101=100+1,99=100-1,根据算式的规律n2-1=(n+1)×(n-1),可得101×99=(100+1)×(100-1)=1002-1,据此求解即可。
【详解】(1)根据分析可得规律:n2-1=(n+1)×(n-1)
52-1=6×4=24(答案不唯一)
(2)101×99
=(100+1)×(100-1)
=1002-1
=10000-1
=9999
同课章节目录
