2025学年小升初数学专题训练:图形的拼切(含解析)
文档属性
| 名称 | 2025学年小升初数学专题训练:图形的拼切(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 327.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 08:00:39 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2025学年小升初数学专题训练:图形的拼切
一、选择题
1.用两个完全一样的三角形,拼成平行四边形,三角形的边长分别为6厘米,5厘米,8厘米,这个平行四边形的周长最大是( )厘米。
A.22 B.26 C.28 D.38
2.把一个高6分米,底面半径2分米的圆柱切成若干等份,拼成一个近似的长方体(如图)。这时表面积( )。
A.不变 B.增加了12平方分米
C.增加了24平方分米 D.减少了24平方分米
3.将一个平行四边形沿高剪拼成一个长方形(如下图),剪拼成的长方形和原来的平行四边形相比,( )。
A.周长不变,面积也不变 B.周长不变,面积变了
C.周长变了,面积不变 D.周长变了,面积也变了
4.下图是由一个圆分成若干等份后,拼成的一个近似长方形,这个圆的周长与长方形的周长相差约4厘米,这个圆的周长约是( )厘米。
A.6.28 B.9.42 C.12.56 D.无法计算
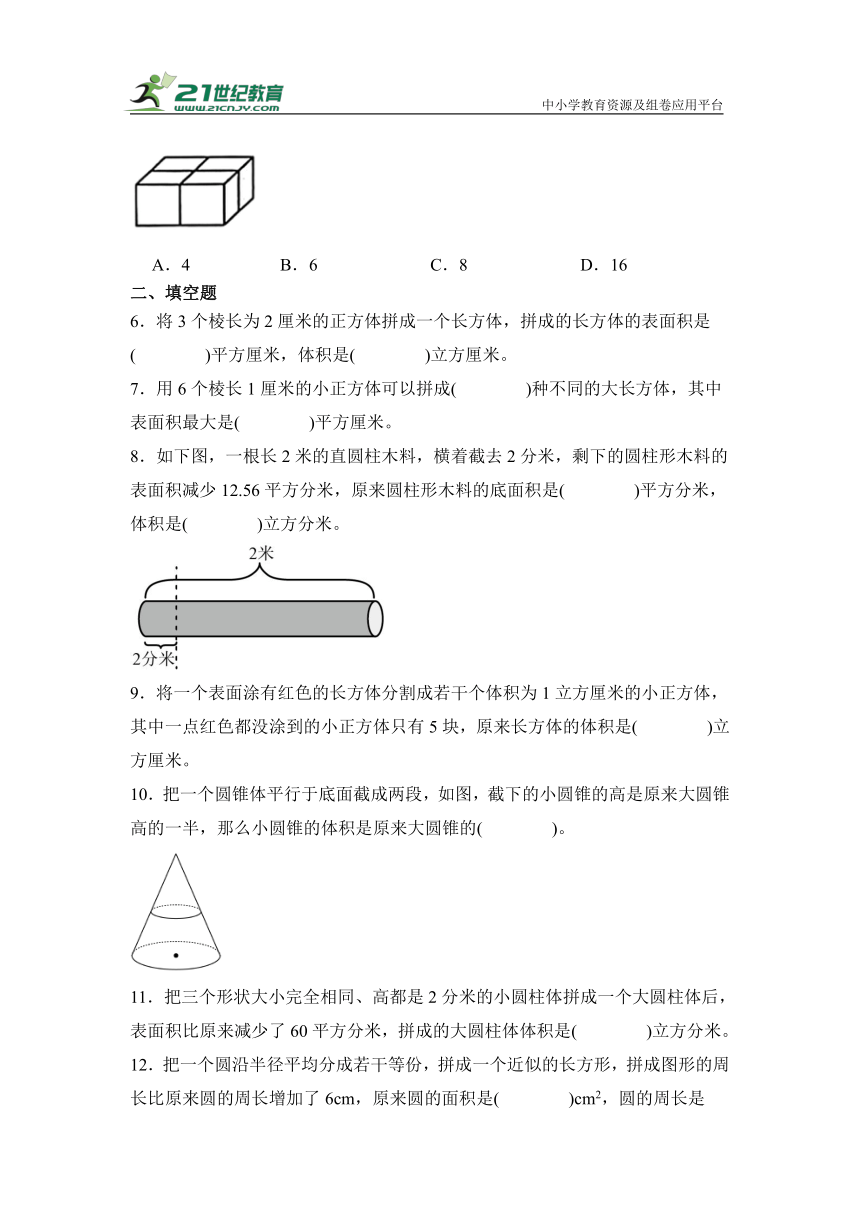
5.四个棱长为1cm的正方体拼成如图的长方体,表面积减少了( )。
A.4 B.6 C.8 D.16
二、填空题
6.将3个棱长为2厘米的正方体拼成一个长方体,拼成的长方体的表面积是( )平方厘米,体积是( )立方厘米。
7.用6个棱长1厘米的小正方体可以拼成( )种不同的大长方体,其中表面积最大是( )平方厘米。
8.如下图,一根长2米的直圆柱木料,横着截去2分米,剩下的圆柱形木料的表面积减少12.56平方分米,原来圆柱形木料的底面积是( )平方分米,体积是( )立方分米。
9.将一个表面涂有红色的长方体分割成若干个体积为1立方厘米的小正方体,其中一点红色都没涂到的小正方体只有5块,原来长方体的体积是( )立方厘米。
10.把一个圆锥体平行于底面截成两段,如图,截下的小圆锥的高是原来大圆锥高的一半,那么小圆锥的体积是原来大圆锥的( )。
11.把三个形状大小完全相同、高都是2分米的小圆柱体拼成一个大圆柱体后,表面积比原来减少了60平方分米,拼成的大圆柱体体积是( )立方分米。
12.把一个圆沿半径平均分成若干等份,拼成一个近似的长方形,拼成图形的周长比原来圆的周长增加了6cm,原来圆的面积是( )cm2,圆的周长是( )cm。
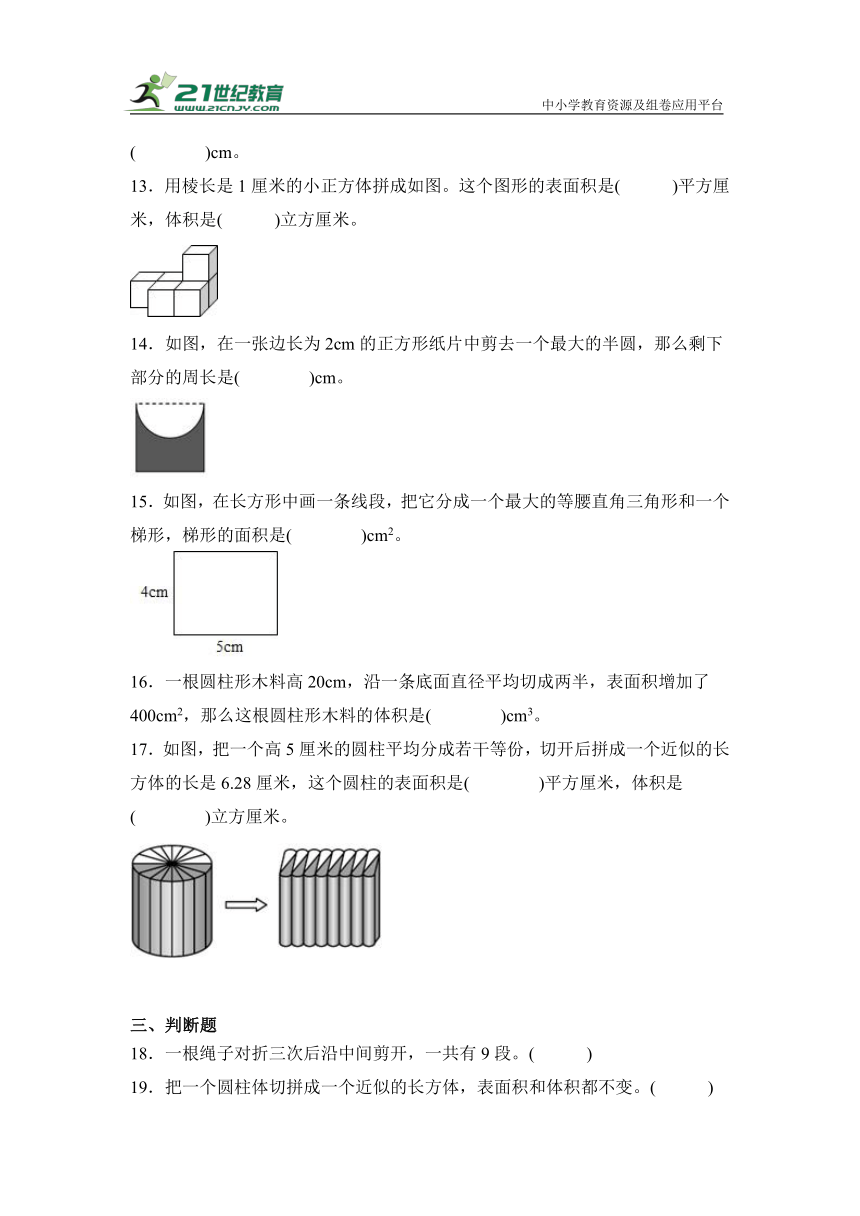
13.用棱长是1厘米的小正方体拼成如图。这个图形的表面积是( )平方厘米,体积是( )立方厘米。
14.如图,在一张边长为2cm的正方形纸片中剪去一个最大的半圆,那么剩下部分的周长是( )cm。
15.如图,在长方形中画一条线段,把它分成一个最大的等腰直角三角形和一个梯形,梯形的面积是( )cm2。
16.一根圆柱形木料高20cm,沿一条底面直径平均切成两半,表面积增加了400cm2,那么这根圆柱形木料的体积是( )cm3。
17.如图,把一个高5厘米的圆柱平均分成若干等份,切开后拼成一个近似的长方体的长是6.28厘米,这个圆柱的表面积是( )平方厘米,体积是( )立方厘米。
三、判断题
18.一根绳子对折三次后沿中间剪开,一共有9段。( )
19.把一个圆柱体切拼成一个近似的长方体,表面积和体积都不变。( )
20.等底等高的两个三角形一定可以拼成一个平行四边形。( )
21.把一个长方体切成两个相同的小长方体后,表面积增加了,体积不变。( )
22.两个面积相等的三角形都可以拼成一个平行四边形。( )
四、计算题
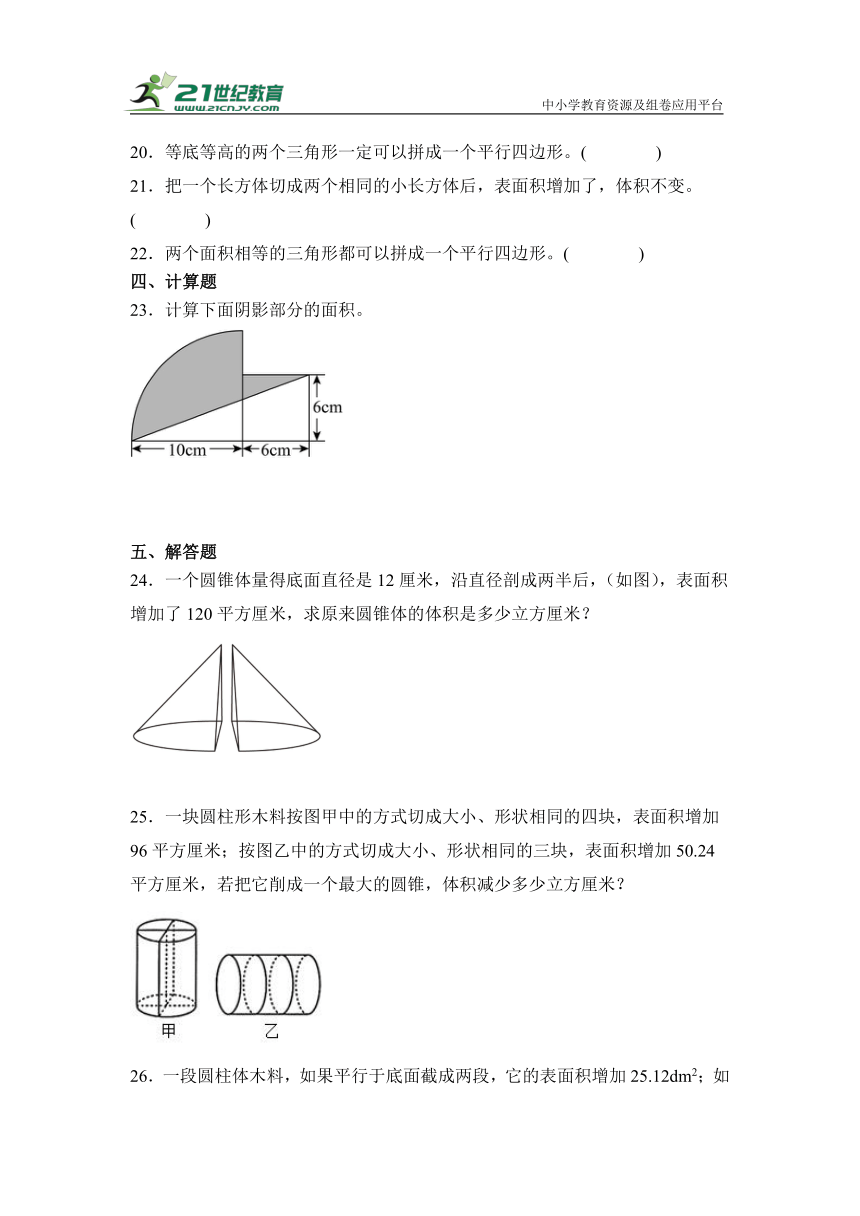
23.计算下面阴影部分的面积。
五、解答题
24.一个圆锥体量得底面直径是12厘米,沿直径剖成两半后,(如图),表面积增加了120平方厘米,求原来圆锥体的体积是多少立方厘米?
25.一块圆柱形木料按图甲中的方式切成大小、形状相同的四块,表面积增加96平方厘米;按图乙中的方式切成大小、形状相同的三块,表面积增加50.24平方厘米,若把它削成一个最大的圆锥,体积减少多少立方厘米?
26.一段圆柱体木料,如果平行于底面截成两段,它的表面积增加25.12dm2;如果沿底面直径竖直切成两个部分,它的表面积增加80dm2,这段圆柱体木料的表面积是( )dm2。
27.把一个棱长为20厘米的正方体木块,削成一个最大的圆柱,这个圆柱的表面积是多少平方厘米?
28.把60厘米长的圆柱按照7∶3截成两个小圆柱后,表面积比原来增加6平方厘米,这两段圆柱体积相差多少立方厘米?
29.把一根长的圆柱形木料沿底面横切,平均截成3段,表面积一共增加了,每段木料的体积是多少?
30.一根2米长的圆柱形木料,横截面的半径是10厘米,沿横截面的直径垂直锯开,分成相等的两块,每块的体积和表面积各是多少?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2025学年小升初数学专题训练:图形的拼切》参考答案
题号 1 2 3 4 5
答案 C C C C C
1.C
【分析】要使两个三角形拼成的平行四边形周长最大,那么要把这两个三角形最短的边拼在一起,使较长的两条边作为平行四边形的一组邻边。三角形的边长分别为6厘米,5厘米,8厘米,则拼成的平行四边形相邻的两条边最大是6厘米和8厘米。平行四边形的对边相等,则用一组相邻边的和乘2,可得周长。
【详解】通过分析可得:
(6+8)×2
=14×2
=28(厘米)
则这个平行四边形的周长最大是28厘米。
故答案为:C
2.C
【分析】根据圆柱体积公式的推导过程可知,把一个圆柱切拼成一个近似长方体后,体积不变,表面积增加了两个切面的面积,每个切面的长等于圆柱的高,切面的宽等于圆柱的底面半径,根据长方形的面积公式:S=ab,把数据代入公式解答。
【详解】6×2×2
=12×2
=24(平方分米)
即表面积增加了24平方分米。
故答案为:C
【点睛】此题考查的目的是理解掌握圆柱体积公式的推导过程,以及圆柱表面积的意义及应用。
3.C
【分析】把平行四边形剪拼成长方形,平行四边形的底相当于长方形的长,平行四边形的高相当于长方形的宽,平行四边形底边的邻边大于底边上的高,利用平行四边形和长方形的周长和面积公式分别表示出它们的周长和面积,最后比较大小,据此解答。
【详解】假设平行四边形的底边为a,底边的邻边为b,高为h。
平行四边形的面积:ah
长方形的面积:ah
所以,平行四边形的面积=长方形的面积。
平行四边形的周长:(a+b)×2
长方形的周长:(a+h)×2
因为b>h,则(a+b)×2>(a+h)×2,所以平行四边形的周长>长方形的周长。
故答案为:C
【点睛】分析平行四边形底与高和长方形长与宽的对应关系是解答题目的关键。
4.C
【分析】拼成长方形的长相当于圆周长的一半,长方形的宽相当于圆的半径,长方形的周长比圆的周长多两条半径的长度,则圆和长方形的周长差就是圆的直径,最后利用“”求出这个圆的周长,据此解答。
【详解】分析可知,这个圆的周长为:3.14×4=12.56(厘米)
故答案为:C
【点睛】找出长方形和圆的对应关系并掌握圆的周长计算公式是解答题目的关键。
5.C
【分析】观察可知,拼成长方体后,表面积减少了8个小正方形,求出一个小正方形面积,乘8即可。
【详解】1×1×8=8(平方厘米)
故答案为:C
【点睛】立体图形(比如正方体之间)拼起来,因为面数目减少,所以表面积减少。
6. 56 24
【分析】将3个棱长为2厘米的正方体拼成一个长方体,则该长方体的长为2×3=6厘米,宽为2厘米,高也为2厘米,然后根据长方体的表面积公式:S=(ab+ah+bh)×2,长方体的体积公式:V=abh,据此进行计算即可。
【详解】2×3=6(厘米)
(6×2+6×2+2×2)×2
=(12+12+4)×2
=28×2
=56(平方厘米)
6×2×2
=12×2
=24(立方厘米)
则拼成的长方体的表面积是56平方厘米,体积是24立方厘米。
【点睛】本题考查长方体的表面积和体积,熟记公式是解题的关键。
7. 2 26
【分析】根据正方体拼组长方体的方法,可以将6个正方体拼一排,或者6个小正方体一排3个,有2排,所以有两种情况,这两种情况一种是长为3厘米、宽为2厘米、高为1厘米的长方体,另一种长是6厘米,宽是1厘米,高是1厘米的长方体,根据长方体的表面积公式解答即可。
【详解】由分析可知:
6个小正方体拼成长方体有两种情况,即用6个小正方体可以组成长为3厘米、宽为2厘米、高为1厘米;另一种长是6厘米,宽是1厘米,高是1厘米的长方体。
长是6厘米,宽是1厘米,高是1厘米的长方体表面积:
(6×1+6×1+1×1)×2
=13×2
=26(平方厘米)
棱长分别为3厘米、2厘米、1厘米的长方体,表面积是:
(3×2+3×1+2×1)×2
=(6+3+2)×2
=11×2
=22(平方厘米)
26>22,所以表面积最大是26平方厘米。
可以拼成2种不同的长方体,其中表面积最大的是26平方厘米。
【点睛】本题主要考查长方体表面积公式,熟练掌握长方体的表面积公式并灵活运用。
8. 3.14 62.8
【分析】根据题意可知,表面积减少12.56平方分米,也就是侧面减少了一些面积,根据圆柱的侧面积公式:S=Ch,用12.56÷2即可求出圆柱形木料的底面周长,再根据周长公式,用12.56÷2÷3.14÷2即可求出底面半径,然后根据圆柱的底面积公式:S=πr2,代入数据即可求出圆柱形木料的底面积;最后根据圆柱的体积公式:V=Sh,代入数据解答即可。
【详解】12.56÷2÷3.14÷2
=6.28÷3.14÷2
=1(分米)
3.14×12
=3.14×1
=3.14(平方分米)
2米=20分米
3.14×20=62.8(立方分米)
原来圆柱形木料的底面积是3.14平方分米,体积是62.8立方分米。
【点睛】本题主要考查了圆柱的侧面积公式、表面积公式、体积公式的灵活应用,关键是明确表面积减少了哪些面。
9.63
【分析】每个小正方体的棱长都是1厘米,由“其中没有涂色的小正方体只有5块”可知这个长方体的长是5+2=7厘米,宽和高都是1+2=3厘米,由此即可解决问题。
【详解】原来长方体的体积为∶(5+2)×(1+2)×(1+2)
=7×3×3
=21×3
=63(立方厘米)
原来长方体的体积是63立方厘米。
【点睛】抓住长方体切割正方体的特点,以及表面没有涂色的正方体都在长方体的内部的特点即可解决问题。
10.
【分析】根据圆锥的体积公式:V=πr2h,设小圆锥的底面半径为r,高为h,则大圆锥的底面半径为2r,高为2h,把数据代入公式求出大小圆锥的体积,再根据求一个数是另一个数的几分之几,用除法解答。
【详解】设小圆锥的底面半径为r,高为h,则大圆锥的底面半径为2r,高为2h,
πr2h÷[π×(2r)2×2h]
=πr2h÷[π×4r2×2h]
=πr2h÷π÷8r2h
=1÷8
=
则小圆锥的体积是原来大圆锥的。
【点睛】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
11.90
【分析】把三个形状大小完全相同、高都是2分米的小圆柱体拼成一个大圆柱体后,表面积比原来减少了4个底面积,即60平方分米,据此求出圆柱体的底面积,再根据圆柱的体积公式:V=Sh,据此进行计算即可。
【详解】2+2+2=6(分米)
60÷4×6
=15×6
=90(立方分米)
则大圆柱体体积是90立方分米。
【点睛】本题考查圆柱的体积,求出圆柱的底面积是解题的关键。
12. 28.26 18.84
【分析】周长多出的部分是两条半径的长度,所以用6cm除以2,可以求出圆的半径。将半径的数据代入圆的周长和面积公式中,求出对应圆的周长和面积即可。
【详解】6÷2=3(cm)
3.14×32=28.26(cm2)
2×3.14×3=18.84(cm)
所以,原来圆的面积是28.26cm2,圆的周长是18.84cm。
【点睛】本题考查了圆的周长和面积,熟记公式是解题的关键。
13. 24 6
【分析】这个立体图形的每个面都是小正方形,根据正方形的面积=边长×边长,求出每个小正方形的面积;观察这个立体图形的上、下面都是5个面,左、右面都是3个面,前、后面都是4个面,据此算出小正方形的总个数,再乘每个小正方形的面积,即是这个立体图形的表面积;
这个立体图形是由6个小正方体组成的,根据正方体的体积=棱长×棱长×棱长,求出每个小正方体的体积,再乘6即可。
【详解】小正方形的个数:
(5+4+3)×2
=12×2
=24(个)
这个图形的表面积是:
1×1×24=24(平方厘米)
这个图形的体积:
1×1×1×6=6(立方厘米)
【点睛】掌握不规则的立体图形的表面积、体积的计算方法是解题的关键。
14.9.14
【分析】如图,要剪去一个最大的半圆,那么这个最大的半圆的直径等于正方形的边长,为2厘米,剩下部分的周长=圆的周长的一半+正方形的三条边长,利用圆的周长公式:C=,再除以2,求出圆的周长的一半,再加上正方形三条边长的长度,即可得解。
【详解】3.14×2÷2+2×3
=3.14+6
=9.14(cm)
剩下部分的周长是9.14cm。
【点睛】此题考查了图形的切拼,找到最大的半圆是解决此题的关键,利用圆的周长公式,求出结果。
15.12
【分析】要把这个长方形分成一个最大等腰直角三角形和一个梯形,则所画的等腰直角三角形的腰等于长方形的宽,据此画出即可;
通过画图可知,梯形的上底为(5-4=1)厘米,下底为5厘米,高为4厘米,依据梯形的面积=(上底+下底)×高÷2,即可求得梯形的面积。
【详解】根据分析画图如下:
(5-4+5)×4÷2
=6×4÷2
=12(cm2)
梯形的面积是12cm2。
【点睛】本题主要考查等腰直角三角形的特征及梯形面积公式的实际运用,确定以长方形的宽为等腰直角三角形的直角边是关键。
16.1570
【分析】根据题意可知,把一根圆柱形木料沿一条底面直径平均切成两半,表面积增加的是两个切面的面积,每个切面是一个长等于圆柱的高,宽等于圆柱底面直径的长方形;先用增加的表面积除以2,求出一个长方形的面积,再除以高,求出圆柱的底面直径;最后根据圆柱的体积公式V=πr2h,代入数据计算即可。
【详解】圆柱的底面直径:
400÷2÷20
=200÷20
=10(厘米)
圆柱的体积:
3.14×(10÷2)2×20
=3.14×25×20
=78.5×20
=1570(cm3)
这根圆柱形木料的体积是1570 cm3。
【点睛】掌握圆柱切割的特点,明确表面积增加的是哪些面的面积,分析出圆柱的底面直径和高与切面的关系,求出圆柱的底面直径是解题的关键,最后利用圆柱的体积公式列式计算。
17. 87.92 62.8
【分析】由题意,圆柱切拼后,拼成的近似的长方体的长相当于圆柱底面圆周长的一半,可先把这个长度转化为圆的周长,再根据圆的周长公式,求得半径,列综合算式为:6.28×2÷3.14÷2=2(厘米);
然后结合高为5厘米,再套用圆柱表面积公式、体积公式来求得这个圆柱的表面积及体积。
【详解】6.28×2÷3.14÷2
=12.56÷3.14÷2
=4÷2
=2(厘米)
S圆柱=2πr2+2πrh
=2×3.14×22+2×3.14×2×5
=3.14×8+3.14×20
=25.12+62.8
=87.92(平方厘米)
V圆柱=πr2h
=3.14×22×5
=3.14×20
=62.8(立方厘米)
【点睛】关键是结合图示,确定切拼前后,圆柱体与长方体各部分元素间对应的关系。
18.√
【分析】对折1次后从中间剪开变成2+1=3(段),对折2次后从中间剪开变成2×2+1=4+1=5(段),……,以此类推,对折n次后从中间剪开变成n个2相乘,再加1段;据此解答。
【详解】根据分析:
2×2×2+1
=8+1
=9(段)
即一根绳子对折三次后沿中间剪开,一共有9段,原题说法正确。
故答案为:√
19.×
【分析】长方体的高等于圆柱的高,长方体的长等于圆柱底面周长的一半,长方体的宽等于圆柱体的底面半径,设圆柱的底面半径是r,然后表示出拼成的长方体的长与宽,高是h,再根据长方形的表面积=(长×宽+长×高+宽×高)×2,长方形体积=长×宽×高,圆柱的表面积=2πr2+2πrh,圆柱体积=πr2h ,列式表示出长方体的表面积和体积与原来圆柱的表面积和体积,由此即可进行比较选择。
【详解】设圆柱的底面半径是r,长方体的高等于圆柱的高是h,则长方形的长为πr,宽为r。
圆柱的表面积为: 2πr2+2πrh
圆柱的体积为:πr2h
长方体的表面积为:(πr2+πrh+rh)×2=2πr2+2πrh+2rh
长方体的体积为:πr2h
2πr2+2πrh+2rh> 2πr2+2πrh
πr2h=πr2h
所以这个长方体和原来的圆柱体比较表面积变大了,体积没变。题干说法错误。
故答案为:×
20.×
【分析】有两组对边分别平行且相等的四边形,叫做平行四边形。
因在拼组平行四边形时,平行四边形的两组对边平行且相等,且有公共边,所以只有两个完全一样的三角形才能拼成一个平行四边形。
【详解】如图:
4×2÷2=4(cm2)
等底等高的两个三角形面积相等,但形状不一样时,不能拼成一个平行四边形。
原题说法错误。
故答案为:×
21.√
【分析】把一个长方体切成两个相同的小长方体,因为面数目增加,所以表面积增加,但是体积没变,据此分析。
【详解】
如图,把一个长方体切成两个相同的小长方体后,表面积增加了,体积不变,说法正确。
故答案为:√
22.×
【分析】只有两个一模一样的三角形,才可以拼成一个平行四边形。据此解题。
【详解】两个面积相等的三角形,形状不一定相等,那么不一定能拼成一个平行四边形。
故答案为:×
23.66.5平方厘米
【分析】根据图示,阴影部分面积=(圆的面积+正方形的面积)-白色部分三角形面积,依据圆的面积公式=πr ,正方形面积=边长×边长,三角形的面积=底×高÷2,将数据代入公式计算即可。
【详解】(3.14×10×10×)+(6×6)-(10+6)×6÷2
=314×+36-16×6÷2
=114.5-96÷2
=114.5-48
=66.5(平方厘米)
阴影部分的面积为66.5平方厘米。
24.376.8立方厘米
【分析】通过观察图形可知,把这个圆锥沿直径剖成两半,剖面是三角形,这个三角形的底等于圆锥的底面直径,三角形的高等于圆锥的高,据此可以求出圆锥的高,然后根据圆锥的体积公式:V=πr2h,把数据代入公式解答。
【详解】120÷2=60(平方厘米)
60×2÷12
=120÷12
=10(厘米)
×3.14×(12÷2)2×10
=×3.14×36×10
=3.14×12×10
=3.14×120
=376.8(立方厘米)
答:原来圆锥的体积是376.8立方厘米。
【点睛】此题主要考查圆锥体积公式的灵活运用,关键是求出圆锥的高。
25.50.24立方厘米
【分析】按乙的切法增加了4个底面面积,用增加的面积除以4就是底面面积,根据底面积可求出圆柱底面半径,进而求出直径,按甲的切法,增加了8个长为圆柱高,宽为圆柱底面半径的长方形,据此可求出圆柱的高,切成的最大圆锥与圆柱底面积相等、高相等;等底、等高的圆锥体积是圆锥体积的,去掉的体积是圆柱体积的(1-),根据圆柱的体积计算公式V=Sh,求出圆柱的体积,乘(1-)就是减少的体积。
【详解】50.24÷4=12.56(平方厘米)
设圆柱底面半径为r厘米
3.14×r2=12.56
3.14×r2÷3.14=12.56÷3.14
r2=4
因为22=4
所以r=2
96÷8÷2
=12÷2
=6(厘米)
12.56×6×(1-)
=75.36×
=50.24(立方厘米)
答:体积减少50.24立方厘米。
【点睛】此题较难,关键是先根据乙的切法求出圆柱的底面积,进而求出底面半径,再根据甲的切法求出圆柱的高。
26.150.72
【分析】如果平行于底面截成两段,那么增加的表面积是2个底面的面积;用增加的表面积除以2,求出圆柱的底面积,进而求出底面直径;沿底面直径竖直切成两个部分,增加的表面积是2个以直径为宽,圆柱的高为长的长方形的面积,用增加的表面积除以2,再除以底面直径,即能求出圆柱的高;根据圆柱的侧面积公式S侧=πdh,求出圆柱的侧面积,再加上2个底面积,即是圆柱的表面积。
【详解】圆柱的底面积:25.12÷2=12.56(dm2)
半径的平方:12.56÷3.14=4(dm2)
4=2×2,所以圆柱的底面半径是2 dm;
底面直径:2×2=4(dm)
圆柱的高:
80÷2÷4
=40÷4
=10(dm)
圆柱的侧面积:
3.14×4×10
=12.56×10
=125.6(dm2)
圆柱的表面积:125.6+25.12=150.72(dm2)
答:这段圆柱体木料的表面积是150.72 dm2。
【点睛】明确用不同的方法切圆柱,增加的表面积是哪些面,面的形状、数量以及与原圆柱之间的联系是解题的关键。
27.1884平方厘米
【分析】正方体木块削成最大的圆柱,圆的底面直径和高等于正方体的棱长,根据圆柱的表面积公式:表面积=底面积×2+侧面积,代入数据,即可解答。
【详解】3.14×(20÷2)2×2+3.14×20×20
=3.14×100×2+62.8×20
=314×2+1256
=628+1256
=1884(平方厘米)
答:这个圆柱的表面积是1884平方厘米。
【点睛】本题考查圆柱的表面积公式的应用,关键明确正方体削成最大的圆柱,圆柱的底面直径和高等于正方体的棱长。
28.72立方厘米
【分析】先看截成两个小圆柱后,增加了两个底面圆的面积,也就是6平方厘米,则6÷2=3(平方厘米),是圆柱底面的面积;因为是求大小两个圆柱的体积相差多少,所以要把体积按7∶3的比例分配,再用减法求得这个差即可。
【详解】6÷2=3(平方厘米)
V大=60×3×
=180×
=126(立方厘米)
V小=60×3×
=180×
=54(立方厘米)
126-54=72(立方厘米)
答:这两段圆柱体积相差72立方厘米。
【点睛】将圆柱体积问题与比的应用相结合,使题意稍复杂。需要我们每一步都计算仔细,有的可能要反复计算几遍。
29.0.5
【分析】由题意可知,表面积增加了4个圆柱的底面积,根据表面积一共增加的平方米数÷增加的底面积个数=底面积,每段木料的体积=底面积×高÷3,代入数据计算即可。
【详解】1.2÷4=0.3(平方米)
0.3×5÷3=0.5(立方米)
答:每段木料的体积是0.5。
【点睛】此题主要考查立体图形的切拼问题,明确截成3段,增加的是4个底面积,求出木料的一个底面积是解题关键。
30.31400立方厘米;10594平方厘米
【详解】2米=200厘米
3.14×102×200÷2
=3.14×100×100
=31400(立方厘米)
3.14×10×2×200÷2+10×2×200+3.14×102
=6280+4000+314
=10594(平方厘米)
答:每块的体积是31400立方厘米,每块的表面积是10594平方厘米。
中小学教育资源及组卷应用平台
2025学年小升初数学专题训练:图形的拼切
一、选择题
1.用两个完全一样的三角形,拼成平行四边形,三角形的边长分别为6厘米,5厘米,8厘米,这个平行四边形的周长最大是( )厘米。
A.22 B.26 C.28 D.38
2.把一个高6分米,底面半径2分米的圆柱切成若干等份,拼成一个近似的长方体(如图)。这时表面积( )。
A.不变 B.增加了12平方分米
C.增加了24平方分米 D.减少了24平方分米
3.将一个平行四边形沿高剪拼成一个长方形(如下图),剪拼成的长方形和原来的平行四边形相比,( )。
A.周长不变,面积也不变 B.周长不变,面积变了
C.周长变了,面积不变 D.周长变了,面积也变了
4.下图是由一个圆分成若干等份后,拼成的一个近似长方形,这个圆的周长与长方形的周长相差约4厘米,这个圆的周长约是( )厘米。
A.6.28 B.9.42 C.12.56 D.无法计算
5.四个棱长为1cm的正方体拼成如图的长方体,表面积减少了( )。
A.4 B.6 C.8 D.16
二、填空题
6.将3个棱长为2厘米的正方体拼成一个长方体,拼成的长方体的表面积是( )平方厘米,体积是( )立方厘米。
7.用6个棱长1厘米的小正方体可以拼成( )种不同的大长方体,其中表面积最大是( )平方厘米。
8.如下图,一根长2米的直圆柱木料,横着截去2分米,剩下的圆柱形木料的表面积减少12.56平方分米,原来圆柱形木料的底面积是( )平方分米,体积是( )立方分米。
9.将一个表面涂有红色的长方体分割成若干个体积为1立方厘米的小正方体,其中一点红色都没涂到的小正方体只有5块,原来长方体的体积是( )立方厘米。
10.把一个圆锥体平行于底面截成两段,如图,截下的小圆锥的高是原来大圆锥高的一半,那么小圆锥的体积是原来大圆锥的( )。
11.把三个形状大小完全相同、高都是2分米的小圆柱体拼成一个大圆柱体后,表面积比原来减少了60平方分米,拼成的大圆柱体体积是( )立方分米。
12.把一个圆沿半径平均分成若干等份,拼成一个近似的长方形,拼成图形的周长比原来圆的周长增加了6cm,原来圆的面积是( )cm2,圆的周长是( )cm。
13.用棱长是1厘米的小正方体拼成如图。这个图形的表面积是( )平方厘米,体积是( )立方厘米。
14.如图,在一张边长为2cm的正方形纸片中剪去一个最大的半圆,那么剩下部分的周长是( )cm。
15.如图,在长方形中画一条线段,把它分成一个最大的等腰直角三角形和一个梯形,梯形的面积是( )cm2。
16.一根圆柱形木料高20cm,沿一条底面直径平均切成两半,表面积增加了400cm2,那么这根圆柱形木料的体积是( )cm3。
17.如图,把一个高5厘米的圆柱平均分成若干等份,切开后拼成一个近似的长方体的长是6.28厘米,这个圆柱的表面积是( )平方厘米,体积是( )立方厘米。
三、判断题
18.一根绳子对折三次后沿中间剪开,一共有9段。( )
19.把一个圆柱体切拼成一个近似的长方体,表面积和体积都不变。( )
20.等底等高的两个三角形一定可以拼成一个平行四边形。( )
21.把一个长方体切成两个相同的小长方体后,表面积增加了,体积不变。( )
22.两个面积相等的三角形都可以拼成一个平行四边形。( )
四、计算题
23.计算下面阴影部分的面积。
五、解答题
24.一个圆锥体量得底面直径是12厘米,沿直径剖成两半后,(如图),表面积增加了120平方厘米,求原来圆锥体的体积是多少立方厘米?
25.一块圆柱形木料按图甲中的方式切成大小、形状相同的四块,表面积增加96平方厘米;按图乙中的方式切成大小、形状相同的三块,表面积增加50.24平方厘米,若把它削成一个最大的圆锥,体积减少多少立方厘米?
26.一段圆柱体木料,如果平行于底面截成两段,它的表面积增加25.12dm2;如果沿底面直径竖直切成两个部分,它的表面积增加80dm2,这段圆柱体木料的表面积是( )dm2。
27.把一个棱长为20厘米的正方体木块,削成一个最大的圆柱,这个圆柱的表面积是多少平方厘米?
28.把60厘米长的圆柱按照7∶3截成两个小圆柱后,表面积比原来增加6平方厘米,这两段圆柱体积相差多少立方厘米?
29.把一根长的圆柱形木料沿底面横切,平均截成3段,表面积一共增加了,每段木料的体积是多少?
30.一根2米长的圆柱形木料,横截面的半径是10厘米,沿横截面的直径垂直锯开,分成相等的两块,每块的体积和表面积各是多少?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2025学年小升初数学专题训练:图形的拼切》参考答案
题号 1 2 3 4 5
答案 C C C C C
1.C
【分析】要使两个三角形拼成的平行四边形周长最大,那么要把这两个三角形最短的边拼在一起,使较长的两条边作为平行四边形的一组邻边。三角形的边长分别为6厘米,5厘米,8厘米,则拼成的平行四边形相邻的两条边最大是6厘米和8厘米。平行四边形的对边相等,则用一组相邻边的和乘2,可得周长。
【详解】通过分析可得:
(6+8)×2
=14×2
=28(厘米)
则这个平行四边形的周长最大是28厘米。
故答案为:C
2.C
【分析】根据圆柱体积公式的推导过程可知,把一个圆柱切拼成一个近似长方体后,体积不变,表面积增加了两个切面的面积,每个切面的长等于圆柱的高,切面的宽等于圆柱的底面半径,根据长方形的面积公式:S=ab,把数据代入公式解答。
【详解】6×2×2
=12×2
=24(平方分米)
即表面积增加了24平方分米。
故答案为:C
【点睛】此题考查的目的是理解掌握圆柱体积公式的推导过程,以及圆柱表面积的意义及应用。
3.C
【分析】把平行四边形剪拼成长方形,平行四边形的底相当于长方形的长,平行四边形的高相当于长方形的宽,平行四边形底边的邻边大于底边上的高,利用平行四边形和长方形的周长和面积公式分别表示出它们的周长和面积,最后比较大小,据此解答。
【详解】假设平行四边形的底边为a,底边的邻边为b,高为h。
平行四边形的面积:ah
长方形的面积:ah
所以,平行四边形的面积=长方形的面积。
平行四边形的周长:(a+b)×2
长方形的周长:(a+h)×2
因为b>h,则(a+b)×2>(a+h)×2,所以平行四边形的周长>长方形的周长。
故答案为:C
【点睛】分析平行四边形底与高和长方形长与宽的对应关系是解答题目的关键。
4.C
【分析】拼成长方形的长相当于圆周长的一半,长方形的宽相当于圆的半径,长方形的周长比圆的周长多两条半径的长度,则圆和长方形的周长差就是圆的直径,最后利用“”求出这个圆的周长,据此解答。
【详解】分析可知,这个圆的周长为:3.14×4=12.56(厘米)
故答案为:C
【点睛】找出长方形和圆的对应关系并掌握圆的周长计算公式是解答题目的关键。
5.C
【分析】观察可知,拼成长方体后,表面积减少了8个小正方形,求出一个小正方形面积,乘8即可。
【详解】1×1×8=8(平方厘米)
故答案为:C
【点睛】立体图形(比如正方体之间)拼起来,因为面数目减少,所以表面积减少。
6. 56 24
【分析】将3个棱长为2厘米的正方体拼成一个长方体,则该长方体的长为2×3=6厘米,宽为2厘米,高也为2厘米,然后根据长方体的表面积公式:S=(ab+ah+bh)×2,长方体的体积公式:V=abh,据此进行计算即可。
【详解】2×3=6(厘米)
(6×2+6×2+2×2)×2
=(12+12+4)×2
=28×2
=56(平方厘米)
6×2×2
=12×2
=24(立方厘米)
则拼成的长方体的表面积是56平方厘米,体积是24立方厘米。
【点睛】本题考查长方体的表面积和体积,熟记公式是解题的关键。
7. 2 26
【分析】根据正方体拼组长方体的方法,可以将6个正方体拼一排,或者6个小正方体一排3个,有2排,所以有两种情况,这两种情况一种是长为3厘米、宽为2厘米、高为1厘米的长方体,另一种长是6厘米,宽是1厘米,高是1厘米的长方体,根据长方体的表面积公式解答即可。
【详解】由分析可知:
6个小正方体拼成长方体有两种情况,即用6个小正方体可以组成长为3厘米、宽为2厘米、高为1厘米;另一种长是6厘米,宽是1厘米,高是1厘米的长方体。
长是6厘米,宽是1厘米,高是1厘米的长方体表面积:
(6×1+6×1+1×1)×2
=13×2
=26(平方厘米)
棱长分别为3厘米、2厘米、1厘米的长方体,表面积是:
(3×2+3×1+2×1)×2
=(6+3+2)×2
=11×2
=22(平方厘米)
26>22,所以表面积最大是26平方厘米。
可以拼成2种不同的长方体,其中表面积最大的是26平方厘米。
【点睛】本题主要考查长方体表面积公式,熟练掌握长方体的表面积公式并灵活运用。
8. 3.14 62.8
【分析】根据题意可知,表面积减少12.56平方分米,也就是侧面减少了一些面积,根据圆柱的侧面积公式:S=Ch,用12.56÷2即可求出圆柱形木料的底面周长,再根据周长公式,用12.56÷2÷3.14÷2即可求出底面半径,然后根据圆柱的底面积公式:S=πr2,代入数据即可求出圆柱形木料的底面积;最后根据圆柱的体积公式:V=Sh,代入数据解答即可。
【详解】12.56÷2÷3.14÷2
=6.28÷3.14÷2
=1(分米)
3.14×12
=3.14×1
=3.14(平方分米)
2米=20分米
3.14×20=62.8(立方分米)
原来圆柱形木料的底面积是3.14平方分米,体积是62.8立方分米。
【点睛】本题主要考查了圆柱的侧面积公式、表面积公式、体积公式的灵活应用,关键是明确表面积减少了哪些面。
9.63
【分析】每个小正方体的棱长都是1厘米,由“其中没有涂色的小正方体只有5块”可知这个长方体的长是5+2=7厘米,宽和高都是1+2=3厘米,由此即可解决问题。
【详解】原来长方体的体积为∶(5+2)×(1+2)×(1+2)
=7×3×3
=21×3
=63(立方厘米)
原来长方体的体积是63立方厘米。
【点睛】抓住长方体切割正方体的特点,以及表面没有涂色的正方体都在长方体的内部的特点即可解决问题。
10.
【分析】根据圆锥的体积公式:V=πr2h,设小圆锥的底面半径为r,高为h,则大圆锥的底面半径为2r,高为2h,把数据代入公式求出大小圆锥的体积,再根据求一个数是另一个数的几分之几,用除法解答。
【详解】设小圆锥的底面半径为r,高为h,则大圆锥的底面半径为2r,高为2h,
πr2h÷[π×(2r)2×2h]
=πr2h÷[π×4r2×2h]
=πr2h÷π÷8r2h
=1÷8
=
则小圆锥的体积是原来大圆锥的。
【点睛】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
11.90
【分析】把三个形状大小完全相同、高都是2分米的小圆柱体拼成一个大圆柱体后,表面积比原来减少了4个底面积,即60平方分米,据此求出圆柱体的底面积,再根据圆柱的体积公式:V=Sh,据此进行计算即可。
【详解】2+2+2=6(分米)
60÷4×6
=15×6
=90(立方分米)
则大圆柱体体积是90立方分米。
【点睛】本题考查圆柱的体积,求出圆柱的底面积是解题的关键。
12. 28.26 18.84
【分析】周长多出的部分是两条半径的长度,所以用6cm除以2,可以求出圆的半径。将半径的数据代入圆的周长和面积公式中,求出对应圆的周长和面积即可。
【详解】6÷2=3(cm)
3.14×32=28.26(cm2)
2×3.14×3=18.84(cm)
所以,原来圆的面积是28.26cm2,圆的周长是18.84cm。
【点睛】本题考查了圆的周长和面积,熟记公式是解题的关键。
13. 24 6
【分析】这个立体图形的每个面都是小正方形,根据正方形的面积=边长×边长,求出每个小正方形的面积;观察这个立体图形的上、下面都是5个面,左、右面都是3个面,前、后面都是4个面,据此算出小正方形的总个数,再乘每个小正方形的面积,即是这个立体图形的表面积;
这个立体图形是由6个小正方体组成的,根据正方体的体积=棱长×棱长×棱长,求出每个小正方体的体积,再乘6即可。
【详解】小正方形的个数:
(5+4+3)×2
=12×2
=24(个)
这个图形的表面积是:
1×1×24=24(平方厘米)
这个图形的体积:
1×1×1×6=6(立方厘米)
【点睛】掌握不规则的立体图形的表面积、体积的计算方法是解题的关键。
14.9.14
【分析】如图,要剪去一个最大的半圆,那么这个最大的半圆的直径等于正方形的边长,为2厘米,剩下部分的周长=圆的周长的一半+正方形的三条边长,利用圆的周长公式:C=,再除以2,求出圆的周长的一半,再加上正方形三条边长的长度,即可得解。
【详解】3.14×2÷2+2×3
=3.14+6
=9.14(cm)
剩下部分的周长是9.14cm。
【点睛】此题考查了图形的切拼,找到最大的半圆是解决此题的关键,利用圆的周长公式,求出结果。
15.12
【分析】要把这个长方形分成一个最大等腰直角三角形和一个梯形,则所画的等腰直角三角形的腰等于长方形的宽,据此画出即可;
通过画图可知,梯形的上底为(5-4=1)厘米,下底为5厘米,高为4厘米,依据梯形的面积=(上底+下底)×高÷2,即可求得梯形的面积。
【详解】根据分析画图如下:
(5-4+5)×4÷2
=6×4÷2
=12(cm2)
梯形的面积是12cm2。
【点睛】本题主要考查等腰直角三角形的特征及梯形面积公式的实际运用,确定以长方形的宽为等腰直角三角形的直角边是关键。
16.1570
【分析】根据题意可知,把一根圆柱形木料沿一条底面直径平均切成两半,表面积增加的是两个切面的面积,每个切面是一个长等于圆柱的高,宽等于圆柱底面直径的长方形;先用增加的表面积除以2,求出一个长方形的面积,再除以高,求出圆柱的底面直径;最后根据圆柱的体积公式V=πr2h,代入数据计算即可。
【详解】圆柱的底面直径:
400÷2÷20
=200÷20
=10(厘米)
圆柱的体积:
3.14×(10÷2)2×20
=3.14×25×20
=78.5×20
=1570(cm3)
这根圆柱形木料的体积是1570 cm3。
【点睛】掌握圆柱切割的特点,明确表面积增加的是哪些面的面积,分析出圆柱的底面直径和高与切面的关系,求出圆柱的底面直径是解题的关键,最后利用圆柱的体积公式列式计算。
17. 87.92 62.8
【分析】由题意,圆柱切拼后,拼成的近似的长方体的长相当于圆柱底面圆周长的一半,可先把这个长度转化为圆的周长,再根据圆的周长公式,求得半径,列综合算式为:6.28×2÷3.14÷2=2(厘米);
然后结合高为5厘米,再套用圆柱表面积公式、体积公式来求得这个圆柱的表面积及体积。
【详解】6.28×2÷3.14÷2
=12.56÷3.14÷2
=4÷2
=2(厘米)
S圆柱=2πr2+2πrh
=2×3.14×22+2×3.14×2×5
=3.14×8+3.14×20
=25.12+62.8
=87.92(平方厘米)
V圆柱=πr2h
=3.14×22×5
=3.14×20
=62.8(立方厘米)
【点睛】关键是结合图示,确定切拼前后,圆柱体与长方体各部分元素间对应的关系。
18.√
【分析】对折1次后从中间剪开变成2+1=3(段),对折2次后从中间剪开变成2×2+1=4+1=5(段),……,以此类推,对折n次后从中间剪开变成n个2相乘,再加1段;据此解答。
【详解】根据分析:
2×2×2+1
=8+1
=9(段)
即一根绳子对折三次后沿中间剪开,一共有9段,原题说法正确。
故答案为:√
19.×
【分析】长方体的高等于圆柱的高,长方体的长等于圆柱底面周长的一半,长方体的宽等于圆柱体的底面半径,设圆柱的底面半径是r,然后表示出拼成的长方体的长与宽,高是h,再根据长方形的表面积=(长×宽+长×高+宽×高)×2,长方形体积=长×宽×高,圆柱的表面积=2πr2+2πrh,圆柱体积=πr2h ,列式表示出长方体的表面积和体积与原来圆柱的表面积和体积,由此即可进行比较选择。
【详解】设圆柱的底面半径是r,长方体的高等于圆柱的高是h,则长方形的长为πr,宽为r。
圆柱的表面积为: 2πr2+2πrh
圆柱的体积为:πr2h
长方体的表面积为:(πr2+πrh+rh)×2=2πr2+2πrh+2rh
长方体的体积为:πr2h
2πr2+2πrh+2rh> 2πr2+2πrh
πr2h=πr2h
所以这个长方体和原来的圆柱体比较表面积变大了,体积没变。题干说法错误。
故答案为:×
20.×
【分析】有两组对边分别平行且相等的四边形,叫做平行四边形。
因在拼组平行四边形时,平行四边形的两组对边平行且相等,且有公共边,所以只有两个完全一样的三角形才能拼成一个平行四边形。
【详解】如图:
4×2÷2=4(cm2)
等底等高的两个三角形面积相等,但形状不一样时,不能拼成一个平行四边形。
原题说法错误。
故答案为:×
21.√
【分析】把一个长方体切成两个相同的小长方体,因为面数目增加,所以表面积增加,但是体积没变,据此分析。
【详解】
如图,把一个长方体切成两个相同的小长方体后,表面积增加了,体积不变,说法正确。
故答案为:√
22.×
【分析】只有两个一模一样的三角形,才可以拼成一个平行四边形。据此解题。
【详解】两个面积相等的三角形,形状不一定相等,那么不一定能拼成一个平行四边形。
故答案为:×
23.66.5平方厘米
【分析】根据图示,阴影部分面积=(圆的面积+正方形的面积)-白色部分三角形面积,依据圆的面积公式=πr ,正方形面积=边长×边长,三角形的面积=底×高÷2,将数据代入公式计算即可。
【详解】(3.14×10×10×)+(6×6)-(10+6)×6÷2
=314×+36-16×6÷2
=114.5-96÷2
=114.5-48
=66.5(平方厘米)
阴影部分的面积为66.5平方厘米。
24.376.8立方厘米
【分析】通过观察图形可知,把这个圆锥沿直径剖成两半,剖面是三角形,这个三角形的底等于圆锥的底面直径,三角形的高等于圆锥的高,据此可以求出圆锥的高,然后根据圆锥的体积公式:V=πr2h,把数据代入公式解答。
【详解】120÷2=60(平方厘米)
60×2÷12
=120÷12
=10(厘米)
×3.14×(12÷2)2×10
=×3.14×36×10
=3.14×12×10
=3.14×120
=376.8(立方厘米)
答:原来圆锥的体积是376.8立方厘米。
【点睛】此题主要考查圆锥体积公式的灵活运用,关键是求出圆锥的高。
25.50.24立方厘米
【分析】按乙的切法增加了4个底面面积,用增加的面积除以4就是底面面积,根据底面积可求出圆柱底面半径,进而求出直径,按甲的切法,增加了8个长为圆柱高,宽为圆柱底面半径的长方形,据此可求出圆柱的高,切成的最大圆锥与圆柱底面积相等、高相等;等底、等高的圆锥体积是圆锥体积的,去掉的体积是圆柱体积的(1-),根据圆柱的体积计算公式V=Sh,求出圆柱的体积,乘(1-)就是减少的体积。
【详解】50.24÷4=12.56(平方厘米)
设圆柱底面半径为r厘米
3.14×r2=12.56
3.14×r2÷3.14=12.56÷3.14
r2=4
因为22=4
所以r=2
96÷8÷2
=12÷2
=6(厘米)
12.56×6×(1-)
=75.36×
=50.24(立方厘米)
答:体积减少50.24立方厘米。
【点睛】此题较难,关键是先根据乙的切法求出圆柱的底面积,进而求出底面半径,再根据甲的切法求出圆柱的高。
26.150.72
【分析】如果平行于底面截成两段,那么增加的表面积是2个底面的面积;用增加的表面积除以2,求出圆柱的底面积,进而求出底面直径;沿底面直径竖直切成两个部分,增加的表面积是2个以直径为宽,圆柱的高为长的长方形的面积,用增加的表面积除以2,再除以底面直径,即能求出圆柱的高;根据圆柱的侧面积公式S侧=πdh,求出圆柱的侧面积,再加上2个底面积,即是圆柱的表面积。
【详解】圆柱的底面积:25.12÷2=12.56(dm2)
半径的平方:12.56÷3.14=4(dm2)
4=2×2,所以圆柱的底面半径是2 dm;
底面直径:2×2=4(dm)
圆柱的高:
80÷2÷4
=40÷4
=10(dm)
圆柱的侧面积:
3.14×4×10
=12.56×10
=125.6(dm2)
圆柱的表面积:125.6+25.12=150.72(dm2)
答:这段圆柱体木料的表面积是150.72 dm2。
【点睛】明确用不同的方法切圆柱,增加的表面积是哪些面,面的形状、数量以及与原圆柱之间的联系是解题的关键。
27.1884平方厘米
【分析】正方体木块削成最大的圆柱,圆的底面直径和高等于正方体的棱长,根据圆柱的表面积公式:表面积=底面积×2+侧面积,代入数据,即可解答。
【详解】3.14×(20÷2)2×2+3.14×20×20
=3.14×100×2+62.8×20
=314×2+1256
=628+1256
=1884(平方厘米)
答:这个圆柱的表面积是1884平方厘米。
【点睛】本题考查圆柱的表面积公式的应用,关键明确正方体削成最大的圆柱,圆柱的底面直径和高等于正方体的棱长。
28.72立方厘米
【分析】先看截成两个小圆柱后,增加了两个底面圆的面积,也就是6平方厘米,则6÷2=3(平方厘米),是圆柱底面的面积;因为是求大小两个圆柱的体积相差多少,所以要把体积按7∶3的比例分配,再用减法求得这个差即可。
【详解】6÷2=3(平方厘米)
V大=60×3×
=180×
=126(立方厘米)
V小=60×3×
=180×
=54(立方厘米)
126-54=72(立方厘米)
答:这两段圆柱体积相差72立方厘米。
【点睛】将圆柱体积问题与比的应用相结合,使题意稍复杂。需要我们每一步都计算仔细,有的可能要反复计算几遍。
29.0.5
【分析】由题意可知,表面积增加了4个圆柱的底面积,根据表面积一共增加的平方米数÷增加的底面积个数=底面积,每段木料的体积=底面积×高÷3,代入数据计算即可。
【详解】1.2÷4=0.3(平方米)
0.3×5÷3=0.5(立方米)
答:每段木料的体积是0.5。
【点睛】此题主要考查立体图形的切拼问题,明确截成3段,增加的是4个底面积,求出木料的一个底面积是解题关键。
30.31400立方厘米;10594平方厘米
【详解】2米=200厘米
3.14×102×200÷2
=3.14×100×100
=31400(立方厘米)
3.14×10×2×200÷2+10×2×200+3.14×102
=6280+4000+314
=10594(平方厘米)
答:每块的体积是31400立方厘米,每块的表面积是10594平方厘米。
同课章节目录
