2025学年小升初数学专题训练:图形计算题(含解析)
文档属性
| 名称 | 2025学年小升初数学专题训练:图形计算题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 975.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 08:01:04 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2025学年小升初数学专题训练:图形计算题
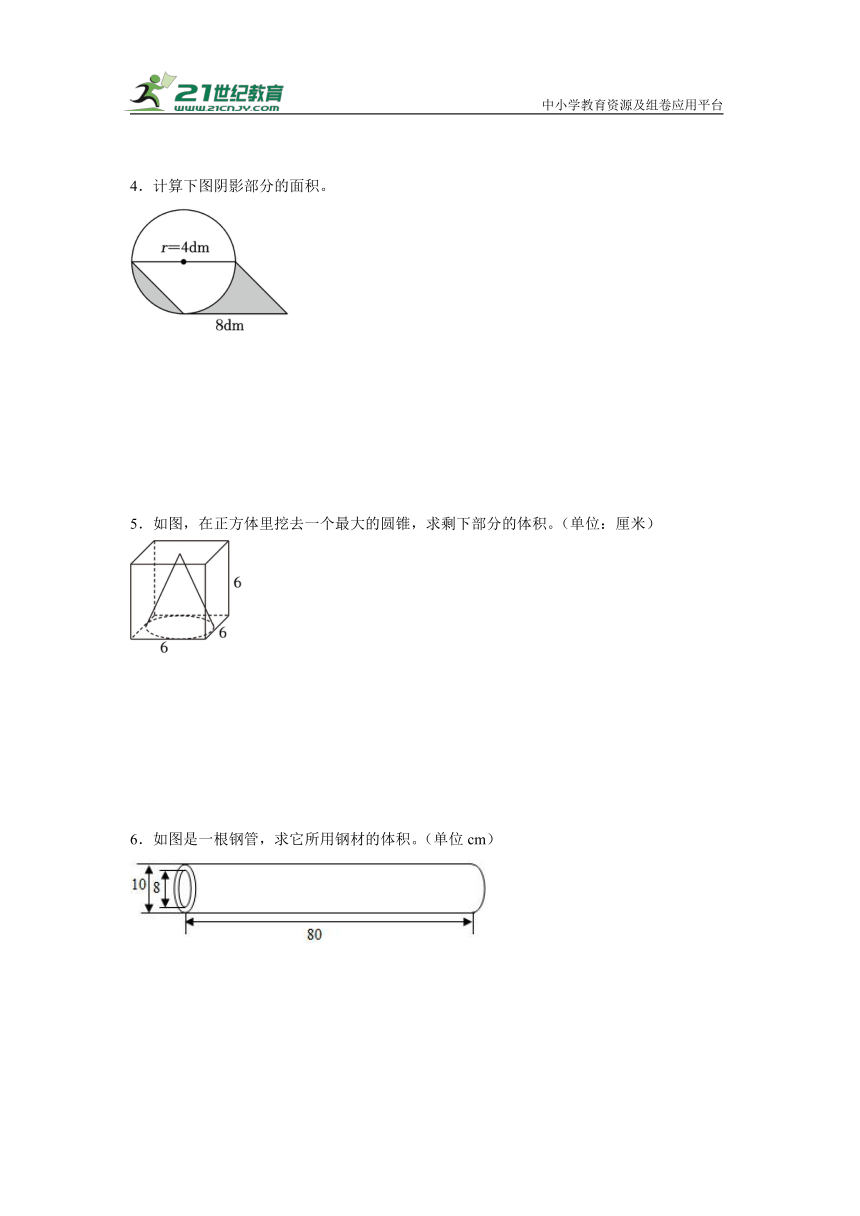
1.求阴影部分的面积。(单位:厘米)
2.求如图的体积。(单位:厘米)
3.求如图阴影部分的面积。
4.计算下图阴影部分的面积。
5.如图,在正方体里挖去一个最大的圆锥,求剩下部分的体积。(单位:厘米)
6.如图是一根钢管,求它所用钢材的体积。(单位cm)
7.如图,已知正方形边长是4dm,求阴影部分的面积。
8.求如图立体图形的体积。
9.求图形的体积(单位:厘米)(π取3.14)。
10.如图,已知平行四边形的面积是100平方厘米。求阴影部分的面积。
11.计算下面阴影部分的面积。
12.计算阴影部分的面积。(单位:厘米)
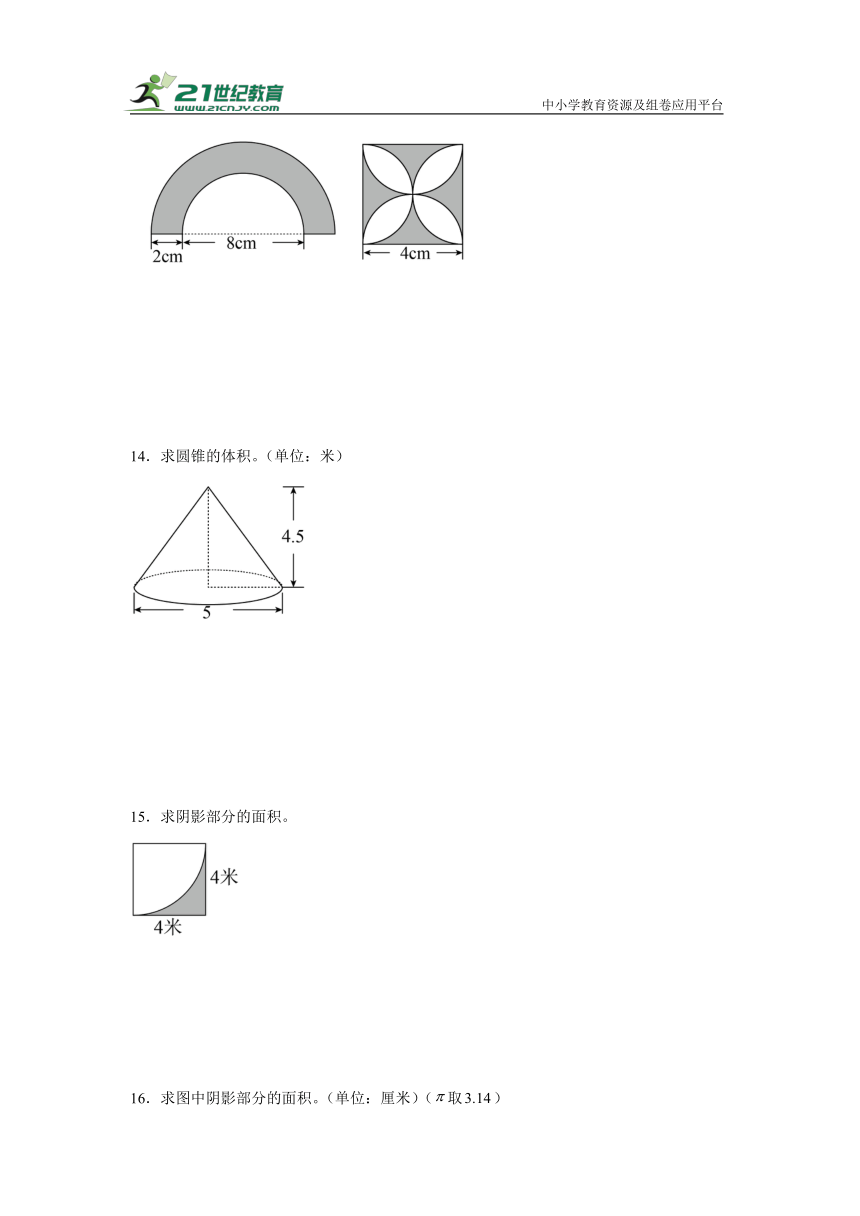
13.求下面图形中阴影部分的周长和面积。
14.求圆锥的体积。(单位:米)
15.求阴影部分的面积。
16.求图中阴影部分的面积。(单位:厘米)(取)
17.求图中阴影部分的面积。(单位:厘米)
18.如图是从圆柱中挖去一个圆锥后的剩余部分,计算它的体积。(单位:cm)
19.求下列图形的体积。
20.求下面图形阴影部分的面积。(单位:厘米)
21.计算阴影部分的面积。(单位:厘米)
22.计算如图中阴影部分的面积。(单位:厘米)
23.根据图中的数据求阴影部分的面积。(单位:米)
24.计算阴影部分的面积。
25.计算下面图形阴影部分的面积。
26.求半圆环的面积。
27.求表面积。
28.计算下面组合图形的体积。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2025学年小升初数学专题训练:图形计算题》参考答案
1.3.44平方厘米
【分析】据图可知,阴影部分的面积等于边长是4厘米的正方形的面积减去一个直径是4厘米的圆的面积,根据圆的面积=π(d÷2)2,正方形的面积=边长×边长列式计算即可。
【详解】4×4-3.14×(4÷2)2
=16-3.14×22
=16-3.14×4
=16-12.56
=3.44(平方厘米)
2.560立方厘米
【分析】依据题意结合图示可知,几何体的体积等于长10厘米、宽8厘米、高10厘米的长方体的体积减去长8厘米、宽5厘米、高6厘米的长方体的体积,由此根据长方体的体积=长×宽×高,V=abh,列式计算。
【详解】10×10×8-8×5×6
=100×8-40×6
=800-240
=560(立方厘米)
体积是560立方厘米。
3.4cm2
【分析】如图:
三角形是等腰直角三角形,所以圆内左边的阴影部分图形等于右边虚线围成的空白弧形部分,所以,阴影部分的面积也就是整个三角形面积的一半,根据三角形的面积公式:S=ah÷2,把数据代入公式解答。
【详解】4×4÷2÷2
=16÷2÷2
=8÷2
=4(cm2)
阴影部分的面积是4cm2。
4.16dm2
【分析】
如图所示连接虚线:
圆内的三角形是等腰直角三角形,所以圆内左边的阴影部分图形等于右边虚线围成的空白弧形部分,所以,阴影部分的面积也就是底为8dm,高4dm的三角形面积,根据三角形的面积公式:S=ah÷2,把数据代入公式解答。
【详解】
8×4÷2
=32÷2
=16(dm2)
阴影部分的面积是16dm2。
5.159.48立方厘米
【分析】根据图意可知,剩下的体积就是这个棱长为6厘米的正方体的体积与高为6厘米的圆锥的体积之差,由此只要求得圆锥的底面半径即可解决问题:圆锥的底面在正方体的底面上,根据正方形内最大圆的特点可知,圆锥的底面半径等于底面边长的一半,据此即可解答。
【详解】6×6×6-×3.14×(6÷2)2×6
=216-×3.14×32×6
=216-×3.14×9×6
=216-56.52
=159.48(立方厘米)
6.2260.8cm2
【分析】由图可知,钢管的体积=底面直径是10cm的圆柱的体积-底面直径是8cm的圆柱的体积,已知圆柱的体积V=πr2h,代入数据计算即可。
【详解】10÷2=5(cm)
8÷2=4(cm)
3.14×(52-42)×80
=3.14×(25-16)×80
=3.14×9×80
=28.26×80
=2260.8(cm2)
钢管的体积是2260.8cm2。
7.9.12dm2
【分析】
如图:,阴影部分面积=(半径是4dm的圆的面积的-底是4dm、高是4dm的三角形面积)×2,根据圆的面积=,三角形面积=底×高÷2,代入数据,即可解答。
【详解】(3.14×42×-4×4÷2)×2
=(3.14×16×-4×4÷2)×2
=(12.56-8)×2
=4.56×2
=9.12(dm2)
阴影部分面积是9.12dm2。
8.173.61立方分米
【分析】正方体的体积=棱长×棱长×棱长,圆柱的体积=底面积×高;用正方体的体积减去圆柱的体积即可求出立体图形的体积;据此解答。
【详解】正方体体积为:
6×6×6
=36×6
=216(dm3)
中间的圆柱体积为:
(3÷2)2×3.14×6
=1.52×3.14×6
=2.25×3.14×6
=7.065×6
=42.39(dm3)
216-42.39=173.61(dm3)
即立体图形的体积是173.61 dm3。
9.214.2立方厘米
【分析】观察图形可知,图形的体积=圆柱的体积×+长方体的体积,根据圆柱的体积公式V=πr2h,长方体的体积公式V=abh,代入数据计算即可求解。
【详解】3.14×22×10×+6×10×2
=3.14×4×10×+60×2
=94.2+120
=214.2(立方厘米)
图形的体积是214.2立方厘米。
10.14.25平方厘米
【分析】由图可知,这个平行四边形的高等于这个圆的半径、平行四边形的底等于这个圆的直径。我们可设圆的半径为r,则平行四边形的底=2r,高=r,因为平行四边形的面积是100平方厘米,根据平行四边形的面积=底×高,即2r×r=100,所以r2=100÷2=50。阴影部分的面积是圆的面积的减去等腰三角形ABO的面积,圆的面积=,三角形的面积=r×r×=r2,把r2=50代入式子中即可解答。
【详解】100÷2=50(平方厘米)
3.14×50×-50×
=39.25-25
=14.25(平方厘米)
阴影部分的面积是14.25平方厘米。
11.66.5平方厘米
【分析】根据图示,阴影部分面积=(圆的面积+正方形的面积)-白色部分三角形面积,依据圆的面积公式=πr ,正方形面积=边长×边长,三角形的面积=底×高÷2,将数据代入公式计算即可。
【详解】(3.14×10×10×)+(6×6)-(10+6)×6÷2
=314×+36-16×6÷2
=114.5-96÷2
=114.5-48
=66.5(平方厘米)
阴影部分的面积为66.5平方厘米。
12.8400平方厘米
【分析】观察题意可知,阴影部分的面积=长方形的面积-正方形的面积-空白梯形的面积,根据长方形的面积公式,用160×100即可求出长方形的面积,再根据正方形的面积公式,用40×40即可求出正方形的面积;
根据题意可知,空白梯形的高是(100-40)厘米,根据梯形的面积公式,用(160+40)×(100-40)÷2即可求出空白梯形的面积,据此用长方形的面积-正方形的面积-空白梯形的面积即可求出阴影部分的面积。
【详解】160×100=16000(平方厘米)
40×40=1600(平方厘米)
(160+40)×(100-40)÷2
=200×60÷2
=6000(平方厘米)
16000-1600-6000=8400(平方厘米)
阴影部分的面积是8400平方厘米。
13.35.4cm;31.4cm2
41.12cm;6.88cm2
【分析】如图所示,圆环的内直径是8cm,外直径是12cm,阴影部分周长等于内外圆周长的一半的和加上圆环宽度的2倍;利用圆环的面积公式求出整个圆环的面积,阴影面积等于圆环面积的一半。
如图所示,阴影部分周长是直径为4cm的圆的周长的2倍与正方形周长的和;正方形面积减去圆的面积是阴影面积的一半,求出一半阴影部分的面积乘2即可。
【详解】周长:
(cm)
第一个阴影部分的周长是35.4cm。
面积:
(cm2)
第一个阴影部分的面积是31.4cm2。
周长:
(cm)
第二个阴影部分的周长是41.12cm。
面积:
(cm2)
第二个阴影部分的面积是6.88cm2。
14.29.4375立方米
【分析】图形中圆锥的底面直径是5,高是4.5。代入圆锥的体积公式计算即可。
【详解】
=
=
=
=29.4375(立方米)
则圆锥的体积是29.4375立方米。
15.3.44平方米
【分析】观察题意可知,阴影部分的面积相当于正方形的面积减去扇形的面积,正方形的边长是4米,根据正方形的面积=边长×边长,用4×4即可求出16平方厘米,扇形的面积相当于一个半径是4米的圆面积的,根据圆面积公式:S=πr2,3.14×42×即可求出扇形的面积,然后用正方形的面积减去扇形的面积,即可求出阴影部分的面积。
【详解】4×4-3.14×42×
=4×4-3.14×16×
=16-12.56
=3.44(平方米)
阴影部分的面积是3.44平方米。
16.平方厘米
【分析】如图,通过割补可知阴影部分面积等于半径为6厘米圆面积的。根据,代入数据计算即可。
【详解】(平方厘米)
即阴影部分面积是平方厘米。
17.3.72平方厘米
【分析】通过观察可知,直角梯形的高等于圆的半径。先根据“梯形的面积=(上底+下底)×高÷2”求出梯形的面积;再根据圆的面积求出圆的面积,用圆的面积÷2求出半圆的面积;最后用梯形的面积-半圆的面积求出阴影部分的面积。
【详解】(4+6)×(4÷2)÷2-3.14×(4÷2)2÷2
=10×2÷2-3.14×22÷2
=20÷2-3.14×4÷2
=10-12.56÷2
=10-6.28
=3.72(平方厘米)
18.1884cm3
【分析】根据圆锥的体积公式:,圆柱的体积公式:,把数据代入公式求出它们的体积差即可。
【详解】
(cm3)
所以,它的体积是1884cm3。
19.125.6cm3;125.6cm3
【分析】左图:用圆柱的体积加上圆锥的体积,求出组合体的体积;
右图:将大圆柱的体积减去小圆柱的体积,求出这个几何体的体积。
【详解】3.14×22×8+×3.14×22×6
=100.48+25.12
=125.6(cm3)
3.14×(6÷2)2×8-3.14×(4÷2)2×8
=3.14×72-3.14×32
=3.14×(72-32)
=3.14×40
=125.6(cm3)
所以,这两个几何体的体积都是125.6cm3。
20.21.98平方厘米
【分析】根据环形面积公式:S=π(R2-r2),把数据代入公式解答。
【详解】3.14×(42-32)
=3.14×(16-9)
=3.14×7
=21.98(平方厘米)
21.18平方厘米;18.84平方厘米
【分析】(1)阴影部分的面积等于以小正方形的边长为上底,以大正方形的边长为下底,高为小正方形的边长的梯形面积加上大正方形面积的一半,减去以大小正方形边长的和为底,高为小正方形边长的三角形的面积,根据梯形的面积公式:S=(a+b)h÷2,正方形的面积公式:S=a2,三角形的面积公式:S=ah÷2,把数据代入公式解答。
(2)阴影部分的面积等于大半圆的面积减去中、小半圆的面积,根据圆的面积公式:S=πr2,把数据代入公式解答。
【详解】(1)(4+6)×4÷2+6×6÷2-(6+4)×4÷2
=10×4÷2+36÷2-10×4÷2
=20+18-20
=18(平方厘米 )
(2)4+6=10(厘米)
3.14×(10÷2)÷2-3.14×(4÷2)÷2-3.14×(6÷2)2÷2
=3.14×25÷2-3.14×4÷2-3.14×9÷2
=39.25-6.28-14.13
=32.97-14.13
=18.84(平方厘米)
22.343平方厘米
【分析】通过观察图形可知,阴影部分的面积等于长方形的面积减去半圆的面积,根据长方形的面积公式:S=ab,圆的面积公式:S=πr2,把数据代入公式解答。
【详解】25×20-3.14×(20÷2)2÷2
=500-3.14×102÷2
=500-3.14×100÷2
=500-157
=343(平方厘米)
23.25.12平方米
【分析】阴影部分的面积=大圆的面积-小圆的面积,根据圆的面积公式S=πr2即可解答。
【详解】阴影部分的面积为:
×3.14×82-×3.14×(8÷2)2
=×3.14×82-×3.14×42
=×3.14×64-×3.14×16
=50.24-25.12
=25.12(平方米)
24.39.25cm2
【分析】三角形内角和180°,3个扇形可以拼成一个半圆,根据半圆面积=πr2÷2,列式计算即可。
【详解】3.14×52÷2
=3.14×25÷2
=39.25(cm2)
25.6.88cm2
【分析】观察图形可知,长方形的长相当于圆的直径,宽相当于圆的半径,阴影部分的面积=长方形的面积-圆的面积的一半,根据圆的面积公式:S=πr2,长方形的面积=长×宽,据此解答即可。
【详解】8×(8÷2)-3.14×(8÷2)2÷2
=8×4-3.14×16÷2
=32-25.12
=6.88(cm2)
26.62.8m2
【分析】先求大圆和小圆的半径,再利用圆的面积公式:S=πr2计算即可。
【详解】18÷2=9(m)
[3.14×(9+2)2-3.14×92]÷2
=[3.14×121-3.14×81]÷2
=[379.94-254.34]÷2
=125.6÷2
=62.8(m2)
27.282.6
【分析】组合图形的表面积等于两个圆柱表面积之和减去重叠面面积,重叠部分是小圆柱的两个底面面积,也就是说,组合图形的表面积相当于大圆柱的表面积+小圆柱的侧面积。
【详解】3.14×(8÷2)2×2+3.14×8×5
=3.14×16×2+125.6
=100.48+125.6
=226.08
3.14×6×3=56.52
226.08+56.52=282.6
28.65.94cm3
【分析】观察图形可知,该组合图形的体积=圆柱的体积+圆锥的体积,根据圆柱的体积公式:V=πr2h,圆锥的体积公式:V=πr2h,据此进行计算即可。
【详解】3.14×(2÷2)2×9+×3.14×(4÷2)2×9
=3.14×1×9+×3.14×4×9
=28.26+37.68
=65.94(cm3)
中小学教育资源及组卷应用平台
2025学年小升初数学专题训练:图形计算题
1.求阴影部分的面积。(单位:厘米)
2.求如图的体积。(单位:厘米)
3.求如图阴影部分的面积。
4.计算下图阴影部分的面积。
5.如图,在正方体里挖去一个最大的圆锥,求剩下部分的体积。(单位:厘米)
6.如图是一根钢管,求它所用钢材的体积。(单位cm)
7.如图,已知正方形边长是4dm,求阴影部分的面积。
8.求如图立体图形的体积。
9.求图形的体积(单位:厘米)(π取3.14)。
10.如图,已知平行四边形的面积是100平方厘米。求阴影部分的面积。
11.计算下面阴影部分的面积。
12.计算阴影部分的面积。(单位:厘米)
13.求下面图形中阴影部分的周长和面积。
14.求圆锥的体积。(单位:米)
15.求阴影部分的面积。
16.求图中阴影部分的面积。(单位:厘米)(取)
17.求图中阴影部分的面积。(单位:厘米)
18.如图是从圆柱中挖去一个圆锥后的剩余部分,计算它的体积。(单位:cm)
19.求下列图形的体积。
20.求下面图形阴影部分的面积。(单位:厘米)
21.计算阴影部分的面积。(单位:厘米)
22.计算如图中阴影部分的面积。(单位:厘米)
23.根据图中的数据求阴影部分的面积。(单位:米)
24.计算阴影部分的面积。
25.计算下面图形阴影部分的面积。
26.求半圆环的面积。
27.求表面积。
28.计算下面组合图形的体积。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2025学年小升初数学专题训练:图形计算题》参考答案
1.3.44平方厘米
【分析】据图可知,阴影部分的面积等于边长是4厘米的正方形的面积减去一个直径是4厘米的圆的面积,根据圆的面积=π(d÷2)2,正方形的面积=边长×边长列式计算即可。
【详解】4×4-3.14×(4÷2)2
=16-3.14×22
=16-3.14×4
=16-12.56
=3.44(平方厘米)
2.560立方厘米
【分析】依据题意结合图示可知,几何体的体积等于长10厘米、宽8厘米、高10厘米的长方体的体积减去长8厘米、宽5厘米、高6厘米的长方体的体积,由此根据长方体的体积=长×宽×高,V=abh,列式计算。
【详解】10×10×8-8×5×6
=100×8-40×6
=800-240
=560(立方厘米)
体积是560立方厘米。
3.4cm2
【分析】如图:
三角形是等腰直角三角形,所以圆内左边的阴影部分图形等于右边虚线围成的空白弧形部分,所以,阴影部分的面积也就是整个三角形面积的一半,根据三角形的面积公式:S=ah÷2,把数据代入公式解答。
【详解】4×4÷2÷2
=16÷2÷2
=8÷2
=4(cm2)
阴影部分的面积是4cm2。
4.16dm2
【分析】
如图所示连接虚线:
圆内的三角形是等腰直角三角形,所以圆内左边的阴影部分图形等于右边虚线围成的空白弧形部分,所以,阴影部分的面积也就是底为8dm,高4dm的三角形面积,根据三角形的面积公式:S=ah÷2,把数据代入公式解答。
【详解】
8×4÷2
=32÷2
=16(dm2)
阴影部分的面积是16dm2。
5.159.48立方厘米
【分析】根据图意可知,剩下的体积就是这个棱长为6厘米的正方体的体积与高为6厘米的圆锥的体积之差,由此只要求得圆锥的底面半径即可解决问题:圆锥的底面在正方体的底面上,根据正方形内最大圆的特点可知,圆锥的底面半径等于底面边长的一半,据此即可解答。
【详解】6×6×6-×3.14×(6÷2)2×6
=216-×3.14×32×6
=216-×3.14×9×6
=216-56.52
=159.48(立方厘米)
6.2260.8cm2
【分析】由图可知,钢管的体积=底面直径是10cm的圆柱的体积-底面直径是8cm的圆柱的体积,已知圆柱的体积V=πr2h,代入数据计算即可。
【详解】10÷2=5(cm)
8÷2=4(cm)
3.14×(52-42)×80
=3.14×(25-16)×80
=3.14×9×80
=28.26×80
=2260.8(cm2)
钢管的体积是2260.8cm2。
7.9.12dm2
【分析】
如图:,阴影部分面积=(半径是4dm的圆的面积的-底是4dm、高是4dm的三角形面积)×2,根据圆的面积=,三角形面积=底×高÷2,代入数据,即可解答。
【详解】(3.14×42×-4×4÷2)×2
=(3.14×16×-4×4÷2)×2
=(12.56-8)×2
=4.56×2
=9.12(dm2)
阴影部分面积是9.12dm2。
8.173.61立方分米
【分析】正方体的体积=棱长×棱长×棱长,圆柱的体积=底面积×高;用正方体的体积减去圆柱的体积即可求出立体图形的体积;据此解答。
【详解】正方体体积为:
6×6×6
=36×6
=216(dm3)
中间的圆柱体积为:
(3÷2)2×3.14×6
=1.52×3.14×6
=2.25×3.14×6
=7.065×6
=42.39(dm3)
216-42.39=173.61(dm3)
即立体图形的体积是173.61 dm3。
9.214.2立方厘米
【分析】观察图形可知,图形的体积=圆柱的体积×+长方体的体积,根据圆柱的体积公式V=πr2h,长方体的体积公式V=abh,代入数据计算即可求解。
【详解】3.14×22×10×+6×10×2
=3.14×4×10×+60×2
=94.2+120
=214.2(立方厘米)
图形的体积是214.2立方厘米。
10.14.25平方厘米
【分析】由图可知,这个平行四边形的高等于这个圆的半径、平行四边形的底等于这个圆的直径。我们可设圆的半径为r,则平行四边形的底=2r,高=r,因为平行四边形的面积是100平方厘米,根据平行四边形的面积=底×高,即2r×r=100,所以r2=100÷2=50。阴影部分的面积是圆的面积的减去等腰三角形ABO的面积,圆的面积=,三角形的面积=r×r×=r2,把r2=50代入式子中即可解答。
【详解】100÷2=50(平方厘米)
3.14×50×-50×
=39.25-25
=14.25(平方厘米)
阴影部分的面积是14.25平方厘米。
11.66.5平方厘米
【分析】根据图示,阴影部分面积=(圆的面积+正方形的面积)-白色部分三角形面积,依据圆的面积公式=πr ,正方形面积=边长×边长,三角形的面积=底×高÷2,将数据代入公式计算即可。
【详解】(3.14×10×10×)+(6×6)-(10+6)×6÷2
=314×+36-16×6÷2
=114.5-96÷2
=114.5-48
=66.5(平方厘米)
阴影部分的面积为66.5平方厘米。
12.8400平方厘米
【分析】观察题意可知,阴影部分的面积=长方形的面积-正方形的面积-空白梯形的面积,根据长方形的面积公式,用160×100即可求出长方形的面积,再根据正方形的面积公式,用40×40即可求出正方形的面积;
根据题意可知,空白梯形的高是(100-40)厘米,根据梯形的面积公式,用(160+40)×(100-40)÷2即可求出空白梯形的面积,据此用长方形的面积-正方形的面积-空白梯形的面积即可求出阴影部分的面积。
【详解】160×100=16000(平方厘米)
40×40=1600(平方厘米)
(160+40)×(100-40)÷2
=200×60÷2
=6000(平方厘米)
16000-1600-6000=8400(平方厘米)
阴影部分的面积是8400平方厘米。
13.35.4cm;31.4cm2
41.12cm;6.88cm2
【分析】如图所示,圆环的内直径是8cm,外直径是12cm,阴影部分周长等于内外圆周长的一半的和加上圆环宽度的2倍;利用圆环的面积公式求出整个圆环的面积,阴影面积等于圆环面积的一半。
如图所示,阴影部分周长是直径为4cm的圆的周长的2倍与正方形周长的和;正方形面积减去圆的面积是阴影面积的一半,求出一半阴影部分的面积乘2即可。
【详解】周长:
(cm)
第一个阴影部分的周长是35.4cm。
面积:
(cm2)
第一个阴影部分的面积是31.4cm2。
周长:
(cm)
第二个阴影部分的周长是41.12cm。
面积:
(cm2)
第二个阴影部分的面积是6.88cm2。
14.29.4375立方米
【分析】图形中圆锥的底面直径是5,高是4.5。代入圆锥的体积公式计算即可。
【详解】
=
=
=
=29.4375(立方米)
则圆锥的体积是29.4375立方米。
15.3.44平方米
【分析】观察题意可知,阴影部分的面积相当于正方形的面积减去扇形的面积,正方形的边长是4米,根据正方形的面积=边长×边长,用4×4即可求出16平方厘米,扇形的面积相当于一个半径是4米的圆面积的,根据圆面积公式:S=πr2,3.14×42×即可求出扇形的面积,然后用正方形的面积减去扇形的面积,即可求出阴影部分的面积。
【详解】4×4-3.14×42×
=4×4-3.14×16×
=16-12.56
=3.44(平方米)
阴影部分的面积是3.44平方米。
16.平方厘米
【分析】如图,通过割补可知阴影部分面积等于半径为6厘米圆面积的。根据,代入数据计算即可。
【详解】(平方厘米)
即阴影部分面积是平方厘米。
17.3.72平方厘米
【分析】通过观察可知,直角梯形的高等于圆的半径。先根据“梯形的面积=(上底+下底)×高÷2”求出梯形的面积;再根据圆的面积求出圆的面积,用圆的面积÷2求出半圆的面积;最后用梯形的面积-半圆的面积求出阴影部分的面积。
【详解】(4+6)×(4÷2)÷2-3.14×(4÷2)2÷2
=10×2÷2-3.14×22÷2
=20÷2-3.14×4÷2
=10-12.56÷2
=10-6.28
=3.72(平方厘米)
18.1884cm3
【分析】根据圆锥的体积公式:,圆柱的体积公式:,把数据代入公式求出它们的体积差即可。
【详解】
(cm3)
所以,它的体积是1884cm3。
19.125.6cm3;125.6cm3
【分析】左图:用圆柱的体积加上圆锥的体积,求出组合体的体积;
右图:将大圆柱的体积减去小圆柱的体积,求出这个几何体的体积。
【详解】3.14×22×8+×3.14×22×6
=100.48+25.12
=125.6(cm3)
3.14×(6÷2)2×8-3.14×(4÷2)2×8
=3.14×72-3.14×32
=3.14×(72-32)
=3.14×40
=125.6(cm3)
所以,这两个几何体的体积都是125.6cm3。
20.21.98平方厘米
【分析】根据环形面积公式:S=π(R2-r2),把数据代入公式解答。
【详解】3.14×(42-32)
=3.14×(16-9)
=3.14×7
=21.98(平方厘米)
21.18平方厘米;18.84平方厘米
【分析】(1)阴影部分的面积等于以小正方形的边长为上底,以大正方形的边长为下底,高为小正方形的边长的梯形面积加上大正方形面积的一半,减去以大小正方形边长的和为底,高为小正方形边长的三角形的面积,根据梯形的面积公式:S=(a+b)h÷2,正方形的面积公式:S=a2,三角形的面积公式:S=ah÷2,把数据代入公式解答。
(2)阴影部分的面积等于大半圆的面积减去中、小半圆的面积,根据圆的面积公式:S=πr2,把数据代入公式解答。
【详解】(1)(4+6)×4÷2+6×6÷2-(6+4)×4÷2
=10×4÷2+36÷2-10×4÷2
=20+18-20
=18(平方厘米 )
(2)4+6=10(厘米)
3.14×(10÷2)÷2-3.14×(4÷2)÷2-3.14×(6÷2)2÷2
=3.14×25÷2-3.14×4÷2-3.14×9÷2
=39.25-6.28-14.13
=32.97-14.13
=18.84(平方厘米)
22.343平方厘米
【分析】通过观察图形可知,阴影部分的面积等于长方形的面积减去半圆的面积,根据长方形的面积公式:S=ab,圆的面积公式:S=πr2,把数据代入公式解答。
【详解】25×20-3.14×(20÷2)2÷2
=500-3.14×102÷2
=500-3.14×100÷2
=500-157
=343(平方厘米)
23.25.12平方米
【分析】阴影部分的面积=大圆的面积-小圆的面积,根据圆的面积公式S=πr2即可解答。
【详解】阴影部分的面积为:
×3.14×82-×3.14×(8÷2)2
=×3.14×82-×3.14×42
=×3.14×64-×3.14×16
=50.24-25.12
=25.12(平方米)
24.39.25cm2
【分析】三角形内角和180°,3个扇形可以拼成一个半圆,根据半圆面积=πr2÷2,列式计算即可。
【详解】3.14×52÷2
=3.14×25÷2
=39.25(cm2)
25.6.88cm2
【分析】观察图形可知,长方形的长相当于圆的直径,宽相当于圆的半径,阴影部分的面积=长方形的面积-圆的面积的一半,根据圆的面积公式:S=πr2,长方形的面积=长×宽,据此解答即可。
【详解】8×(8÷2)-3.14×(8÷2)2÷2
=8×4-3.14×16÷2
=32-25.12
=6.88(cm2)
26.62.8m2
【分析】先求大圆和小圆的半径,再利用圆的面积公式:S=πr2计算即可。
【详解】18÷2=9(m)
[3.14×(9+2)2-3.14×92]÷2
=[3.14×121-3.14×81]÷2
=[379.94-254.34]÷2
=125.6÷2
=62.8(m2)
27.282.6
【分析】组合图形的表面积等于两个圆柱表面积之和减去重叠面面积,重叠部分是小圆柱的两个底面面积,也就是说,组合图形的表面积相当于大圆柱的表面积+小圆柱的侧面积。
【详解】3.14×(8÷2)2×2+3.14×8×5
=3.14×16×2+125.6
=100.48+125.6
=226.08
3.14×6×3=56.52
226.08+56.52=282.6
28.65.94cm3
【分析】观察图形可知,该组合图形的体积=圆柱的体积+圆锥的体积,根据圆柱的体积公式:V=πr2h,圆锥的体积公式:V=πr2h,据此进行计算即可。
【详解】3.14×(2÷2)2×9+×3.14×(4÷2)2×9
=3.14×1×9+×3.14×4×9
=28.26+37.68
=65.94(cm3)
同课章节目录
