2024-2025学年九年级(下)期中数学试卷(含解析)
文档属性
| 名称 | 2024-2025学年九年级(下)期中数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 195.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 16:22:05 | ||
图片预览



文档简介
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
2024-2025学年九年级(下)期中数学试卷
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的平方根是( )
A. B. C. D.
2.汉字,是中华民族文化的化石,汉字之美,美在形体、美在风骨、美在精髓、美在真情以下汉字中,可近似看作轴对称字形的个数有个( )
A. B. C. D.
3.据报道,年春节假期兰州市接待游客约万人次,旅游收入同比增长近三成将用科学记数法表示应为( )
A. B. C. D.
4.若,则的余角等于( )
A. B. C. D.
5.若为正整数,要使有意义,则满足条件的的值可能是( )
A. B. C. D.
6.每一个内角都是的正多边形是( )
A. 正四边形 B. 正六边形 C. 正七边形 D. 正八边形
7.若关于的一元二次方程有两个相等的实数根,则实数的值为( )
A. B. C. D.
8.现有三张背面花色完全一样的扑克牌,它们的正面分别写有“”兰、州、好”,若将这三张扑克牌背面朝上,洗匀后从中随机抽取一张,则正好抽到“好”字的概率为( )
A. B. C. D.
9.某商店售货时,在进价基础上加一定利润,其数量与售价如表所示,则售价与数量的函数关系式为( )
数量件
售价元
A. B. C. D.
10.为扎实推进“五育”并举工作,加强劳动教育,东营市某中学针对七年级学生开设了“跟我学面点”烹饪课程课程开设后学校花费元购进第一批面粉,用完后学校又花费元购进了第二批面粉,第二批面粉的采购量是第一批采购量的倍,但每千克面粉价格提高了元设第一批面粉采购量为千克,依题意所列方程正确的是( )
A. B.
C. D.
11.如图,为半圆的直径,平分,交半圆于点,,交于点,则的度数是( )
A. B. C. D.
12.如图所示,是菱形的对角线上一动点,过点作垂直于的直线交菱形的边于、两点,设,,,的面积为,则关于的函数图象的大致形状是( )
A. B.
C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.因式分解:______.
14.如图,在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点的对应点的坐标是 .
15.如图,在 中,,的半径为,则图中阴影部分的面积是______.
16.从甲地到乙地有,,三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了个班次的公交车,收集了这些班次的公交车用时单位:分钟的数据,统计如下:
早高峰期间,乘坐 填“”,“”或“”线路上的公交车,从甲地到乙地“用时不超过分钟”的可能性最大.
三、解答题:本题共9小题,共48分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:.
18.本小题分
解不等式组:.
19.本小题分
先化简,再求值:,其中.
20.本小题分
已知:如图,为锐角三角形,,.
求作:线段,使得点在直线上,且.
作法:以点为圆心,长为半径画圆,交直线于,两点;
连接.
线段就是所求作的线段.
使用直尺和圆规,依作法补全图形保留作图痕迹;
完成下面的证明.
证明:,
______.
,
点在上.
又点,都在上,
______填推理的依据.
.
21.本小题分
某年级共有名学生.为了解该年级学生,两门课程的学习情况,从中随机抽取名学生进行测试,获得了他们的成绩百分制,并对数据成绩进行整理、描述和分析.下面给出了部分信息.
课程成绩的频数分布直方图如上图所示数据分成组:,,,,,;
课程成绩在这一组的是:,,,,,,,,,,,,,;
,两门课程成绩的平均数、中位数、众数如下:
课程 平均数 中位数 众数
根据以上信息,回答下列问题:
写出表中的值;
在此次测试中,某学生的课程成绩为分,课程成绩为分,这名学生成绩排名更靠前的课程是______填““或““,理由是______;
假设该年级学生都参加此次测试,估计课程成绩超过分的人数.
22.本小题分
如图,已知、是一次函数的图象与反比例函数的图象的两个交点.
求此反比例函数和一次函数的解析式;
求的面积.
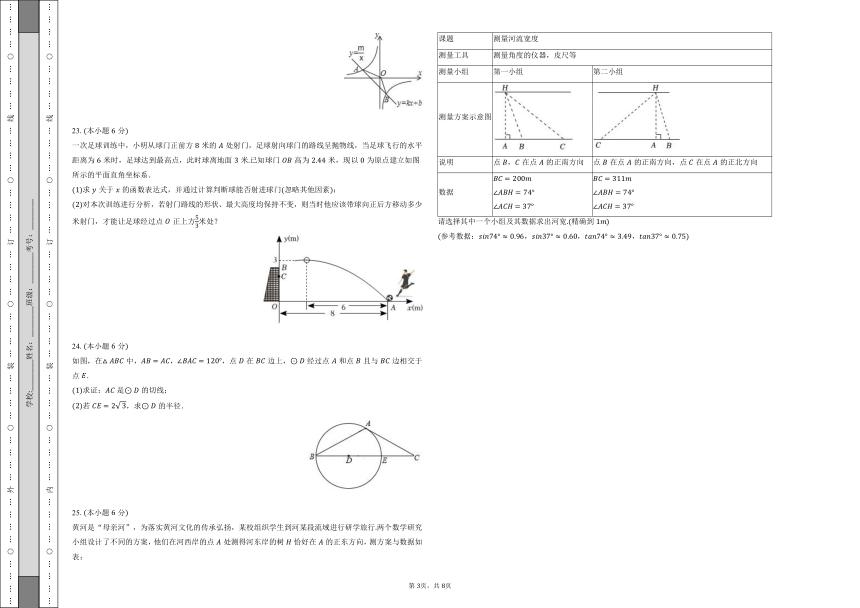
23.本小题分
一次足球训练中,小明从球门正前方米的处射门,足球射向球门的路线呈抛物线,当足球飞行的水平距离为米时,足球达到最高点,此时球离地面米已知球门高为米,现以为原点建立如图所示的平面直角坐标系.
求关于的函数表达式,并通过计算判断球能否射进球门忽略其他因素;
对本次训练进行分析,若射门路线的形状、最大高度均保持不变,则当时他应该带球向正后方移动多少米射门,才能让足球经过点正上方米处?
24.本小题分
如图,在中,,,点在边上,经过点和点且与边相交于点.
求证:是的切线;
若,求的半径.
25.本小题分
黄河是“母亲河”,为落实黄河文化的传承弘扬,某校组织学生到河某段流域进行研学旅行两个数学研究小组设计了不同的方案,他们在河西岸的点处测得河东岸的树恰好在的正东方向,测方案与数据如表:
课题 测量河流宽度
测量工具 测量角度的仪器,皮尺等
测量小组 第一小组 第二小组
测量方案示意图
说明 点,在点的正南方向 点在点的正南方向,点在点的正北方向
数据
请选择其中一个小组及其数据求出河宽精确到
参考数据:,,,
答案和解析
1.【答案】
【解析】【解答】
解:的平方根是.
故选:.
【分析】
根据平方根的定义和求法,可得的平方根是:,据此解答即可.
此题主要考查了平方根的性质和应用,要熟练掌握,解答此题的关键是要明确:一个正数有两个平方根,这两个平方根互为相反数,零的平方根是零,负数没有平方根.
2.【答案】
【解析】解:其中可近似看作轴对称字形的汉字有:黄、美,共个.
故选:.
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,由此即可判断.
本题考查轴对称图形,关键是掌握轴对称图形的定义.
3.【答案】
【解析】解:.
故选:.
科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正数;当原数的绝对值时,是负数.
此题考查科学记数法的表示方法.科学记数法的表示形式为的形式,其中,为整数,表示时关键要正确确定的值以及的值.
4.【答案】
【解析】解:根据题意得,.
故选:.
根据余角的和等于,列式计算即可求解.
本题考查了余角和补角,解题的关键是掌握如果两个角的和等于直角,就说这两个角互为余角.
5.【答案】
【解析】解:有意义,
,
解得,
满足条件.
故选:.
利用被开方数为非负数得到,再解不等式得到的取值范围,然后利用的取值范围对各选项进行判断.
本题考查了二次根式有意义的条件:根据二次根式中的被开方数是非负数来确定二次根式被开方数中字母的取值范围.
6.【答案】
【解析】解:因为正多边形的每一个内角都是,
所以正多边形的每一个外角都是,
所以正多边形的边数是,即这个正多边形是正八边形.
故选:.
先根据邻补角性质得出:正多边形的每一个外角都是,再根据多边形的外角和等于进行计算,即可得出答案.
本题考查了多边形的外角和,邻补角性质,掌握多边形的外角和,邻补角性质是解题的关键.
7.【答案】
【解析】解:根据题意得,
解得.
故选:.
根据根的判别式的意义得到,然后解一次方程即可.
本题考查了根的判别式:一元二次方程的根与有如下关系:当时,方程有两个不相等的实数根;当时,方程有两个相等的实数根;当时,方程无实数根.
8.【答案】
【解析】解:现有三张背面花色完全一样的扑克牌,它们的正面分别写有“”兰、州、好”,
洗匀后从中随机抽取一张,则正好抽到“好”字的概率为,
故选:.
直接由概率公式求解即可.
本题考查了概率公式:概率所求情况数与总情况数之比.熟记概率公式是解题的关键.
9.【答案】
【解析】解:由题意得,.
故选:.
依据题意,根据数量与售价如下表所示所提供的信息,列出售价与数量的函数关系式.
本题主要考查了函数关系式.关键找到函数和自变量的关系,用待定系数法求函数的解析式.
10.【答案】
【解析】解:由题意得:.
故选:.
根据第二批面粉比第一批面粉的每千克面粉价格提高了元列方程即可.
本题考查由实际问题抽象出分式方程,解答本题的关键是明确题意,找出等量关系,列出相应的分式方程.
11.【答案】
【解析】解:,
,
平分,
,
,
,
.
故选:.
根据,得出,再根据平分,得出,再根据同弧所对的圆周角和圆心角的关系得出,再根据三角形内角和定理求得的度数,最后根据对顶角相等即可得出答案.
此题主要考查了圆周角定理,用到的知识点是圆周角定理,三角形的内角和,对顶角相等,掌握相关知识是解题关键.
12.【答案】
【解析】解:当时,如图,
在菱形中,,,,且;
,;
∽,
,
即,;
,
,函数图象开口向上;
当,如图,
同理证得,∽,
,
即,;
,
;
,函数图象开口向下;
综上,答案C的图象大致符合;
故选:.
的面积,通过题干已知条件,用分别表示出、,根据所得的函数,利用其图象,可分两种情况解答:;;
本题考查了二次函数的图象,考查了学生从图象中读取信息的数形结合能力,体现了分类讨论的思想.
13.【答案】
【解析】【分析】
本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.
先提取公因式,再对余下的多项式利用完全平方公式继续分解.
【解答】
解:
.
故答案为.
14.【答案】或
【解析】【分析】
把点的横纵坐标分别乘以或即可得到点的坐标.
本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为,那么位似图形中对应点的坐标的比等于或.
【解答】
解:位似中心为原点,相似比为,
点的对应点的坐标为或,即或.
故答案为或.
15.【答案】
【解析】【分析】
此题主要考查了平行四边形的性质以及扇形面积求法,正确记忆扇形面积公式是解题关键.
直接利用平行四边形的性质得出的度数,再利用扇形面积求法得出答案.
【解答】
解:在 中,,
,
的半径为,
图中阴影部分的面积是:.
故答案为:.
16.【答案】
【解析】【分析】
本题主要考查可能性的大小,难度不大.
分别计算出,,三个线路的公交车用时不超过分钟的可能性大小即可得.
【解答】
解:线路公交车用时不超过分钟的可能性为,
线路公交车用时不超过分钟的可能性为,
线路公交车用时不超过分钟的可能性为,
,
线路上公交车用时不超过分钟的可能性最大.
故答案为:.
17.【答案】
【解析】解:原式
.
根据实数的运算法则进行计算即可.
本题考查了实数的运算,解题的关键是掌握运算法则.
18.【答案】.
【解析】解:解不等式得,,
解不等式得,,
所以不等式组的解集为:.
根据解一元一次不等式组的步骤,对所给不等式组进行求解即可.
本题主要考查了解一元一次不等式组,熟知解一元一次不等式组的步骤是解题的关键.
19.【答案】,.
【解析】解:
,
当时,原式.
根据完全平方公式、平方差公式、单项式乘多项式的运算法则、合并同类项把原式化简,把的值代入计算得到答案.
本题考查的是整式的混合运算化简求值,掌握整式的混合运算法则是解题的关键.
20.【答案】解:如图,即为补全的图形;
;同弧所对的圆周角等于圆心角的一半.
【解析】【分析】
本题考查了作图、等腰三角形的性质、圆周角定理,解决本题的关键是综合运用以上知识.
根据作法即可补全图形;
根据等腰三角形的性质和同弧所对圆周角等于圆心角的一半即可完成下面的证明.
【解答】
解:见答案;
证明:,
.
,
点在上.
又点,都在上,
同弧所对的圆周角等于圆心角的一半,
.
故答案为:,同弧所对的圆周角等于圆心角的一半.
21.【答案】解:课程总人数为,
中位数为第、个数据的平均数,
中位数在这一组,
第、个数为、,
课程的中位数为,即;
;该学生的成绩小于课程的中位数,而大于课程的中位数;
估计课程成绩超过分的人数为人.
答:估计课程成绩超过分的人数为人.
【解析】本题主要考查频数分布直方图、中位数、用样本估计总体等,解题的关键是根据直方图得出解题所需数据及中位数的定义和意义、样本估计总体思想的运用.
先确定课程的中位数落在第小组,再由此分组具体数据得出第、个数据的平均数即可;
根据两个课程的中位数定义解答可得;
用总人数乘以样本中超过分的人数所占比例可得.
22.【答案】解:把代入得,则.
则反比例函数的解析式是;
把代入得,
则的坐标是.
根据题意得:,
解得,
则一次函数的解析式是;
设与轴的交点是,则的坐标是.
则,
,,
则.
【解析】把的坐标代入反比例函数解析式求得的值,从而求得反比例函数解析式,然后把的坐标代入可求得的值,再利用待定系数法求得一次函数的解析式;
求得与轴的交点,然后根据三角形的面积公式求解;
本题考查待定系数法求函数的解析式以及三角形面积的求法,熟练掌握利用点的坐标求函数解析式的方法是关键.
23.【答案】抛物线的函数表达式为;球不能射进球门;
当时他应该带球向正后方移动米射门,才能让足球经过点正上方米处.
【解析】解:根据题意得,抛物线的顶点坐标为,
设抛物线 ,
把点代入得:,
.
抛物线的函数表达式为.
又当时,,
,
球不能射进球门.
设应该带球向正后方移动米,
则移动后的抛物线为,
把点代入得:,
舍去或.
当时球员应该带球向正后方移动米射门,才能让足球经过点正上方米处.
依据题意,用待定系数法求出解析式,然后由时,求出的值可以判断得解;
依据题意,移动后的抛物线为,把点代入得:,即可判断得解.
本题主要考查二次函数的应用,解题的关键是读懂题意,把实际问题转化为数学问题解决.
24.【答案】证明:连接,
,,
,
,
,
,
,即,
是的半径,
是的切线;
解:连接,
,,
是等边三角形,
,,
,
,
,
,
故的半径为.
【解析】本题考查了切线的判定,等腰三角形的性质,等边三角形的判定和性质,正确的作出辅助线是解题的关键.
连接,根据等腰三角形的性质得到,,求得,根据三角形的内角和得到,于是得到是的切线;
连接,推出是等边三角形,得到,,求得,得到,于是得到结论.
25.【答案】河宽约为.
【解析】若选择方案一:
是的一个外角,,,
,
,
,
在中,,
河宽约为;
若选择方案二:
设,
在中,,
,
在中,,
,
,
,
解得:,
,
河宽约为.
若选择方案一:先根据三角形的外角性质可得,从而可得,然后在中,利用锐角三角函数的定义进行计算即可解答;若选择方案二:设,先在中,利用锐角三角函数的定义求出的长,然后在中,利用锐角三角函数的定义求出的长,最后根据,列出关于的方程进行计算,即可解答.
本题考查了解直角三角形的应用,熟练掌握锐角三角函数的定义是解题的关键.
第2页,共2页
第1页,共1页
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
2024-2025学年九年级(下)期中数学试卷
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的平方根是( )
A. B. C. D.
2.汉字,是中华民族文化的化石,汉字之美,美在形体、美在风骨、美在精髓、美在真情以下汉字中,可近似看作轴对称字形的个数有个( )
A. B. C. D.
3.据报道,年春节假期兰州市接待游客约万人次,旅游收入同比增长近三成将用科学记数法表示应为( )
A. B. C. D.
4.若,则的余角等于( )
A. B. C. D.
5.若为正整数,要使有意义,则满足条件的的值可能是( )
A. B. C. D.
6.每一个内角都是的正多边形是( )
A. 正四边形 B. 正六边形 C. 正七边形 D. 正八边形
7.若关于的一元二次方程有两个相等的实数根,则实数的值为( )
A. B. C. D.
8.现有三张背面花色完全一样的扑克牌,它们的正面分别写有“”兰、州、好”,若将这三张扑克牌背面朝上,洗匀后从中随机抽取一张,则正好抽到“好”字的概率为( )
A. B. C. D.
9.某商店售货时,在进价基础上加一定利润,其数量与售价如表所示,则售价与数量的函数关系式为( )
数量件
售价元
A. B. C. D.
10.为扎实推进“五育”并举工作,加强劳动教育,东营市某中学针对七年级学生开设了“跟我学面点”烹饪课程课程开设后学校花费元购进第一批面粉,用完后学校又花费元购进了第二批面粉,第二批面粉的采购量是第一批采购量的倍,但每千克面粉价格提高了元设第一批面粉采购量为千克,依题意所列方程正确的是( )
A. B.
C. D.
11.如图,为半圆的直径,平分,交半圆于点,,交于点,则的度数是( )
A. B. C. D.
12.如图所示,是菱形的对角线上一动点,过点作垂直于的直线交菱形的边于、两点,设,,,的面积为,则关于的函数图象的大致形状是( )
A. B.
C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.因式分解:______.
14.如图,在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点的对应点的坐标是 .
15.如图,在 中,,的半径为,则图中阴影部分的面积是______.
16.从甲地到乙地有,,三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了个班次的公交车,收集了这些班次的公交车用时单位:分钟的数据,统计如下:
早高峰期间,乘坐 填“”,“”或“”线路上的公交车,从甲地到乙地“用时不超过分钟”的可能性最大.
三、解答题:本题共9小题,共48分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:.
18.本小题分
解不等式组:.
19.本小题分
先化简,再求值:,其中.
20.本小题分
已知:如图,为锐角三角形,,.
求作:线段,使得点在直线上,且.
作法:以点为圆心,长为半径画圆,交直线于,两点;
连接.
线段就是所求作的线段.
使用直尺和圆规,依作法补全图形保留作图痕迹;
完成下面的证明.
证明:,
______.
,
点在上.
又点,都在上,
______填推理的依据.
.
21.本小题分
某年级共有名学生.为了解该年级学生,两门课程的学习情况,从中随机抽取名学生进行测试,获得了他们的成绩百分制,并对数据成绩进行整理、描述和分析.下面给出了部分信息.
课程成绩的频数分布直方图如上图所示数据分成组:,,,,,;
课程成绩在这一组的是:,,,,,,,,,,,,,;
,两门课程成绩的平均数、中位数、众数如下:
课程 平均数 中位数 众数
根据以上信息,回答下列问题:
写出表中的值;
在此次测试中,某学生的课程成绩为分,课程成绩为分,这名学生成绩排名更靠前的课程是______填““或““,理由是______;
假设该年级学生都参加此次测试,估计课程成绩超过分的人数.
22.本小题分
如图,已知、是一次函数的图象与反比例函数的图象的两个交点.
求此反比例函数和一次函数的解析式;
求的面积.
23.本小题分
一次足球训练中,小明从球门正前方米的处射门,足球射向球门的路线呈抛物线,当足球飞行的水平距离为米时,足球达到最高点,此时球离地面米已知球门高为米,现以为原点建立如图所示的平面直角坐标系.
求关于的函数表达式,并通过计算判断球能否射进球门忽略其他因素;
对本次训练进行分析,若射门路线的形状、最大高度均保持不变,则当时他应该带球向正后方移动多少米射门,才能让足球经过点正上方米处?
24.本小题分
如图,在中,,,点在边上,经过点和点且与边相交于点.
求证:是的切线;
若,求的半径.
25.本小题分
黄河是“母亲河”,为落实黄河文化的传承弘扬,某校组织学生到河某段流域进行研学旅行两个数学研究小组设计了不同的方案,他们在河西岸的点处测得河东岸的树恰好在的正东方向,测方案与数据如表:
课题 测量河流宽度
测量工具 测量角度的仪器,皮尺等
测量小组 第一小组 第二小组
测量方案示意图
说明 点,在点的正南方向 点在点的正南方向,点在点的正北方向
数据
请选择其中一个小组及其数据求出河宽精确到
参考数据:,,,
答案和解析
1.【答案】
【解析】【解答】
解:的平方根是.
故选:.
【分析】
根据平方根的定义和求法,可得的平方根是:,据此解答即可.
此题主要考查了平方根的性质和应用,要熟练掌握,解答此题的关键是要明确:一个正数有两个平方根,这两个平方根互为相反数,零的平方根是零,负数没有平方根.
2.【答案】
【解析】解:其中可近似看作轴对称字形的汉字有:黄、美,共个.
故选:.
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,由此即可判断.
本题考查轴对称图形,关键是掌握轴对称图形的定义.
3.【答案】
【解析】解:.
故选:.
科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正数;当原数的绝对值时,是负数.
此题考查科学记数法的表示方法.科学记数法的表示形式为的形式,其中,为整数,表示时关键要正确确定的值以及的值.
4.【答案】
【解析】解:根据题意得,.
故选:.
根据余角的和等于,列式计算即可求解.
本题考查了余角和补角,解题的关键是掌握如果两个角的和等于直角,就说这两个角互为余角.
5.【答案】
【解析】解:有意义,
,
解得,
满足条件.
故选:.
利用被开方数为非负数得到,再解不等式得到的取值范围,然后利用的取值范围对各选项进行判断.
本题考查了二次根式有意义的条件:根据二次根式中的被开方数是非负数来确定二次根式被开方数中字母的取值范围.
6.【答案】
【解析】解:因为正多边形的每一个内角都是,
所以正多边形的每一个外角都是,
所以正多边形的边数是,即这个正多边形是正八边形.
故选:.
先根据邻补角性质得出:正多边形的每一个外角都是,再根据多边形的外角和等于进行计算,即可得出答案.
本题考查了多边形的外角和,邻补角性质,掌握多边形的外角和,邻补角性质是解题的关键.
7.【答案】
【解析】解:根据题意得,
解得.
故选:.
根据根的判别式的意义得到,然后解一次方程即可.
本题考查了根的判别式:一元二次方程的根与有如下关系:当时,方程有两个不相等的实数根;当时,方程有两个相等的实数根;当时,方程无实数根.
8.【答案】
【解析】解:现有三张背面花色完全一样的扑克牌,它们的正面分别写有“”兰、州、好”,
洗匀后从中随机抽取一张,则正好抽到“好”字的概率为,
故选:.
直接由概率公式求解即可.
本题考查了概率公式:概率所求情况数与总情况数之比.熟记概率公式是解题的关键.
9.【答案】
【解析】解:由题意得,.
故选:.
依据题意,根据数量与售价如下表所示所提供的信息,列出售价与数量的函数关系式.
本题主要考查了函数关系式.关键找到函数和自变量的关系,用待定系数法求函数的解析式.
10.【答案】
【解析】解:由题意得:.
故选:.
根据第二批面粉比第一批面粉的每千克面粉价格提高了元列方程即可.
本题考查由实际问题抽象出分式方程,解答本题的关键是明确题意,找出等量关系,列出相应的分式方程.
11.【答案】
【解析】解:,
,
平分,
,
,
,
.
故选:.
根据,得出,再根据平分,得出,再根据同弧所对的圆周角和圆心角的关系得出,再根据三角形内角和定理求得的度数,最后根据对顶角相等即可得出答案.
此题主要考查了圆周角定理,用到的知识点是圆周角定理,三角形的内角和,对顶角相等,掌握相关知识是解题关键.
12.【答案】
【解析】解:当时,如图,
在菱形中,,,,且;
,;
∽,
,
即,;
,
,函数图象开口向上;
当,如图,
同理证得,∽,
,
即,;
,
;
,函数图象开口向下;
综上,答案C的图象大致符合;
故选:.
的面积,通过题干已知条件,用分别表示出、,根据所得的函数,利用其图象,可分两种情况解答:;;
本题考查了二次函数的图象,考查了学生从图象中读取信息的数形结合能力,体现了分类讨论的思想.
13.【答案】
【解析】【分析】
本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.
先提取公因式,再对余下的多项式利用完全平方公式继续分解.
【解答】
解:
.
故答案为.
14.【答案】或
【解析】【分析】
把点的横纵坐标分别乘以或即可得到点的坐标.
本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为,那么位似图形中对应点的坐标的比等于或.
【解答】
解:位似中心为原点,相似比为,
点的对应点的坐标为或,即或.
故答案为或.
15.【答案】
【解析】【分析】
此题主要考查了平行四边形的性质以及扇形面积求法,正确记忆扇形面积公式是解题关键.
直接利用平行四边形的性质得出的度数,再利用扇形面积求法得出答案.
【解答】
解:在 中,,
,
的半径为,
图中阴影部分的面积是:.
故答案为:.
16.【答案】
【解析】【分析】
本题主要考查可能性的大小,难度不大.
分别计算出,,三个线路的公交车用时不超过分钟的可能性大小即可得.
【解答】
解:线路公交车用时不超过分钟的可能性为,
线路公交车用时不超过分钟的可能性为,
线路公交车用时不超过分钟的可能性为,
,
线路上公交车用时不超过分钟的可能性最大.
故答案为:.
17.【答案】
【解析】解:原式
.
根据实数的运算法则进行计算即可.
本题考查了实数的运算,解题的关键是掌握运算法则.
18.【答案】.
【解析】解:解不等式得,,
解不等式得,,
所以不等式组的解集为:.
根据解一元一次不等式组的步骤,对所给不等式组进行求解即可.
本题主要考查了解一元一次不等式组,熟知解一元一次不等式组的步骤是解题的关键.
19.【答案】,.
【解析】解:
,
当时,原式.
根据完全平方公式、平方差公式、单项式乘多项式的运算法则、合并同类项把原式化简,把的值代入计算得到答案.
本题考查的是整式的混合运算化简求值,掌握整式的混合运算法则是解题的关键.
20.【答案】解:如图,即为补全的图形;
;同弧所对的圆周角等于圆心角的一半.
【解析】【分析】
本题考查了作图、等腰三角形的性质、圆周角定理,解决本题的关键是综合运用以上知识.
根据作法即可补全图形;
根据等腰三角形的性质和同弧所对圆周角等于圆心角的一半即可完成下面的证明.
【解答】
解:见答案;
证明:,
.
,
点在上.
又点,都在上,
同弧所对的圆周角等于圆心角的一半,
.
故答案为:,同弧所对的圆周角等于圆心角的一半.
21.【答案】解:课程总人数为,
中位数为第、个数据的平均数,
中位数在这一组,
第、个数为、,
课程的中位数为,即;
;该学生的成绩小于课程的中位数,而大于课程的中位数;
估计课程成绩超过分的人数为人.
答:估计课程成绩超过分的人数为人.
【解析】本题主要考查频数分布直方图、中位数、用样本估计总体等,解题的关键是根据直方图得出解题所需数据及中位数的定义和意义、样本估计总体思想的运用.
先确定课程的中位数落在第小组,再由此分组具体数据得出第、个数据的平均数即可;
根据两个课程的中位数定义解答可得;
用总人数乘以样本中超过分的人数所占比例可得.
22.【答案】解:把代入得,则.
则反比例函数的解析式是;
把代入得,
则的坐标是.
根据题意得:,
解得,
则一次函数的解析式是;
设与轴的交点是,则的坐标是.
则,
,,
则.
【解析】把的坐标代入反比例函数解析式求得的值,从而求得反比例函数解析式,然后把的坐标代入可求得的值,再利用待定系数法求得一次函数的解析式;
求得与轴的交点,然后根据三角形的面积公式求解;
本题考查待定系数法求函数的解析式以及三角形面积的求法,熟练掌握利用点的坐标求函数解析式的方法是关键.
23.【答案】抛物线的函数表达式为;球不能射进球门;
当时他应该带球向正后方移动米射门,才能让足球经过点正上方米处.
【解析】解:根据题意得,抛物线的顶点坐标为,
设抛物线 ,
把点代入得:,
.
抛物线的函数表达式为.
又当时,,
,
球不能射进球门.
设应该带球向正后方移动米,
则移动后的抛物线为,
把点代入得:,
舍去或.
当时球员应该带球向正后方移动米射门,才能让足球经过点正上方米处.
依据题意,用待定系数法求出解析式,然后由时,求出的值可以判断得解;
依据题意,移动后的抛物线为,把点代入得:,即可判断得解.
本题主要考查二次函数的应用,解题的关键是读懂题意,把实际问题转化为数学问题解决.
24.【答案】证明:连接,
,,
,
,
,
,
,即,
是的半径,
是的切线;
解:连接,
,,
是等边三角形,
,,
,
,
,
,
故的半径为.
【解析】本题考查了切线的判定,等腰三角形的性质,等边三角形的判定和性质,正确的作出辅助线是解题的关键.
连接,根据等腰三角形的性质得到,,求得,根据三角形的内角和得到,于是得到是的切线;
连接,推出是等边三角形,得到,,求得,得到,于是得到结论.
25.【答案】河宽约为.
【解析】若选择方案一:
是的一个外角,,,
,
,
,
在中,,
河宽约为;
若选择方案二:
设,
在中,,
,
在中,,
,
,
,
解得:,
,
河宽约为.
若选择方案一:先根据三角形的外角性质可得,从而可得,然后在中,利用锐角三角函数的定义进行计算即可解答;若选择方案二:设,先在中,利用锐角三角函数的定义求出的长,然后在中,利用锐角三角函数的定义求出的长,最后根据,列出关于的方程进行计算,即可解答.
本题考查了解直角三角形的应用,熟练掌握锐角三角函数的定义是解题的关键.
第2页,共2页
第1页,共1页
同课章节目录
