2025年九年级中考数学三轮复习相似三角形专题之一线三垂直模型训练(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮复习相似三角形专题之一线三垂直模型训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 16:35:01 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮复习相似三角形专题之一线三垂直模型训练
1.如图,在正方形ABCD中,E,F分别是边AD,AB上的点,连接CE,EF,CF.
(1)若正方形ABCD的边长为2,E是AD的中点.
①如图1,当∠FEC=90°时,求证:△AEF∽△DCE;
②如图2,当tan∠FCE时,求AF的长;
(2)如图3,延长CF,DA交于点G,当GE=DE,sin∠FCE时,求证:AE=AF.
2.在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF折叠,使点A的对应点P落在边CD上,点B的对应点为点G,PG交BC于点H.
(1)如图1,求证:△DEP∽△CPH;
(2)如图2,当P为CD的中点,AB=2,AD=3时,求GH的长;
(3)如图3,连接BG,当P,H分别为CD,BC的中点时,探究BG与AB的数量关系,并说明理由.
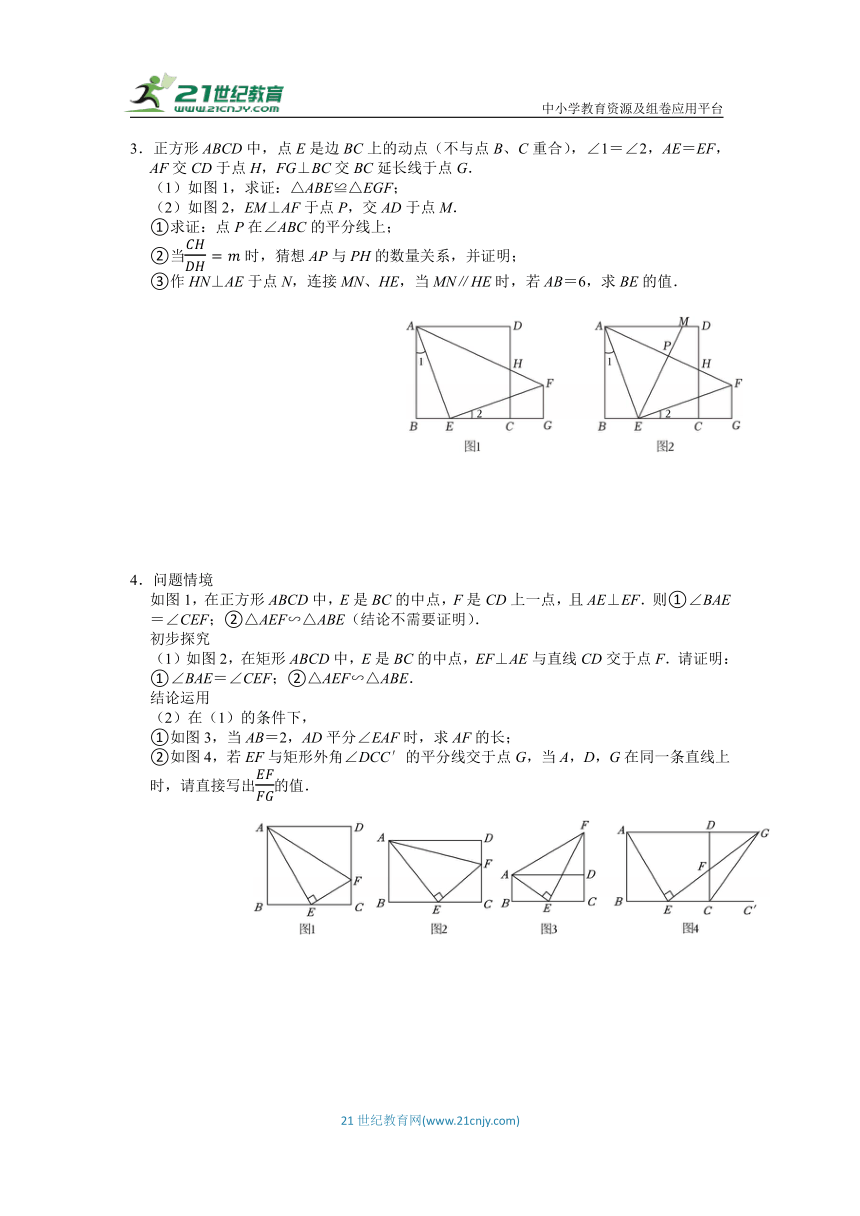
3.正方形ABCD中,点E是边BC上的动点(不与点B、C重合),∠1=∠2,AE=EF,AF交CD于点H,FG⊥BC交BC延长线于点G.
(1)如图1,求证:△ABE≌△EGF;
(2)如图2,EM⊥AF于点P,交AD于点M.
①求证:点P在∠ABC的平分线上;
②当时,猜想AP与PH的数量关系,并证明;
③作HN⊥AE于点N,连接MN、HE,当MN∥HE时,若AB=6,求BE的值.
4.问题情境
如图1,在正方形ABCD中,E是BC的中点,F是CD上一点,且AE⊥EF.则①∠BAE=∠CEF;②△AEF∽△ABE(结论不需要证明).
初步探究
(1)如图2,在矩形ABCD中,E是BC的中点,EF⊥AE与直线CD交于点F.请证明:①∠BAE=∠CEF;②△AEF∽△ABE.
结论运用
(2)在(1)的条件下,
①如图3,当AB=2,AD平分∠EAF时,求AF的长;
②如图4,若EF与矩形外角∠DCC′的平分线交于点G,当A,D,G在同一条直线上时,请直接写出的值.
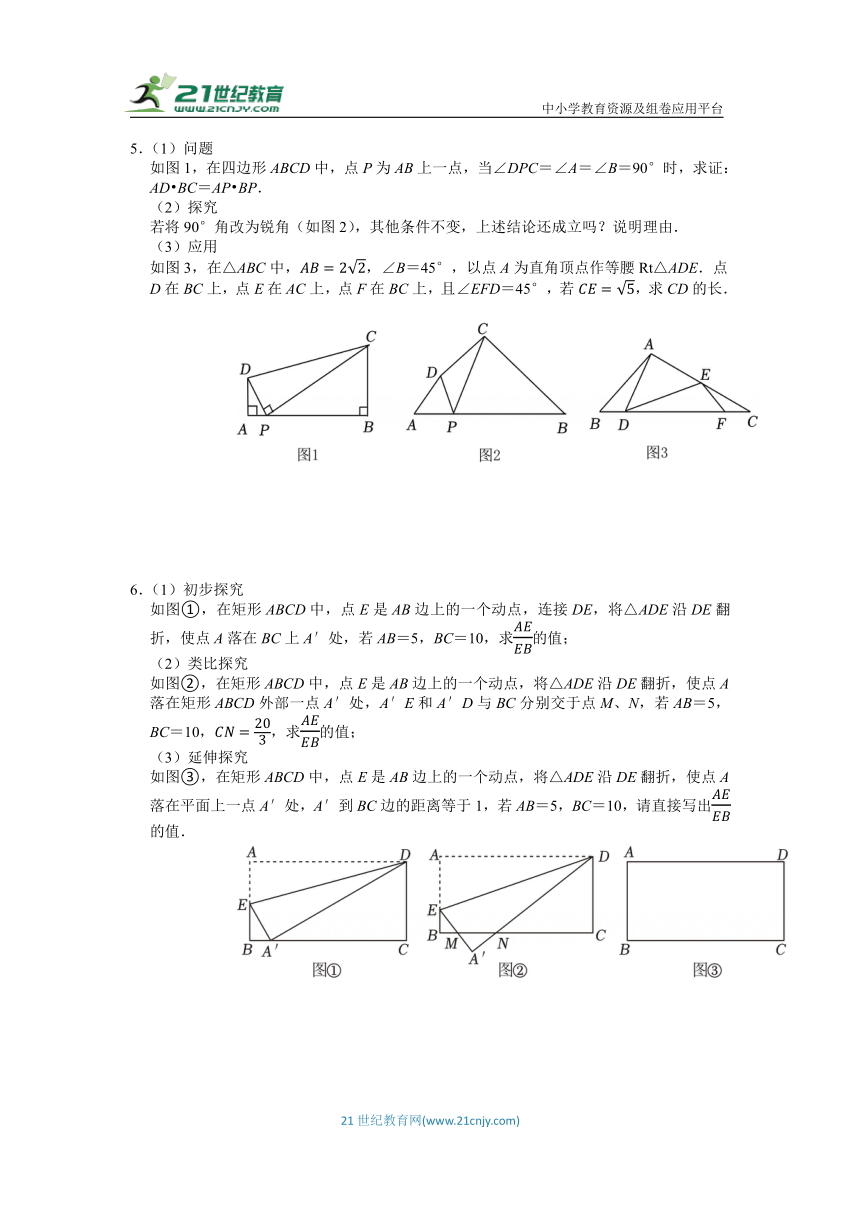
5.(1)问题
如图1,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=90°时,求证:AD BC=AP BP.
(2)探究
若将90°角改为锐角(如图2),其他条件不变,上述结论还成立吗?说明理由.
(3)应用
如图3,在△ABC中,,∠B=45°,以点A为直角顶点作等腰Rt△ADE.点D在BC上,点E在AC上,点F在BC上,且∠EFD=45°,若,求CD的长.
6.(1)初步探究
如图①,在矩形ABCD中,点E是AB边上的一个动点,连接DE,将△ADE沿DE翻折,使点A落在BC上A′处,若AB=5,BC=10,求的值;
(2)类比探究
如图②,在矩形ABCD中,点E是AB边上的一个动点,将△ADE沿DE翻折,使点A落在矩形ABCD外部一点A′处,A′E和A′D与BC分别交于点M、N,若AB=5,BC=10,,求的值;
(3)延伸探究
如图③,在矩形ABCD中,点E是AB边上的一个动点,将△ADE沿DE翻折,使点A落在平面上一点A′处,A′到BC边的距离等于1,若AB=5,BC=10,请直接写出的值.
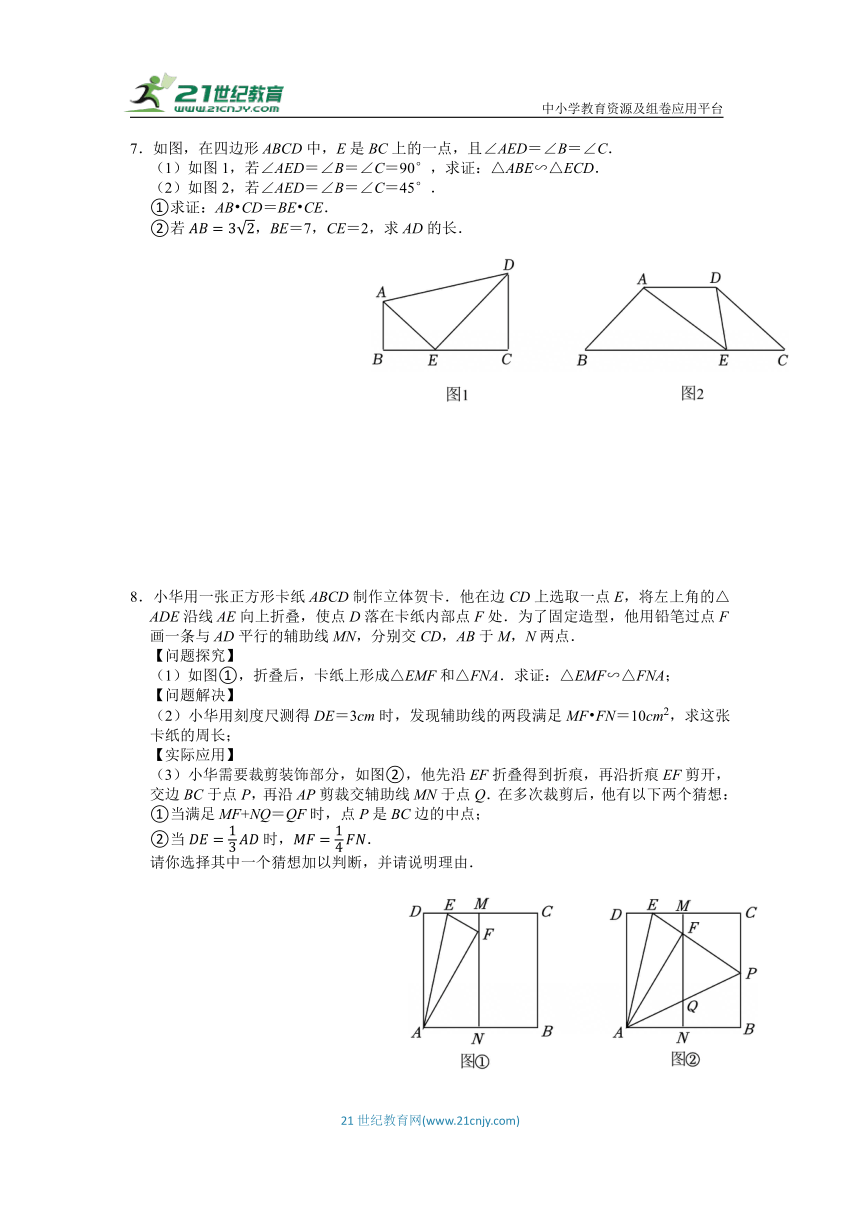
7.如图,在四边形ABCD中,E是BC上的一点,且∠AED=∠B=∠C.
(1)如图1,若∠AED=∠B=∠C=90°,求证:△ABE∽△ECD.
(2)如图2,若∠AED=∠B=∠C=45°.
①求证:AB CD=BE CE.
②若,BE=7,CE=2,求AD的长.
8.小华用一张正方形卡纸ABCD制作立体贺卡.他在边CD上选取一点E,将左上角的△ADE沿线AE向上折叠,使点D落在卡纸内部点F处.为了固定造型,他用铅笔过点F画一条与AD平行的辅助线MN,分别交CD,AB于M,N两点.
【问题探究】
(1)如图①,折叠后,卡纸上形成△EMF和△FNA.求证:△EMF∽△FNA;
【问题解决】
(2)小华用刻度尺测得DE=3cm时,发现辅助线的两段满足MF FN=10cm2,求这张卡纸的周长;
【实际应用】
(3)小华需要裁剪装饰部分,如图②,他先沿EF折叠得到折痕,再沿折痕EF剪开,交边BC于点P,再沿AP剪裁交辅助线MN于点Q.在多次裁剪后,他有以下两个猜想:
①当满足MF+NQ=QF时,点P是BC边的中点;
②当时,.
请你选择其中一个猜想加以判断,并请说明理由.
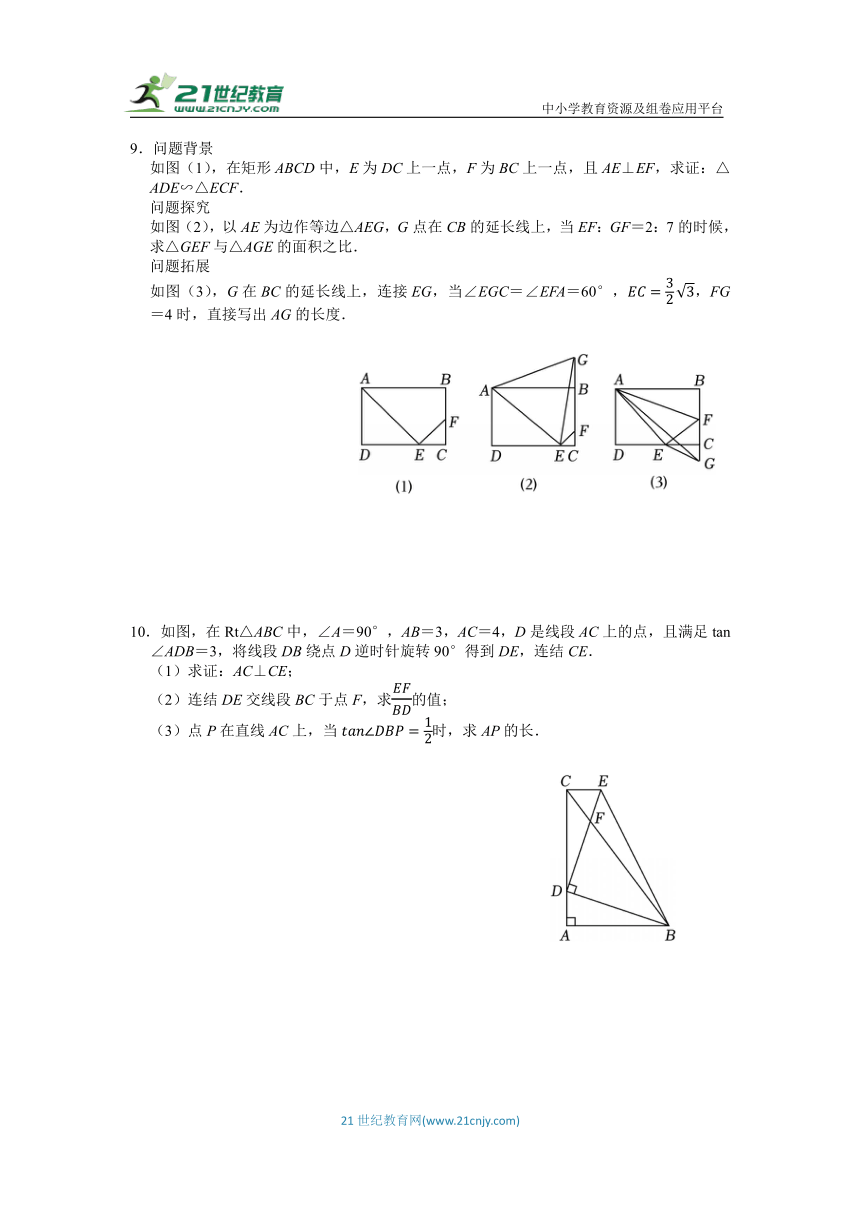
9.问题背景
如图(1),在矩形ABCD中,E为DC上一点,F为BC上一点,且AE⊥EF,求证:△ADE∽△ECF.
问题探究
如图(2),以AE为边作等边△AEG,G点在CB的延长线上,当EF:GF=2:7的时候,求△GEF与△AGE的面积之比.
问题拓展
如图(3),G在BC的延长线上,连接EG,当∠EGC=∠EFA=60°,,FG=4时,直接写出AG的长度.
10.如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,D是线段AC上的点,且满足tan∠ADB=3,将线段DB绕点D逆时针旋转90°得到DE,连结CE.
(1)求证:AC⊥CE;
(2)连结DE交线段BC于点F,求的值;
(3)点P在直线AC上,当时,求AP的长.
11.如图,等腰直角三角形ABC中,∠C=90°,D为BC中点,以D为直角顶点作等腰直角三角形MDN,M在N的左侧.
(1)若点M与点A重合,DN与MB相交于点P.
①若AC=2,求MN的长;
②求证:DP PN=AP PB;
(2)若点M在AC左侧,且∠AMC=90°时,过点D作DE⊥BC交AB于点E,连接ME、CN,在线段CN上取一点F且满足∠NDF=∠EMD,求证:.
12.如图,在矩形ABCD中,AB=6,BC=8,点P在射线AD上运动,以BP为直角边向右作Rt△PBQ,使得∠BPQ=90°,BP=2PQ,连接CQ.
(1)若△ABP与△BPQ相似,则AP= ;
(2)当AP=2时,求CQ的值;
(3)求CQ的最小值.
13.如图,在正方形ABCD中,M为BC边上一动点(点M不与B,C重合),连接DM,将线段DM绕点M逆时针旋转90°得到线段MN,连接BD、BN、DN,DN交AB边于点P.
(1)如图1,求证:△DCM∽△DBN;
(2)如图2,设,,
①当x=1时,请探究得出y的值;
②求出y与x之间满足的关系式.并解决问题:如图3所示,连接MP,若,当∠PMN=30°时,求CM的长.
14.如图,矩形ABCD中,E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在CD上,B的对称点为G,PG交BC于H.
【知识技能】(1)求证:△EDP∽△PCH;
【数学理解】(2)若P为CD中点,且AB=2,BC=3,求GH长;
【拓展探究】(3)连接BG,若P为CD中点,H为BC中点,探究BG与AB的数量关系并说明理由.
15.如图,在Rt△ABC中,∠A=90°,AB=2AC,点M为AB边上一个动点,连接CM,过点M在AB上方作MN⊥CM,且MN=2CM,连接CN,BN.
(1)如图1,①求证:△ABC∽△MNC;②求:∠CBN的度数;
(2)如图2,当AN经过BC中点O时,求的值.
参考答案
1.【解答】(1)①证明:如图1中,∵四边形ABCD是正方形,
∴∠A=∠D=90°,
∵∠CEF=90°,
∴∠AEF+∠CED=90°,∠ECD+∠CED=90°,
∴∠AEF=∠ECD,
∴△AEF∽△DCE;
②解:如图2中,延长DA交CF的延长线于点G,过点G作GH⊥CE交CE的延长线于点H.
∵∠H=∠D=90°,∠GEH=∠CED,
∴△GEH∽△CED,
∴,
∵CD=2,AE=ED=1,
∴GH=2HE,
设EH=m,GH=2m.
∵CE,
∴CH=m,
∵tan∠ECF,
∴,
∴m,
∴EH,GH,
∴EG,
∴AG=EG﹣AE1,DG=EG+DE1,
∵AF∥CD,
∴,
∴,
∴AF;
(3)证明:如图3中,过点G作GH⊥CE交CE的延长线于点H.
设AD=CD=a,GE=DE=t,EH=x,GH=y,CE=n,
∵∠H=∠D=90°,∠GEH=∠CED,
∴△GEH∽△CED,
∴
∴,
∴x,y,
在Rt△CGH中,sin∠ECF,
∴CG=3GH,CH=2GH,
∴,
∴2y=x+n,
∴2n,
∴2at=t2+n2,
在Rt△CDE中,n2=t2+a2,
∴2at=2t2+a2,
∴at,
∵AF∥CD,
∴,
∴,
∴AFaa﹣t,
∵AE=a﹣t,
∴AE=AF.
解法二:设AE=x,则DE=EG=1﹣x,DG=2﹣2x,
∴S△CDE=S△CEG,
∴(1﹣x)×1 ,
解得x=1(负根已经舍去),
∴AE=1,
由AF:CD=AG:DG,可得AF:1=(1):,
∴AF=1.
∴AE=AF.
2.【解答】(1)证明:如图,
∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∴∠1+∠3=90°,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在DC上,
∴∠EPH=∠A=90°,
∴∠1+∠2=90°,
∴∠3=∠2,
∴△EDP∽△PCH;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=3,∠A=∠D=∠C=90°,
∵P为CD中点,
∴DP=CP1,
设EP=AE=x,
∴ED=AD﹣x=3﹣x,
在Rt△EDP中,EP2=ED2+DP2,
即x2=(3﹣x)2+1,
解得x,
∴EP=AP=x,
∴ED=AD﹣AE,
∵△EDP∽△PCH,
∴,即,
∴PH,
∵PG=AB=2,
∴GH=PG﹣PH.
(3)解:如图,延长AB,PG交于一点M,连接AP,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在CD上,
∴AP⊥EF,BG⊥直线EF,
∴BG∥AP,
∵AE=EP,
∴∠EAP=∠EPA,
∴∠BAP=∠GPA,
∴△MAP是等腰三角形,
∴MA=MP,
∵P为CD中点,
∴设DP=CP=y,
∴AB=PG=CD=2y,
∵H为BC中点,
∴BH=CH,
∵∠BHM=∠CHP,∠CBM=∠PCH,
∴△MBH≌△PCH(ASA),
∴BM=CP=y,HM=HP,
∴MP=MA=MB+AB=3y,
∴HPPMy,
在Rt△PCH中,CHy,
∴BC=2CHy,
∴AD=BCy,
在Rt△APD中,APy,
∵BG∥AP,
∴△BMG∽△AMP,
∴,
∴BGy,
∴,
∴ABBG.
3.【解答】(1)证明:∵正方形ABCD,
∴∠B=90°,
∵FG⊥BC,
∴∠G=90°,
由∠B=∠G,∠1=∠2,AE=EF,
得△ABE≌△EGF(AAS);
(2)①证明:连BP.
由(1)得△ABE≌△EGF,
∴∠AEB=∠EFG,
∴∠AEB+∠GEF=∠AEB+∠BAE=90°,
即∠AEF=90°,
∴△AEF是等腰直角三角形,
∵EM⊥AF,
∴∠APE=90°,∠AEP=∠FEP=45°,
∵∠ABE=90°,
∴A、B、E、P四点共圆,
∴∠ABP=∠AEP=45°,
∵∠ABE=90°,∠ABP=∠CBP=45°,
∴点
P
在∠ABC的平分线上;
②m+1.
理由如下:
由①得点
P
在∠ABC的平分线即正方形的对角线上,如图:
∵正方形ABCD,
∴AB∥HD,
∴△ABP∽△HDP,
∴,
∵m,
∴HC=mHD,
∴DC=DH+HC=(m+1)HD,
∴m+1;
③由①得点
P
在∠ABC的平分线即正方形的对角线上,
∴∠PDH=45°,
同理M、D、H、P四点共圆,
∴∠PMH=∠PDH=45°,
∵∠AEP=∠NEM=45°,
∴∠EMH=∠NEM=45°,
∴MH∥EN,
∵MN∥HE,
∴四边形MNEH是平行四边形,
∵△AEF是等腰直角三角形,
∴△PHQ和△PHM都是等腰直角三角形,
设PM=PH=a,则MQ=2a,ME=2MQ=4a,
∵PM=PH,PA=PE,
∴AH=ME=4a,
∴AP=3a,
则AE=3a,
∴BE,
∵∠APM=∠ADH,
∴△APM∽△ADH,
∴,
∴DH,
∴AH2,
∵AH=4a,
∴4a=2,
∴a,
∴BE3.
4.【解答】(1)证明:①∵四边形ABCD是矩形,EF⊥AE与直线CD交于点F,
∴∠B=∠C=90°,∠AEF=90°,
∴∠BAE+∠AEB=∠AEB+∠CEF,
∴∠BAE=∠CEF;
②∵EF⊥AE与直线CD交于点F,
∴∠AEF=∠B=∠C=90°,
∵由①得∠BAE=∠CEF,
∴△ABE∽△ECF,
∴,
在矩形ABCD中,E是BC的中点,
设AB=x、BE=CE=y、AE=a,
∵,
∴,
∴,
∴,,
∴且∠AEF=∠B=90°,
∴△AEF∽△ABE;
(2)解:①∵AD平分∠EAF,
∴∠FAD=∠DAE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠AEB,
∴∠FAD=∠AEB,
∵∠FDA=∠B=90°,
∴△ABE∽△FDA,
设BE=EC=x,则AD=2x,
∴,
∴∠AFE=30°,
由(1)得△AEF∽△ABE,
∴∠AFE=∠AEB,
∴∠AFE=∠AEB=30°,
∴AE=2AB=4,
∴,
∴AF=8.
②;理由如下:
∵∠ECF=∠GDF=90°,∠CFE=∠DFG,
∴△ECF∽△GDF,
设AB=CD=x,BE=EC=y,
∵CG平分∠DCC′,
∴∠DCG=∠GCC′=45°,
∵AG∥BC′,
∴∠DGC=∠GCC′=45°,
∴DG=DC=x,
∴.
∵由(1)得△ABE∽△ECF,
∴,
∴,
∴,,
∵,
∴,
∴,
∴xy=x2﹣y2,
∴,
设,
∴t=1﹣t2,
解得:,(t2<0,舍去),
∴.
5.【解答】解:(1)证明:如图1,∵∠DPC=90°,
∴∠BPC+∠APD=90°,
∵∠A=90°,
∴∠ADP+∠APD=90°,
∴∠ADP=∠BPC,
又∵∠A=∠B=90°,
∴△ADP∽△BPC,
∴AD:BP=AP:BC,
∴AD BC=AP BP;
(2)结论AD BC=AP BP仍成立;
理由:如图2,∵∠BPD=∠DPC+∠BPC,
又∵∠BPD=∠A+∠ADP,
∴∠DPC+∠BPC=∠A+∠ADP,
∵∠DPC=∠A=α,
∴∠BPC=∠ADP,
又∵∠A=∠B=α,
∴△ADP∽△BPC,
∴AD:BP=AP:BC,
∴AD BC=AP BP;
(3)∵∠EFD=45°,
∴∠B=∠ADE=45°,
∴∠BAD=∠EDF,
∴△ABD∽△DFE,
∴AB:DF=AD:DE,
∵△ADE是等腰直角三角形,
∴,
∴,
∵,
∴DF=4,
∵△ADE是等腰直角三角形,
∴∠AED=45°,
∵∠EFD=45°,
∴∠DEC=∠EFC=180°﹣45°=135°,
又∵∠C=∠C,
∴△DEC∽△EFC,
∴DC:EC=EC:CF,即EC2=FC (4+FC),
∵,
∴5=FC(4+FC),
∴FC=1,
解得CD=5.
6.【解答】解:(1)∵四边形ABCD是矩形,
∴CD=AB=5,∠A=∠B=∠C=90°,AD=BC=10,
由翻折性质得:AE=A′E,AD=A′D=10,∠A=∠EA′D=90°,
在Rt△A′CD中,,,
∴∠DA′C=30°,
∴∠BA′E=60°,
∴,,
∴;
(2)如图,过点A′作CD的垂线交直线CD于点G,交直线AB于点K,
∵四边形ABCD是矩形,
∴CD=AB=5,AD=BC=10,∠A=∠B=∠C=90°,
由翻折性质得:∠A=∠EA′D=90°,AE=A′E,AD=A′D=10,
在Rt△NCD中,,
∵∠NDC=∠A′DG,∠NCD=∠A′GD=90°,
∴△NDC∽△A′DG,
∴,即,
∴A′G=8,DG=6,A′K=KG﹣A′G=AD﹣A′G=2,
∵∠EKA′=∠EA′D=90°,
∴∠DA′G+∠EA′K=90°,∠KEA′+∠EA′K=90°,
∴∠DA′G=∠KEA′,
∴△EA′K∽△A′DG,
∴,即,
∴,,
∴;
(3)由题意得,分两种情况讨论:
①当A′在四边形ABCD内部时,如图所示:
过点A′作HG⊥AB,HG⊥DC分别交直线AB,DC于H,G,
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=90°,AD=BC=10,CD=AB=5,
由翻折性质得:AE=A′E,∠A=∠EA′D=90°,AD=A′D=10,
又∵A′到BC边的距离等于1,
∴DG=5﹣1=4,
∵,
∴,
∵∠HEA′+∠HA′E=∠DA′C+∠HA′E,∠EA′D=90°,
∴∠DA′C=∠HEA′,
∴△EHA′∽△A′GD,
∴,即,
∴,
∴,
∴,
∴;
②当A′在四边形ABCD外部时,如图所示:
过点A′作A′G⊥DC,HA′⊥AB分别交直线AB,DC于H,G,
设EB=x,则AE=5﹣x,
∴EH=x+1,
∵CG=1,DC=5,
∴DG=6,
∴A′H=2,A′G=8,
(5﹣x)2=22+(x+1)2,
,
∴AE=AB=BE=5,
∴,
综上所述:的值为或2.
7.【解答】(1)证明:∵∠AED=∠B=90°,
∴∠BAE+∠BEA=90°,∠BEA+∠CED=90°,
∴∠BAE=∠CED,
∵∠B=∠C=90°,
∴△ABE∽△ECD;
(2)①证明:∵∠AED=∠B=45°,
∴∠BAE+∠BEA=135°,∠BEA+∠CED=135°,
∴∠BAE=∠CED.
∵∠B=∠C=45°,
∴△ABE∽△ECD,
∴,
∴AB CD=BE CE;
②解:如图,过点A作AM⊥BC于点M,过点D作 DN⊥AE于点N,
∵∠B=45°,AB=3,
∴BM=AM=AB sin45°=3.
∵BE=7,
∴EM=BE﹣BM=4,
∴在Rt△AME中,AE5,
由①知△ABE∽△ECD,
∴,
∵CE=2,
∴,
∴DE,
∵∠AED=45°,
∴DN=NE=DE sin45°,
∴AN=AE﹣NE,
在Rt△ADN中,AD.
8.【解答】(1)证明:∵∠FME=∠ANF=90°,∠AFE=∠D=90°,
∴∠EFM=∠FAN=90°﹣∠AFN,
∴△EMF∽△FNA;
(2)解:∵∠FME=∠ANF=90°,∠AFE=∠D=90°,
∴∠EFM=∠FAN=90°﹣∠AFN,
∴△FME∽△ANF,
∴,
∴EM NA=MF FN=10,
∵FE=DE=3,
∴NA=DM=EM+3,
∴EM(EM+3)=10,
解得EM=2或EM=﹣5(不符合题意,舍去),
∴NA=DM=2+3=5,
∴MF,
∴FN2,
∴AD=MN=MF+FN23,
∴正方形ABCD的周长为12;
(3)证明:①∵AF=AD,AB=AD,∠AFE=∠D=∠C=90°,
延长EF即交CB边于点P,连接AP交MN于点O,如图②,
∴AF=AB,∠AFP=∠B=90°,
在Rt△APF和Rt△APB中,
,
∴Rt△APF≌Rt△APB(HL),
∴PF=PB,∠APF=∠APB,
∵MN∥AD,BC∥AB,
∴MN∥BC,
∴∠PQF=∠APB,
∴∠APF=∠PQF,
∴QF=PF=PB,
∵MF+NQ=QF,
∴QFMNADBC,
∴BPBC,
∴P为BC的中点;
②∵DEAD,
∴可以假设AD=3k,DE=k,
∴EF=DE=k,AF=AD=3k,
∵△EMF∽△FNA;
∴,
设FM=a,则AN=3a,EM=3a﹣k,FN=9a﹣3k,
∵AD=MN=3k,
∴a+9a﹣3k=3k,
∴ak,
∴FN=9a﹣3kk﹣3kk,
∴,
∴FMFN.
9.【解答】解:问题背景:在矩形ABCD中,AE⊥EF,
∴∠D=∠C=90°,∠AED+∠FEC=90°,
∴∠AED+∠DAE=90°,
∴∠DAE=∠FEC,
∴△ADE∽△ECF;
问题探究:如图2,过F作FH⊥EG,过G作GK⊥AE,
设EF=2x,则CG=2x,CF=5x,GF=7x,
∵△AEG是等边三角形,
∴,GE=AE,∠AEG=∠AGE=60°,
∴∠HEF=∠AEF﹣∠AEG=30°,
∴,
∴,
∴,
∵∠KGE=30°,GK⊥AE,
∴,
∴,
∴;
问题拓展:AG的长度为;理由如下:
当∠EGC=∠EFA=60°,,FG=4时,
∵∠BCE=90°,
∴∠GEC=30°,
∴,,
∴,
∴,
∵∠EFA=60°,∠AEF=90°,
∴,
∵△ADE∽△ECF,
∴,即,
解得:,
∴,
∴,
∴.
10.【解答】(1)证明:在Rt△ABC中,∠A=90°,
∵tan,AB=3,
∴AD=1,CD=AC﹣AD=3,
由旋转的性质得:DB=DE,
∴∠ADB+∠ABD=∠ADB+∠CDE=90°,
∴∠ABD=∠CDE,
在△ABD和△CDE中,
,
∴△ABD≌△CDE(SAS),
∴∠DCE=∠BAD=90°,
∴AC⊥CE;
(2)解:如图2,过点D作DG∥AB交BC于点G,
∴△CDG∽△CAB,
∴,
即
∴,
由(1)知CE∥AB,CE=AD=1,
∴DG∥CE,
∴△CEF∽△GDF,
∴,
即,
∴,
∵BD=ED,
∴,
(3)解:在Rt△ADB中,,
①当点P在点D下方时,
如图3,连结PB,过点P作PM⊥BD于点M,
在Rt△PBM中,tan,
设PM=a,则BM=2a,
在Rt△PDM和Rt△ADB中,
tan,
∴,
∵BD=DM+BM,
∴,
解得,
∴,
在Rt△ADB中,sin,
在Rt△PDM中,sin,
∴,
∴,
∴,
②当点P在点D上方时,
如图4,连结PB,过点P作PN⊥BD交BD的延长线于点N
在Rt△PBN中,tan,
设PN=b,则BN=2b,
∵∠ADB=∠NDP,
∴tan∠ADB=tan∠NDP,
∴,
∴,
∴,
∴,
∵∠ADB=∠NDP,
∴sin∠ADB=sin∠NDP,
∴,
∴,
∴AP=DP+AD=3,
综上所述:AP的长为.
11.【解答】(1)①解:如图1,过点N作NK⊥CB交CB延长线于点K,则∠K=90°;
∵∠ACB=90°,CB=CA,
∴AC=BC=2,
∴由勾股定理得,
∵点D为BC中点,
∴CD=BD=1,
∵△MDN是等腰直角三角形,
∴MD=ND,∠MDN=90°,
∴∠NDK+∠ADC=∠DAC+∠ADC=90°,
∴∠NDK=∠DAC,
∵∠C=∠K=90°,
∴△ACD≌△DKN,
∴DK=AC=2,NK=CD=1,
在Rt△DKN中,由勾股定理得:,
在Rt△MDN中,由勾股定理得:;
②证明:由①得△ACD≌△DKN,
∴DK=AC=BC,NK=CD=BD,
∴CD=BK,
∴NK=BK,
∴△BKN是等腰直角三角形,
∴∠NBK=45°,
∴∠ABN=180°﹣45°﹣45°=90°=∠ADN,
∵∠APD=∠NPB,
∴△APD∽△NPB,
∴,
∴DP PN=AP PB;
(2)解:过点E作ME的垂线与MC的延长线交于点J,连接CE,BN,
∵∠ACB=90°,
∴AC⊥BC,
∵DE⊥BC,
∴DE∥AC,
∴,
∴点E为AB中点,
∵CA=CB,
∴CE⊥AB,
∴∠5+∠6=∠6+∠7=90°,
∴∠5=∠7,
∵CA=CB,∠ACB=90°,
∴∠CAB=∠CBA=45°,
∵∠AMC=90°,∠AEC=90°,
∴∠AMC+∠AEC=180°,
∴A,M,C,E四点共圆,
∴∠EMC=∠CAB=45°,
∴△MEJ为等腰直角三角形,∠AME=∠AMC﹣∠EMC=45°,
∴EM=EJ,∠J=45°,
∴∠J=∠AME,
∵CE⊥AB,∠CAB=45°,
∴△CEA为等腰直角三角形,
∴CE=AE,
在△EAM和△ECJ中,
,
∴△EAM≌△ECJ(ASA),
∴AM=CJ,
∵同理可得△EDB为等腰直角三角形,
∴DE=DB,
∵△MDN为等腰直角三角形,
同理可证明:△MDE≌△NDB,
∴EM=BN,∠2=∠4,
∵∠2=∠3,
∴∠3=∠4,
∴DF∥BN,
∴△CDF∽△CBN,
∴,则BN=2DF,
在等腰Rt△MEJ中,由勾股定理得,
∴,
∵,
∴,
∴,
∴(AM+CM)2=8DF2,即AM2+CM2+2AM×CM=8DF2,
∴AC2+2AM×CM=8DF2,
∵,,
∴AC2=2S△ABC,AM×CM=2S△AMC,
∴,
∴.
12.【解答】解:(1)∵四边形ABCD是矩形,
∴∠A=90°,
∴∠BPQ=∠A=90°,
∵△ABP与△BPQ相似,
∴或,
∵AB=6,BP=2PQ,
∴或,
∴AP=3或AP=12,
故答案为:3或12;
(2)解:过点Q作MN⊥AD于点M,与BC交于点N,
则∠A=∠PMQ=∠CNQ=90°,AB=MN=6,
∵∠BPQ=90°,
∴∠APB+∠MPQ=∠MPQ+∠PQM=90°,
∴∠APB=∠MQP,
∴△APB∽△MQP,
∴,
设MQ=x,则NQ=6﹣x,
∵BP=2PQ,AP=2,
∴2,
∴x=1,MP=3,
∴CN=DM=AD﹣MP﹣AP=8﹣3﹣2=3,
∴CQ2=QN2+CN2=52+32=34,
∴CQ;
(3)由(2)得,△APB∽△MQP,
∴,
设MQ=x,则NQ=6﹣x,
∵BP=2PQ,
∴2,
∴AP=2x,MP=3,
∴CN=DM=AD﹣MP﹣AP=8﹣3﹣2x=5﹣2x,
∴CQ2=QN2+CN2=(6﹣x)2+(5﹣2x)2,
=5(x)2,
当x时,CQ2的最小值为,
∴CQ长的最小值为.
13.【解答】(1)证明:如图1中,过点N作NH⊥CB交CB的延长线于点H.
∵MD=MN,∠DMN=90°,
∴△DMN是等腰直角三角形,
∴∠MDN=45°,
∵四边形ABCD是正方形,
∴CD=CB,∠C=∠ABC=90°,∠BDC=∠DBC=45°,
∵NH⊥CH,
∴∠H=∠DCM=90°,
∵∠NMH+∠DMC=90°,∠DMC+∠CDM=90°,
∴∠NMH=∠CDM,
∵MD=MN,
∴△DCM≌△MHN(AAS),
∴CD=MH=BC,CM=NH,
∴BH=CM=NH,
∴∠NBH=45°,
∴∠DBN=∠DCM=90°,
∵∠NDM=∠BDC,
∴∠NDB=∠MDC,
∴△DCM∽△DBN;
(2)解:①如图2中,过点P作PE⊥BD于点E,PF⊥BN于点F,NH⊥CB交CB的延长线于点H.
当x=1时,设CM=BM=a,则BD=2a,
由(1)可知NH=BH=CM=a,
∴BNa,
∵∠PBN=∠PBD=45°,PE⊥BD.PF⊥BN,
∴PE=PF,
∴,
∴,
∴y;
②如图3中,延长BC到T,使得CT=AP.
∵AD=CD,∠DAP=∠DCT=90°,AP=CT,
∴△DAP≌△DCT(SAS),
∴∠ADP=∠CDT,DP=DT,
∴∠PDT=∠ADC=90°,
∵∠PDM=45°,
∴∠PDM=∠TDM,
∵DM=DM,
∴△DMP≌△DMT(SAS),
∴∠DMP=∠DMT,
∵∠PMN=30°,∠DMN=90°,
∴∠DMT=∠DMP=90°﹣30°=60°,
∵CD=AB=2,
∴tan60°,
∴,
∴CM=2.
14.【解答】(1)证明:如图:
∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∴∠1+∠3=90°,
∵E、F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在DC上,
∴∠EPH=∠A=90°,
∴∠1+∠2=90°,
∴∠3=∠2,
∴△EDP∽△PCH;
(2)解:如图:
∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=3,∠A=∠D=∠C=90°,
∵P为CD中点,
∴,
设EP=AP=x,
∴ED=AD﹣x=3﹣x,
在Rt△EDP中,EP2=ED2+DP2,
即x2=(3﹣x)2+1,
解得,
∴,
∴ED=AD﹣AE,
∵△EDP∽△PCH,
∴,
∴,
解得,
∵PG=AB=2,
∴;
(3)解:如图:延长AB,PG交于一点M,连接AP,
∵E、F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在CD上,
∴AP⊥EF,BG⊥直线EF,
∴BG∥AP,
∵AE=EP,
∴∠EAP=∠EPA,
∴∠BAP=∠GPA,
∴△MAP是等腰三角形,
∴MA=MP,
∵P为CD中点,
∴设DP=CP=y,
∴AB=PG=CD=2y,
∵H为BC中点,
∴BH=CH,
∵∠BHM=∠CHP,∠CBM=∠PCH,
∴△MBH≌△PCH(ASA),
∴BM=CP=y,HM=HP,
∴MP=MA=MB+AB=3y,
∴,
在Rt△PCH中,,
∴,
∴,
在Rt△APD中,,
∵BG∥AP,
∴△BMG∽△MAP,
∴,
∴,
∴,
∴.
15.【解答】(1)①证明:∵AB=2AC,MN=2CM,
∴,
∴,
∵∠A=∠CMN=90°,
∴△ABC∽△MNC;
②解:过N作NG⊥AB,交AB延长线于点G,设MN与BC交于点P,
∵∠A=∠CMN=90°,
∴∠ACM=∠GMN=90°﹣∠CMA,
∵∠A=∠G=90°,
∴△CAM∽△MGN,
∴,
∴MG=2AC=AB,
由①知,△ABC∽△MNC,
∴∠CNM=∠CBM,,
∴,即,
∵∠CPN=∠MPB,
∴∠BCN=∠GMN,
∴△CBN∽△MGN,
∴∠CBN=∠MGN=90°;
(2)解:过N作NG⊥AB,交AB延长线于点G,
设AM=a,AC=b,则AB=2b,
由(1)②可知△CAM∽△MGN,
∴,
∴MG=2AC=2b,NG=2AM=2a,
∴AM=BG=a,
∴AG=AB+BG=a+2b,
过B作BH∥AC交AN于点H,
∴∠CAO=∠BHO,∠ABH=∠BAC=90°,
∵O是BC中点,
∴OC=OB,
∵∠COA=∠BOH,
∴△COA≌△BOH(SAS),
∴BH=AC=b,
∵∠ABH=∠G=90°,∠BAH=∠GAN,
∴△ABH∽△AGN,
∴,即,
整理可得ab,
∴.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮复习相似三角形专题之一线三垂直模型训练
1.如图,在正方形ABCD中,E,F分别是边AD,AB上的点,连接CE,EF,CF.
(1)若正方形ABCD的边长为2,E是AD的中点.
①如图1,当∠FEC=90°时,求证:△AEF∽△DCE;
②如图2,当tan∠FCE时,求AF的长;
(2)如图3,延长CF,DA交于点G,当GE=DE,sin∠FCE时,求证:AE=AF.
2.在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF折叠,使点A的对应点P落在边CD上,点B的对应点为点G,PG交BC于点H.
(1)如图1,求证:△DEP∽△CPH;
(2)如图2,当P为CD的中点,AB=2,AD=3时,求GH的长;
(3)如图3,连接BG,当P,H分别为CD,BC的中点时,探究BG与AB的数量关系,并说明理由.
3.正方形ABCD中,点E是边BC上的动点(不与点B、C重合),∠1=∠2,AE=EF,AF交CD于点H,FG⊥BC交BC延长线于点G.
(1)如图1,求证:△ABE≌△EGF;
(2)如图2,EM⊥AF于点P,交AD于点M.
①求证:点P在∠ABC的平分线上;
②当时,猜想AP与PH的数量关系,并证明;
③作HN⊥AE于点N,连接MN、HE,当MN∥HE时,若AB=6,求BE的值.
4.问题情境
如图1,在正方形ABCD中,E是BC的中点,F是CD上一点,且AE⊥EF.则①∠BAE=∠CEF;②△AEF∽△ABE(结论不需要证明).
初步探究
(1)如图2,在矩形ABCD中,E是BC的中点,EF⊥AE与直线CD交于点F.请证明:①∠BAE=∠CEF;②△AEF∽△ABE.
结论运用
(2)在(1)的条件下,
①如图3,当AB=2,AD平分∠EAF时,求AF的长;
②如图4,若EF与矩形外角∠DCC′的平分线交于点G,当A,D,G在同一条直线上时,请直接写出的值.
5.(1)问题
如图1,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=90°时,求证:AD BC=AP BP.
(2)探究
若将90°角改为锐角(如图2),其他条件不变,上述结论还成立吗?说明理由.
(3)应用
如图3,在△ABC中,,∠B=45°,以点A为直角顶点作等腰Rt△ADE.点D在BC上,点E在AC上,点F在BC上,且∠EFD=45°,若,求CD的长.
6.(1)初步探究
如图①,在矩形ABCD中,点E是AB边上的一个动点,连接DE,将△ADE沿DE翻折,使点A落在BC上A′处,若AB=5,BC=10,求的值;
(2)类比探究
如图②,在矩形ABCD中,点E是AB边上的一个动点,将△ADE沿DE翻折,使点A落在矩形ABCD外部一点A′处,A′E和A′D与BC分别交于点M、N,若AB=5,BC=10,,求的值;
(3)延伸探究
如图③,在矩形ABCD中,点E是AB边上的一个动点,将△ADE沿DE翻折,使点A落在平面上一点A′处,A′到BC边的距离等于1,若AB=5,BC=10,请直接写出的值.
7.如图,在四边形ABCD中,E是BC上的一点,且∠AED=∠B=∠C.
(1)如图1,若∠AED=∠B=∠C=90°,求证:△ABE∽△ECD.
(2)如图2,若∠AED=∠B=∠C=45°.
①求证:AB CD=BE CE.
②若,BE=7,CE=2,求AD的长.
8.小华用一张正方形卡纸ABCD制作立体贺卡.他在边CD上选取一点E,将左上角的△ADE沿线AE向上折叠,使点D落在卡纸内部点F处.为了固定造型,他用铅笔过点F画一条与AD平行的辅助线MN,分别交CD,AB于M,N两点.
【问题探究】
(1)如图①,折叠后,卡纸上形成△EMF和△FNA.求证:△EMF∽△FNA;
【问题解决】
(2)小华用刻度尺测得DE=3cm时,发现辅助线的两段满足MF FN=10cm2,求这张卡纸的周长;
【实际应用】
(3)小华需要裁剪装饰部分,如图②,他先沿EF折叠得到折痕,再沿折痕EF剪开,交边BC于点P,再沿AP剪裁交辅助线MN于点Q.在多次裁剪后,他有以下两个猜想:
①当满足MF+NQ=QF时,点P是BC边的中点;
②当时,.
请你选择其中一个猜想加以判断,并请说明理由.
9.问题背景
如图(1),在矩形ABCD中,E为DC上一点,F为BC上一点,且AE⊥EF,求证:△ADE∽△ECF.
问题探究
如图(2),以AE为边作等边△AEG,G点在CB的延长线上,当EF:GF=2:7的时候,求△GEF与△AGE的面积之比.
问题拓展
如图(3),G在BC的延长线上,连接EG,当∠EGC=∠EFA=60°,,FG=4时,直接写出AG的长度.
10.如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,D是线段AC上的点,且满足tan∠ADB=3,将线段DB绕点D逆时针旋转90°得到DE,连结CE.
(1)求证:AC⊥CE;
(2)连结DE交线段BC于点F,求的值;
(3)点P在直线AC上,当时,求AP的长.
11.如图,等腰直角三角形ABC中,∠C=90°,D为BC中点,以D为直角顶点作等腰直角三角形MDN,M在N的左侧.
(1)若点M与点A重合,DN与MB相交于点P.
①若AC=2,求MN的长;
②求证:DP PN=AP PB;
(2)若点M在AC左侧,且∠AMC=90°时,过点D作DE⊥BC交AB于点E,连接ME、CN,在线段CN上取一点F且满足∠NDF=∠EMD,求证:.
12.如图,在矩形ABCD中,AB=6,BC=8,点P在射线AD上运动,以BP为直角边向右作Rt△PBQ,使得∠BPQ=90°,BP=2PQ,连接CQ.
(1)若△ABP与△BPQ相似,则AP= ;
(2)当AP=2时,求CQ的值;
(3)求CQ的最小值.
13.如图,在正方形ABCD中,M为BC边上一动点(点M不与B,C重合),连接DM,将线段DM绕点M逆时针旋转90°得到线段MN,连接BD、BN、DN,DN交AB边于点P.
(1)如图1,求证:△DCM∽△DBN;
(2)如图2,设,,
①当x=1时,请探究得出y的值;
②求出y与x之间满足的关系式.并解决问题:如图3所示,连接MP,若,当∠PMN=30°时,求CM的长.
14.如图,矩形ABCD中,E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在CD上,B的对称点为G,PG交BC于H.
【知识技能】(1)求证:△EDP∽△PCH;
【数学理解】(2)若P为CD中点,且AB=2,BC=3,求GH长;
【拓展探究】(3)连接BG,若P为CD中点,H为BC中点,探究BG与AB的数量关系并说明理由.
15.如图,在Rt△ABC中,∠A=90°,AB=2AC,点M为AB边上一个动点,连接CM,过点M在AB上方作MN⊥CM,且MN=2CM,连接CN,BN.
(1)如图1,①求证:△ABC∽△MNC;②求:∠CBN的度数;
(2)如图2,当AN经过BC中点O时,求的值.
参考答案
1.【解答】(1)①证明:如图1中,∵四边形ABCD是正方形,
∴∠A=∠D=90°,
∵∠CEF=90°,
∴∠AEF+∠CED=90°,∠ECD+∠CED=90°,
∴∠AEF=∠ECD,
∴△AEF∽△DCE;
②解:如图2中,延长DA交CF的延长线于点G,过点G作GH⊥CE交CE的延长线于点H.
∵∠H=∠D=90°,∠GEH=∠CED,
∴△GEH∽△CED,
∴,
∵CD=2,AE=ED=1,
∴GH=2HE,
设EH=m,GH=2m.
∵CE,
∴CH=m,
∵tan∠ECF,
∴,
∴m,
∴EH,GH,
∴EG,
∴AG=EG﹣AE1,DG=EG+DE1,
∵AF∥CD,
∴,
∴,
∴AF;
(3)证明:如图3中,过点G作GH⊥CE交CE的延长线于点H.
设AD=CD=a,GE=DE=t,EH=x,GH=y,CE=n,
∵∠H=∠D=90°,∠GEH=∠CED,
∴△GEH∽△CED,
∴
∴,
∴x,y,
在Rt△CGH中,sin∠ECF,
∴CG=3GH,CH=2GH,
∴,
∴2y=x+n,
∴2n,
∴2at=t2+n2,
在Rt△CDE中,n2=t2+a2,
∴2at=2t2+a2,
∴at,
∵AF∥CD,
∴,
∴,
∴AFaa﹣t,
∵AE=a﹣t,
∴AE=AF.
解法二:设AE=x,则DE=EG=1﹣x,DG=2﹣2x,
∴S△CDE=S△CEG,
∴(1﹣x)×1 ,
解得x=1(负根已经舍去),
∴AE=1,
由AF:CD=AG:DG,可得AF:1=(1):,
∴AF=1.
∴AE=AF.
2.【解答】(1)证明:如图,
∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∴∠1+∠3=90°,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在DC上,
∴∠EPH=∠A=90°,
∴∠1+∠2=90°,
∴∠3=∠2,
∴△EDP∽△PCH;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=3,∠A=∠D=∠C=90°,
∵P为CD中点,
∴DP=CP1,
设EP=AE=x,
∴ED=AD﹣x=3﹣x,
在Rt△EDP中,EP2=ED2+DP2,
即x2=(3﹣x)2+1,
解得x,
∴EP=AP=x,
∴ED=AD﹣AE,
∵△EDP∽△PCH,
∴,即,
∴PH,
∵PG=AB=2,
∴GH=PG﹣PH.
(3)解:如图,延长AB,PG交于一点M,连接AP,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在CD上,
∴AP⊥EF,BG⊥直线EF,
∴BG∥AP,
∵AE=EP,
∴∠EAP=∠EPA,
∴∠BAP=∠GPA,
∴△MAP是等腰三角形,
∴MA=MP,
∵P为CD中点,
∴设DP=CP=y,
∴AB=PG=CD=2y,
∵H为BC中点,
∴BH=CH,
∵∠BHM=∠CHP,∠CBM=∠PCH,
∴△MBH≌△PCH(ASA),
∴BM=CP=y,HM=HP,
∴MP=MA=MB+AB=3y,
∴HPPMy,
在Rt△PCH中,CHy,
∴BC=2CHy,
∴AD=BCy,
在Rt△APD中,APy,
∵BG∥AP,
∴△BMG∽△AMP,
∴,
∴BGy,
∴,
∴ABBG.
3.【解答】(1)证明:∵正方形ABCD,
∴∠B=90°,
∵FG⊥BC,
∴∠G=90°,
由∠B=∠G,∠1=∠2,AE=EF,
得△ABE≌△EGF(AAS);
(2)①证明:连BP.
由(1)得△ABE≌△EGF,
∴∠AEB=∠EFG,
∴∠AEB+∠GEF=∠AEB+∠BAE=90°,
即∠AEF=90°,
∴△AEF是等腰直角三角形,
∵EM⊥AF,
∴∠APE=90°,∠AEP=∠FEP=45°,
∵∠ABE=90°,
∴A、B、E、P四点共圆,
∴∠ABP=∠AEP=45°,
∵∠ABE=90°,∠ABP=∠CBP=45°,
∴点
P
在∠ABC的平分线上;
②m+1.
理由如下:
由①得点
P
在∠ABC的平分线即正方形的对角线上,如图:
∵正方形ABCD,
∴AB∥HD,
∴△ABP∽△HDP,
∴,
∵m,
∴HC=mHD,
∴DC=DH+HC=(m+1)HD,
∴m+1;
③由①得点
P
在∠ABC的平分线即正方形的对角线上,
∴∠PDH=45°,
同理M、D、H、P四点共圆,
∴∠PMH=∠PDH=45°,
∵∠AEP=∠NEM=45°,
∴∠EMH=∠NEM=45°,
∴MH∥EN,
∵MN∥HE,
∴四边形MNEH是平行四边形,
∵△AEF是等腰直角三角形,
∴△PHQ和△PHM都是等腰直角三角形,
设PM=PH=a,则MQ=2a,ME=2MQ=4a,
∵PM=PH,PA=PE,
∴AH=ME=4a,
∴AP=3a,
则AE=3a,
∴BE,
∵∠APM=∠ADH,
∴△APM∽△ADH,
∴,
∴DH,
∴AH2,
∵AH=4a,
∴4a=2,
∴a,
∴BE3.
4.【解答】(1)证明:①∵四边形ABCD是矩形,EF⊥AE与直线CD交于点F,
∴∠B=∠C=90°,∠AEF=90°,
∴∠BAE+∠AEB=∠AEB+∠CEF,
∴∠BAE=∠CEF;
②∵EF⊥AE与直线CD交于点F,
∴∠AEF=∠B=∠C=90°,
∵由①得∠BAE=∠CEF,
∴△ABE∽△ECF,
∴,
在矩形ABCD中,E是BC的中点,
设AB=x、BE=CE=y、AE=a,
∵,
∴,
∴,
∴,,
∴且∠AEF=∠B=90°,
∴△AEF∽△ABE;
(2)解:①∵AD平分∠EAF,
∴∠FAD=∠DAE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠AEB,
∴∠FAD=∠AEB,
∵∠FDA=∠B=90°,
∴△ABE∽△FDA,
设BE=EC=x,则AD=2x,
∴,
∴∠AFE=30°,
由(1)得△AEF∽△ABE,
∴∠AFE=∠AEB,
∴∠AFE=∠AEB=30°,
∴AE=2AB=4,
∴,
∴AF=8.
②;理由如下:
∵∠ECF=∠GDF=90°,∠CFE=∠DFG,
∴△ECF∽△GDF,
设AB=CD=x,BE=EC=y,
∵CG平分∠DCC′,
∴∠DCG=∠GCC′=45°,
∵AG∥BC′,
∴∠DGC=∠GCC′=45°,
∴DG=DC=x,
∴.
∵由(1)得△ABE∽△ECF,
∴,
∴,
∴,,
∵,
∴,
∴,
∴xy=x2﹣y2,
∴,
设,
∴t=1﹣t2,
解得:,(t2<0,舍去),
∴.
5.【解答】解:(1)证明:如图1,∵∠DPC=90°,
∴∠BPC+∠APD=90°,
∵∠A=90°,
∴∠ADP+∠APD=90°,
∴∠ADP=∠BPC,
又∵∠A=∠B=90°,
∴△ADP∽△BPC,
∴AD:BP=AP:BC,
∴AD BC=AP BP;
(2)结论AD BC=AP BP仍成立;
理由:如图2,∵∠BPD=∠DPC+∠BPC,
又∵∠BPD=∠A+∠ADP,
∴∠DPC+∠BPC=∠A+∠ADP,
∵∠DPC=∠A=α,
∴∠BPC=∠ADP,
又∵∠A=∠B=α,
∴△ADP∽△BPC,
∴AD:BP=AP:BC,
∴AD BC=AP BP;
(3)∵∠EFD=45°,
∴∠B=∠ADE=45°,
∴∠BAD=∠EDF,
∴△ABD∽△DFE,
∴AB:DF=AD:DE,
∵△ADE是等腰直角三角形,
∴,
∴,
∵,
∴DF=4,
∵△ADE是等腰直角三角形,
∴∠AED=45°,
∵∠EFD=45°,
∴∠DEC=∠EFC=180°﹣45°=135°,
又∵∠C=∠C,
∴△DEC∽△EFC,
∴DC:EC=EC:CF,即EC2=FC (4+FC),
∵,
∴5=FC(4+FC),
∴FC=1,
解得CD=5.
6.【解答】解:(1)∵四边形ABCD是矩形,
∴CD=AB=5,∠A=∠B=∠C=90°,AD=BC=10,
由翻折性质得:AE=A′E,AD=A′D=10,∠A=∠EA′D=90°,
在Rt△A′CD中,,,
∴∠DA′C=30°,
∴∠BA′E=60°,
∴,,
∴;
(2)如图,过点A′作CD的垂线交直线CD于点G,交直线AB于点K,
∵四边形ABCD是矩形,
∴CD=AB=5,AD=BC=10,∠A=∠B=∠C=90°,
由翻折性质得:∠A=∠EA′D=90°,AE=A′E,AD=A′D=10,
在Rt△NCD中,,
∵∠NDC=∠A′DG,∠NCD=∠A′GD=90°,
∴△NDC∽△A′DG,
∴,即,
∴A′G=8,DG=6,A′K=KG﹣A′G=AD﹣A′G=2,
∵∠EKA′=∠EA′D=90°,
∴∠DA′G+∠EA′K=90°,∠KEA′+∠EA′K=90°,
∴∠DA′G=∠KEA′,
∴△EA′K∽△A′DG,
∴,即,
∴,,
∴;
(3)由题意得,分两种情况讨论:
①当A′在四边形ABCD内部时,如图所示:
过点A′作HG⊥AB,HG⊥DC分别交直线AB,DC于H,G,
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=90°,AD=BC=10,CD=AB=5,
由翻折性质得:AE=A′E,∠A=∠EA′D=90°,AD=A′D=10,
又∵A′到BC边的距离等于1,
∴DG=5﹣1=4,
∵,
∴,
∵∠HEA′+∠HA′E=∠DA′C+∠HA′E,∠EA′D=90°,
∴∠DA′C=∠HEA′,
∴△EHA′∽△A′GD,
∴,即,
∴,
∴,
∴,
∴;
②当A′在四边形ABCD外部时,如图所示:
过点A′作A′G⊥DC,HA′⊥AB分别交直线AB,DC于H,G,
设EB=x,则AE=5﹣x,
∴EH=x+1,
∵CG=1,DC=5,
∴DG=6,
∴A′H=2,A′G=8,
(5﹣x)2=22+(x+1)2,
,
∴AE=AB=BE=5,
∴,
综上所述:的值为或2.
7.【解答】(1)证明:∵∠AED=∠B=90°,
∴∠BAE+∠BEA=90°,∠BEA+∠CED=90°,
∴∠BAE=∠CED,
∵∠B=∠C=90°,
∴△ABE∽△ECD;
(2)①证明:∵∠AED=∠B=45°,
∴∠BAE+∠BEA=135°,∠BEA+∠CED=135°,
∴∠BAE=∠CED.
∵∠B=∠C=45°,
∴△ABE∽△ECD,
∴,
∴AB CD=BE CE;
②解:如图,过点A作AM⊥BC于点M,过点D作 DN⊥AE于点N,
∵∠B=45°,AB=3,
∴BM=AM=AB sin45°=3.
∵BE=7,
∴EM=BE﹣BM=4,
∴在Rt△AME中,AE5,
由①知△ABE∽△ECD,
∴,
∵CE=2,
∴,
∴DE,
∵∠AED=45°,
∴DN=NE=DE sin45°,
∴AN=AE﹣NE,
在Rt△ADN中,AD.
8.【解答】(1)证明:∵∠FME=∠ANF=90°,∠AFE=∠D=90°,
∴∠EFM=∠FAN=90°﹣∠AFN,
∴△EMF∽△FNA;
(2)解:∵∠FME=∠ANF=90°,∠AFE=∠D=90°,
∴∠EFM=∠FAN=90°﹣∠AFN,
∴△FME∽△ANF,
∴,
∴EM NA=MF FN=10,
∵FE=DE=3,
∴NA=DM=EM+3,
∴EM(EM+3)=10,
解得EM=2或EM=﹣5(不符合题意,舍去),
∴NA=DM=2+3=5,
∴MF,
∴FN2,
∴AD=MN=MF+FN23,
∴正方形ABCD的周长为12;
(3)证明:①∵AF=AD,AB=AD,∠AFE=∠D=∠C=90°,
延长EF即交CB边于点P,连接AP交MN于点O,如图②,
∴AF=AB,∠AFP=∠B=90°,
在Rt△APF和Rt△APB中,
,
∴Rt△APF≌Rt△APB(HL),
∴PF=PB,∠APF=∠APB,
∵MN∥AD,BC∥AB,
∴MN∥BC,
∴∠PQF=∠APB,
∴∠APF=∠PQF,
∴QF=PF=PB,
∵MF+NQ=QF,
∴QFMNADBC,
∴BPBC,
∴P为BC的中点;
②∵DEAD,
∴可以假设AD=3k,DE=k,
∴EF=DE=k,AF=AD=3k,
∵△EMF∽△FNA;
∴,
设FM=a,则AN=3a,EM=3a﹣k,FN=9a﹣3k,
∵AD=MN=3k,
∴a+9a﹣3k=3k,
∴ak,
∴FN=9a﹣3kk﹣3kk,
∴,
∴FMFN.
9.【解答】解:问题背景:在矩形ABCD中,AE⊥EF,
∴∠D=∠C=90°,∠AED+∠FEC=90°,
∴∠AED+∠DAE=90°,
∴∠DAE=∠FEC,
∴△ADE∽△ECF;
问题探究:如图2,过F作FH⊥EG,过G作GK⊥AE,
设EF=2x,则CG=2x,CF=5x,GF=7x,
∵△AEG是等边三角形,
∴,GE=AE,∠AEG=∠AGE=60°,
∴∠HEF=∠AEF﹣∠AEG=30°,
∴,
∴,
∴,
∵∠KGE=30°,GK⊥AE,
∴,
∴,
∴;
问题拓展:AG的长度为;理由如下:
当∠EGC=∠EFA=60°,,FG=4时,
∵∠BCE=90°,
∴∠GEC=30°,
∴,,
∴,
∴,
∵∠EFA=60°,∠AEF=90°,
∴,
∵△ADE∽△ECF,
∴,即,
解得:,
∴,
∴,
∴.
10.【解答】(1)证明:在Rt△ABC中,∠A=90°,
∵tan,AB=3,
∴AD=1,CD=AC﹣AD=3,
由旋转的性质得:DB=DE,
∴∠ADB+∠ABD=∠ADB+∠CDE=90°,
∴∠ABD=∠CDE,
在△ABD和△CDE中,
,
∴△ABD≌△CDE(SAS),
∴∠DCE=∠BAD=90°,
∴AC⊥CE;
(2)解:如图2,过点D作DG∥AB交BC于点G,
∴△CDG∽△CAB,
∴,
即
∴,
由(1)知CE∥AB,CE=AD=1,
∴DG∥CE,
∴△CEF∽△GDF,
∴,
即,
∴,
∵BD=ED,
∴,
(3)解:在Rt△ADB中,,
①当点P在点D下方时,
如图3,连结PB,过点P作PM⊥BD于点M,
在Rt△PBM中,tan,
设PM=a,则BM=2a,
在Rt△PDM和Rt△ADB中,
tan,
∴,
∵BD=DM+BM,
∴,
解得,
∴,
在Rt△ADB中,sin,
在Rt△PDM中,sin,
∴,
∴,
∴,
②当点P在点D上方时,
如图4,连结PB,过点P作PN⊥BD交BD的延长线于点N
在Rt△PBN中,tan,
设PN=b,则BN=2b,
∵∠ADB=∠NDP,
∴tan∠ADB=tan∠NDP,
∴,
∴,
∴,
∴,
∵∠ADB=∠NDP,
∴sin∠ADB=sin∠NDP,
∴,
∴,
∴AP=DP+AD=3,
综上所述:AP的长为.
11.【解答】(1)①解:如图1,过点N作NK⊥CB交CB延长线于点K,则∠K=90°;
∵∠ACB=90°,CB=CA,
∴AC=BC=2,
∴由勾股定理得,
∵点D为BC中点,
∴CD=BD=1,
∵△MDN是等腰直角三角形,
∴MD=ND,∠MDN=90°,
∴∠NDK+∠ADC=∠DAC+∠ADC=90°,
∴∠NDK=∠DAC,
∵∠C=∠K=90°,
∴△ACD≌△DKN,
∴DK=AC=2,NK=CD=1,
在Rt△DKN中,由勾股定理得:,
在Rt△MDN中,由勾股定理得:;
②证明:由①得△ACD≌△DKN,
∴DK=AC=BC,NK=CD=BD,
∴CD=BK,
∴NK=BK,
∴△BKN是等腰直角三角形,
∴∠NBK=45°,
∴∠ABN=180°﹣45°﹣45°=90°=∠ADN,
∵∠APD=∠NPB,
∴△APD∽△NPB,
∴,
∴DP PN=AP PB;
(2)解:过点E作ME的垂线与MC的延长线交于点J,连接CE,BN,
∵∠ACB=90°,
∴AC⊥BC,
∵DE⊥BC,
∴DE∥AC,
∴,
∴点E为AB中点,
∵CA=CB,
∴CE⊥AB,
∴∠5+∠6=∠6+∠7=90°,
∴∠5=∠7,
∵CA=CB,∠ACB=90°,
∴∠CAB=∠CBA=45°,
∵∠AMC=90°,∠AEC=90°,
∴∠AMC+∠AEC=180°,
∴A,M,C,E四点共圆,
∴∠EMC=∠CAB=45°,
∴△MEJ为等腰直角三角形,∠AME=∠AMC﹣∠EMC=45°,
∴EM=EJ,∠J=45°,
∴∠J=∠AME,
∵CE⊥AB,∠CAB=45°,
∴△CEA为等腰直角三角形,
∴CE=AE,
在△EAM和△ECJ中,
,
∴△EAM≌△ECJ(ASA),
∴AM=CJ,
∵同理可得△EDB为等腰直角三角形,
∴DE=DB,
∵△MDN为等腰直角三角形,
同理可证明:△MDE≌△NDB,
∴EM=BN,∠2=∠4,
∵∠2=∠3,
∴∠3=∠4,
∴DF∥BN,
∴△CDF∽△CBN,
∴,则BN=2DF,
在等腰Rt△MEJ中,由勾股定理得,
∴,
∵,
∴,
∴,
∴(AM+CM)2=8DF2,即AM2+CM2+2AM×CM=8DF2,
∴AC2+2AM×CM=8DF2,
∵,,
∴AC2=2S△ABC,AM×CM=2S△AMC,
∴,
∴.
12.【解答】解:(1)∵四边形ABCD是矩形,
∴∠A=90°,
∴∠BPQ=∠A=90°,
∵△ABP与△BPQ相似,
∴或,
∵AB=6,BP=2PQ,
∴或,
∴AP=3或AP=12,
故答案为:3或12;
(2)解:过点Q作MN⊥AD于点M,与BC交于点N,
则∠A=∠PMQ=∠CNQ=90°,AB=MN=6,
∵∠BPQ=90°,
∴∠APB+∠MPQ=∠MPQ+∠PQM=90°,
∴∠APB=∠MQP,
∴△APB∽△MQP,
∴,
设MQ=x,则NQ=6﹣x,
∵BP=2PQ,AP=2,
∴2,
∴x=1,MP=3,
∴CN=DM=AD﹣MP﹣AP=8﹣3﹣2=3,
∴CQ2=QN2+CN2=52+32=34,
∴CQ;
(3)由(2)得,△APB∽△MQP,
∴,
设MQ=x,则NQ=6﹣x,
∵BP=2PQ,
∴2,
∴AP=2x,MP=3,
∴CN=DM=AD﹣MP﹣AP=8﹣3﹣2x=5﹣2x,
∴CQ2=QN2+CN2=(6﹣x)2+(5﹣2x)2,
=5(x)2,
当x时,CQ2的最小值为,
∴CQ长的最小值为.
13.【解答】(1)证明:如图1中,过点N作NH⊥CB交CB的延长线于点H.
∵MD=MN,∠DMN=90°,
∴△DMN是等腰直角三角形,
∴∠MDN=45°,
∵四边形ABCD是正方形,
∴CD=CB,∠C=∠ABC=90°,∠BDC=∠DBC=45°,
∵NH⊥CH,
∴∠H=∠DCM=90°,
∵∠NMH+∠DMC=90°,∠DMC+∠CDM=90°,
∴∠NMH=∠CDM,
∵MD=MN,
∴△DCM≌△MHN(AAS),
∴CD=MH=BC,CM=NH,
∴BH=CM=NH,
∴∠NBH=45°,
∴∠DBN=∠DCM=90°,
∵∠NDM=∠BDC,
∴∠NDB=∠MDC,
∴△DCM∽△DBN;
(2)解:①如图2中,过点P作PE⊥BD于点E,PF⊥BN于点F,NH⊥CB交CB的延长线于点H.
当x=1时,设CM=BM=a,则BD=2a,
由(1)可知NH=BH=CM=a,
∴BNa,
∵∠PBN=∠PBD=45°,PE⊥BD.PF⊥BN,
∴PE=PF,
∴,
∴,
∴y;
②如图3中,延长BC到T,使得CT=AP.
∵AD=CD,∠DAP=∠DCT=90°,AP=CT,
∴△DAP≌△DCT(SAS),
∴∠ADP=∠CDT,DP=DT,
∴∠PDT=∠ADC=90°,
∵∠PDM=45°,
∴∠PDM=∠TDM,
∵DM=DM,
∴△DMP≌△DMT(SAS),
∴∠DMP=∠DMT,
∵∠PMN=30°,∠DMN=90°,
∴∠DMT=∠DMP=90°﹣30°=60°,
∵CD=AB=2,
∴tan60°,
∴,
∴CM=2.
14.【解答】(1)证明:如图:
∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∴∠1+∠3=90°,
∵E、F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在DC上,
∴∠EPH=∠A=90°,
∴∠1+∠2=90°,
∴∠3=∠2,
∴△EDP∽△PCH;
(2)解:如图:
∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=3,∠A=∠D=∠C=90°,
∵P为CD中点,
∴,
设EP=AP=x,
∴ED=AD﹣x=3﹣x,
在Rt△EDP中,EP2=ED2+DP2,
即x2=(3﹣x)2+1,
解得,
∴,
∴ED=AD﹣AE,
∵△EDP∽△PCH,
∴,
∴,
解得,
∵PG=AB=2,
∴;
(3)解:如图:延长AB,PG交于一点M,连接AP,
∵E、F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在CD上,
∴AP⊥EF,BG⊥直线EF,
∴BG∥AP,
∵AE=EP,
∴∠EAP=∠EPA,
∴∠BAP=∠GPA,
∴△MAP是等腰三角形,
∴MA=MP,
∵P为CD中点,
∴设DP=CP=y,
∴AB=PG=CD=2y,
∵H为BC中点,
∴BH=CH,
∵∠BHM=∠CHP,∠CBM=∠PCH,
∴△MBH≌△PCH(ASA),
∴BM=CP=y,HM=HP,
∴MP=MA=MB+AB=3y,
∴,
在Rt△PCH中,,
∴,
∴,
在Rt△APD中,,
∵BG∥AP,
∴△BMG∽△MAP,
∴,
∴,
∴,
∴.
15.【解答】(1)①证明:∵AB=2AC,MN=2CM,
∴,
∴,
∵∠A=∠CMN=90°,
∴△ABC∽△MNC;
②解:过N作NG⊥AB,交AB延长线于点G,设MN与BC交于点P,
∵∠A=∠CMN=90°,
∴∠ACM=∠GMN=90°﹣∠CMA,
∵∠A=∠G=90°,
∴△CAM∽△MGN,
∴,
∴MG=2AC=AB,
由①知,△ABC∽△MNC,
∴∠CNM=∠CBM,,
∴,即,
∵∠CPN=∠MPB,
∴∠BCN=∠GMN,
∴△CBN∽△MGN,
∴∠CBN=∠MGN=90°;
(2)解:过N作NG⊥AB,交AB延长线于点G,
设AM=a,AC=b,则AB=2b,
由(1)②可知△CAM∽△MGN,
∴,
∴MG=2AC=2b,NG=2AM=2a,
∴AM=BG=a,
∴AG=AB+BG=a+2b,
过B作BH∥AC交AN于点H,
∴∠CAO=∠BHO,∠ABH=∠BAC=90°,
∵O是BC中点,
∴OC=OB,
∵∠COA=∠BOH,
∴△COA≌△BOH(SAS),
∴BH=AC=b,
∵∠ABH=∠G=90°,∠BAH=∠GAN,
∴△ABH∽△AGN,
∴,即,
整理可得ab,
∴.
21世纪教育网(www.21cnjy.com)
同课章节目录
