2025年中考数学三轮冲刺练习圆中相似三角形和锐角三角函数综合训练(含解析)
文档属性
| 名称 | 2025年中考数学三轮冲刺练习圆中相似三角形和锐角三角函数综合训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 16:25:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年中考数学三轮冲刺练习圆中相似三角形和锐角三角函数综合训练
1.如图1,在Rt△ABC中,∠ACB=90°,⊙O是△ABC的外接圆,点D是的中点,连结CD交AB于点E.
(1)求∠DCB的度数.
(2)如图2,过点A作AF⊥CD,连结OD,若,.
①若,求.
②连结OF,求OF的长.
2.如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,将△ABC沿直线AB翻折到△ABD,点D在⊙O上.连接CD,交AB于点E,延长BD,CA,两线相交于点P,过点A作⊙O的切线交BP于点G.
(1)求证:AG∥CD;
(2)求证:PA2=PG PB;
(3)若,求tan∠AGB的值.
3.如图,BC是⊙O的直径,点A在上,点E是AC的中点,连接OE并延长交于点D,过点D作DF∥AC交BC的延长线于点F.
(1)求证:DF是⊙O的切线:
(2)若点A为的中点,求证:四边形ACFD是平行四边形;
(3)在(2)的条件下,若⊙O的半径长为4,连接BE,求tan∠OBE的值.
4.如图,AB为⊙O的直径,点C在BA的延长线上,D为⊙O上一点,连接AD,BD,E,F分别是AD,BD的中点,连接OE,OF,延长CD,OF交于点P.
(1)求证:四边形OFDE是矩形;
(2)若∠ADC=∠EOA,求证:CD是⊙O的切线;
(3)在(2)的条件下,若,,求⊙O的半径.
5.如图,AB是半圆O的直径,动点C在半圆上,OD平分∠COB与圆O交于点D,连接CA.
(1)求证:OD∥AC;
(2)过点B作EB⊥AB,交OD的延长线于点E,设△OAC的面积为S1,△OBE的面积为S2.
①若,求tan∠ACO;
②若S1=S2,则tan∠ACO= (直接写出答案).
6.如图1,在等腰Rt△ABC中,AB=BC,∠ABC=90°,D为AC的中点,E为边BC上一点,连结AE,过点B作BG⊥AE于点G,⊙O经过点C,D,G,E,交射线BG于点F,连结CF.
(1)求证:△BEG∽△BFC.
(2)连结DF,CG,如图2,若∠DCG=∠FBC.记BF交AC于点H,求的值.
(3)当时(点D,G不重合),求tan∠BAE的值.
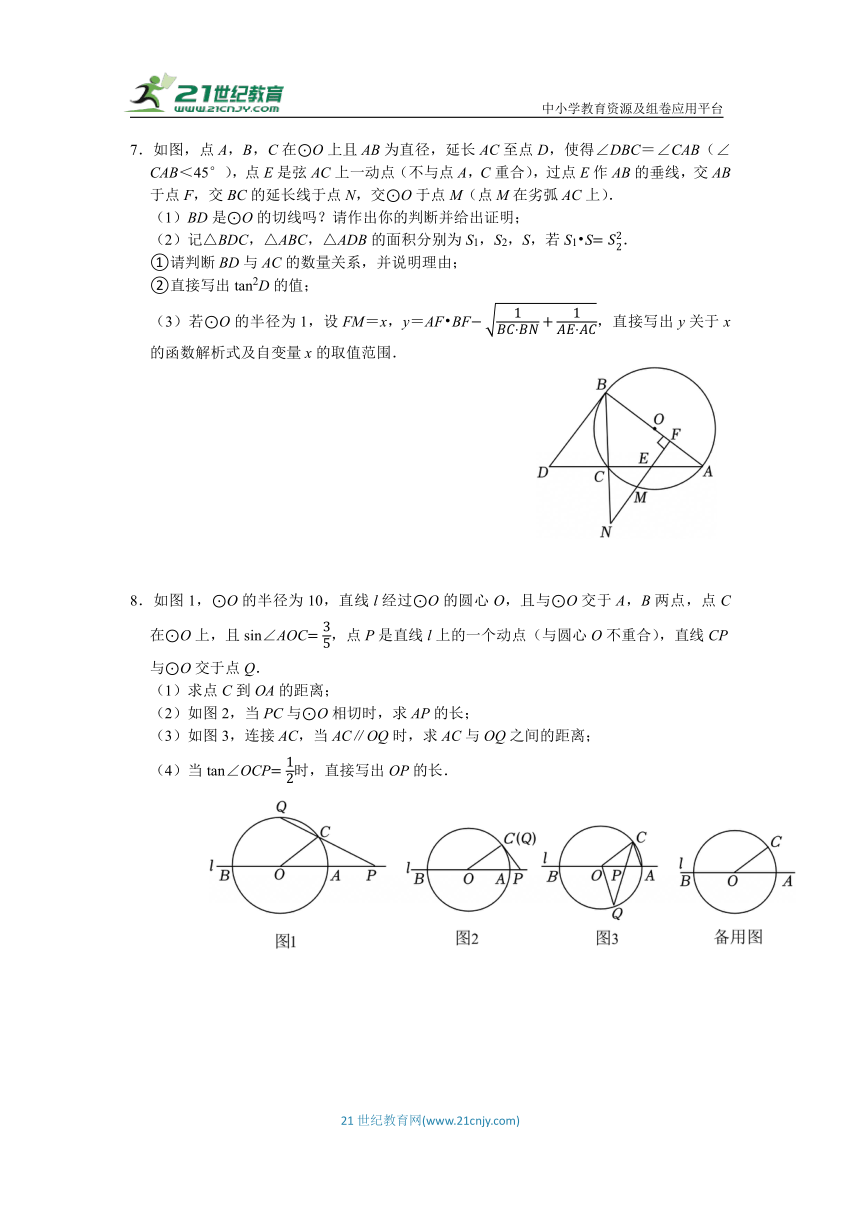
7.如图,点A,B,C在⊙O上且AB为直径,延长AC至点D,使得∠DBC=∠CAB(∠CAB<45°),点E是弦AC上一动点(不与点A,C重合),过点E作AB的垂线,交AB于点F,交BC的延长线于点N,交⊙O于点M(点M在劣弧AC上).
(1)BD是⊙O的切线吗?请作出你的判断并给出证明;
(2)记△BDC,△ABC,△ADB的面积分别为S1,S2,S,若S1 S.
①请判断BD与AC的数量关系,并说明理由;
②直接写出tan2D的值;
(3)若⊙O的半径为1,设FM=x,y=AF BF,直接写出y关于x的函数解析式及自变量x的取值范围.
8.如图1,⊙O的半径为10,直线l经过⊙O的圆心O,且与⊙O交于A,B两点,点C在⊙O上,且sin∠AOC,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O交于点Q.
(1)求点C到OA的距离;
(2)如图2,当PC与⊙O相切时,求AP的长;
(3)如图3,连接AC,当AC∥OQ时,求AC与OQ之间的距离;
(4)当tan∠OCP时,直接写出OP的长.
9.如图1,以点M(1,0)为圆心的圆与y轴、x轴分别交于点A、B、C、D,直线y与⊙M相切于点H,交x轴于点E,交y轴于点F.
(1)填空:OE的长为 ;OF的长为 ;⊙M的半径为 ;CH的长为 ;
(2)如图2,点P是直径CD上的一个动点(不与C、D重合),连结HP并延长交⊙M于点Q.
①当DP:PH=3:2时,求cos∠QHC的值;
②设tan∠QHC=x,y,求y与x的函数关系式.
10.已知点A,P,B,C在⊙O上,AB=AC,点D在BP的延长线上,连接AD.
(1)如图1,若AD∥BC,求证:AD是⊙O的切线;
(2)如图2,若,ADPD,BP=PD,,求AD的长.
11.如图,⊙O是锐角三角形ABC的外接圆,且满足AB<AC.D是BC的中点,连结DO并延长交AC于点E,与BA的延长线交于点F,连结CO并延长交⊙O于点G,连结FG,AG.
(1)若∠BAC=60°,,求OC的长.
(2)若FG与⊙O相切,G为切点.
①求证:△BDF∽△GAC;
②若∠BAC=45°,直接写出tanB和的值.
12.如图,AB为⊙O的直径,弦CD⊥AB于E,F为弦CD上一点,且∠DAF=∠C,射线AF与射线DB相交于点P.
(1)求证:F为AP的中点.
(2)①若sin∠DAF,求的值.
②当△CDP为直角三角形时,求∠DAF的正切值.
13.如图,在△ABC的外接圆中,弦BD平分∠ABC(∠ABC>90°),连结CD.延长BC至点E,使CE=CD,EF∥AC交CD于点F.
(1)若∠ABC=100°,求∠CFE的度数;
(2)①求证:BD=EF;
②若AB∥CD,,求的值.
14.如图,⊙O是△ABC的外接圆,点D位于⊙O外一点,连接AD,BD,CD.BD交⊙O于点E,连接CE.已知AB=AC=AD.
(1)如图1,求证:∠ACE=∠ADE.
(2)如图2,BD经过圆心O,AB=2CD.
①求cos∠BAC的值;
②若AB=3,求⊙O的半径.
15.如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E是BC的中点,连接BD、DE.
(1)求证:DE是⊙O的切线;
(2)若,求AD的长;
(3)若,点F是直线BC上一动点,连接AF交⊙O于点M,连接BM,求的最大值.
参考答案
一、选择题
1.【解答】解:(1)∵AB是直径,
∴的度数为180°,
∵点D是AB的中点,
∴的度数为90°,
∴∠DCB=45°;
(2)①∵,
设OE=a,则OD=2a,
∵,
∴OE=OD,
∴,
解得,
∵AF⊥CD,
∴∠AFE=90°,
∵∠AEF=∠OED,
∴∠FAE=∠D,
∴
∴,
∴EF=1,AF=2,
∵∠ACD=45°,
∴CF=AF=2,
∴CE=3,
在Rt△OED中,DE2=OE2+OD2=25,DE=5,
∴;
②当时
过点O作OG⊥CD,
∴,
∴EG=DE﹣DG=1,
∵EF=1,
∴GF=2,
∴△OEG∽△OED,
∴,
∴OG=2,
在Rt△OGF中,,
当时,
过点O作OG⊥CD,
∵∠BAF=∠D,
∴,
设OE=b,OD=OA=2b,
∵,
∴,
∴,
∴EF=1,AF=2,
∵△OEG∽△AEF,
∴,
∴OG,
在Rt△ODG中,,
在Rt△ODE中,,
∴,
∴,
∴.
2.【解答】(1)证明:∵将△ABC沿直线AB翻折到△ABD,点D在⊙O上,
∴AB⊥CD,
∵AB为⊙O的直径,AG是切线,
∴AG⊥AB,
∴AG∥CD;
(2)证明:∵AG∥CD,
∴∠PAG=∠PCD,
∵∠PCD=∠PBA,
∴∠PAG=∠PBA,
又∵∠APG=∠BPA,
∴△APG∽△BPA,
∴,即PA2=PG PB;
(3)解:∵,设AD=a,则AP=3a,
∴,
∴,
∵将△ABC沿直线AB翻折到△ABD,点D在⊙O上,
∴AC=AD=a,
∴PC=PA+AC=3a+a=4a,
在Rt△PCB中,,
∴,
∵AD⊥BD,GA⊥AB,
∴∠AGB=90°﹣∠GAD=∠DAB,
∴.
3.【解答】(1)证明:如图,连接OA.
∵点E是AC的中点,OA=OC,
∴OD⊥AC.
∵DF∥AC,
∴OD⊥DF.
∵OD是⊙O的半径,
∴DF是⊙O的切线.
(2)证明:由(1)可知,OD⊥AC,
∴.
∵点A为BD的中点,
∴,
∴,
∴∠ACB=∠CAD,
∴AD∥CF.
又∵DF∥AC,
∴四边形ACFD是平行四边形.
(3)解:如图,连接CD,过点E作EH⊥BC于点H.
由(2)可知,,
∴AD=CD,.
∵OC=OD,
∴△OCD是等边三角形,
∴CD=OC=4,
∴AD=OC=4.
∵∠EAD=∠ECO,∠AED=∠CEO,
∴△DAE≌△OCE(AAS),
∴OE=ED.
∵在Rt△OEH中,∠EOH=60°,OE=2,
∴,
∴BH=OB+OH=4+1=5,
∴,
∴tan∠OBE的值为.
4.【解答】(1)证明:∵AB为⊙O的直径,
∴∠ADB=90°,
∵E,F分别是AD,BD的中点,且OE,OF经过圆心O,
∴OE⊥AD,OF⊥BD,
∴∠EDF=∠DFO=90°,
∴∠EDF=∠DEO=∠DFO=90°,
∴四边形OFDE是矩形.
(2)证明:如图,连接OD.
∵OD=OA,
∴∠ADO=∠DAO,
∵OE⊥AD,
∴∠AEO=90°,
∴∠EAO+∠EOA=90°,
∵∠ADC=∠EOA,∠ADO=∠DAO,
∴∠ADC+∠ADO=90°,
即∠ODC=90°,
∴OD⊥CD,
又∵OD为半径,
∴CD是⊙O的切线.
(3)解:∵∠ODC=90°,
∴tanC,
设OA=OD=3x,CD=4x,
在 Rt△ODC 中,根据勾股定理,得,
∴AC=OC﹣OA=2x,
∵OF⊥BD,
∴∠DFP=90°,
∴∠ADF=∠DFP=90°,
∴AD∥OP,
∴,
即,
∴DP=6x,
∵OD⊥CD,
∴∠ODP=90°,
在Rt△ODP中,根据勾股定理,得,
即.
解得x=1,
∴OD=3x=3,
∴⊙O的半径为3.
5.【解答】(1)证明:∵AB是半圆O的直径,动点C在半圆上,OD平分∠COB与圆O交于点D,
∴,
∵,
∴∠COD=∠BOE=∠CAO,
∴OD∥AC;
(2)解:①过C作CH⊥AO于H,如图2:
∵,
∴,
∴,
∵∠A=∠BOE,
∴tan∠A=tan∠BOE,
∴,
∴,
设AH=m,则BO=2m=AO=CO,
∴OH=2m﹣m=m,
在直角三角形CHO中,由勾股定理得:,
∴,
∵OA=OC,
∴∠A=∠ACO,
∴;
②tan∠ACO=1;理由如下:
同①可知:当S1=S2时,则:,
∴AH=OB=OA,
∴点H与点O重合,
∴△AOC为等腰直角三角形,
∴∠ACO=∠A=45°,
∴tan∠ACO=tan45°=1.
故答案为:1.
6.【解答】(1)证明:BG⊥AE于点G,如图1,连接EF,则EF是⊙O的直径,
∴∠ECF=90°,
∴∠BGE=∠BCF,
又∵∠GBE=∠CBF,
∴△BEG∽△BFC;
(2)解:①如图2,
∵DF∥BC,
∴△DHF∽△CHB,
∴,
∴HFBF,
∵FC=3,BC=6,
∴BF3,则HFBF,
∴BH=BF﹣HF=2,
由(1)可得△BEG∽△BFC,
∴,
∴BG,
∴FG=BF﹣BG=3,
∴;
(3)点D是等腰Rt△ABC斜边AC上的中点,如图3,连接BD,DE,EF,DF,
∴BD=CD,BD⊥AC,
∵,
∴∠DFE=∠DCE=45°,
又∵EF是⊙O的直径,
∴∠FDE=90°,
∴△DEF是等腰直角三角形,
∴DE=DF,
在△BDE和△CDF中,
,
∴△BDE≌△CDF(SAS),
∴BE=CF,
设BE=x,则CF=BE=x,EC=BC﹣BE=6﹣x,
在Rt△ECF中,由勾股定理得:EF2=EC2+FC2=(6﹣x)2+x2,
在Rt△BCF中,由勾股定理得:BF2=FC2+BC2=62+x2,
∵,
∴CG=CDAC=3,
∵,
∴∠BFE=∠BCG,
又∵∠FBE=∠CBG,
∴△FBE∽△CBG,
∴,
∴,即,
∴2,
∴2,
解得:x1=2,x2=6(舍去),
∴BE=2,
∴tan∠BAE.
7.【解答】解:(1)BD是⊙O的切线.
证明: AB是⊙O的直径.
∴∠ACB=90°,
∴∠CAB+∠ABC=90°,
又∠DBC=∠CAB,
∴∠DBC+∠ABC=90°,
∴∠ABD=90°.
即AB⊥BD,
∵OD为半径,
∴BD是⊙O的切线.
(2)①BD=AC,理由如下:
由题意得,S1BC CD,S2BC AC,SAD BC.
∵,
∵.
∴CD AD=AC2,
∵,
即CD AD=BD2,
∴BD=AC;
②∵CD AD=AC.
∴CD(CD+AC)=AC2.
又∵∠D+∠DBC=90°,∠ABC+∠A=90°,∠DBC=∠A,
∴∠D=∠ABC.
∵.
∴,
∴CD(CD+AC)=AC2,
∴,
∴BC4+AC2 BC2=AC4.
∴,
由题意,设(tan∠D)2=m,
∴.
∴1+m=m2
∴,
∵m>0,
∴,
∴;
(3),0<x≤1.
设∠A=α,
∵∠A+∠ABC=∠ABC+∠DBC=∠ABC+∠N=90°,
∴∠A=∠DBC=∠N=α.
如图,连接OM.
∴.
∴,,
∴BF AF=x2,
∴.
∵BC=AB sinα=2sinα.r=1,
∴AB=2,
∴AC=AB cosα=2cosα.
∵,
∴y=AF BFx2
=x2x2x2,
即y=x2,
∵FM⊥AB,
∴FM最大值为F与O重合时,即为1.
∴0<x≤1.
8.【解答】解:(1)过点C作CH⊥AB于点H,如图,
∵CH⊥AB,sin∠AOC,
∴,
∴,
∴CH=6.
∴点C到OA的距离为6;
(2)∵PC与⊙O相切,
∴PC⊥OC,
∴sin∠AOC,
设PC=3k,则OP=5k,
∴OC4k,
∵⊙O的半径为10,
∴4k=10,
∴k,
∴OP=5k,
∴AP=OP﹣OA;
(3)过点C作CH⊥AB于点H,过点O作OE⊥AC于点E,如图,
由(1)知:CH=6,
∴OH8,
∴AH=OA﹣OH=2,
∴AC2.
∵,
∴OE3,
∵AC∥OQ,平行线之间的距离相等,
∴AC与OQ之间的距离为3;
(4)当tan∠OCP时,OP的长为5或25.理由:
①点P在点O的右侧时,过点P作PM⊥OC于点M,如图,
∵tan∠OCP,PM⊥OC,
∴,
设PM=m.则CM=2m,
∵sin∠AOC,PM⊥OC,
∴,
∴OPm,
∴OMm,
∴OC=OM+CMm,
∴m=10,
∴m=3,
∴OPm=5.
②点P在点O的左侧时,过点P作PN⊥OC交CO的延长线于点N,如图,
∵tan∠OCP,PN⊥OC,
∴,
设PN=n.则CN=2n,
∵sin∠AOC,∠AOC=∠PON,
∴sin∠PON,
∵PN⊥OC,
∴,
∴OPn,
∴ONn,
∴CN=ON+OC,
∴n+10=2n,
∴n=15,
∴OPn=25.
综上,当tan∠OCP时,OP的长为5或25.
9.【解答】解:(1)∵直线y交x轴于点E,交y轴于点F,
令y=0得,0,
解得x=5,
∴OE=5;
令x=0得,y,
∴OF;
∵tan∠OEF,
∴∠OEF=30°,
连接MH,则∠MHE=90°,
∵M(1,0),
∴OM=1,
∴EM=4,
∴MHEM=2,即⊙M的半径为2;
∵MC=MH,∠CMH=90°﹣30°=60°,
∴△MCH是等边三角形,
∴CH=2;
故答案为:5,,2,2;
(2)①连接DQ、CQ,
∵,
∴∠QDC=∠QHC,
∵∠QPD=∠CPH,
∴△DPQ∽△HPC,
∴,
∵CH=2,
∴DQ=3,
∵CD为直径,
∴CD=4,∠DQC=90°,
∴cos∠QDC,
∴cos∠QHC;
②由①知∠QDC=∠QHC,
∴tan∠QHC=tan∠QDCx,
如图,作QK⊥x轴于点K,HJ⊥x轴于点J,则HJ∥KQ,
∵∠MCH=60°,CM=2,
∴HJ=CH cos30°,
∵HJ∥KQ,
∴y,
∴KQy,
在Rt△DKQ中,tan∠KDQx,
∴DK,
∵CD=4,
∴CK=CD﹣DK=4,
∵∠DQC=90°,
∴∠KQC=90°﹣∠KQD=∠KDQ,
在Rt△KCQ中,tan∠KQCx,
∴CK=KQ x,即4y x,
整理得(x2+1)y=4x,
∴y与x的函数关系式为y.
10.【解答】(1)证明:如图1,连接AO并延长交BC于M,连接OB、OC,
在△AOB和△AOC中,
,
∴△AOB≌△AOC(SSS),
∴∠BAM=∠CAM,
∵AB=AC,
∴AM⊥BC,
∴∠AMC=90°,
∵AD∥BC,
∴∠DAM=∠AMC=90°,
∴OA⊥AD,
∴AD是⊙O的切线;
(2)解:如图2,过点C作CQ⊥PA交PA的延长线于点Q,
∵ADPD,BP=PD,
∴,,
∴,
又∵∠ADP=∠BDA,
∴△DAP∽△DBA,
∴,
∴,
设AP=a,则ACa,
∵∠APC=∠ABC,
∴tan∠APC=tan∠ABC,
∵PC,
∴QC=1,QP=2,
∴AQ=2﹣a,
在Rt△ACQ中,AQ2+CQ2=AC2,
∴12+(2﹣a)2=(a)2,
解得:a1=﹣5(舍去),a2=1,
∴PA=AQ=QC=1,AC,
由∠DAP=∠DBA=∠ACP,
∴△DPA∽△APC,
∴,
∴,
∴DA
∴AD的长为.
11.【解答】(1)解:连接OB,如图,
∵D是BC的中点,⊙O是锐角三角形ABC的外接圆,
∴BD=CDBC,OD⊥BD,
∵OB=OC,
∴∠DOC∠BOC,
∵∠BOC=2∠BAC=120°,
∴∠DOC=60°.
在Rt△ODC中,
∵sin∠DOC,
∴,
∴OC=2;
(2)①证明:∵CG为圆的直径,
∴∠GAC=90°,
∴∠AGC+∠ACG=90°,
∵∠AGC=∠B,
∴∠B+∠ACG=90°,
由(1)知:OD⊥BD,
∴∠B+∠BFD=90°,
∴∠BFD=∠ACG.
∵∠BDF=∠GAC=90°,
∴△BDF∽△GAC;
②解:连接OB,过点C作CH⊥AB于点H,如图,
设BD=CD=a,则BC=2a,
由(1)知:∠DOCBOC=∠BAC=45°,OD⊥BC,
∴OD=CD=a,
∴OCCDa,
∴GC=2OG=2OC=2a,
∵FG与⊙O相切,OG为圆的半径,
∴OG⊥FG,
∵∠GOF=∠DOC=45°,
∴FOOG=2a,
∴FD=OD+FO=3a,
∴tanB3.
∵CH⊥AB,
∴tanB3,
∴CH=3BH,
设BH=b,则CH=3b,
∵BH2+CH2=BC2,
∴b2+(3b)2=(2a)2,
∵b>0,
∴ba,
∴AH=CHa,BHa.
∴AB=AH+BHa.
∵BFa,
∴AF=BF﹣ABa.
∵∠BAC=∠DOC=45°,
∴∠FAE=∠COE=135°,
由(2)①知:∠BFD=∠ACG,
∴△FAE∽△COE,
∴.
∵CH⊥AB,∠BAC=45°,
∴ACCHa.
设OE=x,AE=y,则EF=2a﹣x,EC=AC﹣AEa﹣y,
∴,
∴,
∴EF=a,
由(2)①知:△BDF∽△GAC,
∴,
∴AGACa,
∴.
12.【解答】(1)证明:∵AB为⊙O的直径,弦CD⊥AB,
∴,
∴∠C=∠ADC,
∵∠DAF=∠C,
∴∠DAF=∠ADC,
∴AF=DF.
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠APD=∠FDP,
∴,
即F为AP的中点.
(2)解:①∵,且∠DAF=∠C=∠ADC,
∴,
设AE=3a,则AD=5a,
∴CE=DE=4a,
∵△DAF∽△DCA,
∴,
∴AD2=DF CD,
∴(5a)2=DF 8a,
解得,
∴.
②(i)当∠PCD=90°时,PC∥AE,
∴∠FAE=∠FPC,
由(1)得FA=FP,
∴△AEF≌△PCF(AAS),
∴CF=EF,AE=PC,
设CF=EF=b,
∴DE=CE=2b,DF=3b,
由(1)知,FD=FA=3b,
∴AE=2b,
∴.
(ii)当∠CPD=90°时,CP∥AD,
∴∠APC=∠PAD.
∵FA=FP,∠AFD=∠PFC,
∴△ADF≌△PCF(ASA),
∴PC=AD,
∴四边形ACPD为平行四边形,
又AC=AD,
∴四边形ACPD为正方形,
∴∠DAF=45°,
∴tan∠DAF=1.
综上,∠DAF的正切值为或1.
13.【解答】(1)解:∵BD平分∠ABC,∠ABC=100°,
∴∠ABD=∠CBD=50°,
∴∠ACD=∠ABD=50°,
∵EF∥AC,
∴∠CFE=∠ACD=50°;
(2)①证明:如图1,连接AD,
∵∠ABD=∠CBD,
∴,
∴AD=CD,
∵CD=CE,
∴AD=CE,
∵四边形ABCD是圆内接四边形,
∴∠FCE=∠BAD,
由(1)知:∠CFE=∠ABD,
∴△DAB≌△ECF(AAS),
∴BD=EF;
②解:如图2,连接AD,DE,过点F作FH⊥DE于点H,
∵AB∥CD,
∴∠ABD=∠BDC,
∴,
∴AD=BC,
∵AD=CE=CD,
∴BC=CD=CE,
∴∠CBD=∠CDB,∠CDE=∠CED,
∵∠CBD+∠CDB+∠CDE+∠CED=180°,
∴∠CDB+∠CDE=90°,
即∠BDE=90°,
∵tan∠CBD,
∴设DE=4a,BD=3a,则BE=5a,
∴CDBE=2.5a,
∵∠CBD+∠BED=90°,∠FDH+∠DFH=90°,
∴∠DFH=∠CBD,
∴tan∠DFH,
∴设DH=4x,FH=3x,则DF=5x,
∴EH=4a﹣4x,
在Rt△EHF中,FH2+EH2=EF2,
∴(3x)2+(4a﹣4x)2=(3a)2,
∴25x2﹣32ax+7a2=0,
(x﹣a)(25x﹣7a)=0,
a1=x(舍),a2,
∴CF=DC﹣DF=2.5a﹣5xx﹣5xx,
∴.
14.【解答】(1)证明:⊙O是△ABC的外接圆,
∴∠ACE=∠ABE,
∵AB=AD,
∴∠ABD=∠ADB,
∴∠ACE=∠ADE.
(2)解:①已知AB=AC=AD,如图2,连接AO,CO,
∵OB=OC,
∴∠AOB=∠AOC.
∵AO=BO=CO,
∴∠OBA=∠OAB=∠OAC=∠OCA,
∴.
∵AC=AD,
∴∠ACD=∠ADC.
∵∠ACE=∠ADE,
∴.
∵∠BAC=∠BEC,
∴∠OBA=∠OAB=∠ECD=∠EDC,
∴△ABO∽△CDE,
∴,
∵AB=2CD,
∴BO=2EC,
∴BE=4EC,
∵BD经过圆心O,
∴BD是⊙O的直径,
∴∠BCE=90°,
∴;
②已知AB=AC,∠OAB=∠OAC,如图3,延长AO交BC于点F,
∴AF⊥BC,
∴∠AFB=90°,BF=CF,
∵O为BE的中点,
∴,
由(2)①可得BO=AO=2CE,
在Rt△BFO中,由勾股定理理:,
在Rt△BFA中,由勾股定理得:,
∴,
∴(负根舍去),
∴.
15.【解答】(1)证明:设AB中点为O,连接OD,如图1,
∵AB为⊙O的直径,
∴∠ADB=∠CDB=90°,
∵∠CBD+∠ABD=∠CAB+∠ABD=90°,
∴∠CBD=∠CAB,
∵AO=DO,
∴∠CAB=∠ADO,
在Rt△BCD中,点E是BC的中点,
∴DE=BE=CE,
∴∠CBD=∠BDE,
∴∠ADO=∠BDE,
∵∠ADO+∠BDO=90°,
∴∠BDE+∠BDO=90°,
∴DE⊥OD,
∵OD是⊙O半径,
∴DE是⊙O的切线;
(2)解:在Rt△BCD中,点E是BC的中点,DE=5,
∴DE=BE=CE=5,
∴BC=10,
∵,
∴AB=20,
∵,
∴AD=2BD,
∴即,
∴(负值舍去);
(3)解:过点M作MG⊥AB,交AB于点G,如图2,
则∠AGM=90°,
∵AB为⊙O的直径,
∴∠AMB=90°,
∵∠AMG+∠MAB=∠AMG+∠BMG=90°,
∴∠MAB=∠BMG,
∵∠AGM=∠ABF=90°,
∴△MGB∽△ABF,
∴,
∵,
∴AB=8,
∴,
∴当MG最大时,有最大值,则当G点与O点重合时,即MG最大,为⊙O的半径,
∴此时,
∴,
∴的最大值为.
21世纪教育网(www.21cnjy.com)
2025年中考数学三轮冲刺练习圆中相似三角形和锐角三角函数综合训练
1.如图1,在Rt△ABC中,∠ACB=90°,⊙O是△ABC的外接圆,点D是的中点,连结CD交AB于点E.
(1)求∠DCB的度数.
(2)如图2,过点A作AF⊥CD,连结OD,若,.
①若,求.
②连结OF,求OF的长.
2.如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,将△ABC沿直线AB翻折到△ABD,点D在⊙O上.连接CD,交AB于点E,延长BD,CA,两线相交于点P,过点A作⊙O的切线交BP于点G.
(1)求证:AG∥CD;
(2)求证:PA2=PG PB;
(3)若,求tan∠AGB的值.
3.如图,BC是⊙O的直径,点A在上,点E是AC的中点,连接OE并延长交于点D,过点D作DF∥AC交BC的延长线于点F.
(1)求证:DF是⊙O的切线:
(2)若点A为的中点,求证:四边形ACFD是平行四边形;
(3)在(2)的条件下,若⊙O的半径长为4,连接BE,求tan∠OBE的值.
4.如图,AB为⊙O的直径,点C在BA的延长线上,D为⊙O上一点,连接AD,BD,E,F分别是AD,BD的中点,连接OE,OF,延长CD,OF交于点P.
(1)求证:四边形OFDE是矩形;
(2)若∠ADC=∠EOA,求证:CD是⊙O的切线;
(3)在(2)的条件下,若,,求⊙O的半径.
5.如图,AB是半圆O的直径,动点C在半圆上,OD平分∠COB与圆O交于点D,连接CA.
(1)求证:OD∥AC;
(2)过点B作EB⊥AB,交OD的延长线于点E,设△OAC的面积为S1,△OBE的面积为S2.
①若,求tan∠ACO;
②若S1=S2,则tan∠ACO= (直接写出答案).
6.如图1,在等腰Rt△ABC中,AB=BC,∠ABC=90°,D为AC的中点,E为边BC上一点,连结AE,过点B作BG⊥AE于点G,⊙O经过点C,D,G,E,交射线BG于点F,连结CF.
(1)求证:△BEG∽△BFC.
(2)连结DF,CG,如图2,若∠DCG=∠FBC.记BF交AC于点H,求的值.
(3)当时(点D,G不重合),求tan∠BAE的值.
7.如图,点A,B,C在⊙O上且AB为直径,延长AC至点D,使得∠DBC=∠CAB(∠CAB<45°),点E是弦AC上一动点(不与点A,C重合),过点E作AB的垂线,交AB于点F,交BC的延长线于点N,交⊙O于点M(点M在劣弧AC上).
(1)BD是⊙O的切线吗?请作出你的判断并给出证明;
(2)记△BDC,△ABC,△ADB的面积分别为S1,S2,S,若S1 S.
①请判断BD与AC的数量关系,并说明理由;
②直接写出tan2D的值;
(3)若⊙O的半径为1,设FM=x,y=AF BF,直接写出y关于x的函数解析式及自变量x的取值范围.
8.如图1,⊙O的半径为10,直线l经过⊙O的圆心O,且与⊙O交于A,B两点,点C在⊙O上,且sin∠AOC,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O交于点Q.
(1)求点C到OA的距离;
(2)如图2,当PC与⊙O相切时,求AP的长;
(3)如图3,连接AC,当AC∥OQ时,求AC与OQ之间的距离;
(4)当tan∠OCP时,直接写出OP的长.
9.如图1,以点M(1,0)为圆心的圆与y轴、x轴分别交于点A、B、C、D,直线y与⊙M相切于点H,交x轴于点E,交y轴于点F.
(1)填空:OE的长为 ;OF的长为 ;⊙M的半径为 ;CH的长为 ;
(2)如图2,点P是直径CD上的一个动点(不与C、D重合),连结HP并延长交⊙M于点Q.
①当DP:PH=3:2时,求cos∠QHC的值;
②设tan∠QHC=x,y,求y与x的函数关系式.
10.已知点A,P,B,C在⊙O上,AB=AC,点D在BP的延长线上,连接AD.
(1)如图1,若AD∥BC,求证:AD是⊙O的切线;
(2)如图2,若,ADPD,BP=PD,,求AD的长.
11.如图,⊙O是锐角三角形ABC的外接圆,且满足AB<AC.D是BC的中点,连结DO并延长交AC于点E,与BA的延长线交于点F,连结CO并延长交⊙O于点G,连结FG,AG.
(1)若∠BAC=60°,,求OC的长.
(2)若FG与⊙O相切,G为切点.
①求证:△BDF∽△GAC;
②若∠BAC=45°,直接写出tanB和的值.
12.如图,AB为⊙O的直径,弦CD⊥AB于E,F为弦CD上一点,且∠DAF=∠C,射线AF与射线DB相交于点P.
(1)求证:F为AP的中点.
(2)①若sin∠DAF,求的值.
②当△CDP为直角三角形时,求∠DAF的正切值.
13.如图,在△ABC的外接圆中,弦BD平分∠ABC(∠ABC>90°),连结CD.延长BC至点E,使CE=CD,EF∥AC交CD于点F.
(1)若∠ABC=100°,求∠CFE的度数;
(2)①求证:BD=EF;
②若AB∥CD,,求的值.
14.如图,⊙O是△ABC的外接圆,点D位于⊙O外一点,连接AD,BD,CD.BD交⊙O于点E,连接CE.已知AB=AC=AD.
(1)如图1,求证:∠ACE=∠ADE.
(2)如图2,BD经过圆心O,AB=2CD.
①求cos∠BAC的值;
②若AB=3,求⊙O的半径.
15.如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E是BC的中点,连接BD、DE.
(1)求证:DE是⊙O的切线;
(2)若,求AD的长;
(3)若,点F是直线BC上一动点,连接AF交⊙O于点M,连接BM,求的最大值.
参考答案
一、选择题
1.【解答】解:(1)∵AB是直径,
∴的度数为180°,
∵点D是AB的中点,
∴的度数为90°,
∴∠DCB=45°;
(2)①∵,
设OE=a,则OD=2a,
∵,
∴OE=OD,
∴,
解得,
∵AF⊥CD,
∴∠AFE=90°,
∵∠AEF=∠OED,
∴∠FAE=∠D,
∴
∴,
∴EF=1,AF=2,
∵∠ACD=45°,
∴CF=AF=2,
∴CE=3,
在Rt△OED中,DE2=OE2+OD2=25,DE=5,
∴;
②当时
过点O作OG⊥CD,
∴,
∴EG=DE﹣DG=1,
∵EF=1,
∴GF=2,
∴△OEG∽△OED,
∴,
∴OG=2,
在Rt△OGF中,,
当时,
过点O作OG⊥CD,
∵∠BAF=∠D,
∴,
设OE=b,OD=OA=2b,
∵,
∴,
∴,
∴EF=1,AF=2,
∵△OEG∽△AEF,
∴,
∴OG,
在Rt△ODG中,,
在Rt△ODE中,,
∴,
∴,
∴.
2.【解答】(1)证明:∵将△ABC沿直线AB翻折到△ABD,点D在⊙O上,
∴AB⊥CD,
∵AB为⊙O的直径,AG是切线,
∴AG⊥AB,
∴AG∥CD;
(2)证明:∵AG∥CD,
∴∠PAG=∠PCD,
∵∠PCD=∠PBA,
∴∠PAG=∠PBA,
又∵∠APG=∠BPA,
∴△APG∽△BPA,
∴,即PA2=PG PB;
(3)解:∵,设AD=a,则AP=3a,
∴,
∴,
∵将△ABC沿直线AB翻折到△ABD,点D在⊙O上,
∴AC=AD=a,
∴PC=PA+AC=3a+a=4a,
在Rt△PCB中,,
∴,
∵AD⊥BD,GA⊥AB,
∴∠AGB=90°﹣∠GAD=∠DAB,
∴.
3.【解答】(1)证明:如图,连接OA.
∵点E是AC的中点,OA=OC,
∴OD⊥AC.
∵DF∥AC,
∴OD⊥DF.
∵OD是⊙O的半径,
∴DF是⊙O的切线.
(2)证明:由(1)可知,OD⊥AC,
∴.
∵点A为BD的中点,
∴,
∴,
∴∠ACB=∠CAD,
∴AD∥CF.
又∵DF∥AC,
∴四边形ACFD是平行四边形.
(3)解:如图,连接CD,过点E作EH⊥BC于点H.
由(2)可知,,
∴AD=CD,.
∵OC=OD,
∴△OCD是等边三角形,
∴CD=OC=4,
∴AD=OC=4.
∵∠EAD=∠ECO,∠AED=∠CEO,
∴△DAE≌△OCE(AAS),
∴OE=ED.
∵在Rt△OEH中,∠EOH=60°,OE=2,
∴,
∴BH=OB+OH=4+1=5,
∴,
∴tan∠OBE的值为.
4.【解答】(1)证明:∵AB为⊙O的直径,
∴∠ADB=90°,
∵E,F分别是AD,BD的中点,且OE,OF经过圆心O,
∴OE⊥AD,OF⊥BD,
∴∠EDF=∠DFO=90°,
∴∠EDF=∠DEO=∠DFO=90°,
∴四边形OFDE是矩形.
(2)证明:如图,连接OD.
∵OD=OA,
∴∠ADO=∠DAO,
∵OE⊥AD,
∴∠AEO=90°,
∴∠EAO+∠EOA=90°,
∵∠ADC=∠EOA,∠ADO=∠DAO,
∴∠ADC+∠ADO=90°,
即∠ODC=90°,
∴OD⊥CD,
又∵OD为半径,
∴CD是⊙O的切线.
(3)解:∵∠ODC=90°,
∴tanC,
设OA=OD=3x,CD=4x,
在 Rt△ODC 中,根据勾股定理,得,
∴AC=OC﹣OA=2x,
∵OF⊥BD,
∴∠DFP=90°,
∴∠ADF=∠DFP=90°,
∴AD∥OP,
∴,
即,
∴DP=6x,
∵OD⊥CD,
∴∠ODP=90°,
在Rt△ODP中,根据勾股定理,得,
即.
解得x=1,
∴OD=3x=3,
∴⊙O的半径为3.
5.【解答】(1)证明:∵AB是半圆O的直径,动点C在半圆上,OD平分∠COB与圆O交于点D,
∴,
∵,
∴∠COD=∠BOE=∠CAO,
∴OD∥AC;
(2)解:①过C作CH⊥AO于H,如图2:
∵,
∴,
∴,
∵∠A=∠BOE,
∴tan∠A=tan∠BOE,
∴,
∴,
设AH=m,则BO=2m=AO=CO,
∴OH=2m﹣m=m,
在直角三角形CHO中,由勾股定理得:,
∴,
∵OA=OC,
∴∠A=∠ACO,
∴;
②tan∠ACO=1;理由如下:
同①可知:当S1=S2时,则:,
∴AH=OB=OA,
∴点H与点O重合,
∴△AOC为等腰直角三角形,
∴∠ACO=∠A=45°,
∴tan∠ACO=tan45°=1.
故答案为:1.
6.【解答】(1)证明:BG⊥AE于点G,如图1,连接EF,则EF是⊙O的直径,
∴∠ECF=90°,
∴∠BGE=∠BCF,
又∵∠GBE=∠CBF,
∴△BEG∽△BFC;
(2)解:①如图2,
∵DF∥BC,
∴△DHF∽△CHB,
∴,
∴HFBF,
∵FC=3,BC=6,
∴BF3,则HFBF,
∴BH=BF﹣HF=2,
由(1)可得△BEG∽△BFC,
∴,
∴BG,
∴FG=BF﹣BG=3,
∴;
(3)点D是等腰Rt△ABC斜边AC上的中点,如图3,连接BD,DE,EF,DF,
∴BD=CD,BD⊥AC,
∵,
∴∠DFE=∠DCE=45°,
又∵EF是⊙O的直径,
∴∠FDE=90°,
∴△DEF是等腰直角三角形,
∴DE=DF,
在△BDE和△CDF中,
,
∴△BDE≌△CDF(SAS),
∴BE=CF,
设BE=x,则CF=BE=x,EC=BC﹣BE=6﹣x,
在Rt△ECF中,由勾股定理得:EF2=EC2+FC2=(6﹣x)2+x2,
在Rt△BCF中,由勾股定理得:BF2=FC2+BC2=62+x2,
∵,
∴CG=CDAC=3,
∵,
∴∠BFE=∠BCG,
又∵∠FBE=∠CBG,
∴△FBE∽△CBG,
∴,
∴,即,
∴2,
∴2,
解得:x1=2,x2=6(舍去),
∴BE=2,
∴tan∠BAE.
7.【解答】解:(1)BD是⊙O的切线.
证明: AB是⊙O的直径.
∴∠ACB=90°,
∴∠CAB+∠ABC=90°,
又∠DBC=∠CAB,
∴∠DBC+∠ABC=90°,
∴∠ABD=90°.
即AB⊥BD,
∵OD为半径,
∴BD是⊙O的切线.
(2)①BD=AC,理由如下:
由题意得,S1BC CD,S2BC AC,SAD BC.
∵,
∵.
∴CD AD=AC2,
∵,
即CD AD=BD2,
∴BD=AC;
②∵CD AD=AC.
∴CD(CD+AC)=AC2.
又∵∠D+∠DBC=90°,∠ABC+∠A=90°,∠DBC=∠A,
∴∠D=∠ABC.
∵.
∴,
∴CD(CD+AC)=AC2,
∴,
∴BC4+AC2 BC2=AC4.
∴,
由题意,设(tan∠D)2=m,
∴.
∴1+m=m2
∴,
∵m>0,
∴,
∴;
(3),0<x≤1.
设∠A=α,
∵∠A+∠ABC=∠ABC+∠DBC=∠ABC+∠N=90°,
∴∠A=∠DBC=∠N=α.
如图,连接OM.
∴.
∴,,
∴BF AF=x2,
∴.
∵BC=AB sinα=2sinα.r=1,
∴AB=2,
∴AC=AB cosα=2cosα.
∵,
∴y=AF BFx2
=x2x2x2,
即y=x2,
∵FM⊥AB,
∴FM最大值为F与O重合时,即为1.
∴0<x≤1.
8.【解答】解:(1)过点C作CH⊥AB于点H,如图,
∵CH⊥AB,sin∠AOC,
∴,
∴,
∴CH=6.
∴点C到OA的距离为6;
(2)∵PC与⊙O相切,
∴PC⊥OC,
∴sin∠AOC,
设PC=3k,则OP=5k,
∴OC4k,
∵⊙O的半径为10,
∴4k=10,
∴k,
∴OP=5k,
∴AP=OP﹣OA;
(3)过点C作CH⊥AB于点H,过点O作OE⊥AC于点E,如图,
由(1)知:CH=6,
∴OH8,
∴AH=OA﹣OH=2,
∴AC2.
∵,
∴OE3,
∵AC∥OQ,平行线之间的距离相等,
∴AC与OQ之间的距离为3;
(4)当tan∠OCP时,OP的长为5或25.理由:
①点P在点O的右侧时,过点P作PM⊥OC于点M,如图,
∵tan∠OCP,PM⊥OC,
∴,
设PM=m.则CM=2m,
∵sin∠AOC,PM⊥OC,
∴,
∴OPm,
∴OMm,
∴OC=OM+CMm,
∴m=10,
∴m=3,
∴OPm=5.
②点P在点O的左侧时,过点P作PN⊥OC交CO的延长线于点N,如图,
∵tan∠OCP,PN⊥OC,
∴,
设PN=n.则CN=2n,
∵sin∠AOC,∠AOC=∠PON,
∴sin∠PON,
∵PN⊥OC,
∴,
∴OPn,
∴ONn,
∴CN=ON+OC,
∴n+10=2n,
∴n=15,
∴OPn=25.
综上,当tan∠OCP时,OP的长为5或25.
9.【解答】解:(1)∵直线y交x轴于点E,交y轴于点F,
令y=0得,0,
解得x=5,
∴OE=5;
令x=0得,y,
∴OF;
∵tan∠OEF,
∴∠OEF=30°,
连接MH,则∠MHE=90°,
∵M(1,0),
∴OM=1,
∴EM=4,
∴MHEM=2,即⊙M的半径为2;
∵MC=MH,∠CMH=90°﹣30°=60°,
∴△MCH是等边三角形,
∴CH=2;
故答案为:5,,2,2;
(2)①连接DQ、CQ,
∵,
∴∠QDC=∠QHC,
∵∠QPD=∠CPH,
∴△DPQ∽△HPC,
∴,
∵CH=2,
∴DQ=3,
∵CD为直径,
∴CD=4,∠DQC=90°,
∴cos∠QDC,
∴cos∠QHC;
②由①知∠QDC=∠QHC,
∴tan∠QHC=tan∠QDCx,
如图,作QK⊥x轴于点K,HJ⊥x轴于点J,则HJ∥KQ,
∵∠MCH=60°,CM=2,
∴HJ=CH cos30°,
∵HJ∥KQ,
∴y,
∴KQy,
在Rt△DKQ中,tan∠KDQx,
∴DK,
∵CD=4,
∴CK=CD﹣DK=4,
∵∠DQC=90°,
∴∠KQC=90°﹣∠KQD=∠KDQ,
在Rt△KCQ中,tan∠KQCx,
∴CK=KQ x,即4y x,
整理得(x2+1)y=4x,
∴y与x的函数关系式为y.
10.【解答】(1)证明:如图1,连接AO并延长交BC于M,连接OB、OC,
在△AOB和△AOC中,
,
∴△AOB≌△AOC(SSS),
∴∠BAM=∠CAM,
∵AB=AC,
∴AM⊥BC,
∴∠AMC=90°,
∵AD∥BC,
∴∠DAM=∠AMC=90°,
∴OA⊥AD,
∴AD是⊙O的切线;
(2)解:如图2,过点C作CQ⊥PA交PA的延长线于点Q,
∵ADPD,BP=PD,
∴,,
∴,
又∵∠ADP=∠BDA,
∴△DAP∽△DBA,
∴,
∴,
设AP=a,则ACa,
∵∠APC=∠ABC,
∴tan∠APC=tan∠ABC,
∵PC,
∴QC=1,QP=2,
∴AQ=2﹣a,
在Rt△ACQ中,AQ2+CQ2=AC2,
∴12+(2﹣a)2=(a)2,
解得:a1=﹣5(舍去),a2=1,
∴PA=AQ=QC=1,AC,
由∠DAP=∠DBA=∠ACP,
∴△DPA∽△APC,
∴,
∴,
∴DA
∴AD的长为.
11.【解答】(1)解:连接OB,如图,
∵D是BC的中点,⊙O是锐角三角形ABC的外接圆,
∴BD=CDBC,OD⊥BD,
∵OB=OC,
∴∠DOC∠BOC,
∵∠BOC=2∠BAC=120°,
∴∠DOC=60°.
在Rt△ODC中,
∵sin∠DOC,
∴,
∴OC=2;
(2)①证明:∵CG为圆的直径,
∴∠GAC=90°,
∴∠AGC+∠ACG=90°,
∵∠AGC=∠B,
∴∠B+∠ACG=90°,
由(1)知:OD⊥BD,
∴∠B+∠BFD=90°,
∴∠BFD=∠ACG.
∵∠BDF=∠GAC=90°,
∴△BDF∽△GAC;
②解:连接OB,过点C作CH⊥AB于点H,如图,
设BD=CD=a,则BC=2a,
由(1)知:∠DOCBOC=∠BAC=45°,OD⊥BC,
∴OD=CD=a,
∴OCCDa,
∴GC=2OG=2OC=2a,
∵FG与⊙O相切,OG为圆的半径,
∴OG⊥FG,
∵∠GOF=∠DOC=45°,
∴FOOG=2a,
∴FD=OD+FO=3a,
∴tanB3.
∵CH⊥AB,
∴tanB3,
∴CH=3BH,
设BH=b,则CH=3b,
∵BH2+CH2=BC2,
∴b2+(3b)2=(2a)2,
∵b>0,
∴ba,
∴AH=CHa,BHa.
∴AB=AH+BHa.
∵BFa,
∴AF=BF﹣ABa.
∵∠BAC=∠DOC=45°,
∴∠FAE=∠COE=135°,
由(2)①知:∠BFD=∠ACG,
∴△FAE∽△COE,
∴.
∵CH⊥AB,∠BAC=45°,
∴ACCHa.
设OE=x,AE=y,则EF=2a﹣x,EC=AC﹣AEa﹣y,
∴,
∴,
∴EF=a,
由(2)①知:△BDF∽△GAC,
∴,
∴AGACa,
∴.
12.【解答】(1)证明:∵AB为⊙O的直径,弦CD⊥AB,
∴,
∴∠C=∠ADC,
∵∠DAF=∠C,
∴∠DAF=∠ADC,
∴AF=DF.
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠APD=∠FDP,
∴,
即F为AP的中点.
(2)解:①∵,且∠DAF=∠C=∠ADC,
∴,
设AE=3a,则AD=5a,
∴CE=DE=4a,
∵△DAF∽△DCA,
∴,
∴AD2=DF CD,
∴(5a)2=DF 8a,
解得,
∴.
②(i)当∠PCD=90°时,PC∥AE,
∴∠FAE=∠FPC,
由(1)得FA=FP,
∴△AEF≌△PCF(AAS),
∴CF=EF,AE=PC,
设CF=EF=b,
∴DE=CE=2b,DF=3b,
由(1)知,FD=FA=3b,
∴AE=2b,
∴.
(ii)当∠CPD=90°时,CP∥AD,
∴∠APC=∠PAD.
∵FA=FP,∠AFD=∠PFC,
∴△ADF≌△PCF(ASA),
∴PC=AD,
∴四边形ACPD为平行四边形,
又AC=AD,
∴四边形ACPD为正方形,
∴∠DAF=45°,
∴tan∠DAF=1.
综上,∠DAF的正切值为或1.
13.【解答】(1)解:∵BD平分∠ABC,∠ABC=100°,
∴∠ABD=∠CBD=50°,
∴∠ACD=∠ABD=50°,
∵EF∥AC,
∴∠CFE=∠ACD=50°;
(2)①证明:如图1,连接AD,
∵∠ABD=∠CBD,
∴,
∴AD=CD,
∵CD=CE,
∴AD=CE,
∵四边形ABCD是圆内接四边形,
∴∠FCE=∠BAD,
由(1)知:∠CFE=∠ABD,
∴△DAB≌△ECF(AAS),
∴BD=EF;
②解:如图2,连接AD,DE,过点F作FH⊥DE于点H,
∵AB∥CD,
∴∠ABD=∠BDC,
∴,
∴AD=BC,
∵AD=CE=CD,
∴BC=CD=CE,
∴∠CBD=∠CDB,∠CDE=∠CED,
∵∠CBD+∠CDB+∠CDE+∠CED=180°,
∴∠CDB+∠CDE=90°,
即∠BDE=90°,
∵tan∠CBD,
∴设DE=4a,BD=3a,则BE=5a,
∴CDBE=2.5a,
∵∠CBD+∠BED=90°,∠FDH+∠DFH=90°,
∴∠DFH=∠CBD,
∴tan∠DFH,
∴设DH=4x,FH=3x,则DF=5x,
∴EH=4a﹣4x,
在Rt△EHF中,FH2+EH2=EF2,
∴(3x)2+(4a﹣4x)2=(3a)2,
∴25x2﹣32ax+7a2=0,
(x﹣a)(25x﹣7a)=0,
a1=x(舍),a2,
∴CF=DC﹣DF=2.5a﹣5xx﹣5xx,
∴.
14.【解答】(1)证明:⊙O是△ABC的外接圆,
∴∠ACE=∠ABE,
∵AB=AD,
∴∠ABD=∠ADB,
∴∠ACE=∠ADE.
(2)解:①已知AB=AC=AD,如图2,连接AO,CO,
∵OB=OC,
∴∠AOB=∠AOC.
∵AO=BO=CO,
∴∠OBA=∠OAB=∠OAC=∠OCA,
∴.
∵AC=AD,
∴∠ACD=∠ADC.
∵∠ACE=∠ADE,
∴.
∵∠BAC=∠BEC,
∴∠OBA=∠OAB=∠ECD=∠EDC,
∴△ABO∽△CDE,
∴,
∵AB=2CD,
∴BO=2EC,
∴BE=4EC,
∵BD经过圆心O,
∴BD是⊙O的直径,
∴∠BCE=90°,
∴;
②已知AB=AC,∠OAB=∠OAC,如图3,延长AO交BC于点F,
∴AF⊥BC,
∴∠AFB=90°,BF=CF,
∵O为BE的中点,
∴,
由(2)①可得BO=AO=2CE,
在Rt△BFO中,由勾股定理理:,
在Rt△BFA中,由勾股定理得:,
∴,
∴(负根舍去),
∴.
15.【解答】(1)证明:设AB中点为O,连接OD,如图1,
∵AB为⊙O的直径,
∴∠ADB=∠CDB=90°,
∵∠CBD+∠ABD=∠CAB+∠ABD=90°,
∴∠CBD=∠CAB,
∵AO=DO,
∴∠CAB=∠ADO,
在Rt△BCD中,点E是BC的中点,
∴DE=BE=CE,
∴∠CBD=∠BDE,
∴∠ADO=∠BDE,
∵∠ADO+∠BDO=90°,
∴∠BDE+∠BDO=90°,
∴DE⊥OD,
∵OD是⊙O半径,
∴DE是⊙O的切线;
(2)解:在Rt△BCD中,点E是BC的中点,DE=5,
∴DE=BE=CE=5,
∴BC=10,
∵,
∴AB=20,
∵,
∴AD=2BD,
∴即,
∴(负值舍去);
(3)解:过点M作MG⊥AB,交AB于点G,如图2,
则∠AGM=90°,
∵AB为⊙O的直径,
∴∠AMB=90°,
∵∠AMG+∠MAB=∠AMG+∠BMG=90°,
∴∠MAB=∠BMG,
∵∠AGM=∠ABF=90°,
∴△MGB∽△ABF,
∴,
∵,
∴AB=8,
∴,
∴当MG最大时,有最大值,则当G点与O点重合时,即MG最大,为⊙O的半径,
∴此时,
∴,
∴的最大值为.
21世纪教育网(www.21cnjy.com)
同课章节目录
