第六章平行四边形期末复习练习(含解析)
文档属性
| 名称 | 第六章平行四边形期末复习练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 712.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第六章平行四边形期末复习练习北师大版2024—2025学年八年级下册
一、选择题
1.如果一个正多边形的内角和是外角和的4倍,那么这个正多边形的边数为( )
A.7 B.8 C.9 D.10
2.观察图,根据所标注的数据能判断其一定是平行四边形的是( )
A.只有③ B.只有② C.①② D.①②③
3.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F.若AE=4,AF=6,且 ABCD的周长为40,则 ABCD的面积为( )
A.24 B.36 C.40 D.48
4.下列关于平行四边形的说法中错误的是( )
A.平行四边形的对角相等,邻角互补
B.一组对边相等,一组对角相等的四边形是平行四边形
C.一组对边平行,一组对角相等的四边形是平行四边形
D.一组对边平行且相等的四边形是平行四边形
5.如图,在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AB=BC B.AD=BC
C.∠A=∠C D.∠B+∠C=180°
6.在平面直角坐标系中, PQMN的三个顶点坐标分别是P(﹣5,﹣10),Q(15,﹣3),M(6,8),则N点坐标是( )
A.(﹣15,5) B.(﹣14,1) C.(﹣14,5) D.(﹣15,1)
7.如图,点D,E,F分别是△ABC的边AB,BC,AC的中点,分别连接DE,EF,DF,AE,AE与DF相交于点O.有下列四个结论:
①;
②S△DEFS△ABC;
③当AB=AC时,点O到四边形ADEF四条边的距离相等;
④当∠ABC=90°时,点O到四边形ADEF四个顶点的距离相等.
其中正确的结论是( )
A.①② B.③④ C.②③ D.①④
8.如图,点O是 ABCD的对角线的交点,∠ABC=120°,∠ADC的平分线DE交AB于点E,AB=2AD,连接OE.下列结论:①S ABCD=AD BD;②DB平分∠CDE;③AO=DE;④OE:BD:6;⑤S△ADE=5S△OFE,其中正确的个数有( )
A.2个 B.3个 C.4个 D.5个
二、填空题
9.在平面直角坐标系中, ABCD的顶点坐标分别是A(0,1),C(3,﹣2),B(a,b),则D的坐标为 .
10.如图,四边形ABCD为长方形,点E、F分别为AD、BC边上一点,将长方形ABCD沿EF翻折,点A、B分别落在G、H处,若∠1=α,则∠2= .(用含α的代数式表示)
11.一个正五边形与一个正六边形按如图所示方式放置,若AB、AC分别平分正五边形与正六边形的一个内角,则∠BAC的度数为 .
12.如图, ABCD的对角线AC,BD相交于点O,DE∥AC,CE∥BD,若AC=3,BD=5,则四边形OCED的周长为 .
三、解答题
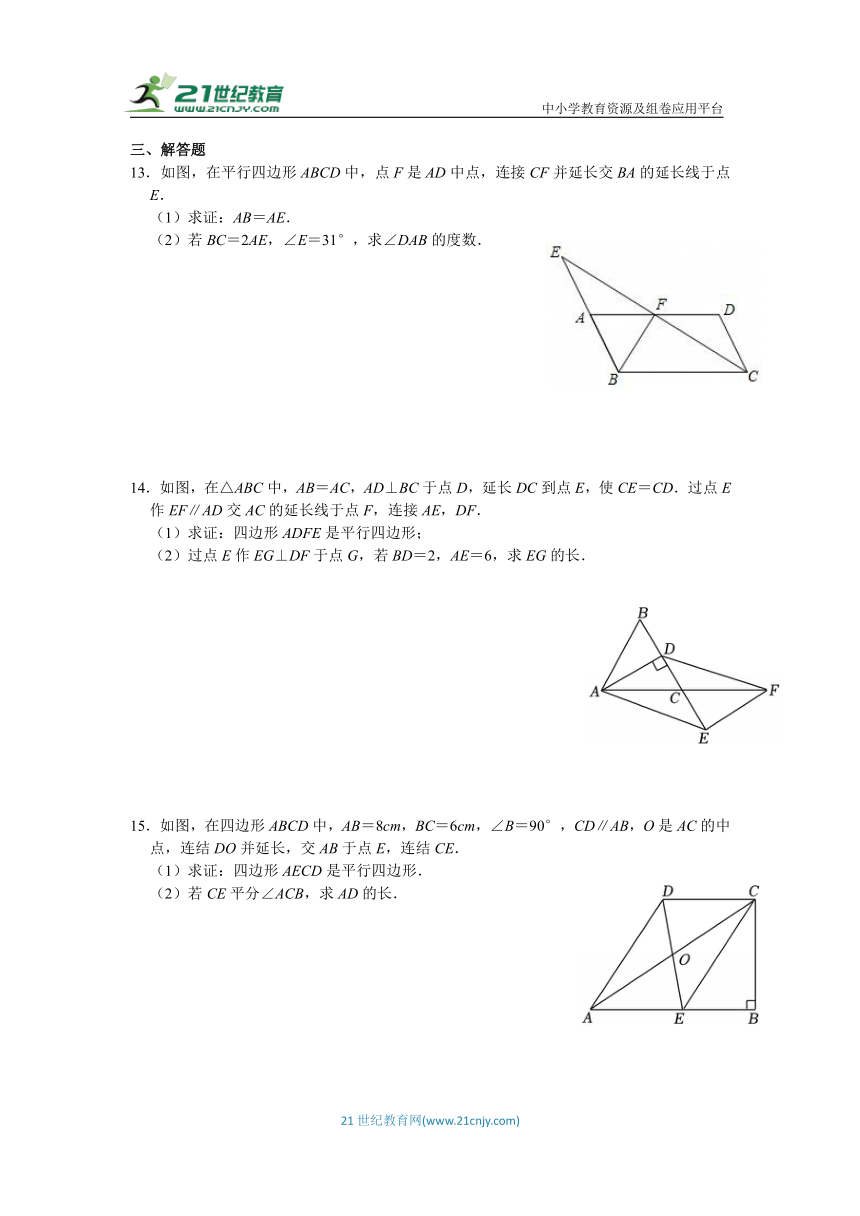
13.如图,在平行四边形ABCD中,点F是AD中点,连接CF并延长交BA的延长线于点E.
(1)求证:AB=AE.
(2)若BC=2AE,∠E=31°,求∠DAB的度数.
14.如图,在△ABC中,AB=AC,AD⊥BC于点D,延长DC到点E,使CE=CD.过点E作EF∥AD交AC的延长线于点F,连接AE,DF.
(1)求证:四边形ADFE是平行四边形;
(2)过点E作EG⊥DF于点G,若BD=2,AE=6,求EG的长.
15.如图,在四边形ABCD中,AB=8cm,BC=6cm,∠B=90°,CD∥AB,O是AC的中点,连结DO并延长,交AB于点E,连结CE.
(1)求证:四边形AECD是平行四边形.
(2)若CE平分∠ACB,求AD的长.
16.如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使CFBC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长;
(3)求四边形DEFC的面积.
17.如图,四边形ABCD为平行四边形,线段AC为对角线,点E、F分别为线段BC、AD的中点,连接EF交AC于点O.
(1)求证:四边形AECF为平行四边形;
(2)若OF=3,求CD的长.
18.【建立模型】如图1,在∠A内部有一点P,连接BP、CP,求证:∠P=∠1+∠A+∠2;
【尝试应用】如图2,利用上面的结论,直接写出五角星中,∠A+∠B+∠C+∠D+∠E= 度;
【拓展创新】如图3,将五角星截去一个角后多出一个角,求∠A+∠B+∠C+∠D+∠E+∠G的度数.
【提升思维】如图4,将五角星的每个角都截去,则一共得到10个角,则这10个角的和∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠J的度数是 度.
参考答案
一、选择题
1.【解答】解:设正多边形的边数为n,由题意得:
(n﹣2) 180°=4×360°,
解得:n=10,
故选:D.
2.【解答】解:①、由同旁内角互补,两直线平行,只能判定四边形的上下一组对边平行,不能判定四边形是平行四边形,故①不符合题意;
②、由同旁内角互补,两直线平行,只能判定四边形的左右一组对边平行,不能判定四边形是平行四边形,故②不符合题意;
③、由同旁内角互补,两直线平行,判定四边形的上下一组对边平行,并且上下一组对边相等,判定四边形是平行四边形,故③符合题意.
∴判定四边形一定是平行四边形的只有③.
故选:A.
3.【解答】解:设BC=x,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵ ABCD的周长为40,
∴BC+CD=20,
∴CD=20﹣x,
∵AE⊥BC于点E,AF⊥CD于点F,
∵ ABCD的面积=BC AE=CD AF,
∴4x=6(20﹣x),
解得:x=12,
∴ ABCD的面积=BC AE=12×4=48.
故选:D.
4.【解答】解:∵平行四边形的对角相等,且两组对边分别平行,
∴平行四边形的邻角互补,
故A不符合题意;
如图1,△ABE中,AE=AB,在BE上取一点C,使CE≠BC,作AC的垂直平分线交AE于点F,连接并延长CF到点D,使DF=EF,连接AD,
∵CF=AF,DF=EF,
∴CF+DF=AF+EF,
∴CD=AE=AB,
在△AFD和△CFE中,
,
∴△AFD≌△CFE(SAS),
∴∠D=∠E=∠B,
∴四边形ABCD是一组对边相等,一组对角相等的四边形,但四边形ABCD不是平行四边形,
∴一组对边相等,一组对角相等的四边形不一定是平行四边形,
故B符合题意;
如图2,AD∥BC,∠A=∠C,∵∠A+∠B=180°,
∴∠C+∠B=180°,
∴CD∥AB,
∴四边形ABCD是平行四边形,
∴一组对平行,一组对角相等的四边形是平行四边形,
故C不符合题意;
根据平行四边形的判定定理,一组对边平行且相等的四边形是平行四边形,
故D不符合题意,
故选:B.
5.【解答】解:一定能判定四边形ABCD是平行四边形的是∠A=∠C,理由如下:
∵AB∥CD,
∴∠A+∠D=180°,
∵∠A=∠C,
∴∠C+∠D=180°,
∴AD∥BC,
又∵AB∥CD,
∴四边形ABCD是平行四边形,
故选:C.
6.【解答】解:设N(x,y),
∵四边形PQMN是平行四边形,P(﹣5,﹣10),Q(15,﹣3),M(6,8),
∴|x﹣6|=|﹣5﹣15|,|y+10|=|8+3|,
∵N点在第二象限,
∴x<0,y>0,
∴x=﹣14,y=1,
∴N(﹣14,1),
故选:B.
7.【解答】解:①∵点D,E,F分别是△ABC的边AB,BC,AC的中点,
∴DFBC,BEAC,DF∥BC,
∴AO=EO,
∴OD是△ABE的中位线,
∴ODBE,故①错误;
②∵点D,E,F分别是△ABC的边AB,BC,AC的中点,
∴DF∥BC,DFBC,BE=CE,DE∥AF,EF∥AD,
∴四边形ADEF和四边形DBEF和四边形DECF是平行四边形,
∴S△ADF=S△DEF=S△BDE=S△CEF,
∴S△DEFS△ABC,故②正确;
③∵AB=AC,
∴AD=AF,
∵四边形ADEF是平行四边形,
∴四边形ADEF是菱形,
∴AE,DF是菱形两组对角的平分线,
∴点O到四边形ADEF四条边的距离相等,故③正确;
④∵∠ABC=90°,四边形ADEF是平行四边形,
∴点O到四边形ADEF四个顶点的距离不相等,故④错误.
综上所述:正确的是②③,共2个,
故选:C.
8.【解答】解:在 ABCD中,
∵∠BAD=∠BCD=60°,∠ADC=120°,DE平分∠ADC,
∴∠ADE=∠DAE=∠AED=60°,
∴△ADE是等边三角形,
∴,
∴E是AB的中点,
∴DE=BE,
∴,
∴∠ADB=90°,即AD⊥BD,
∴S ABCD=AD BD,故①正确;
∵∠CDE=60°,∠BDE=30°,
∴∠CDB=∠CDE﹣∠BDE=60°﹣30°=30°,
∴∠CDB=BDE,
故DB平分∠CDE,故②正确;
依据Rt△AOD中,AO>AD,即可得到AO>DE,故③错误;
∵O是BD中点,E为AB中点,
∴OE是△ABD的中位线,
∴,OE∥AD,
在Rt△ABD中,,
∴,
∴,故④正确;
∵OE∥AD,
∴△ADF∽△OEF,
∴,
∴S△ADF=4S△OEF,S△AEF=2S△OEF
∴S△ADE=S△ADF+S△AEF=6S△OEF,故⑤错误;
∴正确的有3个,
故选:B.
二、填空题
9.【解答】解:∵A(0,1),C(3,﹣2),
∴AC的中点坐标为(,),
即(,),
设点D(x,y),
∵B(a,b),
∴,,
解得:x=﹣a+3,y=﹣b﹣1,
∴点D的坐标为(﹣a+3,﹣b﹣1),
故答案为:(﹣a+3,﹣b﹣1).
10.【解答】解:如图,由折叠可知,∠2=∠4,∠H=∠B=90°,
∵AD∥BC,
∴∠2=∠3,
∵∠1+∠5=180°,
∴∠5=180°﹣∠1=180°﹣α,
∵∠4+∠3+∠5+∠H=360°,
∴2∠2+180°﹣α+90°=360°,
即∠2=45α,
故答案为:45α.
11.【解答】解:根据题意可知,正五边形的内角为:,
正六边形的内角为:,
AB、AC分别平分正八边形与正六边形的一个内角,
∴.
故答案为:114°.
12.【解答】解:∵ ABCD的对角线AC,BD相交于点O,AC=3,BD=5,
∴,
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∴四边形OCED的周长,
故答案为:8.
三、解答题
13.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,BC=AD,
∴∠E=∠DCF,
∵点F是AD中点,
∴AF=DF,
∵∠EFA=∠CFD,
∴△AFE≌△DFC(AAS),
∴CD=AE,
∴AB=AE;
(2)解:由(1)可得AF=DF,BC=AD,
∵BC=2AE,
∴AE=AF,
∵∠E=31°,
∴∠AFE=∠E=31°,
∴∠DAB=2∠E=62°.
14.【解答】(1)证明:∵EF∥AD,
∴∠FEC=∠ADC,
又∵CE=CD,∠FCE=∠ACD,
∴△FCE≌△ACD(ASA),
∴EF=AD,
∴四边形ADFE是平行四边形;
(2)解:如图,
由(1)可知,四边形ADFE是平行四边形,
∴DF=AE=6,
∵AB=AC,AD⊥BC,
∴CD=BD=2,
∴CE=CD=2,
∴DE=2CD=4,
∵EF∥AD,
∴EF⊥BC,
∴∠DEF=90°,
∴EF2,
∵EG⊥DF,
∴S△DEFDF EG EF,
∴EG,
即EG的长为.
15.【解答】(1)证明:∵CD∥AB,
∴∠ACD=∠CAE,
∵O是AC的中点,
∴AO=CO,
在△AOE与△COD中,
,
∴△AOE≌△COD(ASA),
∴AE=CD,又AE∥CD,
∴四边形AECD是平行四边形;
(2)解:如图,过点E作EF⊥AC于F,
在Rt△ABC中,AB=8cm,BC=6cm,∠B=90°,
由勾股定理得:AC10(cm),
∵CE平分∠ACB,∠B=90°,EF⊥AC,
∴EF=EB,
则,
∴,
∵AB=8cm,
∴BE=3cm,
∴CE3(cm),
由(1)可知:四边形AECD是平行四边形,
∴AD=CE=3cm.
16.【解答】解:(1)在△ABC中,
∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DEBC,
∵CFBC,
∴DE=CF.
(2)∵AC=BC,AD=BD,
∴CD⊥AB,
∵BC=4,BD=2,
∴CD2,
∵DE∥CF,DE=CF,
∴四边形DEFC是平行四边形,
∴EF=CD=2.
(3)过点D作DH⊥BC于H.
∵∠DHC=90°,∠DCB=30°,
∴DHDC,
∵DE=CF=2,
∴S四边形DEFC=CF DH=22.
17.【解答】(1)证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
∵点E、F分别为线段BC、AD的中点,
∴AFAD,CEBC,
∴AF=CE,
∵AF∥CE,
∴四边形AECF为平行四边形;
(2)解:∵四边形AECF为平行四边形,
∴OA=OC,
∵AF=DF,
∴OF为△ACD的中位线,
∴CD=2OF=2×3=6.
18.【解答】【建立模型】证明:延长BP交AC于点M,如图1所示:
由三角形外角性质得:∠BPC=∠1+∠PMC,∠PMC=∠A+∠2,
∴∠BPC=∠1+∠A+∠2;
【尝试应用】解:设BD与CE相交于点N,如图2所示:
由【建立模型】得:∠CND=∠A+∠C+∠D,
∵∠BNE=∠CND,
∴∠BNE=∠A+∠C+∠D,
在△BEN中,∠BNE+∠B+∠E=180°,
∴∠A+∠C+∠D+∠B+∠E=180°,
故答案为:180;
【拓展创新】解:延长CA与DG的延长线相交于点K,如图3所示:
∵∠CAG=180°﹣∠KAG,∠DGA=180°﹣∠KGA,
∴∠CAG+∠DGA=360°﹣(∠KAG+∠KGA),
在△KAG中,∠KAG+∠KGA=180°﹣∠K,
∴∠CAG+∠DGA=360°﹣(180°﹣∠K)=180°+∠K,
由【尝试应用】得:∠K+∠B+∠C+∠D+∠E=180°,
∴∠CAG+∠B+∠C+∠D+∠E+∠∠DGA
=∠CAG+∠DGA+∠B+∠C+∠D+∠E
=180°+∠K+∠B+∠C+∠D+∠E
=180°+180°
=360°;
【提升思维】解:由【拓展创新】得:当五角星去掉一个角后多出一个角时,此时所有角的和的度数比五角星的内角和多出180°,
∴当五角星去掉五个角后多出五个角,此时所有角的和的度数为:180°+5×180°=1080°.
故答案为:1080.
21世纪教育网(www.21cnjy.com)
第六章平行四边形期末复习练习北师大版2024—2025学年八年级下册
一、选择题
1.如果一个正多边形的内角和是外角和的4倍,那么这个正多边形的边数为( )
A.7 B.8 C.9 D.10
2.观察图,根据所标注的数据能判断其一定是平行四边形的是( )
A.只有③ B.只有② C.①② D.①②③
3.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F.若AE=4,AF=6,且 ABCD的周长为40,则 ABCD的面积为( )
A.24 B.36 C.40 D.48
4.下列关于平行四边形的说法中错误的是( )
A.平行四边形的对角相等,邻角互补
B.一组对边相等,一组对角相等的四边形是平行四边形
C.一组对边平行,一组对角相等的四边形是平行四边形
D.一组对边平行且相等的四边形是平行四边形
5.如图,在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
A.AB=BC B.AD=BC
C.∠A=∠C D.∠B+∠C=180°
6.在平面直角坐标系中, PQMN的三个顶点坐标分别是P(﹣5,﹣10),Q(15,﹣3),M(6,8),则N点坐标是( )
A.(﹣15,5) B.(﹣14,1) C.(﹣14,5) D.(﹣15,1)
7.如图,点D,E,F分别是△ABC的边AB,BC,AC的中点,分别连接DE,EF,DF,AE,AE与DF相交于点O.有下列四个结论:
①;
②S△DEFS△ABC;
③当AB=AC时,点O到四边形ADEF四条边的距离相等;
④当∠ABC=90°时,点O到四边形ADEF四个顶点的距离相等.
其中正确的结论是( )
A.①② B.③④ C.②③ D.①④
8.如图,点O是 ABCD的对角线的交点,∠ABC=120°,∠ADC的平分线DE交AB于点E,AB=2AD,连接OE.下列结论:①S ABCD=AD BD;②DB平分∠CDE;③AO=DE;④OE:BD:6;⑤S△ADE=5S△OFE,其中正确的个数有( )
A.2个 B.3个 C.4个 D.5个
二、填空题
9.在平面直角坐标系中, ABCD的顶点坐标分别是A(0,1),C(3,﹣2),B(a,b),则D的坐标为 .
10.如图,四边形ABCD为长方形,点E、F分别为AD、BC边上一点,将长方形ABCD沿EF翻折,点A、B分别落在G、H处,若∠1=α,则∠2= .(用含α的代数式表示)
11.一个正五边形与一个正六边形按如图所示方式放置,若AB、AC分别平分正五边形与正六边形的一个内角,则∠BAC的度数为 .
12.如图, ABCD的对角线AC,BD相交于点O,DE∥AC,CE∥BD,若AC=3,BD=5,则四边形OCED的周长为 .
三、解答题
13.如图,在平行四边形ABCD中,点F是AD中点,连接CF并延长交BA的延长线于点E.
(1)求证:AB=AE.
(2)若BC=2AE,∠E=31°,求∠DAB的度数.
14.如图,在△ABC中,AB=AC,AD⊥BC于点D,延长DC到点E,使CE=CD.过点E作EF∥AD交AC的延长线于点F,连接AE,DF.
(1)求证:四边形ADFE是平行四边形;
(2)过点E作EG⊥DF于点G,若BD=2,AE=6,求EG的长.
15.如图,在四边形ABCD中,AB=8cm,BC=6cm,∠B=90°,CD∥AB,O是AC的中点,连结DO并延长,交AB于点E,连结CE.
(1)求证:四边形AECD是平行四边形.
(2)若CE平分∠ACB,求AD的长.
16.如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使CFBC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长;
(3)求四边形DEFC的面积.
17.如图,四边形ABCD为平行四边形,线段AC为对角线,点E、F分别为线段BC、AD的中点,连接EF交AC于点O.
(1)求证:四边形AECF为平行四边形;
(2)若OF=3,求CD的长.
18.【建立模型】如图1,在∠A内部有一点P,连接BP、CP,求证:∠P=∠1+∠A+∠2;
【尝试应用】如图2,利用上面的结论,直接写出五角星中,∠A+∠B+∠C+∠D+∠E= 度;
【拓展创新】如图3,将五角星截去一个角后多出一个角,求∠A+∠B+∠C+∠D+∠E+∠G的度数.
【提升思维】如图4,将五角星的每个角都截去,则一共得到10个角,则这10个角的和∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠J的度数是 度.
参考答案
一、选择题
1.【解答】解:设正多边形的边数为n,由题意得:
(n﹣2) 180°=4×360°,
解得:n=10,
故选:D.
2.【解答】解:①、由同旁内角互补,两直线平行,只能判定四边形的上下一组对边平行,不能判定四边形是平行四边形,故①不符合题意;
②、由同旁内角互补,两直线平行,只能判定四边形的左右一组对边平行,不能判定四边形是平行四边形,故②不符合题意;
③、由同旁内角互补,两直线平行,判定四边形的上下一组对边平行,并且上下一组对边相等,判定四边形是平行四边形,故③符合题意.
∴判定四边形一定是平行四边形的只有③.
故选:A.
3.【解答】解:设BC=x,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵ ABCD的周长为40,
∴BC+CD=20,
∴CD=20﹣x,
∵AE⊥BC于点E,AF⊥CD于点F,
∵ ABCD的面积=BC AE=CD AF,
∴4x=6(20﹣x),
解得:x=12,
∴ ABCD的面积=BC AE=12×4=48.
故选:D.
4.【解答】解:∵平行四边形的对角相等,且两组对边分别平行,
∴平行四边形的邻角互补,
故A不符合题意;
如图1,△ABE中,AE=AB,在BE上取一点C,使CE≠BC,作AC的垂直平分线交AE于点F,连接并延长CF到点D,使DF=EF,连接AD,
∵CF=AF,DF=EF,
∴CF+DF=AF+EF,
∴CD=AE=AB,
在△AFD和△CFE中,
,
∴△AFD≌△CFE(SAS),
∴∠D=∠E=∠B,
∴四边形ABCD是一组对边相等,一组对角相等的四边形,但四边形ABCD不是平行四边形,
∴一组对边相等,一组对角相等的四边形不一定是平行四边形,
故B符合题意;
如图2,AD∥BC,∠A=∠C,∵∠A+∠B=180°,
∴∠C+∠B=180°,
∴CD∥AB,
∴四边形ABCD是平行四边形,
∴一组对平行,一组对角相等的四边形是平行四边形,
故C不符合题意;
根据平行四边形的判定定理,一组对边平行且相等的四边形是平行四边形,
故D不符合题意,
故选:B.
5.【解答】解:一定能判定四边形ABCD是平行四边形的是∠A=∠C,理由如下:
∵AB∥CD,
∴∠A+∠D=180°,
∵∠A=∠C,
∴∠C+∠D=180°,
∴AD∥BC,
又∵AB∥CD,
∴四边形ABCD是平行四边形,
故选:C.
6.【解答】解:设N(x,y),
∵四边形PQMN是平行四边形,P(﹣5,﹣10),Q(15,﹣3),M(6,8),
∴|x﹣6|=|﹣5﹣15|,|y+10|=|8+3|,
∵N点在第二象限,
∴x<0,y>0,
∴x=﹣14,y=1,
∴N(﹣14,1),
故选:B.
7.【解答】解:①∵点D,E,F分别是△ABC的边AB,BC,AC的中点,
∴DFBC,BEAC,DF∥BC,
∴AO=EO,
∴OD是△ABE的中位线,
∴ODBE,故①错误;
②∵点D,E,F分别是△ABC的边AB,BC,AC的中点,
∴DF∥BC,DFBC,BE=CE,DE∥AF,EF∥AD,
∴四边形ADEF和四边形DBEF和四边形DECF是平行四边形,
∴S△ADF=S△DEF=S△BDE=S△CEF,
∴S△DEFS△ABC,故②正确;
③∵AB=AC,
∴AD=AF,
∵四边形ADEF是平行四边形,
∴四边形ADEF是菱形,
∴AE,DF是菱形两组对角的平分线,
∴点O到四边形ADEF四条边的距离相等,故③正确;
④∵∠ABC=90°,四边形ADEF是平行四边形,
∴点O到四边形ADEF四个顶点的距离不相等,故④错误.
综上所述:正确的是②③,共2个,
故选:C.
8.【解答】解:在 ABCD中,
∵∠BAD=∠BCD=60°,∠ADC=120°,DE平分∠ADC,
∴∠ADE=∠DAE=∠AED=60°,
∴△ADE是等边三角形,
∴,
∴E是AB的中点,
∴DE=BE,
∴,
∴∠ADB=90°,即AD⊥BD,
∴S ABCD=AD BD,故①正确;
∵∠CDE=60°,∠BDE=30°,
∴∠CDB=∠CDE﹣∠BDE=60°﹣30°=30°,
∴∠CDB=BDE,
故DB平分∠CDE,故②正确;
依据Rt△AOD中,AO>AD,即可得到AO>DE,故③错误;
∵O是BD中点,E为AB中点,
∴OE是△ABD的中位线,
∴,OE∥AD,
在Rt△ABD中,,
∴,
∴,故④正确;
∵OE∥AD,
∴△ADF∽△OEF,
∴,
∴S△ADF=4S△OEF,S△AEF=2S△OEF
∴S△ADE=S△ADF+S△AEF=6S△OEF,故⑤错误;
∴正确的有3个,
故选:B.
二、填空题
9.【解答】解:∵A(0,1),C(3,﹣2),
∴AC的中点坐标为(,),
即(,),
设点D(x,y),
∵B(a,b),
∴,,
解得:x=﹣a+3,y=﹣b﹣1,
∴点D的坐标为(﹣a+3,﹣b﹣1),
故答案为:(﹣a+3,﹣b﹣1).
10.【解答】解:如图,由折叠可知,∠2=∠4,∠H=∠B=90°,
∵AD∥BC,
∴∠2=∠3,
∵∠1+∠5=180°,
∴∠5=180°﹣∠1=180°﹣α,
∵∠4+∠3+∠5+∠H=360°,
∴2∠2+180°﹣α+90°=360°,
即∠2=45α,
故答案为:45α.
11.【解答】解:根据题意可知,正五边形的内角为:,
正六边形的内角为:,
AB、AC分别平分正八边形与正六边形的一个内角,
∴.
故答案为:114°.
12.【解答】解:∵ ABCD的对角线AC,BD相交于点O,AC=3,BD=5,
∴,
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∴四边形OCED的周长,
故答案为:8.
三、解答题
13.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,BC=AD,
∴∠E=∠DCF,
∵点F是AD中点,
∴AF=DF,
∵∠EFA=∠CFD,
∴△AFE≌△DFC(AAS),
∴CD=AE,
∴AB=AE;
(2)解:由(1)可得AF=DF,BC=AD,
∵BC=2AE,
∴AE=AF,
∵∠E=31°,
∴∠AFE=∠E=31°,
∴∠DAB=2∠E=62°.
14.【解答】(1)证明:∵EF∥AD,
∴∠FEC=∠ADC,
又∵CE=CD,∠FCE=∠ACD,
∴△FCE≌△ACD(ASA),
∴EF=AD,
∴四边形ADFE是平行四边形;
(2)解:如图,
由(1)可知,四边形ADFE是平行四边形,
∴DF=AE=6,
∵AB=AC,AD⊥BC,
∴CD=BD=2,
∴CE=CD=2,
∴DE=2CD=4,
∵EF∥AD,
∴EF⊥BC,
∴∠DEF=90°,
∴EF2,
∵EG⊥DF,
∴S△DEFDF EG EF,
∴EG,
即EG的长为.
15.【解答】(1)证明:∵CD∥AB,
∴∠ACD=∠CAE,
∵O是AC的中点,
∴AO=CO,
在△AOE与△COD中,
,
∴△AOE≌△COD(ASA),
∴AE=CD,又AE∥CD,
∴四边形AECD是平行四边形;
(2)解:如图,过点E作EF⊥AC于F,
在Rt△ABC中,AB=8cm,BC=6cm,∠B=90°,
由勾股定理得:AC10(cm),
∵CE平分∠ACB,∠B=90°,EF⊥AC,
∴EF=EB,
则,
∴,
∵AB=8cm,
∴BE=3cm,
∴CE3(cm),
由(1)可知:四边形AECD是平行四边形,
∴AD=CE=3cm.
16.【解答】解:(1)在△ABC中,
∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DEBC,
∵CFBC,
∴DE=CF.
(2)∵AC=BC,AD=BD,
∴CD⊥AB,
∵BC=4,BD=2,
∴CD2,
∵DE∥CF,DE=CF,
∴四边形DEFC是平行四边形,
∴EF=CD=2.
(3)过点D作DH⊥BC于H.
∵∠DHC=90°,∠DCB=30°,
∴DHDC,
∵DE=CF=2,
∴S四边形DEFC=CF DH=22.
17.【解答】(1)证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
∵点E、F分别为线段BC、AD的中点,
∴AFAD,CEBC,
∴AF=CE,
∵AF∥CE,
∴四边形AECF为平行四边形;
(2)解:∵四边形AECF为平行四边形,
∴OA=OC,
∵AF=DF,
∴OF为△ACD的中位线,
∴CD=2OF=2×3=6.
18.【解答】【建立模型】证明:延长BP交AC于点M,如图1所示:
由三角形外角性质得:∠BPC=∠1+∠PMC,∠PMC=∠A+∠2,
∴∠BPC=∠1+∠A+∠2;
【尝试应用】解:设BD与CE相交于点N,如图2所示:
由【建立模型】得:∠CND=∠A+∠C+∠D,
∵∠BNE=∠CND,
∴∠BNE=∠A+∠C+∠D,
在△BEN中,∠BNE+∠B+∠E=180°,
∴∠A+∠C+∠D+∠B+∠E=180°,
故答案为:180;
【拓展创新】解:延长CA与DG的延长线相交于点K,如图3所示:
∵∠CAG=180°﹣∠KAG,∠DGA=180°﹣∠KGA,
∴∠CAG+∠DGA=360°﹣(∠KAG+∠KGA),
在△KAG中,∠KAG+∠KGA=180°﹣∠K,
∴∠CAG+∠DGA=360°﹣(180°﹣∠K)=180°+∠K,
由【尝试应用】得:∠K+∠B+∠C+∠D+∠E=180°,
∴∠CAG+∠B+∠C+∠D+∠E+∠∠DGA
=∠CAG+∠DGA+∠B+∠C+∠D+∠E
=180°+∠K+∠B+∠C+∠D+∠E
=180°+180°
=360°;
【提升思维】解:由【拓展创新】得:当五角星去掉一个角后多出一个角时,此时所有角的和的度数比五角星的内角和多出180°,
∴当五角星去掉五个角后多出五个角,此时所有角的和的度数为:180°+5×180°=1080°.
故答案为:1080.
21世纪教育网(www.21cnjy.com)
同课章节目录
