第十一章反比例函数期末复习(含解析)
文档属性
| 名称 | 第十一章反比例函数期末复习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 674.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 16:38:01 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十一章反比例函数期末复习苏科版2024—2025学年八年级下册
一、选择题
1.若点A(﹣3,y1),B(1,y2),C(3,y3)都在反比例函数的图象上,则y1,y2,y3的大小关系是( )
A.y1<y3<y2 B.y1<y2<y3 C.y3<y2<y1 D.y2<y3<y1
2.如图,一次函数y=kx+b的图象与反比例函数的图象相交于A(﹣3,1),B(﹣1,3)两点.则不等式的解为( )
A.x<﹣3或x>﹣1 B.﹣3<x<﹣1
C.﹣3<x<﹣1或x>0 D.x<﹣3或﹣1<x<0
3.在平面直角坐标系中,如果反比例函数的图象经过点(2,3),那么此反比例函数的图象也一定经过点( )
A.(﹣2,3) B.(﹣2,﹣3) C.(3,﹣2) D.(﹣3,2)
4.在同一平面直角坐标系中,若反比例函数(a为常数,a≠0)与正比例函数y=bx(b为常数,b≠0)的图象有公共点,则下列关于a,b之间的关系一定正确的是( )
A.a+b>0 B.a+b<0 C.ab<0 D.ab>0
5.如图,A是反比例函数的图象上一点,AB⊥y轴于B,点C在x轴上,若△ABC面积为2,则k的值为( )
A.﹣4 B.1 C.2 D.4
6.如图,直线y=2x﹣4与x轴,y轴分别交于点A,B,与双曲线(k≠0)在第一象限的分支交于点C,过点C作CD⊥y轴于点D,OB=2OD,则k的值为( )
A.6 B.﹣6 C.6或﹣6 D.
7.已知反比例函数与一次函数y=k﹣x的图象的一个交点的横坐标为﹣2,则k的值为( )
A.﹣5 B.﹣51 C.5 D.3
8.如图,点A,B在反比例函数的图象上,CA⊥y轴,垂足为D,BC⊥AC.若四边形AOBC的面积为8,,则k的值为( )
A.1 B.2 C.3 D.4
二、填空题
9.如图,点A是反比例函数在第一象限图象上的任意一点,点B、C分别在x、y轴正半轴上,且AC∥x轴,若△ABC的面积为2,则k的值为 .
10.已知直线y=﹣2x与双曲线的一个交点的坐标为(2,n),则m的值为 .
11.如图,点A,B在反比例函数图象上,点A的横坐标为1,连接OA,OB,AB,若OA=OB,△OAB的面积为4,则k的值为 .
12.如图,正方形ABCD的顶点C,D均在双曲线在第一象限的分支上,顶点A,B分别在x轴、y轴上,则此正方形的边长为 .
三、解答题
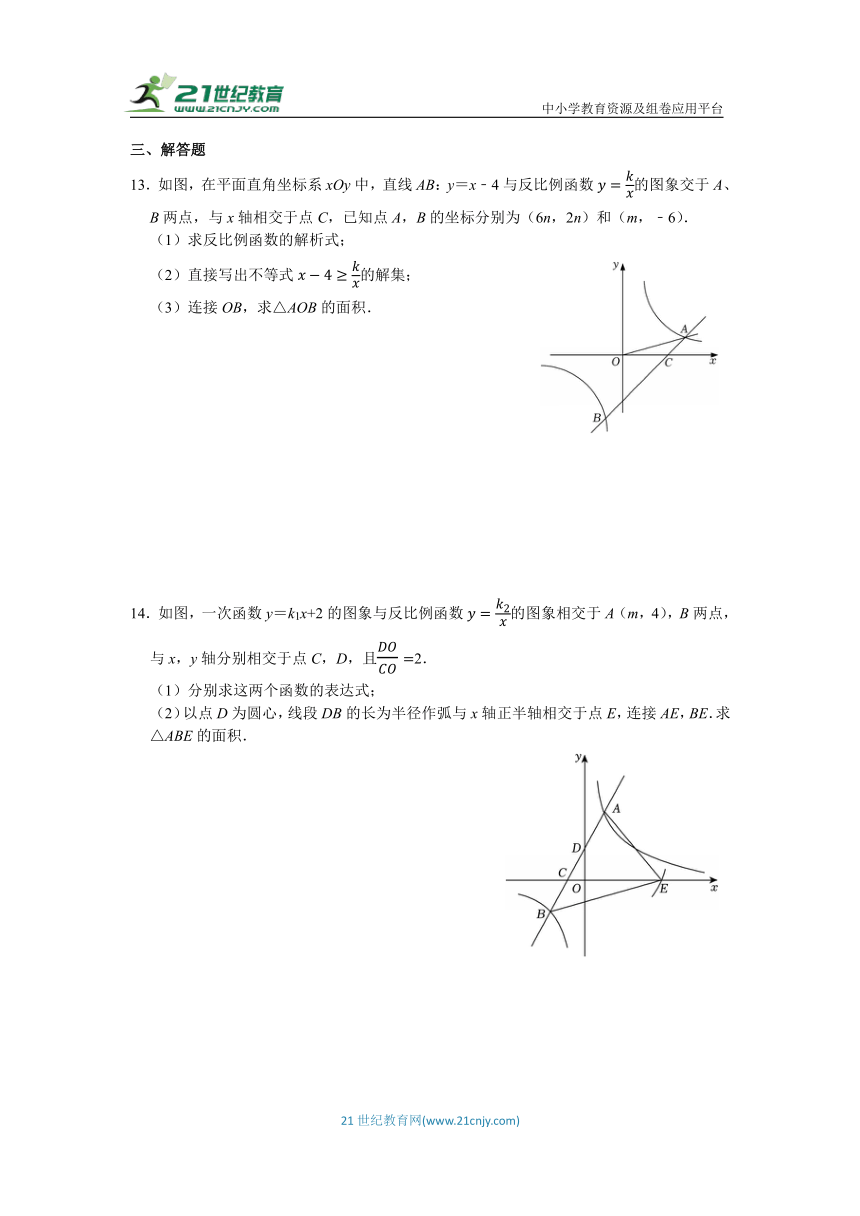
13.如图,在平面直角坐标系xOy中,直线AB:y=x﹣4与反比例函数的图象交于A、B两点,与x轴相交于点C,已知点A,B的坐标分别为(6n,2n)和(m,﹣6).
(1)求反比例函数的解析式;
(2)直接写出不等式的解集;
(3)连接OB,求△AOB的面积.
14.如图,一次函数y=k1x+2的图象与反比例函数的图象相交于A(m,4),B两点,与x,y轴分别相交于点C,D,且2.
(1)分别求这两个函数的表达式;
(2)以点D为圆心,线段DB的长为半径作弧与x轴正半轴相交于点E,连接AE,BE.求△ABE的面积.
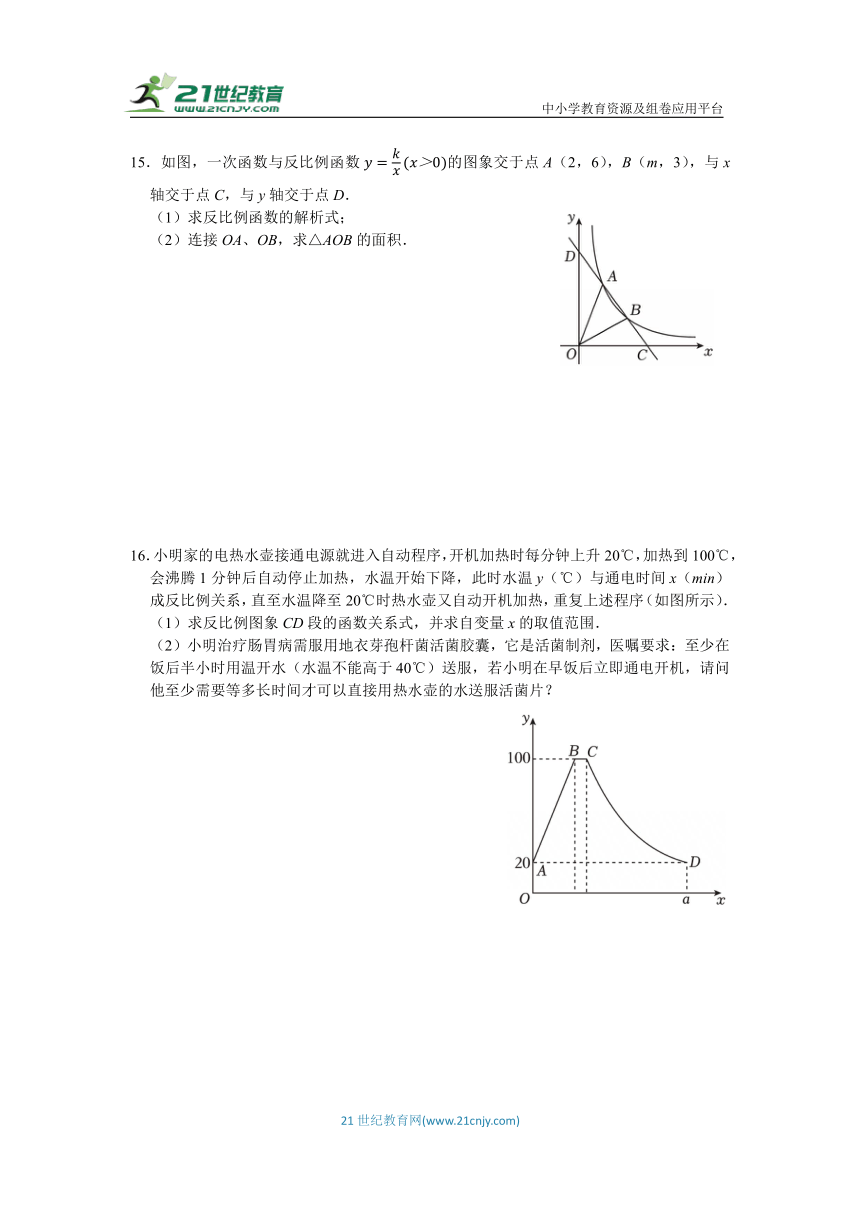
15.如图,一次函数与反比例函数的图象交于点A(2,6),B(m,3),与x轴交于点C,与y轴交于点D.
(1)求反比例函数的解析式;
(2)连接OA、OB,求△AOB的面积.
16.小明家的电热水壶接通电源就进入自动程序,开机加热时每分钟上升20℃,加热到100℃,会沸腾1分钟后自动停止加热,水温开始下降,此时水温y(℃)与通电时间x(min)成反比例关系,直至水温降至20℃时热水壶又自动开机加热,重复上述程序(如图所示).
(1)求反比例图象CD段的函数关系式,并求自变量x的取值范围.
(2)小明治疗肠胃病需服用地衣芽孢杆菌活菌胶囊,它是活菌制剂,医嘱要求:至少在饭后半小时用温开水(水温不能高于40℃)送服,若小明在早饭后立即通电开机,请问他至少需要等多长时间才可以直接用热水壶的水送服活菌片?
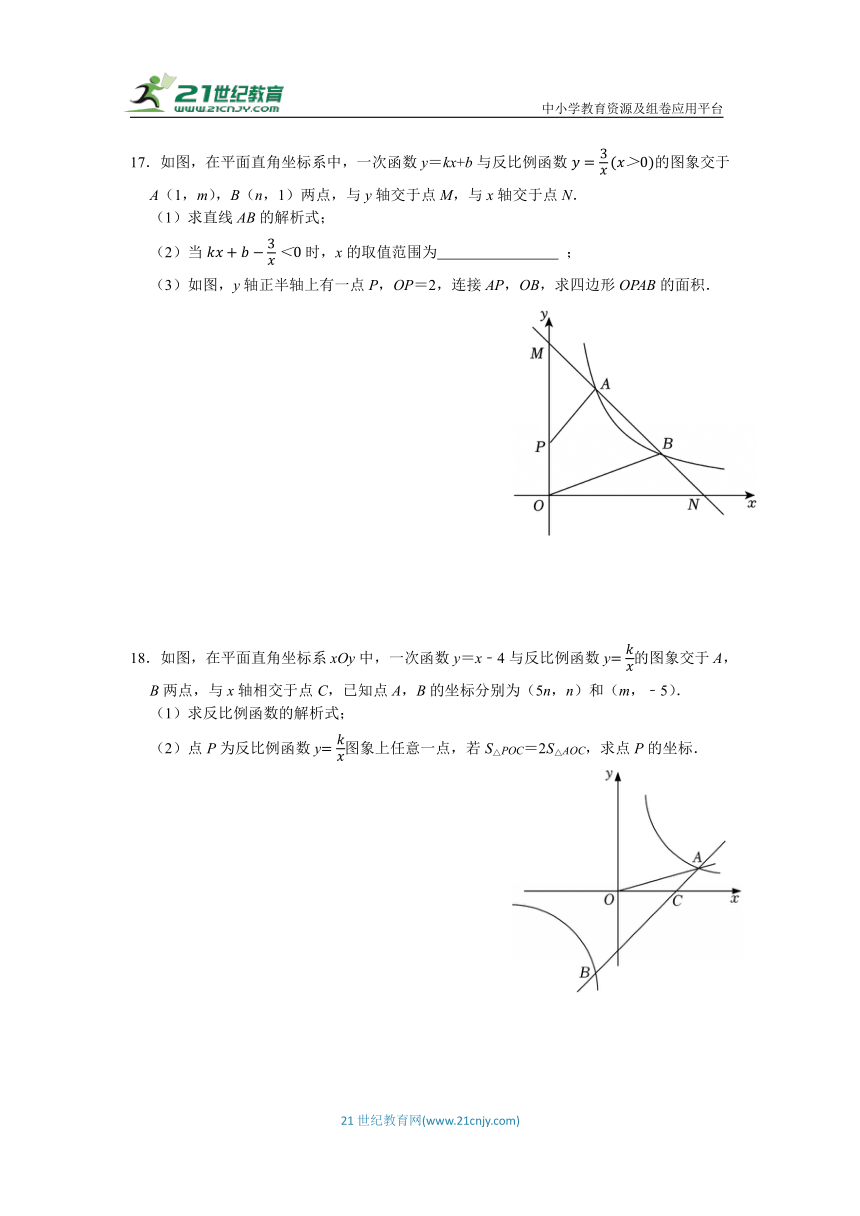
17.如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数的图象交于A(1,m),B(n,1)两点,与y轴交于点M,与x轴交于点N.
(1)求直线AB的解析式;
(2)当时,x的取值范围为 ;
(3)如图,y轴正半轴上有一点P,OP=2,连接AP,OB,求四边形OPAB的面积.
18.如图,在平面直角坐标系xOy中,一次函数y=x﹣4与反比例函数y的图象交于A,B两点,与x轴相交于点C,已知点A,B的坐标分别为(5n,n)和(m,﹣5).
(1)求反比例函数的解析式;
(2)点P为反比例函数y图象上任意一点,若S△POC=2S△AOC,求点P的坐标.
参考答案
一、选择题
1.【解答】解:当x=﹣3时,y1=﹣1,
当x=1时,y2=3,
当x=3时,y3=1,
∴y1<y3<y2.
故选:A.
2.【解答】解:由图象可知:当﹣3<x<﹣1或x>0时,一次函数的图象在反比例函数图象的上方,
∴不等式的解为:﹣3<x<﹣1或x>0.
故选:C.
3.【解答】解:由条件可知k=2×3=6;
A.﹣2×3=﹣6≠6,此反比例函数的图象不经过此点,故选项不符合题意;
B.﹣2×(﹣3)=6,此反比例函数的图象也一定经过此点,故选项符合题意;
C.3×(﹣2)=﹣6≠6,此反比例函数的图象不经过此点,故选项不符合题意;
D.﹣3×2=﹣6≠6,此反比例函数的图象不经过此点,故选项不符合题意;
故选:B.
4.【解答】解:∵正比例函数y=bx的图象与反比例函数y的图象有公共点,
∴a、b同号,
∴ab>0.
故选:D.
5.【解答】解:连接OA,
∵AB⊥y轴,
∴AB∥x轴,
∴S△AOB=S△ABC=2.
又∵点A在反比例函数y的图象上,
∴.
又∵k>0,
∴k=4.
故选:D.
6.【解答】解:将x=0代入y=2x﹣4得,
y=﹣4,
所以点B的坐标为(0,﹣4),
则OB=4.
又因为OB=2OD,
所以OD=2,
所以点D的坐标为(0,2).
又因为CD⊥y轴,
所以yC=2,
则,
所以点C的坐标为().
将点C坐标代入一次函数解析式得,
,
解得k=6.
故选:A.
7.【解答】解:∵反比例函数与一次函数y=k﹣x的图象的一个交点的横坐标为﹣2,
在中,当x=﹣2时,y=﹣3,
∴交点坐标是:(﹣2,﹣3),
代入y=k﹣x,得﹣3=k+2.
解得k=﹣5.
故选:A.
8.【解答】解:设A(a,),则AD=a,OD,
∵,
∴AC=2a,CD=3a,
∵CA⊥y轴,BC⊥AC,
∴BC∥y轴,
∴B(3a,),
∴BC,
∵S梯形OBCD=S△AOD+S四边形AOBC,四边形AOBC的面积为8,
∴()×3ak+8,
解得k=4.
故选:D.
二、填空题
9.【解答】解:如图,连接OA,
∵AC∥x轴,
∴S△ABC=S△AOC=2,
∵点A在反比例函数图象上,
∴k=2S△AOC=2×2=4.
故答案为:4.
10.【解答】解:把x=2代入y=﹣2x得:y=﹣2×2=﹣4,
∴直线y=﹣2x与双曲线y的一个交点坐标为(2,﹣4),
把(2,﹣4)代入双曲线y得:m=2×(﹣4)=﹣8.
故答案为:﹣8.
11.【解答】解:过点A作AC⊥y轴于C,过点B作BD⊥x轴于D,过点A作AE⊥OD于E,
∵点A,B在反比例函数图象上,点A的横坐标为1,
∴A(1,k),
∴AC=OE=1,OC=AE=k,
设,则a>1,
∵OA=OB,
∴AC2+OC2=BD2+OD2,
∴,
整理得,即,
∵a>1,
∴a2﹣1≠0,
∴a2=k2,
∴a=±k,
∵图象在第一象限,
∴k>0,
∴a=k,
∴B(k,1),
∴BD=AC=1,OD=OC=k,
∵,S四边形OABD=S梯形AEDB+S△AEO=S△BDO+S△AOB,
∴S△AOB=S梯形AEDB,
∵S△AOB=4,
∴,
∴k2﹣1=8,
∴k=±3
∵k>0,
∴k=3,
故答案为:3.
12.【解答】解:作DE⊥x轴于E,作CF⊥y轴于F,则∠DEA=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAO+∠DAE=90°,∠DAE+∠ADE=90°,
∴∠DAE=∠ABO,
又∵AB=AD,
∴△ABO≌△DAE(AAS).
同理,△ABO≌△BCF.
设OA=a,AE=b,则OB=b,BF=a,DE=a,CF=b.
则D的坐标是(a+b,a),C的坐标是(b,a+b).
∵C、D的两个顶点在双曲线在第一象限的分支上,
∴a(a+b)=b(a+b)=8,
∴a=b,
∴△ABO是等腰直角三角形.
∴D的坐标是(2a,a),
∵D在双曲线在第一象限的分支上,
∴2a2=8,
∴a2=4,
∴OB2+OA2=4+4=8,
∴,
故答案为:.
三、解答题
13.【解答】解:(1)直线AB:y=x﹣4与反比例函数的图象交于A、B两点,与x轴相交于点C,已知点A,B的坐标分别为(6n,2n)和(m,﹣6),
∴把点A(6n,2n)代入y=x﹣4得,2n=6n﹣4,
解得:n=1,
∴点A的坐标为:(6,2),
∵反比例函数的图象过点A,
∴k=6×2=12,
∴反比例函数的解析式为;
(2)把点B(m,﹣6)代入直线y=x﹣4得,﹣6=m﹣4,
解得m=﹣2,
∴B(﹣2,﹣6),
由函数图象可知:当﹣2<x<0或x>6时,一次函数图象在反比例函数图象的上方,
∴不等式的解集为﹣2≤x<0或x≥6.
(3)连接OB,如图所示,
∵直线AB:y=x﹣4与x轴相交于点C,
当y=0时,x=4,
∴C(4,0),
∴OC=4,
∴.
14.【解答】解:(1)由y=k1x+2得D(0,2),
∴DO=2,
∴2,
∴CO=1,
∴C(﹣1,0),
代入y=k1x+2得k1=2,
∴一次函数解析式为y=2x+2;
过A作AM⊥x轴,如图:
∵AM=4,
∴CM=2,
∴OM=1,
∴A(1,4),
把(1,4)代入y得:k2=4,
∴反比例函数解析式为y;
如图:过A作AN∥y轴,交BE于N,
联立y=2x+2和y得x2+x﹣2=0,
∴x=﹣2或1,
∴B(﹣2,﹣2),
∴BD2,
∴DE=DB=2,
∴OE4,
∴E(4,0),
设直线BE解析式为y=mx+n,
∴,
解得:,
∴直线BE解析式为yx,
∴N(1,﹣1),
∴AN=4+1=5,
∴△ABE面积(4+2)×5=15.
15.【解答】解:(1)将点A、B的坐标代入反比例函数表达式得:k=2×6=3m,
则m=4,k=12,
则反比例函数的表达式为:y;
(2)设直线A、B的表达式为:y=s(x﹣2)+6,
将点B(4,3)代入上式得:3=s(4﹣2)+6,则s,
则直线AB的表达式为:y(x﹣2)+6x+9,则点D(0,9),
则△AOB的面积=S△ODB﹣S△ODAOD×(xB﹣xA)9×(3﹣2).
16.【解答】解:(1)由题意可得:开机加热到 100°C 所需时间为: (分钟),
∴点B坐标为(4,100),
∵加热到100℃,会沸腾1分钟后自动停止加热,
∴点C坐标为(5,100),
设反比例图象CD段的函数关系式 ,把点C(5,100)代入得:
,
解得:k=500,
,
令y=20时,代入 ,
解得:x=25,
∴点D(25,20),
∴反比例图象CD段的函数关系式 ;
(2)由(1)可知:从水温20°C开机加热到100°C、沸腾停止加热、再到水温下降回20°C 为一个周期共用时25分钟,
∵25<30,
∴小明在第一个周期还不能服药,
当水温第二次加热到40°C所需时间为:,
当水温第二次下降到 40°C 所需时间为:2537.5(分),
∴他至少需要等37.5分钟才可以直接用热水壶的水送服活菌片.
17.【解答】解:(1)把A(1,m),B(n,1)两点坐标分别代入反比例函数,可得,,
∴m=3,n=3,
∴A(1,3),B(3,1).
把A(1,3),B(3,1)代入一次函数y=kx+b,
可得,解得,
∴直线AB的解析式为y=﹣x+4.
(2)由图象可知不等式的解集为:0<x<1或x>3.
(3)如图,过点B作BE⊥y轴于点E,过点A作AF⊥y轴于点F,
∵直线AB的解析式为y=﹣x+4,
∴M点坐标为(0,4),
∴PM=OM﹣OP=4﹣2=2,
∵A(1,3),B(3,1),
∴AF=1,BE=3,
∴四边形OPAB的面积=S△OBM﹣S△PAM
=5.
18.【解答】解:(1)把A(5n,n)代入y=x﹣4中得:5n﹣4=n,
解得n=1,
∴A(5,1),
把A(5,1)代入中得:,
解得k=5,
∴反比例函数解析式为;
(2)在y=x﹣4中,当y=x﹣4=0时,x=4,
∴C(4,0),
∴OC=4,
∴S△AOC4×1=2,
∴S△POC=2S△AOC=4,
∴OC |yP|=4,
∴|yP|=2,
∴yP=±2,
在中,当y=2时,,
当y=﹣2时,,
∴点P的坐标为或.
21世纪教育网(www.21cnjy.com)
第十一章反比例函数期末复习苏科版2024—2025学年八年级下册
一、选择题
1.若点A(﹣3,y1),B(1,y2),C(3,y3)都在反比例函数的图象上,则y1,y2,y3的大小关系是( )
A.y1<y3<y2 B.y1<y2<y3 C.y3<y2<y1 D.y2<y3<y1
2.如图,一次函数y=kx+b的图象与反比例函数的图象相交于A(﹣3,1),B(﹣1,3)两点.则不等式的解为( )
A.x<﹣3或x>﹣1 B.﹣3<x<﹣1
C.﹣3<x<﹣1或x>0 D.x<﹣3或﹣1<x<0
3.在平面直角坐标系中,如果反比例函数的图象经过点(2,3),那么此反比例函数的图象也一定经过点( )
A.(﹣2,3) B.(﹣2,﹣3) C.(3,﹣2) D.(﹣3,2)
4.在同一平面直角坐标系中,若反比例函数(a为常数,a≠0)与正比例函数y=bx(b为常数,b≠0)的图象有公共点,则下列关于a,b之间的关系一定正确的是( )
A.a+b>0 B.a+b<0 C.ab<0 D.ab>0
5.如图,A是反比例函数的图象上一点,AB⊥y轴于B,点C在x轴上,若△ABC面积为2,则k的值为( )
A.﹣4 B.1 C.2 D.4
6.如图,直线y=2x﹣4与x轴,y轴分别交于点A,B,与双曲线(k≠0)在第一象限的分支交于点C,过点C作CD⊥y轴于点D,OB=2OD,则k的值为( )
A.6 B.﹣6 C.6或﹣6 D.
7.已知反比例函数与一次函数y=k﹣x的图象的一个交点的横坐标为﹣2,则k的值为( )
A.﹣5 B.﹣51 C.5 D.3
8.如图,点A,B在反比例函数的图象上,CA⊥y轴,垂足为D,BC⊥AC.若四边形AOBC的面积为8,,则k的值为( )
A.1 B.2 C.3 D.4
二、填空题
9.如图,点A是反比例函数在第一象限图象上的任意一点,点B、C分别在x、y轴正半轴上,且AC∥x轴,若△ABC的面积为2,则k的值为 .
10.已知直线y=﹣2x与双曲线的一个交点的坐标为(2,n),则m的值为 .
11.如图,点A,B在反比例函数图象上,点A的横坐标为1,连接OA,OB,AB,若OA=OB,△OAB的面积为4,则k的值为 .
12.如图,正方形ABCD的顶点C,D均在双曲线在第一象限的分支上,顶点A,B分别在x轴、y轴上,则此正方形的边长为 .
三、解答题
13.如图,在平面直角坐标系xOy中,直线AB:y=x﹣4与反比例函数的图象交于A、B两点,与x轴相交于点C,已知点A,B的坐标分别为(6n,2n)和(m,﹣6).
(1)求反比例函数的解析式;
(2)直接写出不等式的解集;
(3)连接OB,求△AOB的面积.
14.如图,一次函数y=k1x+2的图象与反比例函数的图象相交于A(m,4),B两点,与x,y轴分别相交于点C,D,且2.
(1)分别求这两个函数的表达式;
(2)以点D为圆心,线段DB的长为半径作弧与x轴正半轴相交于点E,连接AE,BE.求△ABE的面积.
15.如图,一次函数与反比例函数的图象交于点A(2,6),B(m,3),与x轴交于点C,与y轴交于点D.
(1)求反比例函数的解析式;
(2)连接OA、OB,求△AOB的面积.
16.小明家的电热水壶接通电源就进入自动程序,开机加热时每分钟上升20℃,加热到100℃,会沸腾1分钟后自动停止加热,水温开始下降,此时水温y(℃)与通电时间x(min)成反比例关系,直至水温降至20℃时热水壶又自动开机加热,重复上述程序(如图所示).
(1)求反比例图象CD段的函数关系式,并求自变量x的取值范围.
(2)小明治疗肠胃病需服用地衣芽孢杆菌活菌胶囊,它是活菌制剂,医嘱要求:至少在饭后半小时用温开水(水温不能高于40℃)送服,若小明在早饭后立即通电开机,请问他至少需要等多长时间才可以直接用热水壶的水送服活菌片?
17.如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数的图象交于A(1,m),B(n,1)两点,与y轴交于点M,与x轴交于点N.
(1)求直线AB的解析式;
(2)当时,x的取值范围为 ;
(3)如图,y轴正半轴上有一点P,OP=2,连接AP,OB,求四边形OPAB的面积.
18.如图,在平面直角坐标系xOy中,一次函数y=x﹣4与反比例函数y的图象交于A,B两点,与x轴相交于点C,已知点A,B的坐标分别为(5n,n)和(m,﹣5).
(1)求反比例函数的解析式;
(2)点P为反比例函数y图象上任意一点,若S△POC=2S△AOC,求点P的坐标.
参考答案
一、选择题
1.【解答】解:当x=﹣3时,y1=﹣1,
当x=1时,y2=3,
当x=3时,y3=1,
∴y1<y3<y2.
故选:A.
2.【解答】解:由图象可知:当﹣3<x<﹣1或x>0时,一次函数的图象在反比例函数图象的上方,
∴不等式的解为:﹣3<x<﹣1或x>0.
故选:C.
3.【解答】解:由条件可知k=2×3=6;
A.﹣2×3=﹣6≠6,此反比例函数的图象不经过此点,故选项不符合题意;
B.﹣2×(﹣3)=6,此反比例函数的图象也一定经过此点,故选项符合题意;
C.3×(﹣2)=﹣6≠6,此反比例函数的图象不经过此点,故选项不符合题意;
D.﹣3×2=﹣6≠6,此反比例函数的图象不经过此点,故选项不符合题意;
故选:B.
4.【解答】解:∵正比例函数y=bx的图象与反比例函数y的图象有公共点,
∴a、b同号,
∴ab>0.
故选:D.
5.【解答】解:连接OA,
∵AB⊥y轴,
∴AB∥x轴,
∴S△AOB=S△ABC=2.
又∵点A在反比例函数y的图象上,
∴.
又∵k>0,
∴k=4.
故选:D.
6.【解答】解:将x=0代入y=2x﹣4得,
y=﹣4,
所以点B的坐标为(0,﹣4),
则OB=4.
又因为OB=2OD,
所以OD=2,
所以点D的坐标为(0,2).
又因为CD⊥y轴,
所以yC=2,
则,
所以点C的坐标为().
将点C坐标代入一次函数解析式得,
,
解得k=6.
故选:A.
7.【解答】解:∵反比例函数与一次函数y=k﹣x的图象的一个交点的横坐标为﹣2,
在中,当x=﹣2时,y=﹣3,
∴交点坐标是:(﹣2,﹣3),
代入y=k﹣x,得﹣3=k+2.
解得k=﹣5.
故选:A.
8.【解答】解:设A(a,),则AD=a,OD,
∵,
∴AC=2a,CD=3a,
∵CA⊥y轴,BC⊥AC,
∴BC∥y轴,
∴B(3a,),
∴BC,
∵S梯形OBCD=S△AOD+S四边形AOBC,四边形AOBC的面积为8,
∴()×3ak+8,
解得k=4.
故选:D.
二、填空题
9.【解答】解:如图,连接OA,
∵AC∥x轴,
∴S△ABC=S△AOC=2,
∵点A在反比例函数图象上,
∴k=2S△AOC=2×2=4.
故答案为:4.
10.【解答】解:把x=2代入y=﹣2x得:y=﹣2×2=﹣4,
∴直线y=﹣2x与双曲线y的一个交点坐标为(2,﹣4),
把(2,﹣4)代入双曲线y得:m=2×(﹣4)=﹣8.
故答案为:﹣8.
11.【解答】解:过点A作AC⊥y轴于C,过点B作BD⊥x轴于D,过点A作AE⊥OD于E,
∵点A,B在反比例函数图象上,点A的横坐标为1,
∴A(1,k),
∴AC=OE=1,OC=AE=k,
设,则a>1,
∵OA=OB,
∴AC2+OC2=BD2+OD2,
∴,
整理得,即,
∵a>1,
∴a2﹣1≠0,
∴a2=k2,
∴a=±k,
∵图象在第一象限,
∴k>0,
∴a=k,
∴B(k,1),
∴BD=AC=1,OD=OC=k,
∵,S四边形OABD=S梯形AEDB+S△AEO=S△BDO+S△AOB,
∴S△AOB=S梯形AEDB,
∵S△AOB=4,
∴,
∴k2﹣1=8,
∴k=±3
∵k>0,
∴k=3,
故答案为:3.
12.【解答】解:作DE⊥x轴于E,作CF⊥y轴于F,则∠DEA=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAO+∠DAE=90°,∠DAE+∠ADE=90°,
∴∠DAE=∠ABO,
又∵AB=AD,
∴△ABO≌△DAE(AAS).
同理,△ABO≌△BCF.
设OA=a,AE=b,则OB=b,BF=a,DE=a,CF=b.
则D的坐标是(a+b,a),C的坐标是(b,a+b).
∵C、D的两个顶点在双曲线在第一象限的分支上,
∴a(a+b)=b(a+b)=8,
∴a=b,
∴△ABO是等腰直角三角形.
∴D的坐标是(2a,a),
∵D在双曲线在第一象限的分支上,
∴2a2=8,
∴a2=4,
∴OB2+OA2=4+4=8,
∴,
故答案为:.
三、解答题
13.【解答】解:(1)直线AB:y=x﹣4与反比例函数的图象交于A、B两点,与x轴相交于点C,已知点A,B的坐标分别为(6n,2n)和(m,﹣6),
∴把点A(6n,2n)代入y=x﹣4得,2n=6n﹣4,
解得:n=1,
∴点A的坐标为:(6,2),
∵反比例函数的图象过点A,
∴k=6×2=12,
∴反比例函数的解析式为;
(2)把点B(m,﹣6)代入直线y=x﹣4得,﹣6=m﹣4,
解得m=﹣2,
∴B(﹣2,﹣6),
由函数图象可知:当﹣2<x<0或x>6时,一次函数图象在反比例函数图象的上方,
∴不等式的解集为﹣2≤x<0或x≥6.
(3)连接OB,如图所示,
∵直线AB:y=x﹣4与x轴相交于点C,
当y=0时,x=4,
∴C(4,0),
∴OC=4,
∴.
14.【解答】解:(1)由y=k1x+2得D(0,2),
∴DO=2,
∴2,
∴CO=1,
∴C(﹣1,0),
代入y=k1x+2得k1=2,
∴一次函数解析式为y=2x+2;
过A作AM⊥x轴,如图:
∵AM=4,
∴CM=2,
∴OM=1,
∴A(1,4),
把(1,4)代入y得:k2=4,
∴反比例函数解析式为y;
如图:过A作AN∥y轴,交BE于N,
联立y=2x+2和y得x2+x﹣2=0,
∴x=﹣2或1,
∴B(﹣2,﹣2),
∴BD2,
∴DE=DB=2,
∴OE4,
∴E(4,0),
设直线BE解析式为y=mx+n,
∴,
解得:,
∴直线BE解析式为yx,
∴N(1,﹣1),
∴AN=4+1=5,
∴△ABE面积(4+2)×5=15.
15.【解答】解:(1)将点A、B的坐标代入反比例函数表达式得:k=2×6=3m,
则m=4,k=12,
则反比例函数的表达式为:y;
(2)设直线A、B的表达式为:y=s(x﹣2)+6,
将点B(4,3)代入上式得:3=s(4﹣2)+6,则s,
则直线AB的表达式为:y(x﹣2)+6x+9,则点D(0,9),
则△AOB的面积=S△ODB﹣S△ODAOD×(xB﹣xA)9×(3﹣2).
16.【解答】解:(1)由题意可得:开机加热到 100°C 所需时间为: (分钟),
∴点B坐标为(4,100),
∵加热到100℃,会沸腾1分钟后自动停止加热,
∴点C坐标为(5,100),
设反比例图象CD段的函数关系式 ,把点C(5,100)代入得:
,
解得:k=500,
,
令y=20时,代入 ,
解得:x=25,
∴点D(25,20),
∴反比例图象CD段的函数关系式 ;
(2)由(1)可知:从水温20°C开机加热到100°C、沸腾停止加热、再到水温下降回20°C 为一个周期共用时25分钟,
∵25<30,
∴小明在第一个周期还不能服药,
当水温第二次加热到40°C所需时间为:,
当水温第二次下降到 40°C 所需时间为:2537.5(分),
∴他至少需要等37.5分钟才可以直接用热水壶的水送服活菌片.
17.【解答】解:(1)把A(1,m),B(n,1)两点坐标分别代入反比例函数,可得,,
∴m=3,n=3,
∴A(1,3),B(3,1).
把A(1,3),B(3,1)代入一次函数y=kx+b,
可得,解得,
∴直线AB的解析式为y=﹣x+4.
(2)由图象可知不等式的解集为:0<x<1或x>3.
(3)如图,过点B作BE⊥y轴于点E,过点A作AF⊥y轴于点F,
∵直线AB的解析式为y=﹣x+4,
∴M点坐标为(0,4),
∴PM=OM﹣OP=4﹣2=2,
∵A(1,3),B(3,1),
∴AF=1,BE=3,
∴四边形OPAB的面积=S△OBM﹣S△PAM
=5.
18.【解答】解:(1)把A(5n,n)代入y=x﹣4中得:5n﹣4=n,
解得n=1,
∴A(5,1),
把A(5,1)代入中得:,
解得k=5,
∴反比例函数解析式为;
(2)在y=x﹣4中,当y=x﹣4=0时,x=4,
∴C(4,0),
∴OC=4,
∴S△AOC4×1=2,
∴S△POC=2S△AOC=4,
∴OC |yP|=4,
∴|yP|=2,
∴yP=±2,
在中,当y=2时,,
当y=﹣2时,,
∴点P的坐标为或.
21世纪教育网(www.21cnjy.com)
同课章节目录
