人教版九年级数学下册 27.2.2 相似三角形的性质 课时练习(含答案)
文档属性
| 名称 | 人教版九年级数学下册 27.2.2 相似三角形的性质 课时练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 633.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 09:56:31 | ||
图片预览

文档简介
九年级数学下册第二十七章第2.2节《相似三角形的性质》课时练习
一、单选题
1.如果两个相似三角形对应边的比为2∶3,那么它们对应高线的比是( )
A.2∶3 B.2∶5 C.4∶9 D.8∶27
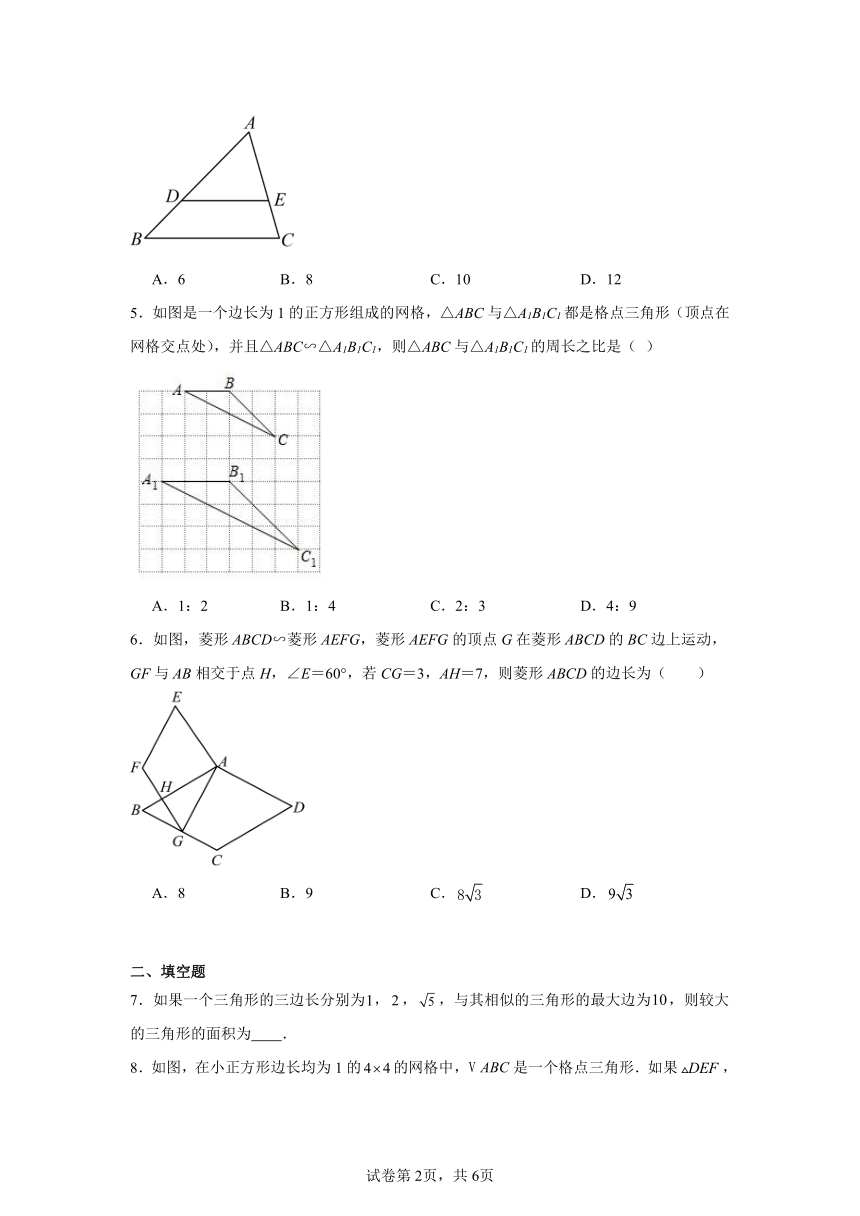
2.如图,在 ABC中,,若,则下列结论中正确的是( )
A.
B.
C.
D.
3.如图,菱形的周长为8,是的中点,,交于点,那么的长是( )
A.4 B.3 C.2 D.1
4.如图,在△ABC中,DE∥BC,AD:BD=5:3,BC=16,则DE的长为( )
A.6 B.8 C.10 D.12
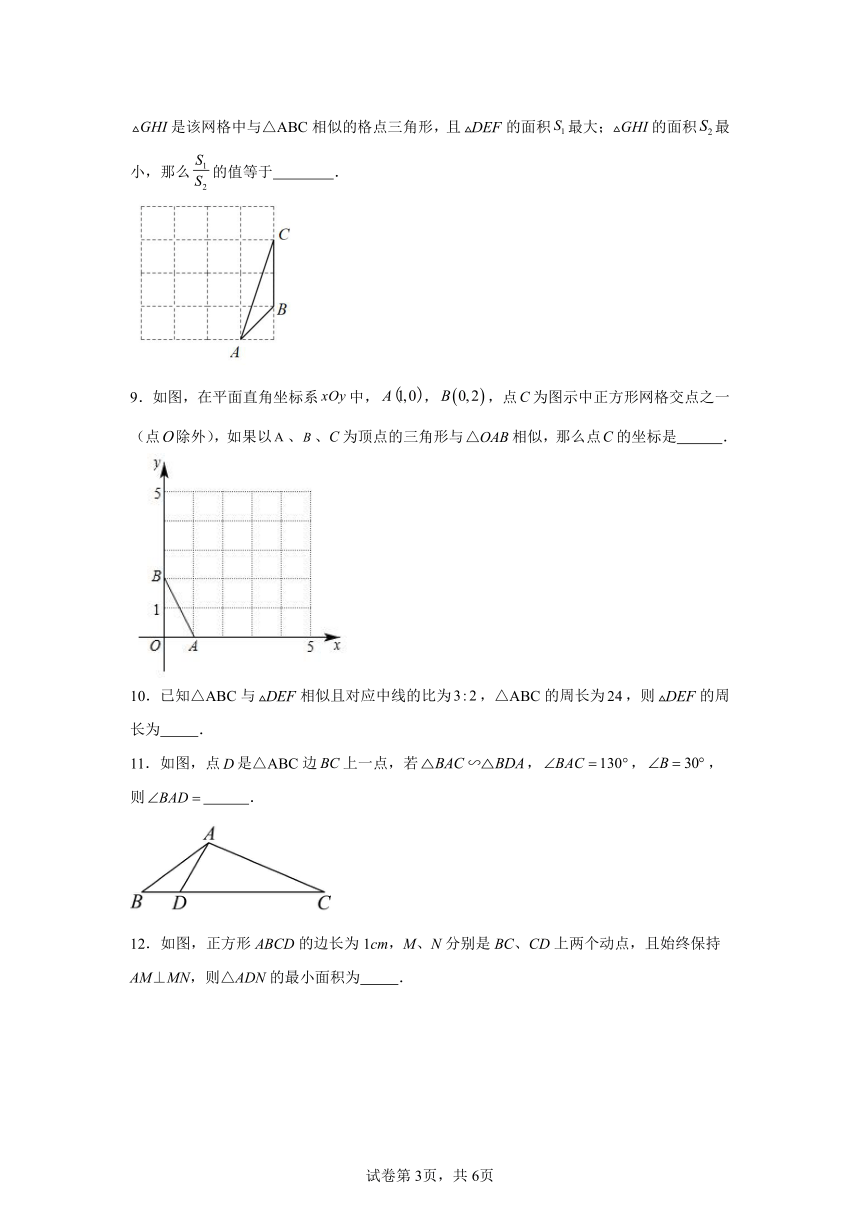
5.如图是一个边长为1的正方形组成的网格,△ABC与△A1B1C1都是格点三角形(顶点在网格交点处),并且△ABC∽△A1B1C1,则△ABC与△A1B1C1的周长之比是( )
A.1:2 B.1:4 C.2:3 D.4:9
6.如图,菱形ABCD∽菱形AEFG,菱形AEFG的顶点G在菱形ABCD的BC边上运动,GF与AB相交于点H,∠E=60°,若CG=3,AH=7,则菱形ABCD的边长为( )
A.8 B.9 C. D.
二、填空题
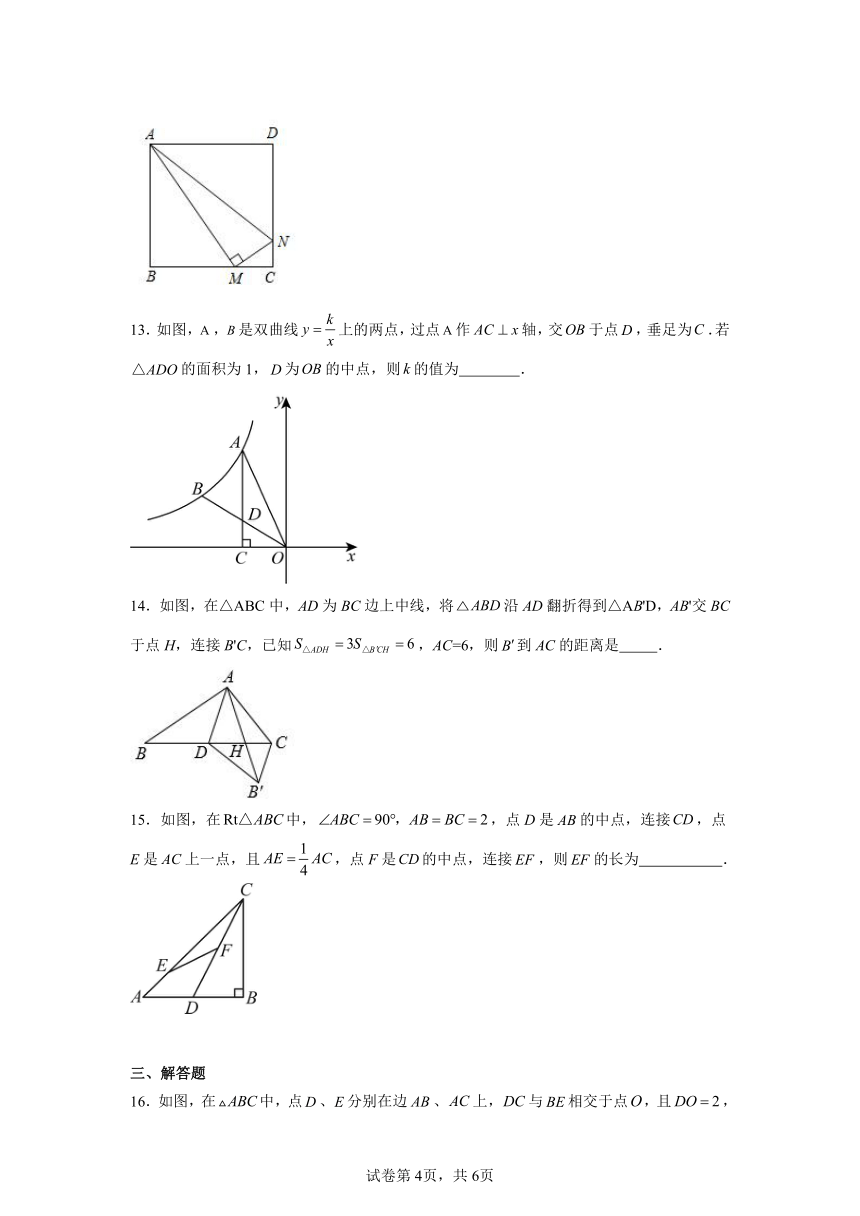
7.如果一个三角形的三边长分别为,,,与其相似的三角形的最大边为,则较大的三角形的面积为 .
8.如图,在小正方形边长均为1的的网格中,是一个格点三角形.如果,是该网格中与△ABC相似的格点三角形,且的面积最大;的面积最小,那么的值等于 .
9.如图,在平面直角坐标系中,,,点为图示中正方形网格交点之一(点除外),如果以、、为顶点的三角形与相似,那么点的坐标是 .
10.已知△ABC与相似且对应中线的比为,△ABC的周长为,则的周长为 .
11.如图,点是△ABC边上一点,若,,,则 .
12.如图,正方形ABCD的边长为1cm,M、N分别是BC、CD上两个动点,且始终保持AM⊥MN,则△ADN的最小面积为 .
13.如图,,是双曲线上的两点,过点作轴,交于点,垂足为.若的面积为1,为的中点,则的值为 .
14.如图,在△ABC中,AD为BC边上中线,将沿AD翻折得到△AB'D,AB'交BC于点H,连接B'C,已知,AC=6,则到AC的距离是 .
15.如图,在中,,点D是的中点,连接,点E是上一点,且,点F是的中点,连接,则的长为 .
三、解答题
16.如图,在中,点、分别在边、上,与相交于点,且,,.
(1)求证:;
(2)已知,求.
17.如图,在Rt△ABC中,∠C=90°,矩形DEFG的顶点G、F分别在AC、BC上,DE在AB上.
(1)求证:△ADG∽△FEB.
(2)若AG=5,AD=4,求BE的长
18.如图,在矩形中,,.点E,F,G分别从点A,B,C三点同时出发,沿矩形的边按逆时针方向移动,点E,G的速度均为,点F的速度为,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,的面积为,
(1)当秒时,S的值是多少?
(2)若点F在矩形的边上移动,当t为何值时,以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形相似?请说明理由.
19.如图所示,已知△ABC中,BC=30cm,AD=10cm.AD是高,矩形EFGH内接于△ABC中,且长边FG在BC边上.设EF=x, FG=y.
(1)求y与x的函数关系式.并求自变量x的取值范围.
(2)若x:y=1:2,求矩形EFGH的面积.
(3)当EF为何值时,矩形EFGH的面积最大?最大面积是多少
20.在△ABC中,,是边的中点,以为角的顶点作.
(1)当射线经过点,交边于点,如图1,不添加辅助线,直接写出图中所有与△ADE相似的三角形(不需要证明);
(2)将绕点D沿逆时针方向旋转,分别交线段于点E、F(点E与点A不重合,如图2).
①求证:;②与是否相似?并证明你的结论.
21.如图,在平面直角坐标系中,二次函数的图象交坐标轴于,,三点,点P是直线上方抛物线上的一个动点.
(1)求这个二次函数的解析式;
(2)动点P运动到什么位置时,的面积最大,求此时P点坐标及面积的最大值;
(3)在y轴上是否存在点Q,使以O,B,Q为顶点的三角形与相似?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学下册第二十七章第2.2节《相似三角形的性质》课时练习》参考答案
题号 1 2 3 4 5 6
答案 A D D C C B
7.
8.5
9.、、
10.
11./20度
12.
13.
14.
15.
16.(1)解:,,,
,,,
,
,
;
解:△ABC COB
,
,
,
,
.
17.解:(1)∵∠C=90°,
∴∠A+∠B=90°;
∵四边形DEFG是矩形,
∴∠GDE=∠FED=90°,
∴∠GDA=∠FED=90°;
∴∠A+∠AGD=90°,
∴∠B=∠AGD且∠GDA=∠FED=90°,
∴△ADG∽△FEB.
(2)在Rt△AGD中,∠GDA=90°由勾股定理得,AD +GD =AG ,
∵AD=4,AG=5,
∴GD=3,
∵△ADG∽△FEB,
∴;
∵四边形DEFG是矩形,
∴FE=DG=3;
∴,
∴ BE =.
18.(1)解:当秒时,则,,,,,
由
(2)解:当点F在矩形的边上的边移动时,在和中,,
①若,即
解得,
经检验,是分式方程的解且符合题意,
所以当时,
②若即,解得
经检验,是分式方程的解且符合题意,
所以当时, ,
综上所述,当或时,以点E、B、F为顶点的三角形与以F、C、G为顶点的三角形相似.
19.解:(1)如图,
∵EF=x, FG=y,
∴DM=EF=x,AM=AD-DM=10-x,
∵EH//BC,
∴,即,
∴y=30-3x;
∵y>0,
∴30-3x>0,即x<10,
∵x>0,
∴x取值范围为0<x<10;
所以:(0<x<10);
(2)∵x:y=1:2,
∴y=2x,
∵y=30-3x,
∴2x=30-3x,
∴x=6,
∴y=12,
∴矩形EFGH的面积=6×12=72;
(3)设四边形EFGH的面积为S,
则 ,
∴当x=5时,即EF=5时,S有最大值为75.
20.(1)解:∵,.
∴,
又∵,是边的中点,
∴,
∵,
∴,
∴,
故答案为:、、;
(2)证明:①∵是的一个外角,
∴.
∵,,
∴.
又∵,
∴;
②,
证明:∵,
∴ ,
∵,
∴,
∴,
又,
∴.
21.(1)解:∵,则设抛物线解析式为,
把A、B两点坐标代入可得,
解得:,
∴抛物线解析式为;
(2)解:∵点P在抛物线上,
∴可设,
过P作轴于点E,交直线于点F,如图,
∵,,
设直线解析式为,
则,
解得,
∴直线解析式为,
∴,
∴,
∴
,
∴当时,最大值为8,此时,
∴当P点坐标为时,的最大面积为8;
(3)解:设,
∵,
∴分和两种情况,
当时,
∴,即,
解得,
∴点的坐标为或;
当时,
∴,即,
解得,
∴点的坐标为或;
综上,点的坐标为或或或.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如果两个相似三角形对应边的比为2∶3,那么它们对应高线的比是( )
A.2∶3 B.2∶5 C.4∶9 D.8∶27
2.如图,在 ABC中,,若,则下列结论中正确的是( )
A.
B.
C.
D.
3.如图,菱形的周长为8,是的中点,,交于点,那么的长是( )
A.4 B.3 C.2 D.1
4.如图,在△ABC中,DE∥BC,AD:BD=5:3,BC=16,则DE的长为( )
A.6 B.8 C.10 D.12
5.如图是一个边长为1的正方形组成的网格,△ABC与△A1B1C1都是格点三角形(顶点在网格交点处),并且△ABC∽△A1B1C1,则△ABC与△A1B1C1的周长之比是( )
A.1:2 B.1:4 C.2:3 D.4:9
6.如图,菱形ABCD∽菱形AEFG,菱形AEFG的顶点G在菱形ABCD的BC边上运动,GF与AB相交于点H,∠E=60°,若CG=3,AH=7,则菱形ABCD的边长为( )
A.8 B.9 C. D.
二、填空题
7.如果一个三角形的三边长分别为,,,与其相似的三角形的最大边为,则较大的三角形的面积为 .
8.如图,在小正方形边长均为1的的网格中,是一个格点三角形.如果,是该网格中与△ABC相似的格点三角形,且的面积最大;的面积最小,那么的值等于 .
9.如图,在平面直角坐标系中,,,点为图示中正方形网格交点之一(点除外),如果以、、为顶点的三角形与相似,那么点的坐标是 .
10.已知△ABC与相似且对应中线的比为,△ABC的周长为,则的周长为 .
11.如图,点是△ABC边上一点,若,,,则 .
12.如图,正方形ABCD的边长为1cm,M、N分别是BC、CD上两个动点,且始终保持AM⊥MN,则△ADN的最小面积为 .
13.如图,,是双曲线上的两点,过点作轴,交于点,垂足为.若的面积为1,为的中点,则的值为 .
14.如图,在△ABC中,AD为BC边上中线,将沿AD翻折得到△AB'D,AB'交BC于点H,连接B'C,已知,AC=6,则到AC的距离是 .
15.如图,在中,,点D是的中点,连接,点E是上一点,且,点F是的中点,连接,则的长为 .
三、解答题
16.如图,在中,点、分别在边、上,与相交于点,且,,.
(1)求证:;
(2)已知,求.
17.如图,在Rt△ABC中,∠C=90°,矩形DEFG的顶点G、F分别在AC、BC上,DE在AB上.
(1)求证:△ADG∽△FEB.
(2)若AG=5,AD=4,求BE的长
18.如图,在矩形中,,.点E,F,G分别从点A,B,C三点同时出发,沿矩形的边按逆时针方向移动,点E,G的速度均为,点F的速度为,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,的面积为,
(1)当秒时,S的值是多少?
(2)若点F在矩形的边上移动,当t为何值时,以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形相似?请说明理由.
19.如图所示,已知△ABC中,BC=30cm,AD=10cm.AD是高,矩形EFGH内接于△ABC中,且长边FG在BC边上.设EF=x, FG=y.
(1)求y与x的函数关系式.并求自变量x的取值范围.
(2)若x:y=1:2,求矩形EFGH的面积.
(3)当EF为何值时,矩形EFGH的面积最大?最大面积是多少
20.在△ABC中,,是边的中点,以为角的顶点作.
(1)当射线经过点,交边于点,如图1,不添加辅助线,直接写出图中所有与△ADE相似的三角形(不需要证明);
(2)将绕点D沿逆时针方向旋转,分别交线段于点E、F(点E与点A不重合,如图2).
①求证:;②与是否相似?并证明你的结论.
21.如图,在平面直角坐标系中,二次函数的图象交坐标轴于,,三点,点P是直线上方抛物线上的一个动点.
(1)求这个二次函数的解析式;
(2)动点P运动到什么位置时,的面积最大,求此时P点坐标及面积的最大值;
(3)在y轴上是否存在点Q,使以O,B,Q为顶点的三角形与相似?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学下册第二十七章第2.2节《相似三角形的性质》课时练习》参考答案
题号 1 2 3 4 5 6
答案 A D D C C B
7.
8.5
9.、、
10.
11./20度
12.
13.
14.
15.
16.(1)解:,,,
,,,
,
,
;
解:△ABC COB
,
,
,
,
.
17.解:(1)∵∠C=90°,
∴∠A+∠B=90°;
∵四边形DEFG是矩形,
∴∠GDE=∠FED=90°,
∴∠GDA=∠FED=90°;
∴∠A+∠AGD=90°,
∴∠B=∠AGD且∠GDA=∠FED=90°,
∴△ADG∽△FEB.
(2)在Rt△AGD中,∠GDA=90°由勾股定理得,AD +GD =AG ,
∵AD=4,AG=5,
∴GD=3,
∵△ADG∽△FEB,
∴;
∵四边形DEFG是矩形,
∴FE=DG=3;
∴,
∴ BE =.
18.(1)解:当秒时,则,,,,,
由
(2)解:当点F在矩形的边上的边移动时,在和中,,
①若,即
解得,
经检验,是分式方程的解且符合题意,
所以当时,
②若即,解得
经检验,是分式方程的解且符合题意,
所以当时, ,
综上所述,当或时,以点E、B、F为顶点的三角形与以F、C、G为顶点的三角形相似.
19.解:(1)如图,
∵EF=x, FG=y,
∴DM=EF=x,AM=AD-DM=10-x,
∵EH//BC,
∴,即,
∴y=30-3x;
∵y>0,
∴30-3x>0,即x<10,
∵x>0,
∴x取值范围为0<x<10;
所以:(0<x<10);
(2)∵x:y=1:2,
∴y=2x,
∵y=30-3x,
∴2x=30-3x,
∴x=6,
∴y=12,
∴矩形EFGH的面积=6×12=72;
(3)设四边形EFGH的面积为S,
则 ,
∴当x=5时,即EF=5时,S有最大值为75.
20.(1)解:∵,.
∴,
又∵,是边的中点,
∴,
∵,
∴,
∴,
故答案为:、、;
(2)证明:①∵是的一个外角,
∴.
∵,,
∴.
又∵,
∴;
②,
证明:∵,
∴ ,
∵,
∴,
∴,
又,
∴.
21.(1)解:∵,则设抛物线解析式为,
把A、B两点坐标代入可得,
解得:,
∴抛物线解析式为;
(2)解:∵点P在抛物线上,
∴可设,
过P作轴于点E,交直线于点F,如图,
∵,,
设直线解析式为,
则,
解得,
∴直线解析式为,
∴,
∴,
∴
,
∴当时,最大值为8,此时,
∴当P点坐标为时,的最大面积为8;
(3)解:设,
∵,
∴分和两种情况,
当时,
∴,即,
解得,
∴点的坐标为或;
当时,
∴,即,
解得,
∴点的坐标为或;
综上,点的坐标为或或或.
答案第1页,共2页
答案第1页,共2页
