2025年中考数学复习--圆的计算证明辅助线压轴题(含解析)
文档属性
| 名称 | 2025年中考数学复习--圆的计算证明辅助线压轴题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 609.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 16:39:02 | ||
图片预览




文档简介
圆的计算证明辅助线压轴题
1如图, AB是⊙O的直径, C、D是⊙O上两点, 且 过点D的直线l 交AC的延长线于点 E,交AB的延长线于点F,连结AD、OE交于点G.
(1) 求证: DE是⊙O的切线;
(2)若 ⊙O的半径为2,求阴影部分的面积;
(3) 连结BE, 在 (2) 的条件下, 求BE的长.
2已知⊙O为△ACD 的外接圆, AD=CD.
(1) 如图1, 延长AD至点B, 使BD=AD, 连接CB.
①求证:△ABC为直角三角形;
②若⊙O的半径为4, AD=5, 求BC的值;
(2)如图2, 若∠ADC=90°, E为⊙O上的一点, 且点D,E位于AC两侧, 作△ADE关于 AD对称的图形△ADQ, 连接QC, 试猜想QA, QC, QD三者之间的数量关系并给予证明.
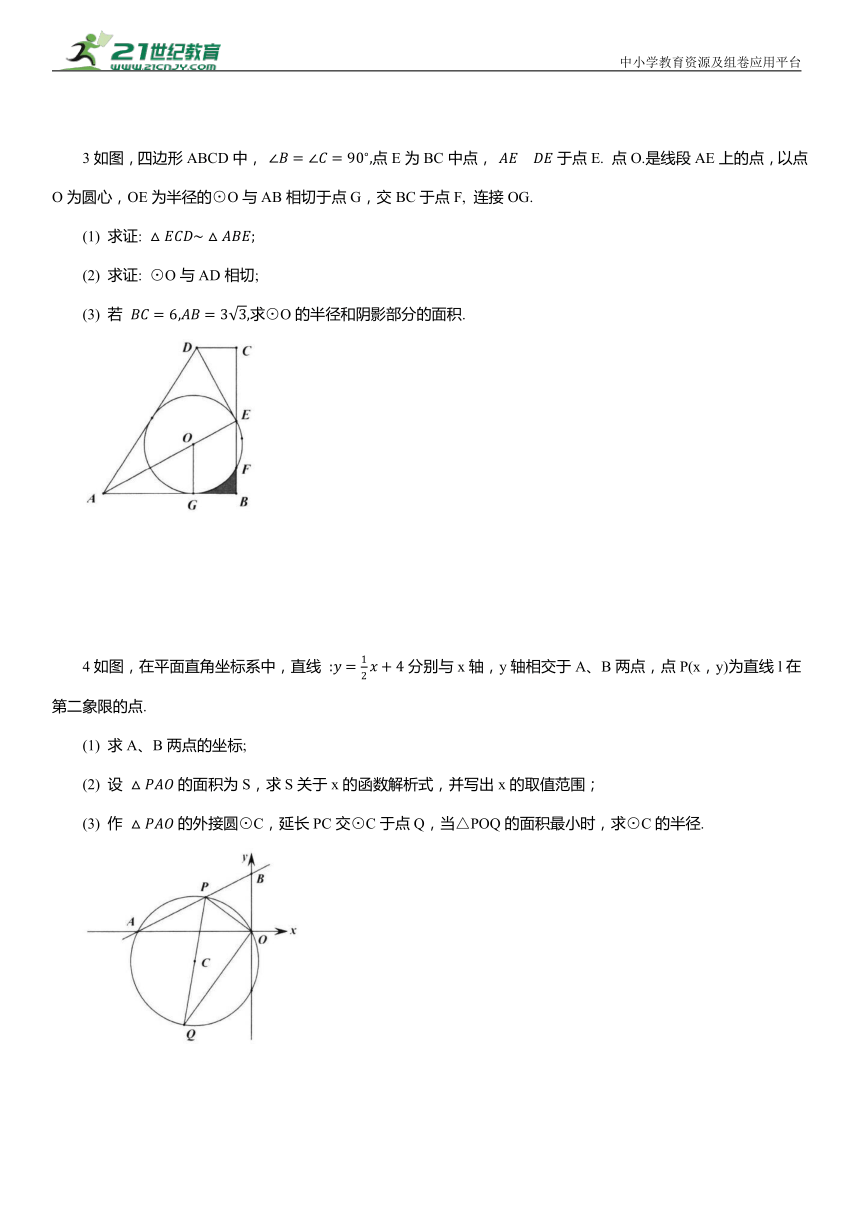
3如图,四边形ABCD中, 点E为BC中点, 于点E. 点O.是线段AE上的点,以点O为圆心,OE为半径的⊙O与AB相切于点G,交BC于点F, 连接OG.
(1) 求证:
(2) 求证: ⊙O与AD相切;
(3) 若 求⊙O的半径和阴影部分的面积.
4如图,在平面直角坐标系中,直线 分别与x轴,y轴相交于A、B两点,点P(x,y)为直线l在第二象限的点.
(1) 求A、B两点的坐标;
(2) 设 的面积为S,求S关于x的函数解析式,并写出x的取值范围;
(3) 作 的外接圆⊙C,延长PC交⊙C于点Q,当△POQ的面积最小时,求⊙C的半径.
5如图,在等腰锐角三角形ABC中, 过点B作 于D, 延长BD 交△学习笔记:ABC 的外接圆于点 E,过点 A 作 于F, AE, BC的延长线交于点G.
(1)判断EA是否平分 并说明理由;
(2) 求证:(
6如图, PA、PB是⊙O的切线, A、B是切点, AC是⊙O的直径, 连接OP, 交⊙O于点D, 交AB于点E.
(1) 求证:
(2)若E恰好是OD的中点,且四边形OAPB的面积是 ,求阴影部分的面积;
(3) 若 且 求切线PA的长.
7如图1,AB是⊙O的直径,点E是⊙O上一动点,且不与A,B两点重合, 的平分线交⊙O于点C,过点C作( 交AE的延长线于点D.
(1) 求证: CD是⊙O的切线;
(2) 求证:
(3) 如图2, 原有条件不变, 连接BE, BC, 延长AB至点M, 的平分线交AC的延长线于点 P, 的平分线交 的平分线于点 Q.求证:无论点E如何运动,总有
8如图,在 中, 以AB为直径的⊙O与BC相交于点D, 垂足为E.
(1) 求证: DE是⊙O的切线;
(2) 若弦MN垂直于AB, 垂足为G, 求⊙O的半径;
(3) 在(2) 的条件下, 当 时,求线段CECE的长.
9问题提出: (1)如图1,在四边形ABCD中, AC=4. 求BC+CD的值.
问题解决: (2)有一个直径为30cm的圆形配件⊙O,如图2所示.现需在该配件上切割出一个四边形孔洞OABC,要求 并使切割出的四边形孔洞OABC 的面积尽可能小,试问,是否存在符合要求的面积最小的四边形OABC 若存在,请求出四边形OABC面积的最小值,及此时OA的长;若不存在,请说明理由.
10如图,在Rt△ABC中, ∠C=90°, AD平分∠BAC交BC于点D, O为AB上一点,经过点A、D的⊙O分别交AB、AC于点E、F.
(1) 求证: BC是⊙O的切线;
(2) 若 求⊙O的半径;
(3) 求证:
11如图,在⊙O中,AB为直径,P为AB上一点, m为常数,且 0). 过点P的弦( Q为 上一动点(与点B不重合), 垂足为H. 连接AD、BQ.
(1) 若 . ①求证:∠OAD=60°; ②求 的值;
(2)用含m的代数式表示 ,请直接写出结果;
(3)存在一个大小确定的⊙O,对于点Q的任意位置,都有 的值是一个定值,求此时∠Q的度数.
12如图, ⊙O是△ABC的外接圆, 点O在BC边上, ∠BAC的平分线交⊙O于点D,连接BD,CD,过点D作⊙O的切线与AC的延长线交于点 P.
(1) 求证: DP∥BC;
(2) 求证:
(3) 当 时,求线段PC 的长.
13如图,四边形ABCD中, 以A为圆心,AD为半径作圆, 延长CD交⊙A 于点F, 延长DA交⊙A于点E, 连结BF, 交DE于点G.
(1) 求证: BC为⊙A 的切线;
(2) 求 的值;
(3) 求线段BG的长.
14如图1,D为⊙O上一点,点C在直径BA的延长线上,且
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2) 若 求⊙O的半径;
(3)如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E,交AB于点F,连接BE. 求 sin∠DBE 的值.
15如图,菱形ABCD中,O是对角线BD上一点( 垂足为E,以 OE为半径的⊙O分别交DC于点H,交EO的延长线于点F,EF与DC交于点G.
(1) 求证: BC是⊙O的切线;
(2) 若G是OF的中点, ①求HE弧的长;② 求AD的长.
16如图,点O为以AB为直径的半圆的圆心,点M,N在直径AB上,点P,Q在AB弧上,四边形MNPQ为正方形,点C在QP弧上运动(点C与点P,Q不重合),连接BC 并延长交MQ的延长线于点 D,连接AC交MQ于点E,连接OQ.
(1) 求 的值;
(2) 求 的值;
(3)令 直径AB=2R(R>0,R 是常数), 求y关于x的函数解析式,并指明自变量x的取值范围.
17如图所示,AB是⊙O的直径,点C、D是⊙O上不同的两点,直线BD交线段OC于点E、交过点C的直线CF于点F,若( 且
(1) 求证: 直线CF 是⊙O的切线;
(2) 连接OD、AD、AC、DC, 若.
①求证:
②过点E作 ,交线段AC于点G,点M为线段AC的中点,若, 求线段MG的长度.
18如图1, 四边形ABCD内接于⊙O, AD为直径, 点C作( 于点E, 连接AC.
(1) 求证:
(2) 若CE是⊙O的切线, 连接OC, 如图2.
①请判断四边形ABCO的形状,并说明理由;
②当AB=2时,求AD,AC与CD弧围成阴影部分的面积.
19如图,BD是半径为3的⊙O的一条弦, 点A是⊙O上的一个动点(不与点B, D重合) , 以A, B, D为顶点作
(1)如图1,若点A 是劣弧BD的中点.
①求证: 是菱形;②求 的面积.
(2)若点A 运动到优弧BD上,且 有一边与⊙O相切.
①求AB的长;②直接写出 对角线所夹锐角的正切值.
20如图,在平面直角坐标系中,⊙M经过原点O,分别交x轴、y轴于点A(2,0),B(0,8),连结AB.直线CM分别交⊙M于点D,E(点D在左侧),交x轴于点C(17,0),连结AE.
(1)求⊙M的半径和直线CM的函数表达式;
(2) 求点D, E的坐标;
(3) 点 P 在线段AC上, 连结PE. 当. 与 的一个内角相等时,求所有满足条件的OP 的长.
1 (1) 证明: 如图1, 连接OD,
∴∠DAB=∠ODA, ∴∠CAD=∠ODA, ∴OD∥AE,
∵DE⊥AC, ∴OD⊥DE,
∵OD是⊙O 的半径, ∴DE是⊙O 的切线;
(2)解:∵OD∥AE,∴△OGD∽△EGA,∴DG=ODDE, ⊙O的半径为2, ∴ = E, ∴AE=3,如图1, 连接BD, ∵AB是⊙O 的直径, DE⊥AE,
∴∠AED=∠ADB=90° , ∵∠CAD=∠DAB ,
即
在Rt△ADB中,
∴∠DAB=30°, ∴∠EAF=60°, ∠DOB=60°,
∴S阴影=SADOF-S扇形
(3) 如图2, 过点E作EM⊥AB于点M , 连接BE ,在Rt△AEM 中,
2.(1) 证明: ①∵AD=CD, BD=AD,
为直角三角形;
解:②连接OA,OD,如图1, ∴OD⊥AC且AH=CH.
∵⊙O 的半径为4, ∴OA=OD=4.
设DH=x, 则OH=4-x,
解得:
由①知: BC⊥AC, ∵OD⊥AC, ∴OD∥BC.
(2) QA , QC , QD 三者之间的数量关系为: 理由如下:
延长QA交⊙O于点 F, 连接DF, FC, 如图2,
∵∠ADC=90°, AD=CD, ∴∠DAC=∠DCA=45°.
∴∠DFA=∠E=∠DCA=45°, ∠DFC=∠DAC=45°.
∵△ADQ与△ADE关于AD 对称, ∴∠DQA=∠E=45°,
∴∠DQA=∠DFA=45°, ∴DQ=DF.
∴∠QDF=180°-∠DQA-∠QFD=90°
即
∵∠QDF=∠ADC=90°, ∴∠QDA=∠CDF .
在△QDA和△FDC中,
∴△QDA≌△FDC(AAS).∴QA=FC.∴QC =2QD +QA
3. 证明: (1) ∵AE⊥DE, ∴∠AED=90°,
∴∠DEC+∠AEB=90°, ∵∠C=90°,
∴∠CDE+∠DEC=90°, ∴∠AEB=∠CDE,
∵∠B=∠C, ∴△ECD∽△ABE;
(2)如图1,延长DE、AB交于点P,作OH⊥AD于H,∵E 为BC的中点, ∴CE=BE, 在△DCE和△PBE中,
∵AE⊥DP, ,∴AE 垂直平分DP, ∴AD=AP,
∴∠DAO=∠GAO, ∵OH⊥AD, OG⊥AB,
∴OH =OG, ∴⊙O与AD相切;
中小学教育资源及组卷应用平台
(3) 如图2, 连接OF,
在Rt△ABE中,∵BC=6,AB=3 由(2)可知CE=BE,
∴∠AEB=60°, ∴△OEF 是等边三角形, ∠EAB=30°
∴AE=2BE=6, 设半径为r, ∴AO=2OG,
∴6-r=2r, ∴r=2,
∵∠GOF =180°-∠EOF-∠AOG=60°,
4. 解: (1) ∵直线 分别与x轴,y轴相交于A、 B两点, ∴当x=0时, y=4;
当y=0时, x=-8, ∴A(-8,0), B(0,4);
(2)∵点P(x,y)为直线l在第二象限的点,P(x, x+4)
∴S=2x+16(-8(3) ∵A(-8,0), B(0,4), ∴OA=8, OB=4,在Rt△AOB中,由勾股定理得:
在⊙C中, ∵PQ是直径, ∴∠POQ=90°,
∴当S△POO最小时, 则OP最小,
∵点P在线段AB 上运动, ∴当OP⊥AB时, OP 最小,
∴⊙C 半径为4.
5.解: (1) EA平分∠DEF, 理由如下:
∵AB=AC, ∴∠ABC=∠ACB,
又∵∠ACB=∠AEB, ∴∠ABC=∠AEB
∵∠ABC+∠AEC=180°, ∠AEF+∠AEC=180°,
∴∠ABC=∠AEF, ∴∠AEB=∠AEF, ∴EA平分∠DEF,
(2) ①由(1) 知: EA平分∠DEF,
∵BD⊥AC, AF⊥CE, ∴AD=AF, 在 Rt△ABD 和 Rt△ACF 中, 易证Rt△ABD≌Rt△ACF(HL) ,
∴BD=CF,
②由(1) 知, ∠AEB=∠AEF,
∵∠AEF=∠CEG, ∴∠AEB=∠CEG,
∵∠BAE+∠BCE=180° , ∠BCE+∠ECG=180° ,
∴∠BAE=∠ECG, ∴△AEB∽△CEG,∴∠E=BE=,
∴BE·CE=AE·EG,
∴BD -DE = (BD+DE) (BD-DE)
即
6 (1) 证明: ∵PA, PB是⊙O的切线, ∴PA=PB,∵OA=OB, ∴OP⊥AB, ∵AC是直径,
∴∠ABC=90°, ∴BC⊥AB, ∴BC∥OP.
(2) 解: ∵OE=DE, AB⊥OD, ∴AO=AD,
∵OA=OD, ∴AD=OA=OD,
∴△AOD是等边三角形, ∴∠AOD=60°,设OE=m, 则AE=BE= m, OA=2m, OP=4m,
∵四边形OAPB的面积是 或-2 (舍去) ,
∵OD⊥AB, ∴AD=BD, ∴∠AOD=∠BOD=60°,
∴∠AOB=2∠AOD=120°,
(3) 解: 在Rt△AOE中,
设OE=x, 则(OA=OD=3x, DE=2x,
在Rt△ADE中,
或-1 (舍去),
∴OE=1, OA=3, AE=2 , ∵PA是切线,
∴PA⊥OA, ∴∠OAP=90°,
∴∠CAB+∠BAP=90°, ∠APO+∠PAE=90°,
∴∠CAB=∠APO,
478.(1) 证明: 如图1, 连接OC,
∵OA=OC, ∴∠OAC=∠OCA, ∴∠BOC=2∠OAC,
∵AC平分∠BAE,∴∠BAE=2∠OAC,∴∠BAE=∠BOC,
∴CO∥AD, ∵CD⊥AE, ∴∠D=90°, ∴∠DCO=90°,
∴OC⊥CD, ∴CD是⊙O 的切线.
(2) 如图2, 连接BC, ∵AC平分∠BAE,
∴∠BAC=∠CAD, ∵AB是⊙O 的直径, ∴∠BCA=90°,
∵∠D=90°, ∴∠D=∠BCA, ∴△BAC∽△CAD,
(3) ∵∠CAB、∠CBM 的角平分线交于点Q,
∵∠QBM 是△QAB的一个外角, ∠CBM 是△ABC 的一个外角,
∵∠ACB=90°, ∴∠Q=45°,
同理可证:
7 (1) 证明: 如图1, 连接OD,
∵OB=OD, ∴∠OBD=∠ODB, ∵AB=AC,
∴∠ABC=∠ACB, ∴∠ODB=∠ACB, ∴OD∥AC,
∵DE⊥AC, ∴DE⊥OD,
∵OD是⊙O的半径, ∴DE是⊙O的切线;
(2)解:如图1,连接OM , ∵AB⊥MN,且AB为⊙O的直径, 设⊙O 的半径为r, 则OM =r, AB=2r,
在Rt△OGM中,根据勾股定理得, 即⊙O 的半径为1;
(3) 如图2, 作∠ABC的平分线交AC于F,在△ABC中, AB=AC, ∠BAC=36°,
∴AF=BF,
设AF=BF=x,在△BCF 中,∠CBF=36°,∠C=72°,
由(2) 知, ⊙O的半径为1, ∴AB=AC=2,
∴CF=AC-AF=2-x, ∵∠CBF=∠CAB,
∴∠C=∠C, ∴△BCF∽△ACB, ∴BCAC=CEB,
或 (舍),
连接AD, ∵AB为⊙O 的直径,
∵DE⊥AC, ∴∠DEC=90°=∠ADC,
∵∠C=∠C, ∴△DEC∽△ADC,∵ =00,
8.解: (1)如图1, ∵∠BCD=∠BAD=90°, AD=AB,
∴∠B+∠ADC=180°,
∴可以将△ABC绕A 点逆时针旋转90°得△ADE,
∴∠ADE=∠B, AE=AC, ∠CAE=90°,
∴∠ADE+∠ADC=180°,∴C、D、E在同一条直线上,
(2) 如图2, 连接OB, ∵∠AOC=60°, OA=OC,
∴将△AOB绕O点顺时针旋转60°至△COE , 连接BE ,
∴∠BOE=60°, OE=OB, ∴△BOE 是等边三角形,
∴BE=OB=15, ∠BEO=60°, ∠CBE=∠ABO=∠CEO,
∴∠CBE+∠CEB=60°, ∴∠BCE=120°,
当△BCE的面积最大时,四边形OABC 的面积最小
∵BE=BO=15, ∠BCE=120° , 均为定值
∴C 是△BCE 外接圆的BE 弧上运动,作它的外接圆⊙I,当CI⊥BE时, CF 即为△BCE 底边 BE 上的高的最大值,此时O、C、F、I四点共线.
此时
9.解: (1) 如图1, 连接OD, 则OA=OD,
∴∠ODA=∠OAD , ∵AD是∠BAC 的平分线,
∴∠OAD=∠CAD, ∴∠ODA=∠CAD,
∴OD∥AC, ∴∠ODB=∠C=90°,
∵点D 在⊙O 上, ∴BC是⊙O 的切线;
∴OD=5, ∴⊙O的半径为5;
(3) 如图2, 连接EF, ∵AE 是直径,
∴∠AFE=90°=∠ACB, ∴EF∥BC, ∴∠AEF=∠B,
又∵∠AEF=∠ADF , ∴∠B=∠ADF,
又∵∠OAD=∠CAD , ∴△DAB∽△FAD,
10. 解: (1) ①连接OD, 如图1:
∵m=3即PB=3, AP=1, ∴AB=AP+PB=4,
∴P是OA中点, 又CD⊥AB, ∴CD是OA的垂直平分线, ∴AD=OD=OA=2, 即△AOD是等边三角形,∴∠OAD=60°;
②连接AQ,如图1:∵AB是⊙O 直径,∴∠AQB=90°,∵AH⊥DQ, ∴∠AHD=90°, ∴∠AQB=∠AHD,∵AQ=AQ, ∴∠ADH =∠ABQ, ∴△ADH∽△ABQ, 由①知: AB=4, AD=2,∴B /DH=2;(2) 连接AQ、 BD,如图2:
∵AB是⊙O 直径, ∴∠ADB=90°, ∴∠ADB=∠APD,又∠PAD=∠DAB, ∴△APD∽△ADB, ∴ADAB=APA,∵AP=1, PB=m, ∴AB=1+m,ADm= D ,
与(1)中②同理,可得:
(3) 由 (2) 得
即
若 是定值,则 的值与DH 无关, 即当m=1时, 的定值为1,此时P与O重合,如图3
∵AB⊥CD, OA=OD=1, ∴△AOD是等腰直角三角形,
故存在半径为1 的⊙O , 对Q 的任意位置, 都有 是定值1, 此时∠BQD为45°.
11.解:(1)连接OD,∵DP是⊙O 的切线,∴DO⊥DP,
∵AD是∠BAC的平分线, ∴∠BAD=∠CAD,
∵BC是圆的直径, ∴∠BAC=90°,
∴∠BAD=45°, ∴∠BOD=90°,
∴OD⊥BC, ∴DP∥BC;
(2) ∵DP∥BC, ∴∠ACB=∠P, ∵∠ACB=∠ADB,∴∠P=∠ADB,
∵OD=OC, ∴∠ODC=45°∴∠CDP=45°,
∵∠BAD=∠DAC=45°, ∴∠BAD=∠CDP,
∴△ABD∽△DCP;
(3) ∵AB=5cm, AC=12cm, ∠BAC=90°,
∴BC=13cm,∴OC=OB=OD= cm
在等腰Rt△COD中,
在等腰 Rt△BOD中, BD=13 / , ∵△ABD∽△DCP ,
12.(1) 证明: ∵AD⊥AB, ∴∠BAD=90°,∵AD∥BC, ∴∠ABC=180°-∠BAD=90°,又∵AB是圆的半径, ∴BC为⊙A的切线;
(2) 解: 如图1, 过点D作DH⊥BC于H,
∴∠DHB=90°, 由 (1) 知, ∠BAD=∠ABC=90°,
∴∠ABC=∠BAD=∠BHD=90°,
∴四边形ABHD为矩形, ∵AB=AD=1,
∴矩形ABHD 是正方形, ∴BH=DH=AB=1,
在Rt△DHC中, 根据勾股定理得,
∵AD∥BC, ∴∠EDF=∠C,
(3) 如图2, 过点A作AM⊥DF于M,则DF=2DM , ∠AMD=90°,
在Rt△AMD中,
∵AD∥BC, ∴△DFG∽△CFB, ∴DF=DGBC,
由(2)知,
在Rt△BAG中,
13.解: (1) CD与⊙O 相切,理由: 如图1,连接OD,
∵OB=OD, ∴∠ODB=∠CBD,
∵∠CDA=∠CBD, ∴∠CDA=∠ODB,
∵AB为⊙O 的直径, ∴∠ADB=∠ADO+∠ODB=90°,
∴∠CDA+∠ADO=90°, ∴∠CDO=90°,
∴OD⊥CD, ∴CD与⊙O 相切;
(2) 由(1) 知,∠CBD=∠ADC, ∵tan∠ADC=
在Rt△ADB中,
∵∠C=∠C, ∠ADC=∠CBD, ∴△CAD∽△CDB,
∴ ∴CD=2CA=4 ,
∴CB=2CD=8,
∴AB=CB-CA=8-2=6, ∴OA=OB= AB=3,∴⊙O的半径为3;
(3) 如图2, 连接OE, 过点E作EG⊥BD于G,∵DE平分∠ADB, ∴∠ADE=∠BDE=45°,
∴∠BOE=2∠BDE=90°, . 在Rt△ABD中,
∵EG⊥BD, ∠BDE=45°,
∴∠DEG=∠BDE=45°, ∴DG=EG,
设DG=EG=x, 则
在Rt△BEG中,
或 (舍),
14解: (1)证明:如图1,过点O作OM⊥BC于点M ,∵BD是菱形ABCD的对角线, ∴∠ABD=∠CBD,∵OM⊥BC, OE⊥AB, ∴OE=OM ,∴BC是⊙O的切线.
(2) ∵G是OF的中点, ∵AB∥CD, OE⊥AB, ∴OF⊥CD, ∴∠OGH=90°, ∴∠HOE=120°, ∵OG=2, ∴OH =4,
∴由弧长公式得到HE 弧的长:
②如图2, 过A作AN⊥BD 于点N,
∵DG=1, OG=2, OE=OH=4,
15. 解: (1) 如图1, 连接OP.
∵四边形MNPQ是正方形, ∴∠OMQ=∠ONP=90°,MQ=PN, ∵OQ=OP, ∴Rt△OMQ≌Rt△ONP(HL),∴OM =ON, 设OM =ON=m, 则MQ=2m,
(2) 由 (1) 可知OM=ON=m, OQ=OA= m,MN=2m, ∴AM=OA-OM= m-m,
(3) ∵AB=2R, ∴OA=OB=OQ=R,
∵AB是直径, ∴∠ACB=∠DCE=90°,
∵∠CED=∠AEM , ∴∠A=∠D
∵∠AME=∠DMB=90°,
当点C与P重合时,
如图2,当C与Q点重合时, 如图3,当C与P点重合时,
488. (1) 证明:
∴∠ECF =90°, ∴OC⊥CF, ∴直线CF是⊙O 的切线.
(2) ①证明: ∵∠COD=2∠DAC, ∠COD=2∠BOC,
∴∠DAC=∠EOB,∵∠DCA=∠EBO, ∴△ACD∽△OBE.
②解: ∵OB=OC, OC=3EC, ∴OB:OE=3:2,
∵AD=4, ∴AC=6,
∵M 是AC的中点, ∴CM =MA=3,
,
∴MG=CM--CG=3-2=1, 即线段MG的长度为1.
489. (1)证明: ∵四边形ABCD是⊙O的内接四边形,
∴∠CBE=∠D,
∵AD为⊙O的直径, ∴∠ACD=90°,
∴∠D+∠CAD=90°, ∴∠CBE+∠CAD=90°,
∵CE⊥AB, ∴∠CBE+∠BCE=90°,
∴∠CAD=∠BCE;
(2) ①四边形ABCO是菱形, 理由:
∵∠CAD=30°, ∴∠COD=2∠CAD=60°,
∵CE 是⊙O 的切线, ∴OC⊥CE,
∵CE⊥AB, ∴OC∥AB, ∴∠DAB=∠COD=60°,由 (1) 知, ∠CBE+∠CAD=90°,
∴BC∥OA,
∴四边形ABCO是平行四边形, ∵OA=OC,
∴□ABCO是菱形;
②由①知,四边形ABCO是菱形,
∴OA=OC=AB=2, ∴AD=2OA=4,
由①知, ∠COD=60°,
在Rt△ACD中, ∠CAD=30°,
∴CD=2, AC=2
∴AD, AC与CD弧围成阴影部分的面积为:
16 (1) ①证明:
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
②解: 如图1, 连接OA交BD于J, 连接OC, OD.
∵AD=AB, ∴OA⊥BD, ∵四边形ABCD是菱形,
∴AC⊥BD, ∴A, O, C共线,
在Rt△OJD中,
∴AJ=OA-OJ =3-1=2,
∵四边形ABCD是菱形, ∴AJ =CJ=2,
(2)①解:分两种情况讨论:
第1种情况,如图2,当CD与⊙O相切时,连接AC交BD于H, 连接OH, OD, 延长DO交AB于P
∵CD 是⊙O 的切线, ∴OD⊥CD,
∵CD∥AB, ∴DP⊥AB, ∴PA=PB,
∵四边形ABCD是平行四边形,.
∴OH⊥BD, ∴∠DHO=∠DPB=90°,
∵∠ODH =∠BDP, ∴△DHO∽△DPB,
第2种情况,如图3,当BC与⊙O 相切时,同法可证.
综上所述,AB的长为4
②解: 如图4, 过点A 作AJ⊥BD于J .
如图3中,同法可得□ABCD对角线所夹锐角的正切值为 综上所述, ABCD对角线所夹锐角的正切值为
17. 解: (1) ∵∠AOB=90°, ∴AB为⊙M 的直径,∵点M 是AB的中点, 则点M(1,4),
则圆的半径为
设直线CM 的表达式为y=kx+b, 则 解得 故直线CM 的表达式为
(2)设点D 的坐标为
由 得: 解得x=5或-3,
故点D、 E 的坐标分别为(-3,5)、(5,3);
(3) 过点 D 作 DH⊥OB 于 点 H , 则 DH=3 ,BH=8-5=3=DH , 故∠DBO=45°,
由点A、 E 的坐标, 同理可得∠EAP=45°;
由点A、 E、 B 、D的坐标得,
同理可得:BD=3 , OB=8,
①当∠AEP=∠DBO=45°时,则△AEP为等腰直角三角形, EP⊥AC ,故点 P 的坐标为(5,0), 故OP=5;
②∠AEP=∠BDO时, ∵∠EAP=∠DBO,
∴△EAP∽△DBO, 即
解得AP=8, 故PO=10;
③∠AEP=∠BOD时, ∵∠EAP=∠DBO,
∴△EAP∽△OBD, ∴AEOB=ABD,即 解得 则 综上所述, OP为5或10或
1如图, AB是⊙O的直径, C、D是⊙O上两点, 且 过点D的直线l 交AC的延长线于点 E,交AB的延长线于点F,连结AD、OE交于点G.
(1) 求证: DE是⊙O的切线;
(2)若 ⊙O的半径为2,求阴影部分的面积;
(3) 连结BE, 在 (2) 的条件下, 求BE的长.
2已知⊙O为△ACD 的外接圆, AD=CD.
(1) 如图1, 延长AD至点B, 使BD=AD, 连接CB.
①求证:△ABC为直角三角形;
②若⊙O的半径为4, AD=5, 求BC的值;
(2)如图2, 若∠ADC=90°, E为⊙O上的一点, 且点D,E位于AC两侧, 作△ADE关于 AD对称的图形△ADQ, 连接QC, 试猜想QA, QC, QD三者之间的数量关系并给予证明.
3如图,四边形ABCD中, 点E为BC中点, 于点E. 点O.是线段AE上的点,以点O为圆心,OE为半径的⊙O与AB相切于点G,交BC于点F, 连接OG.
(1) 求证:
(2) 求证: ⊙O与AD相切;
(3) 若 求⊙O的半径和阴影部分的面积.
4如图,在平面直角坐标系中,直线 分别与x轴,y轴相交于A、B两点,点P(x,y)为直线l在第二象限的点.
(1) 求A、B两点的坐标;
(2) 设 的面积为S,求S关于x的函数解析式,并写出x的取值范围;
(3) 作 的外接圆⊙C,延长PC交⊙C于点Q,当△POQ的面积最小时,求⊙C的半径.
5如图,在等腰锐角三角形ABC中, 过点B作 于D, 延长BD 交△学习笔记:ABC 的外接圆于点 E,过点 A 作 于F, AE, BC的延长线交于点G.
(1)判断EA是否平分 并说明理由;
(2) 求证:(
6如图, PA、PB是⊙O的切线, A、B是切点, AC是⊙O的直径, 连接OP, 交⊙O于点D, 交AB于点E.
(1) 求证:
(2)若E恰好是OD的中点,且四边形OAPB的面积是 ,求阴影部分的面积;
(3) 若 且 求切线PA的长.
7如图1,AB是⊙O的直径,点E是⊙O上一动点,且不与A,B两点重合, 的平分线交⊙O于点C,过点C作( 交AE的延长线于点D.
(1) 求证: CD是⊙O的切线;
(2) 求证:
(3) 如图2, 原有条件不变, 连接BE, BC, 延长AB至点M, 的平分线交AC的延长线于点 P, 的平分线交 的平分线于点 Q.求证:无论点E如何运动,总有
8如图,在 中, 以AB为直径的⊙O与BC相交于点D, 垂足为E.
(1) 求证: DE是⊙O的切线;
(2) 若弦MN垂直于AB, 垂足为G, 求⊙O的半径;
(3) 在(2) 的条件下, 当 时,求线段CECE的长.
9问题提出: (1)如图1,在四边形ABCD中, AC=4. 求BC+CD的值.
问题解决: (2)有一个直径为30cm的圆形配件⊙O,如图2所示.现需在该配件上切割出一个四边形孔洞OABC,要求 并使切割出的四边形孔洞OABC 的面积尽可能小,试问,是否存在符合要求的面积最小的四边形OABC 若存在,请求出四边形OABC面积的最小值,及此时OA的长;若不存在,请说明理由.
10如图,在Rt△ABC中, ∠C=90°, AD平分∠BAC交BC于点D, O为AB上一点,经过点A、D的⊙O分别交AB、AC于点E、F.
(1) 求证: BC是⊙O的切线;
(2) 若 求⊙O的半径;
(3) 求证:
11如图,在⊙O中,AB为直径,P为AB上一点, m为常数,且 0). 过点P的弦( Q为 上一动点(与点B不重合), 垂足为H. 连接AD、BQ.
(1) 若 . ①求证:∠OAD=60°; ②求 的值;
(2)用含m的代数式表示 ,请直接写出结果;
(3)存在一个大小确定的⊙O,对于点Q的任意位置,都有 的值是一个定值,求此时∠Q的度数.
12如图, ⊙O是△ABC的外接圆, 点O在BC边上, ∠BAC的平分线交⊙O于点D,连接BD,CD,过点D作⊙O的切线与AC的延长线交于点 P.
(1) 求证: DP∥BC;
(2) 求证:
(3) 当 时,求线段PC 的长.
13如图,四边形ABCD中, 以A为圆心,AD为半径作圆, 延长CD交⊙A 于点F, 延长DA交⊙A于点E, 连结BF, 交DE于点G.
(1) 求证: BC为⊙A 的切线;
(2) 求 的值;
(3) 求线段BG的长.
14如图1,D为⊙O上一点,点C在直径BA的延长线上,且
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2) 若 求⊙O的半径;
(3)如图2,在(2)的条件下,∠ADB的平分线DE交⊙O于点E,交AB于点F,连接BE. 求 sin∠DBE 的值.
15如图,菱形ABCD中,O是对角线BD上一点( 垂足为E,以 OE为半径的⊙O分别交DC于点H,交EO的延长线于点F,EF与DC交于点G.
(1) 求证: BC是⊙O的切线;
(2) 若G是OF的中点, ①求HE弧的长;② 求AD的长.
16如图,点O为以AB为直径的半圆的圆心,点M,N在直径AB上,点P,Q在AB弧上,四边形MNPQ为正方形,点C在QP弧上运动(点C与点P,Q不重合),连接BC 并延长交MQ的延长线于点 D,连接AC交MQ于点E,连接OQ.
(1) 求 的值;
(2) 求 的值;
(3)令 直径AB=2R(R>0,R 是常数), 求y关于x的函数解析式,并指明自变量x的取值范围.
17如图所示,AB是⊙O的直径,点C、D是⊙O上不同的两点,直线BD交线段OC于点E、交过点C的直线CF于点F,若( 且
(1) 求证: 直线CF 是⊙O的切线;
(2) 连接OD、AD、AC、DC, 若.
①求证:
②过点E作 ,交线段AC于点G,点M为线段AC的中点,若, 求线段MG的长度.
18如图1, 四边形ABCD内接于⊙O, AD为直径, 点C作( 于点E, 连接AC.
(1) 求证:
(2) 若CE是⊙O的切线, 连接OC, 如图2.
①请判断四边形ABCO的形状,并说明理由;
②当AB=2时,求AD,AC与CD弧围成阴影部分的面积.
19如图,BD是半径为3的⊙O的一条弦, 点A是⊙O上的一个动点(不与点B, D重合) , 以A, B, D为顶点作
(1)如图1,若点A 是劣弧BD的中点.
①求证: 是菱形;②求 的面积.
(2)若点A 运动到优弧BD上,且 有一边与⊙O相切.
①求AB的长;②直接写出 对角线所夹锐角的正切值.
20如图,在平面直角坐标系中,⊙M经过原点O,分别交x轴、y轴于点A(2,0),B(0,8),连结AB.直线CM分别交⊙M于点D,E(点D在左侧),交x轴于点C(17,0),连结AE.
(1)求⊙M的半径和直线CM的函数表达式;
(2) 求点D, E的坐标;
(3) 点 P 在线段AC上, 连结PE. 当. 与 的一个内角相等时,求所有满足条件的OP 的长.
1 (1) 证明: 如图1, 连接OD,
∴∠DAB=∠ODA, ∴∠CAD=∠ODA, ∴OD∥AE,
∵DE⊥AC, ∴OD⊥DE,
∵OD是⊙O 的半径, ∴DE是⊙O 的切线;
(2)解:∵OD∥AE,∴△OGD∽△EGA,∴DG=ODDE, ⊙O的半径为2, ∴ = E, ∴AE=3,如图1, 连接BD, ∵AB是⊙O 的直径, DE⊥AE,
∴∠AED=∠ADB=90° , ∵∠CAD=∠DAB ,
即
在Rt△ADB中,
∴∠DAB=30°, ∴∠EAF=60°, ∠DOB=60°,
∴S阴影=SADOF-S扇形
(3) 如图2, 过点E作EM⊥AB于点M , 连接BE ,在Rt△AEM 中,
2.(1) 证明: ①∵AD=CD, BD=AD,
为直角三角形;
解:②连接OA,OD,如图1, ∴OD⊥AC且AH=CH.
∵⊙O 的半径为4, ∴OA=OD=4.
设DH=x, 则OH=4-x,
解得:
由①知: BC⊥AC, ∵OD⊥AC, ∴OD∥BC.
(2) QA , QC , QD 三者之间的数量关系为: 理由如下:
延长QA交⊙O于点 F, 连接DF, FC, 如图2,
∵∠ADC=90°, AD=CD, ∴∠DAC=∠DCA=45°.
∴∠DFA=∠E=∠DCA=45°, ∠DFC=∠DAC=45°.
∵△ADQ与△ADE关于AD 对称, ∴∠DQA=∠E=45°,
∴∠DQA=∠DFA=45°, ∴DQ=DF.
∴∠QDF=180°-∠DQA-∠QFD=90°
即
∵∠QDF=∠ADC=90°, ∴∠QDA=∠CDF .
在△QDA和△FDC中,
∴△QDA≌△FDC(AAS).∴QA=FC.∴QC =2QD +QA
3. 证明: (1) ∵AE⊥DE, ∴∠AED=90°,
∴∠DEC+∠AEB=90°, ∵∠C=90°,
∴∠CDE+∠DEC=90°, ∴∠AEB=∠CDE,
∵∠B=∠C, ∴△ECD∽△ABE;
(2)如图1,延长DE、AB交于点P,作OH⊥AD于H,∵E 为BC的中点, ∴CE=BE, 在△DCE和△PBE中,
∵AE⊥DP, ,∴AE 垂直平分DP, ∴AD=AP,
∴∠DAO=∠GAO, ∵OH⊥AD, OG⊥AB,
∴OH =OG, ∴⊙O与AD相切;
中小学教育资源及组卷应用平台
(3) 如图2, 连接OF,
在Rt△ABE中,∵BC=6,AB=3 由(2)可知CE=BE,
∴∠AEB=60°, ∴△OEF 是等边三角形, ∠EAB=30°
∴AE=2BE=6, 设半径为r, ∴AO=2OG,
∴6-r=2r, ∴r=2,
∵∠GOF =180°-∠EOF-∠AOG=60°,
4. 解: (1) ∵直线 分别与x轴,y轴相交于A、 B两点, ∴当x=0时, y=4;
当y=0时, x=-8, ∴A(-8,0), B(0,4);
(2)∵点P(x,y)为直线l在第二象限的点,P(x, x+4)
∴S=2x+16(-8
在⊙C中, ∵PQ是直径, ∴∠POQ=90°,
∴当S△POO最小时, 则OP最小,
∵点P在线段AB 上运动, ∴当OP⊥AB时, OP 最小,
∴⊙C 半径为4.
5.解: (1) EA平分∠DEF, 理由如下:
∵AB=AC, ∴∠ABC=∠ACB,
又∵∠ACB=∠AEB, ∴∠ABC=∠AEB
∵∠ABC+∠AEC=180°, ∠AEF+∠AEC=180°,
∴∠ABC=∠AEF, ∴∠AEB=∠AEF, ∴EA平分∠DEF,
(2) ①由(1) 知: EA平分∠DEF,
∵BD⊥AC, AF⊥CE, ∴AD=AF, 在 Rt△ABD 和 Rt△ACF 中, 易证Rt△ABD≌Rt△ACF(HL) ,
∴BD=CF,
②由(1) 知, ∠AEB=∠AEF,
∵∠AEF=∠CEG, ∴∠AEB=∠CEG,
∵∠BAE+∠BCE=180° , ∠BCE+∠ECG=180° ,
∴∠BAE=∠ECG, ∴△AEB∽△CEG,∴∠E=BE=,
∴BE·CE=AE·EG,
∴BD -DE = (BD+DE) (BD-DE)
即
6 (1) 证明: ∵PA, PB是⊙O的切线, ∴PA=PB,∵OA=OB, ∴OP⊥AB, ∵AC是直径,
∴∠ABC=90°, ∴BC⊥AB, ∴BC∥OP.
(2) 解: ∵OE=DE, AB⊥OD, ∴AO=AD,
∵OA=OD, ∴AD=OA=OD,
∴△AOD是等边三角形, ∴∠AOD=60°,设OE=m, 则AE=BE= m, OA=2m, OP=4m,
∵四边形OAPB的面积是 或-2 (舍去) ,
∵OD⊥AB, ∴AD=BD, ∴∠AOD=∠BOD=60°,
∴∠AOB=2∠AOD=120°,
(3) 解: 在Rt△AOE中,
设OE=x, 则(OA=OD=3x, DE=2x,
在Rt△ADE中,
或-1 (舍去),
∴OE=1, OA=3, AE=2 , ∵PA是切线,
∴PA⊥OA, ∴∠OAP=90°,
∴∠CAB+∠BAP=90°, ∠APO+∠PAE=90°,
∴∠CAB=∠APO,
478.(1) 证明: 如图1, 连接OC,
∵OA=OC, ∴∠OAC=∠OCA, ∴∠BOC=2∠OAC,
∵AC平分∠BAE,∴∠BAE=2∠OAC,∴∠BAE=∠BOC,
∴CO∥AD, ∵CD⊥AE, ∴∠D=90°, ∴∠DCO=90°,
∴OC⊥CD, ∴CD是⊙O 的切线.
(2) 如图2, 连接BC, ∵AC平分∠BAE,
∴∠BAC=∠CAD, ∵AB是⊙O 的直径, ∴∠BCA=90°,
∵∠D=90°, ∴∠D=∠BCA, ∴△BAC∽△CAD,
(3) ∵∠CAB、∠CBM 的角平分线交于点Q,
∵∠QBM 是△QAB的一个外角, ∠CBM 是△ABC 的一个外角,
∵∠ACB=90°, ∴∠Q=45°,
同理可证:
7 (1) 证明: 如图1, 连接OD,
∵OB=OD, ∴∠OBD=∠ODB, ∵AB=AC,
∴∠ABC=∠ACB, ∴∠ODB=∠ACB, ∴OD∥AC,
∵DE⊥AC, ∴DE⊥OD,
∵OD是⊙O的半径, ∴DE是⊙O的切线;
(2)解:如图1,连接OM , ∵AB⊥MN,且AB为⊙O的直径, 设⊙O 的半径为r, 则OM =r, AB=2r,
在Rt△OGM中,根据勾股定理得, 即⊙O 的半径为1;
(3) 如图2, 作∠ABC的平分线交AC于F,在△ABC中, AB=AC, ∠BAC=36°,
∴AF=BF,
设AF=BF=x,在△BCF 中,∠CBF=36°,∠C=72°,
由(2) 知, ⊙O的半径为1, ∴AB=AC=2,
∴CF=AC-AF=2-x, ∵∠CBF=∠CAB,
∴∠C=∠C, ∴△BCF∽△ACB, ∴BCAC=CEB,
或 (舍),
连接AD, ∵AB为⊙O 的直径,
∵DE⊥AC, ∴∠DEC=90°=∠ADC,
∵∠C=∠C, ∴△DEC∽△ADC,∵ =00,
8.解: (1)如图1, ∵∠BCD=∠BAD=90°, AD=AB,
∴∠B+∠ADC=180°,
∴可以将△ABC绕A 点逆时针旋转90°得△ADE,
∴∠ADE=∠B, AE=AC, ∠CAE=90°,
∴∠ADE+∠ADC=180°,∴C、D、E在同一条直线上,
(2) 如图2, 连接OB, ∵∠AOC=60°, OA=OC,
∴将△AOB绕O点顺时针旋转60°至△COE , 连接BE ,
∴∠BOE=60°, OE=OB, ∴△BOE 是等边三角形,
∴BE=OB=15, ∠BEO=60°, ∠CBE=∠ABO=∠CEO,
∴∠CBE+∠CEB=60°, ∴∠BCE=120°,
当△BCE的面积最大时,四边形OABC 的面积最小
∵BE=BO=15, ∠BCE=120° , 均为定值
∴C 是△BCE 外接圆的BE 弧上运动,作它的外接圆⊙I,当CI⊥BE时, CF 即为△BCE 底边 BE 上的高的最大值,此时O、C、F、I四点共线.
此时
9.解: (1) 如图1, 连接OD, 则OA=OD,
∴∠ODA=∠OAD , ∵AD是∠BAC 的平分线,
∴∠OAD=∠CAD, ∴∠ODA=∠CAD,
∴OD∥AC, ∴∠ODB=∠C=90°,
∵点D 在⊙O 上, ∴BC是⊙O 的切线;
∴OD=5, ∴⊙O的半径为5;
(3) 如图2, 连接EF, ∵AE 是直径,
∴∠AFE=90°=∠ACB, ∴EF∥BC, ∴∠AEF=∠B,
又∵∠AEF=∠ADF , ∴∠B=∠ADF,
又∵∠OAD=∠CAD , ∴△DAB∽△FAD,
10. 解: (1) ①连接OD, 如图1:
∵m=3即PB=3, AP=1, ∴AB=AP+PB=4,
∴P是OA中点, 又CD⊥AB, ∴CD是OA的垂直平分线, ∴AD=OD=OA=2, 即△AOD是等边三角形,∴∠OAD=60°;
②连接AQ,如图1:∵AB是⊙O 直径,∴∠AQB=90°,∵AH⊥DQ, ∴∠AHD=90°, ∴∠AQB=∠AHD,∵AQ=AQ, ∴∠ADH =∠ABQ, ∴△ADH∽△ABQ, 由①知: AB=4, AD=2,∴B /DH=2;(2) 连接AQ、 BD,如图2:
∵AB是⊙O 直径, ∴∠ADB=90°, ∴∠ADB=∠APD,又∠PAD=∠DAB, ∴△APD∽△ADB, ∴ADAB=APA,∵AP=1, PB=m, ∴AB=1+m,ADm= D ,
与(1)中②同理,可得:
(3) 由 (2) 得
即
若 是定值,则 的值与DH 无关, 即当m=1时, 的定值为1,此时P与O重合,如图3
∵AB⊥CD, OA=OD=1, ∴△AOD是等腰直角三角形,
故存在半径为1 的⊙O , 对Q 的任意位置, 都有 是定值1, 此时∠BQD为45°.
11.解:(1)连接OD,∵DP是⊙O 的切线,∴DO⊥DP,
∵AD是∠BAC的平分线, ∴∠BAD=∠CAD,
∵BC是圆的直径, ∴∠BAC=90°,
∴∠BAD=45°, ∴∠BOD=90°,
∴OD⊥BC, ∴DP∥BC;
(2) ∵DP∥BC, ∴∠ACB=∠P, ∵∠ACB=∠ADB,∴∠P=∠ADB,
∵OD=OC, ∴∠ODC=45°∴∠CDP=45°,
∵∠BAD=∠DAC=45°, ∴∠BAD=∠CDP,
∴△ABD∽△DCP;
(3) ∵AB=5cm, AC=12cm, ∠BAC=90°,
∴BC=13cm,∴OC=OB=OD= cm
在等腰Rt△COD中,
在等腰 Rt△BOD中, BD=13 / , ∵△ABD∽△DCP ,
12.(1) 证明: ∵AD⊥AB, ∴∠BAD=90°,∵AD∥BC, ∴∠ABC=180°-∠BAD=90°,又∵AB是圆的半径, ∴BC为⊙A的切线;
(2) 解: 如图1, 过点D作DH⊥BC于H,
∴∠DHB=90°, 由 (1) 知, ∠BAD=∠ABC=90°,
∴∠ABC=∠BAD=∠BHD=90°,
∴四边形ABHD为矩形, ∵AB=AD=1,
∴矩形ABHD 是正方形, ∴BH=DH=AB=1,
在Rt△DHC中, 根据勾股定理得,
∵AD∥BC, ∴∠EDF=∠C,
(3) 如图2, 过点A作AM⊥DF于M,则DF=2DM , ∠AMD=90°,
在Rt△AMD中,
∵AD∥BC, ∴△DFG∽△CFB, ∴DF=DGBC,
由(2)知,
在Rt△BAG中,
13.解: (1) CD与⊙O 相切,理由: 如图1,连接OD,
∵OB=OD, ∴∠ODB=∠CBD,
∵∠CDA=∠CBD, ∴∠CDA=∠ODB,
∵AB为⊙O 的直径, ∴∠ADB=∠ADO+∠ODB=90°,
∴∠CDA+∠ADO=90°, ∴∠CDO=90°,
∴OD⊥CD, ∴CD与⊙O 相切;
(2) 由(1) 知,∠CBD=∠ADC, ∵tan∠ADC=
在Rt△ADB中,
∵∠C=∠C, ∠ADC=∠CBD, ∴△CAD∽△CDB,
∴ ∴CD=2CA=4 ,
∴CB=2CD=8,
∴AB=CB-CA=8-2=6, ∴OA=OB= AB=3,∴⊙O的半径为3;
(3) 如图2, 连接OE, 过点E作EG⊥BD于G,∵DE平分∠ADB, ∴∠ADE=∠BDE=45°,
∴∠BOE=2∠BDE=90°, . 在Rt△ABD中,
∵EG⊥BD, ∠BDE=45°,
∴∠DEG=∠BDE=45°, ∴DG=EG,
设DG=EG=x, 则
在Rt△BEG中,
或 (舍),
14解: (1)证明:如图1,过点O作OM⊥BC于点M ,∵BD是菱形ABCD的对角线, ∴∠ABD=∠CBD,∵OM⊥BC, OE⊥AB, ∴OE=OM ,∴BC是⊙O的切线.
(2) ∵G是OF的中点, ∵AB∥CD, OE⊥AB, ∴OF⊥CD, ∴∠OGH=90°, ∴∠HOE=120°, ∵OG=2, ∴OH =4,
∴由弧长公式得到HE 弧的长:
②如图2, 过A作AN⊥BD 于点N,
∵DG=1, OG=2, OE=OH=4,
15. 解: (1) 如图1, 连接OP.
∵四边形MNPQ是正方形, ∴∠OMQ=∠ONP=90°,MQ=PN, ∵OQ=OP, ∴Rt△OMQ≌Rt△ONP(HL),∴OM =ON, 设OM =ON=m, 则MQ=2m,
(2) 由 (1) 可知OM=ON=m, OQ=OA= m,MN=2m, ∴AM=OA-OM= m-m,
(3) ∵AB=2R, ∴OA=OB=OQ=R,
∵AB是直径, ∴∠ACB=∠DCE=90°,
∵∠CED=∠AEM , ∴∠A=∠D
∵∠AME=∠DMB=90°,
当点C与P重合时,
如图2,当C与Q点重合时, 如图3,当C与P点重合时,
488. (1) 证明:
∴∠ECF =90°, ∴OC⊥CF, ∴直线CF是⊙O 的切线.
(2) ①证明: ∵∠COD=2∠DAC, ∠COD=2∠BOC,
∴∠DAC=∠EOB,∵∠DCA=∠EBO, ∴△ACD∽△OBE.
②解: ∵OB=OC, OC=3EC, ∴OB:OE=3:2,
∵AD=4, ∴AC=6,
∵M 是AC的中点, ∴CM =MA=3,
,
∴MG=CM--CG=3-2=1, 即线段MG的长度为1.
489. (1)证明: ∵四边形ABCD是⊙O的内接四边形,
∴∠CBE=∠D,
∵AD为⊙O的直径, ∴∠ACD=90°,
∴∠D+∠CAD=90°, ∴∠CBE+∠CAD=90°,
∵CE⊥AB, ∴∠CBE+∠BCE=90°,
∴∠CAD=∠BCE;
(2) ①四边形ABCO是菱形, 理由:
∵∠CAD=30°, ∴∠COD=2∠CAD=60°,
∵CE 是⊙O 的切线, ∴OC⊥CE,
∵CE⊥AB, ∴OC∥AB, ∴∠DAB=∠COD=60°,由 (1) 知, ∠CBE+∠CAD=90°,
∴BC∥OA,
∴四边形ABCO是平行四边形, ∵OA=OC,
∴□ABCO是菱形;
②由①知,四边形ABCO是菱形,
∴OA=OC=AB=2, ∴AD=2OA=4,
由①知, ∠COD=60°,
在Rt△ACD中, ∠CAD=30°,
∴CD=2, AC=2
∴AD, AC与CD弧围成阴影部分的面积为:
16 (1) ①证明:
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
②解: 如图1, 连接OA交BD于J, 连接OC, OD.
∵AD=AB, ∴OA⊥BD, ∵四边形ABCD是菱形,
∴AC⊥BD, ∴A, O, C共线,
在Rt△OJD中,
∴AJ=OA-OJ =3-1=2,
∵四边形ABCD是菱形, ∴AJ =CJ=2,
(2)①解:分两种情况讨论:
第1种情况,如图2,当CD与⊙O相切时,连接AC交BD于H, 连接OH, OD, 延长DO交AB于P
∵CD 是⊙O 的切线, ∴OD⊥CD,
∵CD∥AB, ∴DP⊥AB, ∴PA=PB,
∵四边形ABCD是平行四边形,.
∴OH⊥BD, ∴∠DHO=∠DPB=90°,
∵∠ODH =∠BDP, ∴△DHO∽△DPB,
第2种情况,如图3,当BC与⊙O 相切时,同法可证.
综上所述,AB的长为4
②解: 如图4, 过点A 作AJ⊥BD于J .
如图3中,同法可得□ABCD对角线所夹锐角的正切值为 综上所述, ABCD对角线所夹锐角的正切值为
17. 解: (1) ∵∠AOB=90°, ∴AB为⊙M 的直径,∵点M 是AB的中点, 则点M(1,4),
则圆的半径为
设直线CM 的表达式为y=kx+b, 则 解得 故直线CM 的表达式为
(2)设点D 的坐标为
由 得: 解得x=5或-3,
故点D、 E 的坐标分别为(-3,5)、(5,3);
(3) 过点 D 作 DH⊥OB 于 点 H , 则 DH=3 ,BH=8-5=3=DH , 故∠DBO=45°,
由点A、 E 的坐标, 同理可得∠EAP=45°;
由点A、 E、 B 、D的坐标得,
同理可得:BD=3 , OB=8,
①当∠AEP=∠DBO=45°时,则△AEP为等腰直角三角形, EP⊥AC ,故点 P 的坐标为(5,0), 故OP=5;
②∠AEP=∠BDO时, ∵∠EAP=∠DBO,
∴△EAP∽△DBO, 即
解得AP=8, 故PO=10;
③∠AEP=∠BOD时, ∵∠EAP=∠DBO,
∴△EAP∽△OBD, ∴AEOB=ABD,即 解得 则 综上所述, OP为5或10或
同课章节目录
