2025年中考数学复习--十字架模型(弦图模型)(含解析)
文档属性
| 名称 | 2025年中考数学复习--十字架模型(弦图模型)(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 242.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
十字架模型(弦图模型)
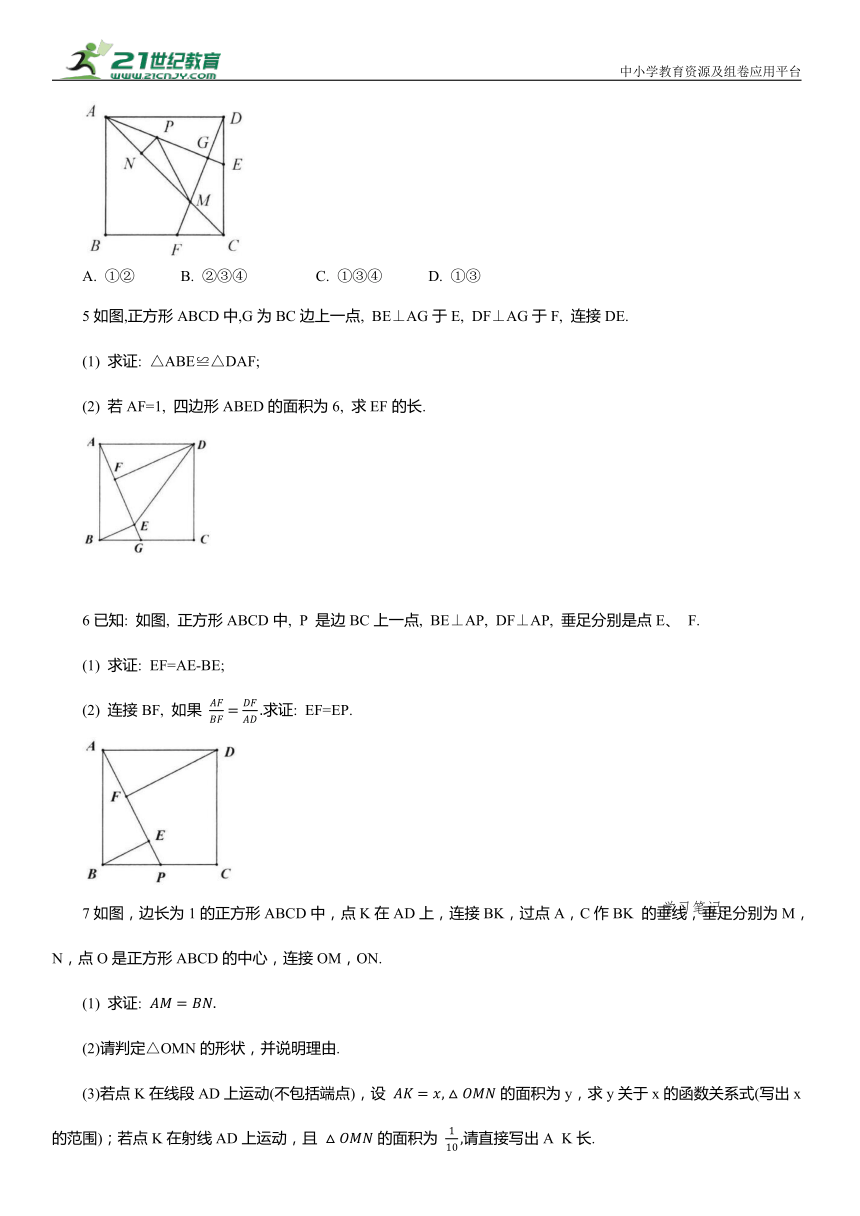
1如图, 在正方形ABCD中, 点E、F分别在CD、BC上, 且 连接BE、AF相交于点G,则下列结论不正确的是 ( )
A. BE=AF B. ∠DAF=∠BEC C. ∠AFB+∠BEC=90° D. AG⊥BE
2如图, 已知正方形ABCD的边长为5, 点E、F分别在AD、DC上, AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则 GH的长为 .
3如图, 在正方形ABCD中, AB=4, 点G在边BC上, 连接AG,作DE⊥AG于点E,BF⊥AG于点F, 连接BE、DF, 设
(1) 求证: AE=BF;
(2) 求证: tanα=k·tanβ;
(3)若点G从点B沿BC边运动至点C停止,求点E,F所经过的路径与边AB围成的图形的面积.
4如图,正方形ABCD的边长为4,点E,F分别在边DC,BC上,且 AE平分 连接DF,分别交AE,AC于点G,M. P 是线段AG上的一个动点,过点P作 垂足为N,连接PM. 有下列四个结论: ①AE 垂直平分DM; ②PM+PN的最小值为3 ; ③CF =GE·AE; ④S△ADM=6 其中正确的是( )
A. ①② B. ②③④ C. ①③④ D. ①③
5如图,正方形ABCD中,G为BC边上一点, BE⊥AG于E, DF⊥AG于F, 连接DE.
(1) 求证: △ABE≌△DAF;
(2) 若AF=1, 四边形ABED的面积为6, 求EF的长.
6已知: 如图, 正方形ABCD中, P 是边BC上一点, BE⊥AP, DF⊥AP, 垂足分别是点E、 F.
(1) 求证: EF=AE-BE;
(2) 连接BF, 如果 求证: EF=EP.
7如图,边长为1的正方形ABCD中,点K在AD上,连接BK,过点A,C作BK 的垂线,垂足分别为M,N,点O是正方形ABCD的中心,连接OM,ON.
(1) 求证:
(2)请判定△OMN的形状,并说明理由.
(3)若点K在线段AD上运动(不包括端点),设 的面积为y,求y关于x的函数关系式(写出x的范围);若点K在射线AD上运动,且 的面积为 请直接写出A K长.
8在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连接BE.
【感知】如图①,过点A作AF⊥BE交BC于点F. 易证△ABF≌△BCE. (不需要证明)
【探究】如图②,取BE的中点M,过点M作FG⊥BE交BC于点F, 交AD于点G.
(1) 求证: BE=FG.
(2) 连接CM, 若CM=1, 则FG的长为 .
【应用】如图③,取BE 的中点M, 连接CM. 过点C作CG⊥BE 交AD 于点G, 连接EG、MG. 若CM=3, 则四边形GMCE 的面积为 .
9如图1,在正方形ABCD中,点E是AB边上的一个动点(点E与点A,B不重合), 学习笔记:连接CE, 过点B作BF⊥CE 于点 G, 交AD于点 F.
(1) 求证: △ABF≌△BCE;
(2) 如图2, 当点E运动到AB中点时, 连接DG, 求证: DC=DG;
(3)如图3,在(2) 的条件下, 过点C作CM⊥DG于点H, 分别交AD, BF于点M, N, 求 的值.
10(1) 证明推断: 如图(1) , 在正方形ABCD中, 点E, Q分别在边BC, AB上,DQ⊥AE于点O, 点G, F分别在边CD, AB上, GF⊥AE.
①求证: DQ=AE;
②推断: 的值为 ;
(2) 类比探究: 如图(2), 在矩形ABCD中, (k为常数). 将矩形 ABCD沿GF 折叠,使点A落在BC边上的点E处,得到四边形FEPG,EP交CD于点H,连接AE交GF于点O.试探究GF与AE之间的数量关系,并说明理由;
(3)拓展应用:在(2)的条件下,连接CP,当 时,若 GF 求CP 的长.
1.∵ABCD 是正方形∴∠ABF=∠C=90° , AB=BC∵BF=CE∴△ABF≌△BCE∴AF=BE(第一个正确)∠BAF=∠CBE, ∠BFA=∠BEC (第三个错误)
∵∠BAF+∠DAF=90°, ∠BAF+∠BFA=90°
∴∠DAF=∠BEC (第二个正确)
∵∠BAF=∠CBE, ∠BAF+∠AFB=90°
∴∠CBE+∠AFB=90°∴AG⊥BE (第四个正确)
所以不正确的是C,故选C.
2. 解: ∵四边形 ABCD为正方形, ∴∠BAE=∠D=90° ,AB=AD,在△ABE和△DAF中,
∴△ABE≌△DAF(SAS), ∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90° , ∴∠DAF+∠BEA=90° ,
∴∠AGE=∠BGF=90°, ∵点H为BF的中点,
∴GH= BF,∵BC=5、CF=CD-DF=5-2=3,
故答案为:
3.解: (1)证明: 在正方形ABCD中,AB=BC=AD,∠BAD=∠ABC=90°, ∵DE⊥AG, BF⊥AG,
∴∠AED=∠BFA=90° , ∴∠ADE+∠DAE=90° ,
∵∠BAF+∠DAE=90°, ∴∠ADE=∠BAF,
∴△ABF≌△DAE (AAS) , ∴AE=BF;
(2) 在 Rt△DEF 和 Rt△EFB中,
由①可知∠ADE=∠BAG, ∠AED=∠GBA=90°,
由①可知,
(3) ∵DE⊥AG, BF⊥AG, ∴∠AED=∠BFA=90°,∴当点G从点 B 沿BC边运动至点C停止时,点E经过的路径是以AD为直径,圆心角为90°的圆弧,同理可得点F经过的路径,两弧交于正方形的中心点 O,如图.
∵AB=AD=4, ∴所围成的图形的面积为:
4. 解: ①∵四边形ABCD 是正方形,∴AD=DC=BC, ∠ADC=∠DCB=90°,∵BF=CE, ∴BC--BF=DC-CE, 即CF=DE,在△ADE和△DCF中,
∴△ADE≌△DCF (SAS), ∴∠DAE=∠CDF,
∵∠CDF+∠ADG=90°, ∴∠DAE+∠ADG=90° ,
∴∠AGD=90° , ∴∠AGM=90° ,
∴∠AGM=∠AGD,
∵AE平分∠CAD, ∴∠MAG=∠DAG,又AG为公共边,
∴△AGM≌△AGD(ASA) , ∴GM=GD,又∵∠AGM=∠AGD=90° ,
∴AE 垂直平分 DM, 故①正确;
②如图, 连接BD与AC交于点O, 连接PD,
∵四边形ABCD是正方形, ∴AC⊥BD, 即DO⊥AM,
∵AE 垂直平分DM, ∴PM=PD,
∴PM+PN=PD+PN
当点 D、P、N三点共线且垂直AC时,PM+PN的值最小,此时 PM+PN的最小值即为DO的长,
∵正方形ABCD的边长为4, 即 PM+PN的最小值为 故②错误;
③∵AE 垂直平分DM, ∴∠DGE=90°,∵∠ADC=90°, ∴∠DGE=∠ADC,又∵∠DEG=∠AED, ∴△DGE∽△ADE, 即
由①知( 故③正确;
④∵AE 垂直平分DM, ∴AM=AD=4,又∵
故④错误;综上,正确的是:①③,故选:D.
5证明: (1) ∵四边形ABCD 是正方形, ∴AB=AD, ∵DF⊥AG, BE⊥AG, ∴∠BAE+∠DAF=90°,∠DAF+∠ADF=90°,∴∠BAE=∠ADF,在△ABE和△DAF中,
(2) 设EF=x, 则AE=DF=x+1,
∵S四
整理得:
解得x=2或-5(舍), ∴EF=2.
6 证明: (1) ∵四边形ABCD为正方形, ∴AB=AD, ∠BAD=90°, ∵BE⊥AP, DF⊥AP, ∴∠BEA=∠AFD=90° , ∵∠1+∠2=90° , ∠2+∠3=90° ,
∴∠1=∠3, 在△ABE和△DAF中,
∴△ABE≌△DAF, ∴BE=AF,
∴EF=AE--AF=AE-BE;
(2)如图,
∴cos∠4=cos∠3, ∴∠4=∠3,
∵∠1=∠3, ∴∠4=∠1, ∵∠5=∠1, ∴∠4=∠5,即BE平分∠FBP, 而BE⊥EP, ∴EF=EP.
7 证明: (1) ∵四边形ABCD 是正方形,∴AB=BC, ∠ABC=90°, ∴∠ABM+∠CBM=90° ,∵AM⊥BM, CN⊥BN, ∴∠AMB=∠BNC=90°,
∴∠MAB+∠MBA=90°, ∴∠MAB=∠CBM,
∴△ABM≌△BCN (AAS) , ∴AM=BN;
(2)△OMN是等腰直角三角形,理由如下:如图,连接OB, ∵点O是正方形ABCD的中心,
∴OA=OB, ∠OBA=∠OAB=45° =∠OBC, AO⊥BO,
∵∠MAB=∠CBM,
∴∠MAB-∠OAB=∠CBM-∠OBC,
∴∠MAO=∠NBO, 又∵AM=BN, OA=OB,
∴△AOM≌△BON (SAS) ,
∴MO=NO, ∠AOM=∠BON,
∵∠AON+∠BON=90° , ∴∠AON+∠AOM=90°,
∴∠MON=90°, ∴△MON是等腰直角三角形;
B
(3) 在 Rt△ABK中,
当点K在线段AD上时,则
解得:x =3(不合题意舍去), 当点K在线段AD 的延长线时,同理可求 解得: (舍去),综上所述:AK的值为3或 时,△OMN的面积为
9. 解: 感知: ∵四边形ABCD是正方形, ∴AB=BC,∠BCE=∠ABC=90°, ∴∠ABE+∠CBE=90°,∵AF⊥BE, ∴∠ABE+∠BAF=90° , ∴∠BAF=∠CBE,在△ABF和△BCE中,
探究: (1)如图②, 过点 G作GP⊥BC于 P, ∵四边形ABCD是正方形, ∴AB=BC, ∠A=∠ABC=90°,∴四边形ABPG是矩形, ∴PG=AB, ∴PG=BC,同感知的方法得, ∠PGF=∠CBE,
在△PGF和△CBE中, ∴△PGF≌△CBE(ASA), ∴BE=FG,
(2) 由 (1) 知, FG=BE, 连接CM,
∵∠BCE=90° , 点M是BE的中点, ∴BE=2CM=2,∴FG=2, 故答案为: 2.
应用: 同探究(2)得, BE=2ME=2CM=6,∴ME=3,同探究(1) 得, CG=BE=6, ∵BE⊥CG,
故答案为9.296. (1) 证明: ∵BF⊥CE, ∴∠CGB=90°,
∴∠GCB+∠CBG=90, ∵四边形ABCD 是正方形,
∴∠CBE=90° =∠A, BC=AB,
∴∠FBA+∠CBG=90, ∴∠GCB=∠FBA,
∴△ABF≌△BCE(ASA);
(2) 证明: 如图2, 过点 D作DQ⊥CE于 Q,
设AB=CD=BC=2a, ∵点E是AB的中点,
在Rt△CEB中, 根据面积相等, 得BG·CE=CB·EB,
∵∠DCE+∠BCE=90°, ∠CBF+∠BCE=90°,
∴∠DCE=∠CBF,∵CD=BC,∠CQD=∠CGB=90°,
=∠GQD=90°, ∴△DGQ≌△DCQ(SAS), ∴CD=GD;
(3) 解: 如图3, 过点D作DQ⊥CE于Q,
在Rt△CQD中, CD=2a,
∵∠MDH+∠HDC=90° ,∠HCD+∠HDC=90° , ∴∠MDH=∠HCD,
在Rt△CHG中,
∠HCG+∠CGH=90°, ∴∠CGH=∠CNG,
10 (1) ①证明: ∵四边形ABCD 是正方形,∴AB=DA, ∠ABE=90° =∠DAQ.
∴∠ADO+∠OAD=90° . ∴∠QAO=∠ADO.
∴△ABE≌△DAQ (ASA) , ∴AE=DQ.
②解:结论: 理由: ∵DQ⊥AE, FG⊥AE,∴DQ∥FG,∵FQ∥DG,∴四边形DQFG是平行四边形,∴FG=DQ, ∵AE=DQ, ∴FG=AE, ∴GFAE=1.故答案为1.
(2) 解: 结论: 理由: 如图1, 作 GM⊥AB于
M. ∵AE⊥GF, ∴∠AOF=∠GMF=∠ABE=90°,
∴∠BAE+∠AFO=90°, ∠AFO+∠FGM=90°,
∴∠BAE=∠FGM, ∴△ABE∽△GMF,
∵∠AMG=∠D=∠DAM=90°, ∴四边形AMGD 是矩 形,
(3) 解: 如图2, 作 PN⊥BC交BC的延长线于 N.
∵FB∥GC, FE∥GP, ∴∠CGP=∠BFE,
∴设BE=3m,BF=4m, EF=AF=5m, ∴AB=BF+AF=9m
或--1(舍弃),1
∴BE=3, AB=9, ∵BC: AB=2: 3,
∴BC=6, ∴BE=CE=3, AD=PE=BC=6,
∵∠EBF=∠FEP=∠PNE=90°,
∴∠FEB+∠PEN=90° , ∠PEN+∠EPN=90° ,
∴∠FEB=∠EPN, ∴△FBE∽△ENP,
∴勾股定理得:
十字架模型(弦图模型)
1如图, 在正方形ABCD中, 点E、F分别在CD、BC上, 且 连接BE、AF相交于点G,则下列结论不正确的是 ( )
A. BE=AF B. ∠DAF=∠BEC C. ∠AFB+∠BEC=90° D. AG⊥BE
2如图, 已知正方形ABCD的边长为5, 点E、F分别在AD、DC上, AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则 GH的长为 .
3如图, 在正方形ABCD中, AB=4, 点G在边BC上, 连接AG,作DE⊥AG于点E,BF⊥AG于点F, 连接BE、DF, 设
(1) 求证: AE=BF;
(2) 求证: tanα=k·tanβ;
(3)若点G从点B沿BC边运动至点C停止,求点E,F所经过的路径与边AB围成的图形的面积.
4如图,正方形ABCD的边长为4,点E,F分别在边DC,BC上,且 AE平分 连接DF,分别交AE,AC于点G,M. P 是线段AG上的一个动点,过点P作 垂足为N,连接PM. 有下列四个结论: ①AE 垂直平分DM; ②PM+PN的最小值为3 ; ③CF =GE·AE; ④S△ADM=6 其中正确的是( )
A. ①② B. ②③④ C. ①③④ D. ①③
5如图,正方形ABCD中,G为BC边上一点, BE⊥AG于E, DF⊥AG于F, 连接DE.
(1) 求证: △ABE≌△DAF;
(2) 若AF=1, 四边形ABED的面积为6, 求EF的长.
6已知: 如图, 正方形ABCD中, P 是边BC上一点, BE⊥AP, DF⊥AP, 垂足分别是点E、 F.
(1) 求证: EF=AE-BE;
(2) 连接BF, 如果 求证: EF=EP.
7如图,边长为1的正方形ABCD中,点K在AD上,连接BK,过点A,C作BK 的垂线,垂足分别为M,N,点O是正方形ABCD的中心,连接OM,ON.
(1) 求证:
(2)请判定△OMN的形状,并说明理由.
(3)若点K在线段AD上运动(不包括端点),设 的面积为y,求y关于x的函数关系式(写出x的范围);若点K在射线AD上运动,且 的面积为 请直接写出A K长.
8在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连接BE.
【感知】如图①,过点A作AF⊥BE交BC于点F. 易证△ABF≌△BCE. (不需要证明)
【探究】如图②,取BE的中点M,过点M作FG⊥BE交BC于点F, 交AD于点G.
(1) 求证: BE=FG.
(2) 连接CM, 若CM=1, 则FG的长为 .
【应用】如图③,取BE 的中点M, 连接CM. 过点C作CG⊥BE 交AD 于点G, 连接EG、MG. 若CM=3, 则四边形GMCE 的面积为 .
9如图1,在正方形ABCD中,点E是AB边上的一个动点(点E与点A,B不重合), 学习笔记:连接CE, 过点B作BF⊥CE 于点 G, 交AD于点 F.
(1) 求证: △ABF≌△BCE;
(2) 如图2, 当点E运动到AB中点时, 连接DG, 求证: DC=DG;
(3)如图3,在(2) 的条件下, 过点C作CM⊥DG于点H, 分别交AD, BF于点M, N, 求 的值.
10(1) 证明推断: 如图(1) , 在正方形ABCD中, 点E, Q分别在边BC, AB上,DQ⊥AE于点O, 点G, F分别在边CD, AB上, GF⊥AE.
①求证: DQ=AE;
②推断: 的值为 ;
(2) 类比探究: 如图(2), 在矩形ABCD中, (k为常数). 将矩形 ABCD沿GF 折叠,使点A落在BC边上的点E处,得到四边形FEPG,EP交CD于点H,连接AE交GF于点O.试探究GF与AE之间的数量关系,并说明理由;
(3)拓展应用:在(2)的条件下,连接CP,当 时,若 GF 求CP 的长.
1.∵ABCD 是正方形∴∠ABF=∠C=90° , AB=BC∵BF=CE∴△ABF≌△BCE∴AF=BE(第一个正确)∠BAF=∠CBE, ∠BFA=∠BEC (第三个错误)
∵∠BAF+∠DAF=90°, ∠BAF+∠BFA=90°
∴∠DAF=∠BEC (第二个正确)
∵∠BAF=∠CBE, ∠BAF+∠AFB=90°
∴∠CBE+∠AFB=90°∴AG⊥BE (第四个正确)
所以不正确的是C,故选C.
2. 解: ∵四边形 ABCD为正方形, ∴∠BAE=∠D=90° ,AB=AD,在△ABE和△DAF中,
∴△ABE≌△DAF(SAS), ∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90° , ∴∠DAF+∠BEA=90° ,
∴∠AGE=∠BGF=90°, ∵点H为BF的中点,
∴GH= BF,∵BC=5、CF=CD-DF=5-2=3,
故答案为:
3.解: (1)证明: 在正方形ABCD中,AB=BC=AD,∠BAD=∠ABC=90°, ∵DE⊥AG, BF⊥AG,
∴∠AED=∠BFA=90° , ∴∠ADE+∠DAE=90° ,
∵∠BAF+∠DAE=90°, ∴∠ADE=∠BAF,
∴△ABF≌△DAE (AAS) , ∴AE=BF;
(2) 在 Rt△DEF 和 Rt△EFB中,
由①可知∠ADE=∠BAG, ∠AED=∠GBA=90°,
由①可知,
(3) ∵DE⊥AG, BF⊥AG, ∴∠AED=∠BFA=90°,∴当点G从点 B 沿BC边运动至点C停止时,点E经过的路径是以AD为直径,圆心角为90°的圆弧,同理可得点F经过的路径,两弧交于正方形的中心点 O,如图.
∵AB=AD=4, ∴所围成的图形的面积为:
4. 解: ①∵四边形ABCD 是正方形,∴AD=DC=BC, ∠ADC=∠DCB=90°,∵BF=CE, ∴BC--BF=DC-CE, 即CF=DE,在△ADE和△DCF中,
∴△ADE≌△DCF (SAS), ∴∠DAE=∠CDF,
∵∠CDF+∠ADG=90°, ∴∠DAE+∠ADG=90° ,
∴∠AGD=90° , ∴∠AGM=90° ,
∴∠AGM=∠AGD,
∵AE平分∠CAD, ∴∠MAG=∠DAG,又AG为公共边,
∴△AGM≌△AGD(ASA) , ∴GM=GD,又∵∠AGM=∠AGD=90° ,
∴AE 垂直平分 DM, 故①正确;
②如图, 连接BD与AC交于点O, 连接PD,
∵四边形ABCD是正方形, ∴AC⊥BD, 即DO⊥AM,
∵AE 垂直平分DM, ∴PM=PD,
∴PM+PN=PD+PN
当点 D、P、N三点共线且垂直AC时,PM+PN的值最小,此时 PM+PN的最小值即为DO的长,
∵正方形ABCD的边长为4, 即 PM+PN的最小值为 故②错误;
③∵AE 垂直平分DM, ∴∠DGE=90°,∵∠ADC=90°, ∴∠DGE=∠ADC,又∵∠DEG=∠AED, ∴△DGE∽△ADE, 即
由①知( 故③正确;
④∵AE 垂直平分DM, ∴AM=AD=4,又∵
故④错误;综上,正确的是:①③,故选:D.
5证明: (1) ∵四边形ABCD 是正方形, ∴AB=AD, ∵DF⊥AG, BE⊥AG, ∴∠BAE+∠DAF=90°,∠DAF+∠ADF=90°,∴∠BAE=∠ADF,在△ABE和△DAF中,
(2) 设EF=x, 则AE=DF=x+1,
∵S四
整理得:
解得x=2或-5(舍), ∴EF=2.
6 证明: (1) ∵四边形ABCD为正方形, ∴AB=AD, ∠BAD=90°, ∵BE⊥AP, DF⊥AP, ∴∠BEA=∠AFD=90° , ∵∠1+∠2=90° , ∠2+∠3=90° ,
∴∠1=∠3, 在△ABE和△DAF中,
∴△ABE≌△DAF, ∴BE=AF,
∴EF=AE--AF=AE-BE;
(2)如图,
∴cos∠4=cos∠3, ∴∠4=∠3,
∵∠1=∠3, ∴∠4=∠1, ∵∠5=∠1, ∴∠4=∠5,即BE平分∠FBP, 而BE⊥EP, ∴EF=EP.
7 证明: (1) ∵四边形ABCD 是正方形,∴AB=BC, ∠ABC=90°, ∴∠ABM+∠CBM=90° ,∵AM⊥BM, CN⊥BN, ∴∠AMB=∠BNC=90°,
∴∠MAB+∠MBA=90°, ∴∠MAB=∠CBM,
∴△ABM≌△BCN (AAS) , ∴AM=BN;
(2)△OMN是等腰直角三角形,理由如下:如图,连接OB, ∵点O是正方形ABCD的中心,
∴OA=OB, ∠OBA=∠OAB=45° =∠OBC, AO⊥BO,
∵∠MAB=∠CBM,
∴∠MAB-∠OAB=∠CBM-∠OBC,
∴∠MAO=∠NBO, 又∵AM=BN, OA=OB,
∴△AOM≌△BON (SAS) ,
∴MO=NO, ∠AOM=∠BON,
∵∠AON+∠BON=90° , ∴∠AON+∠AOM=90°,
∴∠MON=90°, ∴△MON是等腰直角三角形;
B
(3) 在 Rt△ABK中,
当点K在线段AD上时,则
解得:x =3(不合题意舍去), 当点K在线段AD 的延长线时,同理可求 解得: (舍去),综上所述:AK的值为3或 时,△OMN的面积为
9. 解: 感知: ∵四边形ABCD是正方形, ∴AB=BC,∠BCE=∠ABC=90°, ∴∠ABE+∠CBE=90°,∵AF⊥BE, ∴∠ABE+∠BAF=90° , ∴∠BAF=∠CBE,在△ABF和△BCE中,
探究: (1)如图②, 过点 G作GP⊥BC于 P, ∵四边形ABCD是正方形, ∴AB=BC, ∠A=∠ABC=90°,∴四边形ABPG是矩形, ∴PG=AB, ∴PG=BC,同感知的方法得, ∠PGF=∠CBE,
在△PGF和△CBE中, ∴△PGF≌△CBE(ASA), ∴BE=FG,
(2) 由 (1) 知, FG=BE, 连接CM,
∵∠BCE=90° , 点M是BE的中点, ∴BE=2CM=2,∴FG=2, 故答案为: 2.
应用: 同探究(2)得, BE=2ME=2CM=6,∴ME=3,同探究(1) 得, CG=BE=6, ∵BE⊥CG,
故答案为9.296. (1) 证明: ∵BF⊥CE, ∴∠CGB=90°,
∴∠GCB+∠CBG=90, ∵四边形ABCD 是正方形,
∴∠CBE=90° =∠A, BC=AB,
∴∠FBA+∠CBG=90, ∴∠GCB=∠FBA,
∴△ABF≌△BCE(ASA);
(2) 证明: 如图2, 过点 D作DQ⊥CE于 Q,
设AB=CD=BC=2a, ∵点E是AB的中点,
在Rt△CEB中, 根据面积相等, 得BG·CE=CB·EB,
∵∠DCE+∠BCE=90°, ∠CBF+∠BCE=90°,
∴∠DCE=∠CBF,∵CD=BC,∠CQD=∠CGB=90°,
=∠GQD=90°, ∴△DGQ≌△DCQ(SAS), ∴CD=GD;
(3) 解: 如图3, 过点D作DQ⊥CE于Q,
在Rt△CQD中, CD=2a,
∵∠MDH+∠HDC=90° ,∠HCD+∠HDC=90° , ∴∠MDH=∠HCD,
在Rt△CHG中,
∠HCG+∠CGH=90°, ∴∠CGH=∠CNG,
10 (1) ①证明: ∵四边形ABCD 是正方形,∴AB=DA, ∠ABE=90° =∠DAQ.
∴∠ADO+∠OAD=90° . ∴∠QAO=∠ADO.
∴△ABE≌△DAQ (ASA) , ∴AE=DQ.
②解:结论: 理由: ∵DQ⊥AE, FG⊥AE,∴DQ∥FG,∵FQ∥DG,∴四边形DQFG是平行四边形,∴FG=DQ, ∵AE=DQ, ∴FG=AE, ∴GFAE=1.故答案为1.
(2) 解: 结论: 理由: 如图1, 作 GM⊥AB于
M. ∵AE⊥GF, ∴∠AOF=∠GMF=∠ABE=90°,
∴∠BAE+∠AFO=90°, ∠AFO+∠FGM=90°,
∴∠BAE=∠FGM, ∴△ABE∽△GMF,
∵∠AMG=∠D=∠DAM=90°, ∴四边形AMGD 是矩 形,
(3) 解: 如图2, 作 PN⊥BC交BC的延长线于 N.
∵FB∥GC, FE∥GP, ∴∠CGP=∠BFE,
∴设BE=3m,BF=4m, EF=AF=5m, ∴AB=BF+AF=9m
或--1(舍弃),1
∴BE=3, AB=9, ∵BC: AB=2: 3,
∴BC=6, ∴BE=CE=3, AD=PE=BC=6,
∵∠EBF=∠FEP=∠PNE=90°,
∴∠FEB+∠PEN=90° , ∠PEN+∠EPN=90° ,
∴∠FEB=∠EPN, ∴△FBE∽△ENP,
∴勾股定理得:
同课章节目录
