2025年中考数学复习--对角互补模型(含解析)
文档属性
| 名称 | 2025年中考数学复习--对角互补模型(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 255.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
对角互补模型
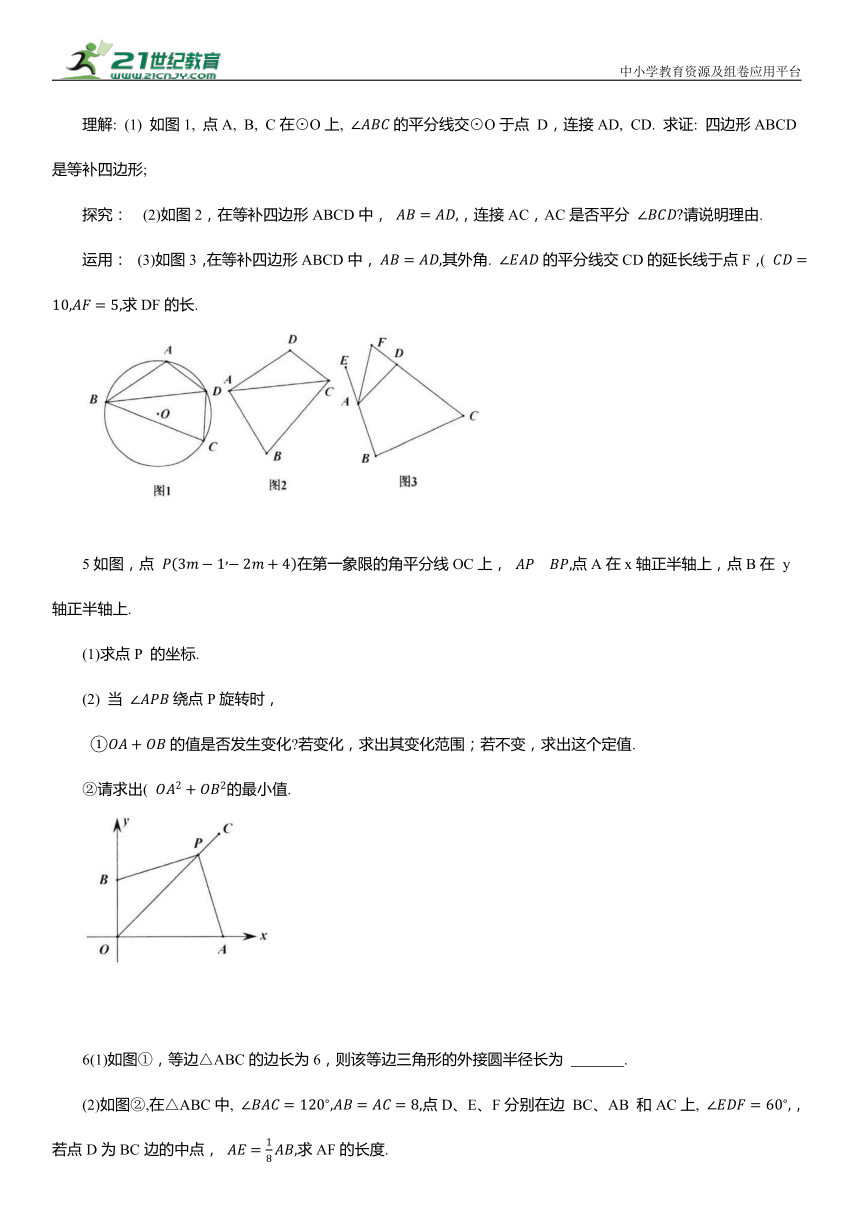
1如图, △ABC为等边三角形, 以AB为边向形外作△ABD, 使∠ADB=120°, 再以点C为旋转中心把△CBD旋转到△CAE,则下列结论:①D、A、E三点共线;②DC平分∠BDA; ③∠E=∠BAC; ④DC=DB+DA. 其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
2如图,正方形ABCD, 点P 是对角线AC上一点, 连接BP, 过P作PQ⊥BP, PQ交CD于Q, 连接BQ交AC于 G, 若 Q为CD中点,则下列结论:
①∠PBC=∠PQD; ②BP=PQ; ③∠BPC=∠BQC; ④正方形ABCD的面积是16;其中正确结论的个数是 ()
A. 4 B. 3 C. 2 D. 1
3已知△ABC中, AC=BC, ∠C=120° , 点D为AB边的中点, ∠EDF=60° , DE、DF分别交 AC、BC于 E、F点.
(1) 如图1, 若EF∥AB. 求证: DE=DF.
(2)如图2,若EF与AB不平行.则问题(1)的结论是否成立 说明理由.
4定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解: (1) 如图1, 点A, B, C在⊙O上, 的平分线交⊙O于点 D,连接AD, CD. 求证: 四边形ABCD是等补四边形;
探究: (2)如图2,在等补四边形ABCD中, ,连接AC,AC是否平分 请说明理由.
运用: (3)如图3,在等补四边形ABCD中, 其外角. 的平分线交CD的延长线于点F,( 求DF的长.
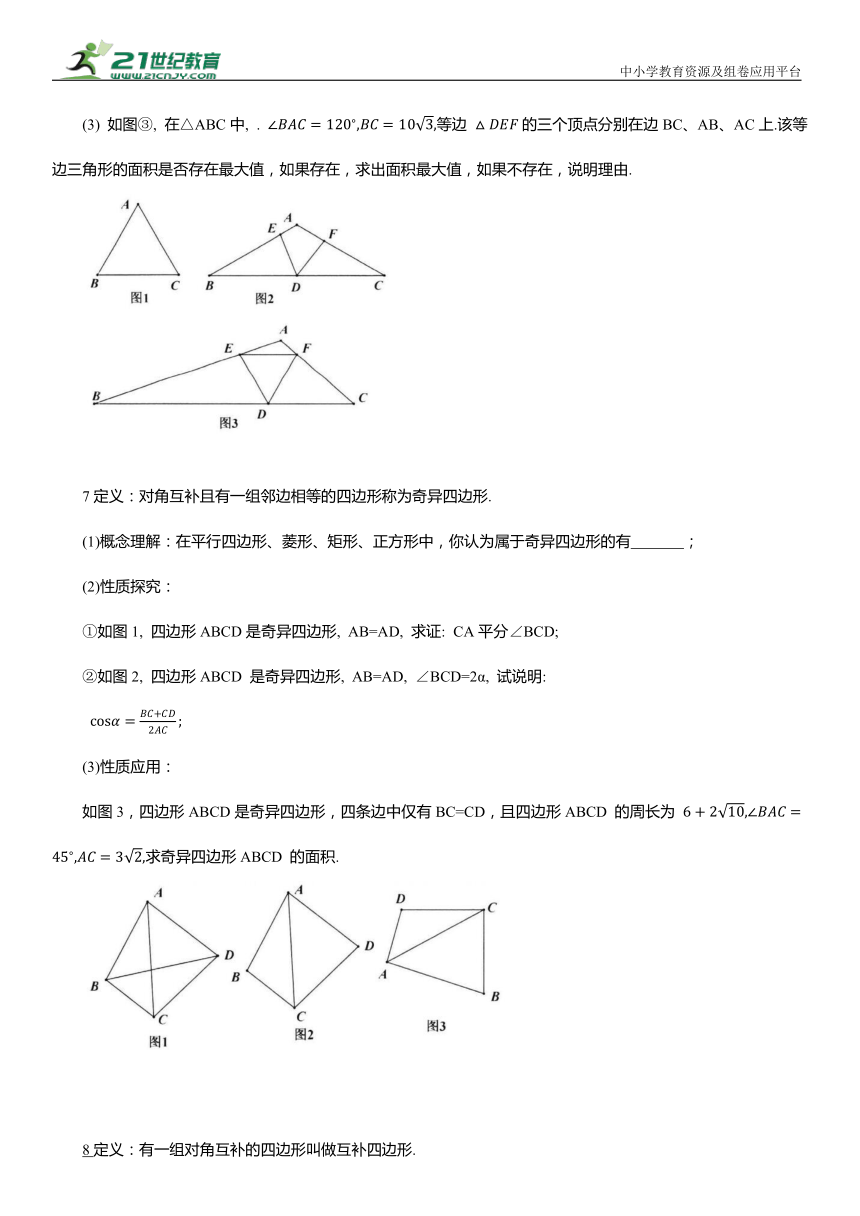
5如图,点 在第一象限的角平分线OC上, 点A在x轴正半轴上,点B在 y 轴正半轴上.
(1)求点P 的坐标.
(2) 当 绕点P旋转时,
的值是否发生变化 若变化,求出其变化范围;若不变,求出这个定值.
②请求出( 的最小值.
6(1)如图①,等边△ABC的边长为6,则该等边三角形的外接圆半径长为 .
(2)如图②,在△ABC中, 点D、E、F分别在边 BC、AB 和AC上, ,若点D为BC边的中点, 求AF的长度.
(3) 如图③, 在△ABC中, . 等边 的三个顶点分别在边BC、AB、AC上.该等边三角形的面积是否存在最大值,如果存在,求出面积最大值,如果不存在,说明理由.
7定义:对角互补且有一组邻边相等的四边形称为奇异四边形.
(1)概念理解:在平行四边形、菱形、矩形、正方形中,你认为属于奇异四边形的有 ;
(2)性质探究:
①如图1, 四边形ABCD是奇异四边形, AB=AD, 求证: CA平分∠BCD;
②如图2, 四边形ABCD 是奇异四边形, AB=AD, ∠BCD=2α, 试说明:
(3)性质应用:
如图3,四边形ABCD是奇异四边形,四条边中仅有BC=CD,且四边形ABCD 的周长为 求奇异四边形ABCD 的面积.
8定义:有一组对角互补的四边形叫做互补四边形.
(1)概念理解:
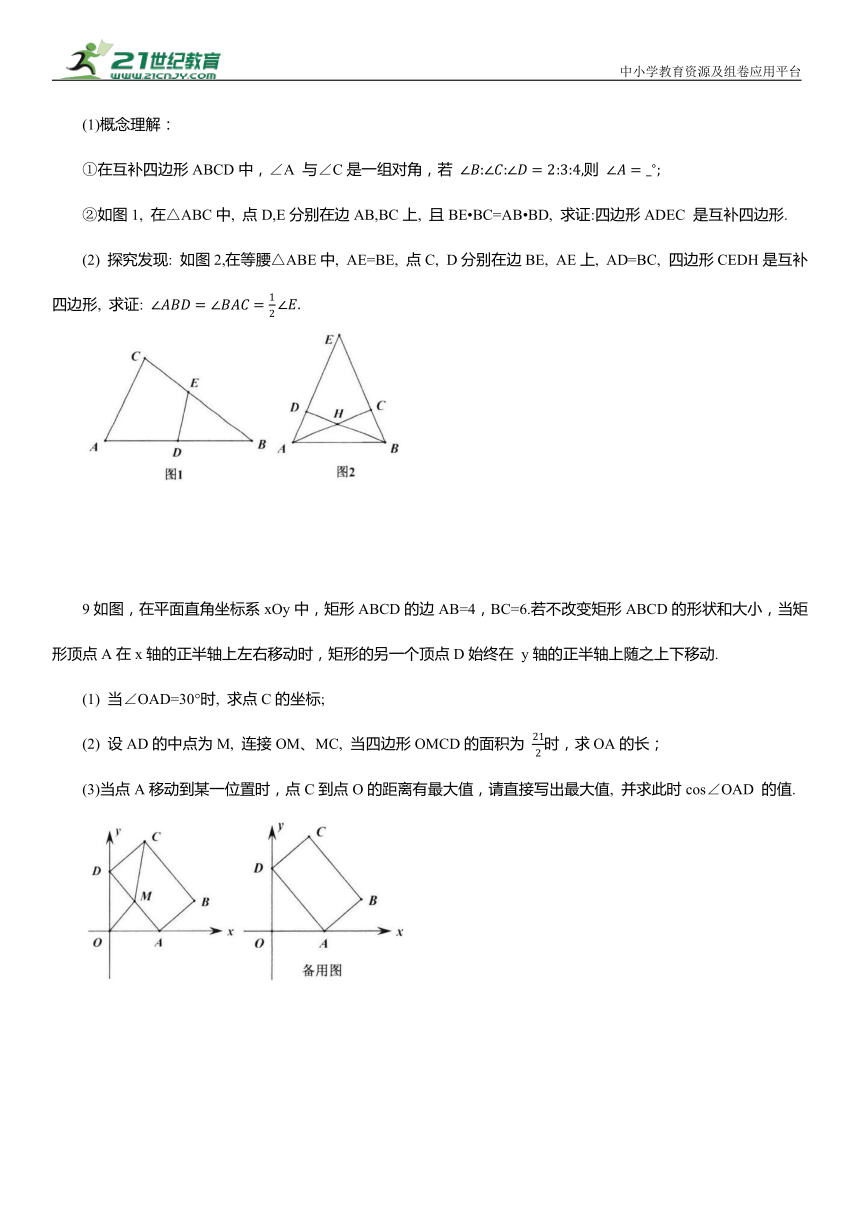
①在互补四边形ABCD中,∠A 与∠C是一组对角,若 则
②如图1, 在△ABC中, 点D,E分别在边AB,BC上, 且BE BC=AB BD, 求证:四边形ADEC 是互补四边形.
(2) 探究发现: 如图2,在等腰△ABE中, AE=BE, 点C, D分别在边BE, AE上, AD=BC, 四边形CEDH是互补四边形, 求证:
9如图,在平面直角坐标系xOy中,矩形ABCD的边AB=4,BC=6.若不改变矩形ABCD的形状和大小,当矩形顶点A在x轴的正半轴上左右移动时,矩形的另一个顶点D始终在 y轴的正半轴上随之上下移动.
(1) 当∠OAD=30°时, 求点C的坐标;
(2) 设AD的中点为M, 连接OM、MC, 当四边形OMCD的面积为 时,求OA的长;
(3)当点A移动到某一位置时,点C到点O的距离有最大值,请直接写出最大值, 并求此时cos∠OAD 的值.
1.解: 如图, ①设∠1=x度, 则∠2= (60-x)°,∠DBC= (x+60) °, 故∠4= (x+60)°,
∴∠2+∠3+∠4=60-x+60+x+60=180°,
∴D、A、E三点共线; 故①正确;
C
②∵△BCD 绕着点 C 按顺时针方向旋转60°得到△ACE, ∴CD=CE, ∠DCE=60°, ∴△CDE为等边三角形,
∴∠E=60° , ∴∠BDC=∠E=60° ,
∴∠CDA=120° -60° =60° ,
∴DC平分∠BDA; 故②正确;
③∵∠BAC=60° , ∠E=60° , ∴∠E=∠BAC.故③正确;
④由旋转可知AE=BD, 又∵∠DAE=180°,
∴DE=AE+AD. ∵△CDE为等边三角形,
∴DC=DB+BA. 故④正确; 故选: A.
2解: ∵四边形ABCD 是正方形, ∴∠BCQ=90°,∵PQ⊥PB,∴∠BPQ=90°,∴∠BPQ+∠BCQ=180° ,∴B、C、Q、P四点共圆, ∴∠PBC=∠PQD, ∠BPC=∠BQC, ∴①正确; ③正确;
∵四边形ABCD 是正方形, ∴∠BCP=∠PCQ=45°,
∴ BP=PQ, ∴②正确;
过P作PE⊥AB于E, PF⊥DC于F, 则E、P、F三点共线, ∵四边形ABCD是正方形, ∴∠PAE=45°, ∴△PAE是等腰直角三角形,
在△BEP 和△PFQ中, 易证△BEP≌△PFQ (ASA) ,∴PE=FQ=1, ∴DQ=1+1=2, ∵Q为CD中点,∴DC=2DQ=4, ∴正方形ABCD的面积是4×4=16,∴④正确; 故选: A.
3 解: (1) ∵EF∥AB. ∴∠FEC=∠A=30° .∠EFC=∠B=30° ∴EC=CF. 又∵AC=BC ,∴AE=BF, 又∵D是AB中点. ∴DB=AD∴△ADE≌△BDF. ∴DE=DF
(2) 如图, 连接CD, ∵△ABC是等腰三角形, 点D为AB边的中点, ∴∠ACD=∠BCD,
在线段AC上取点F',使( 连接F'D,
在△CDF与△CDF' 中,
∴△CDF≌△CDF' (SAS), ∴∠CFD=∠CF' D,在四边形CEDF中, ∠ACB=120° , ∠EDF=60° ,
∴∠CED+∠CFD=180°, ∴∠CED+∠CF' D=180° ,
∵∠CED+∠F' ED=180° , ∴∠EF' D=∠F' ED,
∴DE=DF' , ∵DF' =DF, ∴DE=DF.
方法2(初三): ∵∠ACB=120° , ∠EDF=60°
∴AEDF 四点共圆, ∵∠EAD=∠FAD(三线合一)
∴DE=DF
4解: (1) 证明: ∵四边形ABCD 为圆内接四边形,∴∠A+∠C=180° , ∠ABC+∠ADC=180° ,
∵BD平分∠ABC, ∴∠ABD=∠CBD, ∴AD=CD,
∴四边形ABCD 是等补四边形;
(2) AC平分∠BCD, 理由如下:
如图2, 过点A分别作AE⊥BC于点 E, AF 垂直CD的延长线于点 F, 则∠AEB=∠AFD=90°,
∵四边形ABCD是等补四边形, ∴∠B+∠ADC=180°,又∠ADC+∠ADF=180°, ∴∠B=∠ADF, ∵AB=AD,
∴△ABE≌△ADF (AAS) , ∴AE=AF,
∴AC是∠BCF的平分线, 即 AC平分∠BCD;
(3) 如图3, 连接AC, ∵四边形ABCD是等补四边形,
∴∠BAD+∠BCD=180° , 又∠BAD+∠EAD=180° ,
∴∠EAD=∠BCD, ∵AF平分∠EAD,
由(2)知, AC平分∠BCD,
∴∠FCA= ∠BCD, ∴∠FCA=∠FAD,又∠AFC=∠DFA, ∴△ACF∽△DAF, 即
5.解: (1) ∵点P (3m-1, - 2m+4) 在第一象限的角平分线OC上, ∴3m-1=-2m+4,
∴m=1, ∴P (2, 2) ;
(2)①不变.过点 P作 PM⊥y轴于 M,PN⊥OA于 N.
∵∠PMO=∠PNO=∠MON=90° , PM=PN=2,
∴四边形QMPN是正方形, ∴∠MPN=90°=∠APB,
∴∠MPB=∠NPA.
在△PMB 和△PNA中,
∴△PMB≌△PNA (ASA) , ∴BM=AN,
∴OB+OA=OM--BM+ON+AN=2OM=4,
②连接AB, ∵∠AOB=90°, ∴OA +OB =AB ,
当PA最小时, 也最小.根据垂线段最短原理,PA 最小值为2,
的最小值为8.
303. 解: (1) 如图1, 作BC、AC的垂直平分线, 交△ABC的内部于一点O,O即为等边三角形的外接圆的圆心,则
在Rt△OBD 中, ∴等边三角形的外接圆半径长为
(2) 如图2, 连接AD, 过点D作 DM⊥BA于点 M,DN⊥AC于点 N, 则∠DMA=∠DNA=∠DNF=90°,∵AB=AC, 点D 是BC的中点,
在△ADM和△ADN中,
∴△ADM≌△ADN(AAS) , ∴AM=AN, DM=DN,在四边形AMDN 中, ∠MDN=360°-120° -90° -90°=60° ,∵∠EDF=60°,∴∠MDN=∠EDF,即∠EDN+∠NDF=∠EDN+∠MDE, ∴∠NDF=∠MDE,
在△MDE和△NDF中,
∴△MDE≌△NDF(ASA) , ∴ME=∠NF,
∴AE+AF=AM-ME+AN+NF=2AM,
∵∠BAC=120° , AB=AC=8, ∴∠B=∠C=30° ,
在Rt△ABD中,
在Rt△AMD中,
∴AF=2+1=3.
(3) 如图3, 过点 D作 DG⊥AB于点 G, GH⊥AC于点H, 由(2) 可得: △DEG≌△DFH, △ADG≌ADH,∴DG=DH, ∠DAG=∠DAH=60° ,
且由几何关系可得DF≤AD,
∴AD 取得最大值时,S△DEF取得最大值,作△ABC的外接圆⊙O, 连接OB、OC, 则∠BOC=120°,
∵BC=10 , ∴OB=OC=10,
过点O 作OQ⊥BC交⊙O于M、N, 垂足为Q,则OQ=5, MN平分BC弧, ∴BN弧=CN弧,连接DN, A、D、N共线,
由几何关系可得: DN+AD≤MN,
∴AD≤MN-DN,
∵ND≥QN, ∴当DN最小时, AD存在最大值,
∴当AN为直径时,AD 存在最大值,AD 最大=5,
∴S△DEF最大
6解: (1)根据奇异四边形的定义可知:正方形是奇异四边形,故答案为正方形.
(2)①如图1,过点A作AM⊥CB于M,AN⊥CD于N.,∵∠ABC+∠D=180° , ∠ABM+∠ABC=180°,
∴∠ABM=∠D, ∵∠AMB=∠AND=90° , AB=AD,
∴△AMB≌△AND, ∴AM=AN,
∵AM⊥CB于M, AN⊥CD于N, ∴CA平分∠BCD.
②由①可知: =CD-BM=CD - (CM-BC) =CD - (CN-BC),
在 Rt△ACN中,
(3)如图3中, 由(2) 可知: ∵四边形ABCD的周长为
∴∠DAB=90°, ∵四边形是奇异四边形,
∴∠BCD=90° , ∵AD+AB=6,
9.
7. (1) ①解: ∵四边形ABCD 是互补四边形,∠A与∠C是一组对角,
∵∠B: ∠C: ∠D=2: 3: 4,
∵∠A+∠B+∠C+∠D=360°,
∠A)=360°, ∴∠A=90°, 故答案为: 90;
②证明: 又∵∠B=∠B, ∴△BDE∽△BCA, ∴∠BED=∠A,
∴∠A+∠CED=∠BED+∠CED=180°,
∴四边形ADEC 是互补四边形;
(2) 证明: ∵AE=BE, AD=BC, ∴ED=EC,在△EAC和△EBD中,
∴△EAC≌△EBD (SAS), ∴∠EBD=∠EAC,
∵AE=BE, ∴∠EAB=∠EBA, ∴∠ABD=∠BAC,
∵四边形CEDH是互补四边形,∴∠E+∠DHC=180°,
∵∠AHB=∠DHC, ∴∠E+∠AHB=180° ,
∴∠ABD+∠BAC=∠E, ∴∠ABD=∠BAC= ∠E.
8解: (1) 如图1, 过点C作CE⊥y轴于点 E,∵矩形ABCD 中, CD⊥AD, ∴∠CDE+∠ADO=90° ,又∵∠OAD+∠ADO=90°, ∴∠CDE=∠OAD=30°,∴在 Rt△CED 中, 在Rt△OAD中, ∠OAD=30° ,
∴点C的坐标为
(2) ∵M为AD的中点,∴DM=3, S△DCM=6,又 设OA=x、OD=y, 则 即x=y,将x=y代入 得 解得 (负值舍去),
(3) OC的最大值为8, 如图2, M为AD的中点, ∴OC≤OM+CM=8,
当O、M、C三点在同一直线时,OC有最大值8,
连接OC,则此时OC与AD的交点为M,
过点O作ON⊥AD,垂足为N,∵∠CDM=∠ONM=90°,
∠CMD=∠OMN, ∴△CMD∽△OMN,
即
解得
在 Rt△OAN中,
对角互补模型
1如图, △ABC为等边三角形, 以AB为边向形外作△ABD, 使∠ADB=120°, 再以点C为旋转中心把△CBD旋转到△CAE,则下列结论:①D、A、E三点共线;②DC平分∠BDA; ③∠E=∠BAC; ④DC=DB+DA. 其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
2如图,正方形ABCD, 点P 是对角线AC上一点, 连接BP, 过P作PQ⊥BP, PQ交CD于Q, 连接BQ交AC于 G, 若 Q为CD中点,则下列结论:
①∠PBC=∠PQD; ②BP=PQ; ③∠BPC=∠BQC; ④正方形ABCD的面积是16;其中正确结论的个数是 ()
A. 4 B. 3 C. 2 D. 1
3已知△ABC中, AC=BC, ∠C=120° , 点D为AB边的中点, ∠EDF=60° , DE、DF分别交 AC、BC于 E、F点.
(1) 如图1, 若EF∥AB. 求证: DE=DF.
(2)如图2,若EF与AB不平行.则问题(1)的结论是否成立 说明理由.
4定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解: (1) 如图1, 点A, B, C在⊙O上, 的平分线交⊙O于点 D,连接AD, CD. 求证: 四边形ABCD是等补四边形;
探究: (2)如图2,在等补四边形ABCD中, ,连接AC,AC是否平分 请说明理由.
运用: (3)如图3,在等补四边形ABCD中, 其外角. 的平分线交CD的延长线于点F,( 求DF的长.
5如图,点 在第一象限的角平分线OC上, 点A在x轴正半轴上,点B在 y 轴正半轴上.
(1)求点P 的坐标.
(2) 当 绕点P旋转时,
的值是否发生变化 若变化,求出其变化范围;若不变,求出这个定值.
②请求出( 的最小值.
6(1)如图①,等边△ABC的边长为6,则该等边三角形的外接圆半径长为 .
(2)如图②,在△ABC中, 点D、E、F分别在边 BC、AB 和AC上, ,若点D为BC边的中点, 求AF的长度.
(3) 如图③, 在△ABC中, . 等边 的三个顶点分别在边BC、AB、AC上.该等边三角形的面积是否存在最大值,如果存在,求出面积最大值,如果不存在,说明理由.
7定义:对角互补且有一组邻边相等的四边形称为奇异四边形.
(1)概念理解:在平行四边形、菱形、矩形、正方形中,你认为属于奇异四边形的有 ;
(2)性质探究:
①如图1, 四边形ABCD是奇异四边形, AB=AD, 求证: CA平分∠BCD;
②如图2, 四边形ABCD 是奇异四边形, AB=AD, ∠BCD=2α, 试说明:
(3)性质应用:
如图3,四边形ABCD是奇异四边形,四条边中仅有BC=CD,且四边形ABCD 的周长为 求奇异四边形ABCD 的面积.
8定义:有一组对角互补的四边形叫做互补四边形.
(1)概念理解:
①在互补四边形ABCD中,∠A 与∠C是一组对角,若 则
②如图1, 在△ABC中, 点D,E分别在边AB,BC上, 且BE BC=AB BD, 求证:四边形ADEC 是互补四边形.
(2) 探究发现: 如图2,在等腰△ABE中, AE=BE, 点C, D分别在边BE, AE上, AD=BC, 四边形CEDH是互补四边形, 求证:
9如图,在平面直角坐标系xOy中,矩形ABCD的边AB=4,BC=6.若不改变矩形ABCD的形状和大小,当矩形顶点A在x轴的正半轴上左右移动时,矩形的另一个顶点D始终在 y轴的正半轴上随之上下移动.
(1) 当∠OAD=30°时, 求点C的坐标;
(2) 设AD的中点为M, 连接OM、MC, 当四边形OMCD的面积为 时,求OA的长;
(3)当点A移动到某一位置时,点C到点O的距离有最大值,请直接写出最大值, 并求此时cos∠OAD 的值.
1.解: 如图, ①设∠1=x度, 则∠2= (60-x)°,∠DBC= (x+60) °, 故∠4= (x+60)°,
∴∠2+∠3+∠4=60-x+60+x+60=180°,
∴D、A、E三点共线; 故①正确;
C
②∵△BCD 绕着点 C 按顺时针方向旋转60°得到△ACE, ∴CD=CE, ∠DCE=60°, ∴△CDE为等边三角形,
∴∠E=60° , ∴∠BDC=∠E=60° ,
∴∠CDA=120° -60° =60° ,
∴DC平分∠BDA; 故②正确;
③∵∠BAC=60° , ∠E=60° , ∴∠E=∠BAC.故③正确;
④由旋转可知AE=BD, 又∵∠DAE=180°,
∴DE=AE+AD. ∵△CDE为等边三角形,
∴DC=DB+BA. 故④正确; 故选: A.
2解: ∵四边形ABCD 是正方形, ∴∠BCQ=90°,∵PQ⊥PB,∴∠BPQ=90°,∴∠BPQ+∠BCQ=180° ,∴B、C、Q、P四点共圆, ∴∠PBC=∠PQD, ∠BPC=∠BQC, ∴①正确; ③正确;
∵四边形ABCD 是正方形, ∴∠BCP=∠PCQ=45°,
∴ BP=PQ, ∴②正确;
过P作PE⊥AB于E, PF⊥DC于F, 则E、P、F三点共线, ∵四边形ABCD是正方形, ∴∠PAE=45°, ∴△PAE是等腰直角三角形,
在△BEP 和△PFQ中, 易证△BEP≌△PFQ (ASA) ,∴PE=FQ=1, ∴DQ=1+1=2, ∵Q为CD中点,∴DC=2DQ=4, ∴正方形ABCD的面积是4×4=16,∴④正确; 故选: A.
3 解: (1) ∵EF∥AB. ∴∠FEC=∠A=30° .∠EFC=∠B=30° ∴EC=CF. 又∵AC=BC ,∴AE=BF, 又∵D是AB中点. ∴DB=AD∴△ADE≌△BDF. ∴DE=DF
(2) 如图, 连接CD, ∵△ABC是等腰三角形, 点D为AB边的中点, ∴∠ACD=∠BCD,
在线段AC上取点F',使( 连接F'D,
在△CDF与△CDF' 中,
∴△CDF≌△CDF' (SAS), ∴∠CFD=∠CF' D,在四边形CEDF中, ∠ACB=120° , ∠EDF=60° ,
∴∠CED+∠CFD=180°, ∴∠CED+∠CF' D=180° ,
∵∠CED+∠F' ED=180° , ∴∠EF' D=∠F' ED,
∴DE=DF' , ∵DF' =DF, ∴DE=DF.
方法2(初三): ∵∠ACB=120° , ∠EDF=60°
∴AEDF 四点共圆, ∵∠EAD=∠FAD(三线合一)
∴DE=DF
4解: (1) 证明: ∵四边形ABCD 为圆内接四边形,∴∠A+∠C=180° , ∠ABC+∠ADC=180° ,
∵BD平分∠ABC, ∴∠ABD=∠CBD, ∴AD=CD,
∴四边形ABCD 是等补四边形;
(2) AC平分∠BCD, 理由如下:
如图2, 过点A分别作AE⊥BC于点 E, AF 垂直CD的延长线于点 F, 则∠AEB=∠AFD=90°,
∵四边形ABCD是等补四边形, ∴∠B+∠ADC=180°,又∠ADC+∠ADF=180°, ∴∠B=∠ADF, ∵AB=AD,
∴△ABE≌△ADF (AAS) , ∴AE=AF,
∴AC是∠BCF的平分线, 即 AC平分∠BCD;
(3) 如图3, 连接AC, ∵四边形ABCD是等补四边形,
∴∠BAD+∠BCD=180° , 又∠BAD+∠EAD=180° ,
∴∠EAD=∠BCD, ∵AF平分∠EAD,
由(2)知, AC平分∠BCD,
∴∠FCA= ∠BCD, ∴∠FCA=∠FAD,又∠AFC=∠DFA, ∴△ACF∽△DAF, 即
5.解: (1) ∵点P (3m-1, - 2m+4) 在第一象限的角平分线OC上, ∴3m-1=-2m+4,
∴m=1, ∴P (2, 2) ;
(2)①不变.过点 P作 PM⊥y轴于 M,PN⊥OA于 N.
∵∠PMO=∠PNO=∠MON=90° , PM=PN=2,
∴四边形QMPN是正方形, ∴∠MPN=90°=∠APB,
∴∠MPB=∠NPA.
在△PMB 和△PNA中,
∴△PMB≌△PNA (ASA) , ∴BM=AN,
∴OB+OA=OM--BM+ON+AN=2OM=4,
②连接AB, ∵∠AOB=90°, ∴OA +OB =AB ,
当PA最小时, 也最小.根据垂线段最短原理,PA 最小值为2,
的最小值为8.
303. 解: (1) 如图1, 作BC、AC的垂直平分线, 交△ABC的内部于一点O,O即为等边三角形的外接圆的圆心,则
在Rt△OBD 中, ∴等边三角形的外接圆半径长为
(2) 如图2, 连接AD, 过点D作 DM⊥BA于点 M,DN⊥AC于点 N, 则∠DMA=∠DNA=∠DNF=90°,∵AB=AC, 点D 是BC的中点,
在△ADM和△ADN中,
∴△ADM≌△ADN(AAS) , ∴AM=AN, DM=DN,在四边形AMDN 中, ∠MDN=360°-120° -90° -90°=60° ,∵∠EDF=60°,∴∠MDN=∠EDF,即∠EDN+∠NDF=∠EDN+∠MDE, ∴∠NDF=∠MDE,
在△MDE和△NDF中,
∴△MDE≌△NDF(ASA) , ∴ME=∠NF,
∴AE+AF=AM-ME+AN+NF=2AM,
∵∠BAC=120° , AB=AC=8, ∴∠B=∠C=30° ,
在Rt△ABD中,
在Rt△AMD中,
∴AF=2+1=3.
(3) 如图3, 过点 D作 DG⊥AB于点 G, GH⊥AC于点H, 由(2) 可得: △DEG≌△DFH, △ADG≌ADH,∴DG=DH, ∠DAG=∠DAH=60° ,
且由几何关系可得DF≤AD,
∴AD 取得最大值时,S△DEF取得最大值,作△ABC的外接圆⊙O, 连接OB、OC, 则∠BOC=120°,
∵BC=10 , ∴OB=OC=10,
过点O 作OQ⊥BC交⊙O于M、N, 垂足为Q,则OQ=5, MN平分BC弧, ∴BN弧=CN弧,连接DN, A、D、N共线,
由几何关系可得: DN+AD≤MN,
∴AD≤MN-DN,
∵ND≥QN, ∴当DN最小时, AD存在最大值,
∴当AN为直径时,AD 存在最大值,AD 最大=5,
∴S△DEF最大
6解: (1)根据奇异四边形的定义可知:正方形是奇异四边形,故答案为正方形.
(2)①如图1,过点A作AM⊥CB于M,AN⊥CD于N.,∵∠ABC+∠D=180° , ∠ABM+∠ABC=180°,
∴∠ABM=∠D, ∵∠AMB=∠AND=90° , AB=AD,
∴△AMB≌△AND, ∴AM=AN,
∵AM⊥CB于M, AN⊥CD于N, ∴CA平分∠BCD.
②由①可知: =CD-BM=CD - (CM-BC) =CD - (CN-BC),
在 Rt△ACN中,
(3)如图3中, 由(2) 可知: ∵四边形ABCD的周长为
∴∠DAB=90°, ∵四边形是奇异四边形,
∴∠BCD=90° , ∵AD+AB=6,
9.
7. (1) ①解: ∵四边形ABCD 是互补四边形,∠A与∠C是一组对角,
∵∠B: ∠C: ∠D=2: 3: 4,
∵∠A+∠B+∠C+∠D=360°,
∠A)=360°, ∴∠A=90°, 故答案为: 90;
②证明: 又∵∠B=∠B, ∴△BDE∽△BCA, ∴∠BED=∠A,
∴∠A+∠CED=∠BED+∠CED=180°,
∴四边形ADEC 是互补四边形;
(2) 证明: ∵AE=BE, AD=BC, ∴ED=EC,在△EAC和△EBD中,
∴△EAC≌△EBD (SAS), ∴∠EBD=∠EAC,
∵AE=BE, ∴∠EAB=∠EBA, ∴∠ABD=∠BAC,
∵四边形CEDH是互补四边形,∴∠E+∠DHC=180°,
∵∠AHB=∠DHC, ∴∠E+∠AHB=180° ,
∴∠ABD+∠BAC=∠E, ∴∠ABD=∠BAC= ∠E.
8解: (1) 如图1, 过点C作CE⊥y轴于点 E,∵矩形ABCD 中, CD⊥AD, ∴∠CDE+∠ADO=90° ,又∵∠OAD+∠ADO=90°, ∴∠CDE=∠OAD=30°,∴在 Rt△CED 中, 在Rt△OAD中, ∠OAD=30° ,
∴点C的坐标为
(2) ∵M为AD的中点,∴DM=3, S△DCM=6,又 设OA=x、OD=y, 则 即x=y,将x=y代入 得 解得 (负值舍去),
(3) OC的最大值为8, 如图2, M为AD的中点, ∴OC≤OM+CM=8,
当O、M、C三点在同一直线时,OC有最大值8,
连接OC,则此时OC与AD的交点为M,
过点O作ON⊥AD,垂足为N,∵∠CDM=∠ONM=90°,
∠CMD=∠OMN, ∴△CMD∽△OMN,
即
解得
在 Rt△OAN中,
同课章节目录
