2025年中考数学复习--二次函数面积问题(含解析)
文档属性
| 名称 | 2025年中考数学复习--二次函数面积问题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 434.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 16:42:03 | ||
图片预览



文档简介
二次函数面积问题
1如图,已知抛物线经过两点A(-3,0),B(0,3),且其对称轴为直线
(1)求此抛物线的解析式;
(2)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求 的面积的最大值,并求出此时点P的坐标.
2如图,在平面直角坐标系xOy中,已知直线 与x轴交于点A,与y轴交于点B,过A、B两点的抛物线 与x轴交于另一点(
(1)求抛物线的解析式;
(2)在抛物线上是否存在一点 P,使 若存在,请求出点 P 的坐标,若不存在,请说明理由;
(3)点M为直线AB下方抛物线上一点,点N为y轴上一点, 当 的面积最大时,求 的最小值.
3在平面直角坐标系中,将二次函数 的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与x轴交于点A、B(点A在点B的左侧), 经过点A 的一次函数 的图象与y轴正半轴交于点C,且与抛物线的另一个交点为D,△ABD的面积为5.
(1)求抛物线和一次函数的解析式;
(2)抛物线上的动点E在一次函数的图象下方,求△ACE面积的最大值,并求出此时点E 的坐标;
(3)若点P为x轴上任意一点,在(2)的结论下,求 的最小值.
4已知抛物线 经过点A(2, 0) 、B(-4, 0) , 与y轴交于点C.
(1)求这条抛物线的解析式;
(2)如图1,点P 是第三象限内抛物线上的一个动点,当四边形ABPC的面积最大时,求点 P 的坐标;
(3)如图2,线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,在直线DE上是否存在一点G,使△CMG的周长最小 若存在,求出点G的坐标;若不存在,请说明理由.
5如图,在平面直角坐标系中,抛物线 与x 轴交于点 点B(4,0),与y轴交于点C(0,8),连接BC.又已知位于y轴右侧且垂直于x轴的动直线l,沿x轴正方向从0运动到B(不含0点和B点),且分别交抛物线、线段BC以及x轴于点 P,D,E.
(1)求抛物线的表达式;
(2)连接AC,AP,当直线l运动时,求使得 和 相似的点P 的坐标;
(3) 作 垂足为F,当直线l运动时,求 面积的最大值.
6如图,抛物线 的图象过点A (-1, 0) 、B(3, 0) 、C(0, 3) .
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在一点P,使得△PAC的周长最小,若存在,请求出点P的坐标及△PAC的周长;若不存在,请说明理由;
(3)在(2)的条件下,在x轴上方的抛物线上是否存在点M(不与C点重合),使得 若存在,请求出点M的坐标;若不存在,请说明理由.
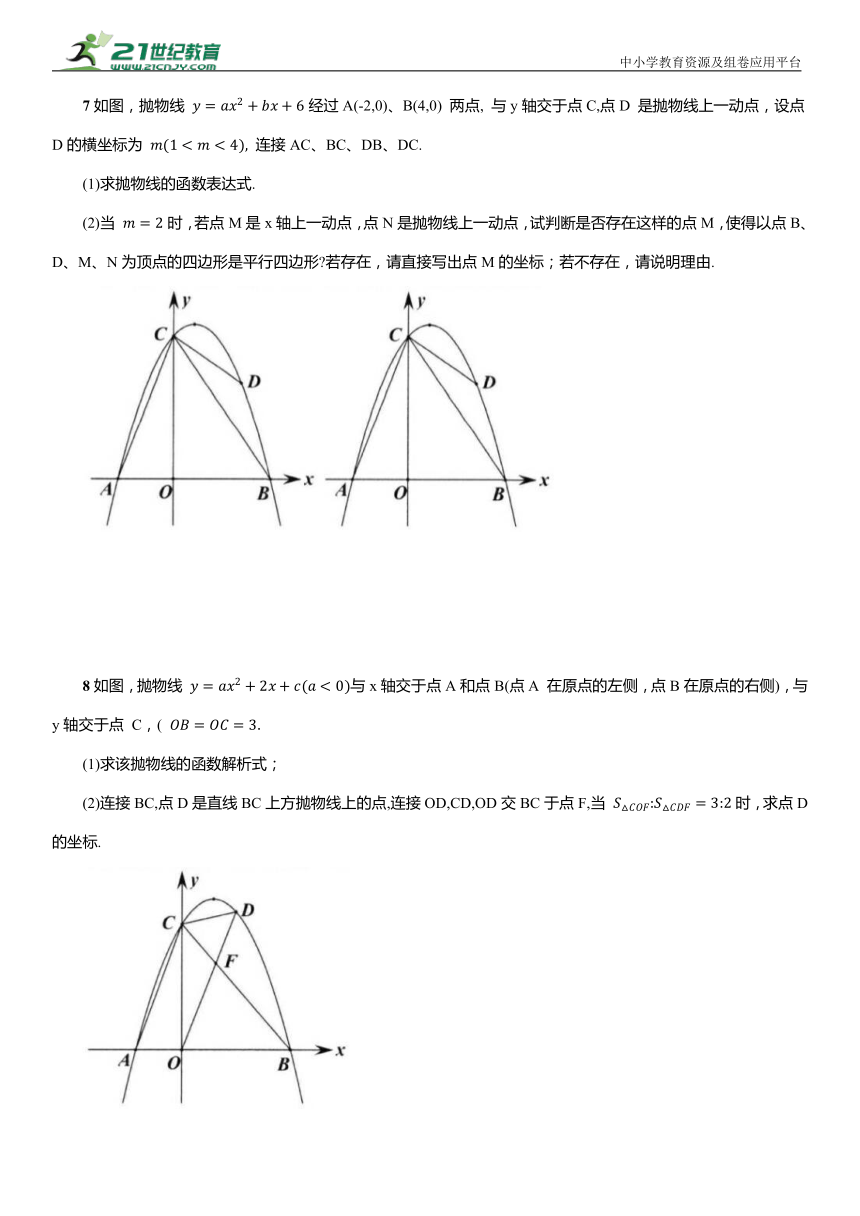
7如图,抛物线 经过A(-2,0)、B(4,0) 两点, 与y轴交于点C,点D 是抛物线上一动点,设点D的横坐标为 连接AC、BC、DB、DC.
(1)求抛物线的函数表达式.
(2)当 时,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B、D、M、N为顶点的四边形是平行四边形 若存在,请直接写出点M的坐标;若不存在,请说明理由.
8如图,抛物线 与x轴交于点A和点B(点A 在原点的左侧,点B在原点的右侧),与y轴交于点 C,(
(1)求该抛物线的函数解析式;
(2)连接BC,点D是直线BC上方抛物线上的点,连接OD,CD,OD交BC于点F,当 时,求点D的坐标.
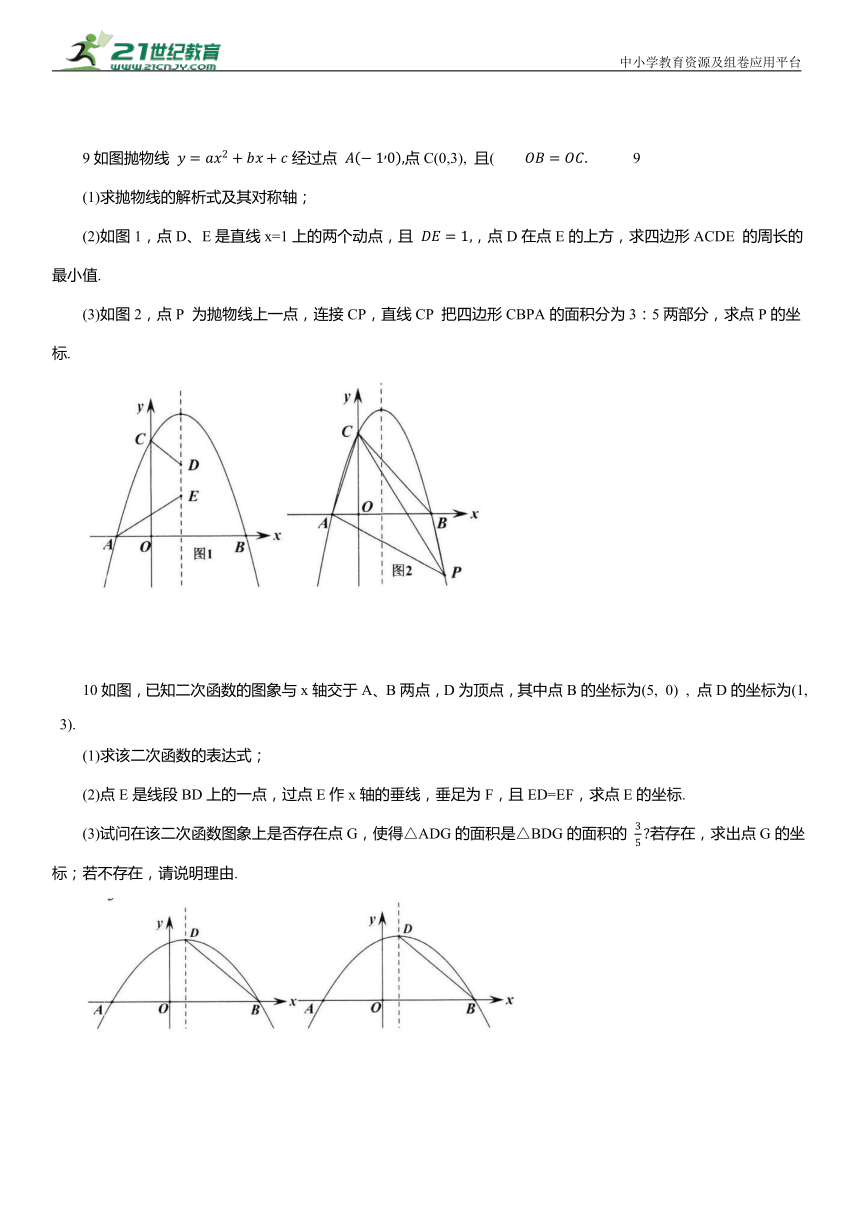
9如图抛物线 经过点 点C(0,3), 且( 9
(1)求抛物线的解析式及其对称轴;
(2)如图1,点D、E是直线x=1上的两个动点,且 ,点D在点E的上方,求四边形ACDE 的周长的最小值.
(3)如图2,点P 为抛物线上一点,连接CP,直线CP 把四边形CBPA的面积分为3:5两部分,求点P的坐标.
10如图,已知二次函数的图象与x轴交于A、B两点,D为顶点,其中点B的坐标为(5, 0) , 点D的坐标为(1, 3).
(1)求该二次函数的表达式;
(2)点E是线段BD上的一点,过点E作x轴的垂线,垂足为F,且ED=EF,求点E的坐标.
(3)试问在该二次函数图象上是否存在点G,使得△ADG的面积是△BDG的面积的 若存在,求出点G的坐标;若不存在,请说明理由.
11在平面直角坐标系xOy中,等腰直角△ABC的直角顶点C在 y轴上,另两个顶点A, B在x轴上, 且AB=4, 抛物线经过A, B, C三点, 如图1所示.
(1)求抛物线所表示的二次函数表达式.
(2)过原点任作直线l交抛物线于M,N两点,如图2所示.
①求△CMN面积的最小值.
②已知 是抛物线上一定点,问抛物线上是否存在点 P,使得点P与点Q关于直线l对称,若存在,求出点P 的坐标及直线l的一次函数表达式;若不存在,请说明理由.
12在平面直角坐标系中,抛物线 交x轴于点A(-1,0),B(3,0),过点B的直线 交抛物线于点 C.
(1)求该抛物线的函数表达式;
(2)若点P是直线BC下方抛物线上的一个动点(P不与点B,C重合),求△PBC面积的最大值;
(3)若点M在抛物线上,将线段OM绕点O旋转90°,得到线段ON,是否存在点M,使点N恰好落在直线BC上 若存在,请直接写出点M的坐标;若不存在,请说明理由.
1 (1)∵抛物线对称轴是直线x=-1且经过点A (-3,0),由抛物线的对称性可知:抛物线还经过点(1, 0) , 设抛物线的解析式为y=a(x-x ) (x-x ) (a≠0)
即: y=a(x-1) (x+3)
把B (0, 3) 代入得:3=-3a, ∴a=-1
∴抛物线的解析式为:
(2) 设直线AB的解析式为y= kx+b, ∵A (-3, 0) ,B(0, 3) , ∴直线AB为y=x+3,如图, 作 PM⊥x轴, 交直线AB于 M,
设 则M(x,x+3),
当 时, 此时,
∴△PAB 的面积的最大值为 此时点P的坐标为
2. 解: (1) ∵直线 与x轴交于点A,与y轴交于点B, ∴点A (4, 0) , 点B (0, - 2) ,∵点C (-1, 0) , 点A (4, 0)
∴ 设抛物线解析式为: y=a(x+1) (x-4) ,
把点B(0, - 2) 代入得:
∴抛物线解析式为:
(2)存在,分两种情况讨论:
①.当点 P在直线AB上方时,过点O作OP∥AB,交抛物线于点 P,如图1中的 P1和 P2,
∵OP∥AB,∴△ABP和△ABO是等底等高的两个三角形,
∵OP∥AB, ∴直线 PO的解析式为
联立方程组可得
解得: 或
∴点 或
②.当点 P在直线AB下方时,在OB的延长线上截取BE=OB=2, 过点E作 EP∥AB, 交抛物线于点 P, 如图1中的P3.
∴AB∥EP3∥OP, OB=BE, ∴S△AP3B=S△ABO,
∵EP"∥AB, 且过点E (0, - 4) ,
∴直线EP3 解析式为 联立方程组可得: 解得 ∴点 P3 (2, - 3) ,综上所述:点P 坐标为 或 或(2, - 3);
(3) 如图2, 过点M作MF⊥AC, 交AB于F,设点 则点 = - (m-2) +4,
∴当m=2时, △MAB的面积有最大值,
∴点 M (2, - 3) ,
再过点O作∠HOB=30°, 过点N作GN⊥OH于G点,则
当M、N、G三点共线,且垂直OH时, 最小,作MH⊥OH于H点,,MH即为所求的最小值,
中小学教育资源及组卷应用平台
设OH与MF交于点Q, 则 又易得
的最小值为
3. 解: (1) 将二次函数 的图象向右平移1个单位,再向下平移2个单位,得到的抛物线解析式为
∵OA=1, ∴点A的坐标为(-1, 0), 代入抛物线的解析式得,
∴抛物线的解析式为: 即
令y=0, 解得x =-1, x =3, ∴B (3, 0) ,∴AB=OA+OB=4,
∵△ABD的面积为5,
把 代入抛物线解析式
得: 解得:x =-2, x =4,
设直线AD的解析式为y= kx+b,
把A(-1, 0)、D (4, 代入得:
解得: ∴直线AD的解析式为
(2)过点E作 EM⊥x轴交AD于M,如图1, 设E(x, 则
∴当 时,△ACE的面积有最大值,最大值是 此时 E 点坐标为
(3).作E关于x轴的对称点 F,连接EF交x轴于点 G,
过点P作 PQ⊥AF于点 Q, 则
当E、P、Q三点共线,且垂直AF时, 有最小值,作EH⊥AF,则 EH 即为所求.
由三角形面积得:
解得: EH=3
的最小值是3.
4解: (1) ∵抛物线y= ax+ bx-4经过点A (2,0),B (-4, 0) , . 解得 ∴抛物线解析式为
(2) 如图1, 连接OP, 设点 其中-4由题意得(
∵--1<0,开口向下, S有最大值, ∴当x=-2时, 四边形ABPC的面积最大, 此时, y=-4, 即 P(-2, -4) .
因此当四边形ABPC的面积最大时,
点P 的坐标为(-2, - 4) .
解法二:连接BC,过点P作x轴的垂线,交 BC 于点 E,用铅垂定理也可.
∴顶点 如图2,连接AM交直线DE于点 G,此时,△CMG的周长最小.设直线AM的解析式为y= kx+b, 且过点A (2, 0) , 解得: ∴直线AM的解析式为
在 Rt△AOC中,
∵D为AC的中点,
∴AE=5, ∴OE=AE-AO=5-2=3, ∴E(-3,0),由图可知D (1, -2),设直线DE 的函数解析式为y= mx+n,把D(1,-2)、E(-3,0),代入得: 解得: 直线 DE的解析式为 . ∴联立得: 解得:
5解: (1)将点A、B、C的坐标代入二次函数表达式
得: 解得:
故抛物线的表达式为:
(2) ∵点A(-2, 0)、 C(0, 8), ∴OA=2, OC=8,∵l⊥x轴, ∴∠PEA=∠AOC=90° ,
∵∠PAE≠∠CAO,
∴只有当∠PAE=∠ACO时, △PEA∽△AOC,此时 即: 设点 P 的纵坐标为k, 则 PE=k, AE=4k,
∴OE=4k-2, 将点 P坐标(4k-2, k) 代入二次函数表达式并解得:k=0(舍去)或 则点
(3) 在 Rt△PFD中, ∠PFD=∠COB=90°,
∵l∥y轴, ∴∠PDF=∠OCB, ∴Rt△PFD∽Rt△BCO,
而
即当PD取得最大值时,S△PDF最大,
将B、C坐标代入一次函数表达式并解得:直线BC的表达式为: y=-2x+8,
设点 则点 D (m, - 2m+8),则 当m=2时, PD的最大值为4, 故当PD=4时,
6 解: (1) ∵抛物线与x轴交于点A(-1,0) 、B(3, 0) ∴可设交点式y=a(x+1) (x-3)
把点 C(0, 3)代入得: - 3a=3, ∴a=-1
∴y= - (x+1) (x-3) =-x +2x+3
∴抛物线解析式为
(2)在抛物线的对称轴上存在一点 P,使得△PAC的周长最小. 如图1, 连接PB、BC
∵点P在抛物线对称轴直线x=1上,点A、B关于对称轴对称, ∴PA=PB, ∴C△PAC=AC+PC+PA=AC+PC+PB
∵当C、P、B在同一直线上时, PC+PB=CB 最小,
∵A(-1, 0) 、B (3, 0) 、 C(0, 3)
∴由两点距离公式可得:
最小
设直线 BC解析式为y= kx+3, 把点 B 代入得: 3k+3=0,解得: k=-1, ∴直线.BC: y=-x+3, ∴yp=-1+3=2∴点 P(1,2)使△PAC的周长最小,最小值为
(3)存在满足条件的点 M,使得
∵ 当以PA为底时,两个三角形等高时,两个三角形面积相等,
∴点 M 和点 C到直线 PA距离相等时,现在,分两种情况讨论:
①若点M在点 P 上方,过点 C作CM∥PA,交抛物线于点 M,如图2中的M1, ∵A(-1,0), P(1,2),设直线AP 解析式为
解得: ∴直线AP: y=x+1
∴直线 CM解析式为:y=x+3,联立得:
解得: (即点C), ∴点 M 坐标(1, 4)
②若点 M在点 P 下方,如图3中的 M ,
同理, C'M ∥PA, 由题意可知, 且直线C'M 到PA的距离等于直线y=x+3到PA的距离,
∴直线 AP: y=x+1向下平移2个单位得y=x-1即为直线C'M 的解析式,联立得:
解得: 或
∵点M在x轴上方∴y>0
∴点M坐标为
综上所述,点M 坐标为(1,4)或 时,
7 解: (1) 由抛物线交点式表达式得: y=a(x+2)
即--8a=6, 解得:
故抛物线的表达式为:
(2) 由抛物线的表达式知, 点C (0, 6),
由点B、C的坐标,得直线BC的表达式为: 如图1, 过点D作DH⊥x轴, 交直线BC于点 H,
设点 则点 则
解得: m=1或3(舍去1) , 故m=3;
(3)当m=2时, 点D (2, 6), 设点M(x, 0), 点N(t, n) , 则
第一种情况:当BD是边时,则N的纵坐标为6或者-6,点B 向左平移2个单位向上平移6个单位得到点 D,同样点M (N)向左平移2个单位向上平移6个单位得到点N(M), 故 或
解得: x=2或 (不合题意的值已舍去);
故点 M的坐标为 )或 或(2, 0);
第二种情况:当BD 是对角线时,由中点公式得:
联立①③并解得x=6, 故点M的坐标为(6, 0),综上,点M 的坐标为 或 或(2, 0) 或(6, 0).
8. 解: (1) ∵OB=OC=3. ∴c=3, .点B (3, 0) ,将点 B 的坐标代入抛物线表达式: 并解得:a= - 1,故抛物线的表达式为:
(2) 如图, 过点D作DH⊥x轴于点H, 交BC于点 M,
则OF: FD=3: 2,
∵DH∥CO, 故CO: DM=3: 2, 则 由 B、C的坐标得:直线BC的表达式为: y=-x+3,
设点 则点 M (x, - x+3) ,
解得: x=1或2, 故点D (1, 4) 或(2, 3).
9解: (1) ∵OB=OC, ∴点B (3, 0),则抛物线的表达式为: y=a(x+1) (x-3) =a(x - 故-3a=3, 解得: a=-1,故抛物线的表达式为: 函数的对称轴为:x=1;
(2) 四边形ACDE的周长=AC+DE+CD+AE, 其中AC 是定值,故CD+AE 最小时,周长最小.取点C关于直线x=1对称点C' (2,3),则CD=C' D, 取点A' (-1, 1) , 则A' D=AE,
故: 则当A′、D、C′三点共线时, 最小,周长也最小,
四边形 ACDE 的周长的最小值=AC+DE+CD+AE=
(3) 设直线 CP交x轴于点 E,
直线 CP把四边形CBPA的面积分为3:5两部分,又∵ -yp) =BE: AE, 则BE: AE=3: 5或5: 3, 则AE= 或
即:点E的坐标为( , 0) 或( ,0),将点 E 的坐标代入直线CP的表达式:y=kx+3,解得: k=-6或-2,
故直线CP 的表达式为: y=-2x+3或y=-6x+3…②联立①②并解得:x=4或8(不合题意值已舍去),故点 P的坐标为(4, - 5) 或 (8, - 45) .
10解: (1)设二次函数的解析式为 将点B代入得0=a(5-1) +3,得
∴二次函数的表达式为:
(2) 依题意, 点B (5, 0) , 点D (1, 3) , 设直线BD 的解析式为y= kx+b, 代入得 解得: ∴线段BD 所在的直线为
设点 E的坐标为: 则F (x, 0)
整理得 解得 (舍去).
故点 E的纵坐标为
∴点E 的坐标为(
(3)存在满足条件的点G,分两种情况讨论:
①.当点 G在x轴的上方时,如图1,设直线DG交x轴于P, 设P (t, 0) , 作AE⊥DG于E, BF⊥DG于F.
由题意: AE: BF=3: 5,
∵BF∥AE, ∴AP: BP=AE: BF=3: 5,
∴ (-3-t) : (5-t) =3: 5, 解得t=-15,
∴ P (-15, 0) , 由点 P (-15, 0) , 点D (1, 3) 可
得:直线DG 的解析式为
联立方程组得:
解得或
②当点G在x轴下方时,如图2,令y=0,
解得: x =-3, x =5,
∴A(-3, 0)、B(5, 0), ∴AO: OB=3: 5
当点 G 在 DO的延长线上与抛物线的交点时,存在点G使得 此时,DG的直线经过原点,设直线 DG的解析式为y= kx, 将点 D (1, 3) 代入得:k=3, 故y=3x, 则有
整理得, (x-1) (x+15) =0,
得x =1(舍去),x =-15, 当x=-15时, y=-45,故点G为(-15, - 45).
综上所述,点G的坐标为(0, 或(-15, - 45).
11.解: (1)设抛物线的解析式为 0), 在等腰Rt△ABC中, OC 垂直平分AB, 且AB=4,∴OA=OB=OC=2,
∴A (-2, 0) , B (2, 0), C(0, - 2) ,
代入得: 解得,
∴抛物线的解析式为
(2) ①设直线l的解析式为y= kx, M(x , y ) , N(x , y ) , 由可得
∴x +x =2k, x ·x =-4,
∴当k=0时 取最小值为4.此时直线1与x轴重合,∴△CMN面积的最小值为4.
②假设抛物线上存在点 使得点 P与点 Q关于直线l对称,
∴OQ=OP, 即 解得, ∵m =1, m =-1不合题意,舍去,
当 时,点 线段PQ的中点为 代入 y= kx得:
∴直线l的表达式为: 当 时,点 线段PQ的中点为 代入y= kx得: ∴直线l的解析式为
综上,点 直线l解析式为 点 直线l解析式为
12解: (1)将点A(-1,0),B(3,0)代入 -3 中, 得: 解得:
∴该抛物线表达式为
(2) 如图1, 过点 P作 PE⊥x轴, 交 BC于点 E, 连接PB, PC,
设点. 则点
联立方程组:
解得: 或
∵点B 坐标为(3,0), ∴点 C 的坐标为
∴B、C之间的水平宽度为
(其中
∴当 时,S△PBC的最大值为
(3)分两种情况讨论:
①.如图2,线段OM 绕点 O逆时针旋转90°,得到线段ON, 设.M(t, t -2t-3), N (n, n-2),作MG⊥y轴于点 G, NH⊥x轴于H,
∴∠OGM=∠OHN=90° ,
∴OM=ON, ∠MON=90° ,
∵∠GOH=90° , ∴∠MOG=∠NOH,
在△OGM与△OHN中,
∴△OGM≌△OHN(AAS) , ∴GM=NH, OG=OH,
解得: 或
②.如图3,线段OM绕点O顺时针旋转90°,得到线段ON, 设.M(t,t -2t-3), N(n, n-2),作MG⊥x轴于点 G, NH⊥x轴于 H,
∴∠OGM=∠OHN=90° ,
∵线段OM 绕点 O 旋转90°, 得到线段ON,
∴OM=ON, ∠MON=90° ,
∵∠GOH=90°, ∴∠MOG=∠NOH,在△OGM与△OHN中,
∴△OGM≌△OHN (AAS) , ∴GM=NH, OG=OH, 解得:
综上所述,点M的坐标为M (0, - 3), M (
1如图,已知抛物线经过两点A(-3,0),B(0,3),且其对称轴为直线
(1)求此抛物线的解析式;
(2)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求 的面积的最大值,并求出此时点P的坐标.
2如图,在平面直角坐标系xOy中,已知直线 与x轴交于点A,与y轴交于点B,过A、B两点的抛物线 与x轴交于另一点(
(1)求抛物线的解析式;
(2)在抛物线上是否存在一点 P,使 若存在,请求出点 P 的坐标,若不存在,请说明理由;
(3)点M为直线AB下方抛物线上一点,点N为y轴上一点, 当 的面积最大时,求 的最小值.
3在平面直角坐标系中,将二次函数 的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与x轴交于点A、B(点A在点B的左侧), 经过点A 的一次函数 的图象与y轴正半轴交于点C,且与抛物线的另一个交点为D,△ABD的面积为5.
(1)求抛物线和一次函数的解析式;
(2)抛物线上的动点E在一次函数的图象下方,求△ACE面积的最大值,并求出此时点E 的坐标;
(3)若点P为x轴上任意一点,在(2)的结论下,求 的最小值.
4已知抛物线 经过点A(2, 0) 、B(-4, 0) , 与y轴交于点C.
(1)求这条抛物线的解析式;
(2)如图1,点P 是第三象限内抛物线上的一个动点,当四边形ABPC的面积最大时,求点 P 的坐标;
(3)如图2,线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,在直线DE上是否存在一点G,使△CMG的周长最小 若存在,求出点G的坐标;若不存在,请说明理由.
5如图,在平面直角坐标系中,抛物线 与x 轴交于点 点B(4,0),与y轴交于点C(0,8),连接BC.又已知位于y轴右侧且垂直于x轴的动直线l,沿x轴正方向从0运动到B(不含0点和B点),且分别交抛物线、线段BC以及x轴于点 P,D,E.
(1)求抛物线的表达式;
(2)连接AC,AP,当直线l运动时,求使得 和 相似的点P 的坐标;
(3) 作 垂足为F,当直线l运动时,求 面积的最大值.
6如图,抛物线 的图象过点A (-1, 0) 、B(3, 0) 、C(0, 3) .
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在一点P,使得△PAC的周长最小,若存在,请求出点P的坐标及△PAC的周长;若不存在,请说明理由;
(3)在(2)的条件下,在x轴上方的抛物线上是否存在点M(不与C点重合),使得 若存在,请求出点M的坐标;若不存在,请说明理由.
7如图,抛物线 经过A(-2,0)、B(4,0) 两点, 与y轴交于点C,点D 是抛物线上一动点,设点D的横坐标为 连接AC、BC、DB、DC.
(1)求抛物线的函数表达式.
(2)当 时,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B、D、M、N为顶点的四边形是平行四边形 若存在,请直接写出点M的坐标;若不存在,请说明理由.
8如图,抛物线 与x轴交于点A和点B(点A 在原点的左侧,点B在原点的右侧),与y轴交于点 C,(
(1)求该抛物线的函数解析式;
(2)连接BC,点D是直线BC上方抛物线上的点,连接OD,CD,OD交BC于点F,当 时,求点D的坐标.
9如图抛物线 经过点 点C(0,3), 且( 9
(1)求抛物线的解析式及其对称轴;
(2)如图1,点D、E是直线x=1上的两个动点,且 ,点D在点E的上方,求四边形ACDE 的周长的最小值.
(3)如图2,点P 为抛物线上一点,连接CP,直线CP 把四边形CBPA的面积分为3:5两部分,求点P的坐标.
10如图,已知二次函数的图象与x轴交于A、B两点,D为顶点,其中点B的坐标为(5, 0) , 点D的坐标为(1, 3).
(1)求该二次函数的表达式;
(2)点E是线段BD上的一点,过点E作x轴的垂线,垂足为F,且ED=EF,求点E的坐标.
(3)试问在该二次函数图象上是否存在点G,使得△ADG的面积是△BDG的面积的 若存在,求出点G的坐标;若不存在,请说明理由.
11在平面直角坐标系xOy中,等腰直角△ABC的直角顶点C在 y轴上,另两个顶点A, B在x轴上, 且AB=4, 抛物线经过A, B, C三点, 如图1所示.
(1)求抛物线所表示的二次函数表达式.
(2)过原点任作直线l交抛物线于M,N两点,如图2所示.
①求△CMN面积的最小值.
②已知 是抛物线上一定点,问抛物线上是否存在点 P,使得点P与点Q关于直线l对称,若存在,求出点P 的坐标及直线l的一次函数表达式;若不存在,请说明理由.
12在平面直角坐标系中,抛物线 交x轴于点A(-1,0),B(3,0),过点B的直线 交抛物线于点 C.
(1)求该抛物线的函数表达式;
(2)若点P是直线BC下方抛物线上的一个动点(P不与点B,C重合),求△PBC面积的最大值;
(3)若点M在抛物线上,将线段OM绕点O旋转90°,得到线段ON,是否存在点M,使点N恰好落在直线BC上 若存在,请直接写出点M的坐标;若不存在,请说明理由.
1 (1)∵抛物线对称轴是直线x=-1且经过点A (-3,0),由抛物线的对称性可知:抛物线还经过点(1, 0) , 设抛物线的解析式为y=a(x-x ) (x-x ) (a≠0)
即: y=a(x-1) (x+3)
把B (0, 3) 代入得:3=-3a, ∴a=-1
∴抛物线的解析式为:
(2) 设直线AB的解析式为y= kx+b, ∵A (-3, 0) ,B(0, 3) , ∴直线AB为y=x+3,如图, 作 PM⊥x轴, 交直线AB于 M,
设 则M(x,x+3),
当 时, 此时,
∴△PAB 的面积的最大值为 此时点P的坐标为
2. 解: (1) ∵直线 与x轴交于点A,与y轴交于点B, ∴点A (4, 0) , 点B (0, - 2) ,∵点C (-1, 0) , 点A (4, 0)
∴ 设抛物线解析式为: y=a(x+1) (x-4) ,
把点B(0, - 2) 代入得:
∴抛物线解析式为:
(2)存在,分两种情况讨论:
①.当点 P在直线AB上方时,过点O作OP∥AB,交抛物线于点 P,如图1中的 P1和 P2,
∵OP∥AB,∴△ABP和△ABO是等底等高的两个三角形,
∵OP∥AB, ∴直线 PO的解析式为
联立方程组可得
解得: 或
∴点 或
②.当点 P在直线AB下方时,在OB的延长线上截取BE=OB=2, 过点E作 EP∥AB, 交抛物线于点 P, 如图1中的P3.
∴AB∥EP3∥OP, OB=BE, ∴S△AP3B=S△ABO,
∵EP"∥AB, 且过点E (0, - 4) ,
∴直线EP3 解析式为 联立方程组可得: 解得 ∴点 P3 (2, - 3) ,综上所述:点P 坐标为 或 或(2, - 3);
(3) 如图2, 过点M作MF⊥AC, 交AB于F,设点 则点 = - (m-2) +4,
∴当m=2时, △MAB的面积有最大值,
∴点 M (2, - 3) ,
再过点O作∠HOB=30°, 过点N作GN⊥OH于G点,则
当M、N、G三点共线,且垂直OH时, 最小,作MH⊥OH于H点,,MH即为所求的最小值,
中小学教育资源及组卷应用平台
设OH与MF交于点Q, 则 又易得
的最小值为
3. 解: (1) 将二次函数 的图象向右平移1个单位,再向下平移2个单位,得到的抛物线解析式为
∵OA=1, ∴点A的坐标为(-1, 0), 代入抛物线的解析式得,
∴抛物线的解析式为: 即
令y=0, 解得x =-1, x =3, ∴B (3, 0) ,∴AB=OA+OB=4,
∵△ABD的面积为5,
把 代入抛物线解析式
得: 解得:x =-2, x =4,
设直线AD的解析式为y= kx+b,
把A(-1, 0)、D (4, 代入得:
解得: ∴直线AD的解析式为
(2)过点E作 EM⊥x轴交AD于M,如图1, 设E(x, 则
∴当 时,△ACE的面积有最大值,最大值是 此时 E 点坐标为
(3).作E关于x轴的对称点 F,连接EF交x轴于点 G,
过点P作 PQ⊥AF于点 Q, 则
当E、P、Q三点共线,且垂直AF时, 有最小值,作EH⊥AF,则 EH 即为所求.
由三角形面积得:
解得: EH=3
的最小值是3.
4解: (1) ∵抛物线y= ax+ bx-4经过点A (2,0),B (-4, 0) , . 解得 ∴抛物线解析式为
(2) 如图1, 连接OP, 设点 其中-4
∵--1<0,开口向下, S有最大值, ∴当x=-2时, 四边形ABPC的面积最大, 此时, y=-4, 即 P(-2, -4) .
因此当四边形ABPC的面积最大时,
点P 的坐标为(-2, - 4) .
解法二:连接BC,过点P作x轴的垂线,交 BC 于点 E,用铅垂定理也可.
∴顶点 如图2,连接AM交直线DE于点 G,此时,△CMG的周长最小.设直线AM的解析式为y= kx+b, 且过点A (2, 0) , 解得: ∴直线AM的解析式为
在 Rt△AOC中,
∵D为AC的中点,
∴AE=5, ∴OE=AE-AO=5-2=3, ∴E(-3,0),由图可知D (1, -2),设直线DE 的函数解析式为y= mx+n,把D(1,-2)、E(-3,0),代入得: 解得: 直线 DE的解析式为 . ∴联立得: 解得:
5解: (1)将点A、B、C的坐标代入二次函数表达式
得: 解得:
故抛物线的表达式为:
(2) ∵点A(-2, 0)、 C(0, 8), ∴OA=2, OC=8,∵l⊥x轴, ∴∠PEA=∠AOC=90° ,
∵∠PAE≠∠CAO,
∴只有当∠PAE=∠ACO时, △PEA∽△AOC,此时 即: 设点 P 的纵坐标为k, 则 PE=k, AE=4k,
∴OE=4k-2, 将点 P坐标(4k-2, k) 代入二次函数表达式并解得:k=0(舍去)或 则点
(3) 在 Rt△PFD中, ∠PFD=∠COB=90°,
∵l∥y轴, ∴∠PDF=∠OCB, ∴Rt△PFD∽Rt△BCO,
而
即当PD取得最大值时,S△PDF最大,
将B、C坐标代入一次函数表达式并解得:直线BC的表达式为: y=-2x+8,
设点 则点 D (m, - 2m+8),则 当m=2时, PD的最大值为4, 故当PD=4时,
6 解: (1) ∵抛物线与x轴交于点A(-1,0) 、B(3, 0) ∴可设交点式y=a(x+1) (x-3)
把点 C(0, 3)代入得: - 3a=3, ∴a=-1
∴y= - (x+1) (x-3) =-x +2x+3
∴抛物线解析式为
(2)在抛物线的对称轴上存在一点 P,使得△PAC的周长最小. 如图1, 连接PB、BC
∵点P在抛物线对称轴直线x=1上,点A、B关于对称轴对称, ∴PA=PB, ∴C△PAC=AC+PC+PA=AC+PC+PB
∵当C、P、B在同一直线上时, PC+PB=CB 最小,
∵A(-1, 0) 、B (3, 0) 、 C(0, 3)
∴由两点距离公式可得:
最小
设直线 BC解析式为y= kx+3, 把点 B 代入得: 3k+3=0,解得: k=-1, ∴直线.BC: y=-x+3, ∴yp=-1+3=2∴点 P(1,2)使△PAC的周长最小,最小值为
(3)存在满足条件的点 M,使得
∵ 当以PA为底时,两个三角形等高时,两个三角形面积相等,
∴点 M 和点 C到直线 PA距离相等时,现在,分两种情况讨论:
①若点M在点 P 上方,过点 C作CM∥PA,交抛物线于点 M,如图2中的M1, ∵A(-1,0), P(1,2),设直线AP 解析式为
解得: ∴直线AP: y=x+1
∴直线 CM解析式为:y=x+3,联立得:
解得: (即点C), ∴点 M 坐标(1, 4)
②若点 M在点 P 下方,如图3中的 M ,
同理, C'M ∥PA, 由题意可知, 且直线C'M 到PA的距离等于直线y=x+3到PA的距离,
∴直线 AP: y=x+1向下平移2个单位得y=x-1即为直线C'M 的解析式,联立得:
解得: 或
∵点M在x轴上方∴y>0
∴点M坐标为
综上所述,点M 坐标为(1,4)或 时,
7 解: (1) 由抛物线交点式表达式得: y=a(x+2)
即--8a=6, 解得:
故抛物线的表达式为:
(2) 由抛物线的表达式知, 点C (0, 6),
由点B、C的坐标,得直线BC的表达式为: 如图1, 过点D作DH⊥x轴, 交直线BC于点 H,
设点 则点 则
解得: m=1或3(舍去1) , 故m=3;
(3)当m=2时, 点D (2, 6), 设点M(x, 0), 点N(t, n) , 则
第一种情况:当BD是边时,则N的纵坐标为6或者-6,点B 向左平移2个单位向上平移6个单位得到点 D,同样点M (N)向左平移2个单位向上平移6个单位得到点N(M), 故 或
解得: x=2或 (不合题意的值已舍去);
故点 M的坐标为 )或 或(2, 0);
第二种情况:当BD 是对角线时,由中点公式得:
联立①③并解得x=6, 故点M的坐标为(6, 0),综上,点M 的坐标为 或 或(2, 0) 或(6, 0).
8. 解: (1) ∵OB=OC=3. ∴c=3, .点B (3, 0) ,将点 B 的坐标代入抛物线表达式: 并解得:a= - 1,故抛物线的表达式为:
(2) 如图, 过点D作DH⊥x轴于点H, 交BC于点 M,
则OF: FD=3: 2,
∵DH∥CO, 故CO: DM=3: 2, 则 由 B、C的坐标得:直线BC的表达式为: y=-x+3,
设点 则点 M (x, - x+3) ,
解得: x=1或2, 故点D (1, 4) 或(2, 3).
9解: (1) ∵OB=OC, ∴点B (3, 0),则抛物线的表达式为: y=a(x+1) (x-3) =a(x - 故-3a=3, 解得: a=-1,故抛物线的表达式为: 函数的对称轴为:x=1;
(2) 四边形ACDE的周长=AC+DE+CD+AE, 其中AC 是定值,故CD+AE 最小时,周长最小.取点C关于直线x=1对称点C' (2,3),则CD=C' D, 取点A' (-1, 1) , 则A' D=AE,
故: 则当A′、D、C′三点共线时, 最小,周长也最小,
四边形 ACDE 的周长的最小值=AC+DE+CD+AE=
(3) 设直线 CP交x轴于点 E,
直线 CP把四边形CBPA的面积分为3:5两部分,又∵ -yp) =BE: AE, 则BE: AE=3: 5或5: 3, 则AE= 或
即:点E的坐标为( , 0) 或( ,0),将点 E 的坐标代入直线CP的表达式:y=kx+3,解得: k=-6或-2,
故直线CP 的表达式为: y=-2x+3或y=-6x+3…②联立①②并解得:x=4或8(不合题意值已舍去),故点 P的坐标为(4, - 5) 或 (8, - 45) .
10解: (1)设二次函数的解析式为 将点B代入得0=a(5-1) +3,得
∴二次函数的表达式为:
(2) 依题意, 点B (5, 0) , 点D (1, 3) , 设直线BD 的解析式为y= kx+b, 代入得 解得: ∴线段BD 所在的直线为
设点 E的坐标为: 则F (x, 0)
整理得 解得 (舍去).
故点 E的纵坐标为
∴点E 的坐标为(
(3)存在满足条件的点G,分两种情况讨论:
①.当点 G在x轴的上方时,如图1,设直线DG交x轴于P, 设P (t, 0) , 作AE⊥DG于E, BF⊥DG于F.
由题意: AE: BF=3: 5,
∵BF∥AE, ∴AP: BP=AE: BF=3: 5,
∴ (-3-t) : (5-t) =3: 5, 解得t=-15,
∴ P (-15, 0) , 由点 P (-15, 0) , 点D (1, 3) 可
得:直线DG 的解析式为
联立方程组得:
解得或
②当点G在x轴下方时,如图2,令y=0,
解得: x =-3, x =5,
∴A(-3, 0)、B(5, 0), ∴AO: OB=3: 5
当点 G 在 DO的延长线上与抛物线的交点时,存在点G使得 此时,DG的直线经过原点,设直线 DG的解析式为y= kx, 将点 D (1, 3) 代入得:k=3, 故y=3x, 则有
整理得, (x-1) (x+15) =0,
得x =1(舍去),x =-15, 当x=-15时, y=-45,故点G为(-15, - 45).
综上所述,点G的坐标为(0, 或(-15, - 45).
11.解: (1)设抛物线的解析式为 0), 在等腰Rt△ABC中, OC 垂直平分AB, 且AB=4,∴OA=OB=OC=2,
∴A (-2, 0) , B (2, 0), C(0, - 2) ,
代入得: 解得,
∴抛物线的解析式为
(2) ①设直线l的解析式为y= kx, M(x , y ) , N(x , y ) , 由可得
∴x +x =2k, x ·x =-4,
∴当k=0时 取最小值为4.此时直线1与x轴重合,∴△CMN面积的最小值为4.
②假设抛物线上存在点 使得点 P与点 Q关于直线l对称,
∴OQ=OP, 即 解得, ∵m =1, m =-1不合题意,舍去,
当 时,点 线段PQ的中点为 代入 y= kx得:
∴直线l的表达式为: 当 时,点 线段PQ的中点为 代入y= kx得: ∴直线l的解析式为
综上,点 直线l解析式为 点 直线l解析式为
12解: (1)将点A(-1,0),B(3,0)代入 -3 中, 得: 解得:
∴该抛物线表达式为
(2) 如图1, 过点 P作 PE⊥x轴, 交 BC于点 E, 连接PB, PC,
设点. 则点
联立方程组:
解得: 或
∵点B 坐标为(3,0), ∴点 C 的坐标为
∴B、C之间的水平宽度为
(其中
∴当 时,S△PBC的最大值为
(3)分两种情况讨论:
①.如图2,线段OM 绕点 O逆时针旋转90°,得到线段ON, 设.M(t, t -2t-3), N (n, n-2),作MG⊥y轴于点 G, NH⊥x轴于H,
∴∠OGM=∠OHN=90° ,
∴OM=ON, ∠MON=90° ,
∵∠GOH=90° , ∴∠MOG=∠NOH,
在△OGM与△OHN中,
∴△OGM≌△OHN(AAS) , ∴GM=NH, OG=OH,
解得: 或
②.如图3,线段OM绕点O顺时针旋转90°,得到线段ON, 设.M(t,t -2t-3), N(n, n-2),作MG⊥x轴于点 G, NH⊥x轴于 H,
∴∠OGM=∠OHN=90° ,
∵线段OM 绕点 O 旋转90°, 得到线段ON,
∴OM=ON, ∠MON=90° ,
∵∠GOH=90°, ∴∠MOG=∠NOH,在△OGM与△OHN中,
∴△OGM≌△OHN (AAS) , ∴GM=NH, OG=OH, 解得:
综上所述,点M的坐标为M (0, - 3), M (
同课章节目录
