2025年中考数学复习--图形变换 多解选填压轴题(含解析)
文档属性
| 名称 | 2025年中考数学复习--图形变换 多解选填压轴题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 200.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 16:43:02 | ||
图片预览



文档简介
图形变换 多解选填压轴题
1在 中, ,有一个锐角为( 若点P在直线AB上(不与点A, B重合) ,且. 则 CP的长为 .
2在矩形纸片ABCD中, ,E是边BC上的点,将纸片沿AE 折叠,使点B 落在点F 处,连接FC, 当 为直角三角形时,BE 的长为 .
3菱形翻折 对应点落在对角线上多解题(初三)如图,在菱形ABCD中, 点M为AB边上一点, 点N为AD边上的一动点,沿MN将 翻折,点A 落在点P处,当点P 在菱形的对角线上时,AN的长度为 .
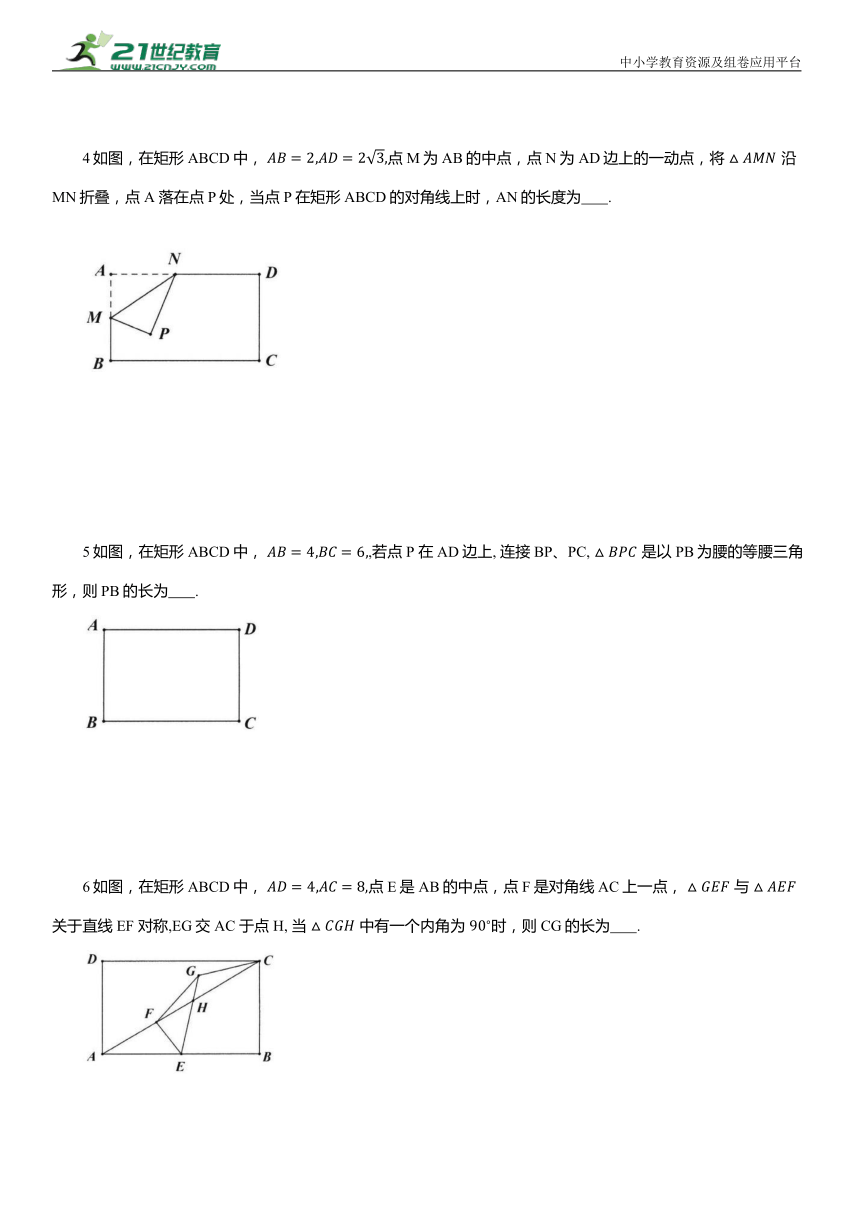
4如图,在矩形ABCD中, 点M为AB的中点,点N为AD边上的一动点,将 沿MN折叠,点A 落在点P处,当点P在矩形ABCD的对角线上时,AN的长度为 .
5如图,在矩形ABCD中, ,若点P 在AD边上, 连接BP、PC, 是以PB为腰的等腰三角形,则PB的长为 .
6如图,在矩形ABCD中, 点E是AB的中点,点F是对角线AC上一点, 与 关于直线EF 对称,EG交AC 于点H, 当 中有一个内角为 时,则CG的长为 .
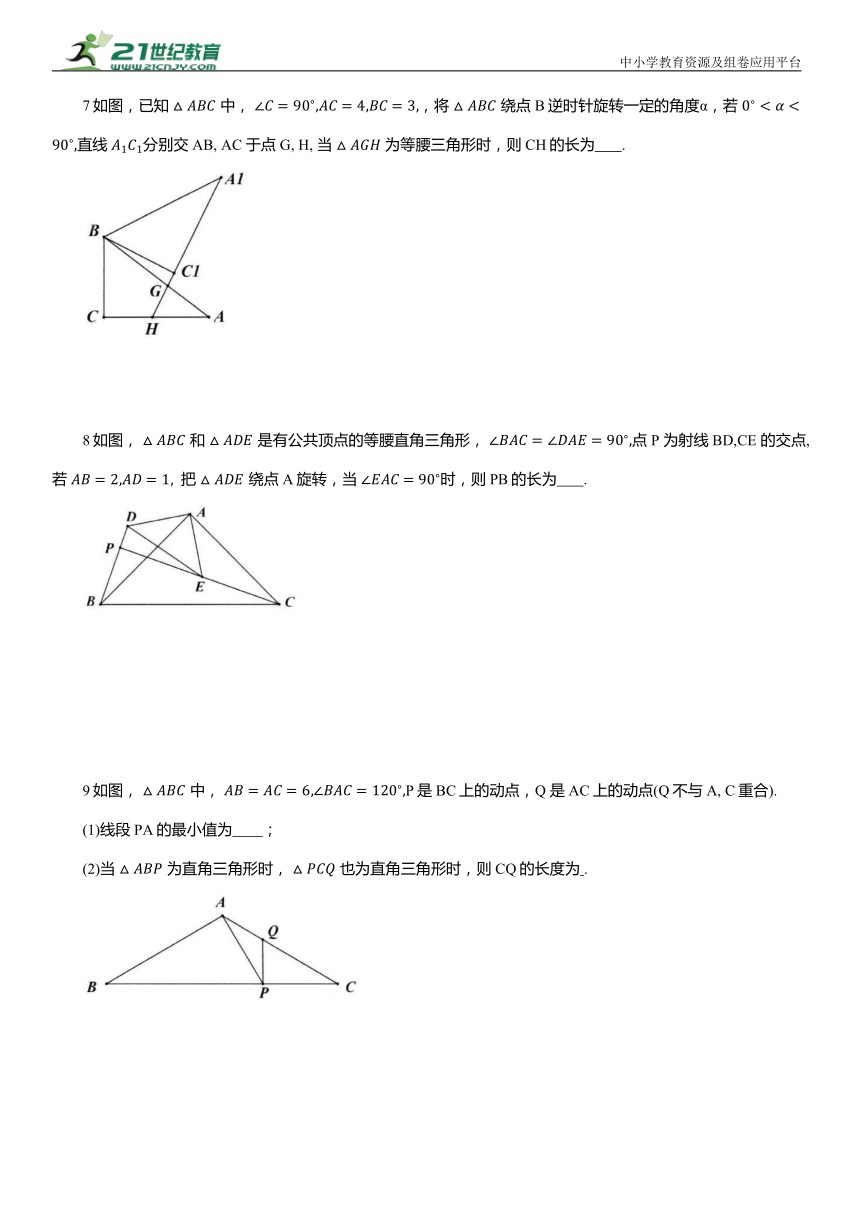
7如图,已知 中, ,将 绕点B逆时针旋转一定的角度α,若 直线 分别交AB, AC 于点G, H, 当 为等腰三角形时,则CH的长为 .
8如图, 和 是有公共顶点的等腰直角三角形, 点 P 为射线BD,CE 的交点,若 把 绕点A旋转,当 时,则PB的长为 .
9如图, 中, P是BC上的动点,Q 是AC上的动点(Q不与A, C重合).
(1)线段PA的最小值为 ;
(2)当 为直角三角形时, 也为直角三角形时,则CQ的长度为 .
1解: (1) 当∠ABC=60°时, 则
①.如图1, 当点 P 在线段AB上时, ∵∠PCB=30°,∴CP⊥AB, ,则
②如图2,当点 P在AB的延长线上,
∵∠PCB=30° , ∠ABC=60° , ∴∠BCP=30°,
(2) 当∠ABC=30°时, 如图3, ∵∠PCB=30°,∠ACB=90° , ∴∠ACP=60° ,
∵∠BAC=60°, ∴△PAC为等边三角形. ∴PC=AC,
∴PC=2. 综上, PC的长为: 2或 或2 故答案为2或 或
493. 解: ∵AD=8, AB=6, 四边形ABCD为矩形,∴BC=AD=8, ∠B=90° ,
△EFC 为直角三角形分两种情况:
①当∠EFC=90°时, 如图1所示.
∵∠AFE=∠B=90° , ∠EFC=90° ,
∴点F在对角线AC上, ∴AE平分∠BAC,
②当∠FEC=90°时, 如图2所示. ∵∠FEC=90°,
∴∠FEB=90° , ∴∠AEF=∠BEA=45° ,
∴四边形ABEF为正方形, ∴BE=AB=6.
综上所述:BE 的长为3或6.故答案为:3或6.
2解:分两种情况:
①.如图1,当点 P在菱形对角线AC上时,:由折叠的性质得: AN=PN, AM=PM,
∵四边形ABCD 是菱形, ∠BAD=60°,
∴∠PAM=∠PAN=30° ,
∴AN=AM=2;
②.如图2,当点 P 在菱形对角线BD上时,设AN=x,由折叠的性质得: PM=AM=2, PN=AN=x, ∠MPN=∠A=60° , ∵AB=3, ∴BM=AB--AM=1,
∵四边形ABCD是菱形,∴
∴∠BPM=∠DNP, ∴△PDN∽△MBP,
即
解得: 或 (不合题意舍去),
综上所述,AN的长为2或
故答案为:2或
3解:分两种情况讨论:
第一种情况:如图1,当点 P 落在BD 上时,
∵点M为AB的中点,
∵将△AMN沿MN折叠, 点 A 落在点 P 处,
∴AM=MP, AN=NP,
∴AM=MP=BM, ∠NAP=∠NPA, ∴∠APB=90°,
∴∠NAP+∠ADP=90° , ∠APN+∠NPD=90°,
∴∠NPD=∠ADP, ∴AN=ND,
第二种情况,如图2,若点P落在AC上时,连接AC交MN于点H,
∵将△AMN沿MN折叠, ∴AC⊥MN,
∵∠ABC+∠BCH+∠CHM+∠BMH=360°,
∴∠BMH+∠BCH=180° ,
又∵∠AMN+∠BCH=180° , ∴∠AMN=∠BCH,
又∵∠BAD=∠ABC=90° , ∴△MAN∽△CBA,
故答案为:
3解: 如图,在矩形ABCD中, AB=CD=4, BC=AD=6. PB为腰的等腰三角形,有两种情况:
第一种情况:如图1,当PB=PC时,点P是BC的中垂线与AD的交点,则
在Rt△ABP中,由勾股定理得 第二种情况: 如图2,当BP=BC=6时,△BPC也是以PB为腰的等腰三角形.
综上所述,PB的长度是5或6.
故答案为:5或6.
4. 解: ∵四边形ABCD 是矩形,
∴AB=CD, ∠B=90°, BC=AD=4, ∵AC=8,
∵点E是AB的中点,
当△CGH中有一个内角为90°时,根据题意,∠GCH不会等于 90°,现在分两种情况讨论:
①当∠CGH=90°时, 如图1, 连接CE,则 AE=GE=BE, 在 Rt△CGE 和 Rt△CBE 中,
∴Rt△CGE≌Rt△CBE(HL), ∴CG=BC=4;
②如图2, 当∠CHG=90°时, 则∠AHE=90°,
∴CH=AC-AH=8-3=5,
由折叠的性质得:
综上所述,当△CGH中有一个内角为90°时,则CG的长为4或 故答案为:4或
5. 解: 如图1中, 当AG=AH时, ∵AG=AH,
∴∠AHG=∠AGH, ∵∠A=∠A , ∠AGH=∠A GB,
∴∠AHG=∠A BG, ∴∠A GB=∠A BG,
∴AH=AG=AB-BG=5-
如图2中, 当GA=GH时, 过点G作GM⊥AH于M.
同法可证, GB=GA , 设(
则有 解得
.=4M/ , ∴AM= ,∵OA=GH, GM⊥AH,
∴AM=HM, ∴AH=3, ∴CH=AC-AH=1.
综上所述,满足条件的 CH 的值为 或1.
6. 解: ∵△ABC和△ADE是等腰直角三角形, ∠BAC=∠DAE=90° , ∴AB=AC, AD=AE,∠DAB=∠CAE, ∴△ADB≌△AEC(SAS),①当点 E在AB上时, BE=AB--AE=1,
∵∠EAC=90° , ∴
∵△ADB≌△AEC, ∴∠DBA=∠ECA,
中小学教育资源及组卷应用平台
∵∠PEB=∠AEC, ∴△PEB∽△AEC,
②当点 E在 BA 延长线上时, BE=3,
∵△ADB≌△AEC, ∴∠DBA=∠ECA,
∵∠BEP=∠CEA, ∴△PEB∽△AEC,
综上所述,PB 的长为 或
故答案为: 或
7. 解: (1)如图1, 由垂线段最短可知, 作AP⊥BC于 P,此时 PA就是最小值
∵△ABC中, AB=AC=6, ∠BAC=120° ,
线段 PA的最小值为 故答案为:3;
(2)当△ABP为直角三角形时,△PCQ也为直角三角形,一共有3种不同的情况:
第一种情况: 如图2, ∠APB=90°, ∠PQC=90°时,
第二种情况: 如图3, ∠BAP=90°, ∠QPC=90°时, 即
解得 (负值舍去),
过点 A 作AD⊥BC于点 D,
∴BC=6 , ∴CP=BC-AP=2
第三种情况, 如图4, ∠BAP=90°, ∠PQC=90°时,同第二种情况,可得
综上所述,CQ的长度为4.5或4或3.
故答案为: 4.5或4或3.
1在 中, ,有一个锐角为( 若点P在直线AB上(不与点A, B重合) ,且. 则 CP的长为 .
2在矩形纸片ABCD中, ,E是边BC上的点,将纸片沿AE 折叠,使点B 落在点F 处,连接FC, 当 为直角三角形时,BE 的长为 .
3菱形翻折 对应点落在对角线上多解题(初三)如图,在菱形ABCD中, 点M为AB边上一点, 点N为AD边上的一动点,沿MN将 翻折,点A 落在点P处,当点P 在菱形的对角线上时,AN的长度为 .
4如图,在矩形ABCD中, 点M为AB的中点,点N为AD边上的一动点,将 沿MN折叠,点A 落在点P处,当点P在矩形ABCD的对角线上时,AN的长度为 .
5如图,在矩形ABCD中, ,若点P 在AD边上, 连接BP、PC, 是以PB为腰的等腰三角形,则PB的长为 .
6如图,在矩形ABCD中, 点E是AB的中点,点F是对角线AC上一点, 与 关于直线EF 对称,EG交AC 于点H, 当 中有一个内角为 时,则CG的长为 .
7如图,已知 中, ,将 绕点B逆时针旋转一定的角度α,若 直线 分别交AB, AC 于点G, H, 当 为等腰三角形时,则CH的长为 .
8如图, 和 是有公共顶点的等腰直角三角形, 点 P 为射线BD,CE 的交点,若 把 绕点A旋转,当 时,则PB的长为 .
9如图, 中, P是BC上的动点,Q 是AC上的动点(Q不与A, C重合).
(1)线段PA的最小值为 ;
(2)当 为直角三角形时, 也为直角三角形时,则CQ的长度为 .
1解: (1) 当∠ABC=60°时, 则
①.如图1, 当点 P 在线段AB上时, ∵∠PCB=30°,∴CP⊥AB, ,则
②如图2,当点 P在AB的延长线上,
∵∠PCB=30° , ∠ABC=60° , ∴∠BCP=30°,
(2) 当∠ABC=30°时, 如图3, ∵∠PCB=30°,∠ACB=90° , ∴∠ACP=60° ,
∵∠BAC=60°, ∴△PAC为等边三角形. ∴PC=AC,
∴PC=2. 综上, PC的长为: 2或 或2 故答案为2或 或
493. 解: ∵AD=8, AB=6, 四边形ABCD为矩形,∴BC=AD=8, ∠B=90° ,
△EFC 为直角三角形分两种情况:
①当∠EFC=90°时, 如图1所示.
∵∠AFE=∠B=90° , ∠EFC=90° ,
∴点F在对角线AC上, ∴AE平分∠BAC,
②当∠FEC=90°时, 如图2所示. ∵∠FEC=90°,
∴∠FEB=90° , ∴∠AEF=∠BEA=45° ,
∴四边形ABEF为正方形, ∴BE=AB=6.
综上所述:BE 的长为3或6.故答案为:3或6.
2解:分两种情况:
①.如图1,当点 P在菱形对角线AC上时,:由折叠的性质得: AN=PN, AM=PM,
∵四边形ABCD 是菱形, ∠BAD=60°,
∴∠PAM=∠PAN=30° ,
∴AN=AM=2;
②.如图2,当点 P 在菱形对角线BD上时,设AN=x,由折叠的性质得: PM=AM=2, PN=AN=x, ∠MPN=∠A=60° , ∵AB=3, ∴BM=AB--AM=1,
∵四边形ABCD是菱形,∴
∴∠BPM=∠DNP, ∴△PDN∽△MBP,
即
解得: 或 (不合题意舍去),
综上所述,AN的长为2或
故答案为:2或
3解:分两种情况讨论:
第一种情况:如图1,当点 P 落在BD 上时,
∵点M为AB的中点,
∵将△AMN沿MN折叠, 点 A 落在点 P 处,
∴AM=MP, AN=NP,
∴AM=MP=BM, ∠NAP=∠NPA, ∴∠APB=90°,
∴∠NAP+∠ADP=90° , ∠APN+∠NPD=90°,
∴∠NPD=∠ADP, ∴AN=ND,
第二种情况,如图2,若点P落在AC上时,连接AC交MN于点H,
∵将△AMN沿MN折叠, ∴AC⊥MN,
∵∠ABC+∠BCH+∠CHM+∠BMH=360°,
∴∠BMH+∠BCH=180° ,
又∵∠AMN+∠BCH=180° , ∴∠AMN=∠BCH,
又∵∠BAD=∠ABC=90° , ∴△MAN∽△CBA,
故答案为:
3解: 如图,在矩形ABCD中, AB=CD=4, BC=AD=6. PB为腰的等腰三角形,有两种情况:
第一种情况:如图1,当PB=PC时,点P是BC的中垂线与AD的交点,则
在Rt△ABP中,由勾股定理得 第二种情况: 如图2,当BP=BC=6时,△BPC也是以PB为腰的等腰三角形.
综上所述,PB的长度是5或6.
故答案为:5或6.
4. 解: ∵四边形ABCD 是矩形,
∴AB=CD, ∠B=90°, BC=AD=4, ∵AC=8,
∵点E是AB的中点,
当△CGH中有一个内角为90°时,根据题意,∠GCH不会等于 90°,现在分两种情况讨论:
①当∠CGH=90°时, 如图1, 连接CE,则 AE=GE=BE, 在 Rt△CGE 和 Rt△CBE 中,
∴Rt△CGE≌Rt△CBE(HL), ∴CG=BC=4;
②如图2, 当∠CHG=90°时, 则∠AHE=90°,
∴CH=AC-AH=8-3=5,
由折叠的性质得:
综上所述,当△CGH中有一个内角为90°时,则CG的长为4或 故答案为:4或
5. 解: 如图1中, 当AG=AH时, ∵AG=AH,
∴∠AHG=∠AGH, ∵∠A=∠A , ∠AGH=∠A GB,
∴∠AHG=∠A BG, ∴∠A GB=∠A BG,
∴AH=AG=AB-BG=5-
如图2中, 当GA=GH时, 过点G作GM⊥AH于M.
同法可证, GB=GA , 设(
则有 解得
.=4M/ , ∴AM= ,∵OA=GH, GM⊥AH,
∴AM=HM, ∴AH=3, ∴CH=AC-AH=1.
综上所述,满足条件的 CH 的值为 或1.
6. 解: ∵△ABC和△ADE是等腰直角三角形, ∠BAC=∠DAE=90° , ∴AB=AC, AD=AE,∠DAB=∠CAE, ∴△ADB≌△AEC(SAS),①当点 E在AB上时, BE=AB--AE=1,
∵∠EAC=90° , ∴
∵△ADB≌△AEC, ∴∠DBA=∠ECA,
中小学教育资源及组卷应用平台
∵∠PEB=∠AEC, ∴△PEB∽△AEC,
②当点 E在 BA 延长线上时, BE=3,
∵△ADB≌△AEC, ∴∠DBA=∠ECA,
∵∠BEP=∠CEA, ∴△PEB∽△AEC,
综上所述,PB 的长为 或
故答案为: 或
7. 解: (1)如图1, 由垂线段最短可知, 作AP⊥BC于 P,此时 PA就是最小值
∵△ABC中, AB=AC=6, ∠BAC=120° ,
线段 PA的最小值为 故答案为:3;
(2)当△ABP为直角三角形时,△PCQ也为直角三角形,一共有3种不同的情况:
第一种情况: 如图2, ∠APB=90°, ∠PQC=90°时,
第二种情况: 如图3, ∠BAP=90°, ∠QPC=90°时, 即
解得 (负值舍去),
过点 A 作AD⊥BC于点 D,
∴BC=6 , ∴CP=BC-AP=2
第三种情况, 如图4, ∠BAP=90°, ∠PQC=90°时,同第二种情况,可得
综上所述,CQ的长度为4.5或4或3.
故答案为: 4.5或4或3.
同课章节目录
