2025年中考数学复习--二次函数的图像与系数的关系(含解析)
文档属性
| 名称 | 2025年中考数学复习--二次函数的图像与系数的关系(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 186.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 16:47:18 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
二次函数的图像与系数的关系
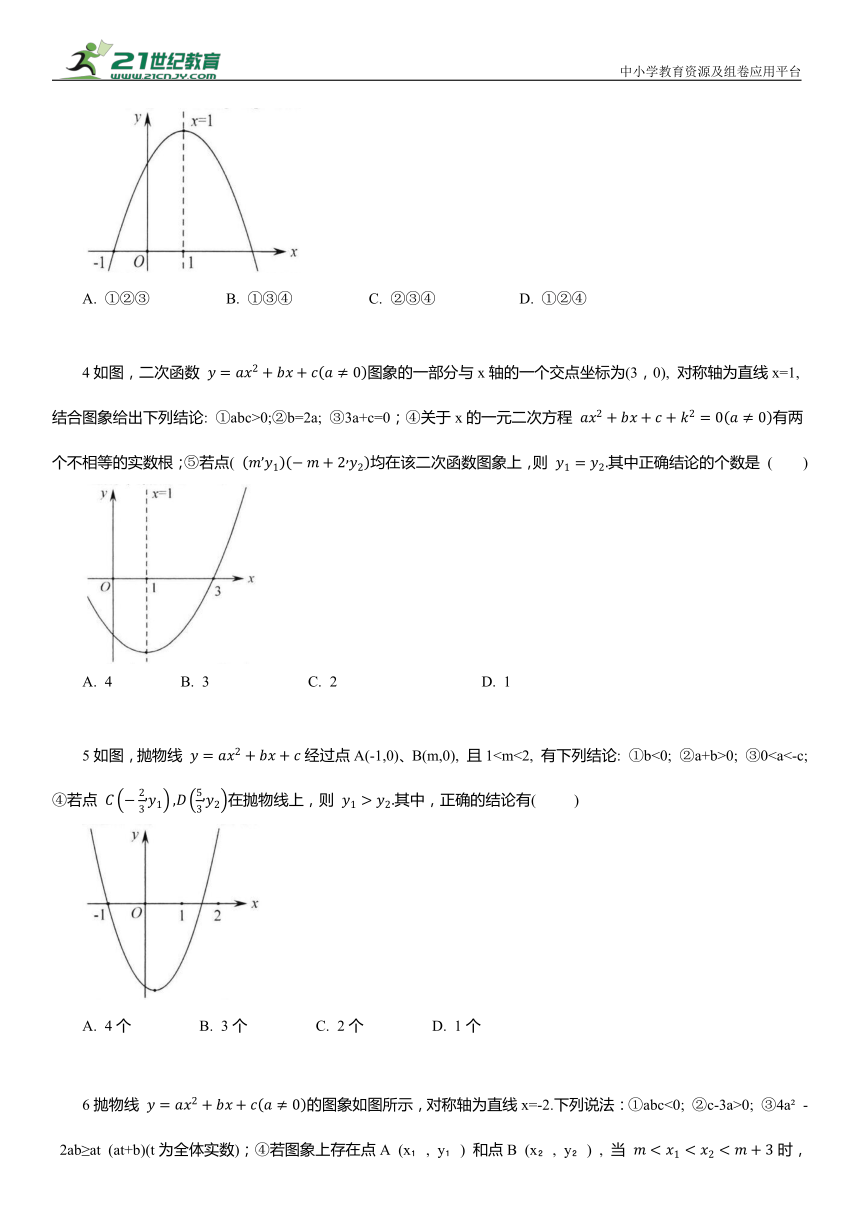
1已知二次函数 的部分图象如图所示,图象经过点(0,2),其对称轴为直线x=-1. 下列结论: ①3a+c>0; ②若点 (-4, y ), (3, y )均在二次函数图象上,则 ③关于x的一元二次方程 有两个相等的实数根;④满足 的x的取值范围为-2A. 1个 B. 2个 C. 3个 D. 4个
2二次函数 的图象如图所示,对称轴是直线x=1,下列结论:①abc<0; ②方程 必有一个根大于2且小于3;③若(0,y ) , ( , y )是抛物线上的两点, 那么 y0;⑤对于任意实数m, 都有m(am+b) ≥a+b, 其中正确结论的个数是 ( )
A. 5 B. 4 C. 3 D. 2
3如图,已知抛物线 的对称轴是直线x=1,且过点(-1,0),顶点在第一象限,其部分图象如图所示.给出以下结论:①ab<0;②4a+2b+c>0; ③3a+c>0; ④若 (其中 是抛物线上的两点,且 则 其中正确的选项是 ( )
A. ①②③ B. ①③④ C. ②③④ D. ①②④
4如图,二次函数 图象的一部分与x轴的一个交点坐标为(3,0), 对称轴为直线x=1, 结合图象给出下列结论: ①abc>0;②b=2a; ③3a+c=0;④关于x的一元二次方程 有两个不相等的实数根;⑤若点( 均在该二次函数图象上,则 其中正确结论的个数是 ( )
A. 4 B. 3 C. 2 D. 1
5如图,抛物线 经过点A(-1,0)、B(m,0), 且10; ③0A. 4个 B. 3个 C. 2个 D. 1个
6抛物线 的图象如图所示,对称轴为直线x=-2.下列说法:①abc<0; ②c-3a>0; ③4a - 2ab≥at (at+b)(t为全体实数);④若图象上存在点A (x , y ) 和点B (x , y ) , 当 时,满足 则m的取值范围为-5A. 1个 B. 2个 C. 3个 D. 4个
1解: ∵对称轴为直线 =2a,
∵当x=1时, y=a+b+c<0, ∴3a+c<0, 故①错误,
∵抛物线开口向下,
∴在对称轴的右侧y随x的增大而减小,
∵(-4, y ) 关于直线x=-1对称的点为(2, y ),又∵2<3, ∴y >y , 故②正确,
方程( 的解,可看做抛物线 与直线y=-1的交点,由图象可知抛物线. 与直线y=-1有两个交点,
∴关于x的一元二次方程 有两个不相等的实数根,故③错误,
不等式 的解集,可看做抛物线y=ax + bx+c的图象在直线y=2上方的部分,
∵ (0,2)关于直线x=-1对称的点为(-2, 2) ,∴x的取值范围为-22解: ①根据图象可知: a>0, c<0,
∵对称轴是直线 即b= -2a.
∴b<0, ∴abc>0. 故①错误.
②方程 即为二次函数 与x轴的交点,根据图象已知一个交点-1③∵对称轴是直线x=1,∴点( ,y )离对称轴更近,∴y >y , 故③错误.
根据图象,令x=-1,y=a+2a+c=3a+c>0,∴6a+2c>0,∵a>0, ∴11a+2c>0, 故④正确.
即证:
∴m为任意实数, 恒成立.故⑤正确.
综上②④⑤正确, 故选: C.
3解: ∵二次函数开口向下, 则a<0,
∵二次函数对称轴为x=1,则
∴b=-2a, b>0, ∴ab<0, 故①正确;
∵过点(-1,0), ∴由对称可得二次函数与x轴的另一交点为 (3, 0) , 由函数图象可得x=2时y>0,
∴4a+2b+c>0, 故②正确;
∵x=-1时y=0, ∴a-b+c=0,
b=-2a代入得: 3a+c=0, 故③错误;
∵对称轴是直线x=1,
∴若 即 时, y =y ,
当 时,点A (x ,y )到对称轴的距离小于点 B(x , y )到对称轴的距离,
∵二次函数图象开口向下,∴y >y , i故④正确.
综上所述,正确的选项是①②④.故选 D.
4 解: ∵抛物线开口向上, ∴a>0,
∵对称轴在y轴右侧, ∴b<0,
∵抛物线与y轴交于负半轴, ∴c<0,
∴abc>0, 故①正确,
故②错误,
∵抛物线与x轴的一个交点为(3,0),对称轴为x=1,
∴抛物线与x轴的另一个交点为(-1,0),
∴a-b+c=0,
∵b=-2a, ∴3a+c=0, 故③正确,
方程 的解可看做 ≠0) 与y=-k 的交点,
∵-k ≤0,
∴当 过抛物线 顶点时,两函数只有一个交点,即方程 有两个相等的实数根,故④错误,∵点(m, y ) (-m+2, y ) 关于直线x=1对称,
∴y =y , 故⑤正确. 故选: B.
6解: ∵抛物线开口向上, ∴a>0,
∵抛物线的对称轴在y轴的右侧,∴b<0,故①正确;
∵抛物线与y轴的交点在x轴下方, ∴c<0,
∵抛物线经过点A(-1, 0),
∴a-b+c=0, ∴c=b-a,
∵当x=2时, y>0, ∴4a+2b+c>0,
∴4a+2b+b-a>0, ∴3a+3b>0,∴a+b>0,故②正确;
∵a-b+c=0, ∴a+c=b, ∵b<0, ∴a+c<0,
∴0∵点 到对称轴的距离比点 到对称轴的距离近,∴y 故选: B.
7. 解: ①.因图象开口向下, 可知: a<0;
又∵对称轴为直线x=-2,
整理得: b=4a, 即a、b同号.
由图象可知, 当x=4时, y<0,
又∵对称轴为直线x=-2,可知: 当x=0时, y<0;即c<0; ∴abc<0, 故①正确.
②.由①得: b=4a. 代入原解析式得: 由图象可知, 当x=-1时, y>0.
即: 整理得: c-3a>0, 故②正确.
③.由①得: b=4a. 不等式 等价于 整理得: 0, ∵t为全体实数, 故③错误.
④.由题意得,x 、x 是一元二次方程 的两个根,从图象上看,因二次函数有对称性,x 、x 关于x=-2对称,
∴当且仅当m<-2故本题选:C.
二次函数的图像与系数的关系
1已知二次函数 的部分图象如图所示,图象经过点(0,2),其对称轴为直线x=-1. 下列结论: ①3a+c>0; ②若点 (-4, y ), (3, y )均在二次函数图象上,则 ③关于x的一元二次方程 有两个相等的实数根;④满足 的x的取值范围为-2
2二次函数 的图象如图所示,对称轴是直线x=1,下列结论:①abc<0; ②方程 必有一个根大于2且小于3;③若(0,y ) , ( , y )是抛物线上的两点, 那么 y
A. 5 B. 4 C. 3 D. 2
3如图,已知抛物线 的对称轴是直线x=1,且过点(-1,0),顶点在第一象限,其部分图象如图所示.给出以下结论:①ab<0;②4a+2b+c>0; ③3a+c>0; ④若 (其中 是抛物线上的两点,且 则 其中正确的选项是 ( )
A. ①②③ B. ①③④ C. ②③④ D. ①②④
4如图,二次函数 图象的一部分与x轴的一个交点坐标为(3,0), 对称轴为直线x=1, 结合图象给出下列结论: ①abc>0;②b=2a; ③3a+c=0;④关于x的一元二次方程 有两个不相等的实数根;⑤若点( 均在该二次函数图象上,则 其中正确结论的个数是 ( )
A. 4 B. 3 C. 2 D. 1
5如图,抛物线 经过点A(-1,0)、B(m,0), 且1
6抛物线 的图象如图所示,对称轴为直线x=-2.下列说法:①abc<0; ②c-3a>0; ③4a - 2ab≥at (at+b)(t为全体实数);④若图象上存在点A (x , y ) 和点B (x , y ) , 当 时,满足 则m的取值范围为-5
1解: ∵对称轴为直线 =2a,
∵当x=1时, y=a+b+c<0, ∴3a+c<0, 故①错误,
∵抛物线开口向下,
∴在对称轴的右侧y随x的增大而减小,
∵(-4, y ) 关于直线x=-1对称的点为(2, y ),又∵2<3, ∴y >y , 故②正确,
方程( 的解,可看做抛物线 与直线y=-1的交点,由图象可知抛物线. 与直线y=-1有两个交点,
∴关于x的一元二次方程 有两个不相等的实数根,故③错误,
不等式 的解集,可看做抛物线y=ax + bx+c的图象在直线y=2上方的部分,
∵ (0,2)关于直线x=-1对称的点为(-2, 2) ,∴x的取值范围为-2
∵对称轴是直线 即b= -2a.
∴b<0, ∴abc>0. 故①错误.
②方程 即为二次函数 与x轴的交点,根据图象已知一个交点-1
根据图象,令x=-1,y=a+2a+c=3a+c>0,∴6a+2c>0,∵a>0, ∴11a+2c>0, 故④正确.
即证:
∴m为任意实数, 恒成立.故⑤正确.
综上②④⑤正确, 故选: C.
3解: ∵二次函数开口向下, 则a<0,
∵二次函数对称轴为x=1,则
∴b=-2a, b>0, ∴ab<0, 故①正确;
∵过点(-1,0), ∴由对称可得二次函数与x轴的另一交点为 (3, 0) , 由函数图象可得x=2时y>0,
∴4a+2b+c>0, 故②正确;
∵x=-1时y=0, ∴a-b+c=0,
b=-2a代入得: 3a+c=0, 故③错误;
∵对称轴是直线x=1,
∴若 即 时, y =y ,
当 时,点A (x ,y )到对称轴的距离小于点 B(x , y )到对称轴的距离,
∵二次函数图象开口向下,∴y >y , i故④正确.
综上所述,正确的选项是①②④.故选 D.
4 解: ∵抛物线开口向上, ∴a>0,
∵对称轴在y轴右侧, ∴b<0,
∵抛物线与y轴交于负半轴, ∴c<0,
∴abc>0, 故①正确,
故②错误,
∵抛物线与x轴的一个交点为(3,0),对称轴为x=1,
∴抛物线与x轴的另一个交点为(-1,0),
∴a-b+c=0,
∵b=-2a, ∴3a+c=0, 故③正确,
方程 的解可看做 ≠0) 与y=-k 的交点,
∵-k ≤0,
∴当 过抛物线 顶点时,两函数只有一个交点,即方程 有两个相等的实数根,故④错误,∵点(m, y ) (-m+2, y ) 关于直线x=1对称,
∴y =y , 故⑤正确. 故选: B.
6解: ∵抛物线开口向上, ∴a>0,
∵抛物线的对称轴在y轴的右侧,∴b<0,故①正确;
∵抛物线与y轴的交点在x轴下方, ∴c<0,
∵抛物线经过点A(-1, 0),
∴a-b+c=0, ∴c=b-a,
∵当x=2时, y>0, ∴4a+2b+c>0,
∴4a+2b+b-a>0, ∴3a+3b>0,∴a+b>0,故②正确;
∵a-b+c=0, ∴a+c=b, ∵b<0, ∴a+c<0,
∴0
7. 解: ①.因图象开口向下, 可知: a<0;
又∵对称轴为直线x=-2,
整理得: b=4a, 即a、b同号.
由图象可知, 当x=4时, y<0,
又∵对称轴为直线x=-2,可知: 当x=0时, y<0;即c<0; ∴abc<0, 故①正确.
②.由①得: b=4a. 代入原解析式得: 由图象可知, 当x=-1时, y>0.
即: 整理得: c-3a>0, 故②正确.
③.由①得: b=4a. 不等式 等价于 整理得: 0, ∵t为全体实数, 故③错误.
④.由题意得,x 、x 是一元二次方程 的两个根,从图象上看,因二次函数有对称性,x 、x 关于x=-2对称,
∴当且仅当m<-2
同课章节目录
