2025年中考数学复习--二次函数直角三角形存在性问题(含解析)
文档属性
| 名称 | 2025年中考数学复习--二次函数直角三角形存在性问题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 202.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 16:50:03 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
二次函数直角三角形存在性问题
1如图,已知抛物线 经过A (-1, 0) 、B(3, 0) 两点, 且与y轴相交于点C,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点C的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且. 为直角三角形,请直接写出所有符合条件的点M的坐标.
2如图1,抛物线 与x轴交于点A (-2, 0) , B(6, 0) , 与y轴交于点C,顶点为D,直线AD交 y轴于点E.
(1)求抛物线的解析式.
(2) 如图2, 将 沿直线AD平移得到
①当点M落在抛物线上时,求点 M的坐标.
②在 移动过程中,存在点M使 为直角三角形,请直接写出所有符合条件的点M的坐标.
3如图,二次函数 的图象交x轴于点A (-1, 0), B (4, 0) 两点,交y轴于点C.动点M从点A出发,以每秒2个单位长度的速度沿AB方向运动,过点M作MN⊥x轴交直线BC于点N,交抛物线于点D,连接AC,设运动的时间为t秒.
(1)求二次函数 的表达式;
(2) 连接BD,当 时, 求△DNB的面积;
(3)在直线MN上存在一点P,当△PBC是以∠BPC为直角的等腰直角三角形时,求此时点D的坐标;
(4)当 时,在直线MN上存在一点Q,使得. 求点Q的坐标.
4如图,已知抛物线 的对称轴为直线x=-1,且抛物线与x轴交于A、B两点, 与y轴交于C点, 其中A(1,0),C(0,3).
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=-1上的一个动点,求使 为直角三角形的点P的坐标.
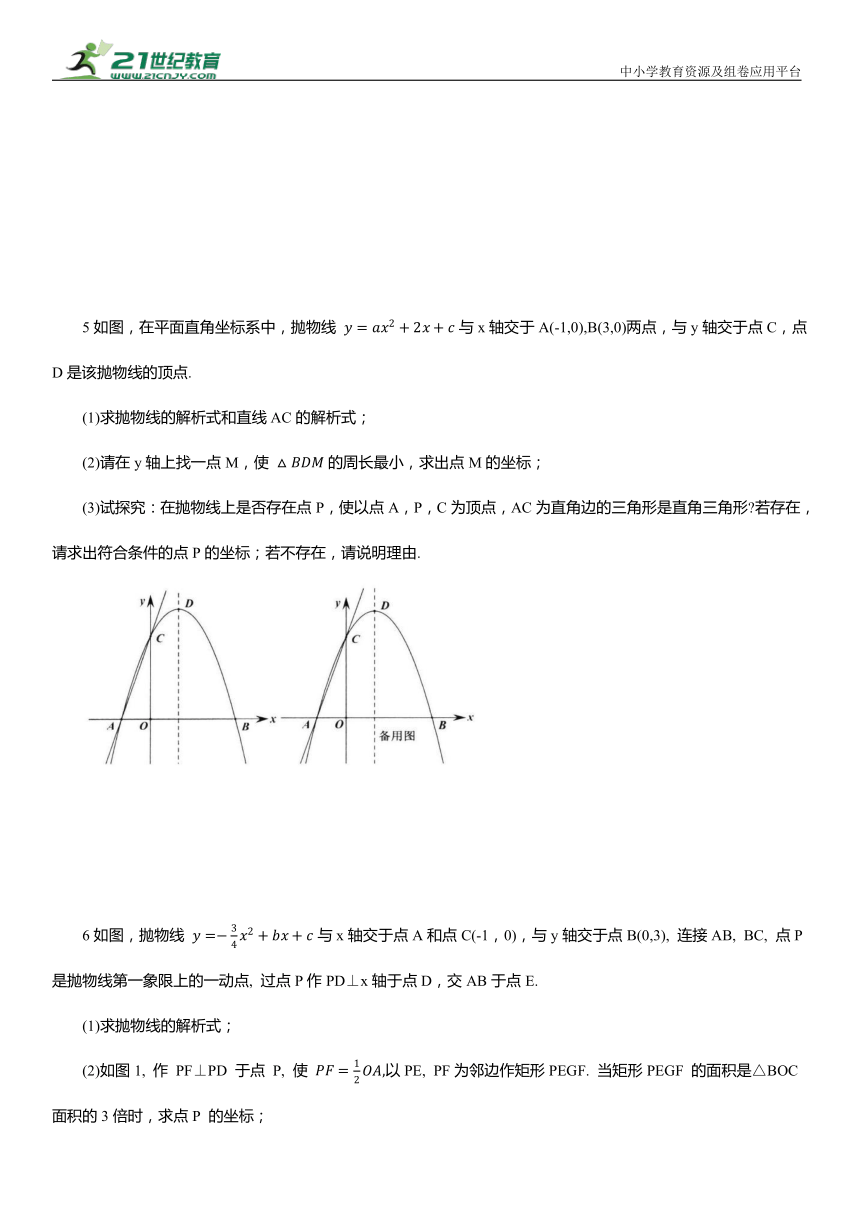
5如图,在平面直角坐标系中,抛物线 与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使 的周长最小,求出点M的坐标;
(3)试探究:在抛物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形 若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
6如图,抛物线 与x轴交于点A和点C(-1,0),与y轴交于点B(0,3), 连接AB, BC, 点P是抛物线第一象限上的一动点, 过点P作PD⊥x轴于点D,交AB于点E.
(1)求抛物线的解析式;
(2)如图1, 作 PF⊥PD 于点 P, 使 以PE, PF为邻边作矩形PEGF. 当矩形PEGF 的面积是△BOC 面积的3倍时,求点P 的坐标;
(3)如图2,当点P运动到抛物线的顶点时,点Q在直线PD上,若以点Q、A、B为顶点的三角形是锐角三角形,请直接写出点Q纵坐标n的取值范围.
1解: ∵抛物线 经过A(-1, 0) 、B(3,0) 两点,
∴抛物线的解析式为
(2) 如图, ∵点A, B关于直线l对称,
∴连接BC交直线l于点 P,此时即为要求的P点.
由 (1)知,抛物线的解析式为
∴直线l: x=1, C (0, - 3) , ∵B(3, 0) ,
∴直线 BC的解析式为y=x-3,
当x=1时, y=-2, ∴P (1, - 2) ,
(3) 设点M (1, m), ∵A(-1, 0), C(0, - 3), ∵△MAC为直角三角形,分三种情况讨论:
①当∠ACM=90°时,
②当∠CAM=90°时,
③当∠AMC=90°时,
或m=-2,
∴M(1, - 1) 或(1, - 2) ,
综上所述,满足条件的点 M 的坐标为:
或( (1, 或(1, - 1)或(1, - 2) .
2解: (1) 抛物线的表达式为: y=a(x+2) (x-6) 即: - 12a=6,解得: 故抛物线的表达式为:
(2) 令y=0, 解得: x=4或-2, 故点A(-2,0) ,函数的对称轴为: 直线x=2, 故点 D (2, 8);
由点 A、D的坐标得, 直线AD的表达式为: y=2x+4,
设点N(n,2n+4),∵MN=OA=2,则点 M(n+2,2n+4),
①将点 M 的坐标代入抛物线表达式得: 解得:
故点 M 的坐标为 或
②点M(n+2, 2n+4), 点 B、D的坐标分别为(6,0)、(2, 8) ,
则.
当∠BMD为直角时,则
由勾股定理得: (2n-4) ,解得:
当∠MBD为直角时,则
同理可得: n=-4,
当∠MDB为直角时,则
同理可得:
故点 M 的坐标为: (-2, - 4)或 或 或
3.解:(1)将点(-1,0),B(4,0)代入.
(2) C (0, 2) , ∴BC的直线解析式为 当 时, AM=3, ∵AB=5, ∴MB=2, ∴OM=2∴M(2, 0) , N(2, 1) , D (2, 3), ∴DN=2∴S△DNBE的面积
(3).由题意可知, MN只能在CB之间, 即0.5如图1,当点 P在 BC的下方时,过点 P作PE⊥y轴于E,过点 B 作BF⊥PE 于点 F,由题意可知PE=OM=2t-1利用一线三等角, 可证△CPE≌△PBF.
∴PE=BF=2t-1=OE, CE=PF
则CE=CO+OE=2+2t-1=2t+1, ∴PF=CE=2t+1,
∴EF=PE+PF=2t-1+2t+1=4t
∵EF=OB=4, ∴4t=4, ∴t=1, ∴M(1, 0), ∴D (1, 3)同理,当P在 BC 的上方时,可得2t-1+2t-3=4,解得t=2
∴ M (3, 0) , ∴D (3, 2) ;
(4) 当 时, ∴点Q在抛物线对称轴 上,
∴连接MC,勾股定理得:
以M为圆心AB为直径构造圆M,如图2,圆与对称轴的交点,分别为Q 与Q ,即为所求的Q点
∵QM⊥x轴,且
即Q 点坐标分别为
4 解: (1)依题意得: 解之得:
∴抛物线解析式为
∵对称轴为直线x=-1, 且抛物线经过A (1, 0),
∴把B(-3, 0) 、C(0,3) 分别代入直线y= mx+n,得: 解之得:
∴直线y=mx+n的解析式为y=x+3;
(2)由对称性质可知,直线BC与对称轴x=-1的交点即为所求的 M 点,则此时MA+MC的值最小.
把x=-1代入直线y=x+3得, y=2, ∴M(-1, 2),即当点M到点A的距离与到点C的距离之和最小时M的坐标为( - 1, 2) ;
(3) 设P (-1, t), 又∵B(-3, 0) , C(0, 3),
①若点B为直角顶点,则
即: 解之得: t=-2;
②若点C为直角顶点,则
即: 解之得: t=4,
③若点 P 为直角顶点,则 即: 解之得: 综上所述,P的坐标为((--1, - 2)或(-1,4)或(- 或
5. 解: (1)设抛物线解析式为y=a(x+1) (x-3),即y=ax -2ax-3a, ∴-2a=2, 解得a=-1,
∴抛物线解析式为
当x=0时, 则C(0,3),设直线 AC 的解析式为y= px+q,
把A(-1,0),C(0,3)代入得 解得 ∴直线AC的解析式为y=3x+3;
, ∴顶点 D 的坐标为(1,4),如图1,作B点关于y轴的对称点B',连接DB' 交y轴于M, 则B' (-3, 0) ,
∵MB=MB' , ∴MB+MD=MB' +MD=DB' ,此时MB+MD 的值最小,而 BD的值不变,
∴此时△BDM的周长最小,
易得直线DB'的解析式为y=x+3,当x=0时, y=x+3=3, ∴点M的坐标为(0, 3);
(3)存在.如图2中的P1和P1 两种情况:
过点 C作AC的垂线交抛物线于另一点 P ,∵直线AC的解析式为y=3x+3,
∴直线 P C的解析式可设为 把C(0, 3)代入得b=3,∴直线P C的解析式为 解方程组 解得 马 则此时 P 点坐标为
过点A 作AC 的垂线交抛物线于另一点 P ,直线AP 的解析式可设为
把A (-1, 0) 代入得 解得 ∴直线AP 的解析式为 解方程组: 解得 可 则此时 P 点坐标为
综上所述,符合条件的点 P 的坐标为 或
6 解: (1) 由题意得: 解得 故抛物线的表达式为
(2)对于 令 解得x=4或-1, 故点A的坐标为(4, 0) , 则PF=2,由点A、B的坐标得,直线AB 的表达式为 设点P 的坐标为
点
解得x=1或3, ∴点P的坐标为(1, 或(3, 3);
(4)由抛物线的表达式知,其对称轴为 故设点Q的坐标为( ,n),又∵A (4, 0) , B(0, 3)
如图,先当以点 Q、A、B为顶点的三角形为直角三角形时,分三种情况讨论:
①.当∠ABQ为直角时, 则有: 解得: n=5,此时为
②.当∠BQA为直角时, 则有:
解得:
此时为
③当∠BAQ为直角时,则有:
解得:
此时为
综上,以点Q、A、B为顶点的三角形是锐角三角形,则△ABQ 不为直角三角形,也不为钝角三角形,即Q在Q 至Q 之间,或者在Q 至Q 之间的范围内,符合题意。
故点 Q 纵坐标n的取值范围为: 或
二次函数直角三角形存在性问题
1如图,已知抛物线 经过A (-1, 0) 、B(3, 0) 两点, 且与y轴相交于点C,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点C的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且. 为直角三角形,请直接写出所有符合条件的点M的坐标.
2如图1,抛物线 与x轴交于点A (-2, 0) , B(6, 0) , 与y轴交于点C,顶点为D,直线AD交 y轴于点E.
(1)求抛物线的解析式.
(2) 如图2, 将 沿直线AD平移得到
①当点M落在抛物线上时,求点 M的坐标.
②在 移动过程中,存在点M使 为直角三角形,请直接写出所有符合条件的点M的坐标.
3如图,二次函数 的图象交x轴于点A (-1, 0), B (4, 0) 两点,交y轴于点C.动点M从点A出发,以每秒2个单位长度的速度沿AB方向运动,过点M作MN⊥x轴交直线BC于点N,交抛物线于点D,连接AC,设运动的时间为t秒.
(1)求二次函数 的表达式;
(2) 连接BD,当 时, 求△DNB的面积;
(3)在直线MN上存在一点P,当△PBC是以∠BPC为直角的等腰直角三角形时,求此时点D的坐标;
(4)当 时,在直线MN上存在一点Q,使得. 求点Q的坐标.
4如图,已知抛物线 的对称轴为直线x=-1,且抛物线与x轴交于A、B两点, 与y轴交于C点, 其中A(1,0),C(0,3).
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=-1上的一个动点,求使 为直角三角形的点P的坐标.
5如图,在平面直角坐标系中,抛物线 与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使 的周长最小,求出点M的坐标;
(3)试探究:在抛物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形 若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
6如图,抛物线 与x轴交于点A和点C(-1,0),与y轴交于点B(0,3), 连接AB, BC, 点P是抛物线第一象限上的一动点, 过点P作PD⊥x轴于点D,交AB于点E.
(1)求抛物线的解析式;
(2)如图1, 作 PF⊥PD 于点 P, 使 以PE, PF为邻边作矩形PEGF. 当矩形PEGF 的面积是△BOC 面积的3倍时,求点P 的坐标;
(3)如图2,当点P运动到抛物线的顶点时,点Q在直线PD上,若以点Q、A、B为顶点的三角形是锐角三角形,请直接写出点Q纵坐标n的取值范围.
1解: ∵抛物线 经过A(-1, 0) 、B(3,0) 两点,
∴抛物线的解析式为
(2) 如图, ∵点A, B关于直线l对称,
∴连接BC交直线l于点 P,此时即为要求的P点.
由 (1)知,抛物线的解析式为
∴直线l: x=1, C (0, - 3) , ∵B(3, 0) ,
∴直线 BC的解析式为y=x-3,
当x=1时, y=-2, ∴P (1, - 2) ,
(3) 设点M (1, m), ∵A(-1, 0), C(0, - 3), ∵△MAC为直角三角形,分三种情况讨论:
①当∠ACM=90°时,
②当∠CAM=90°时,
③当∠AMC=90°时,
或m=-2,
∴M(1, - 1) 或(1, - 2) ,
综上所述,满足条件的点 M 的坐标为:
或( (1, 或(1, - 1)或(1, - 2) .
2解: (1) 抛物线的表达式为: y=a(x+2) (x-6) 即: - 12a=6,解得: 故抛物线的表达式为:
(2) 令y=0, 解得: x=4或-2, 故点A(-2,0) ,函数的对称轴为: 直线x=2, 故点 D (2, 8);
由点 A、D的坐标得, 直线AD的表达式为: y=2x+4,
设点N(n,2n+4),∵MN=OA=2,则点 M(n+2,2n+4),
①将点 M 的坐标代入抛物线表达式得: 解得:
故点 M 的坐标为 或
②点M(n+2, 2n+4), 点 B、D的坐标分别为(6,0)、(2, 8) ,
则.
当∠BMD为直角时,则
由勾股定理得: (2n-4) ,解得:
当∠MBD为直角时,则
同理可得: n=-4,
当∠MDB为直角时,则
同理可得:
故点 M 的坐标为: (-2, - 4)或 或 或
3.解:(1)将点(-1,0),B(4,0)代入.
(2) C (0, 2) , ∴BC的直线解析式为 当 时, AM=3, ∵AB=5, ∴MB=2, ∴OM=2∴M(2, 0) , N(2, 1) , D (2, 3), ∴DN=2∴S△DNBE的面积
(3).由题意可知, MN只能在CB之间, 即0.5
∴PE=BF=2t-1=OE, CE=PF
则CE=CO+OE=2+2t-1=2t+1, ∴PF=CE=2t+1,
∴EF=PE+PF=2t-1+2t+1=4t
∵EF=OB=4, ∴4t=4, ∴t=1, ∴M(1, 0), ∴D (1, 3)同理,当P在 BC 的上方时,可得2t-1+2t-3=4,解得t=2
∴ M (3, 0) , ∴D (3, 2) ;
(4) 当 时, ∴点Q在抛物线对称轴 上,
∴连接MC,勾股定理得:
以M为圆心AB为直径构造圆M,如图2,圆与对称轴的交点,分别为Q 与Q ,即为所求的Q点
∵QM⊥x轴,且
即Q 点坐标分别为
4 解: (1)依题意得: 解之得:
∴抛物线解析式为
∵对称轴为直线x=-1, 且抛物线经过A (1, 0),
∴把B(-3, 0) 、C(0,3) 分别代入直线y= mx+n,得: 解之得:
∴直线y=mx+n的解析式为y=x+3;
(2)由对称性质可知,直线BC与对称轴x=-1的交点即为所求的 M 点,则此时MA+MC的值最小.
把x=-1代入直线y=x+3得, y=2, ∴M(-1, 2),即当点M到点A的距离与到点C的距离之和最小时M的坐标为( - 1, 2) ;
(3) 设P (-1, t), 又∵B(-3, 0) , C(0, 3),
①若点B为直角顶点,则
即: 解之得: t=-2;
②若点C为直角顶点,则
即: 解之得: t=4,
③若点 P 为直角顶点,则 即: 解之得: 综上所述,P的坐标为((--1, - 2)或(-1,4)或(- 或
5. 解: (1)设抛物线解析式为y=a(x+1) (x-3),即y=ax -2ax-3a, ∴-2a=2, 解得a=-1,
∴抛物线解析式为
当x=0时, 则C(0,3),设直线 AC 的解析式为y= px+q,
把A(-1,0),C(0,3)代入得 解得 ∴直线AC的解析式为y=3x+3;
, ∴顶点 D 的坐标为(1,4),如图1,作B点关于y轴的对称点B',连接DB' 交y轴于M, 则B' (-3, 0) ,
∵MB=MB' , ∴MB+MD=MB' +MD=DB' ,此时MB+MD 的值最小,而 BD的值不变,
∴此时△BDM的周长最小,
易得直线DB'的解析式为y=x+3,当x=0时, y=x+3=3, ∴点M的坐标为(0, 3);
(3)存在.如图2中的P1和P1 两种情况:
过点 C作AC的垂线交抛物线于另一点 P ,∵直线AC的解析式为y=3x+3,
∴直线 P C的解析式可设为 把C(0, 3)代入得b=3,∴直线P C的解析式为 解方程组 解得 马 则此时 P 点坐标为
过点A 作AC 的垂线交抛物线于另一点 P ,直线AP 的解析式可设为
把A (-1, 0) 代入得 解得 ∴直线AP 的解析式为 解方程组: 解得 可 则此时 P 点坐标为
综上所述,符合条件的点 P 的坐标为 或
6 解: (1) 由题意得: 解得 故抛物线的表达式为
(2)对于 令 解得x=4或-1, 故点A的坐标为(4, 0) , 则PF=2,由点A、B的坐标得,直线AB 的表达式为 设点P 的坐标为
点
解得x=1或3, ∴点P的坐标为(1, 或(3, 3);
(4)由抛物线的表达式知,其对称轴为 故设点Q的坐标为( ,n),又∵A (4, 0) , B(0, 3)
如图,先当以点 Q、A、B为顶点的三角形为直角三角形时,分三种情况讨论:
①.当∠ABQ为直角时, 则有: 解得: n=5,此时为
②.当∠BQA为直角时, 则有:
解得:
此时为
③当∠BAQ为直角时,则有:
解得:
此时为
综上,以点Q、A、B为顶点的三角形是锐角三角形,则△ABQ 不为直角三角形,也不为钝角三角形,即Q在Q 至Q 之间,或者在Q 至Q 之间的范围内,符合题意。
故点 Q 纵坐标n的取值范围为: 或
同课章节目录
