2025年中考数学复习--二次函数特殊平行四边形存在性问题(含解析)
文档属性
| 名称 | 2025年中考数学复习--二次函数特殊平行四边形存在性问题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 436.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 16:53:03 | ||
图片预览



文档简介
二次函数特殊平行四边形存在性问题
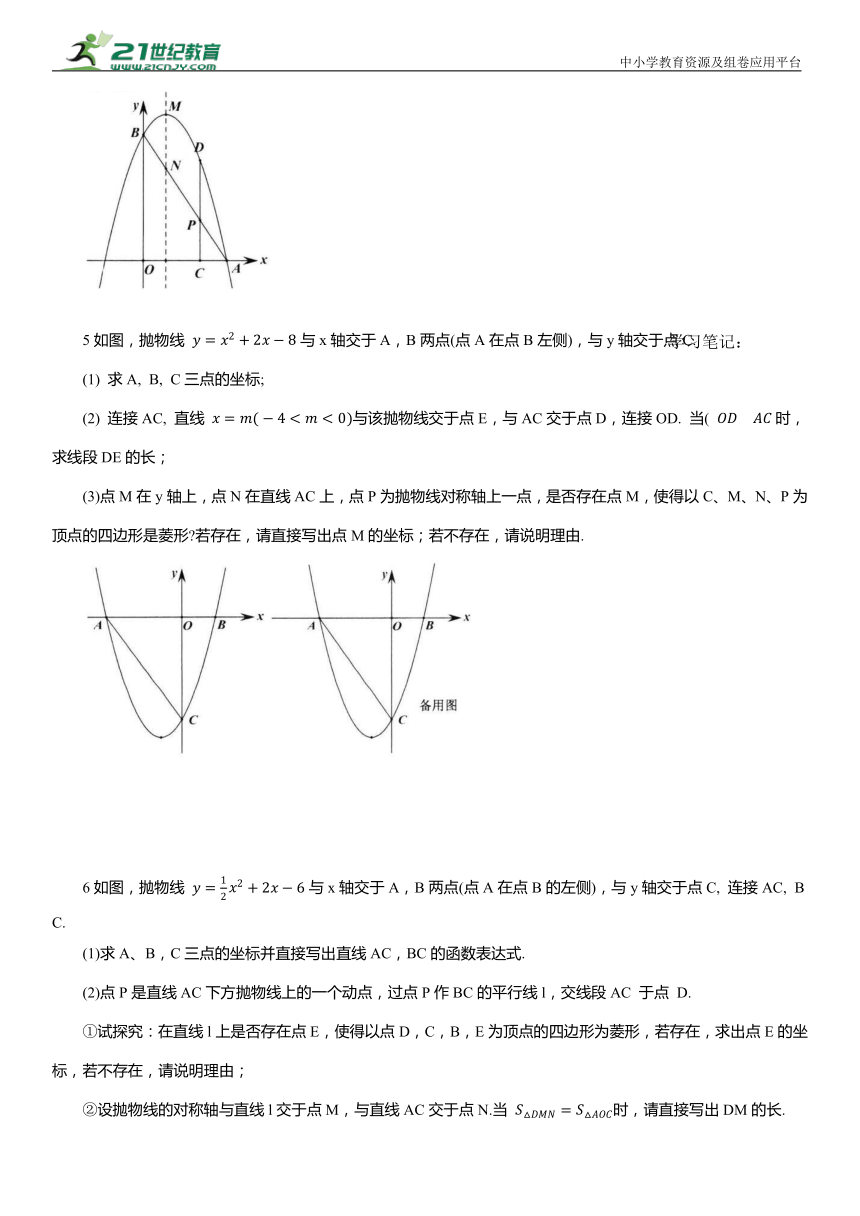
1在平面直角坐标系中,抛物线 交x轴于A(-3,0), B(4, 0)两点,交y轴于点C.
(1)求抛物线的表达式;
(2)如图,直线 与抛物线交于A,D两点,与直线BC交于点 E.若M(m,0)是线段AB上的动点,过点M作x轴的垂线,交抛物线于点 F,交直线AD 于点G, 交直线BC 于点 H.
①当点 F 在直线AD上方的抛物线上,且 时,求m的值;
②在平面内是否存在点 P,使四边形EFHP 为正方形 若存在,请直接写出点 P的坐标;若不存在,请说明理由.
2如图,在平面直角坐标系中,抛物线 与x轴交于点 A、B,与y轴交于点C,连接BC,OA=1,对称轴为直线x=2,点D为此抛物线的顶点.
(1)求抛物线的解析式;
(2)抛物线上C、D两点之间的距离是 ;
(3)点E是第一象限内抛物线上的动点,连接BE 和CE,求 面积的最大值;
(4)点P在抛物线对称轴上,平面内存在点Q,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点 Q的坐标.
3如图,抛物线 与x轴交于点 点 且 OC.
(1)求抛物线的解析式;
(2)点P在抛物线上,且 求点P的坐标;
(3)抛物线上两点M,N,点M的横坐标为m,点N的横坐标为 点 D是抛物线上M,N之间的动点,过点D作y轴的平行线交MN于点E.
①求DE的最大值;
②点D关于点E的对称点为F,当m为何值时,四边形MDNF 为矩形.
4如图, 已知直线y=-2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,点P 是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)若抛物线的解析式为 设其顶点为M,其对称轴交AB于点 N.
①求点 M、N的坐标;
②是否存在点 P,使四边形MNPD为菱形 并说明理由;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似 若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
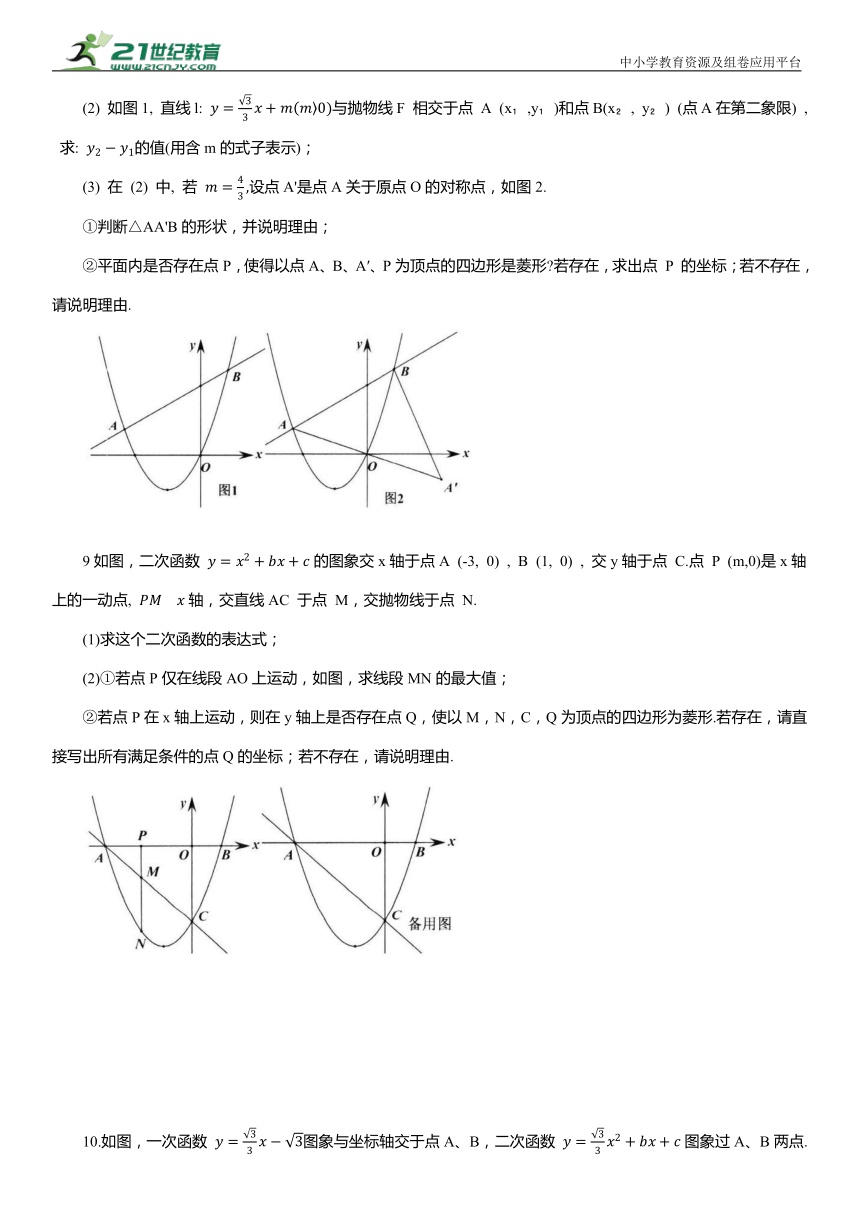
5如图,抛物线 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1) 求A, B, C三点的坐标;
(2) 连接AC, 直线 与该抛物线交于点E,与AC交于点D,连接OD. 当( 时,求线段DE的长;
(3)点M在y轴上,点N在直线AC上,点P为抛物线对称轴上一点,是否存在点M,使得以C、M、N、P为顶点的四边形是菱形 若存在,请直接写出点M的坐标;若不存在,请说明理由.
6如图,抛物线 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C, 连接AC, BC.
(1)求A、B,C三点的坐标并直接写出直线AC,BC的函数表达式.
(2)点P是直线AC下方抛物线上的一个动点,过点P作BC的平行线l,交线段AC 于点 D.
①试探究:在直线l上是否存在点E,使得以点D,C,B,E为顶点的四边形为菱形,若存在,求出点E的坐标,若不存在,请说明理由;
②设抛物线的对称轴与直线l交于点M,与直线AC交于点N.当 时,请直接写出DM的长.
7如图,在平面直角坐标系中,Rt△ABC 的边BC 在 x轴上, 以A为顶点的抛物线 经过点C(3, 0) , 交y轴于点E (0, 3) , 动点P在对称轴上.
(1)求抛物线解析式;
(2)若点P从A点出发,沿A→B方向以1个单位/秒的速度匀速运动到点B停止,设运动时间为t秒,过点 P作PD⊥AB交AC于点D,过点D平行于y轴的直线1交抛物线于点 Q,连接AQ,CQ,当t为何值时, 的面积最大 最大值是多少
(3)若点M是平面内的任意一点,在x轴上方是否存在点P,使得以点P,M,E,C为顶点的四边形是菱形,若存在,请直接写出符合条件的M点坐标;若不存在,请说明理由.
8已知抛物线F: 的图象经过坐标原点O,且与x轴另一交点为
(1)求抛物线F的解析式;
(2) 如图1, 直线l: 与抛物线F 相交于点 A (x ,y )和点B(x , y ) (点A在第二象限) , 求: 的值(用含m的式子表示);
(3) 在 (2) 中, 若 设点A'是点A关于原点O的对称点,如图2.
①判断△AA'B的形状,并说明理由;
②平面内是否存在点P,使得以点A、B、A′、P为顶点的四边形是菱形 若存在,求出点 P 的坐标;若不存在,请说明理由.
9如图,二次函数 的图象交x轴于点A (-3, 0) , B (1, 0) , 交y轴于点 C.点 P (m,0)是x轴上的一动点, 轴,交直线AC 于点 M,交抛物线于点 N.
(1)求这个二次函数的表达式;
(2)①若点P仅在线段AO上运动,如图,求线段MN的最大值;
②若点P在x轴上运动,则在y轴上是否存在点Q,使以M,N,C,Q为顶点的四边形为菱形.若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.
10.如图,一次函数 图象与坐标轴交于点A、B,二次函数 图象过A、B两点.
(1)求二次函数解析式;
(2)点B关于抛物线对称轴的对称点为点C,点P是对称轴上一动点,在抛物线上是否存在点Q,使得以B、C、P、Q为顶点的四边形是菱形 若存在,求出Q点坐标;若不存在,请说明理由.
1 解: (1) ∵抛物线 交x轴于A(-3, 0), B (4, 0) 两点,
(2) ①如图1, ∵B (4, 0) , C (0, 4) ,
∴设BC的解析式为:y= kx+n,则 解得
∴BC的解析式为:
解得: x=1, ∴E(1,3), ∵M(m, 0), 且MH⊥x轴,
和△OEG 的水平宽度相同,
中小学教育资源及组卷应用平台
解得:
②存在, 由①知: E (1, 3), 且
∴过点E 作 AB 的平行线,与抛物线的交点就是正方形EFHP 的顶点 F.
∴FH=EF, ∠EFH=∠FHP=∠HPE=90°,
∵M(m, 0) , 且MH⊥x轴,
分两种情况:
第一种情况: 当-3≤m<1时, 如图1, 点F在EP的左侧,
解得: (舍) , m2
第二种情况:当12. 解: (1) ∵OA=1, ∴A(-1, 0) ,又∵对称轴为x=2, ∴B (5, 0),将A,B代入解析式得: 解得
(2) 由(1)得:C(0, ), D(2, ),∴由两点距离公式可得: 故答案为 (3) ∵B(5,0), C(0, ),
∴直线 BC的解析式为: 设 且0如图, 作EF⊥x轴交 BC 于点 F, 则
当 时,S△BCE有最大值为
(4).设P(2, y), Q (m, n), 由(1)知B(5,0),C(0, ),分三种情况讨论:
①若BC为矩形的对角线,
由中点坐标公式得: 解得:
又∵∠BPC=90°, ∴PC +PB =BC ,
即:
解得y=4或 或n=4,
或Q(3,4),
②若 BP 为矩形的对角线 , 由中点坐标公式得 解得:
又∵∠BCP=90°, BC +CP =Bp
即:
解得 ∴Q(7, 4),
③.若BQ为矩形的对角线,
由中点坐标公式得: 解得:
又∵∠BCQ=90°, ∴BC +CQ =BQ ,
即:
解得
综上,点Q 的坐标为 或(3, 4) , 或(7, 4)或
解法二,也可以构造利用一线三等角三角形相似来解决。
3. 解: (1) ∵抛物线与x轴交于点A (-1, 0) ,点B (-3, 0) ∴设交点式y=a(x+1) (x+3)
∵OC=OB=3, 点C在y轴负半轴, ∴C(0, - 3)
把点C代入抛物线解析式得: 3a=-3, ∴a=-1
∴抛物线解析式为y= - (x+1) (x+3) =-x -4x-3
(2)如图1, 过点A作AG⊥BC于点G, 过点 P作P⊥x轴于点 H, ∴∠AGB=∠AGC=∠PHO=90°
∵∠ACB=∠POB,∴△ACG∽△POH,∴AG/PH=CG/OH,
∴△ABG 是等腰直角三角形,
设
①当p<-3或-1解得:
或
②当-30时,点P在AB之间或在点 C右侧,横纵坐标异号
解得:
∴P (-2, 1) 或
综上所述,点P 坐标为 或 或(-2,1)或
(3)①如图2,∵x=m+4时,
∴M(m, - m -4m-3) , N(m+4, - m -12m-35)
设直线 MN解析式为y=kx+n
解得:
∴直线 MN:
设D (d, - d -4d-3) (m∵DE∥y轴, ∴E(d, (-2m-8) d+m +4m-3)
=--[d - (m+2) ] +4
∴当d=m+2时, DE 的最大值为4.
②如图3, ∵D、F关于点E对称, ∴DE=EF,
∵四边形 MDNF 是矩形,
∴MN=DF, 且MN与DF互相平分
E为MN中点,
由①得当d=m+2时, DE=4, ∴MN=2DE=8
解
得:
或 时,四边形 MDNF为矩形.
4. 解:
∴顶点为M的坐标为
当 时, 则点N坐标为( ,3);
②不存在.理由如下:
设P点坐标为(m, - 2m+4),则. ∵PD∥MN,
当PD=MN时,四边形MNPD为平行四边形,即 解得 (舍去), 此时P 点坐标为
∴由两点距离公式可得: PN= , ∴PN≠MN,
∴平行四边形 MNPD 不为菱形,
∴不存在点 P,使四边形 MNPD 为菱形;
(2) 存在. 由题意知: A (2, 0) , B (0, 4)
∴ OB=4, OA=2, 则.
当x=1时, y=-2x+4=2, 则P (1, 2) ,∴由两点距离公式可得: 设抛物线的解析式为 把A(2, 0) 代入得44a+2b+4=0, 解得b=-2a-2,∴抛物线的解析式为 当x=1时, 则D (1, 2-a) , ∴PD=2-a-2=-a,
∵DC∥OB, ∴∠DPB=∠OBA,
如上图,分两种情况讨论:
①.当 时, △PDB∽△BOA, 即 解得a=-2,此时抛物线解析式为
②.当 时, △PDB∽△BAO, 即 解得 此时抛物线解析式为 综上所述,满足条件的抛物线的解析式为:
或
5 解: (1) 在 中, 令y=0, 得 -8=0, 解得: x =-4,x =2, ∴A(-4, 0), B(2,0) , 令x=0, 得y=-8, ∴C(0, - 8) ;
(2) 如图1, 设直线AC的解析式为y= kx+b,
∵A (-4, 0) , C(0, - 8) ,
解得: ∴直线AC 的解析式为y=-2x-8,
∵直线x=m(-4交于点D, ∴E(m, m +2m-8), D(m, - 2m-8) ,
设DE交x轴于点F, 则 F(m, 0), ∴OF=-m,
∴AF=m - (-4) =m+4, DF=2m+8,
∵OD⊥AC, EF⊥OA,
∴∠ODA=∠OFD=∠DFA=∠AOC=90° ,
∴∠DOF+∠COD=∠OCD+∠COD=90° ,
∴∠DOF=∠OCD, ∴△ACO∽△DOF,
∴8(2m+8) =4(-m) , 解得:
(3)存在,N点为直线AC与抛物线对称轴的交点,即N 抛物线对称轴为直线
∵以C、M、N、P为顶点的四边形是菱形,
∴分三种情况:CM对角线,或CN为对角线,或CP为对角线,
①如图2,当CP为对角线时 为对角线),
∴N点为直线AC与抛物线对称轴的交点,即N(-1, -6),由两点距离公式可得:
②如图3,当CN为对角线时,
设 则
解得:
③.如图4, 当CM对角线(CM )时, PN与CM互相垂直平分,设 则N(1, b), M(0, 2b+8),∵N(1, b)在直线 上,
综上所述,点M的坐标为:
6. 解: (1) 当y=0时,
解得x =-6, x =2, ∴A(-6, 0) , B(2, 0) ,当x=0时, y=-6, ∴C(0, - 6) ,
∵A(-6, 0), C(0, - 6) ,
∴直线AC的函数表达式为y=-x-6,
∵B(2, 0) , C(0, - 6) ,
∴直线 BC的函数表达式为y=3x-6;
(2) ①存在: 设点D 的坐标为(m, - m-6) , 其中-6∵DE∥BC, ∴当DE=BC时, 以点 D, C, B, E为顶点的四边形为平行四边形,现在分分两种情况讨论:
第一种情况:如图1中的E1,当BD=BC时, 四边形BDEC为菱形,∴BD =BC , ∴ (m-2) +(m+6) =40, 解得:m =-4, m =0(舍去) ,
∴点 D 的坐标为(-4, - 2) ,
∵点B 点向左移动2各单位长度,向下移动6个单位长度得到点C
∴ 点 D 向左移动2各单位长度,向下移动6个单位长度得到点 E, ∴点E的坐标为(-6, - 8) ;
第二种情况,如图2,当CD=CB时,四边形CBED为菱形,
解得: (舍去),
∴点 D 的坐标为
∵ 点C向右移动2个单位长度,向上移动6个单位长度得到点B,
∴点D 向右移动2个单位长度,向上移动6个单位长度得到点E,
∴点 E 的坐标为
综上,使得以点D,C,B,E为顶点的四边形为菱形,点E的坐标为 ( - 6, - 8) 或
②.如图3, 设点D的坐标为(m, - m-6) , 其中-6∴抛物线的对称轴为直线x=-2,
∵直线BC的函数表达式为y=3x-6, 直线l∥BC,
∴设直线l的解析式为y=3x+b,
∵点D的坐标(m, - m-6) ,
∴b=-4m-6, ∴ 直线l的解析式为y=3x-4m-6,
∴当x=-2时, y=-4m-12 ∴ M(-2, - 4m-12) ,
∵抛物线的对称轴与直线AC交于点 N.
∴N(-2, - 4) , ∴MN=-4m-12+4=-4m-8,
整理得: 解得: m =-5,m =1(舍去),∴点D 的坐标为(-5, - 1) , ∴点M 的坐标为(-2,8), ∴由两点距离公式得: 故DM的长为
7.解: (1)将点 C、E的坐标代入二次函数表达式得: 解得:
故抛物线的解析式为: 则点A (1, 4);
(2) 设直线AC的解析式为: y= kx+h, 由题意可得: 解得: ∴直线AC的表达式为:
y=-2x+6, 点 P (1, 4-t) , 则点 设点
故S△ACQ有最大值,
∴ 当t=2时,其最大值为1;
(3) 设点P (1, m), 点M(x, y), 分两种情况讨论:
①当EC是菱形一条边时,当点 M在点 P 右方时,如图1中的M1.
点E向右平移3个单位、向下平移3个单位得到C,则点 P向右平移3个单位、向下平移3个单位得到M,则1+3=x=4, m-3=y, 即M(4, m-3)
而MP=EP得: 1 解得: 故点
当点 M在点 P 左方时,如图1中的 M2.
同理可得:点.
②如图2,当EC是菱形一对角线时,则EC中点即为PM中点, ,则x+1=3, y+m=3,
而PE=PC, 即 解得: m=1,故x=2, y=3-m=3-1=2,故点 M (2, 2);
综上所述, 点M(4, ) 或( 或M(2,2) .
8. 解: (1) ∵抛物线 的图象经过点 (0,0)和解得: ∴抛物线 F的解析式为
(2) 将 和 联立方程组,解得:
∴点 A 的坐标为 点B的坐标为 ∵点A'是点A 关于原点O的对称点,∴点A'的坐标为
①△AA'B为等边三角形,理由如下:
∴分别有两点距离公式可得:
∴AA' =AB=A' B, ∴△AA' B为等边三角形.
②∵△AA'B为等边三角形,∴存在符合题意的点 P,且以点A、B、A′、P为顶点的菱形
设点 P 的坐标为(x,y).现在分三种情况讨论:
第一种情况:当A'B为对角线时,
解得:
∴点 P 的坐标为
第二种情况:当AB为对角线时,有
解得: . .点 P 的坐标为
第三种情况:当AA'为对角线时,有
解得: ∴点 P的坐标为
综上所述:平面内存在点 P,使得以点A、B、A'、P为顶点的四边形是菱形,点P 的坐标为 (- 和
9. 解: (1)把A(-3,0), B(1,0)代入 中,得: 解得
(2)①设直线AC的表达式为y= kx+b' ,把A(-3,0),C(0, - 3) 代入. 得
解得:
∵点 P (m, 0) 是x轴上的 一动点, 且PM⊥x轴.
∴M(m, - m-3) , N(m, m +2m-3) ,
∴.此函数有最大值.
又∵点 P 在线段OA 上运动,且
∴当 时,MN有最大值
(3).存在,分三种情况讨论:
①.如图1中, 当点M在线段AC上, MN=MC, 四边形MNQC 是菱形时.
解得 或0(舍弃)
②.如图2中,当 MC 是菱形的对角线时,四边形 MNCQ是正方形, 此时CN=MN=CQ=2,可得Q (0, - 1) .
③.如图3中, 当点 M在CA延长线上时, MN=CM, 四边形MNQC 是菱形时,则有, 解得 或0(舍弃),
当点 P在y轴的右侧时,显然MN>CM,此时满足条件的菱形不存在.
综上所述,满足条件的点 Q 的坐标为 或(0, - 1) 或(0, 3-1).
10.解:(1)在 中,令x=0得y= - 令y=0得x=3, ∴A(3, 0) , B(0, - ) ,∵二次函数 图象过A、B两点, 解得:
∴二次函数解析式为
(2)存在,理由如下:由二次函数 可得其对称轴为直线 设P(1,m), 而 ∵C与B关于直线x=1对称, ①当BC、PQ为对角线时, 如图1:
此时BC的中点即是PQ的中点,而此时的Q 点即为抛物线的顶点 且此时
∴四边形BQCP 是菱形,∴此时
②BP、CQ为对角线时, 如图2中的Q2, 同理BP、CQ中点重合,可得:
解得: ∴当P(1,0), Q (-1, 0)时,四边形BCPQ是平行四边形,由.P (1, 0) , B (0, - ) , 可得:
∴四边形BCPQ是菱形, ∴此时Q (-1, 0) ;
③以BQ、CP为对角线,如图2中的Q3(此时与A 点重合) , RO CP中占重合, 可得.
解得:
∴P (1,0) , Q (3, 0)时, 四边形 BCQP 是平行四边形, 由P(1,0) , B(0, - ) , C(2, - 可得: ∴四边形BCQP 是菱形,
∴此时 Q (3, 0) ;
综上所述,Q的坐标为: 或(-1, 0)或(3, 0) .
1在平面直角坐标系中,抛物线 交x轴于A(-3,0), B(4, 0)两点,交y轴于点C.
(1)求抛物线的表达式;
(2)如图,直线 与抛物线交于A,D两点,与直线BC交于点 E.若M(m,0)是线段AB上的动点,过点M作x轴的垂线,交抛物线于点 F,交直线AD 于点G, 交直线BC 于点 H.
①当点 F 在直线AD上方的抛物线上,且 时,求m的值;
②在平面内是否存在点 P,使四边形EFHP 为正方形 若存在,请直接写出点 P的坐标;若不存在,请说明理由.
2如图,在平面直角坐标系中,抛物线 与x轴交于点 A、B,与y轴交于点C,连接BC,OA=1,对称轴为直线x=2,点D为此抛物线的顶点.
(1)求抛物线的解析式;
(2)抛物线上C、D两点之间的距离是 ;
(3)点E是第一象限内抛物线上的动点,连接BE 和CE,求 面积的最大值;
(4)点P在抛物线对称轴上,平面内存在点Q,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点 Q的坐标.
3如图,抛物线 与x轴交于点 点 且 OC.
(1)求抛物线的解析式;
(2)点P在抛物线上,且 求点P的坐标;
(3)抛物线上两点M,N,点M的横坐标为m,点N的横坐标为 点 D是抛物线上M,N之间的动点,过点D作y轴的平行线交MN于点E.
①求DE的最大值;
②点D关于点E的对称点为F,当m为何值时,四边形MDNF 为矩形.
4如图, 已知直线y=-2x+4分别交x轴、y轴于点A、B,抛物线过A,B两点,点P 是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)若抛物线的解析式为 设其顶点为M,其对称轴交AB于点 N.
①求点 M、N的坐标;
②是否存在点 P,使四边形MNPD为菱形 并说明理由;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似 若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
5如图,抛物线 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1) 求A, B, C三点的坐标;
(2) 连接AC, 直线 与该抛物线交于点E,与AC交于点D,连接OD. 当( 时,求线段DE的长;
(3)点M在y轴上,点N在直线AC上,点P为抛物线对称轴上一点,是否存在点M,使得以C、M、N、P为顶点的四边形是菱形 若存在,请直接写出点M的坐标;若不存在,请说明理由.
6如图,抛物线 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C, 连接AC, BC.
(1)求A、B,C三点的坐标并直接写出直线AC,BC的函数表达式.
(2)点P是直线AC下方抛物线上的一个动点,过点P作BC的平行线l,交线段AC 于点 D.
①试探究:在直线l上是否存在点E,使得以点D,C,B,E为顶点的四边形为菱形,若存在,求出点E的坐标,若不存在,请说明理由;
②设抛物线的对称轴与直线l交于点M,与直线AC交于点N.当 时,请直接写出DM的长.
7如图,在平面直角坐标系中,Rt△ABC 的边BC 在 x轴上, 以A为顶点的抛物线 经过点C(3, 0) , 交y轴于点E (0, 3) , 动点P在对称轴上.
(1)求抛物线解析式;
(2)若点P从A点出发,沿A→B方向以1个单位/秒的速度匀速运动到点B停止,设运动时间为t秒,过点 P作PD⊥AB交AC于点D,过点D平行于y轴的直线1交抛物线于点 Q,连接AQ,CQ,当t为何值时, 的面积最大 最大值是多少
(3)若点M是平面内的任意一点,在x轴上方是否存在点P,使得以点P,M,E,C为顶点的四边形是菱形,若存在,请直接写出符合条件的M点坐标;若不存在,请说明理由.
8已知抛物线F: 的图象经过坐标原点O,且与x轴另一交点为
(1)求抛物线F的解析式;
(2) 如图1, 直线l: 与抛物线F 相交于点 A (x ,y )和点B(x , y ) (点A在第二象限) , 求: 的值(用含m的式子表示);
(3) 在 (2) 中, 若 设点A'是点A关于原点O的对称点,如图2.
①判断△AA'B的形状,并说明理由;
②平面内是否存在点P,使得以点A、B、A′、P为顶点的四边形是菱形 若存在,求出点 P 的坐标;若不存在,请说明理由.
9如图,二次函数 的图象交x轴于点A (-3, 0) , B (1, 0) , 交y轴于点 C.点 P (m,0)是x轴上的一动点, 轴,交直线AC 于点 M,交抛物线于点 N.
(1)求这个二次函数的表达式;
(2)①若点P仅在线段AO上运动,如图,求线段MN的最大值;
②若点P在x轴上运动,则在y轴上是否存在点Q,使以M,N,C,Q为顶点的四边形为菱形.若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.
10.如图,一次函数 图象与坐标轴交于点A、B,二次函数 图象过A、B两点.
(1)求二次函数解析式;
(2)点B关于抛物线对称轴的对称点为点C,点P是对称轴上一动点,在抛物线上是否存在点Q,使得以B、C、P、Q为顶点的四边形是菱形 若存在,求出Q点坐标;若不存在,请说明理由.
1 解: (1) ∵抛物线 交x轴于A(-3, 0), B (4, 0) 两点,
(2) ①如图1, ∵B (4, 0) , C (0, 4) ,
∴设BC的解析式为:y= kx+n,则 解得
∴BC的解析式为:
解得: x=1, ∴E(1,3), ∵M(m, 0), 且MH⊥x轴,
和△OEG 的水平宽度相同,
中小学教育资源及组卷应用平台
解得:
②存在, 由①知: E (1, 3), 且
∴过点E 作 AB 的平行线,与抛物线的交点就是正方形EFHP 的顶点 F.
∴FH=EF, ∠EFH=∠FHP=∠HPE=90°,
∵M(m, 0) , 且MH⊥x轴,
分两种情况:
第一种情况: 当-3≤m<1时, 如图1, 点F在EP的左侧,
解得: (舍) , m2
第二种情况:当1
(2) 由(1)得:C(0, ), D(2, ),∴由两点距离公式可得: 故答案为 (3) ∵B(5,0), C(0, ),
∴直线 BC的解析式为: 设 且0
当 时,S△BCE有最大值为
(4).设P(2, y), Q (m, n), 由(1)知B(5,0),C(0, ),分三种情况讨论:
①若BC为矩形的对角线,
由中点坐标公式得: 解得:
又∵∠BPC=90°, ∴PC +PB =BC ,
即:
解得y=4或 或n=4,
或Q(3,4),
②若 BP 为矩形的对角线 , 由中点坐标公式得 解得:
又∵∠BCP=90°, BC +CP =Bp
即:
解得 ∴Q(7, 4),
③.若BQ为矩形的对角线,
由中点坐标公式得: 解得:
又∵∠BCQ=90°, ∴BC +CQ =BQ ,
即:
解得
综上,点Q 的坐标为 或(3, 4) , 或(7, 4)或
解法二,也可以构造利用一线三等角三角形相似来解决。
3. 解: (1) ∵抛物线与x轴交于点A (-1, 0) ,点B (-3, 0) ∴设交点式y=a(x+1) (x+3)
∵OC=OB=3, 点C在y轴负半轴, ∴C(0, - 3)
把点C代入抛物线解析式得: 3a=-3, ∴a=-1
∴抛物线解析式为y= - (x+1) (x+3) =-x -4x-3
(2)如图1, 过点A作AG⊥BC于点G, 过点 P作P⊥x轴于点 H, ∴∠AGB=∠AGC=∠PHO=90°
∵∠ACB=∠POB,∴△ACG∽△POH,∴AG/PH=CG/OH,
∴△ABG 是等腰直角三角形,
设
①当p<-3或-1
或
②当-3
解得:
∴P (-2, 1) 或
综上所述,点P 坐标为 或 或(-2,1)或
(3)①如图2,∵x=m+4时,
∴M(m, - m -4m-3) , N(m+4, - m -12m-35)
设直线 MN解析式为y=kx+n
解得:
∴直线 MN:
设D (d, - d -4d-3) (m
=--[d - (m+2) ] +4
∴当d=m+2时, DE 的最大值为4.
②如图3, ∵D、F关于点E对称, ∴DE=EF,
∵四边形 MDNF 是矩形,
∴MN=DF, 且MN与DF互相平分
E为MN中点,
由①得当d=m+2时, DE=4, ∴MN=2DE=8
解
得:
或 时,四边形 MDNF为矩形.
4. 解:
∴顶点为M的坐标为
当 时, 则点N坐标为( ,3);
②不存在.理由如下:
设P点坐标为(m, - 2m+4),则. ∵PD∥MN,
当PD=MN时,四边形MNPD为平行四边形,即 解得 (舍去), 此时P 点坐标为
∴由两点距离公式可得: PN= , ∴PN≠MN,
∴平行四边形 MNPD 不为菱形,
∴不存在点 P,使四边形 MNPD 为菱形;
(2) 存在. 由题意知: A (2, 0) , B (0, 4)
∴ OB=4, OA=2, 则.
当x=1时, y=-2x+4=2, 则P (1, 2) ,∴由两点距离公式可得: 设抛物线的解析式为 把A(2, 0) 代入得44a+2b+4=0, 解得b=-2a-2,∴抛物线的解析式为 当x=1时, 则D (1, 2-a) , ∴PD=2-a-2=-a,
∵DC∥OB, ∴∠DPB=∠OBA,
如上图,分两种情况讨论:
①.当 时, △PDB∽△BOA, 即 解得a=-2,此时抛物线解析式为
②.当 时, △PDB∽△BAO, 即 解得 此时抛物线解析式为 综上所述,满足条件的抛物线的解析式为:
或
5 解: (1) 在 中, 令y=0, 得 -8=0, 解得: x =-4,x =2, ∴A(-4, 0), B(2,0) , 令x=0, 得y=-8, ∴C(0, - 8) ;
(2) 如图1, 设直线AC的解析式为y= kx+b,
∵A (-4, 0) , C(0, - 8) ,
解得: ∴直线AC 的解析式为y=-2x-8,
∵直线x=m(-4
设DE交x轴于点F, 则 F(m, 0), ∴OF=-m,
∴AF=m - (-4) =m+4, DF=2m+8,
∵OD⊥AC, EF⊥OA,
∴∠ODA=∠OFD=∠DFA=∠AOC=90° ,
∴∠DOF+∠COD=∠OCD+∠COD=90° ,
∴∠DOF=∠OCD, ∴△ACO∽△DOF,
∴8(2m+8) =4(-m) , 解得:
(3)存在,N点为直线AC与抛物线对称轴的交点,即N 抛物线对称轴为直线
∵以C、M、N、P为顶点的四边形是菱形,
∴分三种情况:CM对角线,或CN为对角线,或CP为对角线,
①如图2,当CP为对角线时 为对角线),
∴N点为直线AC与抛物线对称轴的交点,即N(-1, -6),由两点距离公式可得:
②如图3,当CN为对角线时,
设 则
解得:
③.如图4, 当CM对角线(CM )时, PN与CM互相垂直平分,设 则N(1, b), M(0, 2b+8),∵N(1, b)在直线 上,
综上所述,点M的坐标为:
6. 解: (1) 当y=0时,
解得x =-6, x =2, ∴A(-6, 0) , B(2, 0) ,当x=0时, y=-6, ∴C(0, - 6) ,
∵A(-6, 0), C(0, - 6) ,
∴直线AC的函数表达式为y=-x-6,
∵B(2, 0) , C(0, - 6) ,
∴直线 BC的函数表达式为y=3x-6;
(2) ①存在: 设点D 的坐标为(m, - m-6) , 其中-6
第一种情况:如图1中的E1,当BD=BC时, 四边形BDEC为菱形,∴BD =BC , ∴ (m-2) +(m+6) =40, 解得:m =-4, m =0(舍去) ,
∴点 D 的坐标为(-4, - 2) ,
∵点B 点向左移动2各单位长度,向下移动6个单位长度得到点C
∴ 点 D 向左移动2各单位长度,向下移动6个单位长度得到点 E, ∴点E的坐标为(-6, - 8) ;
第二种情况,如图2,当CD=CB时,四边形CBED为菱形,
解得: (舍去),
∴点 D 的坐标为
∵ 点C向右移动2个单位长度,向上移动6个单位长度得到点B,
∴点D 向右移动2个单位长度,向上移动6个单位长度得到点E,
∴点 E 的坐标为
综上,使得以点D,C,B,E为顶点的四边形为菱形,点E的坐标为 ( - 6, - 8) 或
②.如图3, 设点D的坐标为(m, - m-6) , 其中-6
∵直线BC的函数表达式为y=3x-6, 直线l∥BC,
∴设直线l的解析式为y=3x+b,
∵点D的坐标(m, - m-6) ,
∴b=-4m-6, ∴ 直线l的解析式为y=3x-4m-6,
∴当x=-2时, y=-4m-12 ∴ M(-2, - 4m-12) ,
∵抛物线的对称轴与直线AC交于点 N.
∴N(-2, - 4) , ∴MN=-4m-12+4=-4m-8,
整理得: 解得: m =-5,m =1(舍去),∴点D 的坐标为(-5, - 1) , ∴点M 的坐标为(-2,8), ∴由两点距离公式得: 故DM的长为
7.解: (1)将点 C、E的坐标代入二次函数表达式得: 解得:
故抛物线的解析式为: 则点A (1, 4);
(2) 设直线AC的解析式为: y= kx+h, 由题意可得: 解得: ∴直线AC的表达式为:
y=-2x+6, 点 P (1, 4-t) , 则点 设点
故S△ACQ有最大值,
∴ 当t=2时,其最大值为1;
(3) 设点P (1, m), 点M(x, y), 分两种情况讨论:
①当EC是菱形一条边时,当点 M在点 P 右方时,如图1中的M1.
点E向右平移3个单位、向下平移3个单位得到C,则点 P向右平移3个单位、向下平移3个单位得到M,则1+3=x=4, m-3=y, 即M(4, m-3)
而MP=EP得: 1 解得: 故点
当点 M在点 P 左方时,如图1中的 M2.
同理可得:点.
②如图2,当EC是菱形一对角线时,则EC中点即为PM中点, ,则x+1=3, y+m=3,
而PE=PC, 即 解得: m=1,故x=2, y=3-m=3-1=2,故点 M (2, 2);
综上所述, 点M(4, ) 或( 或M(2,2) .
8. 解: (1) ∵抛物线 的图象经过点 (0,0)和解得: ∴抛物线 F的解析式为
(2) 将 和 联立方程组,解得:
∴点 A 的坐标为 点B的坐标为 ∵点A'是点A 关于原点O的对称点,∴点A'的坐标为
①△AA'B为等边三角形,理由如下:
∴分别有两点距离公式可得:
∴AA' =AB=A' B, ∴△AA' B为等边三角形.
②∵△AA'B为等边三角形,∴存在符合题意的点 P,且以点A、B、A′、P为顶点的菱形
设点 P 的坐标为(x,y).现在分三种情况讨论:
第一种情况:当A'B为对角线时,
解得:
∴点 P 的坐标为
第二种情况:当AB为对角线时,有
解得: . .点 P 的坐标为
第三种情况:当AA'为对角线时,有
解得: ∴点 P的坐标为
综上所述:平面内存在点 P,使得以点A、B、A'、P为顶点的四边形是菱形,点P 的坐标为 (- 和
9. 解: (1)把A(-3,0), B(1,0)代入 中,得: 解得
(2)①设直线AC的表达式为y= kx+b' ,把A(-3,0),C(0, - 3) 代入. 得
解得:
∵点 P (m, 0) 是x轴上的 一动点, 且PM⊥x轴.
∴M(m, - m-3) , N(m, m +2m-3) ,
∴.此函数有最大值.
又∵点 P 在线段OA 上运动,且
∴当 时,MN有最大值
(3).存在,分三种情况讨论:
①.如图1中, 当点M在线段AC上, MN=MC, 四边形MNQC 是菱形时.
解得 或0(舍弃)
②.如图2中,当 MC 是菱形的对角线时,四边形 MNCQ是正方形, 此时CN=MN=CQ=2,可得Q (0, - 1) .
③.如图3中, 当点 M在CA延长线上时, MN=CM, 四边形MNQC 是菱形时,则有, 解得 或0(舍弃),
当点 P在y轴的右侧时,显然MN>CM,此时满足条件的菱形不存在.
综上所述,满足条件的点 Q 的坐标为 或(0, - 1) 或(0, 3-1).
10.解:(1)在 中,令x=0得y= - 令y=0得x=3, ∴A(3, 0) , B(0, - ) ,∵二次函数 图象过A、B两点, 解得:
∴二次函数解析式为
(2)存在,理由如下:由二次函数 可得其对称轴为直线 设P(1,m), 而 ∵C与B关于直线x=1对称, ①当BC、PQ为对角线时, 如图1:
此时BC的中点即是PQ的中点,而此时的Q 点即为抛物线的顶点 且此时
∴四边形BQCP 是菱形,∴此时
②BP、CQ为对角线时, 如图2中的Q2, 同理BP、CQ中点重合,可得:
解得: ∴当P(1,0), Q (-1, 0)时,四边形BCPQ是平行四边形,由.P (1, 0) , B (0, - ) , 可得:
∴四边形BCPQ是菱形, ∴此时Q (-1, 0) ;
③以BQ、CP为对角线,如图2中的Q3(此时与A 点重合) , RO CP中占重合, 可得.
解得:
∴P (1,0) , Q (3, 0)时, 四边形 BCQP 是平行四边形, 由P(1,0) , B(0, - ) , C(2, - 可得: ∴四边形BCQP 是菱形,
∴此时 Q (3, 0) ;
综上所述,Q的坐标为: 或(-1, 0)或(3, 0) .
同课章节目录
