2025年中考数学复习--中点模型(含解析)
文档属性
| 名称 | 2025年中考数学复习--中点模型(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 383.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 16:56:29 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中点模型
1如图,抛物线 与x轴交于A、B两点, P是以点C (0, 3) 为圆心, 2为半径的圆上的动点,Q是线段PA的中点,连接OQ,则线段OQ的最大值是( )
A. 3 C. D. 4
2如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB, 且PA、PB与x轴分别交于A、B两点, 若点A、点B关于原点O对称,则AB的最小值为( )
A. 3 B. 4 C. 6 D. 8
3平行四边形的延长类中线求线段的值 中点模型(初二)如图, 在 ABCD中, AB=5, BC=8. E是边BC的中点, F是 ABCD内一点,且∠BFC=90°. 连接AF 并延长, 交CD于点G. 若EF∥AB, 则DG的长为( )
A. B. C. 3 D. 2
4如图,在边长为2 的正方形ABCD中,点E,F分别是边AB,BC的中点,连接EC, FD, 点G, H分别是EC, FD的中点, 连接GH, 则GH的长度为 .
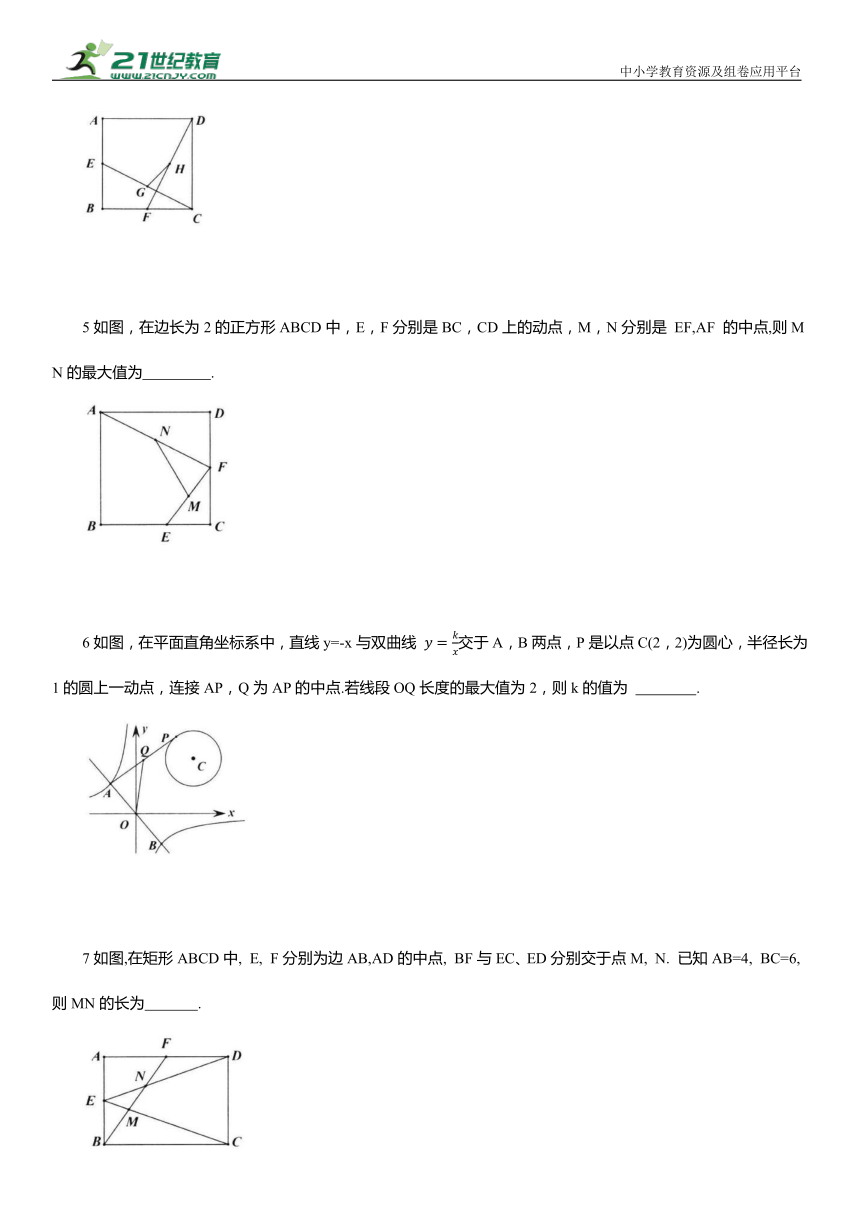
5如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是 EF,AF 的中点,则MN的最大值为 .
6如图,在平面直角坐标系中,直线y=-x与双曲线 交于A,B两点,P是以点C(2,2)为圆心,半径长为1的圆上一动点,连接AP,Q为AP的中点.若线段OQ长度的最大值为2,则k的值为 .
7如图,在矩形ABCD中, E, F分别为边AB,AD的中点, BF与EC、ED分别交于点M, N. 已知AB=4, BC=6, 则MN的长为 .
8已知: 如图, Rt△ABC中, ∠ABC=90° , AB=4, BC=3, 两直角顶点 A、B分别在x轴、y轴的正半轴上滑动,点C在第一象限,连接OC,则OC长的最大值是 .
9如图, 的顶点C在等边 的边BF上,点E在AB的延长线上,G为DE的中点,连接CG.若. , 则CG 的长为 .
10如图,矩形纸片ABCD, ,E为边CD上一点.将 沿BE所在的直线折叠,点C恰好落在AD边上的点F处,过点F作 垂足为点M,取AF 的中点N, 连接MN, 则 MN= cm.
11如图,已知点E在正方形ABCD的边AB上,以BE 为边向正方形ABCD外部作正方形BEFG, 连接DF, M、N分别是DC、DF的中点, 连接MN. 若 则MN= .
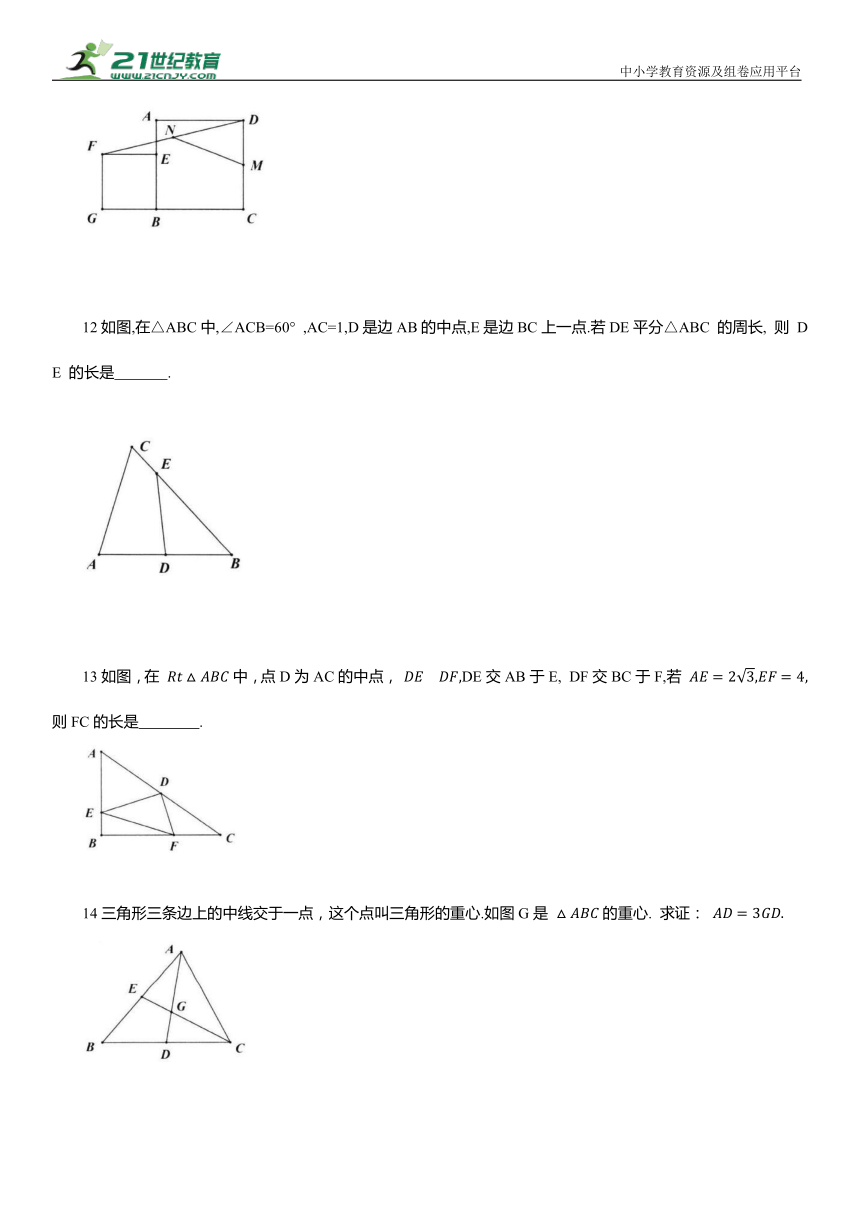
12如图,在△ABC中,∠ACB=60° ,AC=1,D是边AB的中点,E是边BC上一点.若DE平分△ABC 的周长, 则 DE 的长是 .
13如图,在 中,点D为AC的中点, DE交AB于E, DF交BC于F,若 则FC的长是 .
14三角形三条边上的中线交于一点,这个点叫三角形的重心.如图G是 的重心. 求证:
15如图, 在四边形ABCD中, AB∥CD, AB=AD, AC平分∠BAD.
(1) 求证: 四边形ABCD是菱形;
(2) 若菱形ABCD的边长为13, 对角线AC=24, 点E、F分别是边CD、BC的中点,连接EF 并延长,与AB的延长线相交于点G,求EG的长.
16若△ABC 和△AED 均为等腰三角形,且.
(1)如图(1),点B是DE的中点,判定四边形BEAC的形状,并说明理由;
(2) 如图(2) , 若点G是EC的中点, 连接GB并延长至点F, 使CF=CD.
求证: ①EB=DC, ②∠EBG=∠BFC.
17如图,在矩形ABCD中, 点P、M、N分别在边AB、AD、BC上运动, 学习笔记:且线段 MN始终经过矩形的对称中心,则 周长的最小值为 .
18(1)如图1, 在四边形ABCD中,AB=CD, E,F分别是AD,BC的中点, 连接FE并延长,分别与BA,CD的延长线交于点M,N.求证:
(2)如图2,在△ABC中,F是BC边的中点, D是AC边上一点,E是AD的中点,直线FE 交 BA的延长线于点G,若AB=DC=2, ∠FEC=45° , 求FE的长度.
19如图,在△ABC中,点D为BC边上任意一点.
(1) 如图1, 若D为BC的中点.
①若AB=7, AC=5, 则△ABD与△ACD的周长之差为 ;
②E 是AD上一点, 延长BE 交AC 于F, AF=EF, 求证: AC=BE;
(2) 如图2, AD为∠BAC的平分线. 若AC+CD=AB, 求证: ∠C=2∠B.
20【问题情境】课外兴趣小组活动时,老师提出了如下问题:
如图①, 中,若 求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使 连接BE.请根据小明的方法思考:
(1)由已知和作图能得到 依据是 .
A. SAS B. SSS C. AAS D. HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、 “中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=4, EC=3, 求线段BF的长.
【灵活运用】如图③, 在△ABC中, ∠A=90° , D为BC中点, DE⊥DF, DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的数量关系,并证明你的结论.
1解: 连接BP, 如图,当y=0时, 解得x =4, x =-4, 则A(-4, 0) , B(4, 0) ,∵Q 是线段 PA 的中点, ∴OQ为△ABP 的中位线,
当BP 最大时,OQ 最大,而BP 过圆心C时, PB 最大, =7, ∴线段 OQ的最大值是 . 故选: C.
2解: 连接PO, ∵PA⊥PB, ∴∠APB=90°,∵AO=BO, ∴AB=2PO, 若要使AB取得最小值,则PO需取得最小值,连接O、P、M三点共线时,PO最小, 过点M 作 ME⊥y轴于点 E, 在 Rt△MOE 中, 此时 PO 最小值为5-2=3,
∴AB的最小值是6, 故选: C.
3解: 如图, 延长BF交CD的延长线于 H,
∵四边形ABCD是平行四边形,∴AB=CD=5,AB∥CD,
∴∠H=∠ABF, ∵EF∥AB, ∴EF∥CD,
∵E是边 BC的中点, ∴EF是△BCH的中位线,
∴BF=FH, ∵∠BFC=90°, ∴CF⊥BF, ∴CF是BH的中垂线, ∴BC=CH=8, ∴DH=CH-CD=3,
在△ABF和△GHF中,
∴△ABF≌△GFH(ASA) , ∴AB=GH=5,
∴DG=GH-DH=2, 故选: D.
解法二: 由梯形中位线可知: 2EF=AB+CG, EF=4,∴2×4=5+CG, ∴CG=3, ∴DG=CD-CG=5-3=2
4解: 连接CH 并延长交AD于 P, 连接PE,∵四边形ABCD是正方形, ∴∠A=90°, AD∥BC, AB=AD=BC=2 , ∵E,F分别是边AB, BC的中点,∴
∵AD∥BC, ∴∠DPH=∠FCH, ∵∠DHP=∠FHC, DH=FH, ∴△PDH≌△CFH (AAS) , ∴PD=CF= ∵点G, H分别是EC, CP的中点,
5解: 如图所示, 连接AE,
∵M, N分别是EF, AF的中点,
∴MN是△AEF的中位线,
∴当AE 取最大值时,MN有最大值.
∵四边形ABCD 是正方形, ∠B=90°,
∴当BE 最大时,AE 最大,此时MN 最大,
∵点E 是BC上的动点,
∴当点E 和点C重合时,BE最大,即BC的长度,∴此时
∴MN的最大值为
故答案为:
6解:连接BP,点O 是AB的中点,则OQ是△ABP的中位线,则 当B、C、P三点共线时,PB 最大,则OQ有最大值.而 OQ 的最大值为2,故BP的最大值为4, 则BC=BP-PC=4-1=3,设点B (m, - m) , ∵C(2, 2)
则 解得: 故答案为
7解: 如图1, 延长CE、DA 交于Q, ∵四边形ABCD是矩形, BC=6, ∴∠BAD=90° , AD=BC=6, AD∥BC, ∵F为AD中点, ∴AF=DF=3,
在 Rt△BAF 中,由勾股定理得: ∵AD∥BC, ∴∠Q=∠ECB,
∵E为AB的中点, AB=4, ∴AE=BE=2,在△QAE 和△CBE中, CBE (AAS) , ∴AQ=BC=6, 即QF=6+3=9,
∵BF=5, ∴BM=2, FM=3,
如图2, 延长BF和CD, 交于W, 同理AB=DW=4,CW=8,BF=FW=5, ∵AB∥CD, ∴△BNE∽△WND, 解得:BN=
故答案为:
8解:取AB中点 P,连接OP、CP,则 =2, 由勾股定理得, 利用三角形两边之和大于点三边可知:OC≤OP+PC= 即当O、P、C三点共线时OC有最大值,OC的长的最大值为 故答案为:
9解: ∵四边形ABCD 是平行四边形, ∴AD=BC, CD=AB, DC∥AB, ∵AD=3, AB=CF=2,
∴CD=2, BC=3, ∴BF=BC+CF=5, ∵△BEF是等边三角形, G为DE的中点, ∴BF=BE=5, DG=EG,
延长CG交BE于点 H, ∵DC∥AB, ∴∠CDG=∠HEG,
在△DCG和△EHG中, △DCG≌△EHG(ASA), ∴DC=EH, CG=HG, ∵CD=2,BE=5,
∴HE=2, BH=3, ∵∠CBH=60° , BC=BH=3,
∴△CBH是等边三角形, ∴CH=BC=3,
故答案为:
解法二:延长DC 交 FE于点 M,则CG 是△DEM的中位线,则
10解:连接AC,MC.由翻折的性质可知,BE 垂直平分线段CF, ∵FM⊥BE, ∴F. M, C共线, FM=MC,
, ∵四边形ABCD 是矩形,
故答案为5.
11解: 连接CF,
∵正方形ABCD和正方形BEFG中, AB=7, BE=5,∴GF=GB=5, BC=7, ∴GC=GB+BC=5+7=12,∴CF=√GF +GC =13. ∵M、1N分别是DC、DF的中点, 故答案为:
12解: 延长BC至M, 使CM=CA,连接AM, 作CN⊥AM于 N, ∵DE平分△ABC的周长, ∴ME=EB,
又∵AD=DB,∴DE是△ABM的中位线,
DE∥AM, ∵∠ACB=60° , ∴∠ACM=120°,
∵CM=CA, ∴∠ACN=60° , AN=MN, ∠NAC=30°
故答案为:
13解: 如图, 过点 C作 CG∥AB交ED的延长线于点G, 连接FG, ∵点D是AB的中点, ∴AD=CD,∵AB∥GC, ∴∠B=∠BCG=90°,
在△ADE和△CDG中, △CDG(ASA),∴EF=FG,EA=GC,∴FG =FC +GG , 在Rt△BEF 中, 2, 故答案为: 2.
14 证明: 连接DE,
∵点G是△ABC的重心,∴点E 和点 D 分别是AB 和BC的中点, ∴DE 是△ABC的中位线, ∴DE∥AC且 即AD=3GD.
15 解: (1) ∵AC平分∠BAD, AB∥CD,
∴∠DAC=∠BAC, ∠DCA=∠BAC,
∴∠DAC=∠DCA, ∴AD=DC,又∵AB∥CD, AB=AD,
∴AB∥CD且AB=CD, ∴四边形ABCD 是平行四边形,∵AB=AD, ∴四边形ABCD 是菱形.
(2) 连接BD, 交AC于点O, (自行画图)
∵菱形ABCD的边长为13, 对角线AC=24, ∴CD=13,AO=CO=12, ∵点E、F分别是边 CD、BC的中点,
∴EF∥BD(中位线), ∵AC、BD是菱形的对角线,
∴AC⊥BD, OB=OD, 又∵AB∥CD, EF∥BD,
∴DE∥BG, BD∥EG, ∴四边形BDEG是平行四边形,
∴BD=EG. 在△COD中. ∵OC⊥OD, CD=13,
16解: (1)四边形BEAC是平行四边形,理由如下:
∵△AED 为等腰三角形,∠EAD=90°, B是DE的中点,
∴∠E=∠BAE=45° , ∠ABE=90° ,
∵△ABC 是等腰三角形, ∠BAC=90°,
∴∠ABC=∠BAE=45° , ∠ABE=∠BAC=90° ,
∴BC∥AE, AC∥BE, ∴四边形BEAC是平行四边形;
(2) ①∵△ABC和△AED 均为等腰直角三角形,∠BAC=∠EAD=90° , ∴AE=AD, AB=AC,∠BAE=∠CAD, ∴△AEB≌△ADC(SAS) ,∴BE=CD;
②延长FG至点H, 使GH=FG,
∵G是EC的中点, ∴EG=CG,
又∵∠EGH=∠FGC, ∴△EGH≌△CGF(SAS),
∴∠BFC=∠H, CF=EH,
∵CF=CD, CD=BE,
∴EH=BE, ∴∠H=∠EBG, ∴∠EBG=∠BFC.
17 解: 取MP的中点Q, 连接AQ, OQ, AO,∴AQ是 Rt△APM 斜边上的中线, 又∵ 线段 MN始终经过矩形的对称中心,
∴O是MN的中点, ∴OQ 是△MPN的中位线,
∴C△PMN=PM+PN+MN=2AQ+2OQ+2ON
=2(AQ+OQ+ON) =2(AO+ON)
∵点O 是固定点,∴AO 是定值, 当ON取最小时,2(AO+ON)有最小值,即为所求△MPN周长的最小值.
作OG⊥BC,垂足为G,此时OG=2即为ON的最小值,∴△PMN周长的最小值为
故答案为:
18 (1) 证明: 如图1, 连接BD, 取DB的中点 H,连接EH, FH, ∵E, H分别是AD, BD的中点.
∴EH 是△ABD的中位线 ∴∠BME=∠HEF, ∵F, H分别是BC, BD的中点,∴FH 是△BCD的中位线 ∴∠CNE=∠HFE, ∵AB=CD∴HE=FH,
∴∠HEF=∠HFE∴∠BME=∠CNE;
(2)如图2,连接BD,取DB的中点H,连接EH, FH,∵E, F分别是AD, BC的中点, ∴EH是△ABD的中位线, FH 是△BCD的中位线, CD, FH∥AC, ∴∠HFE=∠FEC=45°, ∵AB=CD=2, ∴HF=HE=1, ∴∠HEF=∠HFE=45° , ∴△EFH 是等腰直角三角形,
19 解: ①∵D为BC的中点, ∴BD=CD,
∴△ABD 与△ACD的周长之差为 (AB+AD+BD)(AC+AD+CD) =AB--AC. ∵AB=7, AC=5,
②证明:如图1,延长AD至G,使DG=AD,连接BG,∵D是BC的中点, ∴BD=CD,
在△BDG和△CDA中,
∴△BDG≌△CDA(SAS), ∴∠G=∠CAD,BG=AC,
∵AF=EF, ∴∠CAD=∠AEF, ∴∠G=∠AEF=∠BEG, ∴BE=BG, ∴AC=BE;
(2) 证明: 如图2, 在AB上截取AE=AC, 连接DE,∵AD是∠BAC的平分线, ∴∠BAD=∠CAD,
在△EAD和△CAD中,
∴△EAD≌△CAD(SAS), ∴∠AED=∠C, ED=CD,
∵AC+CD=AB, 且AB=AE+EB, ∴CD=ED=EB,∴∠B=∠BDE, ∴∠AED=∠B+∠BDE=2∠B,即∠C=2∠B.
20【问题情境】解: (1) 在△ADC和△EDB中,
(2) 由 (1) 得: △ADC≌△EDB, ∴AC=BE=6,在△ABE中, AB--BE【初步运用】解: 延长AD到M, 使AD=DM, 连接BM,如图②所示: ∵AE=EF. EF=4, ∴AC=AE+EC=4+3=7, ∵AD是△ABC中线, ∴CD=BD,
∵在△ADC和△MDB中,
∴△ADC≌△MDB(SAS), ∴BM=AC, ∠CAD=∠M,
∵AE=EF, ∴∠CAD=∠AFE, ∵∠AFE=∠BFD,
∴∠BFD=∠CAD=∠M, ∴BF=BM=AC=7;
【灵活运用】解:线段BE、CF、EF之间的等量关系为: 理由如下:延长ED 到点G,使DG=ED,连接GF, GC, 如图③所示:
∵ED⊥DF, ∴EF=GF, ∵D是BC的中点,
∴BD=CD, 在△BDE和△CDG中,
∴△DBE≌△DCG(SAS) , ∴BE=CG, ∵∠A=90°,
∴∠B+∠ACB=90° ,
∵△DBE≌△DCG, EF=GF,
∴BE=CG, ∠B=∠GCD, ∴∠GCD+∠ACB=90°, 即∠GCF=90° ,
∴Rt△CFG中, 由勾股定理得:
中点模型
1如图,抛物线 与x轴交于A、B两点, P是以点C (0, 3) 为圆心, 2为半径的圆上的动点,Q是线段PA的中点,连接OQ,则线段OQ的最大值是( )
A. 3 C. D. 4
2如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB, 且PA、PB与x轴分别交于A、B两点, 若点A、点B关于原点O对称,则AB的最小值为( )
A. 3 B. 4 C. 6 D. 8
3平行四边形的延长类中线求线段的值 中点模型(初二)如图, 在 ABCD中, AB=5, BC=8. E是边BC的中点, F是 ABCD内一点,且∠BFC=90°. 连接AF 并延长, 交CD于点G. 若EF∥AB, 则DG的长为( )
A. B. C. 3 D. 2
4如图,在边长为2 的正方形ABCD中,点E,F分别是边AB,BC的中点,连接EC, FD, 点G, H分别是EC, FD的中点, 连接GH, 则GH的长度为 .
5如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是 EF,AF 的中点,则MN的最大值为 .
6如图,在平面直角坐标系中,直线y=-x与双曲线 交于A,B两点,P是以点C(2,2)为圆心,半径长为1的圆上一动点,连接AP,Q为AP的中点.若线段OQ长度的最大值为2,则k的值为 .
7如图,在矩形ABCD中, E, F分别为边AB,AD的中点, BF与EC、ED分别交于点M, N. 已知AB=4, BC=6, 则MN的长为 .
8已知: 如图, Rt△ABC中, ∠ABC=90° , AB=4, BC=3, 两直角顶点 A、B分别在x轴、y轴的正半轴上滑动,点C在第一象限,连接OC,则OC长的最大值是 .
9如图, 的顶点C在等边 的边BF上,点E在AB的延长线上,G为DE的中点,连接CG.若. , 则CG 的长为 .
10如图,矩形纸片ABCD, ,E为边CD上一点.将 沿BE所在的直线折叠,点C恰好落在AD边上的点F处,过点F作 垂足为点M,取AF 的中点N, 连接MN, 则 MN= cm.
11如图,已知点E在正方形ABCD的边AB上,以BE 为边向正方形ABCD外部作正方形BEFG, 连接DF, M、N分别是DC、DF的中点, 连接MN. 若 则MN= .
12如图,在△ABC中,∠ACB=60° ,AC=1,D是边AB的中点,E是边BC上一点.若DE平分△ABC 的周长, 则 DE 的长是 .
13如图,在 中,点D为AC的中点, DE交AB于E, DF交BC于F,若 则FC的长是 .
14三角形三条边上的中线交于一点,这个点叫三角形的重心.如图G是 的重心. 求证:
15如图, 在四边形ABCD中, AB∥CD, AB=AD, AC平分∠BAD.
(1) 求证: 四边形ABCD是菱形;
(2) 若菱形ABCD的边长为13, 对角线AC=24, 点E、F分别是边CD、BC的中点,连接EF 并延长,与AB的延长线相交于点G,求EG的长.
16若△ABC 和△AED 均为等腰三角形,且.
(1)如图(1),点B是DE的中点,判定四边形BEAC的形状,并说明理由;
(2) 如图(2) , 若点G是EC的中点, 连接GB并延长至点F, 使CF=CD.
求证: ①EB=DC, ②∠EBG=∠BFC.
17如图,在矩形ABCD中, 点P、M、N分别在边AB、AD、BC上运动, 学习笔记:且线段 MN始终经过矩形的对称中心,则 周长的最小值为 .
18(1)如图1, 在四边形ABCD中,AB=CD, E,F分别是AD,BC的中点, 连接FE并延长,分别与BA,CD的延长线交于点M,N.求证:
(2)如图2,在△ABC中,F是BC边的中点, D是AC边上一点,E是AD的中点,直线FE 交 BA的延长线于点G,若AB=DC=2, ∠FEC=45° , 求FE的长度.
19如图,在△ABC中,点D为BC边上任意一点.
(1) 如图1, 若D为BC的中点.
①若AB=7, AC=5, 则△ABD与△ACD的周长之差为 ;
②E 是AD上一点, 延长BE 交AC 于F, AF=EF, 求证: AC=BE;
(2) 如图2, AD为∠BAC的平分线. 若AC+CD=AB, 求证: ∠C=2∠B.
20【问题情境】课外兴趣小组活动时,老师提出了如下问题:
如图①, 中,若 求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使 连接BE.请根据小明的方法思考:
(1)由已知和作图能得到 依据是 .
A. SAS B. SSS C. AAS D. HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、 “中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=4, EC=3, 求线段BF的长.
【灵活运用】如图③, 在△ABC中, ∠A=90° , D为BC中点, DE⊥DF, DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的数量关系,并证明你的结论.
1解: 连接BP, 如图,当y=0时, 解得x =4, x =-4, 则A(-4, 0) , B(4, 0) ,∵Q 是线段 PA 的中点, ∴OQ为△ABP 的中位线,
当BP 最大时,OQ 最大,而BP 过圆心C时, PB 最大, =7, ∴线段 OQ的最大值是 . 故选: C.
2解: 连接PO, ∵PA⊥PB, ∴∠APB=90°,∵AO=BO, ∴AB=2PO, 若要使AB取得最小值,则PO需取得最小值,连接O、P、M三点共线时,PO最小, 过点M 作 ME⊥y轴于点 E, 在 Rt△MOE 中, 此时 PO 最小值为5-2=3,
∴AB的最小值是6, 故选: C.
3解: 如图, 延长BF交CD的延长线于 H,
∵四边形ABCD是平行四边形,∴AB=CD=5,AB∥CD,
∴∠H=∠ABF, ∵EF∥AB, ∴EF∥CD,
∵E是边 BC的中点, ∴EF是△BCH的中位线,
∴BF=FH, ∵∠BFC=90°, ∴CF⊥BF, ∴CF是BH的中垂线, ∴BC=CH=8, ∴DH=CH-CD=3,
在△ABF和△GHF中,
∴△ABF≌△GFH(ASA) , ∴AB=GH=5,
∴DG=GH-DH=2, 故选: D.
解法二: 由梯形中位线可知: 2EF=AB+CG, EF=4,∴2×4=5+CG, ∴CG=3, ∴DG=CD-CG=5-3=2
4解: 连接CH 并延长交AD于 P, 连接PE,∵四边形ABCD是正方形, ∴∠A=90°, AD∥BC, AB=AD=BC=2 , ∵E,F分别是边AB, BC的中点,∴
∵AD∥BC, ∴∠DPH=∠FCH, ∵∠DHP=∠FHC, DH=FH, ∴△PDH≌△CFH (AAS) , ∴PD=CF= ∵点G, H分别是EC, CP的中点,
5解: 如图所示, 连接AE,
∵M, N分别是EF, AF的中点,
∴MN是△AEF的中位线,
∴当AE 取最大值时,MN有最大值.
∵四边形ABCD 是正方形, ∠B=90°,
∴当BE 最大时,AE 最大,此时MN 最大,
∵点E 是BC上的动点,
∴当点E 和点C重合时,BE最大,即BC的长度,∴此时
∴MN的最大值为
故答案为:
6解:连接BP,点O 是AB的中点,则OQ是△ABP的中位线,则 当B、C、P三点共线时,PB 最大,则OQ有最大值.而 OQ 的最大值为2,故BP的最大值为4, 则BC=BP-PC=4-1=3,设点B (m, - m) , ∵C(2, 2)
则 解得: 故答案为
7解: 如图1, 延长CE、DA 交于Q, ∵四边形ABCD是矩形, BC=6, ∴∠BAD=90° , AD=BC=6, AD∥BC, ∵F为AD中点, ∴AF=DF=3,
在 Rt△BAF 中,由勾股定理得: ∵AD∥BC, ∴∠Q=∠ECB,
∵E为AB的中点, AB=4, ∴AE=BE=2,在△QAE 和△CBE中, CBE (AAS) , ∴AQ=BC=6, 即QF=6+3=9,
∵BF=5, ∴BM=2, FM=3,
如图2, 延长BF和CD, 交于W, 同理AB=DW=4,CW=8,BF=FW=5, ∵AB∥CD, ∴△BNE∽△WND, 解得:BN=
故答案为:
8解:取AB中点 P,连接OP、CP,则 =2, 由勾股定理得, 利用三角形两边之和大于点三边可知:OC≤OP+PC= 即当O、P、C三点共线时OC有最大值,OC的长的最大值为 故答案为:
9解: ∵四边形ABCD 是平行四边形, ∴AD=BC, CD=AB, DC∥AB, ∵AD=3, AB=CF=2,
∴CD=2, BC=3, ∴BF=BC+CF=5, ∵△BEF是等边三角形, G为DE的中点, ∴BF=BE=5, DG=EG,
延长CG交BE于点 H, ∵DC∥AB, ∴∠CDG=∠HEG,
在△DCG和△EHG中, △DCG≌△EHG(ASA), ∴DC=EH, CG=HG, ∵CD=2,BE=5,
∴HE=2, BH=3, ∵∠CBH=60° , BC=BH=3,
∴△CBH是等边三角形, ∴CH=BC=3,
故答案为:
解法二:延长DC 交 FE于点 M,则CG 是△DEM的中位线,则
10解:连接AC,MC.由翻折的性质可知,BE 垂直平分线段CF, ∵FM⊥BE, ∴F. M, C共线, FM=MC,
, ∵四边形ABCD 是矩形,
故答案为5.
11解: 连接CF,
∵正方形ABCD和正方形BEFG中, AB=7, BE=5,∴GF=GB=5, BC=7, ∴GC=GB+BC=5+7=12,∴CF=√GF +GC =13. ∵M、1N分别是DC、DF的中点, 故答案为:
12解: 延长BC至M, 使CM=CA,连接AM, 作CN⊥AM于 N, ∵DE平分△ABC的周长, ∴ME=EB,
又∵AD=DB,∴DE是△ABM的中位线,
DE∥AM, ∵∠ACB=60° , ∴∠ACM=120°,
∵CM=CA, ∴∠ACN=60° , AN=MN, ∠NAC=30°
故答案为:
13解: 如图, 过点 C作 CG∥AB交ED的延长线于点G, 连接FG, ∵点D是AB的中点, ∴AD=CD,∵AB∥GC, ∴∠B=∠BCG=90°,
在△ADE和△CDG中, △CDG(ASA),∴EF=FG,EA=GC,∴FG =FC +GG , 在Rt△BEF 中, 2, 故答案为: 2.
14 证明: 连接DE,
∵点G是△ABC的重心,∴点E 和点 D 分别是AB 和BC的中点, ∴DE 是△ABC的中位线, ∴DE∥AC且 即AD=3GD.
15 解: (1) ∵AC平分∠BAD, AB∥CD,
∴∠DAC=∠BAC, ∠DCA=∠BAC,
∴∠DAC=∠DCA, ∴AD=DC,又∵AB∥CD, AB=AD,
∴AB∥CD且AB=CD, ∴四边形ABCD 是平行四边形,∵AB=AD, ∴四边形ABCD 是菱形.
(2) 连接BD, 交AC于点O, (自行画图)
∵菱形ABCD的边长为13, 对角线AC=24, ∴CD=13,AO=CO=12, ∵点E、F分别是边 CD、BC的中点,
∴EF∥BD(中位线), ∵AC、BD是菱形的对角线,
∴AC⊥BD, OB=OD, 又∵AB∥CD, EF∥BD,
∴DE∥BG, BD∥EG, ∴四边形BDEG是平行四边形,
∴BD=EG. 在△COD中. ∵OC⊥OD, CD=13,
16解: (1)四边形BEAC是平行四边形,理由如下:
∵△AED 为等腰三角形,∠EAD=90°, B是DE的中点,
∴∠E=∠BAE=45° , ∠ABE=90° ,
∵△ABC 是等腰三角形, ∠BAC=90°,
∴∠ABC=∠BAE=45° , ∠ABE=∠BAC=90° ,
∴BC∥AE, AC∥BE, ∴四边形BEAC是平行四边形;
(2) ①∵△ABC和△AED 均为等腰直角三角形,∠BAC=∠EAD=90° , ∴AE=AD, AB=AC,∠BAE=∠CAD, ∴△AEB≌△ADC(SAS) ,∴BE=CD;
②延长FG至点H, 使GH=FG,
∵G是EC的中点, ∴EG=CG,
又∵∠EGH=∠FGC, ∴△EGH≌△CGF(SAS),
∴∠BFC=∠H, CF=EH,
∵CF=CD, CD=BE,
∴EH=BE, ∴∠H=∠EBG, ∴∠EBG=∠BFC.
17 解: 取MP的中点Q, 连接AQ, OQ, AO,∴AQ是 Rt△APM 斜边上的中线, 又∵ 线段 MN始终经过矩形的对称中心,
∴O是MN的中点, ∴OQ 是△MPN的中位线,
∴C△PMN=PM+PN+MN=2AQ+2OQ+2ON
=2(AQ+OQ+ON) =2(AO+ON)
∵点O 是固定点,∴AO 是定值, 当ON取最小时,2(AO+ON)有最小值,即为所求△MPN周长的最小值.
作OG⊥BC,垂足为G,此时OG=2即为ON的最小值,∴△PMN周长的最小值为
故答案为:
18 (1) 证明: 如图1, 连接BD, 取DB的中点 H,连接EH, FH, ∵E, H分别是AD, BD的中点.
∴EH 是△ABD的中位线 ∴∠BME=∠HEF, ∵F, H分别是BC, BD的中点,∴FH 是△BCD的中位线 ∴∠CNE=∠HFE, ∵AB=CD∴HE=FH,
∴∠HEF=∠HFE∴∠BME=∠CNE;
(2)如图2,连接BD,取DB的中点H,连接EH, FH,∵E, F分别是AD, BC的中点, ∴EH是△ABD的中位线, FH 是△BCD的中位线, CD, FH∥AC, ∴∠HFE=∠FEC=45°, ∵AB=CD=2, ∴HF=HE=1, ∴∠HEF=∠HFE=45° , ∴△EFH 是等腰直角三角形,
19 解: ①∵D为BC的中点, ∴BD=CD,
∴△ABD 与△ACD的周长之差为 (AB+AD+BD)(AC+AD+CD) =AB--AC. ∵AB=7, AC=5,
②证明:如图1,延长AD至G,使DG=AD,连接BG,∵D是BC的中点, ∴BD=CD,
在△BDG和△CDA中,
∴△BDG≌△CDA(SAS), ∴∠G=∠CAD,BG=AC,
∵AF=EF, ∴∠CAD=∠AEF, ∴∠G=∠AEF=∠BEG, ∴BE=BG, ∴AC=BE;
(2) 证明: 如图2, 在AB上截取AE=AC, 连接DE,∵AD是∠BAC的平分线, ∴∠BAD=∠CAD,
在△EAD和△CAD中,
∴△EAD≌△CAD(SAS), ∴∠AED=∠C, ED=CD,
∵AC+CD=AB, 且AB=AE+EB, ∴CD=ED=EB,∴∠B=∠BDE, ∴∠AED=∠B+∠BDE=2∠B,即∠C=2∠B.
20【问题情境】解: (1) 在△ADC和△EDB中,
(2) 由 (1) 得: △ADC≌△EDB, ∴AC=BE=6,在△ABE中, AB--BE
∵在△ADC和△MDB中,
∴△ADC≌△MDB(SAS), ∴BM=AC, ∠CAD=∠M,
∵AE=EF, ∴∠CAD=∠AFE, ∵∠AFE=∠BFD,
∴∠BFD=∠CAD=∠M, ∴BF=BM=AC=7;
【灵活运用】解:线段BE、CF、EF之间的等量关系为: 理由如下:延长ED 到点G,使DG=ED,连接GF, GC, 如图③所示:
∵ED⊥DF, ∴EF=GF, ∵D是BC的中点,
∴BD=CD, 在△BDE和△CDG中,
∴△DBE≌△DCG(SAS) , ∴BE=CG, ∵∠A=90°,
∴∠B+∠ACB=90° ,
∵△DBE≌△DCG, EF=GF,
∴BE=CG, ∠B=∠GCD, ∴∠GCD+∠ACB=90°, 即∠GCF=90° ,
∴Rt△CFG中, 由勾股定理得:
同课章节目录
