2025年中考数学复习--旋转模型(含解析)
文档属性
| 名称 | 2025年中考数学复习--旋转模型(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 655.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 00:00:00 | ||
图片预览



文档简介
旋转模型
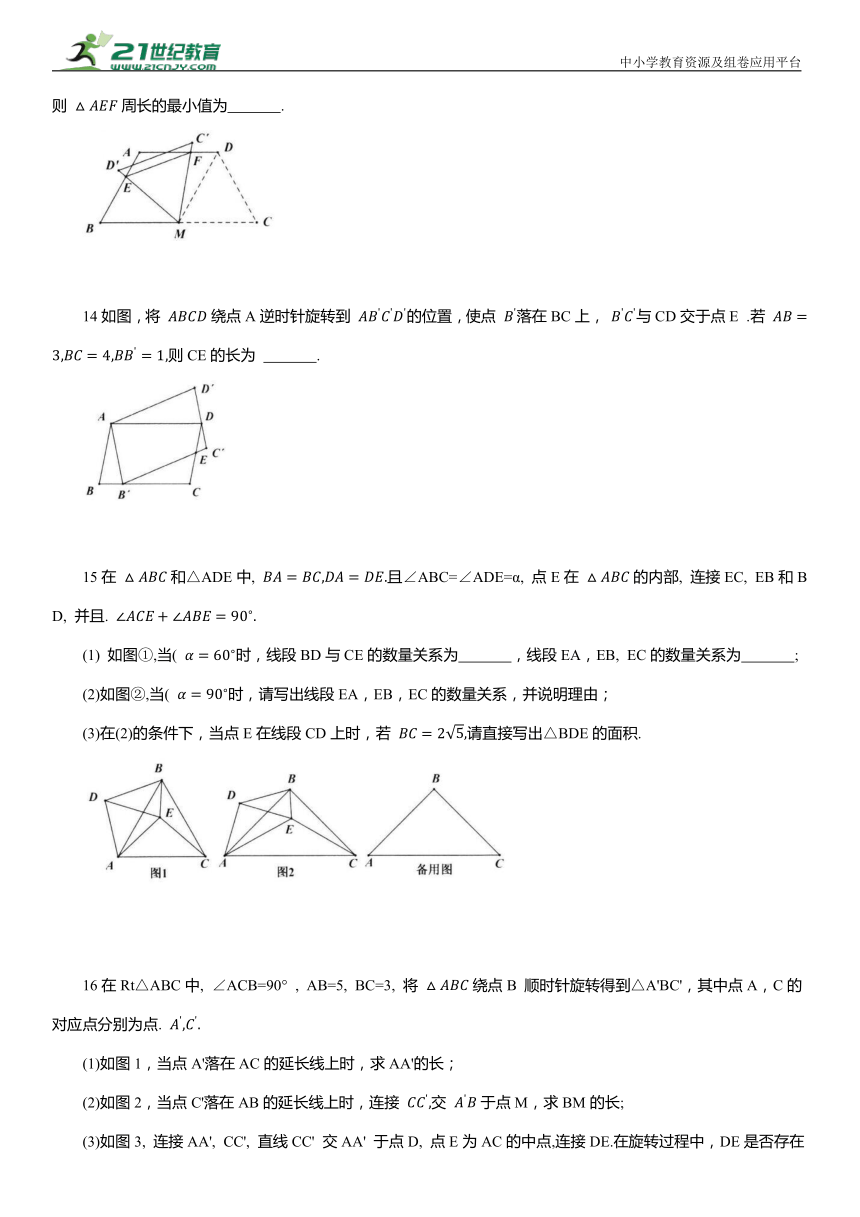
1如图,P为等边三角形ABC内的一点,且P到三个顶点A,B,C的距离分别为34, 5, 则△ABC 的面积为( )
2如图,平面内三点A、B、C,AB=5, AC=3, 以BC为对角线作正方形BDCE, 连接AD,则AD的最大值是( )
C. 4 D. 8
3如图,在矩形ABCD 中, 点E 是 AB的中点, 点F 是 BC的中点, 连接EF, G是EF的中点, 连接DG. 在△BEF中, BE=2, ∠BFE=30°, 若将△BEF 绕点B逆时针旋转,则在旋转的过程中,线段DG长的最大值是 ( )
C. 10 D. 12
4如图,点P 是正方形ABCD内一点,且点P 到点A、B、C的距离分别为 4,则正方形 ABCD的面积为 .
5如图, 在正方形ABCD外取一点E, 连接DE, AE, CE, 过点 D作 DE 的垂线交AE于点P,若] 下列结论: ①△APD≌△CED; ②AE⊥CE; ③点C到直线DE的距离为 ④S 正方形 其中正确结论的序号为 .
6如图,在 中, 将 绕点A逆时针旋转 得到△AB'C',若P为CB上一动点,旋转后点P 的对应点为点P',则线段 PP'长度的最小值是 .
7如图,△ABC是等边三角形,点 D 为BC 边上一点, 以点D为顶点作正方形DEFG, 且DE=BC, 连接AE, AG. 若将正方形DEFG绕点D旋转一周,当AE 取最小值时,AG 的长为 .
8如图1, 在Rt△ABC中, ∠ABC=90° , AB=8, BC=6, D是AB上一点, 且. 2,过点D作DE∥BC交AC于E,将△ADE绕A 点顺时针旋转到图2的位置.则图2中 的值为 .
9如图,已知点A(3,0),点B在y轴正半轴上,将线段AB绕点A顺时针旋转 到线段AC,若点C的坐标为(7,h),则
10如图,边长为 的等边三角形ABC 中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C 逆时针旋转( 得到FC,连接DF,则在点E运动过程中,DF的最小值是 .
11如图,等边三角形ABC 内有一点 P,分别连接AP、BP、CP,若 CP=10. 则
12如图,已知 是等腰三角形, AB=AC, ∠BAC=45°, 点D在AC边上, 将△ABD绕点A逆时针旋转45°得到△ACD',且点D' 、D、B三点在同一条直线上,则 的度数是 .
13如图,等腰梯形ABCD中, ,M是BC的中点.将 学习笔记: 绕点M 旋转,当MD (即 与AB交于一点E, MC(即 同时与AD交于一点F时,点E,F和点A 构成. 则 周长的最小值为 .
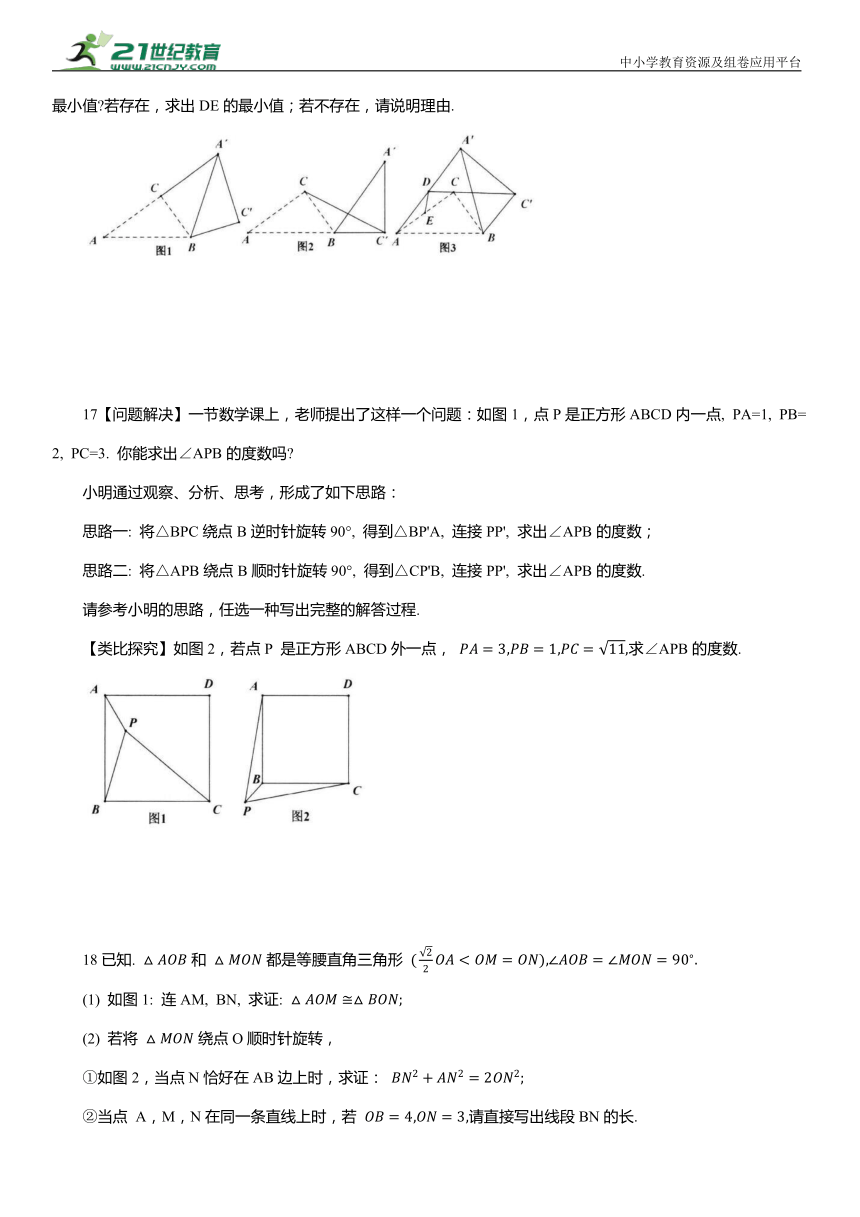
14如图,将 绕点A逆时针旋转到 的位置,使点 落在BC上, 与CD交于点E .若 则CE的长为 .
15在 和△ADE中, 且∠ABC=∠ADE=α, 点E在 的内部, 连接EC, EB和BD, 并且.
(1) 如图①,当( 时,线段BD与CE的数量关系为 ,线段EA,EB, EC的数量关系为 ;
(2)如图②,当( 时,请写出线段EA,EB,EC的数量关系,并说明理由;
(3)在(2)的条件下,当点E在线段CD上时,若 请直接写出△BDE的面积.
16在Rt△ABC中, ∠ACB=90° , AB=5, BC=3, 将 绕点B 顺时针旋转得到△A'BC',其中点A,C的对应点分别为点.
(1)如图1,当点A'落在AC的延长线上时,求AA'的长;
(2)如图2,当点C'落在AB的延长线上时,连接 交 于点M,求BM的长;
(3)如图3, 连接AA', CC', 直线CC' 交AA' 于点D, 点E为AC的中点,连接DE.在旋转过程中,DE是否存在最小值 若存在,求出DE的最小值;若不存在,请说明理由.
17【问题解决】一节数学课上,老师提出了这样一个问题:如图1,点P是正方形ABCD内一点, PA=1, PB=2, PC=3. 你能求出∠APB的度数吗
小明通过观察、分析、思考,形成了如下思路:
思路一: 将△BPC绕点B逆时针旋转90°, 得到△BP'A, 连接PP', 求出∠APB的度数;
思路二: 将△APB绕点B顺时针旋转90°, 得到△CP'B, 连接PP', 求出∠APB的度数.
请参考小明的思路,任选一种写出完整的解答过程.
【类比探究】如图2,若点P 是正方形ABCD外一点, 求∠APB的度数.
18已知. 和 都是等腰直角三角形
(1) 如图1: 连AM, BN, 求证:
(2) 若将 绕点O顺时针旋转,
①如图2,当点N恰好在AB边上时,求证:
②当点 A,M,N在同一条直线上时,若 请直接写出线段BN的长.
19如图1,若四边形ABCD、四边形GFED都是正方形,显然图中有
(1)当正方形GFED绕D 旋转到如图2的位置时, 是否成立 若成立,请给出证明;若不成立,请说明理由;
(2)当正方形GFED 绕D旋转到如图3的位置时,延长CE交AG于H,交AD于M.
①求证:
②当 时,求CH的长.
20已知在 中,0为BC边的中点,连接AO,将 绕点O顺时针方向旋转(旋转角为钝角) , 得到△EOF, 连接AE, CF.
(1)如图1,当∠BAC=90°且AB=AC时,则AE与CF满足的数量关系是 ;
(2) 如图2, 当 且AB≠AC时, (1)中的结论是否仍然成立 若成立,请写出证明过程;若不成立,请说明理由.
(3) 如图3, 延长AO到点D, 使OD=OA, 连接DE, 当. 时,求DE的长.
21在△ABC中, AB=AC,D是边BC上一动点, 连接AD, 将AD绕点A 逆时针旋转至AE的位置, 使得∠DAE+∠BAC=180° .
(1)如图1, 当∠BAC=90°时, 连接BE, 交AC于点F. 若BE平分∠ABC, BD=2, 求AF的长;
(2)如图2,连接BE,取BE的中点G,连接AG.猜想AG与CD存在的数量关系,并证明你的猜想;
(3)如图3, 在(2)的条件下, 连接DG, CE. 若∠BAC=120°, 当BD>CD,∠AEC=150°时, 请直接写出 的值.
22在 中, 中, , 点B,C,E不共线, 点P为直线DE上一点, 且
(1)如图1,点D 在线段BC 延长线上,则. (用含α的代数式表示);
(2) 如图2, 点A, E在直线BC同侧, 求证: BP 平分.
(3) 若 将图3中的 绕点C按顺时针方向旋转,当BP⊥DE时, 直线PC交BD于点G, 点M是PD 中点, 请直接写出GM的长.
23已知 点F在直线BC上,以AF为边作等边三角形AFE,过点E作 于点 D.请解答下列问题:
(1) 如图①, 求证:
(2)如图②、图③,线段AB,BF,BD又有怎样的数量关系 请写出你的猜想,不需要证明.
24如图1, 在△ABC中, ∠C=90° , ∠ABC=30° , AC=1, D为 内部的一动点(不在边上),连接BD,将线段BD绕点D逆时针旋转( ,使点B到达点F的位置;将线段AB绕点B顺时针旋转 ,使点A 到达点E 的位置,连接AD,CD, AE, AF, BF, EF.
(1) 求证: △BDA≌△BFE;
(2) ①CD+DF+FE的最小值为 ;
②当CD+DF+FE 取得最小值时, 求证: AD∥BF.
(3)如图2, M, N, P分别是DF, AF, AE的中点, 连接MP,NP, 在点D运动的过程中,请判断∠MPN的大小是否为定值.若是,求出其度数;若不是,请说明理由.
25如图, 在△ABC中, ,过点A 作射线AM交射线BC于点D,将AM绕点A 逆时针旋转α得到 AN,过点C作CF∥AM交直线AN于点 F, 在 AM上取点E, 使∠AEB=∠ACB.
(1) 当AM与线段BC 相交时,
①如图1, 当α=60°时, 线段AE, CE和CF之间的数量关系为 .
②如图2,当α=90°时,写出线段AE,CE和CF之间的数量关系,并说明理由.
(2)当 时,若△CDE是直角三角形,直接写出AF 的长.
1 解: 为等边三角形, . 可将 绕点 B 逆时针旋转 得 连EP,且延长BP,作 于点F.如图,
C
∴BE=BP=4, AE=PC=5, ∠PBE=60° ,
∴△BPE为等边三角形,∴PE=PB=4,∠BPE=60°,在△AEP中,A ,
∴△APE为直角三角形,且.
∴∠APB=90°+60° =150° . ∴∠APF=30° ,
∴在 Rt△APF 中, ∴在 Rt△ABF中, 则△ABC的面积是 故选: A.
2 解: 如图, 将△BDA 绕点 D 顺时针旋转90°得到△CDM, 由旋转不变性可知: AB=CM=5, DA=DM,∠ADM=90°, ∴△ADM是等腰直角三角形, ∴AD= ∴当AM的值最大时, AD的值最大, ∵AM≤AC+CM, ∴AM≤8, ∴AM的最大值为8, ∴AD的最大值为 故选:B.
3解: 连接BG,△BEF中, BE=2, ∠BFE=30° , ∵G是EF的中点, ∴G在⊙B上,且半径为2,
∴当G在DB 的延长线上时,DG最大,
∵BE=2, BF=2 , 点E是AB的中点, 点F是BC (的中点,∴AB=4, BC=4
∴DG的最大值为8+2=10, 故选: C.
4 解: 如图, 将△ABP 绕点B 顺时针旋转90°得到△CBM, 连接PM, ·
∴PC =CM +PM , ∴∠PMC=90°,
∴∠APB+∠BPM=180°, ∴A, P, M共线, 连接AC,在 Rt△AMC中,
∴正方形ABCD的面积为
5. 解: ①∵DP⊥DE, ∴∠PDE=90°.
∴∠PDC+∠CDE=90°, ∵在正方形ABCD 中, ∠ADC=∠ADP+∠PDC=90° , AD=CD, ∴∠CDE=∠ADP.
在△APD 和△CED中,
∴△APD≌△CED (SAS), 故①正确;
②∵△APD≌△CED, ∴∠APD=∠CED,
又∵∠APD=∠PDE+∠DEP, ∠CED=∠CEA+∠DEP,
∴∠PDE=∠CEA=90°. 即AE⊥CE, 故②正确;
③过点 C作CF⊥DE的延长线于点 F,如图,
∵DE=DP, ∠PDE=90°, ∴∠DPE=∠DEP=45° .
又∵∠CEA=90° , ∴∠CEF=∠FCE=45° .
即点C到直线DE 的距离为 故③错误;
在Rt△CDF中, 故④正确.
中小学教育资源及组卷应用平台
综上所述,正确结论的序号为①②④,故答案为: ①②④.
6解: ∵将△ABC绕点 A 顺时针旋转120°,∴∠PAP=120° , AP=AP', ∴△APP'是顶角为120°的等腰三角形, ∴当PA最小时, PP'有最小值。即当PA⊥BC时,PA有最小值,即 PP'有最小值,此时,
∴线段 PP'长度的最小值
239.解: 连接AD, 在 ADE中, AE≥DE-AD.
∵DE 和AD都是固定值,如下图,当点E在 DA 延长线上时, AE=DE-AD, 此时AE 最小.
过点A作AM⊥BC于M, ·
∴DC=4, ∴BC=BD+DC=2+4=6,
∵△ABC是等边三角形, ∴AB=AC=BC=6,
∴DM=BM--BD=3-2=1, 在 Rt△ABM中, 当点 E 在 DA 延长线上时,AE=DE--AD. 此时AE取最小值,
在Rt△ADM中,
∴在 Rt△ADG中,
故答案为:8.
7.解: ∵∠ABC=90° , AB=8, BC=6,
∵DE∥BC, ∴△ADE∽△ABC,
∵将△ADE绕A 点顺时针旋转到图2的位置,
∴∠DAB=∠EAC, ∴△ADB∽△AEC, 故答案为:
8. 解: 将△AOB 绕点A 顺时针旋转120度, 得到三角形ACD, 延长DC交x轴于点E,
∵ 在直角三角形ADE中,
∴ ∠DEA=30° , 则AE=2AD=2OA=6,
过点C作CF⊥x轴于点F, 则CF=h, AF=7-3=4,
∴ EF=6-4=2,
在直角三角形CEF中, ∠CEF=30°,
故答案为:
9解: 如图, 连接BF, 由旋转可得, CE=FC,∠ECF=60°, ∵△ABC是等边三角形, ∴AC=BC,∠ACB=60°, ∴∠ACE=∠BCF,
在△ACE 和△BCF中,
∴△ACE≌△BCF(SAS), ∴∠CBF=∠CAE,
∵边长为8的等边三角形ABC中,E是对称轴AD上的一个动点, ∴∠CAE=30° , BD=4
∴∠CBF=30°, 即点F的运动轨迹为直线 BF,
∴当DF⊥BF时, DF最短, DH即为所求,此时, ∴DF的最小值是 故答案为
10.解: 如图, 将△BPC绕点 B 逆时针旋转60°后得△AP'B, 连接PP' , 根据旋转的性质可知, 旋转角∠PBP'=∠CAB=60° , BP=BP' , ∴△BPP' 为等边三角形,∴BP' =BP=8=PP'; 由旋转的性质可知, 在△BPP' 中,PP' =8,AP=6,由勾股定理的逆定理得,△APP'是直角三角形,
故答案为:
11.解: ∵将△ABD 绕点 A 逆时针旋转45°得到△ACD' , ∴∠BAC=∠CAD'=45° , AD=AD',
∴∠AD'D=67.5° , ∠D'AB=90° ∴∠ABD=22.5°
故答案为: 22.5°
245. 解: 连接AM, 过点D作 DP⊥BC于点 P, 过点A作AQ⊥BC于点Q, 即AQ∥DP, ∵AD∥BC, ∴四边形ADPQ是平行四边形, ∴AD=QP=AB=CD,
∵∠C=∠B=60° , ∴∠BAQ=∠CDP=30° , ∴CP= 即BC=1+1+2=4,∵点M是BC的中点,∴BM=2=AD, ∴四边形ABMD 是平行四边形,
∵∠C=60° , ∴∠CDP=30° , ∵CD=2, ∴CP=1,
∴由勾股定理得:
连接AM, ∵AB=AD, ∴平行四边形ABMD 是菱形,△MAB, △MAD 和△MC' D' 是等边三角形, ∠BMA=∠BME+∠AME=60° , ∠EMF=∠AMF+∠AME=60° ,
∴∠BME=∠AMF,
在△BME与△AMF中,
△AMF(ASA),∴BE=AF,ME=MF,AE+AF=AE+BE=AB, ∵∠EMF=∠DMC=60°, 故△EMF是等边三角形, EF=MF, ∵MF的最小值为点 M到AD的距离等于 DP的长,即是 即EF的最小值是 , ∴△AEF的周长=AE+AF+EF=AB+EF, ∴△AEF的周长的最小值为 故答案为:
12解:由旋转可知,∠BAB'=∠DAD',AB'=AB=3,AD'=AD=4, ∴ △BAB' ∽△DAD',
∴ AB: BB'=AD: DD'=3: 1, ∠AD'D=∠AB'B=AD'D=∠B=∠AB'B, ∴∠AD'C'=∠AD'D, 即点 D',D, C'在同一条直线上,
又∠C'=∠ECB', ∠DEC'=∠B'EC,
∴△CEB'∽△CED, ∴B'E: DE=CE: C'E=B'C:DC' , 即B' E: DE=CE: C' E=3: 设CE=x, 故答案为:
13.解: (1)∵BA=BC, DA=DE. 且∠ABC=∠ADE=60°, ∴△ABC, △ADE都是等边三角形,
∴AD=AE, AB=AC, ∠DAE=∠BAC=60° ,
∴∠DAB=∠EAC, ∴△DAB≌△EAC(SAS),
∴BD=EC, ∠ABD=∠ACE,
∵∠ACE+∠ABE=90° , ∴∠ABD+∠ABE=90°,
∵EA .故答案为
(2) 结论: 理由:如图②中,∵BA=BC, DA=DE. 且. ABC, △ADE 都是等腰直角三角形, ∴∠DAE=∠BAC ,∠ACE=∠ABD, ∵∠ACE+∠ABE=90°,∴∠ABD+∠ABE=90° , ∴∠DBE=90° ,
(3) 如图, ∵∠AED=45° , D, E, C共线,
∴∠AEC=135° , ∵△ADB∽△AEC,
∴∠ADB=∠AEC=135° ,
∵∠ADE=∠DBE=90° , ∴∠BDE=∠BED=45° ,
∴AD=DE=EC, 设AD=DE=EC=x,
在 Rt△ABC中,
在Rt△ADC中,
(负根已舍),
13.解: (1) ∵∠ACB=90° , AB=5, BC=3,
绕点B
顺时针旋转得到△A'BC',点A'落在AC 的延长线上,
∴∠A'CB=90°, A'B=AB=5,
Rt△A'BC中,
∴AA'=AC+A'C=8;
过C作CE∥A'B交AB于E,过C作CD⊥AB于D,如图2: ∵△ABC绕点 B顺时针旋转得到△A' BC' ,∴∠A'BC=∠ABC, BC=BC=3, ∵CE∥A'B,∴∠A'BC=∠CEB, ∴∠CEB=∠ABC, ∴CE=BC=3,Rt△ABC中, 中, 同理
(3)DE存在最小值,最小值是1,理由如下:如图3左, 连接A'C, 则DE是△A'AC的中位线, 当A'C最小时,DE 有最小值.
如图3右,当A'运动到BC延长线上时,A'C有最小值是A′B-BC=5-3=2, DE 的最小值是1
14解: (问题解决)思路一: 如图1,将△BPC绕点B逆时针旋转90°, 得到△BP' A, 连接PP' ,
∴△ABP'≌△CBP, ∴∠PBP'=90° ,BP'=BP=2,AP'=CP=3,在Rt△PBP'中,BP=BP'=2,∴∠BPP'=45° ,根据勾股定理得,
∴AP +PP' =AP' , ∴△APP'是直角三角形, 且∠APP'=90° ,∴∠APB=∠APP'+∠BPP'=90°+45°=135° ;
(思路探究)如图2,将△BPC绕点B逆时针旋转90°,得到△BP' A, 连接PP' , ∴△ABP'≌△CBP,
∴∠PBP'=90° , BP'=BP=1, AP'=CP= 在Rt△PBP'中, BP=BP'=1, ∴∠BPP'=45° ,根据勾股定理得,
∴△APP'是直角三角形, 且∠APP'=90°,
15 (1) 证明: 如图中, ∵∠AOB=∠MON=90°,∴∠AOM=∠BON,
∵AO=BO, OM=ON, ∴△AOM≌△BON(SAS).
(2) ①证明: 如图2中, 连接AM.
同法可证△AOM≌△BON, ∴AM=BN, ∠OAM=∠B=45° , ∵∠OAB=∠B=45° , ∴∠MAN=∠OAM+ 是等腰直角三角形,
②如图1中,设OA交BN于J, 过点O作OH⊥MN于H.
∵△AOM≌△BON, ∴AM=BN, ∠OAM=∠OBN,
∵∠AJN=∠BJO, ∴∠ANJ=∠JOB=90°,
∵OM=ON=3, ∠MON=90°, OH⊥MN,
如图2中,同法可证
16 (1) 解: AG=CE, 证明如下:
∵四边形ABCD, 四边形EFGD是正方形, ∴DA=DC, DG=DE, ∠ADC=∠GDE=90°, ∴∠GDA=∠EDC,∴△ADG≌△CDE (SAS) , ∴AG=CE.
(2) ①证明: ∵△ADG≌△CDE, ∴∠GAM=∠ECD,∵∠AMH=∠CMD, ∴∠AHN=∠MDC=90°,∴AG⊥CH.
②解: 如图3, 连接GE交AD 于点N, 连接AE,∵四边形EFGD是正方形,DG=2 , ∴GE⊥DF,GE=DF=4, ∴GN=NE=ND=NF=2, ∵AD=8,
∴AN=AD-ND=8-2=6,
17.解: (1) 结论: AE=CF. 理由:
∵AB=AC, ∠BAC=90° , OC=OB, ∴OA=OC=OB,AO⊥BC, ∵∠AOC=∠EOF=90°, ∴∠AOE=∠COF,∵OA=OC, OE=OF,
∴△AOE≌△COF (SAS) , ∴AE=CF.
(2) 结论成立. 理由: ∵∠BAC=90° , OC=OB,
∴OA=OC=OB,∵∠AOC=∠EOF,∴∠AOE=∠COF,
∵OA=OC, OE=OF, ∴△AOE≌△COF(SAS),
∴AE=CF.
(3) 由旋转的性质可知OE=OA, ∵OA=OD,
∴OE=OA=OD=5, ∴∠AED=90° ,
∵OA=OE, OC=OF, ∠AOE=∠COF, ∴ =OEOF,
18.解: (1) 如图1, 过点F作FQ⊥BC于 Q,
∵BE平分∠ABC, ∠BAC=90°, ∴FA=FQ,
∵AB=AC,∴∠ABC=∠ACB=45°,∴FQ= F,
∵∠BAC+∠DAE=180°, ∴∠DAE=∠BAC=90° ,
∴∠BAD=∠CAE, 由旋转知, AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE=2, ∠ABD=∠ACE=45° ,
∴∠BCE=90° , ∴∠CBF+∠BEC=90° ,
∵BE平分∠ABC, ∴∠ABF=∠CBF,
∴∠ABF+∠BEC=90° , ∵∠BAC=90° ,
∴∠ABF+∠AFB=90° ,
∴∠AFB=∠BEC, ∵∠AFB=∠CFE, ∴∠BEC=∠
理由:如图2,延长BA 至点 M,使AM=AB,连接EM, ∵G是BE的中点, ∵∠BAC+∠DAE=∠BAC+∠CAM=180°,
∴∠DAE=∠CAM, ∴∠DAC=∠EAM, ∵AB=AM,AB=AC, ∴AC=AM, ∵AD=AE, ∴△ADC≌△AEM(SAS) , ∴CD=EM, ∴AG= CD;
(3) 如图3, 连接DE, AD与BE的交点记作点 N,
∵∠BAC+∠DAE=180° , ∠BAC=120° ,
∴∠DAE=60°,∵AD=AE,∴△ADE是等边三角形,
∴AE=DE,∠ADE=∠AED=60° ,∵∠AEC=150°,
∴∠DEC=∠AEC-∠AED=90° ,在△ABC中,AB=AC, ∠BAC=120° , ∴∠ACB=∠ABC=30° ,
∵∠AEC=150° , ∴∠ABC+∠AEC=180° ,
∴点A, B, C, E四点共圆, ∴∠BEC=∠BAC=120°,
∴∠BED=∠BEC-∠DEC=30° ,
∴∠DNE=180° -∠BED-∠ADE=90° ,
∵AE=DE, ∴AN=DN, ∴BE是AD的垂直平分线,
∴AG=DG, BA=BD=AC,
∴∠ACE=∠ABE=15° , ∴∠DCE=45°,
∵∠DEC=90°, ∴∠EDC=45°=∠DCE,
∴DE=CE, ∴AD=DE,
设AG=a, 则DG=a, 由(2) 知,
过点D作DH⊥AC于 H, Rt△DHC中, ∠ACB=30°,CD=2a, ∴DH=a, 根据勾股定理得, 在Rt△AHD中,根据勾股定理得, a, ∴AC=AH+CH=a+ a,
19 (1) 解: ∵CE=CD, ∴∠D=∠E=α, ∴∠ECD=180° -2α, ∴∠ECB=∠E+∠D=2α,
∵AB=AC, ∴∠ABC=∠ACB=2α, ∵ PB=PD,
∴∠PBD=∠D=α, ∴∠ABP=∠ABC-∠PBD=α,故答案为: 180° -2α, α.
(2) 证明: 如图2中, 连接BD. ∵CB=CD, PB=PD,
∴∠CBD=∠CDB, ∠PBD=∠PDB,
∴∠PBC=∠PDC=α, ∵∠ABC=2α,
∴∠ABP=∠PBC=α, ∴PB平分∠ABC.
(3) 解: 分两种情况讨论, ①.如图3-1, ∵BP⊥PD, BP=PD, ∴△PBD是等腰直角三角形, ∵CB=CD, PB=PD, ∴PG 垂直平分线段BD, ∴BG=DG, ∵PM=MD,∴GM 是△PBM的中位线,
∵∠ABC=∠ACB=60° ,
是等边三角形,
∵CE=CD, ∴∠CDE=30° ,
∴∠PBC=∠PDC=30° , ∴∠BHC=90° ,
②.如图3-2中,同法可证GM= PB.∵∠PBC=30° ,∠GPB=∠PBC+∠PCB=45° ,
∴∠PCB=∠PCD=15° ,
综上所述,GM的长为 或
255. (1) 证明: 如图①中, 连接BE, 在BC的延长线上截取BT, 使得BT=BA, 连接AT.
∵BA=BT, ∠ABT=60°, ∴△ABT是等边三角形,∵△ABT, △AEF 是等边三角形, ∴AT=AB, AF=AE,∠TAB=∠FAE=60°, ∴∠TAF=∠BAE,
在△ATF与△ABE中,ABE(SAS) , ∴TF=BE, ∠ATB=∠ABE=60°,
∵ED⊥AB, ∴∠DEB=30°, ∴BD= BE,
∴TF=2BD, ∵BT=AB, ∴AB+BF=2BD.
(2) ①如图②, 结论: AB-BF=2BD.
理由:连接BE,在 BC的延长线上截取BT,使得BT=BA, 连接AT. ∵△ABT, △AEF 是等边三角形,
∴AT=AB, AF=AE, ∠TAB=∠FAE=60°,
∴∠TAF=∠BAE,
在△ATF与△ABE中,(4)HEF=6ABE ∴ △ATF≌△
ABE(SAS) , ∴TF=BE, ∠ATF=∠ABE=60° ,
∴∠EBD=60° , ∵ED⊥AB, ∴∠DEB=30° ,
∵BT=AB, ∴AB=2BD, ∴AB-BF=2BD.
②如图③, 结论: BF-AB=2BD. 理由: 连接BE, 在BC上截取 BT, 使得BT=BA, 连接AT.
∵△ABT, △AEF是等边三角形, ∴AT=AB, AF=AE,
∴ ∠TAF = ∠ BAE , 在 △ ATF 与△ABE 中 ,
∴TF=BE, ∠ATF=∠ABE=120° , ∴∠EBD=60°
∵ED⊥AB,∴∠DEB=30°, ∴BD= BE,
∴TF=2BD, ∵BT=AB, ∴BF-AB=2BD
21 解: (1) 证明: ∵∠DBF=∠ABE=60°,∴∠DBF-∠ABF=∠ABE-∠ABF, ∴∠ABD=∠EBF,在△BDA与△BFE中, ∴△BDA≌△BFE(SAS);
(2) ①∵两点之间, 线段最短, 即 C、D、F、E共线时CD+DF+FE 最小, ∴CD+DF+FE 最小值为CE,
∵∠ACB=90° , ∠ABC=30° , AC=1, ∴AB=2,
∴BC= , ∵∠CBE=∠ABC+∠ABE=90°,
故答案为:
②如图1: 证明: ∵BD=BF, ∠DBF=60°,
∴△BDF为等边三角形, 即∠BFD=60°, ∵C、D、F、E共线时CD+DF+FE 最小, ∴∠BFE=120°,
∵△BDA≌△BFE, ∴∠BDA=120°,
∴∠ADF=∠ADB-∠BDF=120° -60° =60° ,
∴∠ADF=∠BFD, ∴AD∥BF;
(3) ∠MPN的大小是为定值, 理由: 如图2, 连接MN,∵M, N, P分别是DF, AF, AE的中点, ∴MN∥AD,
∴AD=EF, ∴NP=MN, ∵AB=BE且∠ABE=60°,
∴△ABE为等边三角形, 设∠BEF=∠BAD=α, ∠PAN=
β, 则∠AEF=∠APN=60° -α, ∠EAD=60°+α,
∴∠PNF=60° -α+β, ∠FNM=∠FAD=60° +α-β,
∴∠PNM=∠PNF+∠FNM=60° -α+β+60° +α-β=
22 解: (1) ①结论: AE=CF+CE.
理由: 如图1中, 作 CT∥AF交AM于T.
∵AB=AC, ∠BAC=60°, ∴△ABC是等边三角形,
∴CA=CB, ∠ACB=60° ,
∵AF∥CT, CF∥AT,
∴四边形AFCT是平行四边形, ∴CF=AT,
∵∠ADC=∠BDE, ∠DEB=∠ACD,
∴△ACD∽△BED,∴AD=CD=ED,∴ADC=BDD,
∵∠ADB=∠CDE, ∴△ADB∽△CDE,
∴∠ABD=∠CED=60°, ∵CT∥AF,
∴∠CTE=∠FAE=60°, ∴△CTE 是等边三角形,
∴EC=ET, ∴AE=AT+ET=CF+CE.
故答案为: AE=CF+CE.
②如图2中,结论:
理由: 过点C作CQ⊥AE于Q. ∵CF∥AM,
∴∠CFA+∠MAN=180° , ∵∠MAN=90° ,
∴∠CFA=∠FAQ=90°, ∵∠CQA=90°, ∴四边形
AFCQ是矩形, ∴CF=AQ, ∵∠ADC=∠BDE,
∴ADDC=BDED,∵∠ADB=∠CDE,∴△ADB∽△CDE,
∴∠ABD=∠CED=45° , ∵∠CQE=90°,
∴CE= EQ, ∴AE-CF=AE-AQ=EQ,
(2) 如图3-1中, 当∠CDE=90°时, 过点 B 作BJ⊥AC于J,过点 F作FK⊥AE 于K. 在 Rt△ABJ中, tan
∵AC=AB=5, ∴CJ=AC-AJ=5-3=2,
∵FK⊥AD, ∴∠CDE=∠FKD=90°, ∴CD∥FK,
∵CF∥DK, ∴四边形CDKF是平行四边形,
∵∠FKD=90°, ∴四边形CDKF是矩形,
如图3-2中, 当∠ECD=90°时, 满足题意
∵∠AEB=∠ACB, ∴ABCE四点共圆,∴∠DAB=90°,∵CF∥AM, ∴∠AKF=∠DAB=90°, 在Rt△ACK中,
∵∠MAN=∠CAB, ∴∠CAN=∠DAB=90°,
∴∠CAB+∠BAF=90° , ∠BAF+∠AFK=90° ,
综上所述,满足条件的AF的值为
1如图,P为等边三角形ABC内的一点,且P到三个顶点A,B,C的距离分别为34, 5, 则△ABC 的面积为( )
2如图,平面内三点A、B、C,AB=5, AC=3, 以BC为对角线作正方形BDCE, 连接AD,则AD的最大值是( )
C. 4 D. 8
3如图,在矩形ABCD 中, 点E 是 AB的中点, 点F 是 BC的中点, 连接EF, G是EF的中点, 连接DG. 在△BEF中, BE=2, ∠BFE=30°, 若将△BEF 绕点B逆时针旋转,则在旋转的过程中,线段DG长的最大值是 ( )
C. 10 D. 12
4如图,点P 是正方形ABCD内一点,且点P 到点A、B、C的距离分别为 4,则正方形 ABCD的面积为 .
5如图, 在正方形ABCD外取一点E, 连接DE, AE, CE, 过点 D作 DE 的垂线交AE于点P,若] 下列结论: ①△APD≌△CED; ②AE⊥CE; ③点C到直线DE的距离为 ④S 正方形 其中正确结论的序号为 .
6如图,在 中, 将 绕点A逆时针旋转 得到△AB'C',若P为CB上一动点,旋转后点P 的对应点为点P',则线段 PP'长度的最小值是 .
7如图,△ABC是等边三角形,点 D 为BC 边上一点, 以点D为顶点作正方形DEFG, 且DE=BC, 连接AE, AG. 若将正方形DEFG绕点D旋转一周,当AE 取最小值时,AG 的长为 .
8如图1, 在Rt△ABC中, ∠ABC=90° , AB=8, BC=6, D是AB上一点, 且. 2,过点D作DE∥BC交AC于E,将△ADE绕A 点顺时针旋转到图2的位置.则图2中 的值为 .
9如图,已知点A(3,0),点B在y轴正半轴上,将线段AB绕点A顺时针旋转 到线段AC,若点C的坐标为(7,h),则
10如图,边长为 的等边三角形ABC 中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C 逆时针旋转( 得到FC,连接DF,则在点E运动过程中,DF的最小值是 .
11如图,等边三角形ABC 内有一点 P,分别连接AP、BP、CP,若 CP=10. 则
12如图,已知 是等腰三角形, AB=AC, ∠BAC=45°, 点D在AC边上, 将△ABD绕点A逆时针旋转45°得到△ACD',且点D' 、D、B三点在同一条直线上,则 的度数是 .
13如图,等腰梯形ABCD中, ,M是BC的中点.将 学习笔记: 绕点M 旋转,当MD (即 与AB交于一点E, MC(即 同时与AD交于一点F时,点E,F和点A 构成. 则 周长的最小值为 .
14如图,将 绕点A逆时针旋转到 的位置,使点 落在BC上, 与CD交于点E .若 则CE的长为 .
15在 和△ADE中, 且∠ABC=∠ADE=α, 点E在 的内部, 连接EC, EB和BD, 并且.
(1) 如图①,当( 时,线段BD与CE的数量关系为 ,线段EA,EB, EC的数量关系为 ;
(2)如图②,当( 时,请写出线段EA,EB,EC的数量关系,并说明理由;
(3)在(2)的条件下,当点E在线段CD上时,若 请直接写出△BDE的面积.
16在Rt△ABC中, ∠ACB=90° , AB=5, BC=3, 将 绕点B 顺时针旋转得到△A'BC',其中点A,C的对应点分别为点.
(1)如图1,当点A'落在AC的延长线上时,求AA'的长;
(2)如图2,当点C'落在AB的延长线上时,连接 交 于点M,求BM的长;
(3)如图3, 连接AA', CC', 直线CC' 交AA' 于点D, 点E为AC的中点,连接DE.在旋转过程中,DE是否存在最小值 若存在,求出DE的最小值;若不存在,请说明理由.
17【问题解决】一节数学课上,老师提出了这样一个问题:如图1,点P是正方形ABCD内一点, PA=1, PB=2, PC=3. 你能求出∠APB的度数吗
小明通过观察、分析、思考,形成了如下思路:
思路一: 将△BPC绕点B逆时针旋转90°, 得到△BP'A, 连接PP', 求出∠APB的度数;
思路二: 将△APB绕点B顺时针旋转90°, 得到△CP'B, 连接PP', 求出∠APB的度数.
请参考小明的思路,任选一种写出完整的解答过程.
【类比探究】如图2,若点P 是正方形ABCD外一点, 求∠APB的度数.
18已知. 和 都是等腰直角三角形
(1) 如图1: 连AM, BN, 求证:
(2) 若将 绕点O顺时针旋转,
①如图2,当点N恰好在AB边上时,求证:
②当点 A,M,N在同一条直线上时,若 请直接写出线段BN的长.
19如图1,若四边形ABCD、四边形GFED都是正方形,显然图中有
(1)当正方形GFED绕D 旋转到如图2的位置时, 是否成立 若成立,请给出证明;若不成立,请说明理由;
(2)当正方形GFED 绕D旋转到如图3的位置时,延长CE交AG于H,交AD于M.
①求证:
②当 时,求CH的长.
20已知在 中,0为BC边的中点,连接AO,将 绕点O顺时针方向旋转(旋转角为钝角) , 得到△EOF, 连接AE, CF.
(1)如图1,当∠BAC=90°且AB=AC时,则AE与CF满足的数量关系是 ;
(2) 如图2, 当 且AB≠AC时, (1)中的结论是否仍然成立 若成立,请写出证明过程;若不成立,请说明理由.
(3) 如图3, 延长AO到点D, 使OD=OA, 连接DE, 当. 时,求DE的长.
21在△ABC中, AB=AC,D是边BC上一动点, 连接AD, 将AD绕点A 逆时针旋转至AE的位置, 使得∠DAE+∠BAC=180° .
(1)如图1, 当∠BAC=90°时, 连接BE, 交AC于点F. 若BE平分∠ABC, BD=2, 求AF的长;
(2)如图2,连接BE,取BE的中点G,连接AG.猜想AG与CD存在的数量关系,并证明你的猜想;
(3)如图3, 在(2)的条件下, 连接DG, CE. 若∠BAC=120°, 当BD>CD,∠AEC=150°时, 请直接写出 的值.
22在 中, 中, , 点B,C,E不共线, 点P为直线DE上一点, 且
(1)如图1,点D 在线段BC 延长线上,则. (用含α的代数式表示);
(2) 如图2, 点A, E在直线BC同侧, 求证: BP 平分.
(3) 若 将图3中的 绕点C按顺时针方向旋转,当BP⊥DE时, 直线PC交BD于点G, 点M是PD 中点, 请直接写出GM的长.
23已知 点F在直线BC上,以AF为边作等边三角形AFE,过点E作 于点 D.请解答下列问题:
(1) 如图①, 求证:
(2)如图②、图③,线段AB,BF,BD又有怎样的数量关系 请写出你的猜想,不需要证明.
24如图1, 在△ABC中, ∠C=90° , ∠ABC=30° , AC=1, D为 内部的一动点(不在边上),连接BD,将线段BD绕点D逆时针旋转( ,使点B到达点F的位置;将线段AB绕点B顺时针旋转 ,使点A 到达点E 的位置,连接AD,CD, AE, AF, BF, EF.
(1) 求证: △BDA≌△BFE;
(2) ①CD+DF+FE的最小值为 ;
②当CD+DF+FE 取得最小值时, 求证: AD∥BF.
(3)如图2, M, N, P分别是DF, AF, AE的中点, 连接MP,NP, 在点D运动的过程中,请判断∠MPN的大小是否为定值.若是,求出其度数;若不是,请说明理由.
25如图, 在△ABC中, ,过点A 作射线AM交射线BC于点D,将AM绕点A 逆时针旋转α得到 AN,过点C作CF∥AM交直线AN于点 F, 在 AM上取点E, 使∠AEB=∠ACB.
(1) 当AM与线段BC 相交时,
①如图1, 当α=60°时, 线段AE, CE和CF之间的数量关系为 .
②如图2,当α=90°时,写出线段AE,CE和CF之间的数量关系,并说明理由.
(2)当 时,若△CDE是直角三角形,直接写出AF 的长.
1 解: 为等边三角形, . 可将 绕点 B 逆时针旋转 得 连EP,且延长BP,作 于点F.如图,
C
∴BE=BP=4, AE=PC=5, ∠PBE=60° ,
∴△BPE为等边三角形,∴PE=PB=4,∠BPE=60°,在△AEP中,A ,
∴△APE为直角三角形,且.
∴∠APB=90°+60° =150° . ∴∠APF=30° ,
∴在 Rt△APF 中, ∴在 Rt△ABF中, 则△ABC的面积是 故选: A.
2 解: 如图, 将△BDA 绕点 D 顺时针旋转90°得到△CDM, 由旋转不变性可知: AB=CM=5, DA=DM,∠ADM=90°, ∴△ADM是等腰直角三角形, ∴AD= ∴当AM的值最大时, AD的值最大, ∵AM≤AC+CM, ∴AM≤8, ∴AM的最大值为8, ∴AD的最大值为 故选:B.
3解: 连接BG,△BEF中, BE=2, ∠BFE=30° , ∵G是EF的中点, ∴G在⊙B上,且半径为2,
∴当G在DB 的延长线上时,DG最大,
∵BE=2, BF=2 , 点E是AB的中点, 点F是BC (的中点,∴AB=4, BC=4
∴DG的最大值为8+2=10, 故选: C.
4 解: 如图, 将△ABP 绕点B 顺时针旋转90°得到△CBM, 连接PM, ·
∴PC =CM +PM , ∴∠PMC=90°,
∴∠APB+∠BPM=180°, ∴A, P, M共线, 连接AC,在 Rt△AMC中,
∴正方形ABCD的面积为
5. 解: ①∵DP⊥DE, ∴∠PDE=90°.
∴∠PDC+∠CDE=90°, ∵在正方形ABCD 中, ∠ADC=∠ADP+∠PDC=90° , AD=CD, ∴∠CDE=∠ADP.
在△APD 和△CED中,
∴△APD≌△CED (SAS), 故①正确;
②∵△APD≌△CED, ∴∠APD=∠CED,
又∵∠APD=∠PDE+∠DEP, ∠CED=∠CEA+∠DEP,
∴∠PDE=∠CEA=90°. 即AE⊥CE, 故②正确;
③过点 C作CF⊥DE的延长线于点 F,如图,
∵DE=DP, ∠PDE=90°, ∴∠DPE=∠DEP=45° .
又∵∠CEA=90° , ∴∠CEF=∠FCE=45° .
即点C到直线DE 的距离为 故③错误;
在Rt△CDF中, 故④正确.
中小学教育资源及组卷应用平台
综上所述,正确结论的序号为①②④,故答案为: ①②④.
6解: ∵将△ABC绕点 A 顺时针旋转120°,∴∠PAP=120° , AP=AP', ∴△APP'是顶角为120°的等腰三角形, ∴当PA最小时, PP'有最小值。即当PA⊥BC时,PA有最小值,即 PP'有最小值,此时,
∴线段 PP'长度的最小值
239.解: 连接AD, 在 ADE中, AE≥DE-AD.
∵DE 和AD都是固定值,如下图,当点E在 DA 延长线上时, AE=DE-AD, 此时AE 最小.
过点A作AM⊥BC于M, ·
∴DC=4, ∴BC=BD+DC=2+4=6,
∵△ABC是等边三角形, ∴AB=AC=BC=6,
∴DM=BM--BD=3-2=1, 在 Rt△ABM中, 当点 E 在 DA 延长线上时,AE=DE--AD. 此时AE取最小值,
在Rt△ADM中,
∴在 Rt△ADG中,
故答案为:8.
7.解: ∵∠ABC=90° , AB=8, BC=6,
∵DE∥BC, ∴△ADE∽△ABC,
∵将△ADE绕A 点顺时针旋转到图2的位置,
∴∠DAB=∠EAC, ∴△ADB∽△AEC, 故答案为:
8. 解: 将△AOB 绕点A 顺时针旋转120度, 得到三角形ACD, 延长DC交x轴于点E,
∵ 在直角三角形ADE中,
∴ ∠DEA=30° , 则AE=2AD=2OA=6,
过点C作CF⊥x轴于点F, 则CF=h, AF=7-3=4,
∴ EF=6-4=2,
在直角三角形CEF中, ∠CEF=30°,
故答案为:
9解: 如图, 连接BF, 由旋转可得, CE=FC,∠ECF=60°, ∵△ABC是等边三角形, ∴AC=BC,∠ACB=60°, ∴∠ACE=∠BCF,
在△ACE 和△BCF中,
∴△ACE≌△BCF(SAS), ∴∠CBF=∠CAE,
∵边长为8的等边三角形ABC中,E是对称轴AD上的一个动点, ∴∠CAE=30° , BD=4
∴∠CBF=30°, 即点F的运动轨迹为直线 BF,
∴当DF⊥BF时, DF最短, DH即为所求,此时, ∴DF的最小值是 故答案为
10.解: 如图, 将△BPC绕点 B 逆时针旋转60°后得△AP'B, 连接PP' , 根据旋转的性质可知, 旋转角∠PBP'=∠CAB=60° , BP=BP' , ∴△BPP' 为等边三角形,∴BP' =BP=8=PP'; 由旋转的性质可知, 在△BPP' 中,PP' =8,AP=6,由勾股定理的逆定理得,△APP'是直角三角形,
故答案为:
11.解: ∵将△ABD 绕点 A 逆时针旋转45°得到△ACD' , ∴∠BAC=∠CAD'=45° , AD=AD',
∴∠AD'D=67.5° , ∠D'AB=90° ∴∠ABD=22.5°
故答案为: 22.5°
245. 解: 连接AM, 过点D作 DP⊥BC于点 P, 过点A作AQ⊥BC于点Q, 即AQ∥DP, ∵AD∥BC, ∴四边形ADPQ是平行四边形, ∴AD=QP=AB=CD,
∵∠C=∠B=60° , ∴∠BAQ=∠CDP=30° , ∴CP= 即BC=1+1+2=4,∵点M是BC的中点,∴BM=2=AD, ∴四边形ABMD 是平行四边形,
∵∠C=60° , ∴∠CDP=30° , ∵CD=2, ∴CP=1,
∴由勾股定理得:
连接AM, ∵AB=AD, ∴平行四边形ABMD 是菱形,△MAB, △MAD 和△MC' D' 是等边三角形, ∠BMA=∠BME+∠AME=60° , ∠EMF=∠AMF+∠AME=60° ,
∴∠BME=∠AMF,
在△BME与△AMF中,
△AMF(ASA),∴BE=AF,ME=MF,AE+AF=AE+BE=AB, ∵∠EMF=∠DMC=60°, 故△EMF是等边三角形, EF=MF, ∵MF的最小值为点 M到AD的距离等于 DP的长,即是 即EF的最小值是 , ∴△AEF的周长=AE+AF+EF=AB+EF, ∴△AEF的周长的最小值为 故答案为:
12解:由旋转可知,∠BAB'=∠DAD',AB'=AB=3,AD'=AD=4, ∴ △BAB' ∽△DAD',
∴ AB: BB'=AD: DD'=3: 1, ∠AD'D=∠AB'B=AD'D=∠B=∠AB'B, ∴∠AD'C'=∠AD'D, 即点 D',D, C'在同一条直线上,
又∠C'=∠ECB', ∠DEC'=∠B'EC,
∴△CEB'∽△CED, ∴B'E: DE=CE: C'E=B'C:DC' , 即B' E: DE=CE: C' E=3: 设CE=x, 故答案为:
13.解: (1)∵BA=BC, DA=DE. 且∠ABC=∠ADE=60°, ∴△ABC, △ADE都是等边三角形,
∴AD=AE, AB=AC, ∠DAE=∠BAC=60° ,
∴∠DAB=∠EAC, ∴△DAB≌△EAC(SAS),
∴BD=EC, ∠ABD=∠ACE,
∵∠ACE+∠ABE=90° , ∴∠ABD+∠ABE=90°,
∵EA .故答案为
(2) 结论: 理由:如图②中,∵BA=BC, DA=DE. 且. ABC, △ADE 都是等腰直角三角形, ∴∠DAE=∠BAC ,∠ACE=∠ABD, ∵∠ACE+∠ABE=90°,∴∠ABD+∠ABE=90° , ∴∠DBE=90° ,
(3) 如图, ∵∠AED=45° , D, E, C共线,
∴∠AEC=135° , ∵△ADB∽△AEC,
∴∠ADB=∠AEC=135° ,
∵∠ADE=∠DBE=90° , ∴∠BDE=∠BED=45° ,
∴AD=DE=EC, 设AD=DE=EC=x,
在 Rt△ABC中,
在Rt△ADC中,
(负根已舍),
13.解: (1) ∵∠ACB=90° , AB=5, BC=3,
绕点B
顺时针旋转得到△A'BC',点A'落在AC 的延长线上,
∴∠A'CB=90°, A'B=AB=5,
Rt△A'BC中,
∴AA'=AC+A'C=8;
过C作CE∥A'B交AB于E,过C作CD⊥AB于D,如图2: ∵△ABC绕点 B顺时针旋转得到△A' BC' ,∴∠A'BC=∠ABC, BC=BC=3, ∵CE∥A'B,∴∠A'BC=∠CEB, ∴∠CEB=∠ABC, ∴CE=BC=3,Rt△ABC中, 中, 同理
(3)DE存在最小值,最小值是1,理由如下:如图3左, 连接A'C, 则DE是△A'AC的中位线, 当A'C最小时,DE 有最小值.
如图3右,当A'运动到BC延长线上时,A'C有最小值是A′B-BC=5-3=2, DE 的最小值是1
14解: (问题解决)思路一: 如图1,将△BPC绕点B逆时针旋转90°, 得到△BP' A, 连接PP' ,
∴△ABP'≌△CBP, ∴∠PBP'=90° ,BP'=BP=2,AP'=CP=3,在Rt△PBP'中,BP=BP'=2,∴∠BPP'=45° ,根据勾股定理得,
∴AP +PP' =AP' , ∴△APP'是直角三角形, 且∠APP'=90° ,∴∠APB=∠APP'+∠BPP'=90°+45°=135° ;
(思路探究)如图2,将△BPC绕点B逆时针旋转90°,得到△BP' A, 连接PP' , ∴△ABP'≌△CBP,
∴∠PBP'=90° , BP'=BP=1, AP'=CP= 在Rt△PBP'中, BP=BP'=1, ∴∠BPP'=45° ,根据勾股定理得,
∴△APP'是直角三角形, 且∠APP'=90°,
15 (1) 证明: 如图中, ∵∠AOB=∠MON=90°,∴∠AOM=∠BON,
∵AO=BO, OM=ON, ∴△AOM≌△BON(SAS).
(2) ①证明: 如图2中, 连接AM.
同法可证△AOM≌△BON, ∴AM=BN, ∠OAM=∠B=45° , ∵∠OAB=∠B=45° , ∴∠MAN=∠OAM+ 是等腰直角三角形,
②如图1中,设OA交BN于J, 过点O作OH⊥MN于H.
∵△AOM≌△BON, ∴AM=BN, ∠OAM=∠OBN,
∵∠AJN=∠BJO, ∴∠ANJ=∠JOB=90°,
∵OM=ON=3, ∠MON=90°, OH⊥MN,
如图2中,同法可证
16 (1) 解: AG=CE, 证明如下:
∵四边形ABCD, 四边形EFGD是正方形, ∴DA=DC, DG=DE, ∠ADC=∠GDE=90°, ∴∠GDA=∠EDC,∴△ADG≌△CDE (SAS) , ∴AG=CE.
(2) ①证明: ∵△ADG≌△CDE, ∴∠GAM=∠ECD,∵∠AMH=∠CMD, ∴∠AHN=∠MDC=90°,∴AG⊥CH.
②解: 如图3, 连接GE交AD 于点N, 连接AE,∵四边形EFGD是正方形,DG=2 , ∴GE⊥DF,GE=DF=4, ∴GN=NE=ND=NF=2, ∵AD=8,
∴AN=AD-ND=8-2=6,
17.解: (1) 结论: AE=CF. 理由:
∵AB=AC, ∠BAC=90° , OC=OB, ∴OA=OC=OB,AO⊥BC, ∵∠AOC=∠EOF=90°, ∴∠AOE=∠COF,∵OA=OC, OE=OF,
∴△AOE≌△COF (SAS) , ∴AE=CF.
(2) 结论成立. 理由: ∵∠BAC=90° , OC=OB,
∴OA=OC=OB,∵∠AOC=∠EOF,∴∠AOE=∠COF,
∵OA=OC, OE=OF, ∴△AOE≌△COF(SAS),
∴AE=CF.
(3) 由旋转的性质可知OE=OA, ∵OA=OD,
∴OE=OA=OD=5, ∴∠AED=90° ,
∵OA=OE, OC=OF, ∠AOE=∠COF, ∴ =OEOF,
18.解: (1) 如图1, 过点F作FQ⊥BC于 Q,
∵BE平分∠ABC, ∠BAC=90°, ∴FA=FQ,
∵AB=AC,∴∠ABC=∠ACB=45°,∴FQ= F,
∵∠BAC+∠DAE=180°, ∴∠DAE=∠BAC=90° ,
∴∠BAD=∠CAE, 由旋转知, AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE=2, ∠ABD=∠ACE=45° ,
∴∠BCE=90° , ∴∠CBF+∠BEC=90° ,
∵BE平分∠ABC, ∴∠ABF=∠CBF,
∴∠ABF+∠BEC=90° , ∵∠BAC=90° ,
∴∠ABF+∠AFB=90° ,
∴∠AFB=∠BEC, ∵∠AFB=∠CFE, ∴∠BEC=∠
理由:如图2,延长BA 至点 M,使AM=AB,连接EM, ∵G是BE的中点, ∵∠BAC+∠DAE=∠BAC+∠CAM=180°,
∴∠DAE=∠CAM, ∴∠DAC=∠EAM, ∵AB=AM,AB=AC, ∴AC=AM, ∵AD=AE, ∴△ADC≌△AEM(SAS) , ∴CD=EM, ∴AG= CD;
(3) 如图3, 连接DE, AD与BE的交点记作点 N,
∵∠BAC+∠DAE=180° , ∠BAC=120° ,
∴∠DAE=60°,∵AD=AE,∴△ADE是等边三角形,
∴AE=DE,∠ADE=∠AED=60° ,∵∠AEC=150°,
∴∠DEC=∠AEC-∠AED=90° ,在△ABC中,AB=AC, ∠BAC=120° , ∴∠ACB=∠ABC=30° ,
∵∠AEC=150° , ∴∠ABC+∠AEC=180° ,
∴点A, B, C, E四点共圆, ∴∠BEC=∠BAC=120°,
∴∠BED=∠BEC-∠DEC=30° ,
∴∠DNE=180° -∠BED-∠ADE=90° ,
∵AE=DE, ∴AN=DN, ∴BE是AD的垂直平分线,
∴AG=DG, BA=BD=AC,
∴∠ACE=∠ABE=15° , ∴∠DCE=45°,
∵∠DEC=90°, ∴∠EDC=45°=∠DCE,
∴DE=CE, ∴AD=DE,
设AG=a, 则DG=a, 由(2) 知,
过点D作DH⊥AC于 H, Rt△DHC中, ∠ACB=30°,CD=2a, ∴DH=a, 根据勾股定理得, 在Rt△AHD中,根据勾股定理得, a, ∴AC=AH+CH=a+ a,
19 (1) 解: ∵CE=CD, ∴∠D=∠E=α, ∴∠ECD=180° -2α, ∴∠ECB=∠E+∠D=2α,
∵AB=AC, ∴∠ABC=∠ACB=2α, ∵ PB=PD,
∴∠PBD=∠D=α, ∴∠ABP=∠ABC-∠PBD=α,故答案为: 180° -2α, α.
(2) 证明: 如图2中, 连接BD. ∵CB=CD, PB=PD,
∴∠CBD=∠CDB, ∠PBD=∠PDB,
∴∠PBC=∠PDC=α, ∵∠ABC=2α,
∴∠ABP=∠PBC=α, ∴PB平分∠ABC.
(3) 解: 分两种情况讨论, ①.如图3-1, ∵BP⊥PD, BP=PD, ∴△PBD是等腰直角三角形, ∵CB=CD, PB=PD, ∴PG 垂直平分线段BD, ∴BG=DG, ∵PM=MD,∴GM 是△PBM的中位线,
∵∠ABC=∠ACB=60° ,
是等边三角形,
∵CE=CD, ∴∠CDE=30° ,
∴∠PBC=∠PDC=30° , ∴∠BHC=90° ,
②.如图3-2中,同法可证GM= PB.∵∠PBC=30° ,∠GPB=∠PBC+∠PCB=45° ,
∴∠PCB=∠PCD=15° ,
综上所述,GM的长为 或
255. (1) 证明: 如图①中, 连接BE, 在BC的延长线上截取BT, 使得BT=BA, 连接AT.
∵BA=BT, ∠ABT=60°, ∴△ABT是等边三角形,∵△ABT, △AEF 是等边三角形, ∴AT=AB, AF=AE,∠TAB=∠FAE=60°, ∴∠TAF=∠BAE,
在△ATF与△ABE中,ABE(SAS) , ∴TF=BE, ∠ATB=∠ABE=60°,
∵ED⊥AB, ∴∠DEB=30°, ∴BD= BE,
∴TF=2BD, ∵BT=AB, ∴AB+BF=2BD.
(2) ①如图②, 结论: AB-BF=2BD.
理由:连接BE,在 BC的延长线上截取BT,使得BT=BA, 连接AT. ∵△ABT, △AEF 是等边三角形,
∴AT=AB, AF=AE, ∠TAB=∠FAE=60°,
∴∠TAF=∠BAE,
在△ATF与△ABE中,(4)HEF=6ABE ∴ △ATF≌△
ABE(SAS) , ∴TF=BE, ∠ATF=∠ABE=60° ,
∴∠EBD=60° , ∵ED⊥AB, ∴∠DEB=30° ,
∵BT=AB, ∴AB=2BD, ∴AB-BF=2BD.
②如图③, 结论: BF-AB=2BD. 理由: 连接BE, 在BC上截取 BT, 使得BT=BA, 连接AT.
∵△ABT, △AEF是等边三角形, ∴AT=AB, AF=AE,
∴ ∠TAF = ∠ BAE , 在 △ ATF 与△ABE 中 ,
∴TF=BE, ∠ATF=∠ABE=120° , ∴∠EBD=60°
∵ED⊥AB,∴∠DEB=30°, ∴BD= BE,
∴TF=2BD, ∵BT=AB, ∴BF-AB=2BD
21 解: (1) 证明: ∵∠DBF=∠ABE=60°,∴∠DBF-∠ABF=∠ABE-∠ABF, ∴∠ABD=∠EBF,在△BDA与△BFE中, ∴△BDA≌△BFE(SAS);
(2) ①∵两点之间, 线段最短, 即 C、D、F、E共线时CD+DF+FE 最小, ∴CD+DF+FE 最小值为CE,
∵∠ACB=90° , ∠ABC=30° , AC=1, ∴AB=2,
∴BC= , ∵∠CBE=∠ABC+∠ABE=90°,
故答案为:
②如图1: 证明: ∵BD=BF, ∠DBF=60°,
∴△BDF为等边三角形, 即∠BFD=60°, ∵C、D、F、E共线时CD+DF+FE 最小, ∴∠BFE=120°,
∵△BDA≌△BFE, ∴∠BDA=120°,
∴∠ADF=∠ADB-∠BDF=120° -60° =60° ,
∴∠ADF=∠BFD, ∴AD∥BF;
(3) ∠MPN的大小是为定值, 理由: 如图2, 连接MN,∵M, N, P分别是DF, AF, AE的中点, ∴MN∥AD,
∴AD=EF, ∴NP=MN, ∵AB=BE且∠ABE=60°,
∴△ABE为等边三角形, 设∠BEF=∠BAD=α, ∠PAN=
β, 则∠AEF=∠APN=60° -α, ∠EAD=60°+α,
∴∠PNF=60° -α+β, ∠FNM=∠FAD=60° +α-β,
∴∠PNM=∠PNF+∠FNM=60° -α+β+60° +α-β=
22 解: (1) ①结论: AE=CF+CE.
理由: 如图1中, 作 CT∥AF交AM于T.
∵AB=AC, ∠BAC=60°, ∴△ABC是等边三角形,
∴CA=CB, ∠ACB=60° ,
∵AF∥CT, CF∥AT,
∴四边形AFCT是平行四边形, ∴CF=AT,
∵∠ADC=∠BDE, ∠DEB=∠ACD,
∴△ACD∽△BED,∴AD=CD=ED,∴ADC=BDD,
∵∠ADB=∠CDE, ∴△ADB∽△CDE,
∴∠ABD=∠CED=60°, ∵CT∥AF,
∴∠CTE=∠FAE=60°, ∴△CTE 是等边三角形,
∴EC=ET, ∴AE=AT+ET=CF+CE.
故答案为: AE=CF+CE.
②如图2中,结论:
理由: 过点C作CQ⊥AE于Q. ∵CF∥AM,
∴∠CFA+∠MAN=180° , ∵∠MAN=90° ,
∴∠CFA=∠FAQ=90°, ∵∠CQA=90°, ∴四边形
AFCQ是矩形, ∴CF=AQ, ∵∠ADC=∠BDE,
∴ADDC=BDED,∵∠ADB=∠CDE,∴△ADB∽△CDE,
∴∠ABD=∠CED=45° , ∵∠CQE=90°,
∴CE= EQ, ∴AE-CF=AE-AQ=EQ,
(2) 如图3-1中, 当∠CDE=90°时, 过点 B 作BJ⊥AC于J,过点 F作FK⊥AE 于K. 在 Rt△ABJ中, tan
∵AC=AB=5, ∴CJ=AC-AJ=5-3=2,
∵FK⊥AD, ∴∠CDE=∠FKD=90°, ∴CD∥FK,
∵CF∥DK, ∴四边形CDKF是平行四边形,
∵∠FKD=90°, ∴四边形CDKF是矩形,
如图3-2中, 当∠ECD=90°时, 满足题意
∵∠AEB=∠ACB, ∴ABCE四点共圆,∴∠DAB=90°,∵CF∥AM, ∴∠AKF=∠DAB=90°, 在Rt△ACK中,
∵∠MAN=∠CAB, ∴∠CAN=∠DAB=90°,
∴∠CAB+∠BAF=90° , ∠BAF+∠AFK=90° ,
综上所述,满足条件的AF的值为
同课章节目录
