2025年中考数学复习--折叠模型(含解析)
文档属性
| 名称 | 2025年中考数学复习--折叠模型(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 508.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 16:58:08 | ||
图片预览

文档简介
折叠模型
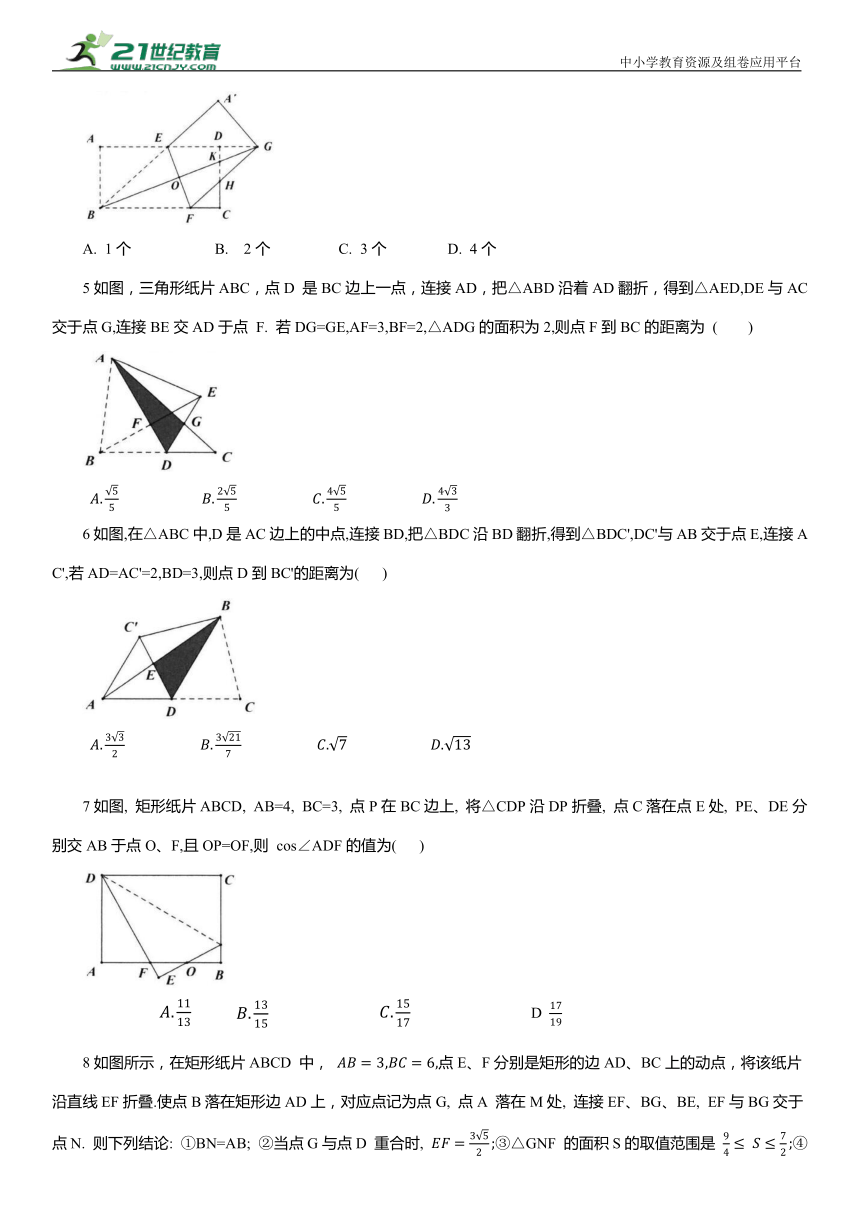
1如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平后再次折叠,使点A落在EF上的点A'处,得到折痕BM,BM与EF 相交于点N.若直线BA' 交直线CD于点O, BC=5, EN=1, 则OD的长为( )
2如图,直线EF 是矩形ABCD的对称轴,点P 在CD边上,将△BCP沿BP 折叠,点C恰好落在线段AP 与 EF 的交点Q处, 则线段AB的长是( )
A. 8 D. 10
3如图,AB是⊙O的直径,BC是⊙O的弦,先将BC弧沿BC 翻折交AB 于点 D,再将BD弧沿AB翻折交 BC于点E. 若BE弧=DE 弧, 设∠ABC=α, 则α所在的范围是( )
4如图, 矩形纸片ABCD中, AB=6, BC=12. 将纸片折叠, 使点B落在边AD 的延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上.连接BG,交CD于点K,FG交CD于点H. 给出以下结论:①EF⊥BG;②GE=GF;③△GDK和△GKH的面积相等;④当点F与点C重合时,∠DEF=75°,其中正确的结论共有( )
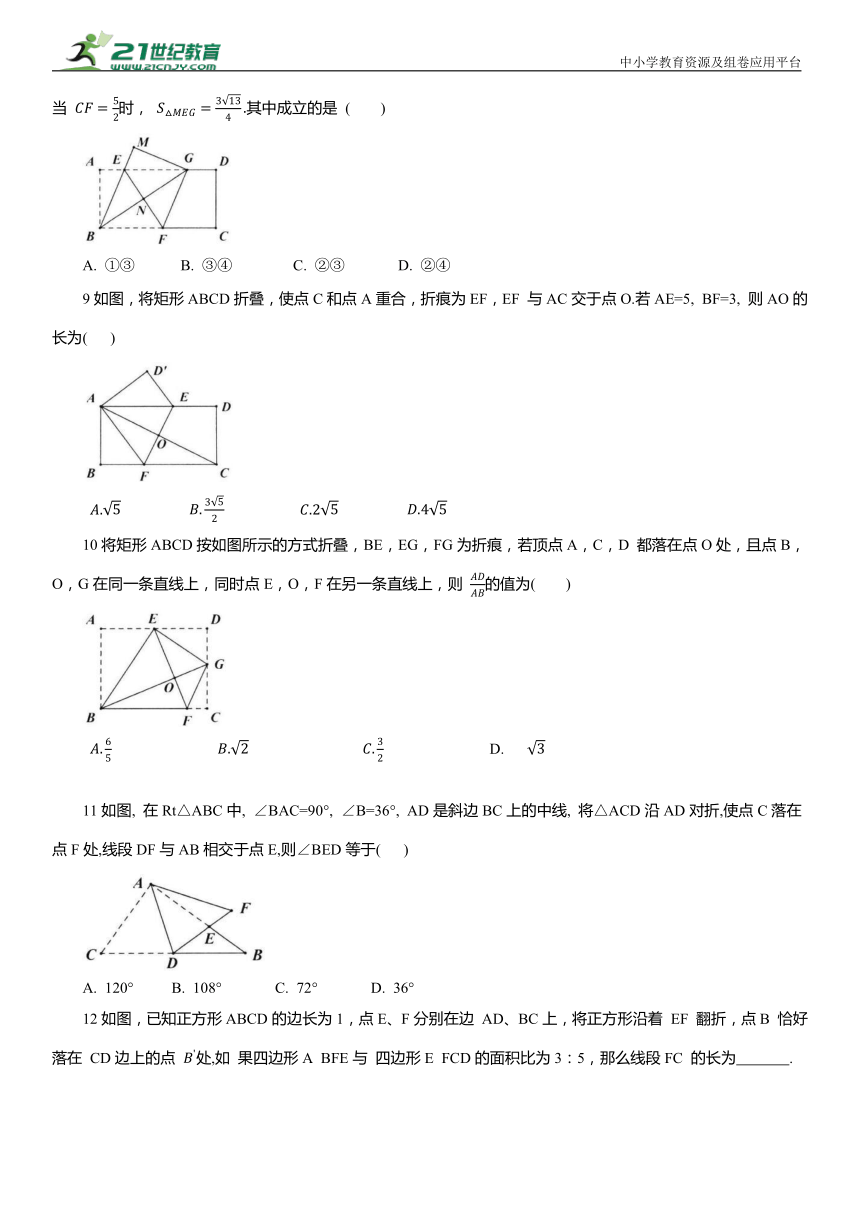
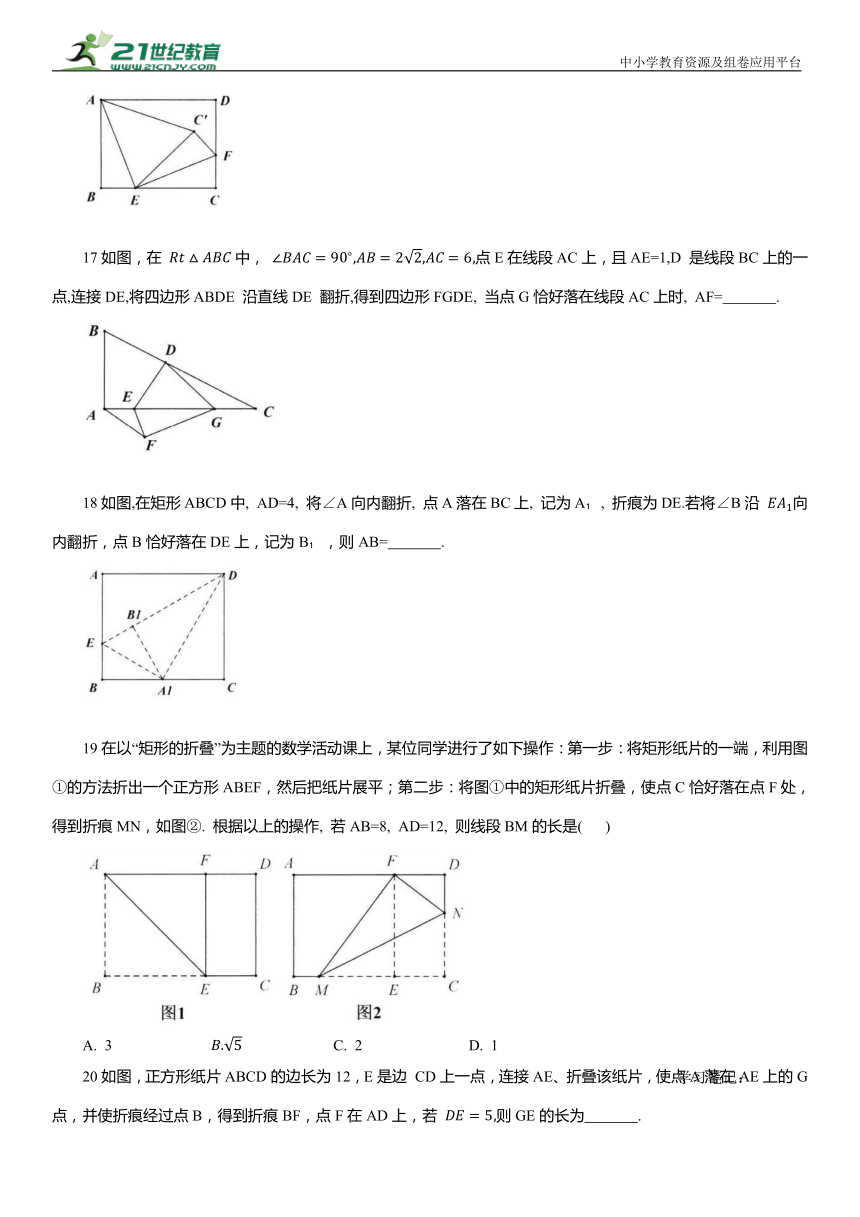
A. 1个 B. 2个 C. 3个 D. 4个
5如图,三角形纸片ABC,点D 是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△AED,DE与AC交于点G,连接BE交AD于点 F. 若DG=GE,AF=3,BF=2,△ADG的面积为2,则点F到BC的距离为 ( )
6如图,在△ABC中,D是AC边上的中点,连接BD,把△BDC沿BD翻折,得到△BDC',DC'与AB交于点E,连接AC',若AD=AC'=2,BD=3,则点D到BC'的距离为( )
7如图, 矩形纸片ABCD, AB=4, BC=3, 点P在BC边上, 将△CDP沿DP折叠, 点C落在点E处, PE、DE分别交AB于点O、F,且OP=OF,则 cos∠ADF的值为( )
8如图所示,在矩形纸片ABCD 中, 点E、F分别是矩形的边AD、BC上的动点,将该纸片沿直线EF折叠.使点B落在矩形边AD上,对应点记为点G, 点A 落在M处, 连接EF、BG、BE, EF与BG交于点N. 则下列结论: ①BN=AB; ②当点G与点D 重合时, ③△GNF 的面积S的取值范围是 ④当 时, 其中成立的是 ( )
A. ①③ B. ③④ C. ②③ D. ②④
9如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF,EF 与AC交于点O.若AE=5, BF=3, 则AO的长为( )
10将矩形ABCD按如图所示的方式折叠,BE,EG,FG为折痕,若顶点A,C,D 都落在点O处,且点B,O,G在同一条直线上,同时点E,O,F在另一条直线上,则 的值为( )
D.
11如图, 在Rt△ABC中, ∠BAC=90°, ∠B=36°, AD是斜边BC上的中线, 将△ACD沿AD对折,使点C落在点F处,线段DF与AB相交于点E,则∠BED等于( )
A. 120° B. 108° C. 72° D. 36°
12如图,已知正方形ABCD的边长为1,点E、F分别在边 AD、BC上,将正方形沿着 EF 翻折,点B 恰好落在 CD边上的点 处,如 果四边形A BFE与 四边形E FCD的面积比为3:5,那么线段FC 的长为 .
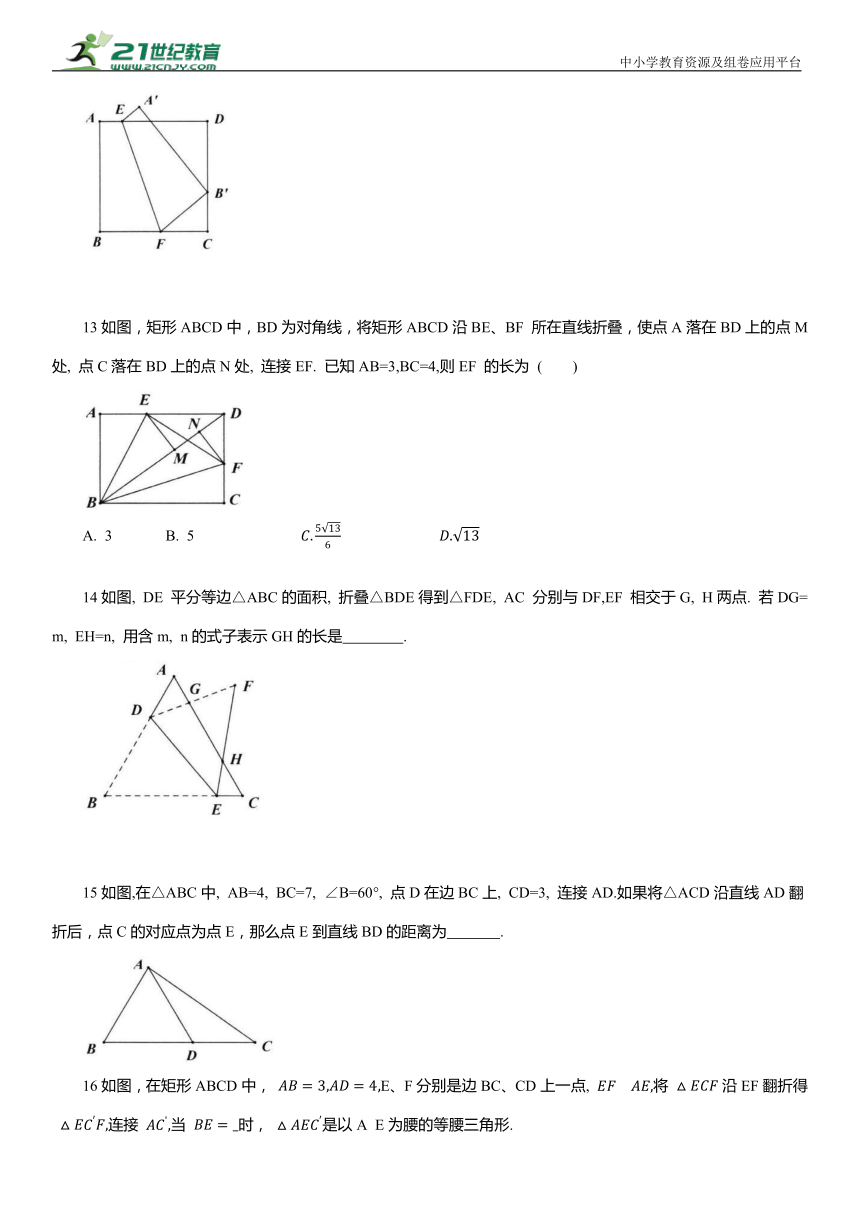
13如图,矩形ABCD中,BD为对角线,将矩形ABCD沿BE、BF 所在直线折叠,使点A落在BD上的点M处, 点C落在BD上的点N处, 连接EF. 已知AB=3,BC=4,则EF 的长为 ( )
A. 3 B. 5
14如图, DE 平分等边△ABC的面积, 折叠△BDE得到△FDE, AC 分别与DF,EF 相交于G, H两点. 若DG=m, EH=n, 用含m, n的式子表示GH的长是 .
15如图,在△ABC中, AB=4, BC=7, ∠B=60°, 点D在边BC上, CD=3, 连接AD.如果将△ACD沿直线AD翻折后,点C的对应点为点E,那么点E到直线BD的距离为 .
16如图,在矩形ABCD中, E、F分别是边BC、CD上一点, 将 沿EF翻折得 连接 当 时, 是以A E为腰的等腰三角形.
17如图,在 中, 点E在线段AC上,且AE=1,D 是线段BC上的一点,连接DE,将四边形ABDE 沿直线DE 翻折,得到四边形FGDE, 当点G恰好落在线段AC上时, AF= .
18如图,在矩形ABCD中, AD=4, 将∠A向内翻折, 点A落在BC上, 记为A , 折痕为DE.若将∠B沿 向内翻折,点B恰好落在DE上,记为B ,则AB= .
19在以“矩形的折叠”为主题的数学活动课上,某位同学进行了如下操作:第一步:将矩形纸片的一端,利用图①的方法折出一个正方形ABEF,然后把纸片展平;第二步:将图①中的矩形纸片折叠,使点C恰好落在点F处,得到折痕MN,如图②. 根据以上的操作, 若AB=8, AD=12, 则线段BM的长是( )
A. 3 C. 2 D. 1
20如图,正方形纸片ABCD的边长为12,E是边 CD上一点,连接AE、折叠该纸片,使点A落在AE上的G点,并使折痕经过点B,得到折痕BF,点F在AD上,若 则GE的长为 .
21如图,是一张矩形纸片,点E 在AB边上,把 沿直线CE对折,使点B 落在对角线AC上的点F处,连接DF.若点E,F,D在同一条直线上, 则D F
22如图, 矩形ABCD中, 点G, E分别在边BC, DC上, 连接AG, EG, AE, 将△ABG和△ECG分别沿AG,EG折叠,使点B,C恰好落在AE上的同一点,记为点F.若CE=3, CG=4, 则 sin∠DAE= .
23如图,矩形ABCD中, E为AD中点, F为AB上一点, 将△AEF沿EF 折叠后,点A 恰好落到CF上的点G 处,则折痕EF 的长是 .
24如图, 已知矩形纸片ABCD,其中AB=3,BC=4,现将纸片进行如下操作:第一步,如图①将纸片对折,使AB与DC重合,折痕为EF,展开后如图②;第二步,再将图②中的纸片沿对角线BD折叠,展开后如图③;
第三步,将图③中的纸片沿过点E的直线折叠,使点C落在对角线BD上的点H处,如图④.则DH的长为( )
A. B. C. D.
25如图,矩形ABCD中,E为边AB上一点,将△ADE沿DE 折叠,使点A的对应点F恰好落在边BC上,连接AF交DE 于点 N,连接BN.若 则矩形ABCD的面积为 .
26在矩形ABCD中,E为DC边上一点,把△ADE 沿AE翻折,使点D 恰好落在 BC边上的点 F.
(1) 求证: △ABF∽△FCE;
(2)若AB=2 , AD=4, 求EC的长;
(3) 若AE-DE=2EC, 记∠BAF=α, ∠FAE=β, 求tanα+tanβ的值.
27矩形ABCD中, .将矩形折叠,使点A落在点P 处,折痕为DE.
(1)如图①,若点P恰好在边BC上,连接AP,求 的值;
(2) 如图②, 若E是AB的中点, EP的延长线交BC于点F, 求BF 的长.
28如图,在 中,
(1)求BC边上的高线长.
(2)点E为线段AB的中点, 点F在边AC上, 连接EF, 沿EF 将 折叠得到
①如图2,当点 P落在BC上时,求 的度数.
②如图3, 连接AP, 当 时,求AP 的长.
29如图,在边长为1的正方形ABCD中,动点E、F分别在边AB、CD上,将正方形ABCD沿直线EF折叠,使点B的对应点M始终落在边AD上(点M不与点A、D重合) , 点C落在点N处, MN与CD交于点P, 设BE=x.
(1)当 时,求x的值;
(2)随着点M在边AD上位置的变化,△PDM的周长是否发生变化 如变化,请说明理由;如不变,请求出该定值;
(3)设四边形BEFC的面积为S,求S与x之间函数表达式,并求出S的最小值.
30如图,在Rt△ABC中,点 P为斜边BC上一动点,将△ABP 沿直线AP 折叠,使得点B的对应点为B',连接A
(1) 如图①, 若PB′⊥AC, 证明:}
(2) 如图②, 若AB=AC, BP=3PC, 求cos∠B'AC的值.
(3) 如图③, 若 是否存在点P,使得. 若存在,求此时 的值;若不存在,请说明理由.
1 解: 连接AA'. ∵EN=1, ∴由中位线定理得AM=2,∵对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,∴A'A=A'B, ∵把纸片展平后再次折叠,使点A 落在EF上的点A'处,得到折痕BM,
∴A'B=AB, ∠ABM=∠A'BM, ∴△ABA'为等边三角形,
∴∠ABA' =∠BA' A=∠A' AB=60° ,
又∵∠ABC=∠BAM=90° ,
∴∠ABM=∠A'BM=∠A'BC=30°,
∴BM=2AM=4, AB= AM=2 =CD.
在Rt△OBC中, ∵∠C=90° , ∠OBC=30° ,
故选: B.
2解: ∵四边形ABCD 是矩形, ∴∠C=90°,
由题意得:
由折叠的性质得: ∠BQP=∠C=90°, BQ=BC,
中小学教育资源及组卷应用平台
∴∠ABQ=30°, 在 Rt△ABQ中, AB=2AQ, 故选: A.
3解: 如图, 连接AC, CD, DE. ∵ED弧=EB弧,
∴ED=EB, ∴∠EDB=∠EBD=α,
∵AC弧=CD弧=DE弧, ∴AC=CD=DE,
∴∠DCE=∠DEC=∠EDB+∠EBD=2α,
∴∠CAD=∠CDA=∠DCE+∠EBD=3α,
∵AB 是直径, ∴∠ACB=90° ,
∴∠CAB+∠ABC=90° , ∴4α=90° , ∴α=22.5° ,故选: B.
4解: 如图, 连接BE, 设EF与BG交于点O,
∵将纸片折叠,使点B落在边AD的延长线上的点G处,
∴EF 垂直平分BG,
∴EF⊥BG, BO=GO, BE=EG, BF=FG, 故①正确,
∵AD∥BC,∴∠EGO=∠FBO, 又∵∠EOG=∠BOF,
∴△BOF≌△GOE (ASA) , ∴BF=EG,
∴BF=EG=GF, 故②正确,
∵BE=EG=BF=FG,∴四边形BEGF是菱形,∴∠BEF=∠GEF,当点F与点 C重合时,则BF=BC=BE=12,
∴∠DEF=75°, 故④正确,
∵BG平分∠EGF, 只有当DG=GH时, DK=KH, 而此时DG≠GH, ∴DK≠KH, ∴S△GDK≠S△GKH, 故③错误;故选:C.
5解: ∵DG=GE, ∴S△ADG=S△AEG=2, ∴S△ADE=4,由翻折可知, △ADB≌△ADE, BE⊥AD,
∴S△ABD=S△ADE=4, ∠BFD=90° ,
设点F到BD 的距离为h,则有 故选: B.
6. 解: 如图, 连接CC', 交 BD 于点 M, 过点 D 作DH⊥BC'于点 H, ∵AD=AC' =2, D是AC边上的中点, ∴DC=AD=2, 由翻折知, △BDC≌△BDC',BD垂直平分CC',∴DC=DC'=2,BC=BC',CM=C'M,∴AD=AC' =DC'=2, ∴△ADC'为等边三角形,∴∠ADC=∠ACD=∠CAC=60° , ∵DC=DC, 在Rt△CDM中, ∠DCC=30° , DC=2, ∴DM=1,CM= DM= , ∴BM=BD-DM=3-1=2,
在 Rt△BMC'中,
故选: B.
7 解: 根据折叠, 可知: △DCP≌△DEP,∴DC=DE=4, CP=EP.
在△OEF 和△OBP中,
∴△OEF≌△OBP(AAS) , ∴OE=OB, EF=BP.
设EF=x, 则BP=x, DF=DE-EF=4-x,
又∵BF=OB+OF=OE+OP=PE=PC,PC=BC-BP=3-x,∴AF=AB-BF=1+x. 在 Rt△DAF中, 即 解得:
故选: C.
8解: ∵AB=3是定值, BG的长是变化的, ∴BN的值也是变化的, ∴BN与AB 不一定相等,故①错误.
∵四边形ABCD是矩形, ∴AD∥BC, ∴∠DEF=∠EFB,由翻折的性质可知FB=FG, ∠EFB=∠EFG,
∴∠GEF=∠EFG, ∴GE=GF=BF, ∵GE∥BF,
∴四边形BEGF 是平行四边形, ∵FB=FG,
∴四边形BEGF 是菱形, ∴BE=EG,
如图, 当D, G重合时, 设BE=DE=x, 在Rt△ABE中,则有
故②正确,
当D,G重合时,△GNF 的面积最大,最大值 3= , ∴S△GNF≤4 故③错误,当 时,
故④正确.故选:D.
9 解: ∵矩形ABCD, ∴AD∥BC, AD=BC, AB=CD, ∴∠EFC=∠AEF, 由折叠得, ∠EFC=∠AFE,∴∠AFE=∠AEF, ∴AE=AF=5,
由折叠得, FC=AF, OA=OC, ∴BC=3+5=8,
在Rt△ABF中,
在Rt△ABC中,
故选: C.
10解: 由折叠可得, AE=OE=DE, CG=OG=DG,∴E, G分别为AD, CD的中点, 设CD=2a, AD=2b,则AB=2a=OB,DG=OG=CG=a,BG=3a,BC=AD=2b, ∵∠C=90° , ∴Rt△BCG中, ( 即 即 的值为 故选: B.
11. 解: ∵在Rt△ABC中,∠BAC=90° , ∠B=36° ,∴∠C=90° -∠B=54°.∵AD是斜边BC上的中线,∴AD=BD=CD, ∴∠BAD=∠B=36° ,∠DAC=∠C=54° , ∴∠ADC=180° -∠DAC-∠C=72° .
∵将△ACD沿AD 对折, 使点 C落在点 F处,
∴∠ADF=∠ADC=72° , ∴∠BED=∠BAD+∠ADF 故选:B.
12 解: 如图, 连接BB', 过点 F作 FH⊥AD,∵已知正方形ABCD 的边长为1,四边形ABFE与四边形EFCD 的面积比为3: 5,
设CF=x, 则DH=x, BF=1-x,
即 解得
由折叠的性质可得BB'⊥EF,
∴∠FBG+∠BFG=∠BGF=90° ,
∵∠EFH+∠BFG=∠BFH=90° ,
∴∠FBG=∠EFH,
又FH=BC=1, ∠EHF=∠C=90° ,
∴△EHF≌△B'CB (ASA) ,
在 Rt△B'FC中,
解得 故答案为:
13.解: 由折叠性质得: BM=AB=3, AE=ME, 由勾股定理的BD=5, 则 MD=BD-BM=2, 在 Rt△DEF 中, 设 ED=x, 则ME=AE=4-x, ∵ME +MD =ED , ∴ (4-x) +2 =x ,解得: 同理: DN=BD-BN=1, 由勾股定理构造方程,得
故选:C
14. 解: ∵△ABC是等边三角形,
∴∠A=∠B=∠C=60° ,
∵折叠△BDE得到△FDE, ∴△BDE≌△FDE,
∴S△BDE=S△FDE, ∠F=∠B=60° =∠A=∠C,
∵DE 平分等边△ABC 的面积,
∴四边形ACED的面积:
∵∠AGD=∠FGH, ∠CHE=∠FHG,
∴△ADG∽△FHG, △CHE∽△FHG,
解得 或 (负值,不合题意舍去),故答案为:
15 解: 如图, 过点 E 作 EH⊥BC于 H.
∵BC=7, CD=3, ∴BD=BC-CD=4,
∵AB=4=BD, ∠B=60°, ∴△ABD 是等边三角形,
∴∠ADB=60° , ∴∠ADC=∠ADE=120° ,
∴∠EDH=60°, ∴∠HED=30°, ∵EH⊥BC,
∴∠EHD=90°, ∵DE=DC=3, DH= DE=
∴E到直线BD的距离为 故答案为
16. 解: 设BE=x, 则EC=4-x, 由翻折得: EC=4-x, △AEC' 是以AE为腰的等腰三角形, 分两种情况讨论:
① 当AE=EC' 时, AE=4-x, ∵矩形ABCD,∴∠B=90°, 由勾股定理得: 解得:
②当AE=AC' 时, 如图, 作AH⊥EC'
∵EF⊥AE, ∴∠AEF=∠AEC' +∠FEC' =90° ,
∴∠BEA+∠FEC=90°,∵△ECF沿EF翻折得△EC'
F, ∴∠FEC' =∠FEC, ∴∠AEB=∠AEH,
∵∠B=∠AHE=90° , AH=AH, ∴△ABE≌△AHE(AAS), ∴BE=HE=x,∵AE=AC' , ∴EC' =2EH,即4-x=2x, 解得 综上所述: 或 故答案为: 或
17解: 如图, 过点F作FH⊥AC于H,
∵将四边形ABDE 沿直线DE 翻折,得到四边形FGDE,∴AB=FG=2 ,AE=EF=1,∠BAC=∠EFG=90° , 故答案为:
18解: 由折叠可得, A D=AD=4, ∠A=∠EA D=90° , ∠BA E=∠B A E, BA =B A , ∠B=∠A B E=90° ,
又∵
中, 故答案为:
19解: 如图1, ∵四边形ABCD是矩形,AB=8, AD=12,
∴DC=AB=8, BC=AD=12, ∠BAD=∠B=90°,由折叠得∠AFE=∠B=90°, ∴四边形ABEF 是矩形,
∵AF=AB=8, ∴四边形ABCD是正方形,
∴BE=EF=AB=8, ∠BEF=90° ,如图2, 由折叠得FM=CM,
∵在Rt△EFM中,
且EM=8-BM, FM=CM=12-BM,
解得BM=2,故选: C.
20. 解: ∵四边形ABCD为正方形, ∴AB=AD=12,∠BAD=∠D=90°, 由折叠及轴对称的性质可知,△ABF≌△GBF,BF垂直平分AG,∴BF⊥AE,AH=GH,
∴∠BAH+∠ABH=90°, 又∵∠FAH+∠BAH=90°,
∴∠ABH=∠FAH, ∴△ABF≌△DAE(ASA),
∴AF=DE=5, 在Rt△ABF中,
故答案为:
21. 解: ∵四边形ABCD是矩形,∴AD=BC, ∠ADC=∠B=∠DAE=90°, ①.∵把△BCE沿直线CE对折, 使点B落在对角线AC上的点F处, ∴CF=BC, ∠CFE=∠B=90°, EF=BE, ∴CF=AD, ∠CFD=90°,
∴∠ADE+∠CDF=∠CDF+∠DCF=90°, ∴∠ADF=∠DCF, ∴△ADE≌△FCD(ASA) , ∴DF=AE=2;
②.∵∠AFE=∠CFD=90°, ∴∠AFE=∠DAE=90°, (负值舍去), 故答案为:2,
22 解: 矩形ABCD中, GC=4, CE=3, ∠C=90°, 由翻折性质得, AF=AB,设AB=AF=x, 则AE=x+3,
在Rt△ABG中,
在Rt△AGE中,
解得:
故答案为:
23. 解: 连接EC, ∵四边形ABCD为矩形,
∴∠A=∠D=90°, BC=AD=12, DC=AB=3
∵E为AD中点, 由折叠性质可知,
AF=FG, AE=GE=DE, 连接EC, 可证△EGC≌EDC,
∴GC=DC=3 设AF=FG=x, 则1FC=FG+GC=x+3 BF=3 -x, 在Rt△BCF中,
解得: 在Rt△BCF 中,
24. 解: 如图, 过点 E 作EM⊥BD于点 M,
∵四边形ABCD为矩形, AB=3, BC=4,
∴AB=CD=3, ∠C=90° ,
在Rt△BCD中,
根据折叠的性质可得,
∴△BHE为等腰三角形 ∴BM=HM
在△BME和△BCD中:
故选: D.
25. 解: ∵将△ADE沿DE 折叠, 使点A 的对应点 F恰好落在边BC上, ∴AF⊥DE, AE=EF,
∵矩形ABCD中, ∠ABF=90°, ∴B, E, N, F四点共圆,
设
∴AE=3x, ∴AB=5x, ∴ AB= BF.
故答案为:
26. (1)证明: ∵四边形ABCD是矩形,∴∠B=∠C
=∠D=90° , 由翻折可知, ∠D=∠AFE=90° ,
∴∠AFB+∠EFC=90° , ∠EFC+∠CEF=90° ,
∴∠AFB=∠FEC, ∴△ABF∽△FCE.
(2) 设EC=x, 由翻折可知, AD=AF=4,
设AB=CD=a, BC=AD=b, DE=x,
∴AE=DE+2CE=x+2(a-x) =2a-x,
∵AD=AF=b, DE=EF=x, ∠B=∠C=∠D=90° ,
整理得,16a -24a b +9b =0, ∴ (4a -3b ) =0,
27.解: (1) 证明: 先证明△ABP 和△DAE相似,
(2)如图中,过点P作GH∥BC交AB于G,交CD于H.则四边形AGHD是矩形, 设EG=x,
∵E是AB的中点, ∴AE=4, ∴EP=AE=4
∵∠A=∠EPD=90° , ∠EGP=∠DHP=90° ,
∴∠EPG+∠DPH=90° , ∠DPH+∠PDH=90° ,
∴∠EPG=∠PDH, ∴△EGP∽△PHD,
d=AG=4+x, 在 Rt△PHD中,
解得 (负值已舍),
在 Rt△EGP 中,
∵GH∥BC, ∴△EGP∽△EBF,
28 解: (1) 如图1中, 过点A 作AD⊥BC于D.
在Rt△ABD中,
(2) ①∵△AEF≌△PEF, ∴AE=EP,∵AE=EB, ∴BE=EP, ∴∠EPB=∠B=45°,
②如图3中, 连接AP,由AE=BE=PE, 可得直角三角形ABP,由PF⊥AC,可得∠AFE=45°,可得∠FAP=45° , 即
29 解: (1) 在 Rt△AEM中, EM=BE=x,
(2) △PDM的周长不变, 为2.
理由:设AM=y,BE=EM=x,则MD=1-y,AE=1-x,在 Rt△AEM中,由勾股定理得 解得1+y =2x, ∴1-x=x-y
∴EMP=90° , ∠A=∠D,
∴ 即
解得 P的周长为2.
(4) 作FH⊥AB 于H. 则四边形BCFH是矩形.连接BM交 EF于O, 交 FH于K. 在 Rt△AEM中,EM=BE=x, AE=1-x,
∵B、M关于EF对称,∴BM⊥EF,∴∠KOF=∠KHB,
∵∠OKF=∠BKH, ∴∠KFO=∠KBH,
∵AB=BC=FH, ∠A=∠FHE=90° ,
∴△ABM≌△HFE, ∴EH=AM= x- ,
当 时,S有最小值
30 解: (1) 证明: ∵PB'⊥AC, ∠CAB=90° ,∴PB'∥AB. ∴∠B'PA=∠BAP,
又由折叠可知∠BAP=∠B'AP, ∴∠B'PA=∠B'AP. 故,
(2) 设AB=AC=B'A=a, AC、PB'交于点D,∵△ABC为等腰直角三角形, 由折叠可知, ∠PB'A=∠B=45° ,
∵∠ACB=45° , ∴∠PB'A=∠ACB,
又∵∠CDP=∠B'DA,∴△CDP∽△B'DA.∴BD=PDDA ①
设B'D=b, 则 由 得: 解得:
过点 D 作DE⊥AB'于点 E, 则△B'DE为等腰直角三角形.
又
(3) 存在点 P, 使得CB'=AB=m. 理由如下:
∵∠ACB=30° , ∠CAB=90° . ∴BC=2m.
①如图3所示,由题意可知,点B'的运动轨迹为以A为圆心、AB为半径的半圆A. 当P为BC中点时, PC=BP , 又∠B=60°, ∴△PAB为等边三角形.又由折叠可得四边形ABPB'为菱形.
∴PB'∥AB, ∴PB'⊥AC. 又∵AP=AB',
则易知AC为PB'的垂直平分线. 故CB'=PC=AB=m,满足题意.此时,
②当点 B'落在 BC 上时, 如图4所示, (2m-m)
此时CB'=AB=m, 则
综上所述, 的值为
1如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平后再次折叠,使点A落在EF上的点A'处,得到折痕BM,BM与EF 相交于点N.若直线BA' 交直线CD于点O, BC=5, EN=1, 则OD的长为( )
2如图,直线EF 是矩形ABCD的对称轴,点P 在CD边上,将△BCP沿BP 折叠,点C恰好落在线段AP 与 EF 的交点Q处, 则线段AB的长是( )
A. 8 D. 10
3如图,AB是⊙O的直径,BC是⊙O的弦,先将BC弧沿BC 翻折交AB 于点 D,再将BD弧沿AB翻折交 BC于点E. 若BE弧=DE 弧, 设∠ABC=α, 则α所在的范围是( )
4如图, 矩形纸片ABCD中, AB=6, BC=12. 将纸片折叠, 使点B落在边AD 的延长线上的点G处,折痕为EF,点E、F分别在边AD和边BC上.连接BG,交CD于点K,FG交CD于点H. 给出以下结论:①EF⊥BG;②GE=GF;③△GDK和△GKH的面积相等;④当点F与点C重合时,∠DEF=75°,其中正确的结论共有( )
A. 1个 B. 2个 C. 3个 D. 4个
5如图,三角形纸片ABC,点D 是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△AED,DE与AC交于点G,连接BE交AD于点 F. 若DG=GE,AF=3,BF=2,△ADG的面积为2,则点F到BC的距离为 ( )
6如图,在△ABC中,D是AC边上的中点,连接BD,把△BDC沿BD翻折,得到△BDC',DC'与AB交于点E,连接AC',若AD=AC'=2,BD=3,则点D到BC'的距离为( )
7如图, 矩形纸片ABCD, AB=4, BC=3, 点P在BC边上, 将△CDP沿DP折叠, 点C落在点E处, PE、DE分别交AB于点O、F,且OP=OF,则 cos∠ADF的值为( )
8如图所示,在矩形纸片ABCD 中, 点E、F分别是矩形的边AD、BC上的动点,将该纸片沿直线EF折叠.使点B落在矩形边AD上,对应点记为点G, 点A 落在M处, 连接EF、BG、BE, EF与BG交于点N. 则下列结论: ①BN=AB; ②当点G与点D 重合时, ③△GNF 的面积S的取值范围是 ④当 时, 其中成立的是 ( )
A. ①③ B. ③④ C. ②③ D. ②④
9如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF,EF 与AC交于点O.若AE=5, BF=3, 则AO的长为( )
10将矩形ABCD按如图所示的方式折叠,BE,EG,FG为折痕,若顶点A,C,D 都落在点O处,且点B,O,G在同一条直线上,同时点E,O,F在另一条直线上,则 的值为( )
D.
11如图, 在Rt△ABC中, ∠BAC=90°, ∠B=36°, AD是斜边BC上的中线, 将△ACD沿AD对折,使点C落在点F处,线段DF与AB相交于点E,则∠BED等于( )
A. 120° B. 108° C. 72° D. 36°
12如图,已知正方形ABCD的边长为1,点E、F分别在边 AD、BC上,将正方形沿着 EF 翻折,点B 恰好落在 CD边上的点 处,如 果四边形A BFE与 四边形E FCD的面积比为3:5,那么线段FC 的长为 .
13如图,矩形ABCD中,BD为对角线,将矩形ABCD沿BE、BF 所在直线折叠,使点A落在BD上的点M处, 点C落在BD上的点N处, 连接EF. 已知AB=3,BC=4,则EF 的长为 ( )
A. 3 B. 5
14如图, DE 平分等边△ABC的面积, 折叠△BDE得到△FDE, AC 分别与DF,EF 相交于G, H两点. 若DG=m, EH=n, 用含m, n的式子表示GH的长是 .
15如图,在△ABC中, AB=4, BC=7, ∠B=60°, 点D在边BC上, CD=3, 连接AD.如果将△ACD沿直线AD翻折后,点C的对应点为点E,那么点E到直线BD的距离为 .
16如图,在矩形ABCD中, E、F分别是边BC、CD上一点, 将 沿EF翻折得 连接 当 时, 是以A E为腰的等腰三角形.
17如图,在 中, 点E在线段AC上,且AE=1,D 是线段BC上的一点,连接DE,将四边形ABDE 沿直线DE 翻折,得到四边形FGDE, 当点G恰好落在线段AC上时, AF= .
18如图,在矩形ABCD中, AD=4, 将∠A向内翻折, 点A落在BC上, 记为A , 折痕为DE.若将∠B沿 向内翻折,点B恰好落在DE上,记为B ,则AB= .
19在以“矩形的折叠”为主题的数学活动课上,某位同学进行了如下操作:第一步:将矩形纸片的一端,利用图①的方法折出一个正方形ABEF,然后把纸片展平;第二步:将图①中的矩形纸片折叠,使点C恰好落在点F处,得到折痕MN,如图②. 根据以上的操作, 若AB=8, AD=12, 则线段BM的长是( )
A. 3 C. 2 D. 1
20如图,正方形纸片ABCD的边长为12,E是边 CD上一点,连接AE、折叠该纸片,使点A落在AE上的G点,并使折痕经过点B,得到折痕BF,点F在AD上,若 则GE的长为 .
21如图,是一张矩形纸片,点E 在AB边上,把 沿直线CE对折,使点B 落在对角线AC上的点F处,连接DF.若点E,F,D在同一条直线上, 则D F
22如图, 矩形ABCD中, 点G, E分别在边BC, DC上, 连接AG, EG, AE, 将△ABG和△ECG分别沿AG,EG折叠,使点B,C恰好落在AE上的同一点,记为点F.若CE=3, CG=4, 则 sin∠DAE= .
23如图,矩形ABCD中, E为AD中点, F为AB上一点, 将△AEF沿EF 折叠后,点A 恰好落到CF上的点G 处,则折痕EF 的长是 .
24如图, 已知矩形纸片ABCD,其中AB=3,BC=4,现将纸片进行如下操作:第一步,如图①将纸片对折,使AB与DC重合,折痕为EF,展开后如图②;第二步,再将图②中的纸片沿对角线BD折叠,展开后如图③;
第三步,将图③中的纸片沿过点E的直线折叠,使点C落在对角线BD上的点H处,如图④.则DH的长为( )
A. B. C. D.
25如图,矩形ABCD中,E为边AB上一点,将△ADE沿DE 折叠,使点A的对应点F恰好落在边BC上,连接AF交DE 于点 N,连接BN.若 则矩形ABCD的面积为 .
26在矩形ABCD中,E为DC边上一点,把△ADE 沿AE翻折,使点D 恰好落在 BC边上的点 F.
(1) 求证: △ABF∽△FCE;
(2)若AB=2 , AD=4, 求EC的长;
(3) 若AE-DE=2EC, 记∠BAF=α, ∠FAE=β, 求tanα+tanβ的值.
27矩形ABCD中, .将矩形折叠,使点A落在点P 处,折痕为DE.
(1)如图①,若点P恰好在边BC上,连接AP,求 的值;
(2) 如图②, 若E是AB的中点, EP的延长线交BC于点F, 求BF 的长.
28如图,在 中,
(1)求BC边上的高线长.
(2)点E为线段AB的中点, 点F在边AC上, 连接EF, 沿EF 将 折叠得到
①如图2,当点 P落在BC上时,求 的度数.
②如图3, 连接AP, 当 时,求AP 的长.
29如图,在边长为1的正方形ABCD中,动点E、F分别在边AB、CD上,将正方形ABCD沿直线EF折叠,使点B的对应点M始终落在边AD上(点M不与点A、D重合) , 点C落在点N处, MN与CD交于点P, 设BE=x.
(1)当 时,求x的值;
(2)随着点M在边AD上位置的变化,△PDM的周长是否发生变化 如变化,请说明理由;如不变,请求出该定值;
(3)设四边形BEFC的面积为S,求S与x之间函数表达式,并求出S的最小值.
30如图,在Rt△ABC中,点 P为斜边BC上一动点,将△ABP 沿直线AP 折叠,使得点B的对应点为B',连接A
(1) 如图①, 若PB′⊥AC, 证明:}
(2) 如图②, 若AB=AC, BP=3PC, 求cos∠B'AC的值.
(3) 如图③, 若 是否存在点P,使得. 若存在,求此时 的值;若不存在,请说明理由.
1 解: 连接AA'. ∵EN=1, ∴由中位线定理得AM=2,∵对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,∴A'A=A'B, ∵把纸片展平后再次折叠,使点A 落在EF上的点A'处,得到折痕BM,
∴A'B=AB, ∠ABM=∠A'BM, ∴△ABA'为等边三角形,
∴∠ABA' =∠BA' A=∠A' AB=60° ,
又∵∠ABC=∠BAM=90° ,
∴∠ABM=∠A'BM=∠A'BC=30°,
∴BM=2AM=4, AB= AM=2 =CD.
在Rt△OBC中, ∵∠C=90° , ∠OBC=30° ,
故选: B.
2解: ∵四边形ABCD 是矩形, ∴∠C=90°,
由题意得:
由折叠的性质得: ∠BQP=∠C=90°, BQ=BC,
中小学教育资源及组卷应用平台
∴∠ABQ=30°, 在 Rt△ABQ中, AB=2AQ, 故选: A.
3解: 如图, 连接AC, CD, DE. ∵ED弧=EB弧,
∴ED=EB, ∴∠EDB=∠EBD=α,
∵AC弧=CD弧=DE弧, ∴AC=CD=DE,
∴∠DCE=∠DEC=∠EDB+∠EBD=2α,
∴∠CAD=∠CDA=∠DCE+∠EBD=3α,
∵AB 是直径, ∴∠ACB=90° ,
∴∠CAB+∠ABC=90° , ∴4α=90° , ∴α=22.5° ,故选: B.
4解: 如图, 连接BE, 设EF与BG交于点O,
∵将纸片折叠,使点B落在边AD的延长线上的点G处,
∴EF 垂直平分BG,
∴EF⊥BG, BO=GO, BE=EG, BF=FG, 故①正确,
∵AD∥BC,∴∠EGO=∠FBO, 又∵∠EOG=∠BOF,
∴△BOF≌△GOE (ASA) , ∴BF=EG,
∴BF=EG=GF, 故②正确,
∵BE=EG=BF=FG,∴四边形BEGF是菱形,∴∠BEF=∠GEF,当点F与点 C重合时,则BF=BC=BE=12,
∴∠DEF=75°, 故④正确,
∵BG平分∠EGF, 只有当DG=GH时, DK=KH, 而此时DG≠GH, ∴DK≠KH, ∴S△GDK≠S△GKH, 故③错误;故选:C.
5解: ∵DG=GE, ∴S△ADG=S△AEG=2, ∴S△ADE=4,由翻折可知, △ADB≌△ADE, BE⊥AD,
∴S△ABD=S△ADE=4, ∠BFD=90° ,
设点F到BD 的距离为h,则有 故选: B.
6. 解: 如图, 连接CC', 交 BD 于点 M, 过点 D 作DH⊥BC'于点 H, ∵AD=AC' =2, D是AC边上的中点, ∴DC=AD=2, 由翻折知, △BDC≌△BDC',BD垂直平分CC',∴DC=DC'=2,BC=BC',CM=C'M,∴AD=AC' =DC'=2, ∴△ADC'为等边三角形,∴∠ADC=∠ACD=∠CAC=60° , ∵DC=DC, 在Rt△CDM中, ∠DCC=30° , DC=2, ∴DM=1,CM= DM= , ∴BM=BD-DM=3-1=2,
在 Rt△BMC'中,
故选: B.
7 解: 根据折叠, 可知: △DCP≌△DEP,∴DC=DE=4, CP=EP.
在△OEF 和△OBP中,
∴△OEF≌△OBP(AAS) , ∴OE=OB, EF=BP.
设EF=x, 则BP=x, DF=DE-EF=4-x,
又∵BF=OB+OF=OE+OP=PE=PC,PC=BC-BP=3-x,∴AF=AB-BF=1+x. 在 Rt△DAF中, 即 解得:
故选: C.
8解: ∵AB=3是定值, BG的长是变化的, ∴BN的值也是变化的, ∴BN与AB 不一定相等,故①错误.
∵四边形ABCD是矩形, ∴AD∥BC, ∴∠DEF=∠EFB,由翻折的性质可知FB=FG, ∠EFB=∠EFG,
∴∠GEF=∠EFG, ∴GE=GF=BF, ∵GE∥BF,
∴四边形BEGF 是平行四边形, ∵FB=FG,
∴四边形BEGF 是菱形, ∴BE=EG,
如图, 当D, G重合时, 设BE=DE=x, 在Rt△ABE中,则有
故②正确,
当D,G重合时,△GNF 的面积最大,最大值 3= , ∴S△GNF≤4 故③错误,当 时,
故④正确.故选:D.
9 解: ∵矩形ABCD, ∴AD∥BC, AD=BC, AB=CD, ∴∠EFC=∠AEF, 由折叠得, ∠EFC=∠AFE,∴∠AFE=∠AEF, ∴AE=AF=5,
由折叠得, FC=AF, OA=OC, ∴BC=3+5=8,
在Rt△ABF中,
在Rt△ABC中,
故选: C.
10解: 由折叠可得, AE=OE=DE, CG=OG=DG,∴E, G分别为AD, CD的中点, 设CD=2a, AD=2b,则AB=2a=OB,DG=OG=CG=a,BG=3a,BC=AD=2b, ∵∠C=90° , ∴Rt△BCG中, ( 即 即 的值为 故选: B.
11. 解: ∵在Rt△ABC中,∠BAC=90° , ∠B=36° ,∴∠C=90° -∠B=54°.∵AD是斜边BC上的中线,∴AD=BD=CD, ∴∠BAD=∠B=36° ,∠DAC=∠C=54° , ∴∠ADC=180° -∠DAC-∠C=72° .
∵将△ACD沿AD 对折, 使点 C落在点 F处,
∴∠ADF=∠ADC=72° , ∴∠BED=∠BAD+∠ADF 故选:B.
12 解: 如图, 连接BB', 过点 F作 FH⊥AD,∵已知正方形ABCD 的边长为1,四边形ABFE与四边形EFCD 的面积比为3: 5,
设CF=x, 则DH=x, BF=1-x,
即 解得
由折叠的性质可得BB'⊥EF,
∴∠FBG+∠BFG=∠BGF=90° ,
∵∠EFH+∠BFG=∠BFH=90° ,
∴∠FBG=∠EFH,
又FH=BC=1, ∠EHF=∠C=90° ,
∴△EHF≌△B'CB (ASA) ,
在 Rt△B'FC中,
解得 故答案为:
13.解: 由折叠性质得: BM=AB=3, AE=ME, 由勾股定理的BD=5, 则 MD=BD-BM=2, 在 Rt△DEF 中, 设 ED=x, 则ME=AE=4-x, ∵ME +MD =ED , ∴ (4-x) +2 =x ,解得: 同理: DN=BD-BN=1, 由勾股定理构造方程,得
故选:C
14. 解: ∵△ABC是等边三角形,
∴∠A=∠B=∠C=60° ,
∵折叠△BDE得到△FDE, ∴△BDE≌△FDE,
∴S△BDE=S△FDE, ∠F=∠B=60° =∠A=∠C,
∵DE 平分等边△ABC 的面积,
∴四边形ACED的面积:
∵∠AGD=∠FGH, ∠CHE=∠FHG,
∴△ADG∽△FHG, △CHE∽△FHG,
解得 或 (负值,不合题意舍去),故答案为:
15 解: 如图, 过点 E 作 EH⊥BC于 H.
∵BC=7, CD=3, ∴BD=BC-CD=4,
∵AB=4=BD, ∠B=60°, ∴△ABD 是等边三角形,
∴∠ADB=60° , ∴∠ADC=∠ADE=120° ,
∴∠EDH=60°, ∴∠HED=30°, ∵EH⊥BC,
∴∠EHD=90°, ∵DE=DC=3, DH= DE=
∴E到直线BD的距离为 故答案为
16. 解: 设BE=x, 则EC=4-x, 由翻折得: EC=4-x, △AEC' 是以AE为腰的等腰三角形, 分两种情况讨论:
① 当AE=EC' 时, AE=4-x, ∵矩形ABCD,∴∠B=90°, 由勾股定理得: 解得:
②当AE=AC' 时, 如图, 作AH⊥EC'
∵EF⊥AE, ∴∠AEF=∠AEC' +∠FEC' =90° ,
∴∠BEA+∠FEC=90°,∵△ECF沿EF翻折得△EC'
F, ∴∠FEC' =∠FEC, ∴∠AEB=∠AEH,
∵∠B=∠AHE=90° , AH=AH, ∴△ABE≌△AHE(AAS), ∴BE=HE=x,∵AE=AC' , ∴EC' =2EH,即4-x=2x, 解得 综上所述: 或 故答案为: 或
17解: 如图, 过点F作FH⊥AC于H,
∵将四边形ABDE 沿直线DE 翻折,得到四边形FGDE,∴AB=FG=2 ,AE=EF=1,∠BAC=∠EFG=90° , 故答案为:
18解: 由折叠可得, A D=AD=4, ∠A=∠EA D=90° , ∠BA E=∠B A E, BA =B A , ∠B=∠A B E=90° ,
又∵
中, 故答案为:
19解: 如图1, ∵四边形ABCD是矩形,AB=8, AD=12,
∴DC=AB=8, BC=AD=12, ∠BAD=∠B=90°,由折叠得∠AFE=∠B=90°, ∴四边形ABEF 是矩形,
∵AF=AB=8, ∴四边形ABCD是正方形,
∴BE=EF=AB=8, ∠BEF=90° ,如图2, 由折叠得FM=CM,
∵在Rt△EFM中,
且EM=8-BM, FM=CM=12-BM,
解得BM=2,故选: C.
20. 解: ∵四边形ABCD为正方形, ∴AB=AD=12,∠BAD=∠D=90°, 由折叠及轴对称的性质可知,△ABF≌△GBF,BF垂直平分AG,∴BF⊥AE,AH=GH,
∴∠BAH+∠ABH=90°, 又∵∠FAH+∠BAH=90°,
∴∠ABH=∠FAH, ∴△ABF≌△DAE(ASA),
∴AF=DE=5, 在Rt△ABF中,
故答案为:
21. 解: ∵四边形ABCD是矩形,∴AD=BC, ∠ADC=∠B=∠DAE=90°, ①.∵把△BCE沿直线CE对折, 使点B落在对角线AC上的点F处, ∴CF=BC, ∠CFE=∠B=90°, EF=BE, ∴CF=AD, ∠CFD=90°,
∴∠ADE+∠CDF=∠CDF+∠DCF=90°, ∴∠ADF=∠DCF, ∴△ADE≌△FCD(ASA) , ∴DF=AE=2;
②.∵∠AFE=∠CFD=90°, ∴∠AFE=∠DAE=90°, (负值舍去), 故答案为:2,
22 解: 矩形ABCD中, GC=4, CE=3, ∠C=90°, 由翻折性质得, AF=AB,设AB=AF=x, 则AE=x+3,
在Rt△ABG中,
在Rt△AGE中,
解得:
故答案为:
23. 解: 连接EC, ∵四边形ABCD为矩形,
∴∠A=∠D=90°, BC=AD=12, DC=AB=3
∵E为AD中点, 由折叠性质可知,
AF=FG, AE=GE=DE, 连接EC, 可证△EGC≌EDC,
∴GC=DC=3 设AF=FG=x, 则1FC=FG+GC=x+3 BF=3 -x, 在Rt△BCF中,
解得: 在Rt△BCF 中,
24. 解: 如图, 过点 E 作EM⊥BD于点 M,
∵四边形ABCD为矩形, AB=3, BC=4,
∴AB=CD=3, ∠C=90° ,
在Rt△BCD中,
根据折叠的性质可得,
∴△BHE为等腰三角形 ∴BM=HM
在△BME和△BCD中:
故选: D.
25. 解: ∵将△ADE沿DE 折叠, 使点A 的对应点 F恰好落在边BC上, ∴AF⊥DE, AE=EF,
∵矩形ABCD中, ∠ABF=90°, ∴B, E, N, F四点共圆,
设
∴AE=3x, ∴AB=5x, ∴ AB= BF.
故答案为:
26. (1)证明: ∵四边形ABCD是矩形,∴∠B=∠C
=∠D=90° , 由翻折可知, ∠D=∠AFE=90° ,
∴∠AFB+∠EFC=90° , ∠EFC+∠CEF=90° ,
∴∠AFB=∠FEC, ∴△ABF∽△FCE.
(2) 设EC=x, 由翻折可知, AD=AF=4,
设AB=CD=a, BC=AD=b, DE=x,
∴AE=DE+2CE=x+2(a-x) =2a-x,
∵AD=AF=b, DE=EF=x, ∠B=∠C=∠D=90° ,
整理得,16a -24a b +9b =0, ∴ (4a -3b ) =0,
27.解: (1) 证明: 先证明△ABP 和△DAE相似,
(2)如图中,过点P作GH∥BC交AB于G,交CD于H.则四边形AGHD是矩形, 设EG=x,
∵E是AB的中点, ∴AE=4, ∴EP=AE=4
∵∠A=∠EPD=90° , ∠EGP=∠DHP=90° ,
∴∠EPG+∠DPH=90° , ∠DPH+∠PDH=90° ,
∴∠EPG=∠PDH, ∴△EGP∽△PHD,
d=AG=4+x, 在 Rt△PHD中,
解得 (负值已舍),
在 Rt△EGP 中,
∵GH∥BC, ∴△EGP∽△EBF,
28 解: (1) 如图1中, 过点A 作AD⊥BC于D.
在Rt△ABD中,
(2) ①∵△AEF≌△PEF, ∴AE=EP,∵AE=EB, ∴BE=EP, ∴∠EPB=∠B=45°,
②如图3中, 连接AP,由AE=BE=PE, 可得直角三角形ABP,由PF⊥AC,可得∠AFE=45°,可得∠FAP=45° , 即
29 解: (1) 在 Rt△AEM中, EM=BE=x,
(2) △PDM的周长不变, 为2.
理由:设AM=y,BE=EM=x,则MD=1-y,AE=1-x,在 Rt△AEM中,由勾股定理得 解得1+y =2x, ∴1-x=x-y
∴EMP=90° , ∠A=∠D,
∴ 即
解得 P的周长为2.
(4) 作FH⊥AB 于H. 则四边形BCFH是矩形.连接BM交 EF于O, 交 FH于K. 在 Rt△AEM中,EM=BE=x, AE=1-x,
∵B、M关于EF对称,∴BM⊥EF,∴∠KOF=∠KHB,
∵∠OKF=∠BKH, ∴∠KFO=∠KBH,
∵AB=BC=FH, ∠A=∠FHE=90° ,
∴△ABM≌△HFE, ∴EH=AM= x- ,
当 时,S有最小值
30 解: (1) 证明: ∵PB'⊥AC, ∠CAB=90° ,∴PB'∥AB. ∴∠B'PA=∠BAP,
又由折叠可知∠BAP=∠B'AP, ∴∠B'PA=∠B'AP. 故,
(2) 设AB=AC=B'A=a, AC、PB'交于点D,∵△ABC为等腰直角三角形, 由折叠可知, ∠PB'A=∠B=45° ,
∵∠ACB=45° , ∴∠PB'A=∠ACB,
又∵∠CDP=∠B'DA,∴△CDP∽△B'DA.∴BD=PDDA ①
设B'D=b, 则 由 得: 解得:
过点 D 作DE⊥AB'于点 E, 则△B'DE为等腰直角三角形.
又
(3) 存在点 P, 使得CB'=AB=m. 理由如下:
∵∠ACB=30° , ∠CAB=90° . ∴BC=2m.
①如图3所示,由题意可知,点B'的运动轨迹为以A为圆心、AB为半径的半圆A. 当P为BC中点时, PC=BP , 又∠B=60°, ∴△PAB为等边三角形.又由折叠可得四边形ABPB'为菱形.
∴PB'∥AB, ∴PB'⊥AC. 又∵AP=AB',
则易知AC为PB'的垂直平分线. 故CB'=PC=AB=m,满足题意.此时,
②当点 B'落在 BC 上时, 如图4所示, (2m-m)
此时CB'=AB=m, 则
综上所述, 的值为
同课章节目录
