2025年济南天桥区泺口实验中学七年级下学期数学期中前测考试试卷(含答案)
文档属性
| 名称 | 2025年济南天桥区泺口实验中学七年级下学期数学期中前测考试试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 243.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 10:45:25 | ||
图片预览


文档简介
2024 - 2025 学年第二学期泺口实验学校七年级(下)4月期中前测数学试卷
(满分150分 时间120分钟)
一、选择题(每小题 4 分,共 40 分)
1.计算 x2·x5的结果是( )
A. x7 B. x5 C. x10 D. x12
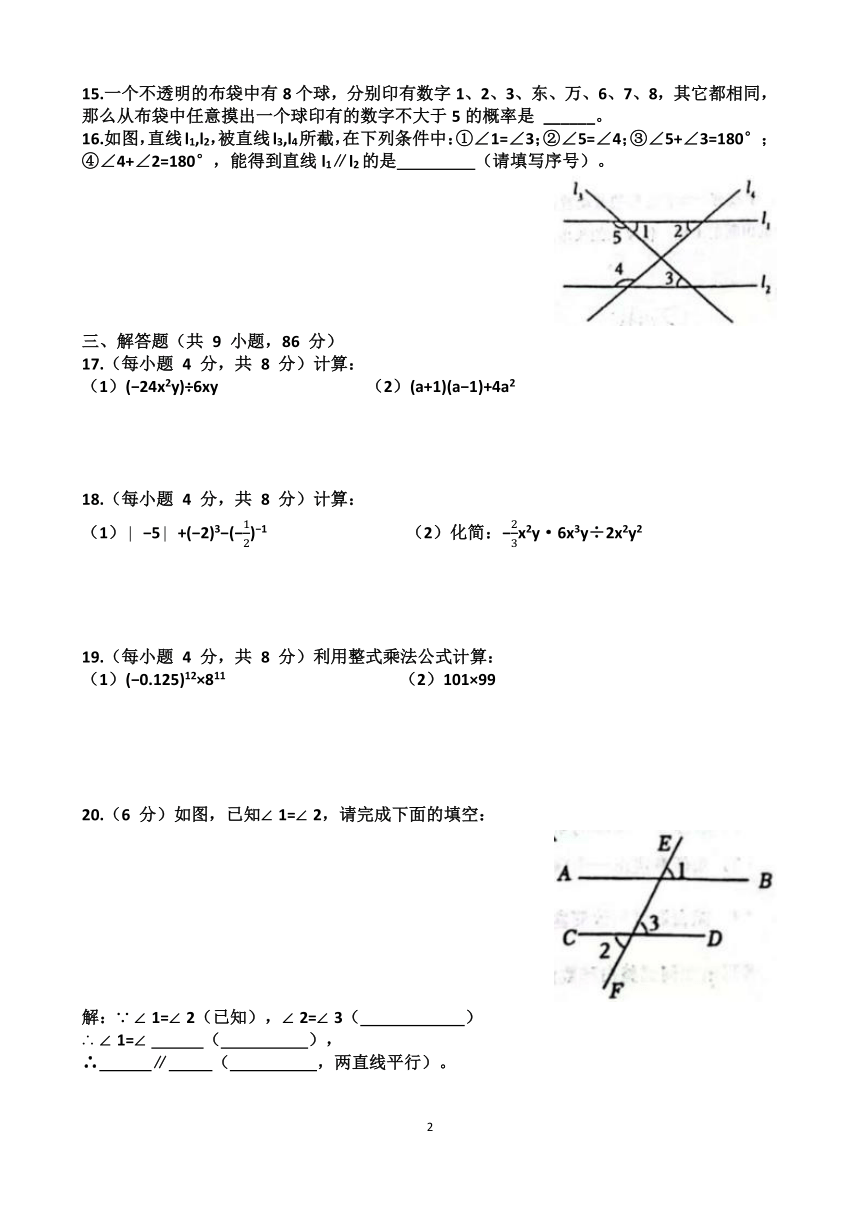
2.在生物课上,老师提到一根人体头发丝的平均直径约为0,000-025米,为了方便记录和计算,请用科学记数法表示这个数值为( )
A. 2.5×10 4 B. 2.5×10 5 C. 2.5×10 6 D. 2.5×10 7
3.下列运算正确的是( )
A. a2·a3=a6 B.(a2)3=a5 C. ( 2xy) 2= 4x2y2 D. a6÷a2=a4
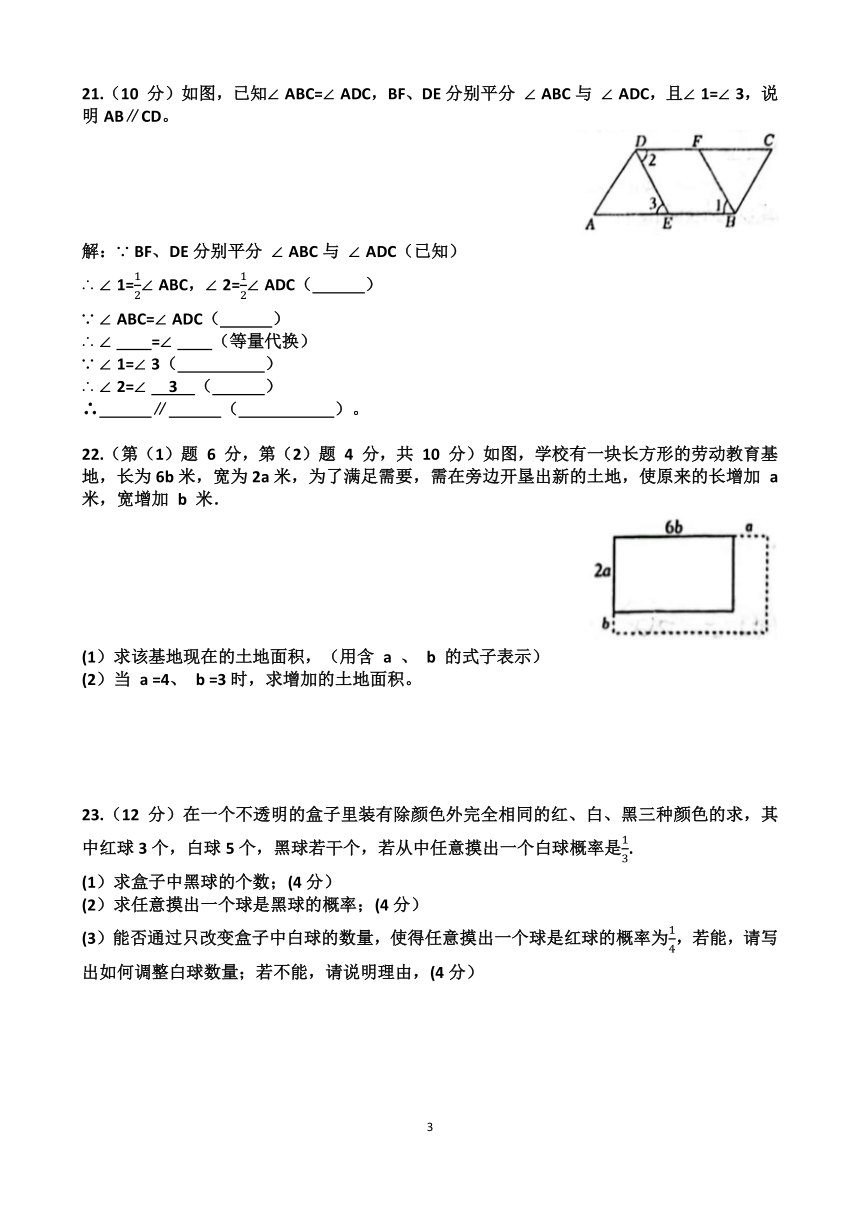
4.已知∠a 与 ∠B 是互余,若 ∠a =20°,则 ∠B 的度数为( )
A. 20° B. 40° C. 70° D. 160°
5.如图所示各图中,∠1与∠2是对顶角的是( )
A. B. C. D.
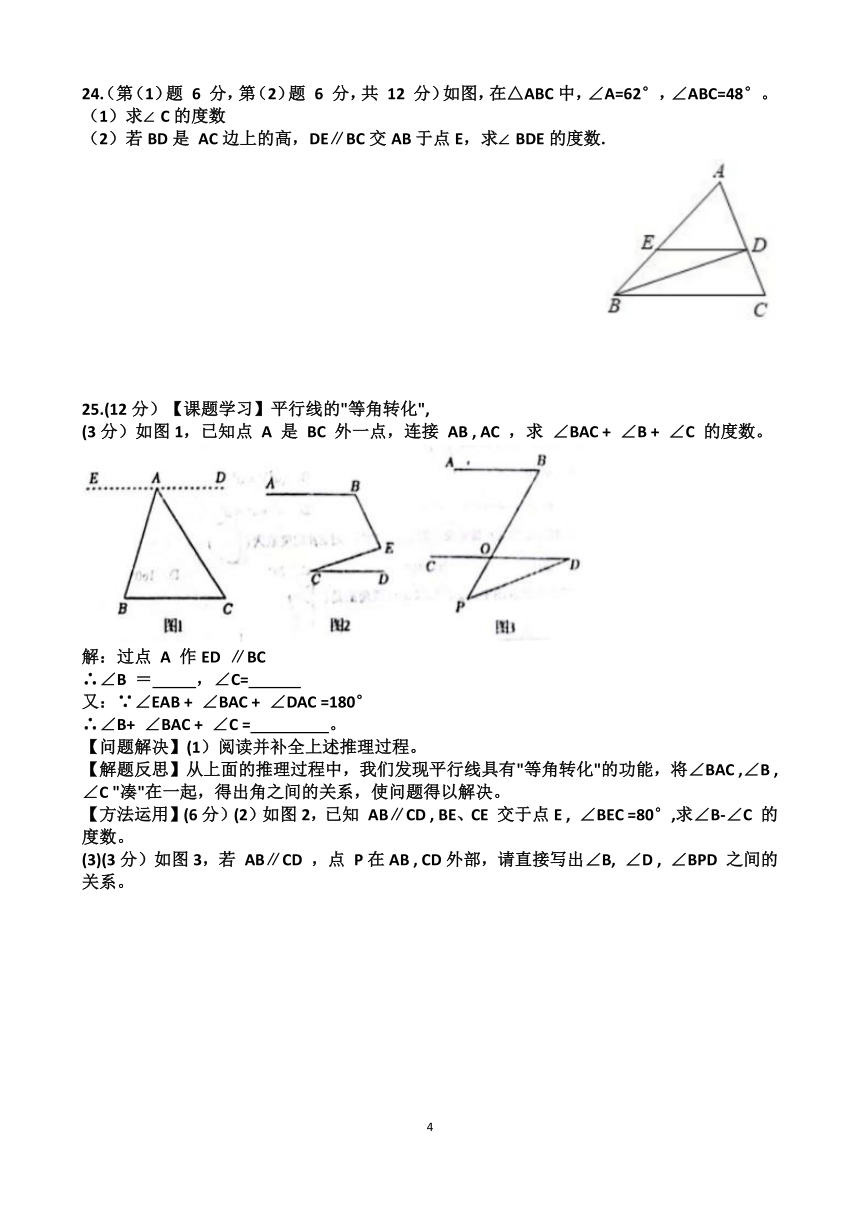
6.汉语是中华民族智慧的结晶,成语又是汉语中的精华,是中华文化的一大瑰宝,具有极强的表现力,下列成语描述的事件属于随机事件的是( )
A. 旭日东升 B. 画饼充饥 C. 守株待兔 D. 竹篮打水
7.下列多项式相乘,能用平方差公式计算的是( )
A. (a+b)(a b) B. (a+2)(2+a) C. (2a+b)(a 2b) D. (a b)(a b)
8.在一个不透明的盒子中装有 a 个除颜色外完全相同的球,这 a 个球中只有4个红球,若每次将球充分搅匀后,任意摸出!个球记下颜色再放回盒子,通过大量重复试验后,发现模到红球的频率稳定在20%左右,则 a 的值大约为( )
A. 16 B. 20 C. 24 D. 28
9.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A. 3cm,4cm,8cm B. 8cm,7cm,15cm C. 5cm,5cm,11cm D. 13cm,12cm,20cm
10.如图,将一条两边沿互相平行的纸带折叠,若 ∠AGE =40,则 ∠ABC( )
A.70° B.65° C.50° D.75°
二、填空题(每小题 4 分,共 24 分)
11.计算4x2y÷2xy=______
12.计算 (x 2)2=______
13.∠A=45°,它的补角等于 ______
14.如图,已知 ∠ACB =100°, OA 平分 ∠BAC , OB 平分 ∠ABC ,则 ∠AOB=______。
15.一个不透明的布袋中有8个球,分别印有数字1、2、3、东、万、6、7、8,其它都相同,那么从布袋中任意摸出一个球印有的数字不大于5的概率是 ______。
16.如图,直线l1,l2,被直线l3,l4所截,在下列条件中:①∠1=∠3;②∠5=∠4;③∠5+∠3=180°;④∠4+∠2=180°,能得到直线l1∥l2的是 (请填写序号)。
三、解答题(共 9 小题,86 分)
17.(每小题 4 分,共 8 分)计算:
(1)( 24x2y)÷6xy (2)(a+1)(a 1)+4a2
18.(每小题 4 分,共 8 分)计算:
(1)∣ 5∣+( 2)3 ( ) 1 (2)化简: x2y·6x3y÷2x2y2
19.(每小题 4 分,共 8 分)利用整式乘法公式计算:
(1)( 0.125)12×811 (2)101×99
20.(6 分)如图,已知∠1=∠2,请完成下面的填空:
解:∵∠1=∠2(已知),∠2=∠3( )
∴∠1=∠ ( ),
∴ ∥ ( ,两直线平行)。
21.(10 分)如图,已知∠ABC=∠ADC,BF、DE分别平分 ∠ABC与 ∠ADC,且∠1=∠3,说明AB∥CD。
解:∵BF、DE分别平分 ∠ABC与 ∠ADC(已知)
∴∠1=∠ABC,∠2=∠ADC( )
∵∠ABC=∠ADC( )
∴∠ =∠ (等量代换)
∵∠1=∠3( )
∴∠2=∠ 3 ( )
∴ ∥ ( )。
22.(第(1)题 6 分,第(2)题 4 分,共 10 分)如图,学校有一块长方形的劳动教育基
地,长为6b米,宽为2a米,为了满足需要,需在旁边开垦出新的土地,使原来的长增加 a 米,宽增加 b 米.
(1)求该基地现在的土地面积,(用含 a 、 b 的式子表示)
(2)当 a =4、 b =3时,求增加的土地面积。
23.(12 分)在一个不透明的盒子里装有除颜色外完全相同的红、白、黑三种颜色的求,其中红球3个,白球5个,黑球若干个,若从中任意摸出一个白球概率是.
(1)求盒子中黑球的个数;(4分)
(2)求任意摸出一个球是黑球的概率;(4分)
(3)能否通过只改变盒子中白球的数量,使得任意摸出一个球是红球的概率为,若能,请写出如何调整白球数量;若不能,请说明理由,(4分)
24.(第(1)题 6 分,第(2)题 6 分,共 12 分)如图,在△ABC中,∠A=62°,∠ABC=48°。
(1)求∠C的度数
(2)若BD是 AC边上的高,DE∥BC交AB于点E,求∠BDE的度数.
25.(12分)【课题学行线的"等角转化",
(3分)如图1,已知点 A 是 BC 外一点,连接 AB , AC ,求 ∠BAC + ∠B + ∠C 的度数。
解:过点 A 作ED ∥BC
∴∠B = ,∠C=
又:∵∠EAB + ∠BAC + ∠DAC =180°
∴∠B+ ∠BAC + ∠C = 。
【问题解决】(1)阅读并补全上述推理过程。
【解题反思】从上面的推理过程中,我们发现平行线具有"等角转化"的功能,将∠BAC ,∠B , ∠C "凑"在一起,得出角之间的关系,使问题得以解决。
【方法运用】(6分)(2)如图2,已知 AB∥CD , BE、CE 交于点E , ∠BEC =80°,求∠B-∠C 的度数。
(3)(3分)如图3,若 AB∥CD ,点 P在AB , CD外部,请直接写出∠B, ∠D , ∠BPD 之间的关系。
答案
一、选择题(每小题 4 分,共 40 分)
1.计算 x2·x5的结果是( )
A. x7 B. x5 C. x10 D. x12
答案:A
2.在生物课上,老师提到一根人体头发丝的平均直径约为0,000-025米,为了方便记录和计算,请用科学记数法表示这个数值为( )
A. 2.5×10 4 B. 2.5×10 5 C. 2.5×10 6 D. 2.5×10 7
答案:B
3.下列运算正确的是( )
A. a2·a3=a6 B.(a2)3=a5 C. ( 2xy) 2= 4x2y2 D. a6÷a2=a4
答案:D
4.已知∠a 与 ∠B 是互余,若 ∠a =20°,则 ∠B 的度数为( )
A. 20° B. 40° C. 70° D. 160°
答案:C
5.如图所示各图中,∠1与∠2是对顶角的是( )
A. B. C. D.
答案:B(根据对顶角定义判断)
6.汉语是中华民族智慧的结晶,成语又是汉语中的精华,是中华文化的一大瑰宝,具有极强的表现力,下列成语描述的事件属于随机事件的是( )
A. 旭日东升 B. 画饼充饥 C. 守株待兔 D. 竹篮打水
答案:C
7.下列多项式相乘,能用平方差公式计算的是( )
A. (a+b)(a b) B. (a+2)(2+a) C. (2a+b)(a 2b) D. (a b)(a b)
答案:A
8.在一个不透明的盒子中装有 a 个除颜色外完全相同的球,这 a 个球中只有4个红球,若每次将球充分搅匀后,任意摸出!个球记下颜色再放回盒子,通过大量重复试验后,发现模到红球的频率稳定在20%左右,则 a 的值大约为( )
A. 16 B. 20 C. 24 D. 28
答案:B(4÷a=20% 解得a=20)
9.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A. 3cm,4cm,8cm B. 8cm,7cm,15cm C. 5cm,5cm,11cm D. 13cm,12cm,20cm
答案:D(13+12>20,满足三边关系)
10.如图,将一条两边沿互相平行的纸带折叠,若 ∠AGE =40,则 ∠ABC( )
A.70° B.65° C.50° D.75°
答案:A(∠ABC= (180° 40°)÷2=70°)
二、填空题(每小题 4 分,共 24 分)
11.计算4x2y÷2xy=______
答案:2x
12.计算 (x 2)2=______
答案:x2 4x+4
13.∠A=45°,它的补角等于 ______
答案:135°(180° 45°=135°)
14.如图,已知 ∠ACB =100°, OA 平分 ∠BAC , OB 平分 ∠ABC ,则 ∠AOB=______。
答案:140°(∠BAC+∠ABC=80°,∠AOB=180° 80°÷2=140°)
15.一个不透明的布袋中有8个球,分别印有数字1、2、3、东、万、6、7、8,其它都相同,那么从布袋中任意摸出一个球印有的数字不大于5的概率是 ______。
答案:(不大于 5 的数有 5 个)
16.如图,直线l1,l2,被直线l3,l4所截,在下列条件中:①∠1=∠3;②∠5=∠4;③∠5+∠3=180°;④∠4+∠2=180°,能得到直线l1∥l2的是 (请填写序号)。
答案:①④(①同位角相等;④同旁内角互补)
三、解答题(共 9 小题,86 分)
17.(每小题 4 分,共 8 分)计算:
(1)( 24x2y)÷6xy (2)(a+1)(a 1)+4a2
=﹣4x =a2﹣1+4a2
=﹣1+5a2
18.(每小题 4 分,共 8 分)计算:
(1)∣ 5∣+( 2)3 ( ) 1 (2)化简: x2y·6x3y÷2x2y2
=5﹣8+2 =﹣4x5y2÷2x2y2
=﹣1 =﹣2x3
19.(每小题 4 分,共 8 分)利用整式乘法公式计算:
(1)( 0.125)12×811 (2)101×99
=﹣0.125×(﹣0.125×8)11 =(100+1)×(100﹣1)
=0.125 =9999
20.(6 分)如图,已知∠1=∠2,请完成下面的填空:
解:∵∠1=∠2(已知),∠2=∠3( 对顶角相等 )
∴∠1=∠ 3 ( 等量代换 ),
∴ AB ∥ CD ( 同位角相等 ,两直线平行)。
21.(10 分)如图,已知∠ABC=∠ADC,BF、DE分别平分 ∠ABC与 ∠ADC,且∠1=∠3,说明AB∥CD。
解:∵BF、DE分别平分 ∠ABC与 ∠ADC(已知)
∴∠1=∠ABC,∠2=∠ADC( 角平分线定义 )
∵∠ABC=∠ADC( 已知 )
∴∠ 1 =∠ 2 (等量代换)
∵∠1=∠3( 已知 )
∴∠2=∠ 3 ( 等量代换 )
∴ AB ∥ CD ( 内错角相等,两直线平行 )。
22.(第(1)题 6 分,第(2)题 4 分,共 10 分)如图,学校有一块长方形的劳动教育基
地,长为6b米,宽为2a米,为了满足需要,需在旁边开垦出新的土地,使原来的长增加 a 米,宽增加 b 米.
(1)求该基地现在的土地面积,(用含 a 、 b 的式子表示)
(2)当 a =4、 b =3时,求增加的土地面积。
(1)(6b+a)(2a+b)=2a2+13ab+6b2
(2)原来面积 12ab=144,现在 2×16+13×12+6×9=242,增加 242 144=98。
23.(12 分)在一个不透明的盒子里装有除颜色外完全相同的红、白、黑三种颜色的求,其中红球3个,白球5个,黑球若干个,若从中任意摸出一个白球概率是.
(1)求盒子中黑球的个数;(4分)
(2)求任意摸出一个球是黑球的概率;(4分)
(3)能否通过只改变盒子中白球的数量,使得任意摸出一个球是红球的概率为,若能,请写出如何调整白球数量;若不能,请说明理由,(4分)
(1)黑球:5÷﹣3﹣5=7个
(2)7÷15=
(3)能
设白球 y个
3÷﹣3﹣7=2
5﹣2=3
∴减少 3 个白球。
24.(第(1)题 6 分,第(2)题 6 分,共 12 分)如图,在△ABC中,∠A=62°,∠ABC=48°。
(1)求∠C的度数
(2)若BD是 AC边上的高,DE∥BC交AB于点E,求∠BDE的度数.
:∵∠A + ∠ABC + ∠C =180°
∴∠C =180°-62°-48°=70°.
(2)∵BD⊥AC
∴∠BDC =90°
∴∠DBC =90°-70°=20°
∵DE // BC
∴∠BDE = ∠CBD =20°.
25.(12分)【课题学行线的"等角转化",
(3分)如图1,已知点 A 是 BC 外一点,连接 AB , AC ,求 ∠BAC + ∠B + ∠C 的度数。
解:过点 A 作ED ∥BC
∴∠B = ,∠C=
又:∵∠EAB + ∠BAC + ∠DAC =180°
∴∠B+ ∠BAC + ∠C = 。
【问题解决】(1)阅读并补全上述推理过程。
【解题反思】从上面的推理过程中,我们发现平行线具有"等角转化"的功能,将 ∠BAC , ∠B , ∠C "凑"在一起,得出角之间的关系,使问题得以解决。
【方法运用】(6分)(2)如图2,已知 AB∥CD , BE、CE 交于点E , ∠BEC =80°,求∠B-∠C 的度数。
(3)(3分)如图3,若 AB∥CD ,点 P在AB , CD外部,请直接写出∠B, ∠D , ∠BPD 之间的关系。
解:(1) ∠EAB ∠DAC 180°
如图,过点 E 作 EF // AB
∴∠B + ∠BEF =180°
∴∠BEF =180°- ∠B
∵AB // CD
∴EF // CD
∴∠FEC = ∠C
∵∠BEC =80°
∴∠BEF + ∠FEC =80°
∴180°-∠B+ ∠C =80°
∴∠B - ∠C =100°.
(3)∠BPD = ∠B - ∠D .
理由:如图,过点 P 作 PE // CD
∴∠D =∠DPE
∵AB // CD
∴AB // PE
∴∠B = ∠BPE
∵∠BPD = ∠BPE - ∠DPE
∴∠BPD = ∠B - ∠D
(满分150分 时间120分钟)
一、选择题(每小题 4 分,共 40 分)
1.计算 x2·x5的结果是( )
A. x7 B. x5 C. x10 D. x12
2.在生物课上,老师提到一根人体头发丝的平均直径约为0,000-025米,为了方便记录和计算,请用科学记数法表示这个数值为( )
A. 2.5×10 4 B. 2.5×10 5 C. 2.5×10 6 D. 2.5×10 7
3.下列运算正确的是( )
A. a2·a3=a6 B.(a2)3=a5 C. ( 2xy) 2= 4x2y2 D. a6÷a2=a4
4.已知∠a 与 ∠B 是互余,若 ∠a =20°,则 ∠B 的度数为( )
A. 20° B. 40° C. 70° D. 160°
5.如图所示各图中,∠1与∠2是对顶角的是( )
A. B. C. D.
6.汉语是中华民族智慧的结晶,成语又是汉语中的精华,是中华文化的一大瑰宝,具有极强的表现力,下列成语描述的事件属于随机事件的是( )
A. 旭日东升 B. 画饼充饥 C. 守株待兔 D. 竹篮打水
7.下列多项式相乘,能用平方差公式计算的是( )
A. (a+b)(a b) B. (a+2)(2+a) C. (2a+b)(a 2b) D. (a b)(a b)
8.在一个不透明的盒子中装有 a 个除颜色外完全相同的球,这 a 个球中只有4个红球,若每次将球充分搅匀后,任意摸出!个球记下颜色再放回盒子,通过大量重复试验后,发现模到红球的频率稳定在20%左右,则 a 的值大约为( )
A. 16 B. 20 C. 24 D. 28
9.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A. 3cm,4cm,8cm B. 8cm,7cm,15cm C. 5cm,5cm,11cm D. 13cm,12cm,20cm
10.如图,将一条两边沿互相平行的纸带折叠,若 ∠AGE =40,则 ∠ABC( )
A.70° B.65° C.50° D.75°
二、填空题(每小题 4 分,共 24 分)
11.计算4x2y÷2xy=______
12.计算 (x 2)2=______
13.∠A=45°,它的补角等于 ______
14.如图,已知 ∠ACB =100°, OA 平分 ∠BAC , OB 平分 ∠ABC ,则 ∠AOB=______。
15.一个不透明的布袋中有8个球,分别印有数字1、2、3、东、万、6、7、8,其它都相同,那么从布袋中任意摸出一个球印有的数字不大于5的概率是 ______。
16.如图,直线l1,l2,被直线l3,l4所截,在下列条件中:①∠1=∠3;②∠5=∠4;③∠5+∠3=180°;④∠4+∠2=180°,能得到直线l1∥l2的是 (请填写序号)。
三、解答题(共 9 小题,86 分)
17.(每小题 4 分,共 8 分)计算:
(1)( 24x2y)÷6xy (2)(a+1)(a 1)+4a2
18.(每小题 4 分,共 8 分)计算:
(1)∣ 5∣+( 2)3 ( ) 1 (2)化简: x2y·6x3y÷2x2y2
19.(每小题 4 分,共 8 分)利用整式乘法公式计算:
(1)( 0.125)12×811 (2)101×99
20.(6 分)如图,已知∠1=∠2,请完成下面的填空:
解:∵∠1=∠2(已知),∠2=∠3( )
∴∠1=∠ ( ),
∴ ∥ ( ,两直线平行)。
21.(10 分)如图,已知∠ABC=∠ADC,BF、DE分别平分 ∠ABC与 ∠ADC,且∠1=∠3,说明AB∥CD。
解:∵BF、DE分别平分 ∠ABC与 ∠ADC(已知)
∴∠1=∠ABC,∠2=∠ADC( )
∵∠ABC=∠ADC( )
∴∠ =∠ (等量代换)
∵∠1=∠3( )
∴∠2=∠ 3 ( )
∴ ∥ ( )。
22.(第(1)题 6 分,第(2)题 4 分,共 10 分)如图,学校有一块长方形的劳动教育基
地,长为6b米,宽为2a米,为了满足需要,需在旁边开垦出新的土地,使原来的长增加 a 米,宽增加 b 米.
(1)求该基地现在的土地面积,(用含 a 、 b 的式子表示)
(2)当 a =4、 b =3时,求增加的土地面积。
23.(12 分)在一个不透明的盒子里装有除颜色外完全相同的红、白、黑三种颜色的求,其中红球3个,白球5个,黑球若干个,若从中任意摸出一个白球概率是.
(1)求盒子中黑球的个数;(4分)
(2)求任意摸出一个球是黑球的概率;(4分)
(3)能否通过只改变盒子中白球的数量,使得任意摸出一个球是红球的概率为,若能,请写出如何调整白球数量;若不能,请说明理由,(4分)
24.(第(1)题 6 分,第(2)题 6 分,共 12 分)如图,在△ABC中,∠A=62°,∠ABC=48°。
(1)求∠C的度数
(2)若BD是 AC边上的高,DE∥BC交AB于点E,求∠BDE的度数.
25.(12分)【课题学行线的"等角转化",
(3分)如图1,已知点 A 是 BC 外一点,连接 AB , AC ,求 ∠BAC + ∠B + ∠C 的度数。
解:过点 A 作ED ∥BC
∴∠B = ,∠C=
又:∵∠EAB + ∠BAC + ∠DAC =180°
∴∠B+ ∠BAC + ∠C = 。
【问题解决】(1)阅读并补全上述推理过程。
【解题反思】从上面的推理过程中,我们发现平行线具有"等角转化"的功能,将∠BAC ,∠B , ∠C "凑"在一起,得出角之间的关系,使问题得以解决。
【方法运用】(6分)(2)如图2,已知 AB∥CD , BE、CE 交于点E , ∠BEC =80°,求∠B-∠C 的度数。
(3)(3分)如图3,若 AB∥CD ,点 P在AB , CD外部,请直接写出∠B, ∠D , ∠BPD 之间的关系。
答案
一、选择题(每小题 4 分,共 40 分)
1.计算 x2·x5的结果是( )
A. x7 B. x5 C. x10 D. x12
答案:A
2.在生物课上,老师提到一根人体头发丝的平均直径约为0,000-025米,为了方便记录和计算,请用科学记数法表示这个数值为( )
A. 2.5×10 4 B. 2.5×10 5 C. 2.5×10 6 D. 2.5×10 7
答案:B
3.下列运算正确的是( )
A. a2·a3=a6 B.(a2)3=a5 C. ( 2xy) 2= 4x2y2 D. a6÷a2=a4
答案:D
4.已知∠a 与 ∠B 是互余,若 ∠a =20°,则 ∠B 的度数为( )
A. 20° B. 40° C. 70° D. 160°
答案:C
5.如图所示各图中,∠1与∠2是对顶角的是( )
A. B. C. D.
答案:B(根据对顶角定义判断)
6.汉语是中华民族智慧的结晶,成语又是汉语中的精华,是中华文化的一大瑰宝,具有极强的表现力,下列成语描述的事件属于随机事件的是( )
A. 旭日东升 B. 画饼充饥 C. 守株待兔 D. 竹篮打水
答案:C
7.下列多项式相乘,能用平方差公式计算的是( )
A. (a+b)(a b) B. (a+2)(2+a) C. (2a+b)(a 2b) D. (a b)(a b)
答案:A
8.在一个不透明的盒子中装有 a 个除颜色外完全相同的球,这 a 个球中只有4个红球,若每次将球充分搅匀后,任意摸出!个球记下颜色再放回盒子,通过大量重复试验后,发现模到红球的频率稳定在20%左右,则 a 的值大约为( )
A. 16 B. 20 C. 24 D. 28
答案:B(4÷a=20% 解得a=20)
9.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A. 3cm,4cm,8cm B. 8cm,7cm,15cm C. 5cm,5cm,11cm D. 13cm,12cm,20cm
答案:D(13+12>20,满足三边关系)
10.如图,将一条两边沿互相平行的纸带折叠,若 ∠AGE =40,则 ∠ABC( )
A.70° B.65° C.50° D.75°
答案:A(∠ABC= (180° 40°)÷2=70°)
二、填空题(每小题 4 分,共 24 分)
11.计算4x2y÷2xy=______
答案:2x
12.计算 (x 2)2=______
答案:x2 4x+4
13.∠A=45°,它的补角等于 ______
答案:135°(180° 45°=135°)
14.如图,已知 ∠ACB =100°, OA 平分 ∠BAC , OB 平分 ∠ABC ,则 ∠AOB=______。
答案:140°(∠BAC+∠ABC=80°,∠AOB=180° 80°÷2=140°)
15.一个不透明的布袋中有8个球,分别印有数字1、2、3、东、万、6、7、8,其它都相同,那么从布袋中任意摸出一个球印有的数字不大于5的概率是 ______。
答案:(不大于 5 的数有 5 个)
16.如图,直线l1,l2,被直线l3,l4所截,在下列条件中:①∠1=∠3;②∠5=∠4;③∠5+∠3=180°;④∠4+∠2=180°,能得到直线l1∥l2的是 (请填写序号)。
答案:①④(①同位角相等;④同旁内角互补)
三、解答题(共 9 小题,86 分)
17.(每小题 4 分,共 8 分)计算:
(1)( 24x2y)÷6xy (2)(a+1)(a 1)+4a2
=﹣4x =a2﹣1+4a2
=﹣1+5a2
18.(每小题 4 分,共 8 分)计算:
(1)∣ 5∣+( 2)3 ( ) 1 (2)化简: x2y·6x3y÷2x2y2
=5﹣8+2 =﹣4x5y2÷2x2y2
=﹣1 =﹣2x3
19.(每小题 4 分,共 8 分)利用整式乘法公式计算:
(1)( 0.125)12×811 (2)101×99
=﹣0.125×(﹣0.125×8)11 =(100+1)×(100﹣1)
=0.125 =9999
20.(6 分)如图,已知∠1=∠2,请完成下面的填空:
解:∵∠1=∠2(已知),∠2=∠3( 对顶角相等 )
∴∠1=∠ 3 ( 等量代换 ),
∴ AB ∥ CD ( 同位角相等 ,两直线平行)。
21.(10 分)如图,已知∠ABC=∠ADC,BF、DE分别平分 ∠ABC与 ∠ADC,且∠1=∠3,说明AB∥CD。
解:∵BF、DE分别平分 ∠ABC与 ∠ADC(已知)
∴∠1=∠ABC,∠2=∠ADC( 角平分线定义 )
∵∠ABC=∠ADC( 已知 )
∴∠ 1 =∠ 2 (等量代换)
∵∠1=∠3( 已知 )
∴∠2=∠ 3 ( 等量代换 )
∴ AB ∥ CD ( 内错角相等,两直线平行 )。
22.(第(1)题 6 分,第(2)题 4 分,共 10 分)如图,学校有一块长方形的劳动教育基
地,长为6b米,宽为2a米,为了满足需要,需在旁边开垦出新的土地,使原来的长增加 a 米,宽增加 b 米.
(1)求该基地现在的土地面积,(用含 a 、 b 的式子表示)
(2)当 a =4、 b =3时,求增加的土地面积。
(1)(6b+a)(2a+b)=2a2+13ab+6b2
(2)原来面积 12ab=144,现在 2×16+13×12+6×9=242,增加 242 144=98。
23.(12 分)在一个不透明的盒子里装有除颜色外完全相同的红、白、黑三种颜色的求,其中红球3个,白球5个,黑球若干个,若从中任意摸出一个白球概率是.
(1)求盒子中黑球的个数;(4分)
(2)求任意摸出一个球是黑球的概率;(4分)
(3)能否通过只改变盒子中白球的数量,使得任意摸出一个球是红球的概率为,若能,请写出如何调整白球数量;若不能,请说明理由,(4分)
(1)黑球:5÷﹣3﹣5=7个
(2)7÷15=
(3)能
设白球 y个
3÷﹣3﹣7=2
5﹣2=3
∴减少 3 个白球。
24.(第(1)题 6 分,第(2)题 6 分,共 12 分)如图,在△ABC中,∠A=62°,∠ABC=48°。
(1)求∠C的度数
(2)若BD是 AC边上的高,DE∥BC交AB于点E,求∠BDE的度数.
:∵∠A + ∠ABC + ∠C =180°
∴∠C =180°-62°-48°=70°.
(2)∵BD⊥AC
∴∠BDC =90°
∴∠DBC =90°-70°=20°
∵DE // BC
∴∠BDE = ∠CBD =20°.
25.(12分)【课题学行线的"等角转化",
(3分)如图1,已知点 A 是 BC 外一点,连接 AB , AC ,求 ∠BAC + ∠B + ∠C 的度数。
解:过点 A 作ED ∥BC
∴∠B = ,∠C=
又:∵∠EAB + ∠BAC + ∠DAC =180°
∴∠B+ ∠BAC + ∠C = 。
【问题解决】(1)阅读并补全上述推理过程。
【解题反思】从上面的推理过程中,我们发现平行线具有"等角转化"的功能,将 ∠BAC , ∠B , ∠C "凑"在一起,得出角之间的关系,使问题得以解决。
【方法运用】(6分)(2)如图2,已知 AB∥CD , BE、CE 交于点E , ∠BEC =80°,求∠B-∠C 的度数。
(3)(3分)如图3,若 AB∥CD ,点 P在AB , CD外部,请直接写出∠B, ∠D , ∠BPD 之间的关系。
解:(1) ∠EAB ∠DAC 180°
如图,过点 E 作 EF // AB
∴∠B + ∠BEF =180°
∴∠BEF =180°- ∠B
∵AB // CD
∴EF // CD
∴∠FEC = ∠C
∵∠BEC =80°
∴∠BEF + ∠FEC =80°
∴180°-∠B+ ∠C =80°
∴∠B - ∠C =100°.
(3)∠BPD = ∠B - ∠D .
理由:如图,过点 P 作 PE // CD
∴∠D =∠DPE
∵AB // CD
∴AB // PE
∴∠B = ∠BPE
∵∠BPD = ∠BPE - ∠DPE
∴∠BPD = ∠B - ∠D
同课章节目录
