3.1.1平面直角坐标系 教案

中小学教育资源及组卷应用平台
分课时教学设计
第1课时《3.1.1平面直角坐标系 》教学设计
课型 新授课√ 复习课口 试卷讲评课口 其他课口
教学内容分析 经历画坐标系，由点找坐标等过程，让学生进一步感受“数形结合”的数学思想，感受“类比”和“坐标”的思想，体验将实际问题数学化的过程与方法．
学习者分析 通过知识的回顾，让学生感受数学的联系，增加学生的学习、探索兴趣.根据班里的座位图回答问题，从而引出有序实数对．
教学目标 能够在给定的直角坐标系中，根据点的坐标指出点的位置，会由点的位置写出点的坐标． 2.认识平面直角坐标系，知道点的坐标及象限的含义．
教学重点 平面直角坐标系．
教学难点 确定点的坐标.
学习活动设计
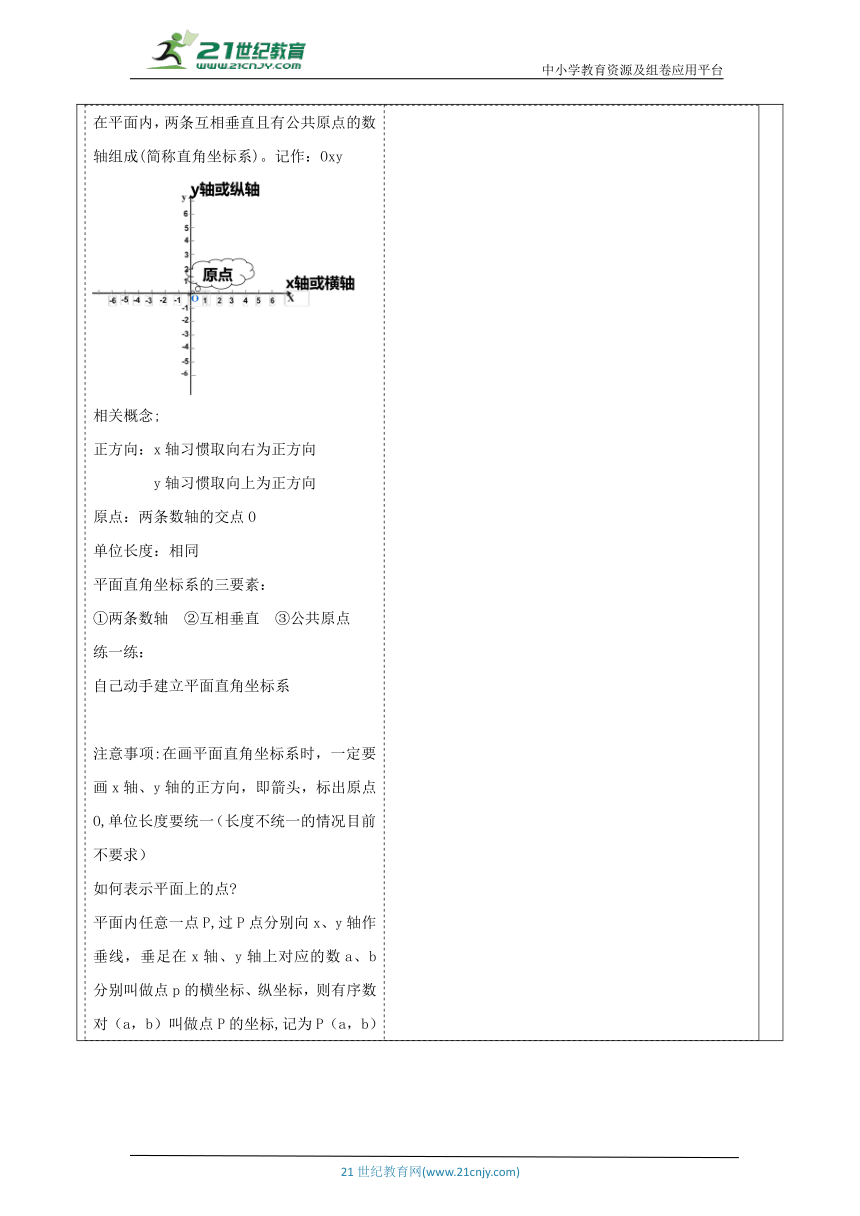
教师活动学生活动环节一：引入新课 如何确定直线上点的位置？ 在直线上规定了原点、正方向、单位长度，就构成了数轴 数轴上的点可以用一个数来表示，这个数叫做这个点在数轴上的坐标． 例如点A在数轴上的坐标为-3，点B在数轴上的坐标为2。反过来，知道数轴上一个点的坐标，这个的点在数轴上的位置也就确定了。 学生活动1： 学生在教师的引导下，能很快回忆相关问题. ? 带着问题参与新课. 活动意图说明：激发学生兴趣,引入新课主题，激发学生的兴趣，理解学生思考，通过知识的回顾，让学生感受数学的联系，增加学生的学习、探索兴趣.根据班里的座位图回答问题，从而引出有序实数对． 环节二：新知探究教师活动2： 问题： 围棋是我们古代就有的一项棋类运动，为了提高自己棋艺，古人往往需要借鉴别人的棋谱进行训练。 那么古时候的棋谱是怎么被记录的呢？ 古人很巧妙的通过给棋盘的行和列加上了数字来解决了这个问题 我们来看：A.(三3)，B.(五6)，C.(二5) 思考：能不能找到一种办法确定平面内的点的位置呢？ 动脑筋 要想确定同学们在教室中的位置只需要2个数据,分别是排数和组数 显示班里的座位图，然后回答问题： 1. 请说出我们班第2组第4排的同学是谁？ 2. 李亮的位置怎么描述呢 学生：我们班第2组第4排的同学是王刚 学生：李亮的位置是第4组第2排 老师：我们可以用一对有顺序的实数（简称为有序实数对）来表示 如：李亮在教室里的座位可以简单地记作（4，２） 请问：(5,2)与(2,5)表示的是同一座位吗 学生：不是 动脑筋 怎样用有序实数对来表示平面内点的位置呢？ 学生;可以在平面内建立平面直角坐标系，然后找出对应的有序实数对。 那么，什么是平面直角坐标系呢？ 在平面内，两条互相垂直且有公共原点的数轴组成(简称直角坐标系)。记作：Oxy 相关概念; 正方向：x轴习惯取向右为正方向 y轴习惯取向上为正方向 原点：两条数轴的交点O 单位长度：相同 平面直角坐标系的三要素： ①两条数轴　②互相垂直 ③公共原点 练一练： 自己动手建立平面直角坐标系 注意事项:在画平面直角坐标系时，一定要画x轴、y轴的正方向，即箭头，标出原点O,单位长度要统一（长度不统一的情况目前不要求） 如何表示平面上的点 平面内任意一点P,过P点分别向x、y轴作垂线，垂足在x轴、y轴上对应的数a、b分别叫做点p的横坐标、纵坐标，则有序数对（a，b）叫做点P的坐标,记为P（a，b） 注意:先横后纵，逗号隔开，加上括号 有序数实数对（3，2）叫做点A的坐标，记作：A（3，2） 在建立平面直角坐标系后，平面上的点与有序实数对一一对应 坐标系的四个象限 注 意:坐标轴上的点不属于任何象限。 想一想 1.原点O的坐标是什么？ 2.x轴和y轴上的点的坐标有什么特征？ 归纳：原点O的坐标是(0,0)； x轴上的点其纵坐标为0 表示为（x，0） y轴上的点其横坐标为0 表示为（0，y）学生活动2： 学生自学、互动。在具体计算时，可以通过小组合作交流，放手让学生去思考、讨论，猜想、发现结论． 学生自主解答，教师适时的进行提示 学生思考 活动意图说明：从旧知识出发，呼应引课问题，学生通过自己解决问题，让学生在小组内共同合作．能够在给定的直角坐标系中，根据点的坐标指出点的位置，会由点的位置写出点的坐标． 环节三：典例精析 例1、如图，写出平面直角坐标系中点A， B， C， D， E， F的坐标. 方法： 先找到表示横坐标与纵坐标的点，然后过这两点分别作x轴与y轴的垂线，垂线的交点就是该坐标对应的点. 例2、在平面直角坐标系中，描出下列各点，并指出它们分别在哪个象限. A（5， 4），B（-3， 4），C（-4， -1），D（2， -4）. 学生活动3： 参与教师分析和讲例题． 活动意图说明：熟练掌握.巩固学的知识，学生通过自己解决问题，充分发挥学习的主动性，进一步感受“数形结合”的数学思想，感受“类比”和“坐标”的思想，体验将实际问题数学化的过程与方法。
板书设计
课堂练习 【知识技能类作业】 必做题： 1.下列关于有序数对的说法正确的是( ) A.(3,2)与（2，3）表示的位置相同 B.（a,b）与（b,a）表示的位置一定不同 C.（3，-2）与(-2,3)是表示不同位置的两个有序数对 D.（4，4）与（4，4）可以表示两个不同的位置 选做题： 2、如图，在平面直角坐标系xOy中，已知点A(3，4)，将OA绕坐标原点O逆时针旋转90°到OA′，则点A′的坐标是_________. 【综合拓展类作业】 3.在平面直角坐标系内，已知点A(1-2k，k-2)在第三象限，且k为整数，求k的值.
课堂总结
作业设计 【知识技能类作业】 必做题： 1.如图，在平面直角坐标系中，点A的坐标是( ) A.(-2，-3) B.(3，-2) C.(2，3) D.(-2，3) 选做题： 2、在平面直角坐标系中，若点P(a，b)在第二象限，则点Q(1-a，-b)在第 象限 【综合拓展类作业】 3.如果点P(3m-2，3-m)到x轴的距离与它到y轴的距离相等，求m的值.
教学反思 这节课你 有哪些收获？你认为自己的表现如何？ 4.各象限中点的特征： 第一象限：（+， +）第二象限：（—， +） 第三象限：（—，—）第四象限：（+， —）
21世纪教育网(www.21cnjy.com)