2024-2025学年北师大版七年级数学下册第一次月考试卷(考试范围:第1~2章) (含解析)
文档属性
| 名称 | 2024-2025学年北师大版七年级数学下册第一次月考试卷(考试范围:第1~2章) (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 944.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 13:19:22 | ||
图片预览



文档简介
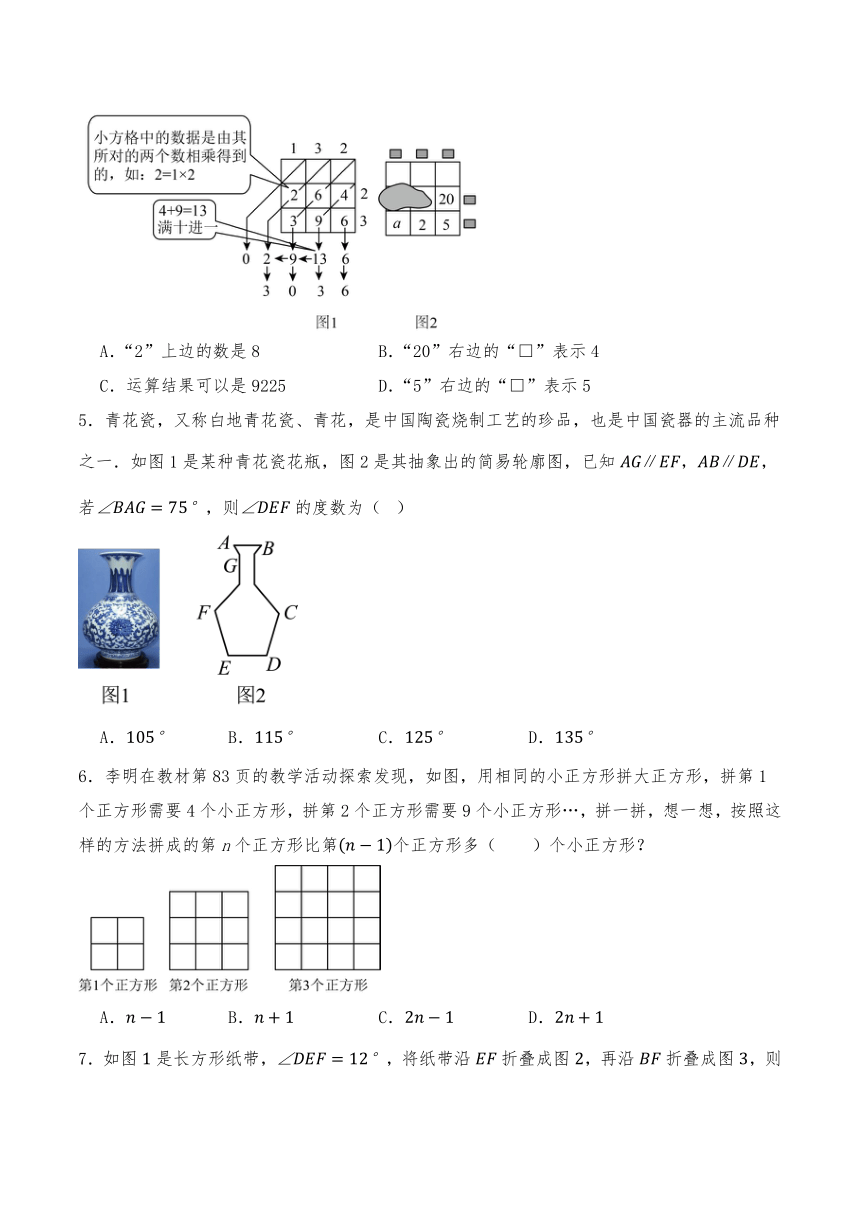
2024-2025学年七年级数学下册第一次月考试卷(考试范围:第1~2章)
一.选择题(共10小题,满分30分,每小题3分)
1.若将展开的结果中不含有项,则,满足的关系式是( )
A. B. C. D.
2.画直线时要按住尺身,推移丁字尺时必须使尺头靠紧图画板的边框.请你说明:利用丁字尺画平行线的理论依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
3.如图,三条直线交于点O,,平分,则的度数是( )
A. B. C. D.
4.“铺地锦”是我国古代一种乘法运算方法,可将多位数乘法运算转化为一位数乘法和简单的加法运算.淇淇受其启发,设计了如图1所示的“表格算法”,图1表示132×23,运算结果为3036.图2表示一个三位数与一个两位数相乘,表格中部分数据被墨迹覆盖,根据图2中现有数据进行推断,错误的是( )
A.“2”上边的数是8 B.“20”右边的“□”表示4
C.运算结果可以是9225 D.“5”右边的“□”表示5
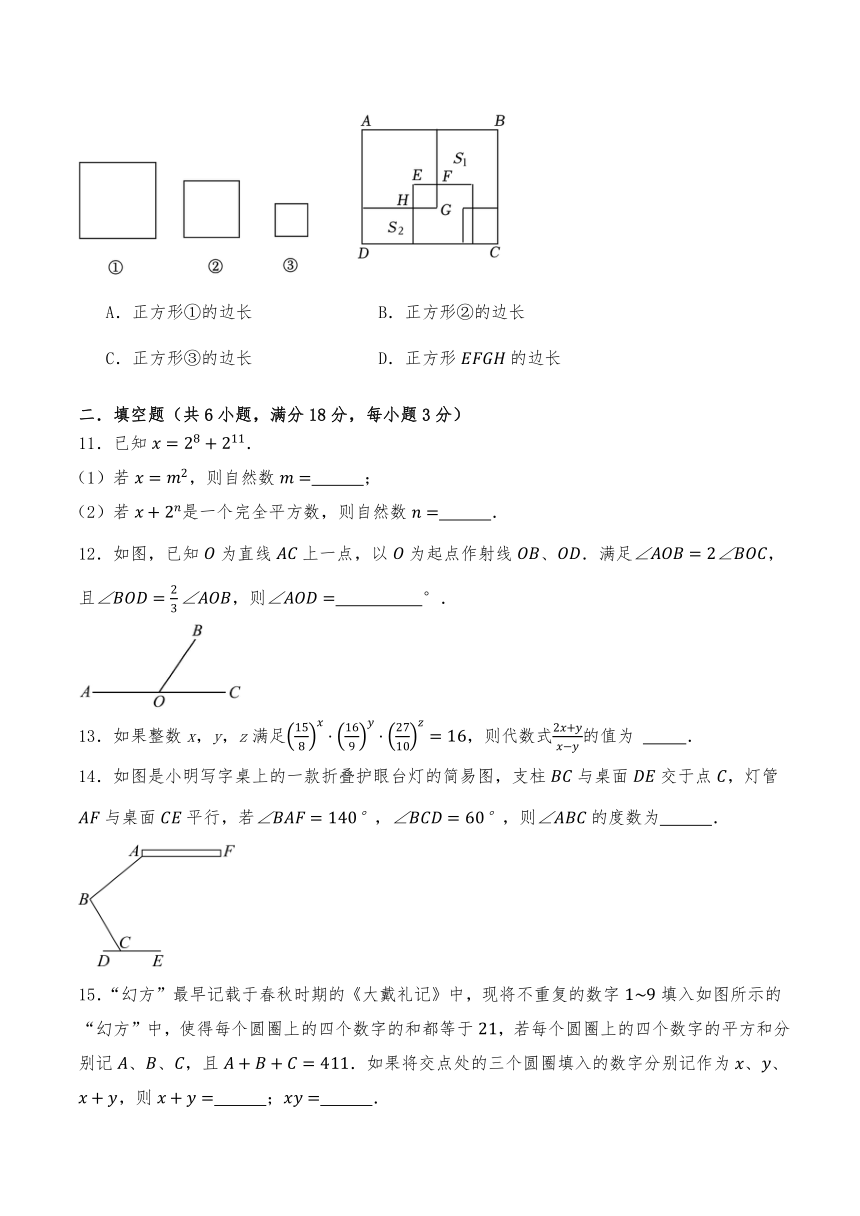
5.青花瓷,又称白地青花瓷、青花,是中国陶瓷烧制工艺的珍品,也是中国瓷器的主流品种之一.如图1是某种青花瓷花瓶,图2是其抽象出的简易轮廓图,已知,若,则的度数为( )
A. B. C. D.
6.李明在教材第83页的教学活动探索发现,如图,用相同的小正方形拼大正方形,拼第1个正方形需要4个小正方形,拼第2个正方形需要9个小正方形…,拼一拼,想一想,按照这样的方法拼成的第n个正方形比第个正方形多( )个小正方形?
A. B. C. D.
7.如图是长方形纸带,,将纸带沿折叠成图,再沿折叠成图,则图中度数是多少( )
A. B. C. D.
8.观察下列各式:
;
;
;
…
根据规律计算: 的值是( )
A. B. C.
9.如图,在锐角三角形中,,将沿着射线方向平移得到(平移后点的对应点分别是),连接.若在整个平移过程中,和的度数之间存在2倍关系,则的度数不可能为( )
A. B. C. D.
10.如图,有三张正方形纸片,将三张纸片按照如图所示的方式放置于一个长方形中,已知中间重叠部分四边形恰好是一个正方形,记图中两块未被覆盖的阴影部分面积分别为和,已知,,若要知道和的面积差,只需要知道( )
A.正方形的边长 B.正方形的边长
C.正方形的边长 D.正方形的边长
二.填空题(共6小题,满分18分,每小题3分)
11.已知.
(1)若,则自然数 ;
(2)若是一个完全平方数,则自然数 .
12.如图,已知为直线上一点,以为起点作射线、.满足,且,则 °.
13.如果整数x,y,z满足,则代数式的值为 .
14.如图是小明写字桌上的一款折叠护眼台灯的简易图,支柱与桌面交于点,灯管与桌面平行,若,,则的度数为 .
15.“幻方”最早记载于春秋时期的《大戴礼记》中,现将不重复的数字填入如图所示的“幻方”中,使得每个圆圈上的四个数字的和都等于,若每个圆圈上的四个数字的平方和分别记、、,且.如果将交点处的三个圆圈填入的数字分别记作为、、,则 ; .
16.如图,,在的两边上分别过点和点向同方向作射线和,且.
(1)若,则的度数为 .
(2)若和的平分线所在的直线交于点(与不重合),则的度数为 .
三.解答题(共8小题,满分72分)
17.(6分)若直线和直线相交于点,为内部的射线,平分,平分.
(1)若,求和的度数?
(2)若是任意角,求的度数?
(3)请猜想,度数会改变吗?若改变,请说明理由;若不改变,则度数是多少?
18.(6分)如图,有三张边长分别为,,的正方形纸片,, 将三张纸片按图1,图2两种不同方式放置于同一长方形中.记图1中阴影部分周长为,面积为;图2中阴影部分周长为,面积为.
(1)若,,图1中阴影部分周长_____,图2中阴影部分周长_____;
(2)求图2中阴影部分面积与图1中阴影部分面积的差(用含,,的代数式表示).
(3)若,那么与满足下列_____关系.
A. B. C. D.
19.(8分)为增强学生体质,某学校将抖空竹引入“阳光体育一小时”活动.图①是某同学抖空竹时的一个瞬间,小聪把它抽象成如图②所示的示意图.已知,,,求的度数.
20.(8分)直线相交于点O,于点O,作射线,且在的内部.
(1)①当在如图1所示位置时,若,求的度数;
②当在如图2所示位置时,若平分,证明:平分;
(2)若,请直接写出与之间的数量关系.
21.(10分)阅读理解:我们在学习了幂的有关知识后,对两个幂与(都是正数,都是正整数)的大小进行比较,并归纳总结了如下两个结论:
①若,则.(底数相同,指数大的幂大)
②若,则.(指数相同,底数大的幂大)
尝试应用:试比较与的大小.
解:因为,
,……(第1步)
又,
所以……(第2步)
问题解决:
(1)在尝试应用的解题过程中,第1步的思路是将底数和指数都不相同的两个幂转化化归为_______;第2步的依据是_______.
(2)请比较下面各组中两个幂的大小:
①与;
②与.
22.(10分)如图1,,过点作,可得.利用平行线的性质,可得:与,之间的数量关系是 , .
利用上面的发现,解决下列问题:
(1)如图2,,点是和平分线的交点,,求的度数;
(2)如图3,,平分,,平分,若比大,则的度数是 .
23.(12分)小明在自学多项式的时候,读到如下一段材料:
已知,,,,,为实数,形如称为关于自变量的多项式,,则称多项式的次数为,设,为两个多项式,且不恒为,则存在唯一的多项式及满足,此时,称为被除式,为除式,为商式,为余式.
小明觉得这个除法与整数的除法有相似之处,因此请你帮助小明完成下列问题:
(1)求一个二次多项式,被除余,被除余,被除余.
(2)已知四次多项式满足,被除余,被除余,被除余,被除余,被除余,当时,求的值.
24.(12分)某地举办电影节,为了主场馆有更好的灯光效果,工作人员设计了灯光组进行舞台投射.如图所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2°,灯B转动的速度是每秒1°,假定主道路是平行的,即,且.
(1)填空:______;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)若两灯同时开始转动,两灯射出的光束交于点C,且,求在灯B射线到达BQ之前,转动的时间为多少秒?直接写出答案.
参考答案
一.选择题
1.C
【分析】本题考查了多项式乘多项式,熟练掌握运算法则是解题的关键.原式利用多项式乘以多项式法则计算,由结果不含项,得出与的关系即可.
【详解】解:原式
展开的结果中不含有项
.
故选:C.
2.A
【分析】本题考查了平行线的判定,根据平行线的判定定理即可判断求解,掌握平行线的判定定理是解题的关键.
【详解】解:由题意可知,按住尺身,使尺头靠紧图画板的边框推移丁字尺是为了使同位角相等,
∴利用丁字尺画平行线的理论依据是:同位角相等,两直线平行,
故选:.
3.A
【分析】本题考查几何图形中的角度计算,先根据垂直的定义得出,再计算出,再根据角平分线的定义得出,最后根据补角的定义可得答案.
【详解】解: ,
,
,
,
平分,
,
,
故选A.
4.D
【分析】本题考查了整式的加法运算,整式的乘法运算,理解题意,正确的逻辑推理时解决本题的关键.
设一个三位数与一个两位数分别为和,则,即,可确定时,则,由题意可判断A、B、D选项,根据题意可得运算结果可以表示为:,把代入,故可判断C选项.
【详解】解:设一个三位数与一个两位数分别为和
如图:
则由题意得:
,
∴,即,
∴当时,不是正整数,不符合题意,故舍;
当时,则,如图:
,
∴A、“2”上边的数是,故本选项不符合题意;
B、“20”右边的“□”表示4,故本选项不符合题意;
C、上面的数应为,如图:
∴运算结果可以表示为:,
∴当时,,
∴C选项不符合题意,
D、“5”右边的“□”表示1,故该选项符合题意,
故选:D.
5.A
【分析】本题考查了平行线的性质.延长,交的延长线于点,根据平行线的性质得出,,代入已知数据即可求解.
【详解】解:如图所示,延长,交的延长线于点,
∵,
∴,,
∴,
故选:A.
6.D
【分析】本题主要考查了图形变化的规律,能根据所给图形发现所需小正方形个数的变化规律是解题的关键.根据所给图形,依次求出图形中正方形的个数,发现规律即可解决问题.
【详解】解:由所给图形可知,
拼第1个正方形需要的小正方形个数为:;
拼第2个正方形需要的小正方形个数为:;
拼第3个正方形需要的小正方形个数为:;
…,
所以拼第n个正方形需要的小正方形个数为个,
则,
即拼第n个正方形比第个正方形多个正方形.
故选:D.
7.A
【分析】本题考查了平行线的性质、折叠—有关角的计算、角的和与差.首先根据四边形是长方形纸带,可得,根据平行线的性质可得,根据邻补角的定义可以求出,从而可求,再根据角之间的关系可以求出的度数.
【详解】解:四边形是长方形纸带,
,
,
如图所示,
,
,
如图所示,
.
故选:A.
8.A
【分析】根据题中规律每一个式子的结果等于两项的差,被减数的指数比第二个因式中第一项大1,减数都为1,即可得到规律为,利用规律,当,时,代入其中即可求解.
本题考查了平方差公式、及数字类的规律题,解题的关键是认真阅读,总结规律,并利用规律解决问题.
【详解】解:由;
;
;
…
观察发现: ,
当,时,得
,
∴,
∴.
故选:A.
9.C
【详解】提示:如图1,当点在线段上时,过点作.因为由平移得到,所以.所以.①当时,设,则.因为,,所以.因为,所以,解得,所以.②当时,设,则.同理可得,.因为,所以.解得,所以.
如图2,当点在线段的延长线上时,过点作.同理可得.③当时,设,则.同理可得.因为,所以,解得,所以.④当时,由图可知,,故不存在这种情况.
综上所述,的度数为或或.
10.C
【分析】本题考查了列代数式,整式的混合运算,延长交于点,则右上角未被覆盖部分阴影部分的面积,分别设正方形的边长分别为,正方形的边长为,表示出,,再作差即可得解,掌握知识点的应用是解题的关键.
【详解】解:如图,延长交于点,则右上角未被覆盖部分阴影部分的面积,
设正方形的边长分别为,正方形的边长为,
则,,,,,,
∴,,
∴
故要知道和的面积差,只需要知道的值即可,即要知道正方形的边长,
故选:.
二.填空题
11.
【分析】本题考查了同底数幂的乘法,幂的乘方的应用;
(1)根据题意得出,进而即可求解;
(2)根据完全平方公式得出,进而得出,即可求解.
【详解】(1)因为,所以,
所以,所以,
所以,
所以自然数;
故答案为:.
(2),
∴只有时,原式为完全平方数,即自然数.
故答案为:.
12.或
【分析】此题考查的知识点是角的计算,涉及邻补角互补,求出的度数是解题的关键.
先根据,,求出,则,再分类讨论,利用角度和差计算即可.
【详解】解:∵,,
∴,
∴,
当点D在上方时,,
当点D在下方时,,
综上所述:或,
故答案为:或.
13.
【分析】先将代为,利用同底数幂的除法可得,由于结果底数是2,故左边5和3的指数应为0,左边和右边2的指数相等,由此可得方程组,解方程组求出x,y,z的值,代入即可求解.
【详解】解:,
则,
,
故,
解得:,
因此,
故答案为:.
14.
【分析】本题考查了平行线的性质,平行公理推论,过作,由平行公理推论得,最后由平行线的性质和角度和差即可求解,掌握平行线的性质,平行公理推论的应用是解题的关键.
【详解】解:如图,过作,
∵,
∴,
∴,,
∵,
∴,
∴,
故答案为:.
15.
【分析】根据、、的位置可知这三个数每个都加了两次,三个圆圈上的数字之和是,但是这个数字之和是,所以可得,从而求出的值;因为,,可以得到,配方得,把代入即可求出的值.
【详解】解:每个圆圈上的四个数字的和都等于,
三个圆上的数字之和应为,
其中的、、这三个数每个都加了两次,
,
,
则有,
解得:;
每个圆圈上的四个数字的平方和分别记、、,且,
,
,
,
,
整理得:,
,
;
,
,
,
解得:.
故答案为:;.
16. 或
【分析】本题考查平行线的性质,角平分线的定义,掌握平行线的性质是解决问题的关键.
(1)过点作,而,可得,证明,,再进一步解答即可;
(2)分两种情况当为锐角时,过点作,过点作,利用平行线的性质可得,,再结合角平分线即可求得;当为钝角时,,,再根据角平分线及平行线性质得.
【详解】解:(1)过点作,而,
∴,
∴,,
∵,
∴,
∵,
∴,
∴;
故答案为:
(2)①当为锐角时,如图所示:
过点作,过点作,
,
,
,,
,,
,即,
,,
,,
,即,
又点为和的角平分线所在的直线的交点,
,,
,
②当为钝角时,如图所示:
过点作,过点作,
,
,
,,
,,
,
,
,
,,
,,
又点为和的角平分线所在的直线的交点,
,,
,
综上所述或
故答案案为:或.
三.解答题
17.(1)解:平分,平分,
,,
,
,
,
,
(2)解:平分,
,
,
,
,
平分,
,
;
(3)解:的度数不变,
平分,平分,
,,
,
.
18.(1)解:根据图形可知,长方形的边长为,宽为,
则,
,
将,,代入,得出,,
故答案为:;.
(2)解:根据图形可知,长方形的边长为,宽为,
则,
,
故.
(3)解:由(1)和(2)得出,,,
故,
将,代入,得,
整理得:,
即,
故答案为:C.
19.解:如图,过点作,
∴,
∵,
∴,
∵,,
∴,
∴,
∴,
∴的度数为.
20.(1)解:①∵于点O,
∴,
∵,
∴,
∴;
∴的度数为;
②∵平分,
∴,
∵,
∴,
∴,
∴,
∴平分.
(2)解:设,则,
当点E,F在直线的同侧时,如图:
,
∴,①
,②
令①×3+②×2可得:,
当点E,F在直线的异侧时,如图:
,
∴,①
,②
令②×2+①可得:,
综上所述:或.
21.(1)解:根据题意,先将底数和指数都不相同的两个幂转化化归为指数相同的两个幂;根据指数相同,底数大的幂大,
故答案为:指数相同的两个幂;指数相同,底数大的幂大.
(2)解:①∵,,
根据底数相同,指数大的幂大
∴,
∴.
②解:∵,
根据指数相同,底数大的幂大,
∴,
∴.
22.解:与,之间的数量关系是:.
理由如下:
,,
,
,,
,
即:;
,理由如下:
,
,,
,
即:,
故答案为:,;
(2)平分,平分,
设,,
,,
由(1)的结论得:
,
,
又,
,
,
;
(3)设,
平分,
,
,
,
由(1)的结论得:
,
,
,
,
,
,
平分,
,
,
比大,
,
即:,
解得:,
.
故答案为:.
23.(1)解: 一个多项式被,整除,被除余,
设这个多项式为,
即
,
∴,即,
∴这个多项式为.
一个多项式被,整除,被除余,
设这个多项式为,
即
,
∴,即,
∴这个多项式为.
一个多项式被,整除,被除余,
设这个多项式为,
即
,
∴,即,
∴这个多项式为,
∴
,
故这个二次多项式.
(2)解:设多项式被除余,
多项式被除余,
多项式被除余,
多项式被除余,
多项式被除余,
∴
,
即,,
,
即,.
,
,
即,.
, 即,.
,
即,,
,
∴.
当时,,
故值为.
24.(1)解: ,,
,
故答案为:120;
(2)解:设灯转动秒,其光束为射线时与灯射线平行.
①当时,则有,
如图1.,
.
,
,
,
,
解得;
②当时,此时的射线已到达再返回,
则有,,
如图2.,
.
,
,
,
,
解得.
综上所述,当灯转动30秒或110秒时,两灯的光束互相平行;
(3)解:转动的时间为110秒或130秒.
由题可知.
,
,.
设灯射线转动时间为秒,
图3中,当时,,或.
又,
,
则,
解得,此时与不相交,不符合题意;
或,
解得;
如图4中,当时,,,
则,
解得.
综上所述,灯射线在到达之前,转动的时间为110秒或130秒.
一.选择题(共10小题,满分30分,每小题3分)
1.若将展开的结果中不含有项,则,满足的关系式是( )
A. B. C. D.
2.画直线时要按住尺身,推移丁字尺时必须使尺头靠紧图画板的边框.请你说明:利用丁字尺画平行线的理论依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
3.如图,三条直线交于点O,,平分,则的度数是( )
A. B. C. D.
4.“铺地锦”是我国古代一种乘法运算方法,可将多位数乘法运算转化为一位数乘法和简单的加法运算.淇淇受其启发,设计了如图1所示的“表格算法”,图1表示132×23,运算结果为3036.图2表示一个三位数与一个两位数相乘,表格中部分数据被墨迹覆盖,根据图2中现有数据进行推断,错误的是( )
A.“2”上边的数是8 B.“20”右边的“□”表示4
C.运算结果可以是9225 D.“5”右边的“□”表示5
5.青花瓷,又称白地青花瓷、青花,是中国陶瓷烧制工艺的珍品,也是中国瓷器的主流品种之一.如图1是某种青花瓷花瓶,图2是其抽象出的简易轮廓图,已知,若,则的度数为( )
A. B. C. D.
6.李明在教材第83页的教学活动探索发现,如图,用相同的小正方形拼大正方形,拼第1个正方形需要4个小正方形,拼第2个正方形需要9个小正方形…,拼一拼,想一想,按照这样的方法拼成的第n个正方形比第个正方形多( )个小正方形?
A. B. C. D.
7.如图是长方形纸带,,将纸带沿折叠成图,再沿折叠成图,则图中度数是多少( )
A. B. C. D.
8.观察下列各式:
;
;
;
…
根据规律计算: 的值是( )
A. B. C.
9.如图,在锐角三角形中,,将沿着射线方向平移得到(平移后点的对应点分别是),连接.若在整个平移过程中,和的度数之间存在2倍关系,则的度数不可能为( )
A. B. C. D.
10.如图,有三张正方形纸片,将三张纸片按照如图所示的方式放置于一个长方形中,已知中间重叠部分四边形恰好是一个正方形,记图中两块未被覆盖的阴影部分面积分别为和,已知,,若要知道和的面积差,只需要知道( )
A.正方形的边长 B.正方形的边长
C.正方形的边长 D.正方形的边长
二.填空题(共6小题,满分18分,每小题3分)
11.已知.
(1)若,则自然数 ;
(2)若是一个完全平方数,则自然数 .
12.如图,已知为直线上一点,以为起点作射线、.满足,且,则 °.
13.如果整数x,y,z满足,则代数式的值为 .
14.如图是小明写字桌上的一款折叠护眼台灯的简易图,支柱与桌面交于点,灯管与桌面平行,若,,则的度数为 .
15.“幻方”最早记载于春秋时期的《大戴礼记》中,现将不重复的数字填入如图所示的“幻方”中,使得每个圆圈上的四个数字的和都等于,若每个圆圈上的四个数字的平方和分别记、、,且.如果将交点处的三个圆圈填入的数字分别记作为、、,则 ; .
16.如图,,在的两边上分别过点和点向同方向作射线和,且.
(1)若,则的度数为 .
(2)若和的平分线所在的直线交于点(与不重合),则的度数为 .
三.解答题(共8小题,满分72分)
17.(6分)若直线和直线相交于点,为内部的射线,平分,平分.
(1)若,求和的度数?
(2)若是任意角,求的度数?
(3)请猜想,度数会改变吗?若改变,请说明理由;若不改变,则度数是多少?
18.(6分)如图,有三张边长分别为,,的正方形纸片,, 将三张纸片按图1,图2两种不同方式放置于同一长方形中.记图1中阴影部分周长为,面积为;图2中阴影部分周长为,面积为.
(1)若,,图1中阴影部分周长_____,图2中阴影部分周长_____;
(2)求图2中阴影部分面积与图1中阴影部分面积的差(用含,,的代数式表示).
(3)若,那么与满足下列_____关系.
A. B. C. D.
19.(8分)为增强学生体质,某学校将抖空竹引入“阳光体育一小时”活动.图①是某同学抖空竹时的一个瞬间,小聪把它抽象成如图②所示的示意图.已知,,,求的度数.
20.(8分)直线相交于点O,于点O,作射线,且在的内部.
(1)①当在如图1所示位置时,若,求的度数;
②当在如图2所示位置时,若平分,证明:平分;
(2)若,请直接写出与之间的数量关系.
21.(10分)阅读理解:我们在学习了幂的有关知识后,对两个幂与(都是正数,都是正整数)的大小进行比较,并归纳总结了如下两个结论:
①若,则.(底数相同,指数大的幂大)
②若,则.(指数相同,底数大的幂大)
尝试应用:试比较与的大小.
解:因为,
,……(第1步)
又,
所以……(第2步)
问题解决:
(1)在尝试应用的解题过程中,第1步的思路是将底数和指数都不相同的两个幂转化化归为_______;第2步的依据是_______.
(2)请比较下面各组中两个幂的大小:
①与;
②与.
22.(10分)如图1,,过点作,可得.利用平行线的性质,可得:与,之间的数量关系是 , .
利用上面的发现,解决下列问题:
(1)如图2,,点是和平分线的交点,,求的度数;
(2)如图3,,平分,,平分,若比大,则的度数是 .
23.(12分)小明在自学多项式的时候,读到如下一段材料:
已知,,,,,为实数,形如称为关于自变量的多项式,,则称多项式的次数为,设,为两个多项式,且不恒为,则存在唯一的多项式及满足,此时,称为被除式,为除式,为商式,为余式.
小明觉得这个除法与整数的除法有相似之处,因此请你帮助小明完成下列问题:
(1)求一个二次多项式,被除余,被除余,被除余.
(2)已知四次多项式满足,被除余,被除余,被除余,被除余,被除余,当时,求的值.
24.(12分)某地举办电影节,为了主场馆有更好的灯光效果,工作人员设计了灯光组进行舞台投射.如图所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2°,灯B转动的速度是每秒1°,假定主道路是平行的,即,且.
(1)填空:______;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)若两灯同时开始转动,两灯射出的光束交于点C,且,求在灯B射线到达BQ之前,转动的时间为多少秒?直接写出答案.
参考答案
一.选择题
1.C
【分析】本题考查了多项式乘多项式,熟练掌握运算法则是解题的关键.原式利用多项式乘以多项式法则计算,由结果不含项,得出与的关系即可.
【详解】解:原式
展开的结果中不含有项
.
故选:C.
2.A
【分析】本题考查了平行线的判定,根据平行线的判定定理即可判断求解,掌握平行线的判定定理是解题的关键.
【详解】解:由题意可知,按住尺身,使尺头靠紧图画板的边框推移丁字尺是为了使同位角相等,
∴利用丁字尺画平行线的理论依据是:同位角相等,两直线平行,
故选:.
3.A
【分析】本题考查几何图形中的角度计算,先根据垂直的定义得出,再计算出,再根据角平分线的定义得出,最后根据补角的定义可得答案.
【详解】解: ,
,
,
,
平分,
,
,
故选A.
4.D
【分析】本题考查了整式的加法运算,整式的乘法运算,理解题意,正确的逻辑推理时解决本题的关键.
设一个三位数与一个两位数分别为和,则,即,可确定时,则,由题意可判断A、B、D选项,根据题意可得运算结果可以表示为:,把代入,故可判断C选项.
【详解】解:设一个三位数与一个两位数分别为和
如图:
则由题意得:
,
∴,即,
∴当时,不是正整数,不符合题意,故舍;
当时,则,如图:
,
∴A、“2”上边的数是,故本选项不符合题意;
B、“20”右边的“□”表示4,故本选项不符合题意;
C、上面的数应为,如图:
∴运算结果可以表示为:,
∴当时,,
∴C选项不符合题意,
D、“5”右边的“□”表示1,故该选项符合题意,
故选:D.
5.A
【分析】本题考查了平行线的性质.延长,交的延长线于点,根据平行线的性质得出,,代入已知数据即可求解.
【详解】解:如图所示,延长,交的延长线于点,
∵,
∴,,
∴,
故选:A.
6.D
【分析】本题主要考查了图形变化的规律,能根据所给图形发现所需小正方形个数的变化规律是解题的关键.根据所给图形,依次求出图形中正方形的个数,发现规律即可解决问题.
【详解】解:由所给图形可知,
拼第1个正方形需要的小正方形个数为:;
拼第2个正方形需要的小正方形个数为:;
拼第3个正方形需要的小正方形个数为:;
…,
所以拼第n个正方形需要的小正方形个数为个,
则,
即拼第n个正方形比第个正方形多个正方形.
故选:D.
7.A
【分析】本题考查了平行线的性质、折叠—有关角的计算、角的和与差.首先根据四边形是长方形纸带,可得,根据平行线的性质可得,根据邻补角的定义可以求出,从而可求,再根据角之间的关系可以求出的度数.
【详解】解:四边形是长方形纸带,
,
,
如图所示,
,
,
如图所示,
.
故选:A.
8.A
【分析】根据题中规律每一个式子的结果等于两项的差,被减数的指数比第二个因式中第一项大1,减数都为1,即可得到规律为,利用规律,当,时,代入其中即可求解.
本题考查了平方差公式、及数字类的规律题,解题的关键是认真阅读,总结规律,并利用规律解决问题.
【详解】解:由;
;
;
…
观察发现: ,
当,时,得
,
∴,
∴.
故选:A.
9.C
【详解】提示:如图1,当点在线段上时,过点作.因为由平移得到,所以.所以.①当时,设,则.因为,,所以.因为,所以,解得,所以.②当时,设,则.同理可得,.因为,所以.解得,所以.
如图2,当点在线段的延长线上时,过点作.同理可得.③当时,设,则.同理可得.因为,所以,解得,所以.④当时,由图可知,,故不存在这种情况.
综上所述,的度数为或或.
10.C
【分析】本题考查了列代数式,整式的混合运算,延长交于点,则右上角未被覆盖部分阴影部分的面积,分别设正方形的边长分别为,正方形的边长为,表示出,,再作差即可得解,掌握知识点的应用是解题的关键.
【详解】解:如图,延长交于点,则右上角未被覆盖部分阴影部分的面积,
设正方形的边长分别为,正方形的边长为,
则,,,,,,
∴,,
∴
故要知道和的面积差,只需要知道的值即可,即要知道正方形的边长,
故选:.
二.填空题
11.
【分析】本题考查了同底数幂的乘法,幂的乘方的应用;
(1)根据题意得出,进而即可求解;
(2)根据完全平方公式得出,进而得出,即可求解.
【详解】(1)因为,所以,
所以,所以,
所以,
所以自然数;
故答案为:.
(2),
∴只有时,原式为完全平方数,即自然数.
故答案为:.
12.或
【分析】此题考查的知识点是角的计算,涉及邻补角互补,求出的度数是解题的关键.
先根据,,求出,则,再分类讨论,利用角度和差计算即可.
【详解】解:∵,,
∴,
∴,
当点D在上方时,,
当点D在下方时,,
综上所述:或,
故答案为:或.
13.
【分析】先将代为,利用同底数幂的除法可得,由于结果底数是2,故左边5和3的指数应为0,左边和右边2的指数相等,由此可得方程组,解方程组求出x,y,z的值,代入即可求解.
【详解】解:,
则,
,
故,
解得:,
因此,
故答案为:.
14.
【分析】本题考查了平行线的性质,平行公理推论,过作,由平行公理推论得,最后由平行线的性质和角度和差即可求解,掌握平行线的性质,平行公理推论的应用是解题的关键.
【详解】解:如图,过作,
∵,
∴,
∴,,
∵,
∴,
∴,
故答案为:.
15.
【分析】根据、、的位置可知这三个数每个都加了两次,三个圆圈上的数字之和是,但是这个数字之和是,所以可得,从而求出的值;因为,,可以得到,配方得,把代入即可求出的值.
【详解】解:每个圆圈上的四个数字的和都等于,
三个圆上的数字之和应为,
其中的、、这三个数每个都加了两次,
,
,
则有,
解得:;
每个圆圈上的四个数字的平方和分别记、、,且,
,
,
,
,
整理得:,
,
;
,
,
,
解得:.
故答案为:;.
16. 或
【分析】本题考查平行线的性质,角平分线的定义,掌握平行线的性质是解决问题的关键.
(1)过点作,而,可得,证明,,再进一步解答即可;
(2)分两种情况当为锐角时,过点作,过点作,利用平行线的性质可得,,再结合角平分线即可求得;当为钝角时,,,再根据角平分线及平行线性质得.
【详解】解:(1)过点作,而,
∴,
∴,,
∵,
∴,
∵,
∴,
∴;
故答案为:
(2)①当为锐角时,如图所示:
过点作,过点作,
,
,
,,
,,
,即,
,,
,,
,即,
又点为和的角平分线所在的直线的交点,
,,
,
②当为钝角时,如图所示:
过点作,过点作,
,
,
,,
,,
,
,
,
,,
,,
又点为和的角平分线所在的直线的交点,
,,
,
综上所述或
故答案案为:或.
三.解答题
17.(1)解:平分,平分,
,,
,
,
,
,
(2)解:平分,
,
,
,
,
平分,
,
;
(3)解:的度数不变,
平分,平分,
,,
,
.
18.(1)解:根据图形可知,长方形的边长为,宽为,
则,
,
将,,代入,得出,,
故答案为:;.
(2)解:根据图形可知,长方形的边长为,宽为,
则,
,
故.
(3)解:由(1)和(2)得出,,,
故,
将,代入,得,
整理得:,
即,
故答案为:C.
19.解:如图,过点作,
∴,
∵,
∴,
∵,,
∴,
∴,
∴,
∴的度数为.
20.(1)解:①∵于点O,
∴,
∵,
∴,
∴;
∴的度数为;
②∵平分,
∴,
∵,
∴,
∴,
∴,
∴平分.
(2)解:设,则,
当点E,F在直线的同侧时,如图:
,
∴,①
,②
令①×3+②×2可得:,
当点E,F在直线的异侧时,如图:
,
∴,①
,②
令②×2+①可得:,
综上所述:或.
21.(1)解:根据题意,先将底数和指数都不相同的两个幂转化化归为指数相同的两个幂;根据指数相同,底数大的幂大,
故答案为:指数相同的两个幂;指数相同,底数大的幂大.
(2)解:①∵,,
根据底数相同,指数大的幂大
∴,
∴.
②解:∵,
根据指数相同,底数大的幂大,
∴,
∴.
22.解:与,之间的数量关系是:.
理由如下:
,,
,
,,
,
即:;
,理由如下:
,
,,
,
即:,
故答案为:,;
(2)平分,平分,
设,,
,,
由(1)的结论得:
,
,
又,
,
,
;
(3)设,
平分,
,
,
,
由(1)的结论得:
,
,
,
,
,
,
平分,
,
,
比大,
,
即:,
解得:,
.
故答案为:.
23.(1)解: 一个多项式被,整除,被除余,
设这个多项式为,
即
,
∴,即,
∴这个多项式为.
一个多项式被,整除,被除余,
设这个多项式为,
即
,
∴,即,
∴这个多项式为.
一个多项式被,整除,被除余,
设这个多项式为,
即
,
∴,即,
∴这个多项式为,
∴
,
故这个二次多项式.
(2)解:设多项式被除余,
多项式被除余,
多项式被除余,
多项式被除余,
多项式被除余,
∴
,
即,,
,
即,.
,
,
即,.
, 即,.
,
即,,
,
∴.
当时,,
故值为.
24.(1)解: ,,
,
故答案为:120;
(2)解:设灯转动秒,其光束为射线时与灯射线平行.
①当时,则有,
如图1.,
.
,
,
,
,
解得;
②当时,此时的射线已到达再返回,
则有,,
如图2.,
.
,
,
,
,
解得.
综上所述,当灯转动30秒或110秒时,两灯的光束互相平行;
(3)解:转动的时间为110秒或130秒.
由题可知.
,
,.
设灯射线转动时间为秒,
图3中,当时,,或.
又,
,
则,
解得,此时与不相交,不符合题意;
或,
解得;
如图4中,当时,,,
则,
解得.
综上所述,灯射线在到达之前,转动的时间为110秒或130秒.
同课章节目录
